1. Introduction
The dark matter hypothesis was proposed by the astronomer Fritz Zwicky after careful analysis of the motions in the Coma Cluster of galaxies [
1]. In the early 1930s he was already convinced that some extra matter should be taken into account, apart from the visible or luminous matter, to explain the dynamics of the galaxies within this cluster.
Nevertheless, dark matter received little attention until the 1970s thanks to the new observations by Rubin and collaborators [
2] as well as Faber and Gallagher [
3]. These authors showed, unmistakably, that the rotation curves of many galaxies exhibit a flat asymptotic behavior that cannot be accommodated with the standard form of Newtonian gravity force and Newtonian dynamics. As the luminous mass of the galaxies is mainly located in the disk and the bulge, one should expect that the orbital velocity of the gas clouds outside the visible mass distribution would decrease with the distance to the center in proportion to the inverse of its square root. This would be the generalization of Kepler’s third law to the whole galaxy.
Surprisingly, these authors found that the orbital velocity of distant particles achieved a constant value and that it does not depend on the distance to the galactic center. This fact, commonly referred to as the flat rotation curves problem, is one of the most fundamental challenges in our understanding of gravity on the galactic scale. In the course of the years, several epistemological approaches to this problem have appeared [
4]:
The dark matter (DM) hypothesis, i.e., the existence of a new particle or a family of particles which interact mainly gravitationally and only very weakly with ordinary matter [
5,
6,
7,
8,
9].
Modified Newtonian dynamics, as proposed by Milgrom in two papers published in 1983 [
10,
11]. According to Milgrom, Newton’s second law should be replaced by:
where
m/s
is a fundamental parameter with units of acceleration, and
is a function of the ratio of the particle’s acceleration with this new constant. This function tends to one for
but it tends to
for
. The reason for this proposal is that the effect of dark matter seems to be switched on when the orbital acceleration goes below this
scale. Moreover, it predicts the relation:
where
v is the asymptotic orbital velocity and
M is the total mass of the galaxy. This agrees with the Tully–Fisher (TF) relation among luminosity and asymptotic velocity if we assume an exponent of 4 (although there is some uncertainty in this exponent as it depends on the galaxy data set [
12,
13,
14]). This is considered as one of the successful predictions of a modification of Newtonian dynamics (MOND) [
15].
A modification of the law of Newtonian attraction in the form:
where
M is the mass source for the gravitation field and
is a fundamental scale of distance, typically of several kiloparsecs (Kpc). Obviously, for
, we should have
in order to recover the standard Newton’s law of gravity. This can also be interpreted in terms of a distance dependence of the gravitational constant,
G. A conspicuous problem with this approach was already pointed out by Milgrom: the asymptotic velocity relation should be given by
and this is at odds with the TF relation [
12].
The are other less radical proposals, such as the suggestion of the existence of a large population of brown and red dwarfs stars with low luminosity [
6]. Nevertheless, after a careful search for microlensing events, this source of DM is now considered negligible. The existence of a dark matter particle (or several different particles) that would comprise most of the DM is the most popular hypothesis in the scientific community. Among the possibilities for a DM candidate particle there are several possibilities found in the literature: (1) axions, a hypothetical particle proposed in the context of the Peccei–Quinn theory for CP violation in QCD [
16,
17]; (2) magnetic monopoles as predicted by Grand Unified theories or string theory [
18,
19]; (3) weakly interacting massive particles (WIMPS) such as the neutralino appearing in supersymmetric extensions of the standard model [
20]; and (4) sterile neutrinos (with a mass around a few keV) formed by oscillations in the early Universe [
21], lepton-number-driven resonant conversion [
22], or the decay of a heavy scalar [
23,
24,
25,
26].
Despite the ongoing effort to find these hypothetical particles in dedicated detectors, there has been no solid evidence of the existence of any of them. Moreover, the problem is that these particles mainly interact through gravity and very weakly through other interactions with ordinary matter. For that reason, the chance of detecting them is very low and relies on several hypotheses about the intensity of this coupling with standard matter [
7,
8]. This makes DM epistemologically not very different from the apparent or phantom matter that would arise from a non-Newtonian law of gravity at large distances.
The most successful alternative to the DM hypothesis is MOND, although it has its problems at the scale of galaxy clusters (where some residual DM must be invoked to explain the observations) and with respect to its theoretical foundations. Despite some relativistic generalizations that have been proposed they are still controversial. A review about its status is found in Sanders and McGaugh [
4].
On the other hand, the MOND approach is now supported by a well-grounded relativistic formulation, the vector–tensor–scalar gravity theory or TeVeS, as proposed by Bekenstein [
27] and recently revisited by Skordis [
28]. For a review about these theories, and their observational status, see Famaey and McGaugh [
29] and also the account of Bekenstein on the small-scale and cosmological consequences of TeVeS [
30].
In this paper we reexamine several proposals for a non-Newtonian law of force and the fitting of the apparent extra dark matter in models of the Milky Way. A possible square-root dependence with total mass of the fundamental distance scale associated with this new force is also discussed in the context of the TF relation. We also propose an alternative force model which implies a finite apparent mass content in the asymptotic distance limit, which avoids the undesirable effect of unlimited gravitational lensing in big clusters. Finally, we comment on the expected anomalies that may arise on the scale of the Solar System as a consequence of the non-Newtonian terms.
2. The Inverse Distance Law
Although there have been several proposals in the literature for an exponential or Yukawa contribution to the gravitational force, a prima facie approach to the flat rotation curves problem in galactic dynamics suggests a modification of Newton’s law in the form:
where
is the force per unit mass,
M is the source mass for the gravitational field,
G is the standard Newton’s constant, and
is a new constant of Nature which can be rewritten in terms of a distance parameter
. This model was firstly proposed by Tohline [
31] and then applied by Kuhn and Kruglyak [
32] to the rotation curves of several galaxies from an empirical point of view. Recently, this force law has been reconsidered by Bel [
33,
34,
35,
36].
In this paper we revisit this approach with the objective of making it consistent with mass distribution models for the Milky Way, the Tully–Fisher relation, and the desirable property of a finite apparent total mass in galaxies and clusters. We notice that inconsistency with the Tully–Fisher relation has been adduced as one of the key inconveniences of this approach [
4]. We will also discuss some controversial observations such as the Bullet Cluster [
37,
38]. We must emphasize that the discussion among the advocates of the dark matter hypothesis and the proponents of the MOND theory and its relativistic formulations is rather polarized, with several problems still unsolved for both alternatives. Although a simple modification of Newton’s law is an old idea that could appear rudimentary in the present phenomenological context, and it is mostly abandoned in modern literature, we think that a reconsideration of this approach could motivate further research in the area of modified gravity theories. In particular, a variable gravitational constant is suggested as a possible explanation of the anomalous rotation curves of galaxies and, perhaps, a fully relativistic theory formulated along this line could provide an alternative cosmology in which the need for dark matter would be unnecessary to tie up all the evidence within a single model.
One obvious feature of the law in Equation (
4) is that the asymptotic rotation velocity outside the visible mass distribution tends to
. Therefore, it does not depend on the distance to the galactic center, so it predicts a flat rotation curve as required. From an equivalent point of view, we can derive a phantom or apparent dark mass from the application of this force model to a mass distribution:
where the first term comes from the integration of the standard Newton’s force contribution in Equation (
4) and the second one is the result of the integration of the non-Newtonian term over the mass distribution. This second term is rewritten as a Newtonian one but with an apparent dark mass
that it is really the result of the non-Newtonian character of the model.
In this section we will analyze the form of the apparent dark mass function, , for several density distributions and its connection with mass models of the Milky Way.
2.1. Uniform Mass Distribution
In the first place we consider a uniform spherical mass distribution of mass
a. This could provide a crude model of elliptical galaxies or the bulge of a disk galaxy. Therefore, we define a volumetric mass density,
, as follows:
If we assume that the superposition principle holds for the non-Newtonian forces also we can write the total contribution at a distance
R from the center of the distribution in the form:
where
is the polar angle. Performing this integration over
yields:
where we have used the uniform mass distribution in Equation (
6) and
denotes the absolute value. To integrate over
r we must consider, separately, the field on a point outside the mass distribution (
) and the field inside (
). In the second case, two integrations are performed for the regions
and
. However, the result can be written as a single expression valid for
:
It is interesting to study the limits for large and small distances from the center of the sphere of visible matter. For
we have:
which means that in this limit the spherical distribution behaves as a point mass, as occurs with the Newtonian force by bounded spherically symmetric mass distributions. On the other hand, for
, Equation (
9) leads to:
According to the interpretation of this anomalous force as originated by DM in Equation (
5) we find that
for
and
for
. Later, we will discuss these limits in connection with the models for the structure of the dark matter halo.
2.2. Bulge and Disk Galactic Models
Spiral galaxies are typically composed of two structural components: (1) the bulge, i.e., a densely packed spheroidal distribution of stars located at the center of the galaxy; and (2) the disk, which extends further away than the bulge in the equatorial plane of the galaxy and whose thickness is only around a one per cent of its diameter [
39,
40]. The disk also contains most of the angular momentum of the galaxy and it is characterized by the presence of spiral arms.
A model for the hydrostatic equilibrium of the Milky Way galactic halo was developed by Kalberla and Kerp [
39,
40]. This model estimates the total mass of the galaxy in
solar masses (
), of which approximately 40% corresponds to the disk. In this model the total mass (including dark matter) is estimated in
. This model can be expressed analytically by Padé approximants of the mass functions, i.e., the mass inside a sphere of given radius,
R [
41]. This way, we can write for the disk:
If we measure the mass in units of
and the distance in Kpc, the parameters
a,
b, and
c are given by:
Similarly, for the bulge we propose:
with
and
.
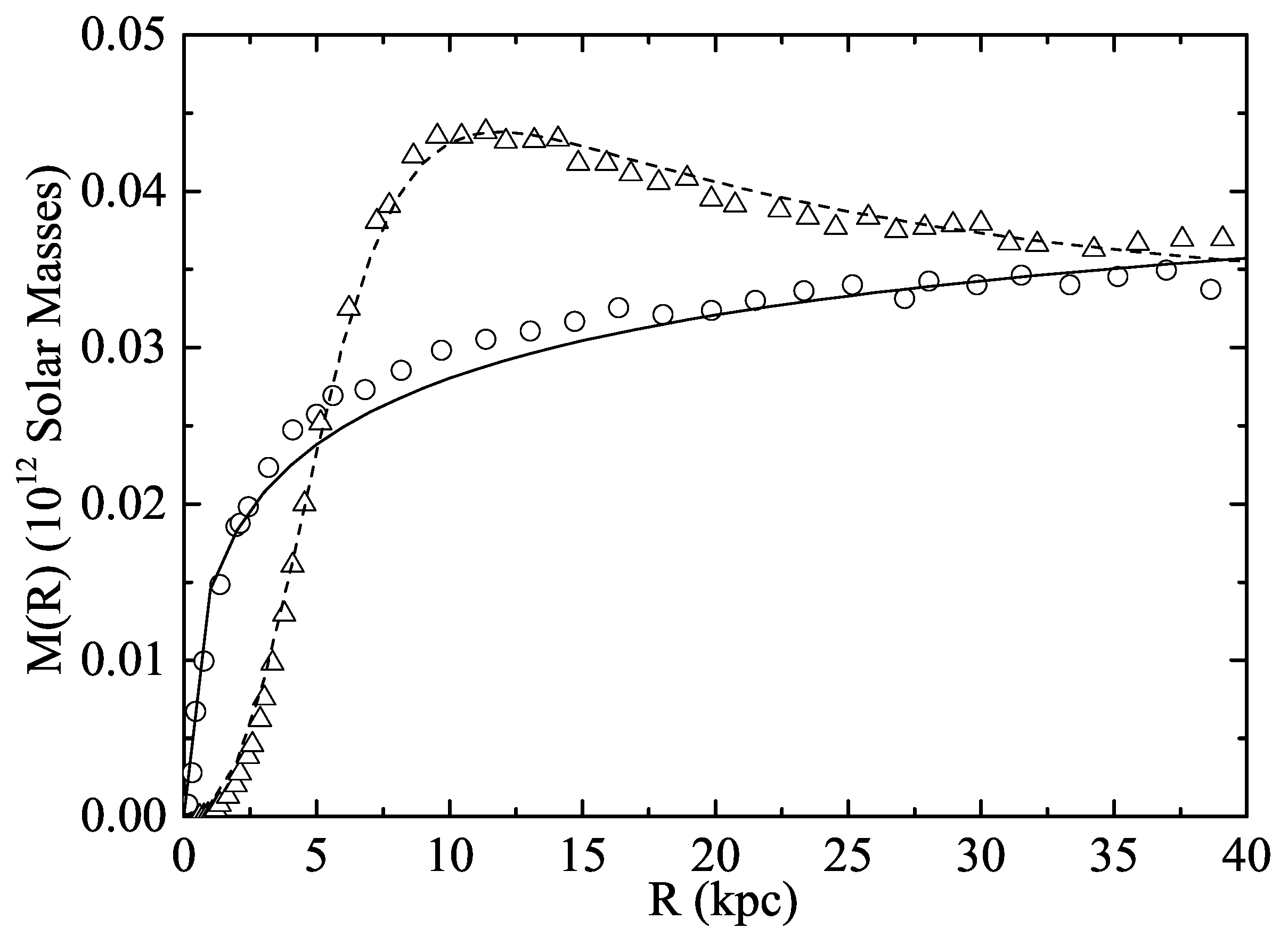
In
Figure 1 we compare these functions in Equations (
13) and (
14) with the Kalberla–Kerp model. These expressions for the mass functions of both disk and bulge are quite convenient for an analytical derivation of the phantom mass in our model. In particular, for the disk the anomalous extra force is given as:
where
is the surface density of the disk. After integration over the azimuthal angle, as before, we obtain:
where
is the mass function for the disk as given in Equations (
12) and (
13). For the bulge, we can define the volumetric density:
Therefore, for the extra non-Newtonian force exerted by the bulge we have:
Then, from Equations (
5), (
15), and (
18) the contributions of the disk and the bulge to the apparent dark mass are given by:
with the total phantom mass given by
. Our objective is now to fit this dark mass function to the dark matter function found in the Kalberla–Kerp model, that can be parametrized by the following Padé approximant:
where
is the total dark mass of the galactic halo estimated as
. If we use units of mass of
and Kpc as before, the parameters are:
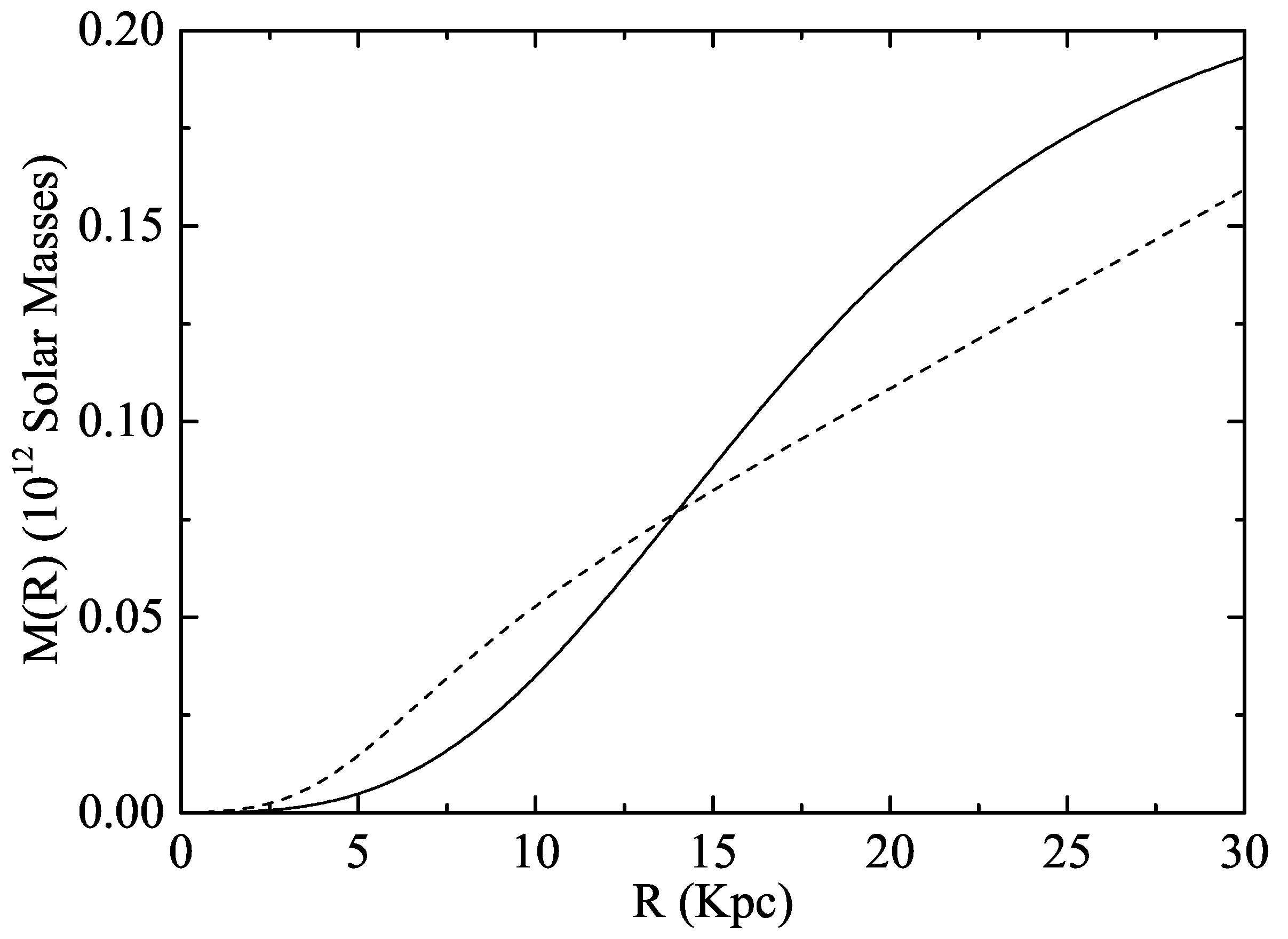
In
Figure 2 we have plotted the results for the best fit of the model in Equation (
19) in comparison with the Kalberla–Kerp hydrostatic model for the Milky Way as given by the Padé approximation in Equation (
20). The best fit corresponds to a distance scale parameter
Kpc. Notice that the fit overestimates the dark mass for distances below
Kpc and underestimates it for
. The same would happen with the uniform mass distribution analyzed in the previous section. Another odd feature of this model is that the apparent dark mass would be raised linearly for unlimited large distances from the center of the galaxy. This would cause problems in the evaluation of gravitational lensing effects if the mass in the Einstein line element for the clusters is replaced by this apparent mass as a first approach for a relativistic generalization of the non-Newtonian model.
In order to solve these shortcomings of the simple force model in Equation (
4), we should study another approach that interpolates between the short and long distance ranges.
2.3. The Interpolated Non-Newtonian Model
It is reasonable to assume that the dark matter halo, although much larger than the bulge or the disk of the typical spiral galaxies, is finite. This is not always very clear from rotation curves because, as pointed out by Kuhn and Kruglyak [
32], there are only a few cases in which the curve turns to lower rotational velocities at large radii (see the review of Faber and Gallagher [
3]).
In any case, there are some practical limitations to the distances at which the rotational velocity can be measured because of the rarefication of ordinary matter in those regions. Moreover, gravitational lensing shows that the dark matter phenomenon is also present in galactic clusters, but nothing indicates that the anomaly extends to infinity. In particular, for the case of the Milky Way, the total mass was estimated in
, which is roughly four times the visible mass. The currently accepted parameters for the standard
-CDM model of cosmology include values of 25.89% for DM in the Universe versus 4.86% for baryonic matter [
42,
43]. This gives a ratio of
among the total mass of the Universe (DM plus ordinary matter) and ordinary matter. This could indicate a peculiarity of the Milky Way or the existence of more DM within clusters or other galaxies.
In any way, to obtain a good fit to the standard view of galactic halos in the
-CDM model, we can propose a non-Newtonian force that becomes Newtonian both for short and large distances. A simple way to achieve this is the expression:
where we have use the hyperbolic tangent to interpolate among the Newtonian behavior at short distances with the source mass
M and the Newtonian law at large distances with the rescaled mass
, which includes the extra phantom mass
. Here,
is a non dimensional parameter,
is a real exponent, and
is a characteristic distance, as before.
The mass functions for the phantom mass arising from the bulge and the disk can be obtained by numerical integration following the approach of the preceding section and replacing the force law by Equation (
22). We then find that a good fit, with the DM halo model for the Milky way, is obtained for
,
, and
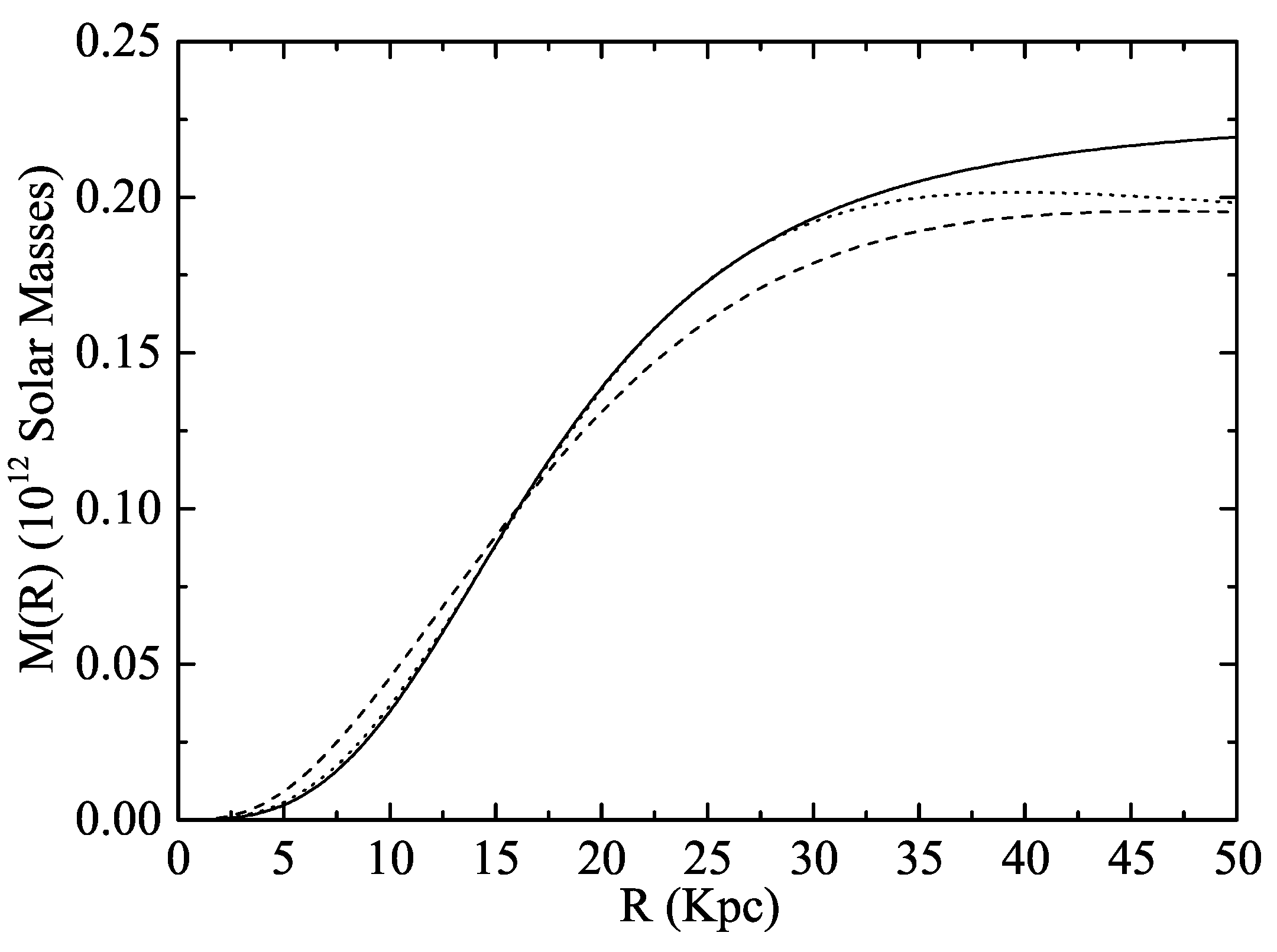
Kpc as shown in
Figure 3. However, a better fit is obtained for
,
, and
Kpc. This second fit is very good in the range
Kpc and it deviates slightly from the Milky Way model for larger distances from the galactic center.
We notice that both fits are good in the interval
Kpc but the total phantom mass associated with this force model for
would be
instead of
as given by Equation (
20). Hence, we obtain a value in agreement with the expected dark mass to baryonic matter ratio in the whole Universe for the
-CDM scenario. This could be relevant, or perhaps it is a mere coincidence of our fitting. In any case, the non-Newtonian force in Equation (
22) provides a good alternative explanation, in terms of phantom mass, to the rotation curve anomalies of the Milky Way as encoded in the dark matter mass function of the galactic halo model.
3. The Tully–Fisher Relation, the Bullet Cluster, and Local Dynamics
The Tully–Fisher (TF) relation is a statistical result obtained from surveys of many galaxies, which shows that the total mass of a galaxy is proportional to a power of the maximum rotation velocity achieved in the plateau of the rotation curve [
12,
13]. This relation is usually written in the form:
where
q and
are constants and we assume that
M is measured in solar masses and
in km/s. In a recent work by Torres–Flores et al. these parameters have been estimated for both the so-called stellar and baryonic TF relation. In the case of the stellar TF relation, only the stars are considered by converting the luminosity of the galaxy to mass with appropriate mass-to-light ratios. The baryonic TF relation also incorporates into
M the gaseous content, i.e., the gas clouds mainly composed of hydrogen and detected through its H
spectra. The results for these coefficients are:
Traditionally, it is assumed that the exponent is (and is thus compatible with both the stellar and the baryonic TF within error bars). The TF relation with is a natural consequence of the MOND approach and it is considered by many authors as one of the successes of this model of modified gravity. On the other hand, the proponents of modified non-Newtonian laws, such as the ones discussed in this paper, have been aware that this approach predicts in notorious disagreement with the TF relations. Although this TF relation does not have the status of a physical law (theoretically or phenomenologically), it seems to be a very robust statistical conclusion derived from the study of many sets of galaxies. For this reason, it is widely accepted as a test for galaxy formation models despite the fact that it is unclear whether its origin comes from cosmology or from star formation processes.
In this section, we analyze an idea that could restore the TF relation for simple non-Newtonian models such as those in Equations (
4) or (
22). The basic supposition is that the new constant
, or the distance parameters
or
, are not really constants but dynamical scalar fields, which depend upon the matter content around the point in which the non-Newtonian force is measured. This would mean that
, i.e., is a functional of the mass density in the galaxy or, more properly, the stress-energy tensor (using its trace as the corresponding scalar,
T). Then,
could satisfy a relativistic scalar field equation with an appropriate distance scale depending upon
T. Further speculations in this direction will be avoided in the present paper but it would be interesting to pursue them in future work. From an effective point of view, we will assume that
is a function of the visible mass alone. In particular, for very large masses in the galactic scale it should be chosen as:
where
is a constant parameter. With this dependence of the total mass, we obtain the asymptotic rotation velocity from the inverse distance force model in Equation (
4) as follows:
which is our expression for the TF relation in the non-Newtonian force model with the gravitational constant as a scalar field of the form in Equation (
25). We know that the value of the prefactor in the TF relation has a large uncertainty and it is different for the stellar and the baryonic case. In our case, if we use Equation (
25) with
Kpc as deduced in
Section 2.2 and the visible mass
we obtain
m/kg
and this implies
m
/kg s
is the coefficient of our TF relation in Equation (
26). This is close to the value predicted by MOND in Equation (
2) with
m/s
, i.e.,
m
/kg s
. We can also check that there are values within the error bars in the parameters of Equation (
24) that lead to this coefficient, so consistency with the latest observation can be achieved. For the following discussion it would be useful to quote the value of
using Kpc as unit of distance and
as the unit of mass (the mass scale for a galaxy). In these units we have
Kpc
.
We should also analyze the hyperbolic tangent model in Equation (
22) with the hypothesis of the mass-dependent distance scale in Equation (
25). We find that the rotation velocity for an object in the galaxy at a distance
R from the galactic center is given by:
where we have equated the centrifugal acceleration with the total gravitational force per unit mass with the first term corresponding to the anomalous force exerted by the bulge, the second one to the anomalous force arising from the disk, and the last term being the classical Newtonian force. If the anomalous force for a point mass is given by Equation (
22) we obtain the following expressions for the anomalous force exerted by the phantom dark matter of the bulge and the disk:
We now use the mass model in Equations (
12)–(
14). Consequently, the total visible mass of the galaxy would be given by
, and the distance scale defined in Equation (
25) is
. From this model and Equations (
27)–(
29) we find that the rotation velocity of the Milky Way at a reference distance
Kpc is
km/s. If we consider a set of hypothetical galaxies with the same mass functions as the Milky Way and the same parameters except for
a and
f, which would be scaled with
,
, 3, …, we find that the plateau velocity of the rotation curves can be obtained by performing the integrations in Equation (
27) at the distance
Kpc. The reason for this is that the distance scale of the galaxy scales linearly as shown in Equation (
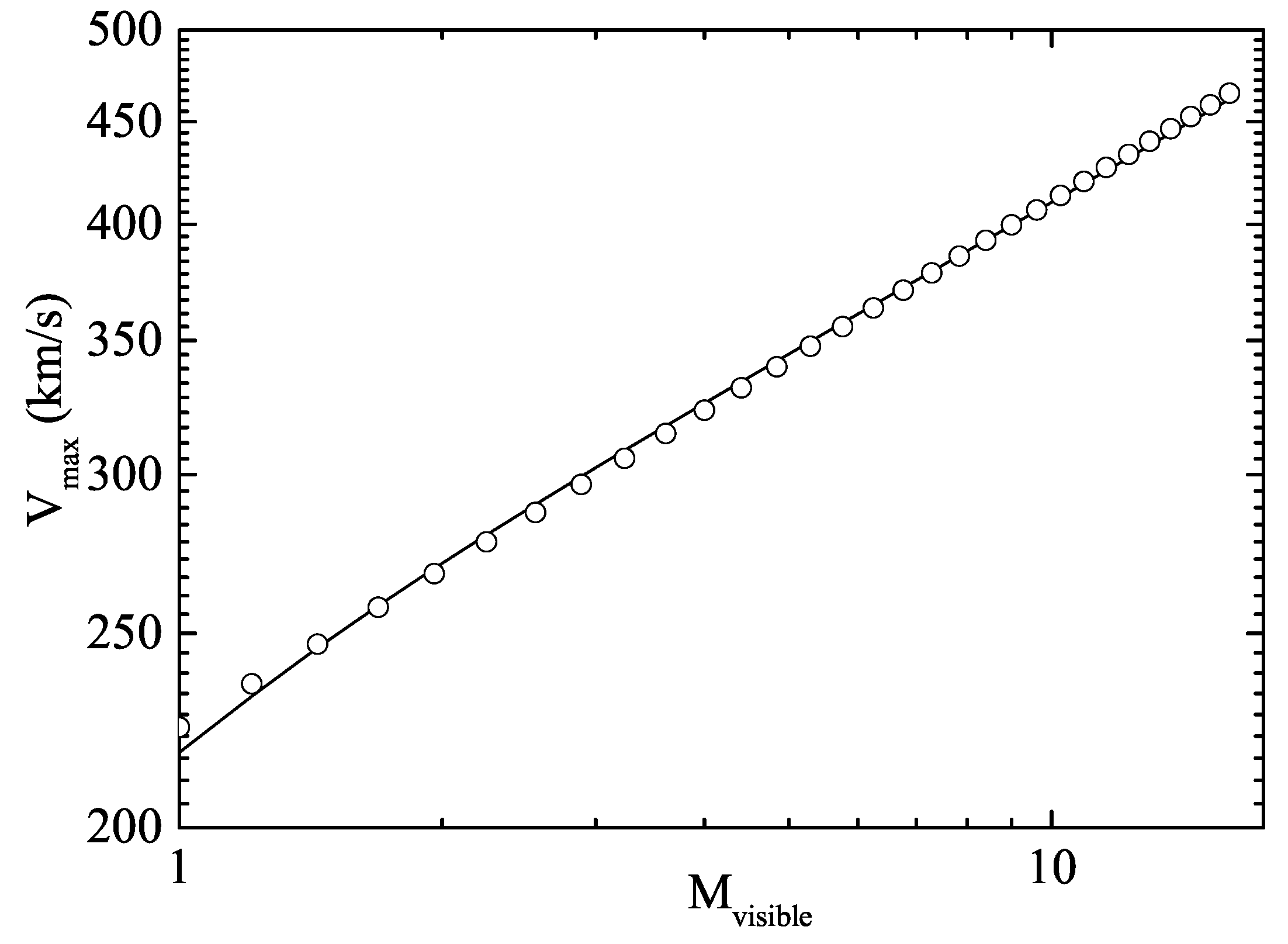
25). The results are plotted in
Figure 4. We notice that in log–log scale the rotation velocity behaves linearly vs the total visible mass. A linear fit gives us:
where the last digit in brackets corresponds to the standard error. Notice that in this expression the visible mass is given in terms of the total mass of the Milky Way as determined by the Kalberla–Kerp model, i.e.,
. If we measure
in solar masses, and
, and
in km/s, as is usual in the standard formulation of the Tully–Fisher relation, the result is:
which is compatible with the baryonic TF relation as deduced from Equations (
23) and (
24).
Finally, we must emphasize that the integration in Equations (
28) and (
29) (or, equivalently, in Equations (
15) and (
18) for the inverse distance force model) is carried out by assuming that the parameter
is a constant for each galaxy but, on the other hand, it depends on the total mass of the galaxy we are considering. Of course, this may seem unphysical from the point of view of a local theory of gravity, although it could be proposed in the context of Mach’s principle. Moreover, one could think that, in the aforementioned integrals,
should depend only on the implicated masses of the corresponding pair of particles and not on the mass of the galaxy as a whole. Nevertheless, it is not our objective in this paper to formulate a fully consistent local theory but to show that there is a rationale for predicting both the TF relation and the dark mass distribution for the halo on the framework of a model for modified Newtonian gravity. In this context, our proposal in Equation (
25) is a simple way to introduce a dependence on the length scale,
, on the particular conditions of a given galaxy. Of course, the underlying relation should be local and the total force should be calculated consistently from these relations, including the equation for the variation of
with the local mass conditions in the galaxy. Our idea is that
depends not on the particular point masses whose interaction we are calculating (to obtain the global interaction of a given test particle with the whole galaxy) but on the local conditions in the galaxy including these particles. It is an open question as to whether the success of our model can be preserved in a local modified gravity theory and this should be addressed in future works.
3.1. Galactic Clusters and DM Distribution
The evidence for DM in the galaxies is, for now, merely indirect. DM candidate particles have not been found and there is no solid evidence on the composition of such new kinds of matter [
6,
9]. For this reason, some researchers have been looking for particular cases in which modified gravity or modified dynamics theories could be tested against the DM hypothesis to elucidate the correct theory by showing that one of the explanations is not possible.
The study of Clowe et al. [
37] on the gravitational lensing by the galactic cluster
0657-558 (also known of the Bullet Cluster) is for some authors the paradigmatic example of a system in which DM manifests itself almost directly. Moreover, the authors of this classical study spoke of the direct empirical proof of the existence of dark matter even in the title of their work. The main reason for this strong statement is the delocalization of the center of mass of the cluster with respect to the plasma distribution as determined by gravitational lensing techniques. It was shown that DM traces the visible distribution of galaxies instead of this plasma, separated from them by the galactic collision. However, the plasma contains most of the baryonic mass and it is assumed that any model of modified gravity should be characterized by perturbations that trace the distribution of this ordinary matter.
In this section, we will show that non-Newtonian models of the general form in Equation (
22) can produce perturbations such that the apparent center of mass of the phantom DM does not coincide with that of the baryonic matter. We start with the apparent DM volumetric density as inferred from Equation (
22):
for
, 2, …. Notice that here we have used the fact that, for a point mass, our proposal in Equation (
22) for the modified Newtonian implies a phantom mass
for a point-like source of baryonic mass
M. The parameter
would be given by Equation (
25) as a function of the total baryonic mass. For our calculation we consider a mass
M such that
Kpc and there is a second point-like mass
at a distance
Kpc from the larger one. The total volumetric density for the phantom DM would be given by:
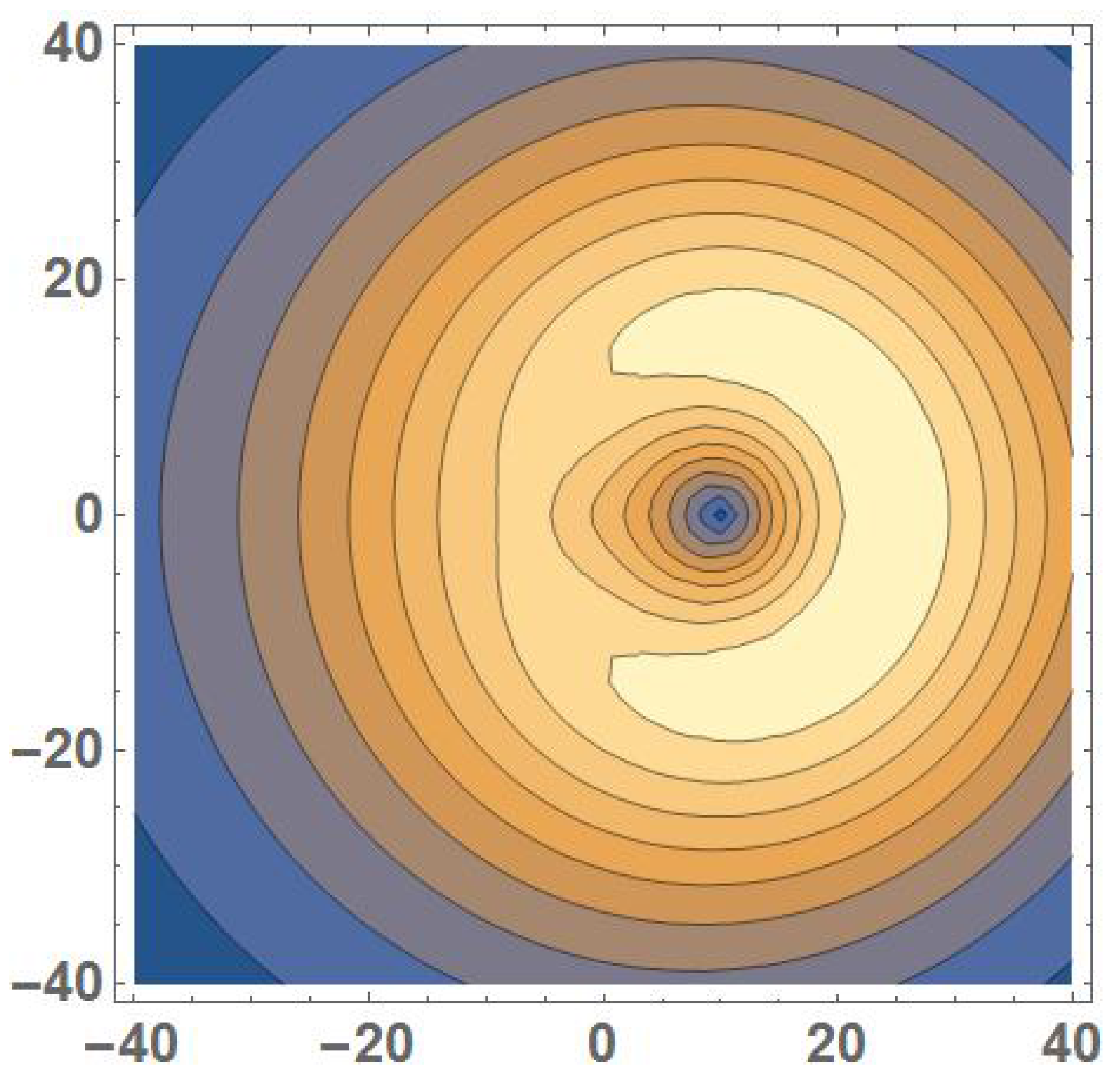
For the parameters
,
, and
Kpc we obtain the contour plot for the phantom mass density in
Figure 5. An interesting fact is that this model predicts a maximum DM density at a distance of 5 Kpc from the smallest component of the cluster and consequently, the apparent DM inferred from this model does not trace the distribution of baryonic mass in the cluster. We find that, for very asymmetric baryonic mass distributions, there are non-Newtonian force models which can predict gravitational effects which do not correlate with that baryonic mass. The strong statement of Clowe et al. [
37] is not generally valid and the bullet cluster cannot be presented as hard evidence in favor of DM. This could also respond to the problem of the likelihood of the bullet cluster in the
CDM cosmology [
38].
3.2. Solar System Dynamics
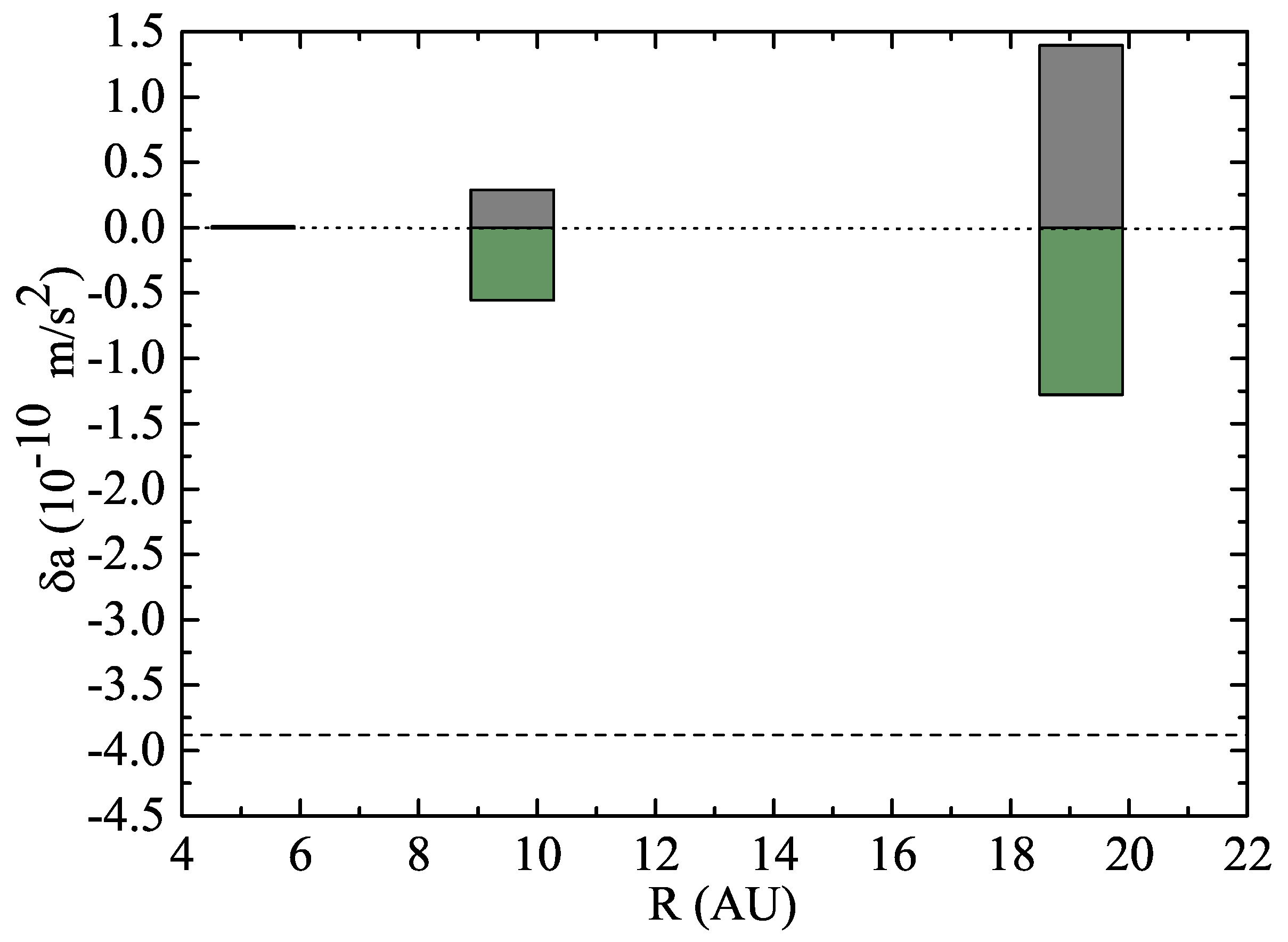
Nowadays very accurate ephemerides are obtained for the planets and satellites of the Solar System by including information about radar ranging, spacecraft missions, optical observations, etc. [
44]. These new ephemerides set very stringent limits on any possible modification to the Newtonian law of gravitation or the refined predictions of general relativity. By measuring extra contributions to the advance of the perihelion and the perturbations on the longitude of the ascending node in all the planets, Pitjeva et al. [
45] have found limits with respect to any possible anomalous contributions to these effects beyond general relativity. In a work by Iorio [
46], these extra precessions are put into correspondence with the magnitude of the anomalous acceleration that would cause them. The magnitude of these accelerations, acting upon the major planets, was estimated as follows:
Notice that all these contributions are compatible with a null effect within the error bars. These results were obtained from the data of Pitjeva et al. in order to rule out the Pioneer anomaly as the effect of an anomalous acceleration acting upon all the bodies in the Solar System. Although there have been other ephemerides published in the last ten years, it would be interesting to compare the extra non-Newtonian acceleration as given by Equations (
22) and (
25) with the values in Equation (
34) by taking
M as the mass of the Sun. Although the parameter
is uncertain, and it would depend on the particular model used for the value quoted in
Section 3, we get
astronomical units (AU) for the mass of the Sun. This distance is equivalent to
% of a light year. By using the model in Equation (
22) and the parameters given in
Section 2.3 for the exponents
and
we obtain the results in
Figure 6. For the case
we obtain the anomalous acceleration
m/s
acting upon a body at the distance of Uranus. For
the result is
m/s
, which is outside the error bars as listed in Equation (
34). Therefore, we conclude that a non-Newtonian model, with a mass-dependent distance scale as given by Equations (
22) and (
25), is not ruled out by the present status of observations in the Solar system. This force model is also in very good agreement with the distribution of apparent DM in the Milky Way according to Kalberla and Kerp [
39,
40].
4. Conclusions
The problem that started with the observations of Fritz Zwicky for the velocity distribution in the Coma Cluster is a lingering one in the field of astrophysics and cosmology [
1,
6]. It can be considered the single oldest and most important question with respect to our understanding of the structure of the Universe on a large scale, apart from the recent interest in accelerated expansion and its relation with the so-called dark energy [
5]. In the late 1970s the detailed study of Rubin et al. [
2] and Faber and Gallagher [
3] of the rotation curves of many galaxies give rise to strong evidence for an anomaly in the internal structure of galaxies that cannot be explained with classical or relativistic dynamics.
Since then, most physicists and astronomers have considered that the best explanation for this anomaly is the existence of a new kind of matter (usually considered in the form of particles with very weak interactions) that would predominate in the Universe and favors the accretion of galaxies and clusters, being six times more abundant than ordinary baryonic matter. The currently accepted model of cosmology incorporates in its premise a form of dark matter constituted by heavy weak interacting particles, also known as weakly interacting massive particles (WIMPs) that would arise in extensions of the standard model of particle physics, for example, the neutralinos predicted by supersymmetric theories with masses in the range of 1–
GeV [
6,
20]. This hypothesis seems to give good results for the evolution of structure on a galactic scale as well as for the location of the acoustic peaks in the cosmic microwave background spectra [
42,
43,
47].
The search for WIMPs has been carried out in experiments such as the DAMA/LIBRA and DAMA/NaI collaborations in which the characteristic signature of an annual variation was found [
7,
8]. This variation would be caused by the variable flux of DM particles through the Earth as it moves around the Sun. However, these results are highly controversial and an alternative explanation in terms of atmospheric muons and solar neutrinos has been proposed [
9]. In the absence of any strong evidence for the existence of good candidates for DM particles some researchers are casting doubts on the reality of the
-CDM cosmology. For example, Kroupa and collaborators have studied the observational data for satellite galaxies in the Local Group and they found that the data disfavors the theory of DM halos because a spherically symmetric distribution of enriched DM dwarf galaxies, predicted in this scenario, is not compatible with observations [
48,
49,
50]. Other important issue is the cuspy halo problem, i.e., the accumulation of DM particles at the core of the galaxies, as predicted by the cold dark matter model [
41], which is not inferred from the rotation curves of galaxies. On the other hand, it have been shown that this problem could be solved by using a warm dark matter (WDM) particle (such as a sterile neutrino) instead of CDM [
41].
Modified Newtonian dynamics (MOND), proposed by Milgrom as early as 1983, have been considered a viable alternative explanation for many years and still have many supporters [
4,
15]. More recently, other modified theories of gravity have been discussed in the literature: (1) Verlinde’s idea based upon an entropic origin of gravity [
51]; (2) non-minimal couplings of curvature and matter implemented as a modification of the Lagrangian [
52]; and (3) bimetric theories of gravity [
53]. On the other hand, there have been several proposals for modifications of Newton’s law at large distances, starting with the work of Finzi in 1963 [
54]. This idea has been revisited in various forms from time to time and it could be also of interest today in face of the present difficulties with standard cosmology.
In this paper we have considered several non-Newtonian models, which can be interpreted as apparent mass at large distances from the galactic center. We have shown that these models can provide a good fit to a hydrostatic model of the galactic halo [
39,
40]. This fit is particularly good for a model that interpolates among a Newton’s law at short distance and another Newton’s law at a very large distance with a constant prefactor, representing the apparent total mass of the system. We have also shown that these models can account for the Tully–Fisher relation [
12,
13] if the characteristic length scale depends upon the square root of the total mass. In any case, one must say that a limitation of our model is that these results have been achieved by proposing this relation among the length scale,
, and the total visible mass,
, of the galaxy and that this should be tested by analyzing other mass distributions inferred from the observation of other galaxies and clusters. The corresponding calibration should yield similar results for the constant parameter
if our approach has an element of truth. On this basis one can also account for the displacement of the observations of extreme systems, such as the Bullet Cluster [
37], in which the center of mass determined by gravitational lensing does not coincide with the center of mass of the baryonic matter. Finally, we have discussed the possibility of detecting the anomalous non-Newtonian force in the Solar System in terms of the new ephemerides for the perihelion precession of the planets. If such an achievement were possible, we would be able to link the local scale with the macro scale of the galaxies and clusters. On the other hand, a validation of the non-Newtonian modification of standard gravity can only be achieved by proposing a universal relativistic theory and this is a pending issue for the proponents of these models that should be attempted in the near future.
The current interest in possible theoretical alternatives to the DM hypothesis is a manifestation of the profound difficulties that have arisen in astrophysics and cosmology. This interest may aid in settling these issues in the face of controversial observations. However, a search in different directions is necessary to evaluate the various possibilities logically consistent with existing data. We expect that these interdisciplinary efforts would finally lead to a solution of the riddles that dark matter and dark energy pose to our understanding of the Universe.