1. Introduction
The Casimir effect (for reviews see [
1,
2,
3]) is among the most interesting manifestations of the influence of boundaries on the properties of quantum vacuum. The boundaries modify the spectrum of zero-point fluctuations of quantum fields, and as a consequence of that the vacuum expectation values (VEVs) of physical observables are shifted. In particular, this gives rise to vacuum forces acting on the boundaries. These forces are sensitive to both the bulk and boundary geometries of the problem at hand.
Closed expressions for the physical characteristics of the vacuum in the Casimir effect can be obtained for highly symmetric background geometries only. In particular, motivated by possible applications in braneworld models and in anti-de Sitter (AdS)/CFT correspondence, the Casimir effect on anti-de Sitter bulk has attracted a great deal of attention. In braneworld models of the Randall–Sundrum type with branes parallel to the AdS boundary, the Casimir forces provide an alternative mechanism for the stabilization of the radion field. The main part of the investigations of the Casimir effect in AdS bulk (see, for instance, references in [
4]) consider global characteristics of the vacuum, such as the Casimir energy and forces, by using either dimensional or zeta function regularization methods. More detailed information on the properties of the vacuum is contained in the local characteristics like the VEV of the energy-momentum tensor. In addition to describing the physical structure of the quantum field at a given point, this VEV acts as the source in the Einstein equations and therefore plays an important role in modelling a self-consistent dynamics involving the gravitational field. The VEV of the energy-momentum tensor for scalar and fermionic fields in the geometry of two branes parallel to the AdS boundary has been investigated in [
5,
6,
7,
8,
9,
10]. Both the global and local characteristics in higher-dimensional generalizations of the AdS spacetime with compact internal spaces are studied in [
11,
12,
13,
14,
15,
16,
17,
18,
19,
20]. The case of a brane perpendicular to the AdS boundary is discussed in [
21]. Induced vacuum currents for a charged scalar field in AdS background with toroidally compactified spatial dimensions and in the presence of branes have been investigated in [
22,
23,
24,
25]. The dynamical Casimir effect for a brane moving in AdS bulk is discussed in [
26] (on the realization of the dynamical Casimir effect in circuit quantum electrodynamics involving superconducting quantum interference devices, see, for instance, [
27,
28]). The renewed interest in physical models on AdS bulk is closely related to application of AdS/CFT correspondence in investigations of strongly coupled condensed matter systems (see, for example, [
29,
30]).
In the present paper, we investigate the VEV of the energy-momentum tensor for the electromagnetic field on a background of
-dimensional AdS spacetime in the presence of a boundary parallel to the AdS horizon. On the boundary, the field obeys the condition that is a generalization of the perfect conductor boundary condition for an arbitrary number of spatial dimensions. The two-point function for the electromagnetic field in the boundary-free AdS spacetime is investigated in [
31]. The two-point functions and the vacuum densities in the presence of a flat brane are evaluated in [
4,
32]. The electromagnetic Casimir densities in de Sitter spacetime for flat boundaries have been investigated in [
33,
34]. The electromagnetic two-point functions and the Casimir effect in the background of more general Friedmann–Robertson–Walker cosmologies are discussed in [
35].
The total Casimir energy for an electromagnetic field in the region between a pair of perfectly conducting plates in a Randall–Sundrum braneworld model with
has been investigated in [
36] at both zero and non-zero temperatures. The corresponding Casimir force at zero temperature has also been discussed in [
37] using the scalar field analogy. It should be emphasized that the Kaluza–Klein masses for electromagnetic and scalar fields are different. Note that in both the papers [
36,
37] the interaction part of the Casimir energy is considered. The latter tends to zero in the limit of large separations between the boundaries. However, in quantum field-theoretical problems with boundaries, a non-zero self energy for separate boundaries may present, similar to the Casimir energy for a single spherical shell widely discussed in the literature.
The paper is organized as follows. In the next section we describe the geometry and present the mode functions and general expressions for the VEV of the energy-momentum tensor. The boundary-induced contribution in the VEVs for the regions on the left and on the right of the boundary are explicitly extracted in
Section 3 and
Section 4. The behavior of these contributions in various asymptotic regions of the parameters is investigated. The main results are summarized in
Section 6.
2. Problem Setup and the Electromagnetic Modes
We consider an electromagnetic field with the vector potential
in the background of
-dimensional AdS spacetime. In the Poincaré coordinates, the line element is given by the expression
where
,
, and
is the metric tensor for
-dimensional Minkowski spacetime. The parameter
is the AdS curvature radius, and for the Ricci scalar one has
. The hypersurfaces
and
correspond to the AdS boundary and horizon, respectively. We assume the presence of a boundary located at
, on which the electromagnetic field obeys the boundary condition
where
is the normal vector to the boundary and
is the dual of the field tensor
. Condition (
2) is a generalization of the perfectly conducting boundary condition in
electrodynamics.
In quantum electrodynamics, the boundary condition (
2) modifies the spectrum of the zero-point fluctuations, and as a consequence, the VEVs of physical observables are changed. This is the well-known Casimir effect, widely discussed in the literature. Among the most important characteristics of the vacuum state is the VEV of the energy-momentum tensor. Expanding the field operator over a complete set of mode functions
, obeying the boundary condition, and using the commutation relations for the annihilation and creation operators, for the VEV one finds the mode-sum formula
where
and the set of quantum numbers
specifies the modes. In (
3), a summation is understood for discrete quantum numbers and an integration over continuous ones. From the invariance of the problem under the Lorentz boosts along the spatial dimensions parallel to the boundary, it follows that the vacuum energy-momentum tensor is diagonal in the subspace perpendicular to the boundary and
From the symmetry of the problem, we also have
for
. The components
and
are related by the covariant conservation equation
, where
is the covariant derivative operator. This equation is reduced to a single equation:
In accordance with the problem symmetry, the dependence of the mode functions
on the coordinates
and on time
can be taken in the form
, with
. Substituting into the Maxwell equations, it can be seen that the
z-dependence of the modes is given by
, where
is a linear combination of cylinder functions and
,
. In the gauge
,
, the mode functions for the vector potential are presented as
where the polarization vectors
,
obey the relations
and
In addition, from the gauge condition one has
and
. With the choice (
6), the set of quantum numbers is specified as
, where
corresponds to different polarizations. From the boundary condition (
2) on the plate
, it follows that
The coefficient
C in (
6) is determined from the normalization condition
where
corresponds to the Kronecker delta for discrete
and to the Dirac delta function for continuous
.
Substituting the mode functions in (
3) for the normal stress, one finds
where we used the relation
for the cylinder functions. In (
10),
is understood as summation for discrete
and the integration for continuous
. The energy density is most easily found from the relation (
5):
To proceed further, we need to specify the region under consideration. Below, the separate regions and will be referred to as L- and R-regions, respectively (left and right regions).
3. VEV of the Energy-Momentum Tensor: L-Region
We start our consideration of the vacuum energy-momentum tensor with the L-region, which corresponds to the region between the AdS boundary and the plate. For the Neumann function
, the normalization integral (
9) diverges in the lower limit of the integration over
z (namely, at
). Consequently, for the normalizable modes we should take
, where
is the Bessel function. Let us denote by
,
the
nth positive zero of the function
:
. From (
8) we obtain the eigenvalues of the quantum number
:
. From (
9) with the
z-integration over
, for the normalization coefficient one gets
where
. Note that we have
.
The expressions for the diagonal components of the VEV of the energy-momentum tensor are presented as (no summation over
):
where
The expression on the right hand side of (
14) diverges. In order to have a finite expression, we assume that some cutoff function is introduced without writing it explicitly. The special form of that function will not be important for the further discussion.
In (
14), the zeros
are given implicitly, and that expression is not convenient for the investigation of the properties. For the transformation of the series over
n, we use the generalized Abel–Plana formula [
38,
39]:
where
and
are the modified Bessel functions and the function
is analytic in the right half plane Re
. After the application of (
16), the VEV is decomposed as
where
and
In (
19) we have introduced the notation
The contribution (
18) comes from the first integral on the right-hand side of (
16). It does not depend on
, whereas the part (
19) vanishes in the limit
. From here we conclude that the term
corresponds to the VEV in AdS spacetime in the absence of the boundary at
and the term
is induced by that boundary. Note that for
the boundary-induced part is finite in the absence of the cutoff function and the renormalization is required for the boundary-free part
only. From the maximal symmetry of the AdS spacetime it follows that the corresponding renormalized VEV should have the structure
.
We can further simplify the boundary-induced contribution (
19). Introducing a new integration variable
instead of
u and passing to polar coordinates in the plane
, after the integration over the angular coordinate we get (no summation over
):
The boundary-induced part depends on
z and
in the form of the ratio
. This property is a consequence of the maximal symmetry of the AdS spacetime. Note that the coordinate
y that measures the physical distance from the boundary is given by
In terms of this coordinate, one has
, where
and
is the proper distance of the observation point from the boundary. By taking (
20) into account, we can see that the boundary-induced contribution to the energy density is negative and the normal stress is positive,
,
.
In the special case
, one gets
for
. In this special case, the electromagnetic field is conformally invariant and the boundary-induced contribution is expressed in terms of the corresponding VEV in the region between two conducting plates in Minkowski bulk by the standard conformal relation.
For
, the boundary-induced contribution diverges on the plate. Near the boundary, the main contribution to the integral in (
21) comes from large values of
x, and to the leading order one gets
where
is the corresponding VEV for a plate in Minkowski spacetime. Note that in Minkowski spacetime the normal stress vanishes
. Near the AdS boundary,
, the boundary- induced VEVs tend to 0 with the leading terms
and
for
.
The Minkowskian limit of (
21) corresponds to
, for a fixed value of the proper distance from the boundary
. In this limit,
and the ratio
is close to 1. By accounting for the fact that the main contribution in (
21) comes from the region
and using the asymptotic expressions for the modified Bessel functions for large arguments, we can see that
for
and
, where
is given by (
24).
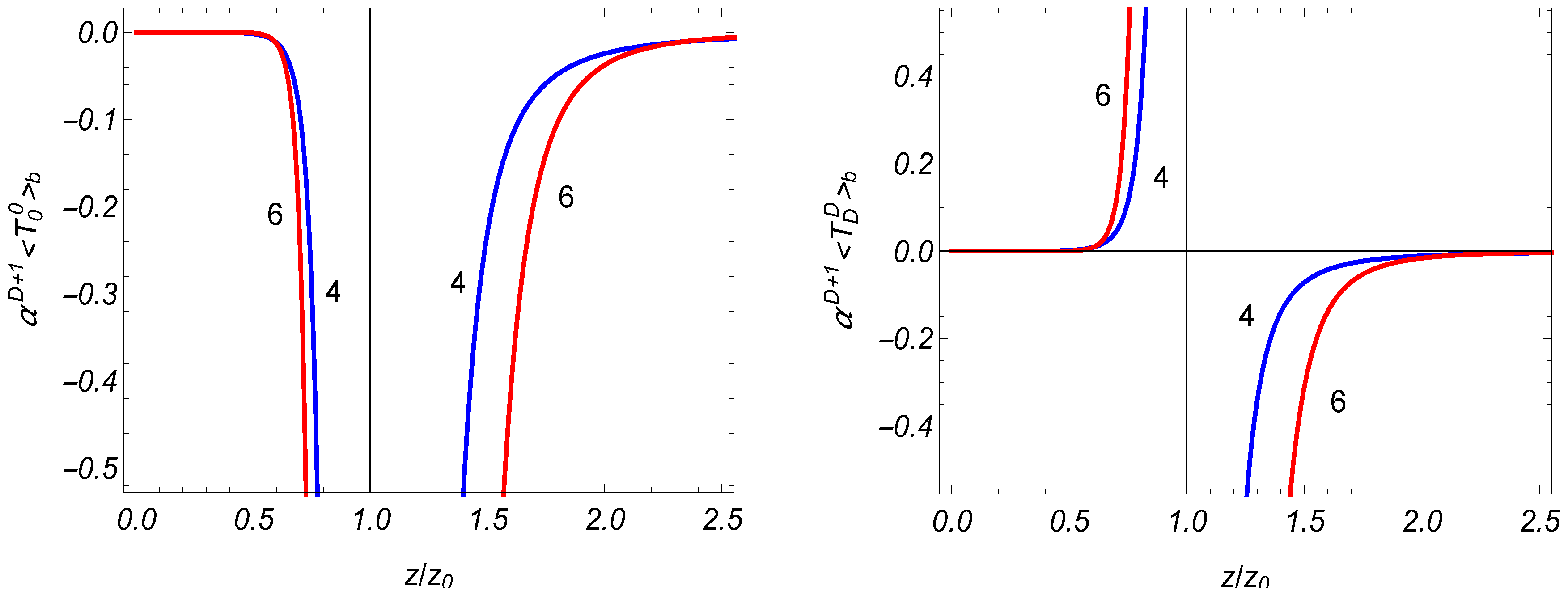
In
Figure 1 we have plotted the boundary-induced contributions in the VEVs of the energy density (left panel) and the normal stress (right panel) as functions of the ratio
for the number of spatial dimensions
(numbers near the curves).
For the evaluation of the mode-sum (
14), we have applied a variant of the generalized Abel–Plana Formula (
16). That allowed us to explicitly extract the boundary-free contribution and to present the boundary-induced contribution in terms of strongly converging integral for points away from the boundary. The latter feature is related to the fact that the Abel–Plana formula automatically rotates the integration contour to the imaginary axis. With the extracted boundary-free part from the VEVs, the renormalization of local observables is reduced to that in the boundary-free geometry. Another important advantage of the procedure based on the Formula (
16) is that the explicit knowledge of the eigenvalues for the quantum number
is not required. Other applications of the generalized Abel–Plana formula to the Casimir effect can be found in [
39]. Note that a similar procedure, widely employed for the evaluation of the global characteristics of the vacuum in the Casimir effect, is based on the argument principle (see, for example, [
1,
2,
3]). In particular, this method has been used for the evaluation of the renormalized Casimir energy in braneworld models on AdS bulk.
4. VEV in the R-Region
Now let us consider the R-region,
. In this region, the function
in (
6) is a linear combination of the Bessel and Neumann functions. The relative coefficient in the linear combination is determined by the boundary condition (
8), and the eigenvalues of the quantum number
are continuous. For the function
, one gets
where
In the normalization condition, the symbol
corresponds to the Dirac delta function
. For the normalization coefficient, we find
For the VEV of the energy-momentum tensor, one gets (no summation over
):
with
As before, the presence of a cutoff function is assumed in (
29). For
, the divergences when one removes the cutoff are the same as those in the boundary-free geometry.
In order to extract the boundary-free contribution from (
29), we use the relation
with
and
. Here
,
, are the Hankel functions. The part in the VEV corresponding to the first term on the right-hand side of (
31) coincides with the boundary-free VEV (
18). In the remaining boundary-induced part, we rotate the integration contour in the complex plane
by the angle
for the term
and by the angle
for the term
. As a result, the VEV in the R-region is decomposed as (
17) with the boundary-induced contribution
and with the functions
The further simplification is similar to that for the L-region, and one gets the final expression
As seen, the boundary-induced VEVs in the L- and R-regions are obtained from each other by the replacements of the modified Bessel functions.
In the special case
, the boundary-induced VEV (
34) vanishes in the R-region. For
, all the components are negative,
. For points near the boundary,
, the ratio
is close to 1 and the contribution of large
x dominates in (
34). By using the corresponding asymptotics for the modified Bessel functions, for the leading terms we obtain the expressions (
24). Near the boundary, the dominant contribution to the VEV comes from wavelengths smaller than the curvature radius, and the influence of the gravity is weak.
At distances from the boundary larger than the AdS curvature radius,
one has
. The dominant contribution to the integral in (
34) comes from small values of
x. By using the corresponding asymptotic expressions for the functions
and
, for the leading order terms we find
with
. As seen, at large distances the boundary-induced VEVs—as functions of the proper distance—are suppressed by the factor
. At distances from the boundary larger than the AdS curvature radius, the effects of gravity are essential and the behavior of the VEV is completely different from that on the Minkowski bulk. In the latter case, the decay of the VEVs, as functions of
, is as power law, as
for the energy density and stresses parallel to the boundary.
For the R-region, the dependence of the boundary-induced energy density and the normal stress on the ratio
is presented in
Figure 1.
5. Applications to Randall–Sundrum Model with a Single Brane
With the results given above, we can find the Casimir densities for the electromagnetic field in Randall–Sundrum braneworld model with a single brane (RSII model) [
40] (for reviews see [
41,
42]). The original model has been formulated on the AdS bulk with
. Here we will consider the generalization for an arbitrary value of the spatial dimension. In terms of the coordinate (
22), measuring the physical distance from the brane located at
, the line element has the form
where
. The absolute value of the
y coordinate in the metric components incorporates the
-symmetry with respect to the brane: the points with the coordinates
y and
are identified. From (
36), it follows that in RSII model only the R-region of the AdS spacetime is employed. In terms of the coordinate
z, the brane is located at
.
The boundary conditions for fields on the brane are dictated by the
-symmetry [
43]. Two types of boundary conditions are realized corresponding to the even and odd fields under the
-symmetry. First let us consider the case of odd fields. These fields obey the boundary condition
. For the modes (
6), this corresponds to the boundary condition (
8). Hence, the electromagnetic Casimir densities in RSII model are obtained from the results given above for the R-region with
. The only difference is that in the RSII model the integration over
y in the normalization integral for the modes (
6) goes over the region
instead of the interval
. This leads to an additional factor
in the normalization coefficient for the mode functions. Consequently, the Casimir densities for odd fields in the RSII model are given by (
34) with an additional factor 1/2. Note that in this case there is no Kaluza–Klein zero mode.
For even fields, the boundary condition on the brane reads
. For the modes (
6) it is reduced to
at
. By taking into account that for cylinder functions one has
, this condition is rewritten as
Note that the boundary condition for even fields can be written in terms of the field tensor as
. This type of boundary condition is used to confine the gluon fields in QCD (in particular, in MIT bag models). The procedure for the evaluation of the vacuum energy-momentum tensor in the R-region for this type of boundary condition is similar to that described in
Section 4. We will omit the details and present the final result for the RSII model (no summation over
):
with
and
. As it has been explained above, the additional factor 2 in the denominator is related to the presence of two regions
and
for the coordinate
y connected by the
-symmetry. The qualitative behavior of the brane-induced energy density and the normal stress is similar to that depicted in
Figure 1. Note that in [
36] the Casimir energy is considered for even fields.
6. Conclusions
For -dimensional AdS spacetime, we have investigated the influence a planar boundary, parallel to the AdS horizon, on the properties of the electromagnetic vacuum. On the boundary, the electromagnetic field obeys the condition that generalizes the perfect conductor boundary condition for . As the local characteristic of the vacuum state we have considered the VEV of the energy-momentum tensor. The latter is among the most important quantities in quantum field theory on curved backgrounds. The vacuum energy-momentum tensor is diagonal, and the stresses parallel to the boundary are equal to the energy-density. The latter property is a direct consequence of the Lorentz invariance with respect to the boosts along the spatial dimensions parallel to the boundary.
The quantum properties of the vacuum are completely different for the region between the boundary and the AdS boundary (region
, referred to here as the L-region) and for the region between the boundary and AdS horizon (region
, referred to as the R-region). In the first region, in addition to the boundary condition at
, the field operator is constrained by the boundary condition on the AdS boundary. The latter is required by the normalizability condition of the mode functions. As a consequence, in the L-region the eigenvalues of the quantum number
form a discrete set determined by the zeros of the Bessel function
. The mode-sum for the energy-momentum tensor contains a summation over these zeros. For the transformation of the corresponding series, we have applied the generalized Abel–Plana formula that allowed the extraction of the boundary-free part from the VEV. For points away from the boundary, the renormalization is required for that part only. The boundary-induced contribution is given by the expression (
21). The vacuum energy density is negative, and the normal stress is positive. In the special case
, the problem for the L-region is conformally related to the problem in Minkowski bulk with two parallel conducting plates, and for the energy-momentum tensor we have a simple result (
23). In this special case, the VEV is finite on the boundary. This is not the case for
, and the VEV diverges on the boundary with the leading terms given by (
24). On the AdS boundary, the boundary-induced contributions vanish like
. As a function of the proper distance from the AdS boundary, this corresponds to the exponential suppression by the factor
with
.
In the R-region, the quantum number
is continuous and the boundary-induced contribution to the VEV of the energy-momentum tensor is presented as (
34). Both the energy density and the normal stress are negative for
. In the case
, the problem in the R-region is conformally related to the Minkowskian problem with a single conducting plate, and the boundary-induced contribution vanishes. For points near the boundary, the main contribution to the VEV comes from the fluctuations with wavelengths smaller than the AdS curvature radius. The influence of the gravitational field on those fluctuations is weak and the leading terms in the asymptotic expansion coincides with those in the Minkowski bulk. The influence of the gravitational field is essential at distances from the boundary larger than the curvature radius. At large distances, the boundary-induced contribution is suppressed by the factor
and it vanishes on the AdS horizon. From the expressions for the VEV of the energy-momentum tensor in the R-region, the corresponding formulas can be obtained for odd and even vector fields in Randall–Sundrum model with a single brane. For odd fields, the boundary condition on the brane is equivalent to the perfectly conducting boundary condition, and the VEV is given by (
34) with
and with an additional factor 1/2. The latter is related to the orbifold nature of the background in Randall–Sundrum models. For even vector fields, the boundary condition is given by (
37). The latter is employed for the confinement of gluon fields in QCD. The corresponding VEV is given by the expression (
38).