1. Introduction
Fourty years after their discovery, the origin of Gamma-Ray Bursts (hereafter GRBs) remains enigmatic. Their central engine, photospheric emission, and emission mechanisms are still under debate. In long-duration GRBs, a massive star collapses and forms a stellar mass black hole, whereas in short-duration GRBs, two compact objects likely merge and also form a black hole, although in that case too the model of a collapsing massive star is not completely rulled out. It is widely discussed in the GRB community (Lee et al. [
1], Wang et al. [
2], McKinney [
3], Komissarov and Barkov [
4], Nagataki [
5]) that a black hole central engine involves the electromagnetic extraction of the black hole rotational energy proposed by Blandford and Znajek [
6] (herefafter BZ). Neutrino annihilation may also work in some cases (e.g., Chen and Beloborodov [
7]), but fails to explain the observed energetics of Ultra Long GRB (Leng and Giannios [
8]). We are proposing that highly conducting matter from the interior of the star will drive the advection of magnetic flux during the collapse, up to the point that an equatorial thick disk (torus) forms and acts as a barrier that holds the advected magnetic flux. What we have in mind here is a rotationally supported hot and highly magnetized torus similar to the one seen in numerical simulations of short gamma-ray bursts (e.g., Rezzolla et al. [
9]) that survives long enough to be able to observe the electromagnetic spindown of the central black hole (see
Figure 1).
The electromagnetic black hole spindown is conceptually similar to the spindown of the so-called Faraday disk, a conducting disk of radius
r, mass
M and angular velocity
threaded by a certain amount of magnetic flux
and magnetic field
B. The magnetic field is not generated by the disk itself, but is generated and held in place by an external medium. If we assume the existence of a conducting path for electric currents to close over the surface of the disk, the spindown rate is proportional to
, and the disk loses rotational kinetic energy at a rate proportional to
. Equating the latter two expressions, we deduce that the Faraday disk spins down exponentially as
, and thus loses rotational energy at a rate
The characteristic decay timescale
is proportional to the mass and the square of the radius, and inversely proportional to the square of the total accumulated magnetic flux, namely
A detailed general relativistic calculation of this process in the case of a slowly rotating black hole yields the BZ timescale for exponential black hole spindown
(see Nathanail and Contopoulos [
11] and Nathanail et al. [
10] for details). We have defined in Equation (
3) a typical value for the accumulated black hole magnetic field
where
c and
are the speed of light and Newton’s gravitational constant respectively.
B can reach very high values during the core-collapse of a massive star, and for
G, the black hole spins down in less than a hundred seconds. It is usually argued that the balance of magnetic pressure with ram pressure from the disk can give an estimate of the possible magnetic flux accumulated around the central object. This argument is reasonable for accreting black hole systems such as AGNs and X-ray binaries,
but not in GRB events where the black hole forms inside a suppermassive star. In the latter, it is reasonable for this magnetic field to be held in place by a massive disk/torus of material that
does not accrete due to centrifugal support (at least during some finite but long enough timescale, similarly to Rezzolla et al. [
9]). This allows us to effectively decouple the Blandford-Znajek mechanism from the accretion process, unlike what is customary to assume in AGN and XRB accretion disks. Obviously, if the massive disk is dispersed faster than the duration of the spindown, the accumulated magnetic flux will not be conserved, and the spindown evolution will not be exponential. Other effects may too ‘contaminate’ the black hole electromagnetic spindown, making it difficult to discern its activation and evolution. One example may be fall-back accretion of large amounts of mass that could lead to black hole spin up with a subsequent different spindown evolution. Moreover, the electromagnetic interaction with the torus formed around the black hole may result in an extra spindown that may too be linked to GRBs (Van Putten and Gupta [
12]). It is interesting to notice here that Equation (
1) cannot distinguish between a black hole and a neutron star/magnetar with field lines that are held open by the surrounding material. Therefore, in principle, we cannot claim that exponential decay is definite proof for the presence of a central black hole; it is, however, a strong suggestion.
If we believe that BZ is the mechanism that powers the burst, we should be able to find its signature in the GRB light curves which allow us to follow the central engine activity for very long times (e.g., Barkov and Pozanenko [
13], Zhang et al. [
14]). Notice that the prolonged activity of the central engine has often been associated with the so called Extended Emission (hundreds of seconds and longer) found in both long and short duration GRBs (e.g., Connaughton [
15], Bostanci, Kaneko and Gogus [
16]). In Nathanail and Contopoulos [
17] and Nathanail et al. [
10], we searched for signatures of exponential decay in the X-ray light curves obtained with the XRT instrument aboard the Swift satellite. In
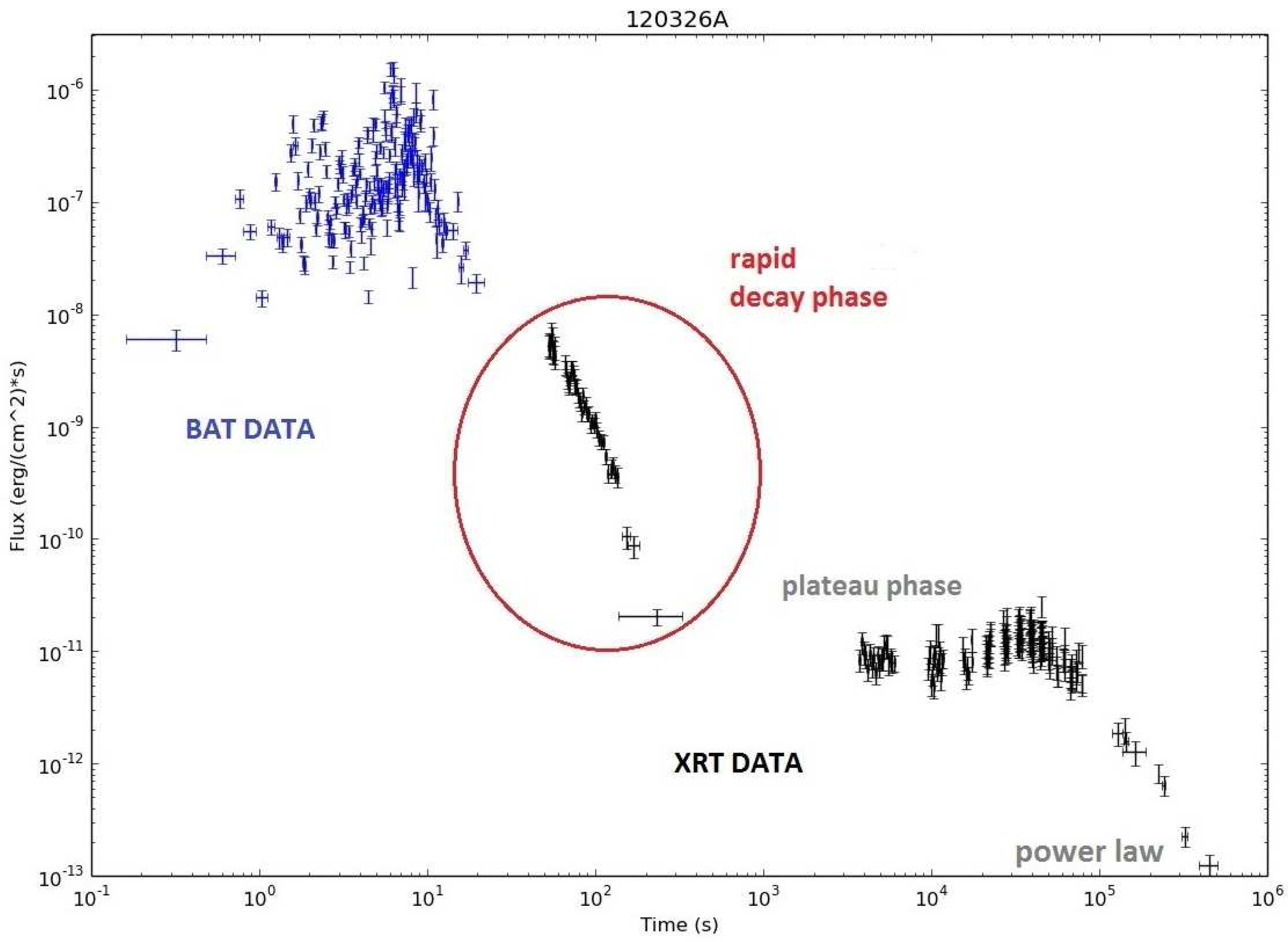
Figure 2, we show the two different components of X-ray GRB light curves, the prompt and the afterglow emission. The prompt emission is usually triggered by BAT, and ends when it decays below the instrument’s sensitivity limit. Anything below that limit is considered as afterglow emission which itself consists of two components separated phenomenologically (O’Brien et al. [
18], Willingale et al. [
19], Ghisellini et al. [
20]). The first afterglow component seems to consist the extension of the prompt emission rapid decay phase, noticed in the first X-ray afterglow detections of Swift (Tagliaferri et al. [
21]). The second afterglow component starts with a plateau, continues in a power law phase, ends with a final fast decay, and most probably involves energy losses through external shocks in the expanding post-explosion stellar material (Meszaros and Rees [
22]). Notice that the prompt emission has some times also been observed by XRT, and even by optical/IR telescopes.
The present report is a summary of the work performed in Nathanail and Contopoulos [
17] and Nathanail et al. [
10] that was presented in the Special Symposium on “Gamma-Ray Bursts: Recent Theoretical Models and Observations” during the 2016 European Week of Astronomy and Space Sciences (EWASS 2016) in Athens Greece. We have found that in about one third of XRT observations where the first rapid decay afterglow phase is clearly observed, parts of it follow closely the theoretical exponential decay dictated by the BZ black hole spindown. This effect has also been observed in Ultra Long GRBs, which lead us to suggest that they lie in the same class together with the usual Long GRBs, and their extraordinary duration may just be due to the small amount of magnetic flux accumulated on the event horizon of the newly formed black hole after the core collapse of the suppermassive star.
2. XRT Observations
Discerning the central engine activity in a GRB light curve is tricky. When the signal drops out of the
-ray band, it continues in the X-rays and this emission can still be of internal origin (Fan and Wei [
23]). At first, the X-ray energy flux shows (in most cases) a very steep decay which is believed to be the tail of the prompt
-ray emission. Then it enters a plateau phase and continues as a power law (Wijers et al. [
24]) that can some times last up to a few weeks and is most probably associated with an external origin (external shocks, e.g., Meszaros and Rees [
22]). Zhang et al. [
14] completed a comprehensive study of Swift XRT light curves and obtained an instrument-independent estimate of the central engine activity duration. We used the same GRB sample with Zhang et al. [
14] since the
-ray signal drops fast and only the X-rays can follow the extended central engine activity. All the XRT light curves are taken from the Swift/XRT website
1 (Evans et al. [
25]) at the UK Swift Science Data Centre (UKSSDC). Our goal was to analyse the first steep decay phase of the light curves for signs of the BZ mechanism.
We considered every light curve from our sample and tried to fit Equation (
1) over some part of it. In order to guarantee good statistical results, we want to be able to follow this decay for more than one order of magnitude, so that we are confident we are following an exponential and not just a steep power law. Cases where data points are too few to claim good statistical results were excluded. For the ones that the rapid decay in the X-rays is less than one order of magnitude we may have lost the first afterglow phase and thus are left out. Furthermore, GRBs with an irregular distribution of data points, i.e., with extra complex physical process going on in parallel, are left undefined. Several effects (such as mass infalls that may result in sudden black hole spin ups) can modify the black hole electromagnetic spindown, making it difficult to discern its activation and evolution. Such secondary events will most probably yield secondary flares, as is frequently seen in GRB light curves (Wu et al. [
26]). There are cases in which, after a big flare, the emission shows a steep decay more than two orders of magnitude (e.g., GRB 121027A). It is very interesting that such rapid emission decays after a flare are also exponential! There are also some GRBs with minor flares that do not disrupt a single exponential fit in which it is not clear whether we are following a black hole spinning down or not. Another physical possibility that would mask the exponential decay is if the surrounding disk disperses faster than the duration of the spindown. In that case, the accumulated magnetic flux will not be conserved, and the spindown evolution will not be exponential.
We decided to focus only on GRBs with a single emission decay event. We thus formulated the following empirical criteria that characterize our sample: (i) emission decay more than one order of magnitude; (ii) full (not sparse) sampling of the light curve in the time interval that we follow the spindown; and (iii) a steep decay emission phase without continuous big flares. No strong conclusions on the central engine activity can be extracted for those few GRBs (∼33) with not enough data in the steep decay phase. By fitting Equation (
1) to the light curve, we find
for every GRB listed in
Table 1 and
Table 2.
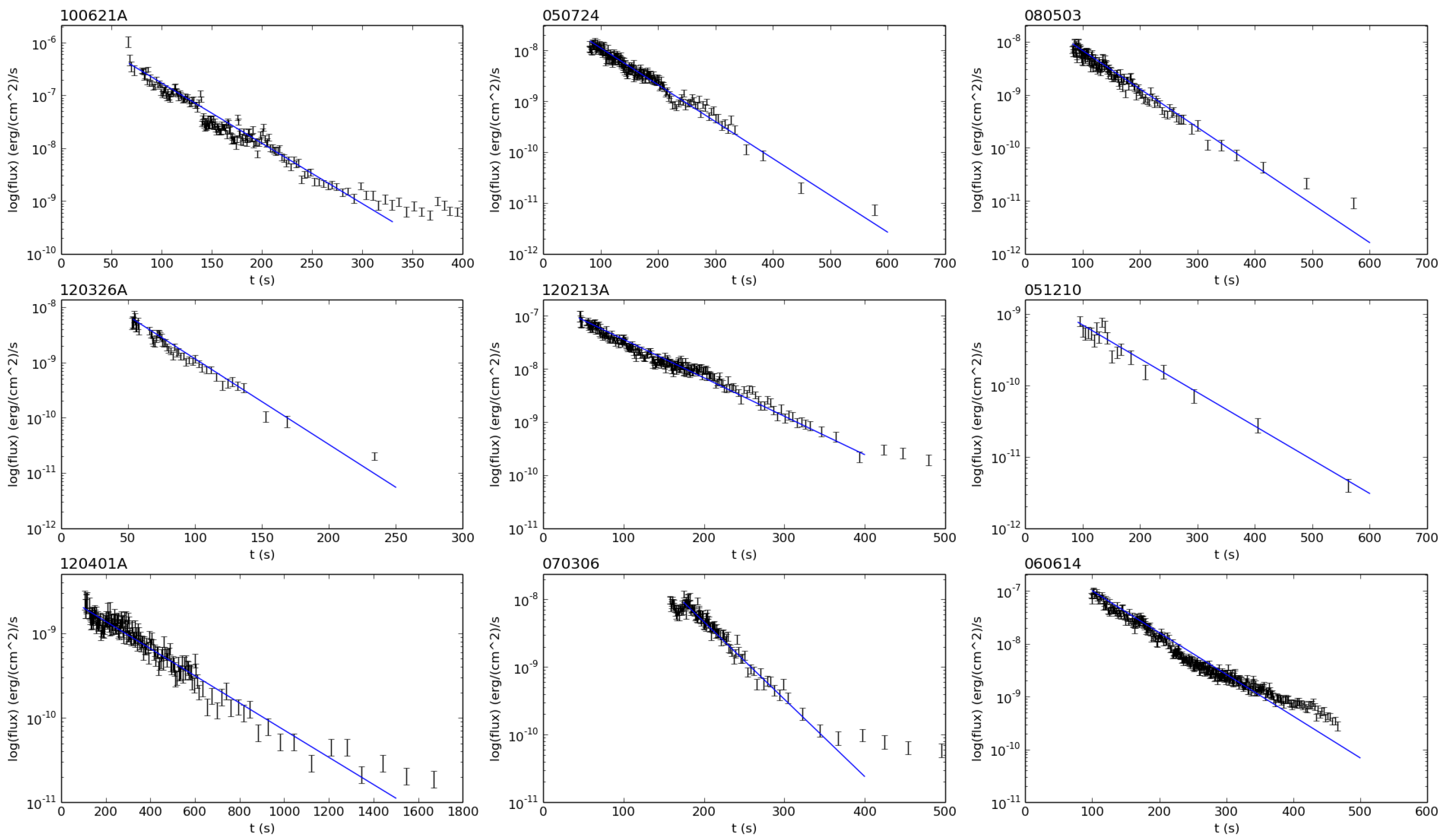
is a really important physical parameter that allows us to estimate the strength of the magnetic field in the vicinity of the black hole. From the primary sample of 343 GRBs, we excluded 33 objects with low number of data in the rapid decay phase, and were left with 310 GRBs. From these GRBs, 60 (∼20%) have a very good exponentially decaying emission event, with
-squared over
for most of them (characteristic examples shown in
Figure 3). In
Table 1 we show the
that we obtained for these objects. In all these events we can follow the exponential decay (black hole spindown) for more than two orders of magnitude combined with a very good fitting result (R-squared more than
). There are many GRBs (31) in which the rapid decay phase is really small and the light curve enters quickly in a plateau phase or goes straight to the plateau phase (33). In these events, the rapid decay can be less than an order of magnitude, thus we cannot support an exponential. In
Table 2 we list 22 objects that have flares with a subsequent exponential decay. A representative example from this class is the Ultra Long GRB 121027 where the X-ray light curve starts with an exponential decay, and after a big flare at around ∼5000 sec (energy flux increases more than two orders of magnitude) it proceeds again with an exponential decay. This big flaring activity may be understood as black hole spinning up because of a large amount of mass infall. Altogether,
(82) of GRBs show an exponential decay in the first phase of the afterglow. There are another 35 GRBs with many small flares in their light curves, for which no conclusion is reached. Notice that we found 28 GRBs in which the whole afterglow can be fitted with a single power law. For the remaining 100 objects no strong conclusions could be reached. There is a possibility that XRT failed to catch their rapid decay phase. It is also possible that the spindown of the central object may be hidden behind a stronger emission of external origin.
3. Summary
The magnetic flux accumulated on the event horizon of a newly formed black hole resulting from the core collapse of a supermassive star can drive the extraction of the black hole rotational energy through the Blandford-Znajek mechanism. We argue that it is possible to hold this magnetic flux for the duration of the burst even without accretion onto the black hole, as seen e.g., in simulations of short gamma ray bursts (Rezzolla et al. [
9]). In that case, the electrodynamic energy release decays exponentially. Clearly, there is a whole spectrum of black hole spins and GRB energies, and in fact some GRBs may release up to ∼10
erg (e.g., GRB 080916C), a value that would correspond to a maximally rotating 10 solar mass black hole.
In order to follow the central engine activity as far as possible, we focused on the XRT X-ray band. We (as well as others before us) propose that the rapid decay phase of Long and Ultra Long GRBs is of internal origin, i.e., it represents the rapid decay of the central engine activity. We further propose to associate this rapid decay with the electromagnetic spindown of the newly formed central black hole. As a result, we suggest that the duration of a GRB depends closely on the magnetic flux accumulated on the event horizon. This in turn can be directly associated, through flux conservation, with the surface magnetic field of the progenitor star. From a sample of 310 Long and Ultra Long duration GRBs, 60 show a clear exponential decay and 22 also proceed with an exponential decay after a flare. In total,
of the events in our sample contain a clear exponentially decaying part. A similar behavior (Fast Rise Exponential Decay-FRED) was observed in the past in
-rays with the BATSE instrument aboard the CGRO satellite (e.g., Peng et al. [
27]). We are well aware that, in the highly dynamical environment of a collapsing stellar core, the accumulated magnetic flux threading the black hole will not always be time independent, and this is why we only observe a clear exponential decay in a fraction of GRB events.
We conclude that, whenever an exponential decay is observed, this may be the signature of the Blandford-Znajek mechanism in action in the central engine of GRBs.