Challenging the Forward Shock Model with the 80 Ms Follow up of the X-ray Afterglow of Gamma-Ray Burst 130427A

Abstract

GRB 130427A was the most luminous gamma-ray burst detected in the last 30 years. With an isotropic energy output of $8.5\times {10}^{53}$ erg and redshift of 0.34, it combined very high energetics with a relative proximity to Earth in an unprecedented way. Sensitive X-ray observatories such as XMM-Newton and Chandra have detected the afterglow of this event for a record-breaking baseline longer than 80 million seconds. The light curve displays a simple power-law over more than three decades in time. In this presentation, we explore the consequences of this result for a few models put forward so far to interpret GRB 130427A, and more in general the implication of this outcome in the context of the standard forward shock model.

1. Introduction

The most energetic gamma-ray bursts—events that release ∼${10}^{54}$ erg—are relatively rare, and are therefore found typically when examining very large cosmological volumes and thus high redshifts (see Figure 1 of [1]). GRB 130427A produced an isotropic energy in gamma-rays $E_{\gamma ,\mathrm{iso}}=8.5\times {10}^{53}$ erg at redshift $z=0.34$. Less than $3\%$ of GRBs produce more energy than 130427A, and less than $4\%$ of bursts are at $z<0.34$ [2,3].

GRB 130427A thus represents a very rare event, and has enabled the GRB community to research the properties of very energetic bursts in an unparalleled fashion. A large corpus of literature has already been written on this GRB; some works deal with the prompt emission (e.g., [4,5]), others present a modeling of the X-ray, optical, and radio afterglow emission (e.g., [1,6,7,8] K13, P14, L13, V14 and M14 henceforth). The studies on the afterglow, however, rely on data taken up to ≃100 days after the GRB trigger.

Taking advantage of the high energy release and proximity of GRB 130427A, we took the opportunity to carry out successful observations of its X-ray afterglow over an unprecedented timescale. Such observations were aimed at testing the models mentioned above.

In this proceedings, we show the X-ray observations of GRB 130427A performed up to ≃83 Ms (i.e., ≃1000 days) by Chandra and XMM-Newton. Even the latest observation led to a significant detection; this is the longest timescale over which the X-ray afterglow of a long GRB has been studied. We also discuss the implication on the scenarios put forward for this exceptional event. For more detailed analysis, we refer the reader to De Pasquale et al. (2016) [9].

We adopt the cosmological parameters determined by the Planck mission; i.e., $H_0=67.8$ km s${}^{-1}$ Mpc ${\mathrm{\Omega }}_m=0.31$, ${\mathrm{\Omega }}_{\mathrm{\Lambda }}=0.69$ [10]. The afterglow emission is described by $F_{\nu }\propto t^{-\alpha }{\nu }^{-\beta }$, where $F_{\nu }$ is the flux density, t the time from trigger, ν the frequency, and α and β are the decay and spectral indices, respectively. Errors are reported at 68% confidence level (C.L.) unless otherwise specified.

XMM-Newton observed GRB 130427A (PI: De Pasquale) seven times: 13 May, 20 June, 14 and 16 November 2013 ($T_0+1.4$ Ms, $T_0+4.7$ Ms, $T_0+17.4$ and $T_0+17.6$ Ms, respectively); 31 May $(T_0+66.1$ Ms), and 12 and 24 December 2015 ($T_0+82.9$ Ms and $T_0+84.0$ Ms, respectively). The science analysis system (sas) version 14.0 was used to reduce the data, and high background periods were excluded from the analysis. Moreover, we used the publicly available Chandra data (PI: Fruchter) obtained at $T_0+25.1$ Ms and $T_0+36.3$ Ms.

In our analysis, we also used the Swift X-ray Telescope (XRT; [11]) data. Swift XRT observed the X-ray afterglow of 130427A up to ≃$15.8$ Ms (≃180 days) after the trigger.

We assumed the XMM-Newton-derived spectral parameters—$\beta =0.79\pm 0.03$ and absorption $N_{\mathrm{H}}=(5.5\pm 0.6)\times {10}^{21}$ cm${}^2$ at $z=0.34$—to translate the measurements from Swift XRT, Chandra, and XMM-Newton to 0.3–10 keV flux units in a consistent fashion. A ten percent uncertainty was added to the errors of the flux data obtained by the three telescopes to account for systematic calibration differences between these instruments.

2. Results

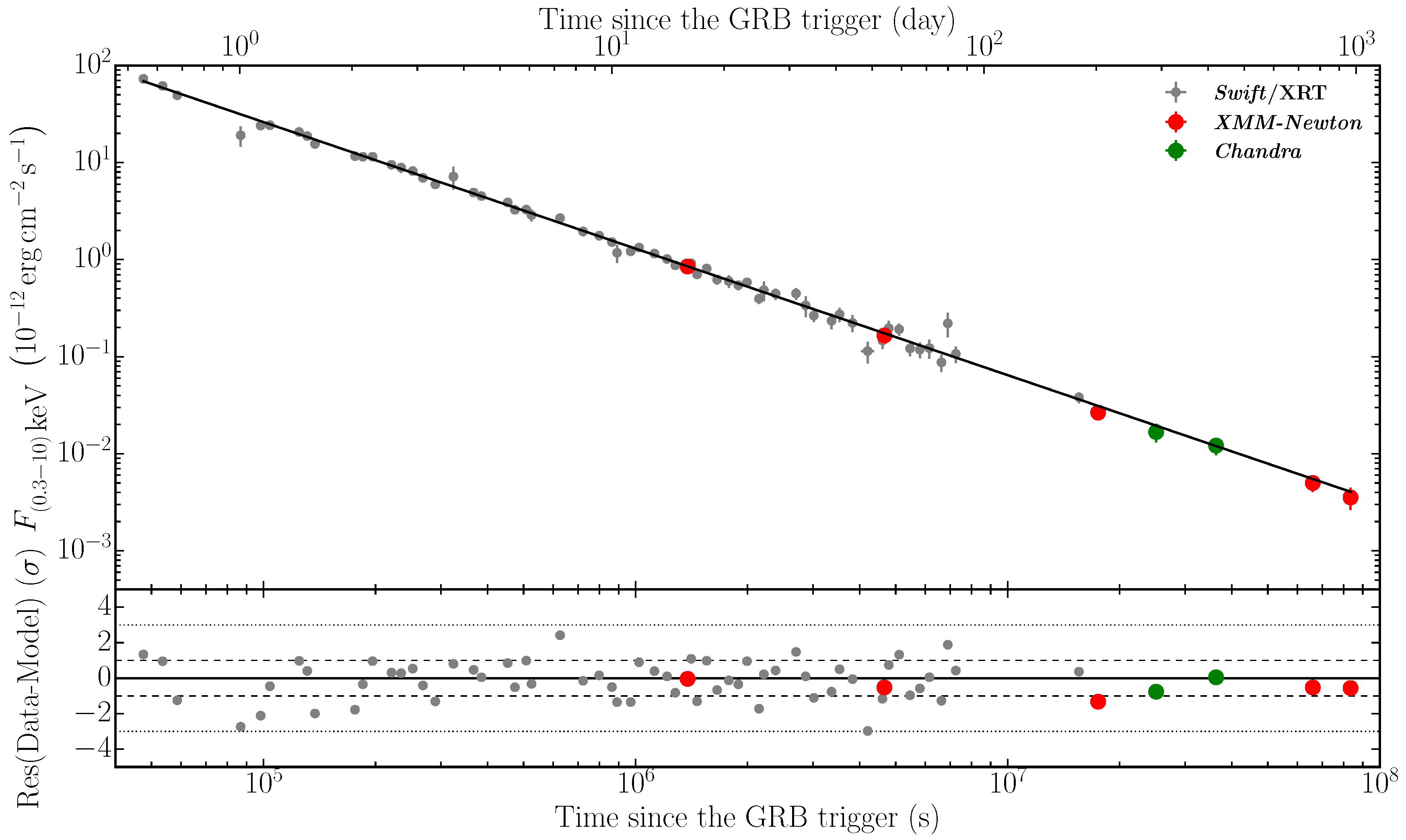
The 83 Ms X-ray Light-Curve of GRB 130427A

We show the X-ray light-curve of GRB 130427A, from 40 ks to 83 Ms, in Figure 1. We have only taken the data from 47 ks into account in our analysis, because we are interested in the late X-ray afterglow; our analysis concentrates on the consistency between models and the late X-ray data.

We find that $\alpha =1.309\pm 0.007$ when fitting this X-ray light-curve with a simple power-law model. This fit model yields ${\chi }^2=75.8$ with 66 degrees of freedom (d.o.f.). The decay index is similar to the previous measurements obtained over a smaller timescale: M14, L13, P14, and K13 determined $\alpha =1.35\pm 0.01$, $\alpha \simeq 1.35$, $\alpha =1.35$, and $\alpha \simeq 1.281\pm 0.004$, respectively, using data up to ≃100 days after the trigger. We have tried one-, two-, and three- broken power-law models to fit the light-curve, but the improvements are not statistically significant. This finding leads us to conclude that a break or multiple breaks are not required by the light-curve.

3. Discussion

The forward shock model [12] predicts phenomena occurring over long timescales in afterglows. Those of interest in our case are:

• Jet break;
• Change of physical parameters of the shock emission: kinetic energy $E_K$ of the ejecta, fraction of energy given to electrons and magnetic field ${ϵ}_{\mathrm{e}}$ and ${ϵ}_{\mathrm{B}}$, fraction of radiating electrons ξ;
• Change of density profile of the circumburst medium.

However, these occurrences put on an appearance in the afterglow light-curve, which depends on the specific environment. In this respect, different authors have made different choices for the modeling. L13 and P14 have adopted a free stellar wind medium, with density of the environment $\rho \propto A{r}^{-2}$, where r is the distance from the centre of the explosion; K13 and V14 settled on a non-standard profile stellar wind, with $\rho \propto A{r}^{-1.4}$ and $\rho \propto A{r}^{-1.7}$, respectively.

3.1. Models in Free Stellar Wind

Both L13 and P14 assumed that the frequency order is ${\nu }_{\mathrm{m}}<{\nu }_{\mathrm{X}}\lesssim {\nu }_{\mathrm{c}}$, where ${\nu }_{\mathrm{m}}$ and ${\nu }_{\mathrm{c}}$ are the synchrotron peak and cooling frequencies, respectively, and ${\nu }_X$ is the X-ray band. The index of power-law energy distribution of radiating electrons $p\simeq 2.2$. Standard formulation predicts that the radius reached by the expanding GRB ejecta is $R=4.8E_{\mathrm{K},\mathrm{iso},54}^{1/2}{A}_{*,-1}^{-1/2}{(t/Ms)}^{1/2}\mathrm{pc}$, where $A_{*}=A/(5\times {10}^{11}\mathrm{g}{\mathrm{cm}}^{-1})$ is the normalization constant for the wind density 1, and we adopt the convention $Q_X\equiv {10}^{X}Q$. Following the classic treatment of Weaver et al. 1977 [13], the stellar wind bubble density profile will be $\rho \propto r^{-2}$ below a certain radius $R_1$, and roughly constant at larger radii, where shocked stellar wind is present. $R_1$ is called the “termination shock”. According to the FS model, when the ejecta enter the constant density medium, the decay slope of the X-ray light curve will be $\alpha =3/4p-3/4=0.9$. With our data, we derive a $95\%$ C.L. lower limit of 48 Ms for any flattening to $\alpha =0.9$ in the X-ray light-curve of 130427A. In other words, at 48 Ms, the ejecta are still moving in the free stellar wind. P14 and L13 find $E_{\mathrm{K},\mathrm{iso},54}=0.3$ and $0.07$ respectively, while both find $A_{*}=\mathbf{0}.\mathbf{003}$. For these values, we have $R_1>105$ (14) and 50 pc (L13). Especially in the first case, the stellar wind bubble must have been extremely large. Given the low mass loss rate, the only way to explain the large $R_1$ is to assume a very low density of the pre-existing material $n_0$. According to Fryer et al. (2006) [14], $R_1={\dot{M_{-5}}}^{1/3}{n}_{0,2}^{1/2}$, where $\dot{M_{-5}}$ is the mass loss rate in units of ${10}^{-5}$ solar masses year${}^{-1}$. Thus, the lower limits on $R_1$ derived above implies $n_0\lesssim 2\times {10}^{-4}$ cm${}^{-3}$ (P14) and $n_0\lesssim 9\times {10}^{-4}$ cm${}^{-3}$ (L13). These values are far too low for star forming regions, where massive progenitors form. Surveys of HII regions [15,16] yield densities > 1 cm${}^{-3}$. Furthermore, we know that GRB 130427A did not occur outside its host galaxy, as Hubble Space Telescope images show [17]. As previously stated, the X-ray spectrum shows an absorption $N_H=(5.5\pm 0.6)\times {10}^{21}$ cm${}^{-3}$ that is taking place at the redshift of the burst, $z=0.34$. This parameter is significantly different from 0, and points to the presence of some medium around the site of the explosion. This is unlikely to happen if the event occurs outside its host galaxy and/or in a low-density environment. One may wonder whether GRB 130427A occurred in a “super bubble”, blown by a super star cluster. These objects have radii of ∼100’s pc. However, numerical simulations [18,19] and the few existing observations show that super bubbles have roughly constant density inside, unless the the number of OB stars is larger than ∼${10}^5$. This requirement would imply extremely massive star clusters, and the presence of such objects in the local Universe has not been ascertained.

3.2. Models in Non-Standard Stellar Wind

According to K13, the GRB afterglow is a pure synchrotron FS emission, with $p=2.34$ and ${\nu }_{\mathrm{m}}<{\nu }_{\mathrm{X}}<{\nu }_{\mathrm{c}}$. By imposing these conditions and observed X-ray flux at 20 ks, we find that the outflow must have a large isotropic kinetic energy $E_{\mathrm{k},\mathrm{iso}}\simeq {10}^{54}$ erg, while $A_{*}\simeq {10}^{-3}$ g cm${}^{-1.6}$. This corresponds to a very thin wind, with a density of ∼${10}^{-7}$ cm${}^{-3}$ 20 pc from the centre of the explosion. Combined, the values inferred from the modeling imply a very large termination radius, $R_1\gtrsim 150$ pc. So, we have the same problem as in the free stellar wind models.

In the model of V14, we have two jets that produce the observed afterglow emission. A few physical parameters of the two components evolve in different fashions; for example ${ϵ}_{\mathrm{e}}$, ${ϵ}_{\mathrm{B}}$; the parameter ξ is chosen to be less than 1, so that the constraint ${ϵ}_{\mathrm{e}}+{ϵ}_{\mathrm{B}}<1$ can be relaxed. The radius reached by the ejecta is quite unconstrained—$R=(0.07-2)\times {10}^{19}{t}_{\mathrm{d}}^{0.43}$ cm—where $t_{\mathrm{d}}$ is the time in days. Applying our lower limit of 48 Ms for any change from a wind medium to a constant density medium, we find $R=3-100$ pc. Wind bubbles with radii towards the low end of this interval do not need an unusually low density of the pre-existing environment. We infer that the model of V14 could explain our late X-ray data. However, we are concerned that it may do so more by virtue of the indeterminacy of some of its parameters—which makes this model difficult to test—than by any particular merits of the physical scenario which it describes.

3.3. Constant Density Medium and Evolving Parameters

M14 assume that GRB 130427A has a jet break at 37 ks that does not lead to a typically steep post-jet break decay slope because of evolving physical parameters of the shock wave. In particular, M14 conjecture that ${ϵ}_{\mathrm{e}}=0.027\times {(t/0.8d)}^{0.6}$, ${ϵ}_{\mathrm{B}}={10}^{-5}{(t/0.8d)}^{0.5}$, and $\xi ={(t/2d)}^{-0.8}$, where d is the time in days. We note that M14 have considered data up 4.2 Ms; the timescale of our observations is ≃20 times longer. FS theory predicts that ${ϵ}_{\mathrm{e}}$ has a saturation value of $1/3$, which would occur at $4.5$ Ms if the modeling of M14 is true. Beyond this epoch, ${ϵ}_{\mathrm{e}}$ should not change any more. Furthermore, the amount of accelerated electrons would be as low as $\xi \simeq {10}^{-3}$ at the end of our observations. It is difficult to understand why the shock wave should accelerate only such a tiny fraction of electrons. Overall, we believe that the model of M14 has difficulty in explaining how the X-ray afterglow of GRB 130427A has the same decay slope of for several tens of Ms.

3.4. A Basic Constant Density Model

One may wonder whether a simple model in constant density medium—in the context of the FS framework—could explain the X-ray light-curve of GRB 130427A at all.

The FS scenario predicts either $\alpha =3/2\beta$ for ${\nu }_{\mathrm{X}}<{\nu }_{\mathrm{c}}$ or $\alpha =(3\beta +5)/8$ for ${\nu }_{\mathrm{X}}>{\nu }_{\mathrm{c}}$ for spherical expansion in constant density medium. The former is satisfied, albeit at ≃$2.5\sigma$ C.L., while the latter is excluded. However, a fundamental question to ask is whether the required parameters, especially energy, are sensible. The total energy corrected for beaming effect is $E_{\mathrm{tot},\mathrm{corr}}=(E_{\gamma ,\mathrm{iso}}+E_{\mathrm{K},\mathrm{iso}})f_{\mathrm{b}}$, where $f_{\mathrm{b}}={\theta }_{\mathrm{jet}}^2/2$ is the beaming factor and ${\theta }_{\mathrm{jet}}$ is the opening angle of the ejecta. We know that ${\theta }_{\mathrm{jet}}=0.12{\left(\frac{t_{\mathrm{jet},\mathrm{d}}}{1+z}\right)}^{3/8}{\left(\frac{E_{\mathrm{K},53,\mathrm{iso}}}{n}\right)}^{-1/8}\mathrm{rad}$ [20], where n is the density of the circumburst medium in cm${}^{-3}$. Remembering that the efficiency of the conversion of kinetic energy into γ-ray prompt emission energy is $\eta =E_{\gamma }/(E_{\gamma }+E_{\mathrm{K}})$, we derive $E_{\mathrm{tot},\mathrm{corr}}\propto {({\eta }^3-{\eta }^4)}^{-1/4}{n}^{1/4}{E}_{\gamma ,\mathrm{iso}}^{3/4}$. For any given n and $E_{\gamma ,\mathrm{iso}}$, the minimum $E_{\mathrm{tot},\mathrm{corr}}$ is obtained for $\eta =3/4$. Now, fitting our X-ray light-curve of GRB 130427A, we derive a 95% C.L. lower limit on a jet break of $t_{\mathrm{jet}}=61$ Ms. Assuming a very low $n={10}^{-3}$, $\eta =3/4$ (the lower limit on the jet break time), we find that the minimum beaming-corrected total energy associated with GRB 130427A is $E_{\mathrm{tot},\mathrm{corr}}=1.23\times {10}^{53}$ erg, for a beaming angle of ${\theta }_{\mathrm{jet}}=0.47$ rad. The value of $E_{\mathrm{tot},\mathrm{corr}}$ would be the largest ever for a GRB event, being one order of magnitude higher than those of the the most energetic bursts [21]. More typical beamed-corrected energetics of GRBs are ≃${10}^{51}$ erg [22,23].

Are there ways to reduce this large energy requirement? One possibility is that the observer is not placed on the symmetry axis of the jet, but off-axis by a certain angle ${\theta }_{\mathrm{obs}}$. In such a condition, the jet break is expected to be visible basically when the observer sees emission from the “far end” of the outflow; that is, when the Lorentz factor ${\mathrm{\Gamma }}^{-1}\simeq ({\theta }_{\mathrm{jet}}+{\theta }_{\mathrm{obs}})$. This way, ${\theta }_{\mathrm{jet}}$ is lower than that calculated above, and $E_{\mathrm{tot},\mathrm{corr}}$ also diminishes. We find that for ${\theta }_{\mathrm{obs}}=0.4{\theta }_{\mathrm{jet}}$, $E_{\mathrm{tot},\mathrm{corr}}\gtrsim 6.5\times {10}^{52}$ erg. This value is roughly half the amount required in the simplest on-axis model. We note, however, that the above ISM model explains the X-ray LC only, but needs testing against data in frequencies other than the X-ray (see P14 on this point).

Another possibility we have explored is the so called “structured jet” [24,25,26]. In this model, the angular density of energy $dE/d\mathrm{\Omega }$ is not constant throughout the emitting surface of the jet. Instead, the jet has a bright “core region" of opening angle ${\theta }_{\mathrm{c}}$, in which the density of energy is assumed to be constant. This region is supposed to produce the very bright prompt emission of 130427A. Outside this region, the energy angular density decreases as $dE/d\mathrm{\Omega }\propto {\theta }^{-k}$, and produces the decaying afterglow emission. The afterglow decay slope measured implies find $k=0.23$, which is a typical value for this scenario [26], while the temporal lower limit on the jet break implies that the outflow has a minimum opening angle of 0.47 rad. By integrating $dE/d\mathrm{\Omega }$ over the whole angular extension of the structured jet, we derive that $E_{\mathrm{tot},\mathrm{corr}}\gtrsim 1.7\times {10}^{53}$ erg. Thus, the structured jet model is not a solution for the problem of the high energy in the constant density model.

4. Conclusions

We presented XMM-Newton and Chandra observations of the X-ray afterglow of GRB 130427A that span 83 Ms from the trigger. This is the longest follow-up for a cosmological GRB X-ray afterglow. We find that the late X-ray afterglow shows a simple power-law decay with slope $\alpha =1.309\pm 0.007$. No jet break or other change of slope is found.

We tested the durability of models built on data gathered up to ∼100 days from the trigger. Our conclusions are as follows.

• Models in free stellar wind (P14, L13): the radius of the stellar wind bubble should be very large (several tens if not hundreds of parsecs in radius), and especially the density of the pre-existing medium should be as low as ∼${10}^{-4}$ cm${}^{-3}$;
• Models in non-standard stellar wind: density should also be very low (K13), or we have evolving and unconstrained parameters (V14);
• The constant density model of M14 assumes an early jet break, which is not very steep because of evolving physical parameters. However, it is difficult to keep the decay slow this way for 83 Ms.

A basic constant density scenario with an observer on-axis requires $E_{\mathrm{tot},\mathrm{corr}}\gtrsim 1.2\times {10}^{53}$ erg. A structured jet does not ease the problem. However, an off-axis model could still explain X-ray observations with $E_{\mathrm{tot},\mathrm{corr}}\gtrsim 6.5\times {10}^{53}$ erg.

To summarize, our late X-ray observations of 130427A challenge the forward shock models proposed for this exceptional event, because they would require extreme values of parameters involved. The least problematic scenario is off-axis jet in ISM, but even this needs atypical parameters. In conclusion, we showed that late time observations of luminous GRBs can robustly test the theoretical models, and sensitivities of future facilities will push the tests even further. Very interestingly, the X-ray flux of the afterglow of GRB 130427A predicted at the launch of the Athena mission (2028) [27] is on the order of ${10}^{-16}$ erg cm${}^{-2}$ s${}^{-1}$, and will be detectable by Athena itself. This will allow the time scale of observations to be extended by about one order of magnitude.