Exploring the Behaviour of Long Gamma-Ray Bursts with Intrinsic Afterglow Correlations: log L200s−α>200s
Abstract
:1. Introduction
2. Results
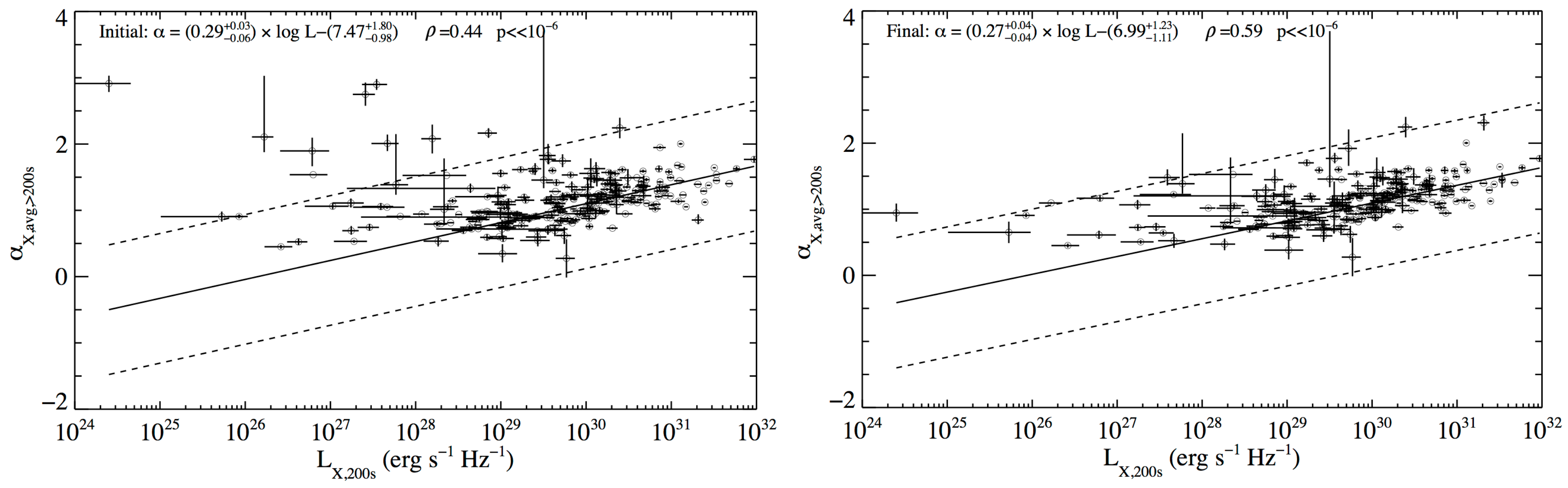
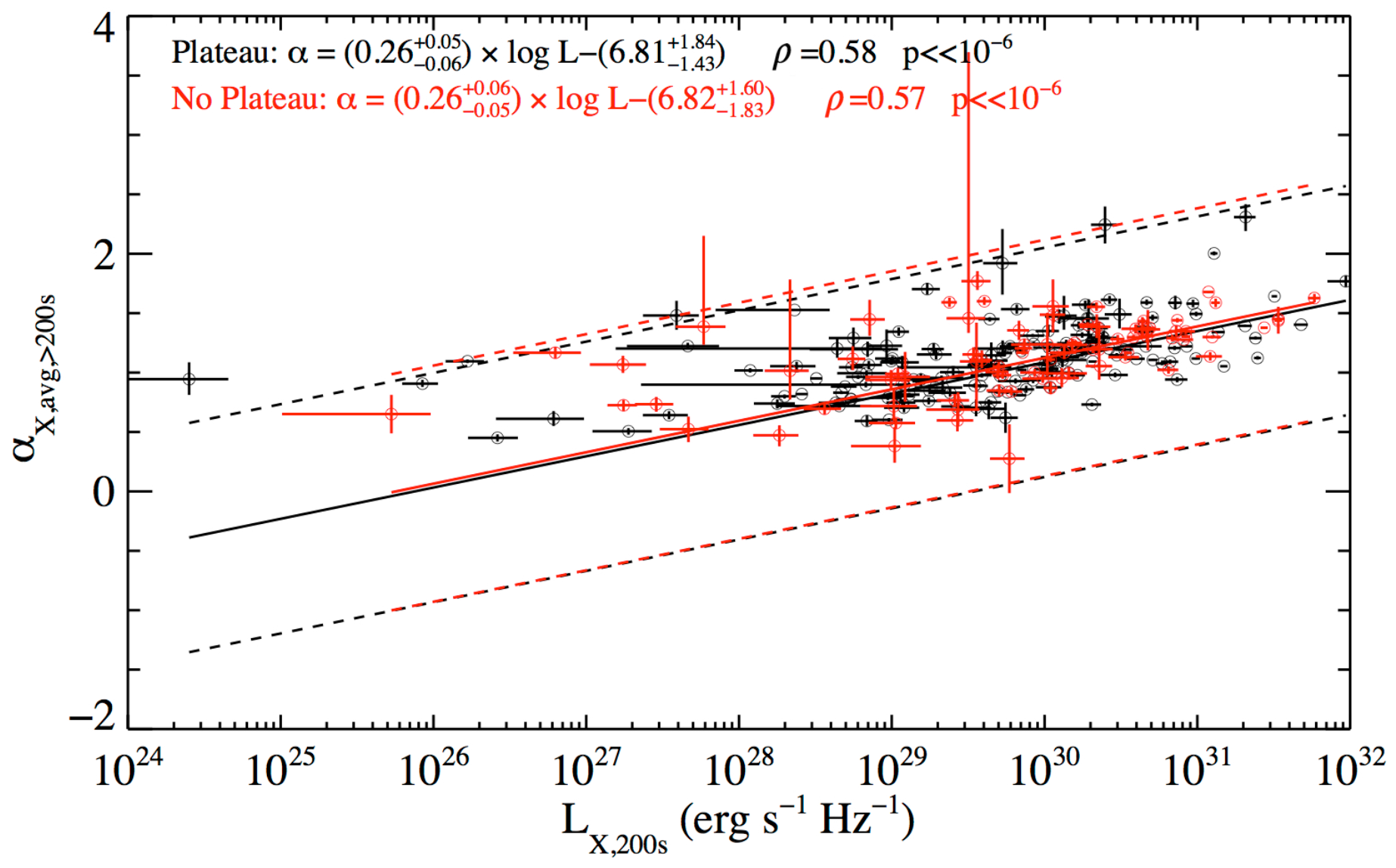
2.1. X-Ray Afterglow Correlation
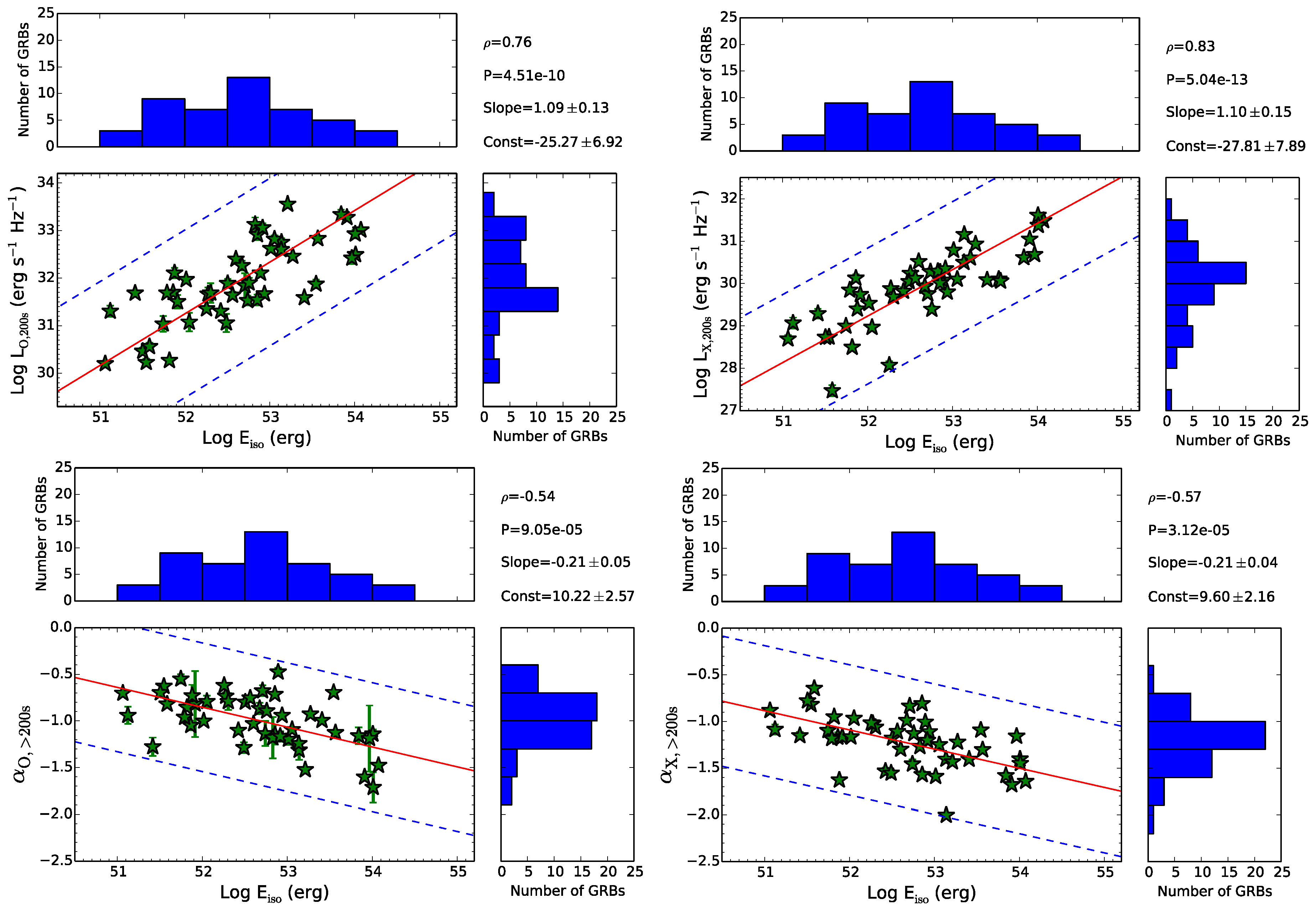
2.2. Comparison of Optical/UV, X-Ray and Prompt Emission
3. Monte Carlo Simulation
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Oates, S.R.; Page, M.J.; De Pasquale, M.; Schady, P.; Breeveld, A.A.; Holland, S.T.; Kuin, N.P.M.; Marshall, F.E. A correlation between the intrinsic brightness and average decay rate of Swift/UVOT gamma-ray burst optical/ultraviolet light curves. Mon. Not. R. Astr. Soc. 2012, 426, L86–L90. [Google Scholar] [CrossRef]
- Racusin, J.L.; Oates, S.R.; de Pasquale, M.; Kocevski, D. A correlation between the intrinsic brightness and average decay rate of gamma-ray burst X-ray afterglow light curves. Astrophys. J. 2016, 826, 45. [Google Scholar] [CrossRef]
- Oates, S.R.; Racusin, J.L.; De Pasquale, M.; Page, M.J.; Castro-Tirado, A.J.; Gorosabel, J.; Smith, P.J.; Breeveld, A.A.; Kuin, N.P.M. Exploring the canonical behaviour of long gamma-ray bursts using an intrinsic multiwavelength afterglow correlation. Mon. Not. R. Astr. Soc. 2015, 453, 4121–4135. [Google Scholar] [CrossRef]
- Panaitescu, A. Jet breaks in the X-ray light-curves of Swift gamma-ray burst afterglows. Mon. Not. R. Astr. Soc. 2007, 380, 374–380. [Google Scholar] [CrossRef]
- Liang, E.; Racusin, J.L.; Zhang, B.; Zhang, B.; Burrows, D.N. A Comprehensive Analysis of Swift XRT Data. III. Jet Break Candidates in X-Ray and Optical Afterglow Light Curves. Astrophys. J. 2008, 675, 528–552. [Google Scholar] [CrossRef]
- Evans, P.A.; Beardmore, A.P.; Page, K.L.; Osborne, J.P.; O’Brien, P.T.; Willingale, R.; Starling, R.L.C.; Burrows, D.N.; Godet, O.; Vetere, L.; et al. Methods and results of an automatic analysis of a complete sample of Swift-XRT observations of GRBs. Mon. Not. R. Astr. Soc. 2009, 397, 1177–1201. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Cardone, V.F.; Capozziello, S. A time-luminosity correlation for γ-ray bursts in the X-rays. Mon. Not. R. Astr. Soc. 2008, 391, L79–L83. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Willingale, R.; Capozziello, S.; Fabrizio Cardone, V.; Ostrowski, M. Discovery of a Tight Correlation for Gamma-ray Burst Afterglows with ”Canonical” Light Curves. Astrophys. J. Lett. 2010, 722, L215–L219. [Google Scholar] [CrossRef]
- Racusin, J.L.; Liang, E.W.; Burrows, D.N.; Falcone, A.; Sakamoto, T.; Zhang, B.B.; Zhang, B.; Evans, P.; Osborne, J. Jet Breaks and Energetics of Swift Gamma-Ray Burst X-Ray Afterglows. Astrophys. J. 2009, 698, 43–74. [Google Scholar] [CrossRef]
- Kann, D.A.; Klose, S.; Zhang, B.; Malesani, D.; Nakar, E.; Pozanenko, A.; Wilson, A.C.; Butler, N.R.; Jakobsson, P.; Schulze, S.; et al. The Afterglows of Swift-era Gamma-ray Bursts. I. Comparing pre-Swift and Swift-era Long/Soft (Type II) GRB Optical Afterglows. Astrophys. J. 2010, 720, 1513–1558. [Google Scholar] [CrossRef]
- D’Avanzo, P.; Salvaterra, R.; Sbarufatti, B.; Nava, L.; Melandri, A.; Bernardini, M.G.; Campana, S.; Covino, S.; Fugazza, D.; Ghirlanda, G.; et al. A complete sample of bright Swift Gamma-ray bursts: X-ray afterglow luminosity and its correlation with the prompt emission. Mon. Not. R. Astr. Soc. 2012, 425, 506–513. [Google Scholar] [CrossRef]
- Margutti, R.; Zaninoni, E.; Bernardini, M.G.; Chincarini, G.; Pasotti, F.; Guidorzi, C.; Angelini, L.; Burrows, D.N.; Capalbi, M.; Evans, P.A.; et al. The prompt-afterglow connection in gamma-ray bursts: A comprehensive statistical analysis of Swift X-ray light curves. Mon. Not. R. Astr. Soc. 2013, 428, 729–742. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T.; Narayan, R. Spectra and Light Curves of Gamma-Ray Burst Afterglows. Astrophys. J. Lett. 1998, 497, L17–L20. [Google Scholar] [CrossRef]
- Panaitescu, A.; Kumar, P. Analytic Light Curves of Gamma-Ray Burst Afterglows: Homogeneous versus Wind External Media. Astrophys. J. 2000, 543, 66–76. [Google Scholar] [CrossRef]
- Zhang, B.; Kobayashi, S.; Mészáros, P. Gamma-Ray Burst Early Optical Afterglows: Implications for the Initial Lorentz Factor and the Central Engine. Astrophys. J. 2003, 595, 950–954. [Google Scholar] [CrossRef]
| Parameters | Spearman Rank | Null | —Best Fit Linear Regression— | ||
|---|---|---|---|---|---|
| -axis | -axis | Coefficient | Hypothesis | Slope | Constant |
| 0.81 (0.05) | 5.26 × 10−12 | 0.91 ± 0.22 | 1.04 ± 6.94 | ||
| 0.77 (0.07) | 1.10 × 10−10 | 0.97 ± 0.10 | −0.25 ± 0.09 | ||
| −0.58 (0.11) | 1.90 × 10−5 | −0.28 ± 0.04 | 7.72 ± 1.31 | ||
| −0.69 (0.09) | 8.03 × 10−8 | −0.26 ± 0.05 | 6.71 ± 1.39 | ||
| −0.60 (0.12) | 6.87 × 10−6 | −0.29 ± 0.03 | 8.13 ± 1.08 | ||
| −0.65 (0.10) | 5.58 × 10−7 | −0.32 ± 0.06 | 8.70 ± 1.68 | ||
| Parameters | Simulated Spearman | —Best Fit Linear Regression for Simulation— | ||
|---|---|---|---|---|
| -axis | -axis | Rank Coefficient | Slope | Constant |
| 0.92 ± 0.02 | 0.82 ± 0.04 | 3.76 ± 1.25 | ||
| 0.74 ± 0.06 | 1.10 ± 0.15 | −0.04 ± 0.17 | ||
| −0.30 ± 0.14 | −0.04 ± 0.02 | 0.31 ± 0.65 | ||
| −0.20 ± 0.14 | −0.04 ± 0.03 | −0.10 ± 0.78 | ||
| −0.06 ± 0.15 | −0.03 ± 0.06 | 0.32 ± 2.91 | ||
| −0.09 ± 0.15 | −0.04 ± 0.06 | 0.76 ± 3.13 | ||
| 0.51 ± 0.11 | 4.43 ± 1.03 | −200.76 ± 54.10 | ||
| 0.54 ± 0.11 | 3.28 ± 0.71 | −142.22 ± 37.33 | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oates, S.R.; Racusin, J.L.; De Pasquale, M.; Kocevski, D.; Page, M.J.; Castro-Tirado, A.J.; Gorosabel, J.; Smith, P.J.; Breeveld, A.A.; Kuin, P.M. Exploring the Behaviour of Long Gamma-Ray Bursts with Intrinsic Afterglow Correlations: log L200s−α>200s. Galaxies 2017, 5, 4. https://doi.org/10.3390/galaxies5010004
Oates SR, Racusin JL, De Pasquale M, Kocevski D, Page MJ, Castro-Tirado AJ, Gorosabel J, Smith PJ, Breeveld AA, Kuin PM. Exploring the Behaviour of Long Gamma-Ray Bursts with Intrinsic Afterglow Correlations: log L200s−α>200s. Galaxies. 2017; 5(1):4. https://doi.org/10.3390/galaxies5010004
Chicago/Turabian StyleOates, Samantha R., Judith L. Racusin, Massimilliano De Pasquale, Daniel Kocevski, Mathew J. Page, Alberto J. Castro-Tirado, Javier Gorosabel, Philip J. Smith, Alice A. Breeveld, and Paul M. Kuin. 2017. "Exploring the Behaviour of Long Gamma-Ray Bursts with Intrinsic Afterglow Correlations: log L200s−α>200s" Galaxies 5, no. 1: 4. https://doi.org/10.3390/galaxies5010004
APA StyleOates, S. R., Racusin, J. L., De Pasquale, M., Kocevski, D., Page, M. J., Castro-Tirado, A. J., Gorosabel, J., Smith, P. J., Breeveld, A. A., & Kuin, P. M. (2017). Exploring the Behaviour of Long Gamma-Ray Bursts with Intrinsic Afterglow Correlations: log L200s−α>200s. Galaxies, 5(1), 4. https://doi.org/10.3390/galaxies5010004





