The Statistical Study of the Daily Fermi Light Curves of 130 Sources
Abstract
:1. Introduction
2. Data and Analysis
2.1. Data and Preprocessing
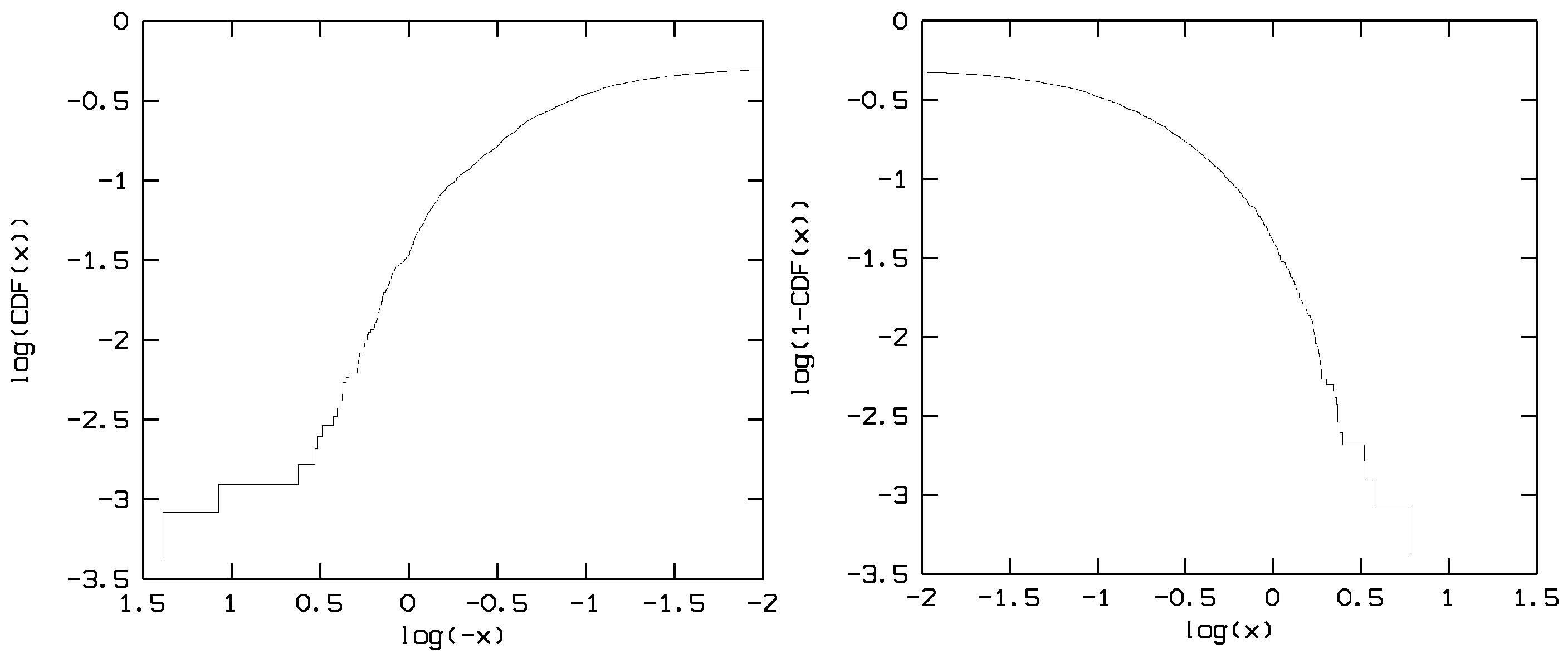
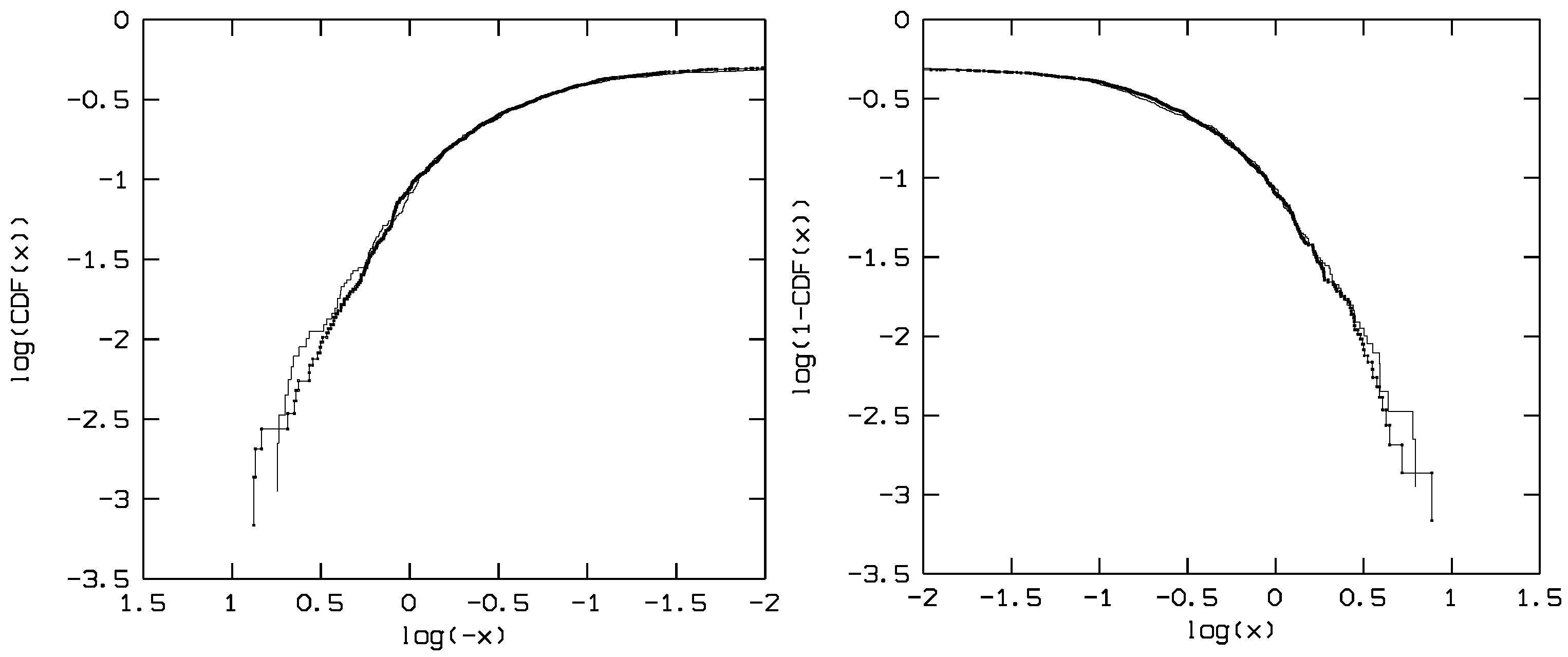
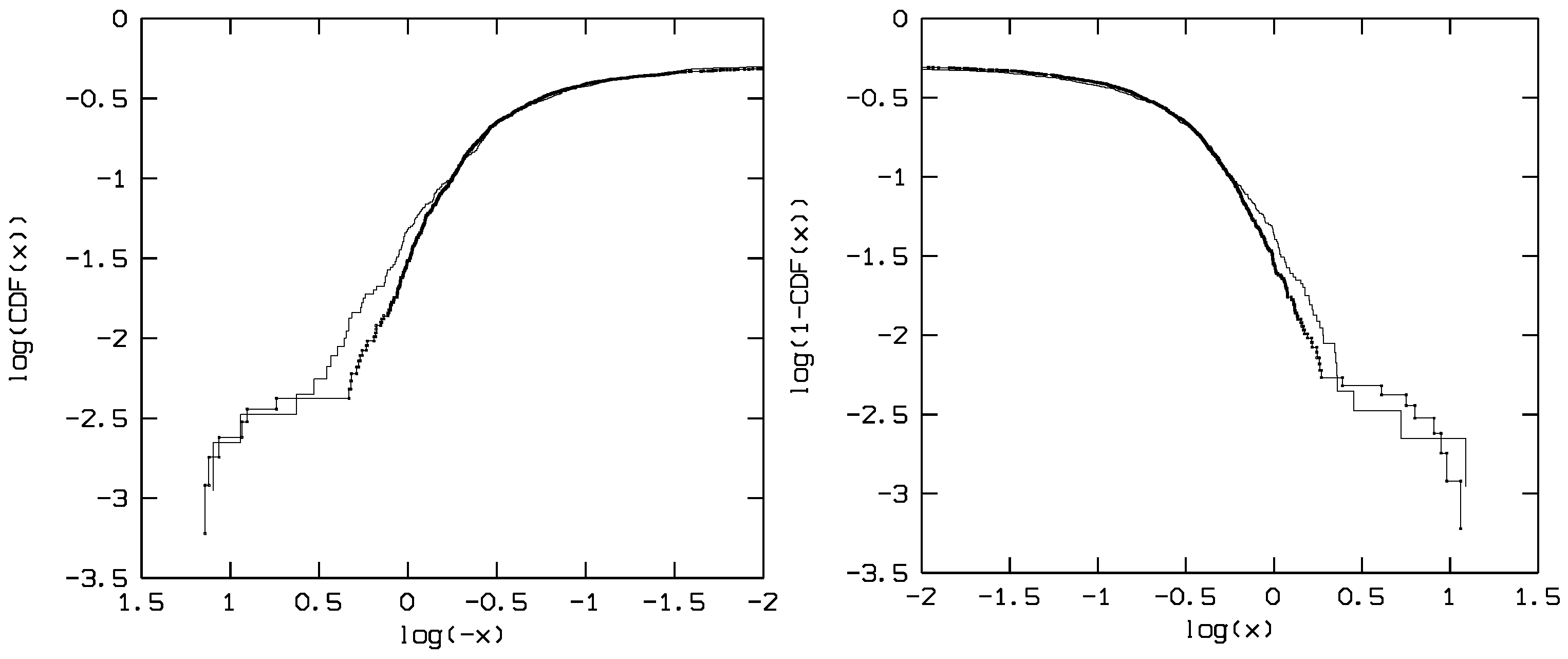
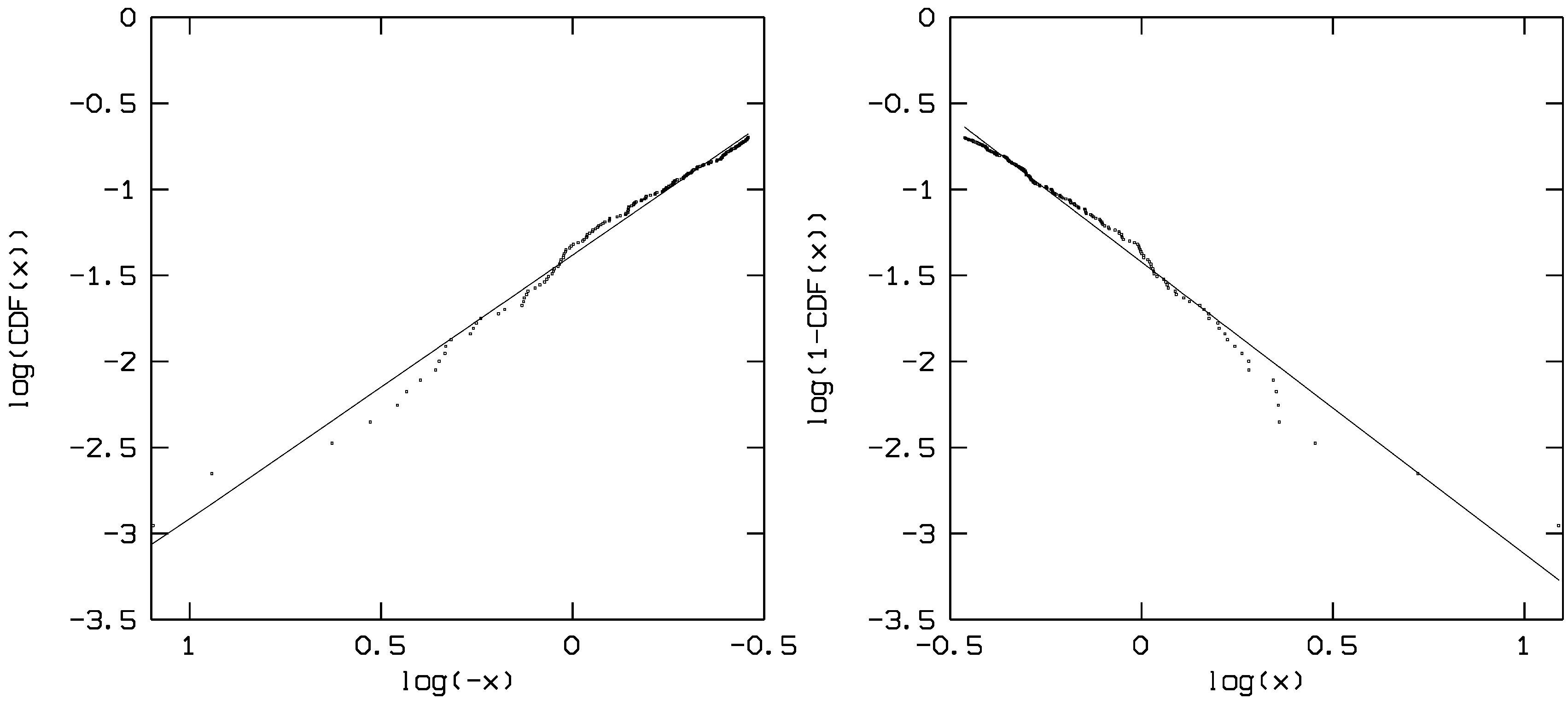
2.2. Test and Pairwise Comparison
3. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fan, J.H.; Xie, G.Z.; Lin, R.G.; Qin, Y.P.; Li, K.H.; Zhang, X. The long-term variability of BL Lac object PKS 0735+178. Astron. Astrophys. Supp. 1997, 125, 525–528. [Google Scholar] [CrossRef]
- Fan, J.H.; Xie, G.Z.; Pecontal, E.; Pecontal, A.; Copin, Y. Historic light curve and long-term optical variation of BL Lacertae 2200+420. Astrophys. J. 1998, 507, 173–178. [Google Scholar] [CrossRef]
- Fan, J.H.; Xie, G.Z.; Adam, G.; Copin, Y.; Lin, R.G.; Bai, J.M.; Qin, Y.P. Long-term Variation of AGNs. BL Lac Phenom. 1999, 159, 99. [Google Scholar]
- Fan, J.H.; Lin, R.G. Optical Variability and Periodicity Analysis for Blazars. I. Light Curves for Radio-selected BL Lacertae Objects. Astrophys. J. 2000, 537, 101–122. [Google Scholar] [CrossRef]
- Fan, J.H.; Lin, R.G.; Xie, G.Z.; Zhang, L.; Mei, D.C.; Su, C.Y.; Peng, Z.M. Optical periodicity analysis for radio selected BL Lacertae objects (RBLs). Astron. Astrophys. 2002, 381, 1–5. [Google Scholar] [CrossRef]
- Fan, J.H. Optical variability of Blazars. Chin. J Astron. Astrophys. 2005, 5, 213–223. [Google Scholar] [CrossRef]
- Fan, J.H.; Liu, Y.; Yuan, Y.H.; Hua, T.X.; Wang, H.G.; Wang, Y.X.; Yang, J.H.; Gupta, A.C.; Li, J.; Zhou, J.L.; et al. Radio variability properties for radio sources. Astron. Astrophys. 2007, 62, 547–552. [Google Scholar] [CrossRef]
- Watson, M.G.; Pounds, K.A.; Elvis, M. Low-frequency divergent X-ray variability in the Seyfert galaxy NGC4051. Nature 1987, 325, 694–696. [Google Scholar]
- Chatterjee, R.; Jorstad, S.G.; Marscher, A.P.; Oh, H.; McHardy, I.M.; Aller, M.F.; Aller, H.D.; Balonek, T.J.; Miller, H.R.; Ryle, W.T.; Tosti, G. Correlated multi-wave band variability in the blazar 3C 279 from 1996 to 2007. Astrophys. J. 2008, 689, 79–94. [Google Scholar] [CrossRef]
- Kataoka, J.; Takahashi, T.; Wagner, S.J.; Iyomoto, N.; Edwards, P.G.; Hayashida, K.; Inoue, S.; Madejski, G.M.; Takahara, F.; Tanihata, C.; Kawai, N. Characteristic x-ray variability of TeV blazars: Probing the link between the jet and the central engine. Astrophys. J. 2001, 560, 659–674. [Google Scholar] [CrossRef]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, W.; Liu, Y.; Fan, J.H. The Statistical Study of the Daily Fermi Light Curves of 130 Sources. Galaxies 2017, 5, 14. https://doi.org/10.3390/galaxies5010014
Cai W, Liu Y, Fan JH. The Statistical Study of the Daily Fermi Light Curves of 130 Sources. Galaxies. 2017; 5(1):14. https://doi.org/10.3390/galaxies5010014
Chicago/Turabian StyleCai, Wei, Yi Liu, and Jun H. Fan. 2017. "The Statistical Study of the Daily Fermi Light Curves of 130 Sources" Galaxies 5, no. 1: 14. https://doi.org/10.3390/galaxies5010014
APA StyleCai, W., Liu, Y., & Fan, J. H. (2017). The Statistical Study of the Daily Fermi Light Curves of 130 Sources. Galaxies, 5(1), 14. https://doi.org/10.3390/galaxies5010014






