Abstract
We derive the thermodynamic products, in particular the area (or entropy) products of for a wide variety of black holes (BHs) in anti-de Sitter (AdS) space. We show by explicit and exact calculations that, for this class of BHs, more complicated functions of the event horizon area and Cauchy horizon area are indeed mass-independent. This mass-independent results indicate that they could turn out to be a “universal” quantity provided that they depend only on the quantized angular momentum, quantized charges, and cosmological constant, etc. Furthermore, these area (or entropy) product relations for several classes of BHs in AdS space gives us strong indication to understanding the nature of non-extremal BH entropy (both inner and outer) at the microscopic level. Moreover, we compute the famous Cosmic Censorship Inequality (which requires Cosmic-Censorship hypothesis) for these classes of BHs in AdS space. Local thermodynamic stability has been discussed for these BHs and under certain conditions, these classes of BHs displayed second order phase transition. The super-entropic BH does not provide any kind of second order phase transition.
1. Introduction
It has been explicitly shown under examination that, for the thermodynamic products for Reissner Nordstrøm (RN) BH, Kerr BH and Kerr-Newman (KN) BH [1], a simple area product of 1 is sufficient to draw a conclusion such that the product of area (or entropy) is a universal quantity. For instance, the product of inner horizon (IH) or Cauchy horizon (CH) area () and outer horizon (OH) or event horizon (EH) area () of a standard four dimensional Kerr-Newman (KN) BH should be [1]
This expression indicates that the IH area and OH area product should depend on the quantized charges and quantized angular momentum but that these are independent of the ADM (Arnowitt-Deser-Misner) mass of the BH space-time. Since this single area product relation is defined on the horizons and independent of the ADM mass parameter, it should be treated as a “universal” relation or “universal” quantity. Alternatively, we can say that a unique product relation/formula only involving horizon quantities could turn out to be universal, but this is the only necessary condition. The “universal” term particularly used here in a sense that when the thermodynamic product of is mass-independent. It may also be noted that the Equation (1) is valid for arbitrary axisymmetric, stationary BH with surrounding matter in an Einstein-Maxwell system when both the charge and angular momentum .
The first motivation comes from the work of Visser [2]. In this work, the author first demonstrated that in case of Schwarzschild-de Sitter (Kottler) BH in four dimensions, the area product of cosmological horizon and EH is not mass independent. Analogously for RN-AdS [2] BH in four dimensions, it has been proved that the product of CH area and EH area is not explicitly mass independent. This means that the mass independence of the area of the two physical horizons ( which is computed perturbatively) is not a generic [2] property.
Since one can not derive a simple area product relation as in Equation (1)2 alternatively, one could derive some complicated function of EH area and CH area for the above described spacetime that might be mass-independent and this mass-independent relation could turn out to be a “universal” quantity. Again these mass independent formulae of two physical horizon areas in spherically symmetry cases are intimately related to the quasi-local quantities which could potentially hold in a wider setting. For example, when we have set in Equation (1), one obtains the area product relation for Kerr BH. In this case ( purely Einstein gravity) a simple area product is sufficient and it only depends on the quantized angular momentum of the BH, as can easily be seen from the exact solution.
This has been extended by Hennig [3] such that for KN-AdS BH, some complicated function of IH and OH area is indeed mass independent and that could turn out to be a universal quantity. Very recently, we have derived a functional relation of area and area for a regular Ayón-Beato and García (ABG) BH [4]. This suggests some complicated function of horizons area that turns out to be universal. However, it is not a simple area product of horizon radii as in the case of RN BH, Kerr BH and KN BH. This has been a very fascinating topic in recent years in the GR (General Relativity) community [1] as well as in the string theory community [5] (see also [6,7,8,9]).
The second motivation comes from the work of Cvetič et al. [5], where the authors argued that if the cosmological constant is quantized then the area (or entropy) product relations for general rotating multicharged BH in four dimensions () and greater than four dimensions () in the case of asymptotically flat and asymptotically AdS space may provide a “looking glass for probing the microscopics of general BHs”. The authors also proposed more specifically, for the BPS (Bogomol’ni-Prasad-Sommerfield) class of BHs in case of string theoretical model, the area products of should be [5]
where is the Planck length. This indicates that the area product should be quantized. Therefore, it is quite interesting to investigate the thermodynamic properties, in particular the area (or entropy) products in AdS space.
However, in this work, we intend to extend our study for several interesting classes of BHs in AdS space for different classes of theory. We derive the formulae for these BHs that involve the area (or entropy) relation in terms of BH horizons and BH parameters with a focus on universal relations that are mass-independent. These mass independent formulae give us a strong indication that they could turn out to be a universal quantity.
Phase transition [10,11] is an important phenomena in BH thermodynamics where the BH changes its phase from stability region to instability region. In case of Schwarzschild-AdS BH, Hawking and Page [10] in 1983 first demonstrated that there exists a first order phase transition between small and large BH. It should be emphasized that the thermodynamic fluctuations and holographic properties of charged AdS BH in the non-extended phase space was first examined by Chamblin et al. [12,13] (see also [14]) where the authors first considered the phase diagram for the canonical (BH charge at infinity) and grand canonical (electric potential at infinity) ensembles. They studied the thermodynamic fluctuations, stability, electric permitivity and also examined the small-large BH phase transitions in the presence of the charge which is quite similar to the liquid-gas phase transitions in fluids which are called the van der Waals-Maxwell liquid-gas phase transitions. They also determined the swallow-tail behaviours of charged AdS BH by computing the free energy. On the other hand, Kubizňák and Mann [11] first showed that second order phase transitions for charged AdS BH could occur in the extended phase space. Furthermore, we compute the specific heat for these class of BHs to examine whether they are locally stable or not. Finally, we examine whether these BHs possesses any kind of second order phase transition or not. This is the another motivation behind this work.
The last and final motivation comes from work of Penrose [15]. In this work, Penrose [15] presented an interesting idea regarding the “Cosmic Censorship Conjecture” (CCC) which is an important issue in the general theory of relativity such that the total ADM (Arnowitt-Deser-Misner) mass M of the Schwarzschild BH spacetime is related to the area of the BH EH by the relation
which is called the Cosmic Censorship Inequality (CCI) or Cosmic Censorship Bound (CCB) [16] and which is a necessary condition for Cosmic-Censorship hypothesis (CCH) [15] (See [17,18,19,20,21]). We derive this inequality for these class of BHs. The physical significance of this inequality is that it states the lower bound on the mass for any time symmetric initial data set which fulfilled the Einstein equations with the negative cosmological constant. Additionally, it also fulfilled the dominant energy condition which possesses no naked singularities. Finally, we consider the thermodynamic properties in the extended phase space [11,22] and in this framework, the cosmological constant is treated as thermodynamic pressure and its conjugate variable as a thermodynamic volume.
First, we consider the static and spherically symmetric solution in Hořava Lifshitz gravity with a cosmological constant. It is a UV complete theory of gravity. It is also a non-relativistic and re-normalizable theory of gravity [23,24,25]. It can be reduced to Einstein’s general theory of relativity in the appropriate limit. This theory manifests a broken Lorentz symmetry in the UV cut-off region.
The fact is that the Horava-Lifshitz gravity is known to suffer from some perturbative instabilities in the IR limit [26,27,28], ultimately due to an extra mode which comes from the explicit breaking of general covariance. Therefore, one of the ways to fix this is to have Horava gravity emerging dynamically in the UV while preserving Lorentz invariance (or rather, not having a preferred foliation) in the IR. This is the proposal behind “covariant renormalizable gravity" proposed in 2009 by Nojiri and Odintsov [29]. The normal GR behaviour is naturally recovered in the IR limit, and the theory is stable [30].
Secondly, we consider the BH solutions in massive gravity [31]. In the holographic framework, “a class of strongly interacting quantum field theory with broken translation symmetry” is described. Massive gravitons are playing key role in this theory. It has a “Lorentz-breaking mass” which is the alternative for “spatial inhomogenities”. Due to this property, it breaks “momentum conservation in the boundary field theory”. Whereas in Einstein’s general theory of relativity, graviton is mass-less. Thus, it is natural to ask the question: does any theory exist where the graviton mass is massive? Vegh [31] obtains a BH solution in AdS space where graviton mass is massive. Thus, it is interesting to study its thermodynamic properties and particularly focus on area (or entropy) product relations which are mass-independent.
Lastly, we consider the another class of BH solution in AdS space where the fields are phantom, which indicates that exotic matter exists. These phantom fields have negative energy density, which will be discussed in Section 4. Finally, we consider another interesting class of BHs which are super-entropic. Their properties are discussed in Section 5.
2. Thermodynamic Product Relations for Hořava Lifshitz BH in AdS Space
The static and spherically symmetric metric of Hořava Lifshitz BH in AdS Space [32] is given by
where the function is defined by
where β and Λ are the integration constant and cosmological constant respectively. Let us choose , where ω is a free parameter that controls the UV characteristics of the theory. When , we get back the solution of Kehagias-Sfetsos (KS) BH [33] in Hořava Lifshitz (HL)3 gravity [23,24,25]. Again we recover the Schwarzschild BH in the IR limit . By inserting , we can rewrite the function as
The BH horizons could be find by setting i.e.,
The roots of the equation can be find by applying Vieta’s theorem:
Case I: Eliminating mass parameter, we obtain only a single mass-independent relation in terms of two horizons:
One can rewrite this formula in terms of area or and it should be
The other mass-independent formula becomes
Case II: For our record, we can write the only mass-dependent relation given by
We find that the CCI for HL BH in AdS Space:
when the inequality becomes equality it is the relation of mass in terms of area. When , we find the CCI for KS BH in HL gravity
where is the area of EH and CH in KS BH [9].
Now let us calculate the specific heat to determine the local thermodynamic stability of the BH. The specific heat is defined by
where,
and
where
where
The local thermodynamic stability requires that and the second order phase transition occurs at , which means the specific heat diverges at that point.
Now if we want to study the thermodynamic behaviour of the HL gravity with AdS space in the extended phase space by considering the cosmological constant as a thermodynamic pressure, i.e., 5 and its conjugate quantity as a thermodynamic volume, i.e., then the ADM mass of an AdS BH may be treated as the enthalpy of AdS space-time, i.e., . Where U is the thermal energy of the system [22]. Therefore, one should write the BH equation of state in the extended phase space as
This is the BH equation of state and the quartic nature of P. It would be interesting if one could study the criticality of this kind of BH by imposing the condition at the point of inflection, i.e.,
This may provide some interesting phase behaviour in the diagram.
Now in the extended phase space, the mass parameter becomes
The thermodynamic volume is defined in the extended phase space as
and it is found to be for HL BH in AdS space:
It is quite interesting that the thermodynamic volume for HL BH in AdS space does not satisfy the formula
that means HL gravity in AdS space violates the naive geometric volume formula. This is the counter example [35,36,37] of any spherically symmetric BH for which the thermodynamic volume is
However, it has been shown that another interesting feature of the thermodynamic volume is called Reverse Isoperimetric Inequality [38] which is defined as
and it is calculated to be for this BH:
It is satisfied for this BH.
Finally, we compute the Gibbs free energy for this AdS BH and it is found to be
This indicates that depends upon both the thermodynamic pressure and coupling constant.
3. Area Products for BH Solutions in Massive Gravity
In this section we would like to derive the thermodynamic product relations, in particular the area product relation for BH solutions in massive gravity [31]. The action for BH solutions in massive gravity in dimension is given by
where m, ℓ and f are graviton mass, AdS radius and reference metric respectively. The reference metric is defined by and represents line element for dimensional Einstein space with constant curvature . Where are the hyperbolic, planar and spherical topology of the BH horizons respectively. The field tensor is given by . and are constants and symmetric polynomials of the eigen values of matrix , i.e.,
More details can be found in Reference [39]. So we do not repeat here. Finally, we obtain the static BH solutions in massive gravity as found in [39] in the form as follows
where the is given by
with the chemical potential at infinity is given by
Since in this work we are restricted in the four dimensional case, thus we choose the parameter . M, Q and are BH mass, BH charge and a positive constant respectively. For convenience, we have set and respectively. These are remnant graviton mass dependent parameters. Also we have set the parameter for BH case. Therefore, the function becomes [40]
The BH horizons correspond to :
To finding the roots we apply the Vieta’s theorem:
Case I:
Since we are interested in finding the mass-independent area product formula in terms of two physical horizons, by eliminating mass parameter from the above Eqs. we have found
If we are working with area of the BH horizons, i.e., then we should find the following mass-independent area functional relation in terms of two BH physical horizons:
Once again the other mass-independent formula becomes
Case II: For our record, we have only single mass dependent area functional relation is given by
The BH temperature in massive gravity is given by
where .
The CCI for this BH should read
Finally the specific heat is given by
The specific heat diverges at
which indicates that the BH in massive gravity shows second order phase transition. This can be seen from the Figure 1.
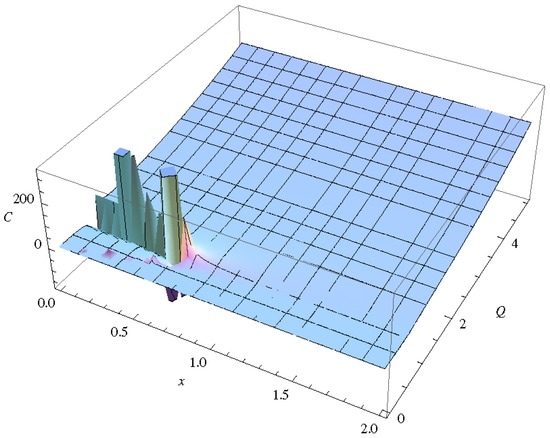
Figure 1.
In this figure, we have plotted the variation of specific heat with horizon radius for massive gravity. Here and .
Now if we consider the extended phase space the mass parameter becomes
The thermodynamic volume is found to be
Unlike HL gravity with AdS space it does satisfied that the thermodynamic volume is equal to the naive geometric volume.
The Gibbs free energy for massive gravity is calculated to be
4. Area Products for Phantom AdS BHs
In this section we would like to compute the thermodynamic product relations of charged phantom spherically symmetric AdS BHs [41]. The main motivation behind this investigation comes from the fact that phantom fields are exotic fields in theoretical physics. This phantom field is due to negative energy density. Current observational data [42] tells us that phantom field can explain the acceleration of our universe. Thus, it is important to study the thermodynamic properties of phantom fields by calculating thermodynamic products, in particular, area (or entropy ) products.
The action for an AdS BH with phantom charge is given by
where the constant η determines the nature of the electro-magnetic (EM) field. For , we obtain the classical EM theory but when , one gets the Maxwell field which is phantom. The spherically symmetric solution of the above action is given by
where the function is
and,
and also M and Q are represents the mass of the BH and charge of the EM source. When , the energy of the EM field to the action becomes negative so it could be interpreted as exotic matter.
Now setting . Therefore, the BH horizons correspond to :
Proceeding analogously, applying Vieta’s theorem we find
Case I:
Again eliminating mass parameter, one finds only single mass-independent relation in terms of two physical horizons:
Similarly, one can rewrite this formula in terms of area :
The other mass-independent formula becomes
Case II:
It may be noted that the only single mass dependent area product relation is
The BH temperature should read
where .
The CCI for phantom BHs should be
The specific heat is calculated to be
The specific heat diverges at
that indicates the phantom BHs possesses second order phase transition. It could be found from the Figure 2.
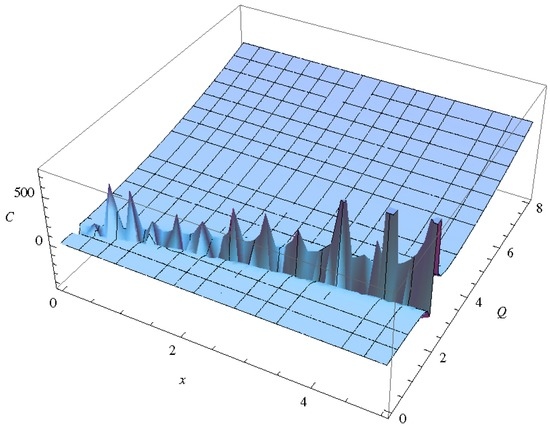
Figure 2.
In this figure, we have plotted the variation of specific heat with horizon radius for phantom AdS BH. Here , and .
In the extended phase space the mass parameter becomes
The thermodynamic volume in this case is found to be
Unlike HL gravity in AdS space, it indeed do satisfied that the thermodynamic volume is equal to the naive geometric volume.
The Gibbs free energy for phantom BH is given by
It may be noted that the product of Gibbs free energy depends upon the mass parameter. In the limit , all the results reduce to for RN-AdS BH and for , one obtain the results for phantom BHs.
5. Area Products for Super-Entropic BHs
This section deals with a new class of spinning AdS BHs having non-compact EHs of finite area in four dimensions and they are the solutions of gauged supergravity [43]. Additionally, their entropy exceeds the maximal bound followed by the conjecture Reverse Isoperimetric Inequality. These types of BHs are called super-entropic BH [44,45,46].
The metric for super-entropic BH [44] (in units where ) is given by
where
The horizon location can be determined by the condition
Applying Vieta’s rule we get
The relevant thermodynamic quantities for the super-entropic BH are
where μ is dimensionless parameter and .
Case I:
Now eliminating the mass parameter, one obtains the mass-independent relation in terms of two physical horizons:
Similarly, one obtains this formula in terms of area :
The other mass-independent formula for super-entropic BHs is
Case II:
The mass dependent area product formula for super-entropic BH should read
The BH temperature should read
where .
The CCI for this BH is calculated to be
The specific heat is found to be
The specific heat diverges for super-entropic BH at the point by solving the following equation
It seems that this equation has no real solution at all and from the Figure 3, it is clear that, in fact, no second order phase transition occurs for four dimensional super-entropic BHs.
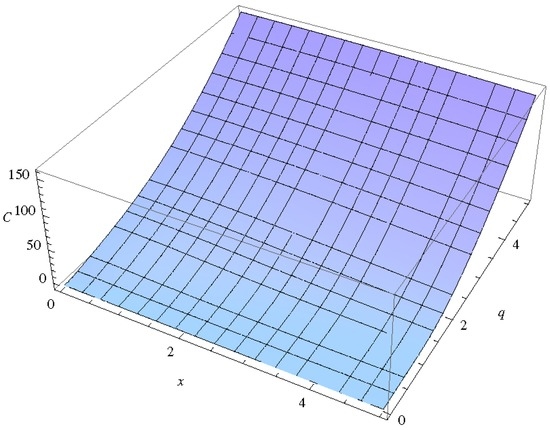
Figure 3.
In this figure, we have plotted the variation of specific heat with horizon radius for super-entropic BH. Here and .
The thermodynamic volume for super-entropic BH is calculated in [44]
which is reminiscent of the naive geometric volume. It follows from the equation is that it is independent of the BH charge. It is also important to note why this BH is called super-entropic. This can be calculated in [44] for :
which means it has not satisfied the condition , this is why it is called super-entropic BH.
If we consider the extended phase space, the mass parameter becomes
Therefore the Gibbs free energy is computed to be
This indicates that the product of Gibbs free energy does depend on the mass parameter, so it is not a mass-independent quantity.
6. Discussion
We studied the intriguing thermodynamic properties for different class of asymptotically spherically symmetric BH solutions in AdS space in Einstein gravity as well as certain modified theories of gravity. The common feature for each AdS BH is that it is quartic in nature for the radial variable. We computed their area (or entropy) product relations. We showed that for each AdS BH, there are more complicated functions of area that are mass-independent and which also relates the different BH parameters.
Also, these mass-independent thermodynamic product relations for multi-horizon BHs have interesting implications in BH thermodynamics. Firstly, these thermodynamic relations signal that they could turn out to be a universal quantity. Secondly, they may provide some insight into the microscopic origin of non-extremal BH entropy (both inner and outer) which is an outstanding issue in quantum theory of gravity. We have also studied the local thermodynamic stability by computing the specific heat at constant pressure. We determined the condition under which the BH possesses second order phase transition. Interestingly, we found that super-entropic BH does not possess any kind of second order phase transition.
Furthermore, we have derived the important inequality in general relativity which is called CCI. This relates the mass and area of the BH. Finally, we computed the Gibbs free energy for each BH. The thermodynamic product relations in case of alternative theories of gravity like gravity can be found in a very recent work [47] by using the extended phase-space formalism.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ansorg, M.; Hennig, J. Inner Cauchy horizon of axisymmetric and stationary black holes with surrounding matter in Einstein-Maxwell theory. Phys. Rev. Lett. 2009, 102, 221102. [Google Scholar] [CrossRef] [PubMed]
- Visser, M. Area products for stationary black hole horizons. Phys. Rev. D 2013, 88, 044014. [Google Scholar] [CrossRef]
- Hennig, J. Geometric relations for rotating and charged AdS black holes. Class. Quant. Grav. 2014, 31, 135005. [Google Scholar] [CrossRef]
- Pradhan, P. Area (or entropy) product formula for a regular black hole. Gen. Relativ. Gravit. 2016, 48, 1–11. [Google Scholar] [CrossRef]
- Cvetič, M.; Gibbons, G.W.; Pope, C.N. Universal Area Product Formulae for Rotating and Charged Black Holes in Four and Higher Dimensions. Phys. Rev. Lett. 2011, 106, 121301. [Google Scholar] [CrossRef] [PubMed]
- Castro, A.; Rodriguez, M.J. Universal properties and the first law of black hole inner mechanics. Phys. Rev. D 2013, 86, 024008. [Google Scholar] [CrossRef]
- Castro, A.; Dehmami, N.; Giribet, G.; Kastor, D. On the universility of inner black hole mechanics and higher curvature gravity. J. High Energy Phys. 2013, 2013, 164. [Google Scholar] [CrossRef]
- Pradhan, P. Black Hole Interior Mass Formula. Eur. Phys. J. C. 2014, 74, 2887. [Google Scholar] [CrossRef]
- Pradhan, P. Thermodynamic product formula for Hořava–Lifshitz black hole. Phys. Lett. B 2015, 747, 64–67. [Google Scholar] [CrossRef]
- Hawking, S.; Page, D.N. Thermodynamics of Black Holes in anti-De Sitter Space. Commun. Math. Phys. 1983, 87, 577. [Google Scholar] [CrossRef]
- Kubizňák, D.; Mann, R.B. P-V criticality of charged AdS black holes. J. High Energy Phys. 2012, 2012, 1207. [Google Scholar] [CrossRef]
- Chamblin, A.; Emparan, R.; Johnson, C.V.; Myers, R.C. Charged AdS black holes and catastrophic holography. Phys. Rev. D 1999, 60, 064018. [Google Scholar] [CrossRef]
- Chamblin, A.; Emparan, R.; Johnson, C.V.; Myers, R.C. Holography, thermodynamics and fluctuations of charged AdS black holes. Phys. Rev. D 1999, 60, 104026. [Google Scholar] [CrossRef]
- Emparan, R.; Johnson, C.V.; Myers, R.C. Surface terms as counterterms in the AdS/CFT correspondence. Phys. Rev. D 1999, 59, 124007. [Google Scholar] [CrossRef]
- Penrose, R. Naked singularities. Ann. N. Y. Acad. Sci. 1973, 224, 125. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Perry, M.J.; Pope, C.N. Bulk/boundary thermodynamic equivalence, and the Bekenstein and cosmic-censorship bounds for rotating charged AdS black holes. Phys. Rev. D 2005, 72, 084028. [Google Scholar] [CrossRef]
- Bray, H.L. Black holes, geometric flows, and the Penrose inequality in general relativity. Not. AMS 2002, 49, 1372–1381. [Google Scholar]
- Bray, H.L.; Piotr, T. Chruściel The Penrose inequality. In The Einstein Equations and the Large Scale Behavior of Gravitational Fields; Birkhǎuser Basel: Basel, Switzerland, 2004; pp. 39–70. [Google Scholar]
- Jang, P.S. The positive energy conjecture and the cosmic censor hypothesis. J. Math. Phys. 1977, 18, 41–44. [Google Scholar] [CrossRef]
- Geroch, R. Energy Extraction. Ann. N. Y. Acad. Sci. 1973, 224, 108–117. [Google Scholar] [CrossRef]
- Gibbons, G.W. Some comments on gravitational entropy and the inverse mean curvature flow. Class. Quant. Grav. 1999, 16, 1677. [Google Scholar] [CrossRef]
- Kastor, D.; Ray, S.; Traschen, J. Enthalpy and the Mechanics of AdS Black Holes. Class. Quant. Grav. 2009, 26, 195011. [Google Scholar] [CrossRef]
- Horava, P. Spectral Dimension of the Universe in Quantum Gravity at a Lifshitz Point. Phys. Rev. Lett. 2009, 102, 161301. [Google Scholar] [CrossRef] [PubMed]
- Horava, P. Quantum Gravity at a Lifshitz Point. Phys. Rev. D 2009, 79, 08400. [Google Scholar] [CrossRef]
- Horava, P. Membranes at Quantum Criticality. J. High Energy Phys. 2009, 2009, 020. [Google Scholar] [CrossRef]
- Blaset, D.; Pujolas, O.; Sibiryakov, S. On the Extra Mode and Inconsistency of Hořava Gravity. J. High Energy Phys. 2009, 2009, 29. [Google Scholar] [CrossRef]
- Charmousis, C.; Niz, G.; Padilla, A.; Saffin, P.M. Strong coupling in Hořava gravity. J. High Energy Phys. 2009, 2009, 070. [Google Scholar] [CrossRef]
- Li, M.; Pang, Y. A Trouble with Hořava-Lifshitz Gravity. J. High Energy Phys. 2009, 2009, 15. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Covariant Hořava-like renormalizable gravity and its FRW cosmology. Phys. Rev. D 2010, 81, 043001. [Google Scholar] [CrossRef]
- Cognola, G.; Myrzakulov, R.; Sebastiani, L.; Vagnozzi, S.; Zerbini, S. Covariant Hořava-like and mimetic Horndeski gravity: Cosmological solutions and perturbations. Class. Quantum Gravity 2016, 33, 225014. [Google Scholar] [CrossRef]
- Vegh, D. Holography without translational symmetry. arXiv, 2013; arXiv:1301.0537. [Google Scholar]
- Park, M.I. The Black Hole and Cosmological Solutions in IR modified Hořava Gravity. J. High Energy Phys. 2009, 2009, 123. [Google Scholar] [CrossRef]
- Kehagias, A. The Black hole and FRW geometries of non-relativistic gravity. Phys. Lett. B 2009, 678, 123. [Google Scholar] [CrossRef]
- Cai, R.G.; Cao, L.M.; Ohta, N. Topological Black Holes in Hořava-Lifshitz Gravity. Phys. Rev. D 2009, 80, 024003. [Google Scholar] [CrossRef]
- Mo, J.X. No P − V criticality for charged topological black holes in Hořava-Lifshitz gravity. Astrophys. Space Sci. 2015, 356, 319. [Google Scholar] [CrossRef]
- Brenna, W.G.; Mann, R.B.; Park, M. Mass and Thermodynamic Volume in Lifshitz Spacetimes. Phys. Rev. D 2015, 92, 044015. [Google Scholar] [CrossRef]
- Pradhan, P. P − V Criticality in Conformal Gravity holography in four Dimensions. arXiv, 2016; arXiv:1603.07750. [Google Scholar]
- Cvetic, M.; Gibbons, G.W.; Kubizňák, D.; Pope, C.N. Black Hole Enthalpy and an Entropy Inequality for the Thermodynamic Volume. Phys. Rev. D 2011, 84, 024037. [Google Scholar] [CrossRef]
- Cai, R.G.; Hu, Y.P.; Pan, Q.Y.; Zhang, Y.L. Thermodynamics of Black Holes in Massive Gravity. Phys. Rev. D 2015, 91, 024032. [Google Scholar] [CrossRef]
- Zeng, X.X.; Zhang, H.; Li, L.F. Phase transition of holographic entanglement entropy in massive gravity. Phys. Lett. B 2016, 756, 170. [Google Scholar] [CrossRef]
- Quevedo, H. Geometrothermodynamics of phantom AdS black holes. Eur. Phys. J. C 2016, 76, 110. [Google Scholar] [CrossRef]
- Dunkle, J.; Komatsu, E.; Nolta, M.R.; Spergel, D.N.; Larson, D.; Hinshaw, G.; Page, L.; Bennett, C.L.; Gold, B.; Jarosik, N.; Weiland, J.L. Five-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Likelihoods and Parameters from the WMAP data. Astrophys. J. Suppl. Ser. 2009, 180, 306. [Google Scholar] [CrossRef]
- Gnecchi, A.; Hristov, K.; Klemm, D.; Toldo, C.; Vaughan, O. Rotating black holes in 4d gauged supergravity. J. High Energy Phys. 2014, 2014, 127. [Google Scholar] [CrossRef]
- Hennigar, R.A.; Mann, R.B.; Kubizňák, D. Entropy Inequality Violations from Ultraspinning Black Holes. Phys. Rev. Lett. 2015, 115, 031101. [Google Scholar] [CrossRef] [PubMed]
- Klemm, D. Four-dimensional black holes with unusual horizons. Phys. Rev. D 2014, 89, 084007. [Google Scholar] [CrossRef]
- Hennigar, R.A.; Kubiznák, D.; Mann, R.B.; Musoke, N. Ultraspinning limits and super-entropic black holes. J. High Energy Phys. 2015, 2015, 96. [Google Scholar] [CrossRef]
- Pradhan, P. Thermodynamic Products in Extended Phase Space. Int. J. Mod. Phys. D 2017, 26, 1750010, Erratum in 2016, 1792001. [Google Scholar] [CrossRef]
- 1. and denote event horizon and Cauchy horizons
- 2.For RN BH, Kerr BH and KN BH, it is very easy to see that the product of is mass-independent. However, for AdS spacetime the task is non-trivial. In this case, a slightly complicated function of is indeed mass-independent. This may be triggered to investigate the various AdS spacetime.
- 3.Within HL gravity, there are some BH solution which is non-asymptotically AdS spacetime [34]. But in our case the BH solution is asymptotically AdS spacetime.
- 4.The entropy in HL gravity is not exactly equal to the area divided by four in addition to that some logarithmic term appears because the entropy computed here by using the formula and by assuming the first law of thermodynamics is always satisfied [34]. In fact, due to some unusual properties of HL gravity the criticality also breaks down [35] in the extended phase space.
- 5.From Equation (5), it follows that the radius of curvature of the asymtotically AdS region is given in terms of the following effective cosmological constant i.e., . It is convenient to define rather .
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).