On the Non-Thermal Energy Content of Cosmic Structures
Abstract
:1. Introduction
2. Results
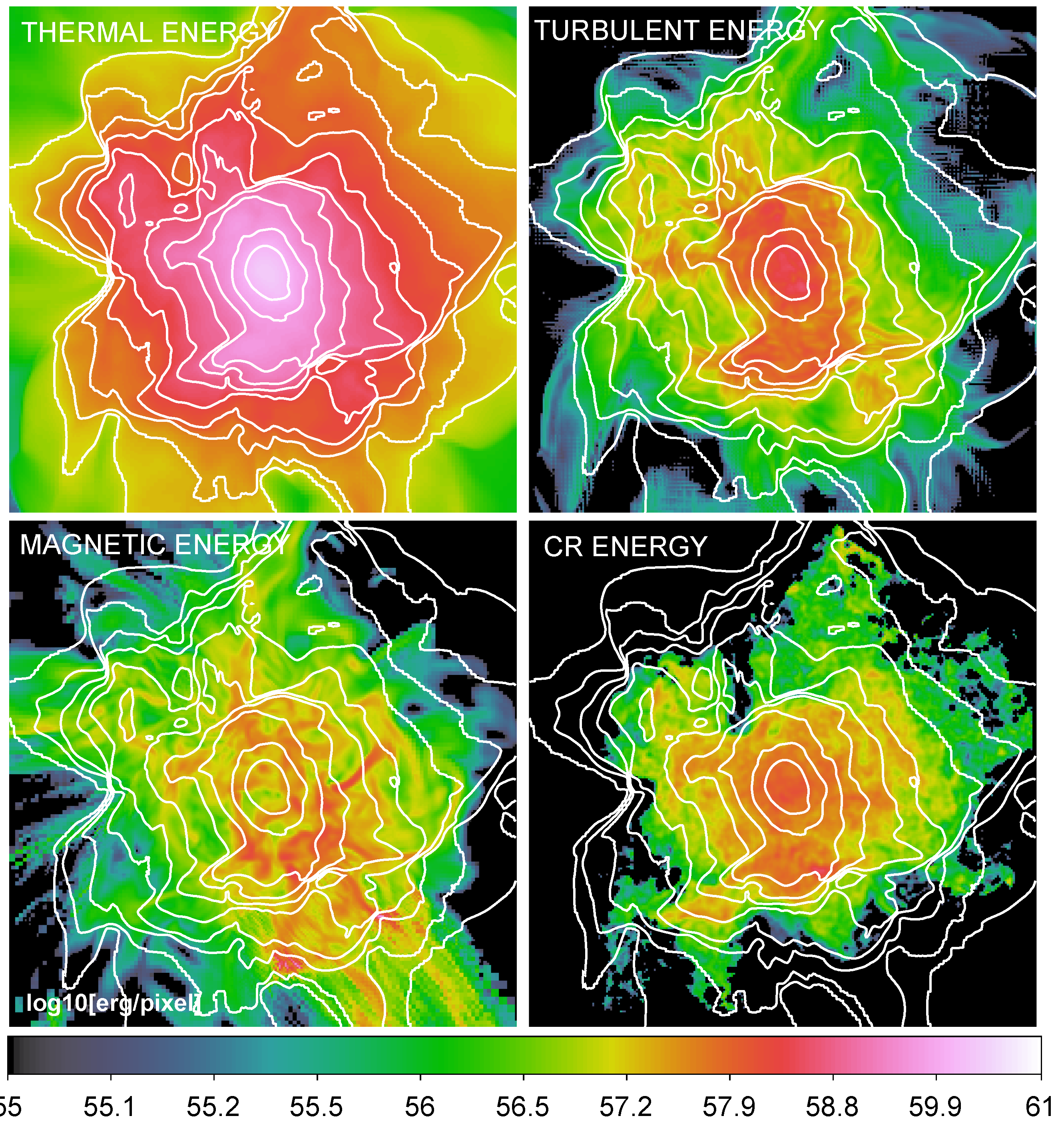
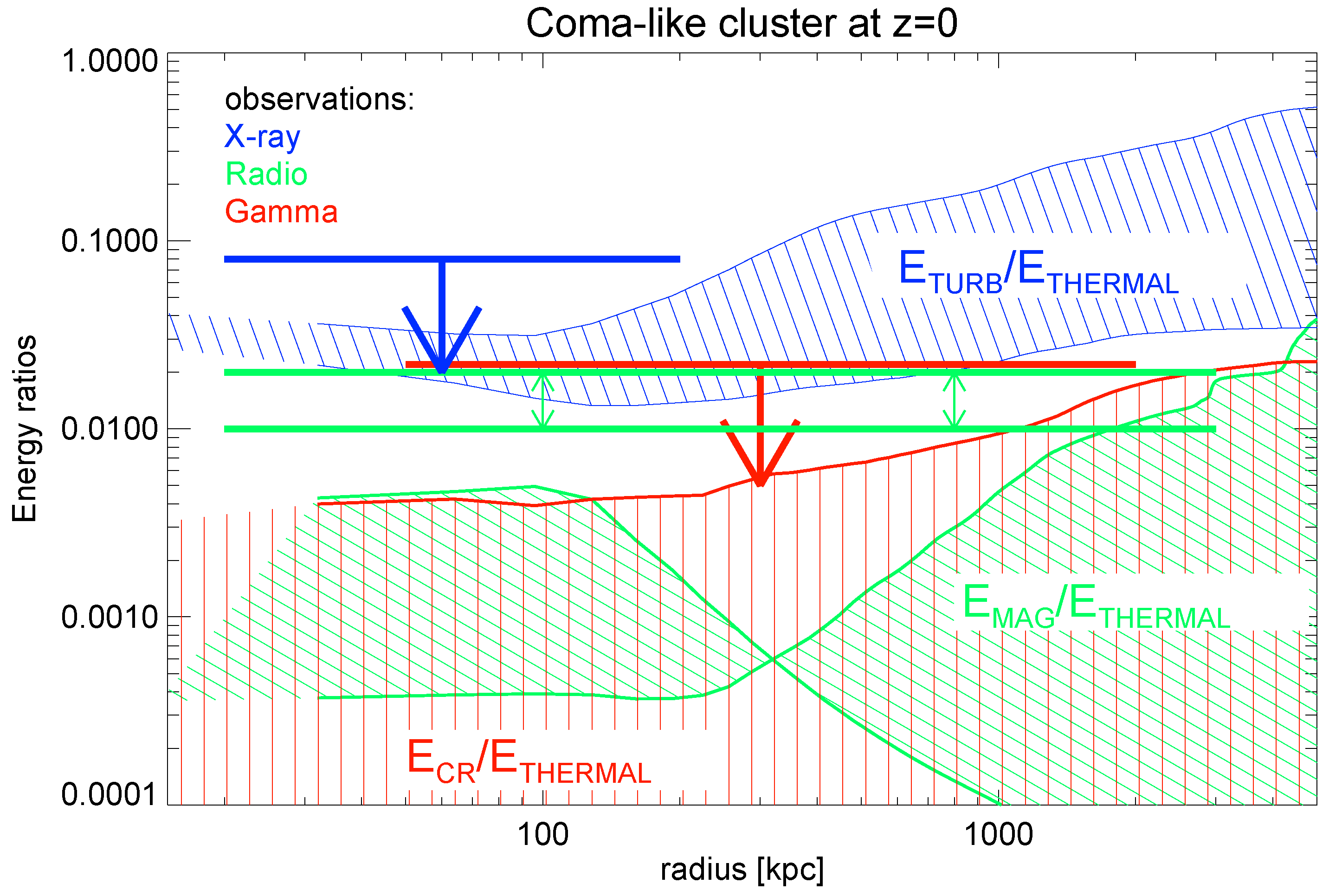
2.1. The Distribution of NT Energy Inside Galaxy Clusters
- The turbulent kinetic energy ranges from the case in which all velocity components larger than are filtered out (lower line), to the upper limit in which all the kinetic energy resolved in the cells is assumed to be turbulent. While our previous studies suggest that the typical outer scale of turbulent motions is of the order of 100–300 kpc, in the presence of large-scale accretion this scale can increase. Hence the hatched region here is meant to bracket the plausible range of ICM turbulence. The turbulent energy support increases with radius, because the driving from infall motions in the outskirts is increasingly supersonic, due to the radial drop in the ICM temperature.
- The magnetic energy ranges from the primordial seed field model (trend increasing with radius) to the trend of the AGN seeding (trend decreasing with radius). In the AGN scenario the magnetic energy drops quickly with radius, as the overall activity by AGN is unable to significantly magnetise large volumes outside of clusters (It shall be noted that also the underlying distribution of the thermal is slightly modified in the astrophysical seeding scenarios, due to the balance of cooling and feedback, which results into a denser cluster core). Both these scenarios are probably underestimating the magnetic energy in the cluster centre, because the finite Reynolds number achieved in our run (, based on , where N is the 1-dimensional size of the high-resolution domain of the simulations, in number of cells, e.g., [48]) likely causes a delayed start of the small-scale dynamo amplification, compared to reality (e.g., [37]). Limited to the single case of the Coma cluster, our primordial seeding run seems to be in better agreement with the observational results of Faraday Rotation (e.g., [49,50]), which suggests a distribution of magnetic energy that scales with the gas thermal energy, and a significant magnetisation in the outskirts (even if limited to a single narrow sector of Coma, e.g., [50]);
- The cosmic-ray energy goes from the upper limit obtained with out post-processing modelling of tracers [39] to zero in case no CR-protons are accelerated by shocks within the cluster. The increasing trend with radius of the CR-energy follows from the sharp increase of the acceleration efficiency as a function of Mach number, which rapidly increase towards cluster outskirts (e.g., [38]).
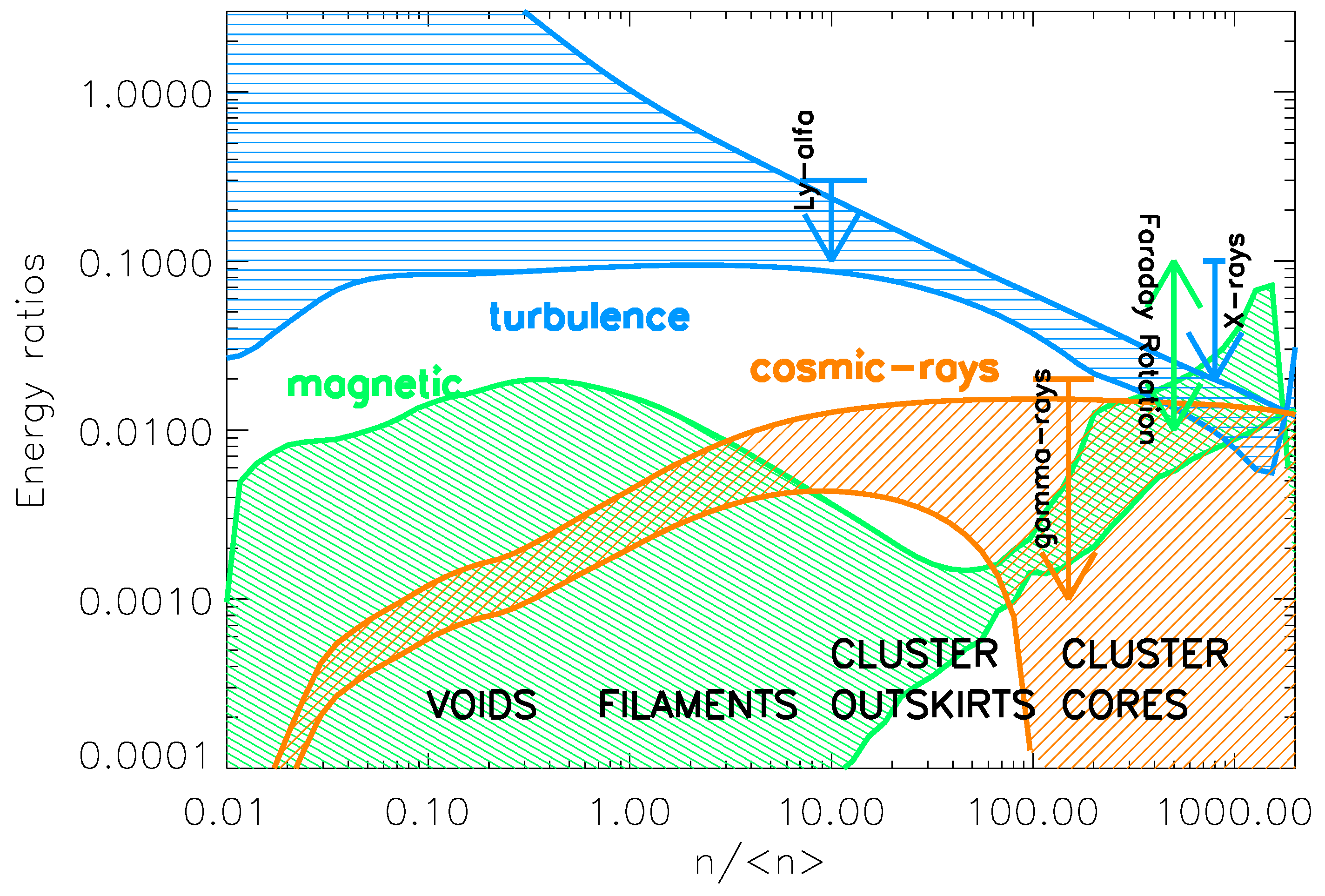
2.2. The Large-Scale Distribution of Non-Thermal Energy
- The turbulent kinetic energy is estimated as in the previous case via small-scale filtering (lower limit), or assuming that the entire post-shock kinetic energy is channeled into turbulence. This second option is particularly significant in the rarefied warm-hot intergalactic medium (WHIM) outside cluster, where our coarse resolution might underestimate vorticity injected by strong accretion shocks [32] . Again, the turbulent kinetic energy budget increases towards lower densities, becoming nearly supersonic at the scale of the linear structures of the Universe (e.g., filaments). At the over density probed through CIV absorption lines in the WHIM, the limits on shear motions at high-z are ∼10% percent of the thermal energy [52], which is at the level of our highest estimate of turbulence. For the cluster cores, the turbulent support is instead in line with present upper limits from X-ray analysis by XMM-Newton observations [53,54], consistent with our estimate at higher resolution in the previous Section.
- The magnetic energy is here measured by combining runs including only primordial seeding at high redshift, or with the additional seeding by AGN at run-time. Outside of clusters the uncertainties are very big because the fields are in the range depending on the seeding model. Even more significantly than in the previous Section, our simulated magnetic fields are found to be smaller than what has been observed through Faraday Rotation (e.g., [49,50,55]), due to the lack of resolution that prevents the formation of a small-scale dynamo. However, in the high density range of our distribution the magnetic energy can be significant, owing to the assumed fixed thermal/magnetic energy per event, which can have a higher impact on low mass systems compared to the previous analysis of the Coma-like cluster.
- The cosmic-ray energy is limited by the requirement of staying within the γ-ray limits by FERMI [27]. While the uncertainties in the acceleration function produce a large uncertainty in the CR energy budget within clusters (owing to the fact that the acceleration efficiency of weak, shocks is very uncertain), the numerical uncertainties are smaller outside clusters, where shocks are predicted to be strong () and the acceleration efficiency is expected to be ∼10%–30% based on the the modelling of strong supernova shocks (e.g., [56]).
3. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mantz, A.; Allen, S.W.; Rapetti, D.; Ebeling, H. The observed growth of massive galaxy clusters—I. Statistical methods and cosmological constraints. Mon. Not. Roy. Astron. Soc. 2010, 406, 1759–1772. [Google Scholar] [CrossRef]
- Kravtsov, A.V.; Borgani, S. Formation of Galaxy Clusters. Ann. Rev. Astron. Astrophys. 2012, 50, 353–409. [Google Scholar] [CrossRef]
- Ryu, D.; Kang, H.; Hallman, E.; Jones, T.W. Cosmological shock waves and their role in the large-scale structure of the universe. Astrophys. J. 2003, 593, 599–610. [Google Scholar] [CrossRef]
- Brüggen, M.; Bykov, A.; Ryu, D.; Röttgering, H. Magnetic Fields, Relativistic Particles, and Shock Waves in Cluster Outskirts. Sci. Space Rev. 2011. [Google Scholar] [CrossRef]
- Subramanian, K.; Shukurov, A.; Haugen, N.E.L. Evolving turbulence and magnetic fields in galaxy clusters. Mon. Not. Roy. Astron. Soc. 2006, 366, 1437–1454. [Google Scholar] [CrossRef]
- Vazza, F.; Brunetti, G.; Gheller, C.; Brunino, R.; Brüggen, M. Massive and refined. II. The statistical properties of turbulent motions in massive galaxy clusters with high spatial resolution. Astron. Astrophys. 2011. [Google Scholar] [CrossRef]
- Miniati, F. The Matryoshka Run: A Eulerian Refinement Strategy to Study the Statistics of Turbulence in Virialized Cosmic Structures. Astrophys. J. 2014, 782, 21. [Google Scholar] [CrossRef]
- Brunetti, G.; Jones, T.W. Cosmic Rays in Galaxy Clusters and Their Nonthermal Emission. Int. J. Mod. Phys. D 2014, 23, 1430007. [Google Scholar] [CrossRef]
- Brüggen, M.; Vazza, F. Turbulence in the Intracluster Medium. In Magnetic Fields in Diffuse Media; Lazarian, A., de Gouveia Dal Pino, E.M., Melioli, C., Eds.; Astrophysics and Space Science Library: Charlottesville, VA, USA, 2015; Volume 407, p. 599. [Google Scholar]
- Bykov, A.M.; Dolag, K.; Durret, F. Cosmological Shock Waves. Sci. Space Rev. 2008, 134, 119–140. [Google Scholar] [CrossRef]
- Dolag, K.; Bykov, A.M.; Diaferio, A. Non-Thermal Processes in Cosmological Simulations. Sci. Space Rev. 2008, 134, 311–335. [Google Scholar] [CrossRef]
- Ferrari, C.; Govoni, F.; Schindler, S.; Bykov, A.M.; Rephaeli, Y. Observations of Extended Radio Emission in Clusters. Sci. Space Rev. 2008, 134, 93–118. [Google Scholar] [CrossRef]
- Feretti, L.; Giovannini, G.; Govoni, F.; Murgia, M. Clusters of galaxies: Observational properties of the diffuse radio emission. Astron. Astrophys. Rev. 2012, 20, 54. [Google Scholar] [CrossRef]
- Rasia, E.; Tormen, G.; Moscardini, L. A dynamical model for the distribution of dark matter and gas in galaxy clusters. Mon. Not. Roy. Astron. Soc. 2004, 351, 237–252. [Google Scholar] [CrossRef]
- Lau, E.T.; Kravtsov, A.V.; Nagai, D. Residual Gas Motions in the Intracluster Medium and Bias in Hydrostatic Measurements of Mass Profiles of Clusters. Astrophys. J. 2009, 705, 1129–1138. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Okabe, N.; Finoguenov, A.; Smith, G.P.; Piffaretti, R.; Valdarnini, R.; Babul, A.; Evrard, A.E.; Mazzotta, P.; Sanderson, A.J.R.; et al. LoCuSS: A Comparison of Cluster Mass Measurements from XMM-Newton and Subaru Testing Deviation from Hydrostatic Equilibrium and Non-thermal Pressure Support. Astrophys. J. 2010, 711, 1033–1043. [Google Scholar] [CrossRef]
- Eckert, D.; Molendi, S.; Vazza, F.; Ettori, S.; Paltani, S. The X-ray/SZ view of the virial region. I. Thermodynamic properties. Astron. Astrophys. 2013, 551, A22. [Google Scholar] [CrossRef]
- Ettori, S.; Dolag, K.; Borgani, S.; Murante, G. The baryon fraction in hydrodynamical simulations of galaxy clusters. Mon. Not. Roy. Astron. Soc. 2006, 365, 1021–1030. [Google Scholar] [CrossRef]
- Battaglia, N.; Bond, J.R.; Pfrommer, C.; Sievers, J.L. On the Cluster Physics of Sunyaev-Zel’dovich and X-ray Surveys. I. The Influence of Feedback, Non-thermal Pressure, and Cluster Shapes on Y-M Scaling Relations. Astrophys. J. 2012, 758, 74. [Google Scholar] [CrossRef]
- Eckert, D.; Ettori, S.; Molendi, S.; Vazza, F.; Paltani, S. The X-ray/SZ view of the virial region. II. Gas mass fraction. Astron. Astrophys. 2013, 551, A23. [Google Scholar] [CrossRef]
- Voit, G.M. Tracing cosmic evolution with clusters of galaxies. Rev. Mod. Phys. 2005, 77, 207–258. [Google Scholar] [CrossRef]
- Vikhlinin, A.; Kravtsov, A.V.; Burenin, R.A.; Ebeling, H.; Forman, W.R.; Hornstrup, A.; Jones, C.; Murray, S.S.; Nagai, D.; Quintana, H.; et al. Chandra Cluster Cosmology Project III: Cosmological Parameter Constraints. Astrophys. J. 2009, 692, 1060–1074. [Google Scholar] [CrossRef]
- Berezinsky, V.S.; Blasi, P.; Ptuskin, V.S. Clusters of Galaxies as Storage Room for Cosmic Rays. Astrophys. J. 1997, 487, 529. [Google Scholar] [CrossRef]
- Völk, H.J.; Atoyan, A.M. Clusters of galaxies: Magnetic fields and nonthermal emission. Astropart. Phys. 1999, 11, 73–82. [Google Scholar] [CrossRef]
- Reimer, O.; Pohl, M.; Sreekumar, P.; Mattox, J.R. EGRET Upper Limits on the High-Energy Gamma-Ray Emission of Galaxy Clusters. Astrophys. J. 2003, 588, 155–164. [Google Scholar] [CrossRef]
- Brunetti, G.; Venturi, T.; Dallacasa, D.; Cassano, R.; Dolag, K.; Giacintucci, S.; Setti, G. Cosmic Rays and Radio Halos in Galaxy Clusters: New Constraints from Radio Observations. Astrophys. J. Lett. 2007, 670, L5–L8. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Albert, A.; Allafort, A.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; et al. Search for Cosmic-Ray-induced Gamma-Ray Emission in Galaxy Clusters. Astrophys. J. 2014, 787, 18. [Google Scholar] [CrossRef]
- Vazza, F.; Eckert, D.; Brüggen, M.; Huber, B. Electron and proton acceleration efficiency by merger shocks in galaxy clusters. Mon. Not. Roy. Astron. Soc. 2015, 451, 2198–2211. [Google Scholar] [CrossRef]
- Vazza, F.; Brüggen, M.; Wittor, D.; Gheller, C.; Eckert, D.; Stubbe, M. Constraining the efficiency of cosmic ray acceleration by cluster shocks. Mon. Not. Roy. Astron. Soc. 2016, 459, 70–83. [Google Scholar] [CrossRef]
- Dolag, K.; Bartelmann, M.; Lesch, H. SPH simulations of magnetic fields in galaxy clusters. Astron. Astrophys. 1999, 348, 351–363. [Google Scholar]
- Schekochihin, A.A.; Cowley, S.C.; Taylor, S.F.; Maron, J.L.; McWilliams, J.C. Simulations of the Small-Scale Turbulent Dynamo. Astrophys. J. 2004, 612, 276–307. [Google Scholar] [CrossRef]
- Ryu, D.; Kang, H.; Cho, J.; Das, S. Turbulence and Magnetic Fields in the Large-Scale Structure of the Universe. Science 2008, 320, 909. [Google Scholar] [CrossRef] [PubMed]
- Cho, J. Origin of Magnetic Field in the Intracluster Medium: Primordial or Astrophysical? Astrophys. J. 2014, 797, 133. [Google Scholar] [CrossRef]
- Vazza, F.; Brüggen, M.; Gheller, C.; Wang, P. On the amplification of magnetic fields in cosmic filaments and galaxy clusters. Mon. Not. Roy. Astron. Soc. 2014, 445, 3706–3722. [Google Scholar] [CrossRef]
- Vazza, F.; Ferrari, C.; Brüggen, M.; Bonafede, A.; Gheller, C.; Wang, P. Forecasts for the detection of the magnetised cosmic web from cosmological simulations. Astron. Astrophys. 2015, 580, A119. [Google Scholar] [CrossRef]
- The Enzo Collaboration; Bryan, G.L.; Norman, M.L.; O’Shea, B.W.; Abel, T.; Wise, J.H.; Turk, M.J.; Reynolds, D.R.; Collins, D.C.; Wang, P.; et al. Enzo: An Adaptive Mesh Refinement Code for Astrophysics. arXiv, 2013; arXiv:astro-ph.IM/1307.2265. [Google Scholar]
- Beresnyak, A.; Miniati, F. Turbulent Amplification and Structure of the Intracluster Magnetic Field. Astrophys. J. 2016, 817, 127. [Google Scholar] [CrossRef]
- Vazza, F.; Brunetti, G.; Gheller, C.; Brunino, R. Massive and refined: A sample of large galaxy clusters simulated at high resolution. I: Thermal gas and properties of shock waves. New Astron. 2010, 15, 695–711. [Google Scholar] [CrossRef]
- Wittor, D.; Vazza, F.; Brüggen, M. Testing cosmic-ray acceleration with radio relics: A high-resolution study using MHD and tracers. arXiv, 2016; arXiv:astro-ph.HE/1610.05305. [Google Scholar]
- Wang, P.; Abel, T.; Kaehler, R. Adaptive mesh fluid simulations on GPU. New Astron. 2010, 15, 581–589. [Google Scholar] [CrossRef]
- Subramanian, K. The Origin, Evolution and Signatures of Primordial Magnetic Fields. arXiv, 2015; arXiv:1504.02311. [Google Scholar]
- Planck Collaboration; Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; et al. Planck 2015 results. XIX. Constraints on primordial magnetic fields. Astron. Astrophys. 2016, 594, A19. [Google Scholar]
- Vazza, F.; Brüggen, M.; Gheller, C. Thermal and non-thermal traces of AGN feedback: Results from cosmological AMR simulations. Mon. Not. Roy. Astron. Soc. 2013, 428, 2366–2388. [Google Scholar] [CrossRef]
- Vazza, F.; Brüggen, M.; Gheller, C.; Brunetti, G. Modelling injection and feedback of cosmic rays in grid-based cosmological simulations: Effects on cluster outskirts. Mon. Not. Roy. Astron. Soc. 2012. [Google Scholar] [CrossRef]
- Caprioli, D.; Spitkovsky, A. Simulations of Ion Acceleration at Non-relativistic Shocks. I. Acceleration Efficiency. Astrophys. J. 2014, 783, 91. [Google Scholar] [CrossRef]
- Kang, H.; Ryu, D. Diffusive Shock Acceleration at Cosmological Shock Waves. Astrophys. J. 2013, 764, 95. [Google Scholar] [CrossRef]
- Vazza, F.; Roediger, E.; Brueggen, M. Turbulence in the ICM from mergers, cool-core sloshing and jets: Results from a new multi-scale filtering approach. arXiv, 2012; arXiv:1202.5882. [Google Scholar]
- Kritsuk, A.G.; Norman, M.L.; Padoan, P. Adaptive Mesh Refinement for Supersonic Molecular Cloud Turbulence. Astrophys. J. Lett. 2006, 638, L25–L28. [Google Scholar] [CrossRef]
- Bonafede, A.; Feretti, L.; Murgia, M.; Govoni, F.; Giovannini, G.; Dallacasa, D.; Dolag, K.; Taylor, G.B. The Coma cluster magnetic field from Faraday rotation measures. Astron. Astrophys. 2010, 513, A30. [Google Scholar] [CrossRef]
- Bonafede, A.; Vazza, F.; Brüggen, M.; Murgia, M.; Govoni, F.; Feretti, L.; Giovannini, G.; Ogrean, G. Measurements and simulation of Faraday rotation across the Coma radio relic. Mon. Not. Roy. Astron. Soc. 2013, 433, 3208–3226. [Google Scholar] [CrossRef]
- Churazov, E.; Vikhlinin, A.; Zhuravleva, I.; Schekochihin, A.; Parrish, I.; Sunyaev, R.; Forman, W.; Böhringer, H.; Randall, S. X-ray surface brightness and gas density fluctuations in the Coma cluster. Mon. Not. Roy. Astron. Soc. 2012, 421, 1123–1135. [Google Scholar] [CrossRef]
- Rauch, M.; Sargent, W.L.W.; Barlow, T.A. Small-Scale Structure at High Redshift. II. Physical Properties of the C IV Absorbing Clouds. Astrophys. J. 2001, 554, 823–840. [Google Scholar] [CrossRef]
- Sanders, J.S.; Fabian, A.C.; Smith, R.K. Constraints on turbulent velocity broadening for a sample of clusters, groups and elliptical galaxies using XMM-Newton. Mon. Not. Roy. Astron. Soc. 2011, 410, 1797–1812. [Google Scholar] [CrossRef]
- Pinto, C.; Sanders, J.S.; Werner, N.; de Plaa, J.; Fabian, A.C.; Zhang, Y.Y.; Kaastra, J.S.; Finoguenov, A.; Ahoranta, J. Chemical Enrichment RGS cluster Sample (CHEERS): Constraints on turbulence. Astron. Astrophys. 2015, 575, A38. [Google Scholar] [CrossRef]
- Murgia, M.; Govoni, F.; Feretti, L.; Giovannini, G.; Dallacasa, D.; Fanti, R.; Taylor, G.B.; Dolag, K. Magnetic fields and Faraday rotation in clusters of galaxies. Astron. Astrophys. 2004, 424, 429–446. [Google Scholar] [CrossRef]
- Caprioli, D. Cosmic-ray acceleration in supernova remnants: Non-linear theory revised. J. Cosmol. Astropart. Phys. 2012, 7, 38. [Google Scholar] [CrossRef]
- Vazza, F.; Brüggen, M.; Gheller, C.; Ferrari, C.; Bonafede, A. Detecting the cosmic web with radio surveys. In Proceedings of the Many Facets of Extragalactic Radio Surveys: Towards New Scientific Challenges, Bologna, Italy, 20–23 October 2015; p. 64.
- Enßlin, T.; Pfrommer, C.; Miniati, F.; Subramanian, K. Cosmic ray transport in galaxy clusters: Implications for radio halos, gamma-ray signatures, and cool core heating. Astron. Astrophys. 2011, 527, A99. [Google Scholar] [CrossRef]
- Brüggen, M. Magnetic field amplification by cosmic ray-driven turbulence—I. Isotropic CR diffusion. Mon. Not. Roy. Astron. Soc. 2013, 436, 294–303. [Google Scholar] [CrossRef]
- Morandi, A.; Limousin, M.; Sayers, J.; Golwala, S.R.; Czakon, N.G.; Pierpaoli, E.; Jullo, E.; Richard, J.; Ameglio, S. X-ray, lensing and Sunyaev-Zel’dovich triaxial analysis of Abell 1835 out to R200. Mon. Not. Roy. Astron. Soc. 2012, 425, 2069–2082. [Google Scholar] [CrossRef]
- AMI Consortium; Rodríguez-Gonzálvez, C.; Shimwell, T.W.; Davies, M.L.; Feroz, F.; Franzen, T.M.O.; Grainge, K.J.B.; Hobson, M.P.; Hurley-Walker, N.; Lasenby, A.N.; et al. Detailed Sunyaev-Zel’dovich study with AMI of 19 LoCuSS galaxy clusters: Masses and temperatures out to the virial radius. Mon. Not. Roy. Astron. Soc. 2012, 425, 162–203. [Google Scholar]
- Fusco-Femiano, R.; Lapi, A. SuperModel Analysis of A1246 and J255: On the Evolution of Galaxy Clusters from High to Low Entropy States. Astrophys. J. 2015, 800, 75. [Google Scholar] [CrossRef]
- Morandi, A.; Sun, M.; Forman, W.; Jones, C. The galaxy cluster outskirts probed by Chandra. Mon. Not. Roy. Astron. Soc. 2015, 450, 2261–2278. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vazza, F.; Wittor, D.; Brüggen, M.; Gheller, C. On the Non-Thermal Energy Content of Cosmic Structures. Galaxies 2016, 4, 60. https://doi.org/10.3390/galaxies4040060
Vazza F, Wittor D, Brüggen M, Gheller C. On the Non-Thermal Energy Content of Cosmic Structures. Galaxies. 2016; 4(4):60. https://doi.org/10.3390/galaxies4040060
Chicago/Turabian StyleVazza, Franco, Denis Wittor, Marcus Brüggen, and Claudio Gheller. 2016. "On the Non-Thermal Energy Content of Cosmic Structures" Galaxies 4, no. 4: 60. https://doi.org/10.3390/galaxies4040060
APA StyleVazza, F., Wittor, D., Brüggen, M., & Gheller, C. (2016). On the Non-Thermal Energy Content of Cosmic Structures. Galaxies, 4(4), 60. https://doi.org/10.3390/galaxies4040060




