1. Introduction
Blazars are highly variable with a high degree of polarized radiation across a wide range of the electromagnetic spectrum [
1,
2,
3]. The understanding of the structure of the field inside a blazar jet, as deduced from polarization observations at radio to optical wavelengths, is closely related to comprehending the formation and propagation of relativistic jets that result from accretion onto supermassive black holes. Many bright
γ-ray blazars that are in the
Fermi-LAT Bright
γ-Ray Source List [
4] have exhibited variations in both their flux and linear polarization [
5,
6,
7]. Degree of polarization is usually higher at optical frequencies than at radio [
8]. This implies that optical emission originates from smaller volumes with more uniform magnetic field compared to radio emission. Such correspondence between the variation in polarization and flux across a wide range of the electromagnetic spectrum can be used to pin down the location of variable emission at all wavebands and shed light on the physical processes responsible for the variability [
7]. But, a largely unexplored aspect of the theoretical understanding of radiation transfer physics in blazar jets has been the magnetic field geometry as revealed by the polarized emission and the connection between the variability in polarization and flux across the spectrum.
In the past, theoretical efforts have been made to calculate high-energy polarization signatures (degree and angle of polarization) for blazar jets [
9]. The authors of [
10] calculated upper limits of polarization signatures of optically thin synchrotron radiation for relativistic jets carrying purely helical magnetic fields. They found that such large-scale magnetic fields could be responsible for polarization properties observed at parsec-scale jets. More recently, the authors of [
11] presented a detailed theoretical analysis of synchrotron polarization signatures for
γ-ray blazars for the case of a shock-in-jet model. Despite such advancements in the theoretical study of polarization signatures of blazar jets a comprehensive study investigating the impact of all possible orientations of the magnetic field on the SEDs and SVPs of blazars is still lacking.
In this paper, we discuss our findings that we have obtained upon extending our MUlti-ZOne Radiation Fedback (MUZORF) model of ([
12], hereafter Paper 2) to address some of the limitations of the models mentioned above. In our study, we include various geometries of the field- parallel, oblique, toroidal- to explore their impact on the time-dependent evolution of the high-energy emission of a generic blazar in terms of its SEDs and SVPs. MUZORF is a time-dependent leptonic jet model that is based on internal shock scenario, which is used to accelerate particles to ultra-relativistic energies ([
13], hereafter Paper 1). It calculates the emission from IR-to-
γ-rays using synchrotron, synchrotron self-Compton (SSC), and external Compton (EC) components for blazar jets. It uses the appropriate photon escape probability functions, for a cylindrical geometry, to accurately evaluate the radiation transfer and include light-travel time delays to calculate the final observed radiation. We calculate EC emission by considering anisotropic radiation fields of the accretion disk, the broad line region (BLR), and the dusty torus (DT) (Paper 2). The evolution of particle and photon populations in the emission region are followed in a time-dependent manner to distances beyond the BLR and into the DT. We assume that before the passage of the shock the magnetic field, of a given geometry, is dynamically unimportant and have not included the effects of the field reverting back to its original strength and direction after the passage of shocks in our study. As shocks pass through their respective emission regions they enhance the ordered magnetic field at their location such that the geometry and strength of this modified field become dynamically important to impact the optically thin synchrotron radiation. The modified synchrotron radiation is further used to calculate the resulting synchrotron self-Compton (SSC) radiation. The radiation from the EC emission is also included in the modified code, with the seed photons assumed to be unpolarized. Throughout this paper, we refer to
α as the photon spectral index such that flux density,
; starred quantities refer to the rest frame of the AGN (lab frame), primed quantities to the comoving frame of the emitting plasma (plasma frame), and unprimed quantities to the observer’s frame; the dimensionless photon energy is denoted by
.
2. Procedure
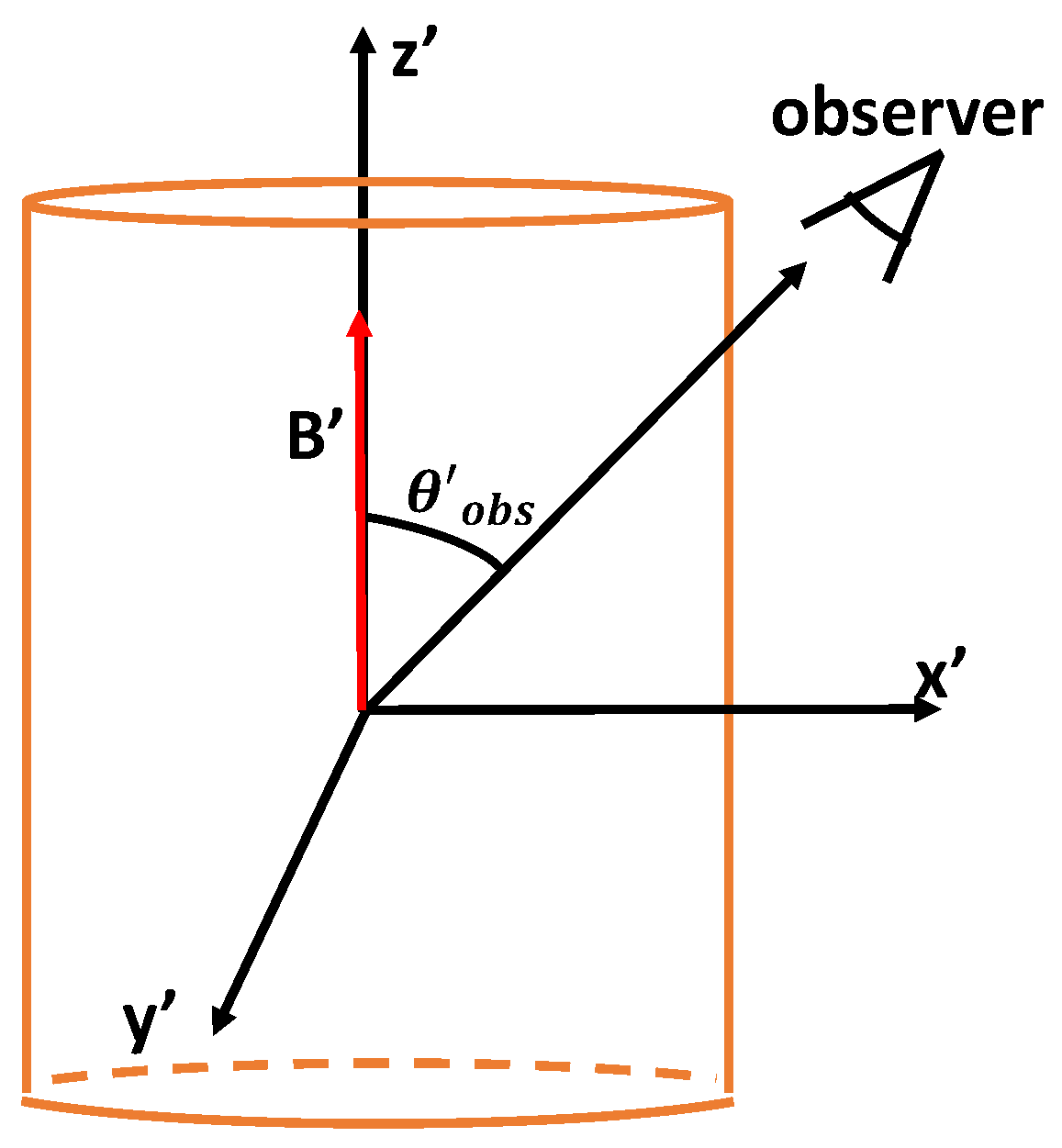
We modify MUZORF to include the effects of magnetic field orientation in the calculation of the optically thin synchrotron radiation. The dependence of the synchrotron emission coefficient,
, on the strength of the magnetic field,
, and the pitch angle,
, that the line of sight (corrected for relativistic aberration) makes with the magnetic field is given by
. We calculate the pitch angle for all geometries of the magnetic field by considering a single cylindrical zone of the emission region. Let
r,
ϕ, and
z be cylindrical coordinates centered on the jet axis and
x,
y, and
z the corresponding rectangular coordinates. Assuming that the jet is being viewed by the observer at an angle
, the observer is located in the
x–
z plane such that the unit vector along the direction of emitted photons is given by
. The bulk velocity of the emission region is directed along the
z-direction with a bulk Lorentz factor of
(see Paper 1) such that the corresponding Doppler boosting factor is given by
, where
. Let
,
, and
be the cylindrical coordinates centered on the jet axis in the plasma frame, such that the comoving magnetic field vector in the jet is denoted by
and
represents a unit vector in the direction of the magnetic field in the plasma frame. We do not consider bulk rotation of the jet in this work. The orientation of the magnetic field with respect to the jet axis, under a particular topology, is assumed to be the same for all zones. Since we are considering a purely ordered magnetic field throughout the emission region our calculations give an upper limit to the impact of the geometry on the SEDs and SVPs of a blazar. We calculate the pitch angle using
, where,
is the unit vector along emitted photons in the plasma frame. Using Lorentz transformation of relativistic wave vector, we can obtain
Magnetic Field Orientation
Figure 1 shows a magnetic field aligned parallel to the jet axis, in the plasma frame, in a single cylindrical zone. The same orientation continues throughout the emission region.
In the case of a parallel geometry the magnetic field vector is given by
. Then,
gives us
This yields the pitch angle for a parallel geometry as,
which can be further reduced to
.
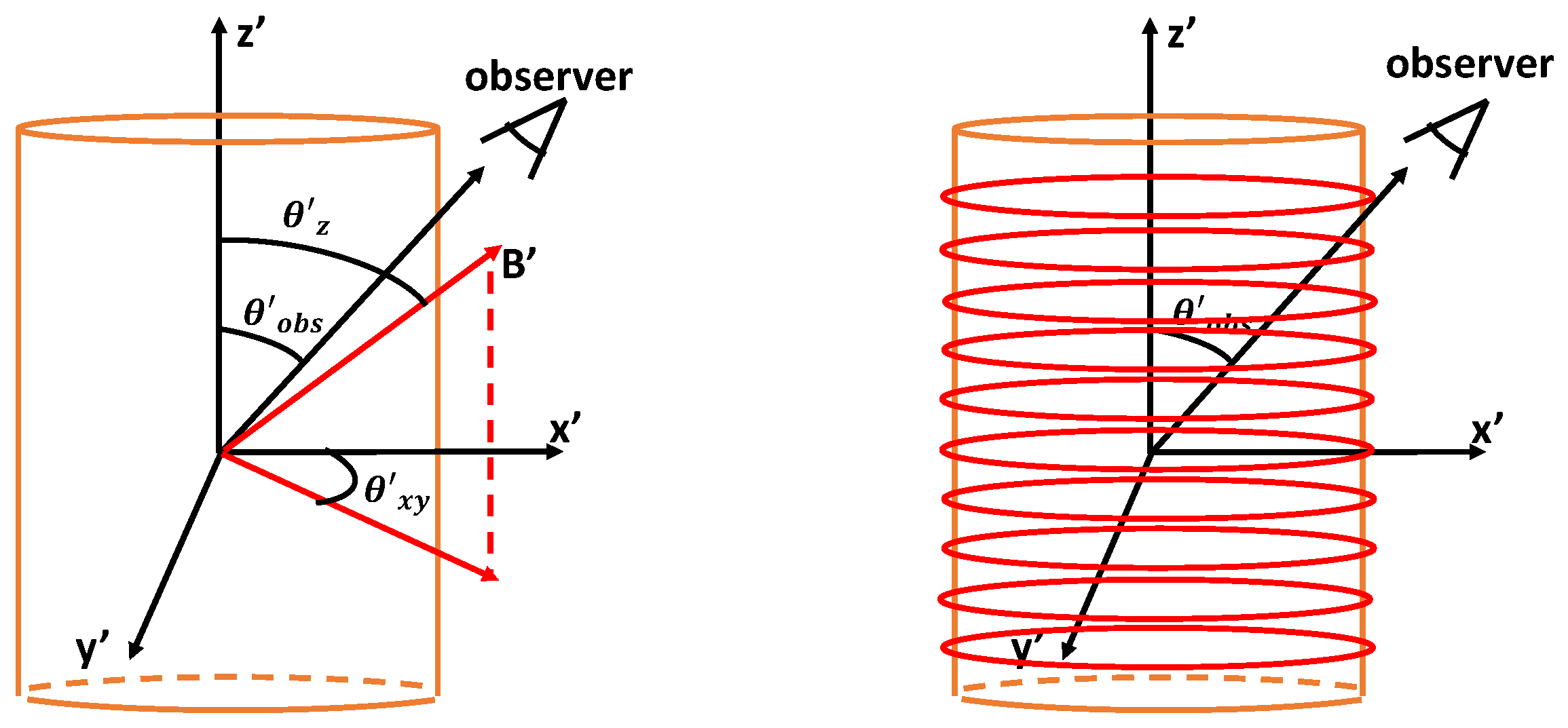
Figure 2 shows the case of an oblique magnetic field aligned at an angle with respect to the jet axis (left panel) and of a purely toroidal field (right panel), in the plasma frame, in a single cylindrical zone. In the case of an oblique geometry, the magnetic field is oriented at an angle
with respect to the jet-axis. The corresponding vector is given by
. Thus, using Equation (
2) we have
and we can obtain the pitch angle for this case using
.
For the case of a purely toroidal magnetic field the corresponding magnetic field vector can be represented as
. Thus using Equation (
2), we obtain the pitch angle for this case to be
In the comoving frame, the synchrotron photon production rate per unit volume in the energy interval
is modified according to the formula
where
and
is as defined in [
14].
The synchrotron self absorption is also modified accordingly. The corresponding energy loss rate and emissivity due to SSC process is calculated according to the prescription given in Paper 1 with the exception that the radiation field available for SSC scattering includes the modified synchrotron emissivity.
3. Parameter Study
The values of input parameters chosen to construct the base set, for conducting the parameter study, are motivated by a fit to the blazar 3C 454.3 for modeling rapid variability on a timescale of ∼1 day. The choice of our input parameters for the base set with a tangled magnetic field, redshift of , and a viewing angle of results in a bulk Lorentz factor (BLF) of and a magnetic field strength of for the emission region. The maximum Lorentz factor of the electron energy distribution is obtained to be while the corresponding minimum Lorentz factors for the forward and reverse emission regions are and respectively. The total widths of the two regions are obtained to be cm and cm, which in turn yield a shock crossing time for the two regions as s and s, respectively. In the observer’s frame, this corresponds to the forward shock leaving the forward emission region in ∼20 h while the reverse shock leaves its respective region in ∼26 h. We set the width and the shock crossing time of each of the emission region such that it is comparable to the variability timescale chosen for our simulations.
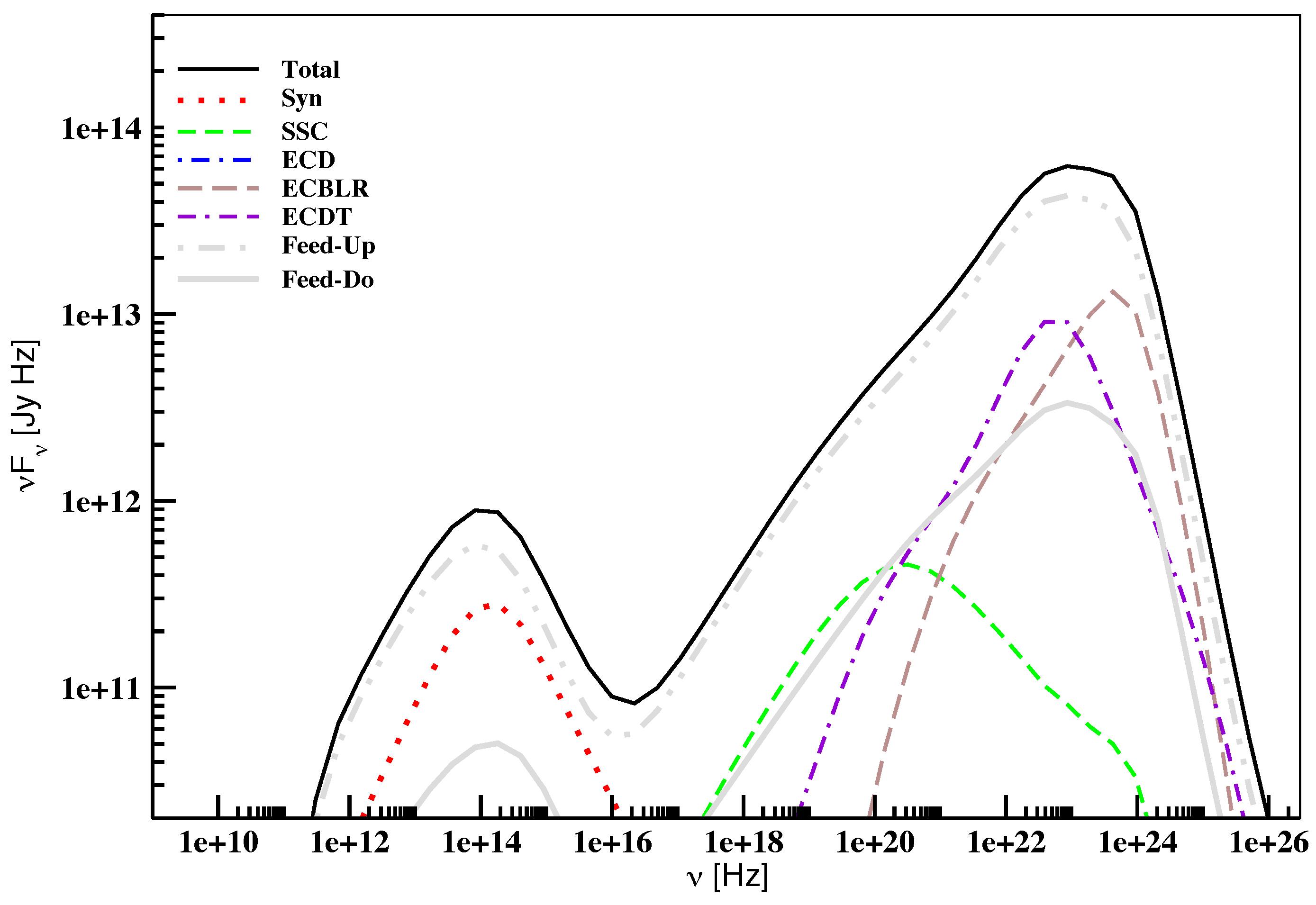
Figure 3 shows the simulated time-averaged SED of the baseline model averaged over a time period of ∼24 h. The overall profile of the SED is governed by various radiative processes- synchrotron, SSC, ECD, ECBLR, ECDT- while the flux level of the SED is guided by the radiative feedback components- forward (Feed-Up) and backward (Feed-Do)- as described in Paper 1. The low-energy component of our baseline model is governed by the synchrotron process and peaks in the near-IR at a frequency of ∼
Hz. It cuts off in the X-rays at ∼5
Hz with the SSC component taking over beyond that till up to about
Hz in the hard X-rays. The ECDT component dominates beyond that till ∼9
Hz in the soft
γ-rays beyond which the high-energy (HE) profile is governed by the ECBLR component into the hard
γ-rays. For the flux level considered in our cases, the ECD component does not play a dominant role. The spectral hardness (SH) of the time-averaged SED is quantified in terms of the photon spectral index. In the X-ray range of 2–10 keV the spectrum is harder with an
On the other hand, the spectrum is softer in the
Fermi range at ∼10 GeV with an
= 2.65.
4. Results
Here, we explore the effects of varying physical parameters that are related to the magnetic field orientation in order to understand their impact on the evolution of SED and SVPs of our generic blazar. For all the cases considered, the simulation run time and the time period over which the SEDs have averaged are the same as that of the base set. The three physical parameters that were varied for this study are the viewing angle (
), the angle that the magnetic field makes in the
–
plane (
), and the angle that the field makes with the
-axis (
).
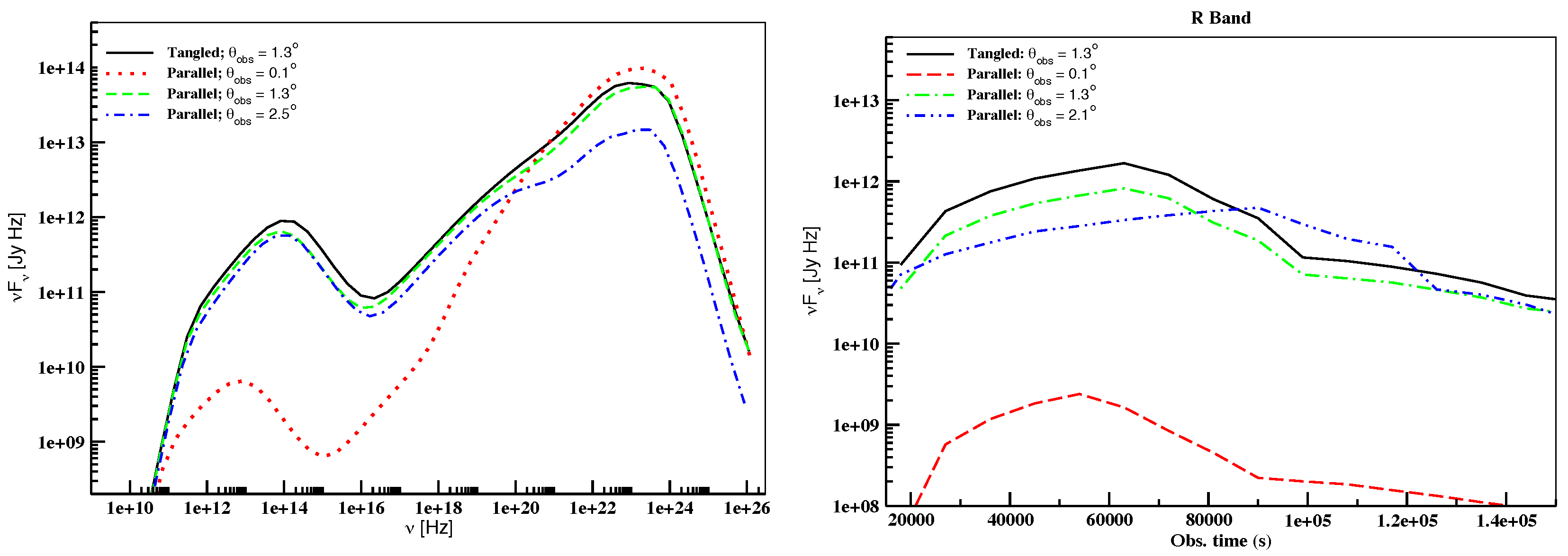
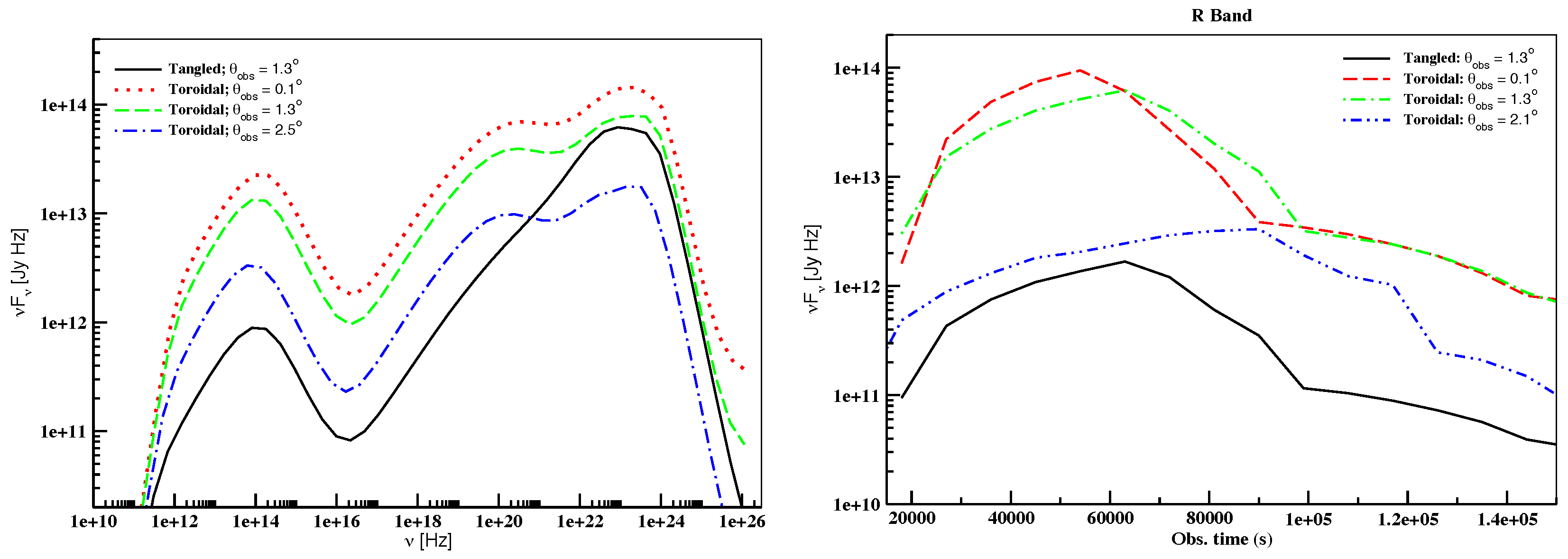
Figure 4 shows the outcome of varying the viewing angle for a parallel geometry on the SEDs (left) and light curves (right) of the generic blazar while
Figure 5 shows the same for a toroidal magnetic field.
As implied by Equation (
4), the value of
is governed by the sine of the viewing angle in the case of a parallel geometry. As a result, the value of the pitch angle reduces with a decrease in the viewing angle that leads to a decline in the synchrotron emission along our line of sight. On the other hand, the HE component of the SED of this generic blazar, which is guided by the EC component, continues to be governed by the Doppler boosting of the radiation in our direction. Thus, for
the synchrotron component goes down while the EC component rises up in flux. The corresponding synchrotron peak frequency,
, and cutoff frequency,
, shift to lower values. On the other hand, for a larger viewing angle of
the EC component is de-boosted in our direction while the synchrotron component is only slightly reduced in flux compared to its baseset counterpart. Hence, the
and
are only slightly affected. Similarly, for the case of the same viewing angle as that of the baseset parameter,
, the synchrotron component decreases slightly according to the value of
while the EC component maintains almost the same level of flux as that of the baseset. Hence, the
shifts slightly to lower values. As far as the SH is concerned, the Fermi range doesn’t get impacted by the parallel geometry of the magnetic field. However, in the X-ray range, a smaller viewing angle increases the hardness of the band. This happens because in the case of
the X-ray range becomes dominated by the rising part of the ECDT instead of the SSC component.
As far as the light curve profiles are concerned, they closely follow that of the baseset when the viewing angle is kept the same. For the sake of brevity, we only show the profile of the optical pulse at the R band. As can be seen from
Figure 4, a decrease or an increase in its value shifts the peaking time of the flare. For a smaller value of the viewing angle the flare profile peaks sooner than its baseset counterpart. This happens because, as explained in Paper 1, the time taken for photons to cover the distance from the far to the near side of the emission region gets shortened in the observer’s frame. Hence, the pulse peaks sooner and lasts for a slightly shorter duration compared to their baseset counterparts. The exact opposite happens for a larger value of the viewing angle.
According to Equation (
6), in the case of a toroidal magnetic field,
has an inverse relationship with the viewing angle. Thus, a smaller value of the viewing angle results in a higher value of
compared to that of a larger viewing angle as long as the viewing angle is within the superluminal cone of the source corresponding to its BLF.
Figure 5 shows the manifestation of this topology on the SEDs and light curves of the generic blazar. As can be seen, the flux level of both the low- and high-energy components is governed by the order in the field along with Doppler boosting in such a way that the EC component is affected the most by de-boosting due to larger viewing angle while the synchrotron component continues to be guided by the geometry of the field. Thus for a lower viewing angle, the
and
shift to higher frequencies but maintain their original values when the viewing angle is kept the same. On the other hand, they shift to lower frequencies for a higher viewing angle. Also, the variation in the flux level of the EC component in comparison to its baseset counterpart, for
, is much more pronounced for a toroidal field. This happens due to the fact that the time-dependent evolution of the electron population in the emission region is dependent on the photon population of the region through radiative cooling. Thus, any change in the synchrotron and SSC photon population brings about a subsequent change in the electron population, which in turn, impacts the EC component. The SH, on the other hand, remains almost the same in both the X-ray and Fermi ranges. As far as the pulse profile is concerned, the amplitude is higher compared to that of the baseset. For the case of
, the R Band pulse profile closely follows that of the baseset but for the other two cases it is guided by boosting effects as explained above. Hence, the peaking time of the pulse is either sooner or later and the duration of the pulse is either smaller or larger depending on the value (small/large) of the viewing angle, respectively.
Figure 6 shows the impact of varying angles
and
on the SEDs of a generic blazar, while keeping the viewing angle constant, for the case of an oblique magnetic field. As shown in
Figure 2, these are the angles that the magnetic field makes in the
x–
y plane and with the
z-axis, respectively, in the frame of the plasma. The figure shows that depending on the obliquity of the magnetic field with respect to the
-axis, the combination of
and
values could result in a scenario where the synchrotron emission is substantially low compared to its counterpart for a tangled field geometry (see the left plot of
Figure 6). For the set of input parameters considered here, this scenario is obtained for a combination of
and
where both the synchrotron and SSC emission decline but the EC emission stays the same. As the obliquity of the field increases for a fixed value of
(see the right plot of
Figure 6), the spread of the synchrotron component of SEDs decreases and converges for higher values of
, such as
&
. This is expected because, as
changes from
to
the field becomes more and more transverse in nature thereby almost reproducing the case of a transverse geometry. Here, we would like to point out that changing the viewing angle while keeping the obliquity of the magnetic field the same will also yield similar results. This, in turn, would make it difficult to distinguish between the two scenarios when analyzing the SEDs alone. Hence, an in-depth analysis of the SVPs would be required in order to separate the two cases.
5. Discussion and Conclusions
The objective of our study is to comprehend the signatures of the magnetic field orientation in blazar jet emission by understanding its impact on some of the observational properties of blazars, such as SEDs and SVPs. The impact can be quantified in terms of the change in the SH, Compton dominance [CD] (ratio of EC and synchrotron flux), and the location of peak synchrotron-flux- and cutoff- frequency. Such a study provides us with an understanding of how the mixture of the two fields would behave in a real source. This study is the first step in the process of exploring the combined effects of the ordered and disordered magnetic fields on the SEDs and SVPs of blazars, and on understanding the intrinsic parameter differences between various blazar subclasses that could arise from the orienation of the magnetic field in the jet.
In order to achieve that goal, we have investigated the effects of a purely ordered field for various topologies, that can exist inside a jet, and have compared the outcome of every field geometry to that of a randomly oriented magnetic field. In this work, we have assumed the magnetic field to be dynamically unimportant before the passage of the shocks. As a result, the effects calculated here represent upper limits of the impact of the magnetic field geometry on the SEDs and SVPs of blazars. We have demonstrated that a field aligned parallel to the jet could give rise to a low-energy component of the SED that follows an inverse relationship with the boosting of the viewing angle. On the other hand, highly ordered fields, such as a toroidal field, boosts the synchrotron, and consequently the SSC, component substantially. This directly influences the CD of a blazar without affecting its SH. Through this work, we have also explored the impact of the obliquity of the magnetic field with respect to the jet axis. We showed that in the case of an oblique geometry, certain combination of angles could result in a substantially low level of synchrotron and SSC emission compared to the case of a tangled field while maintaining the same EC flux level as before. Such a scenario could be used to explain the appearance of
γ-ray orphan flares observed in some blazars, such as PKS 1510-089 [
7], where the directionality of the field creates a difference in the radiation field as seen by an observer versus that seen by the electrons in the emission region.