Magnetic Dissipation in Relativistic Jets
Abstract
:1. Introduction
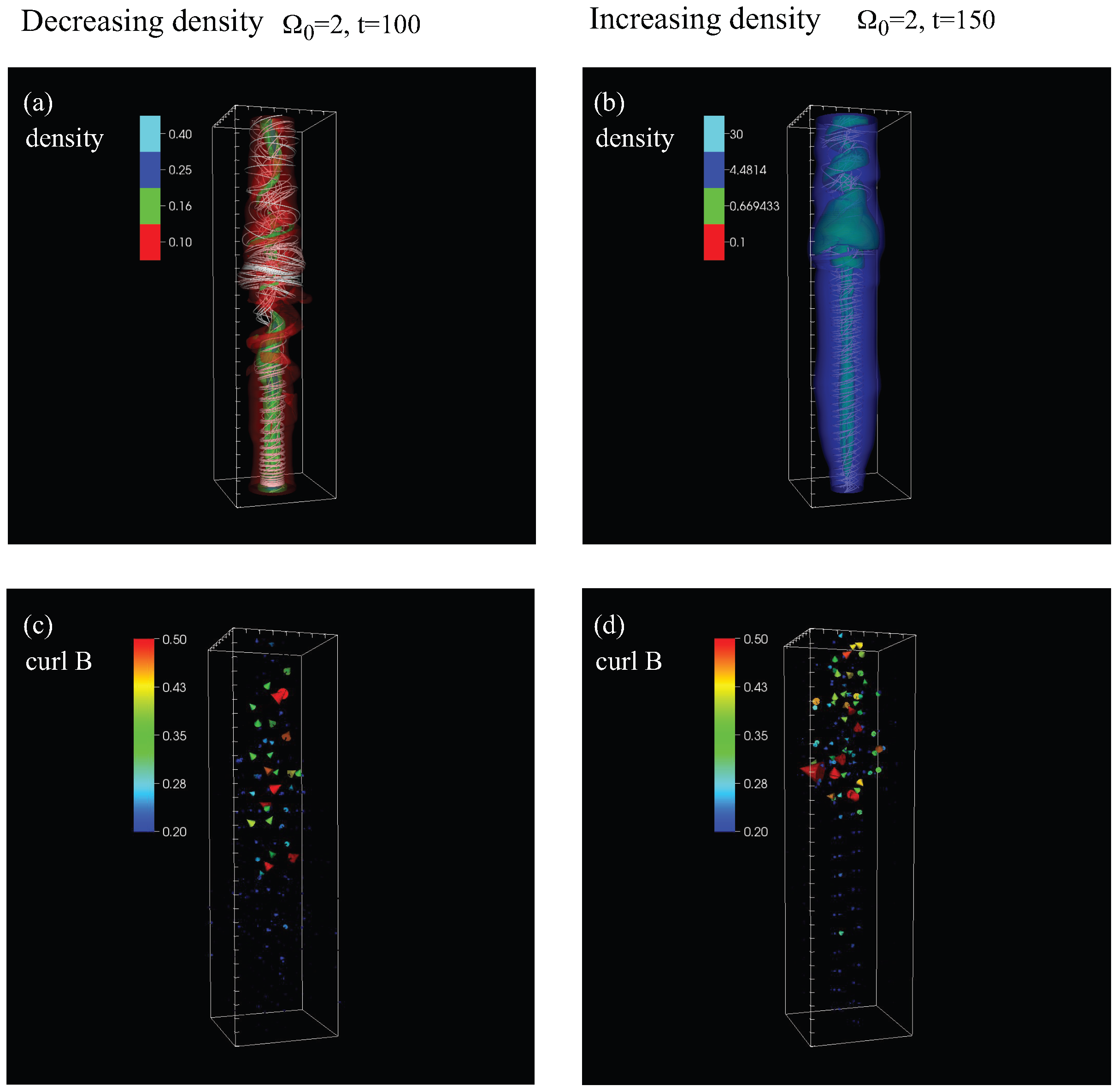
2. Current-Driven Kink Instability
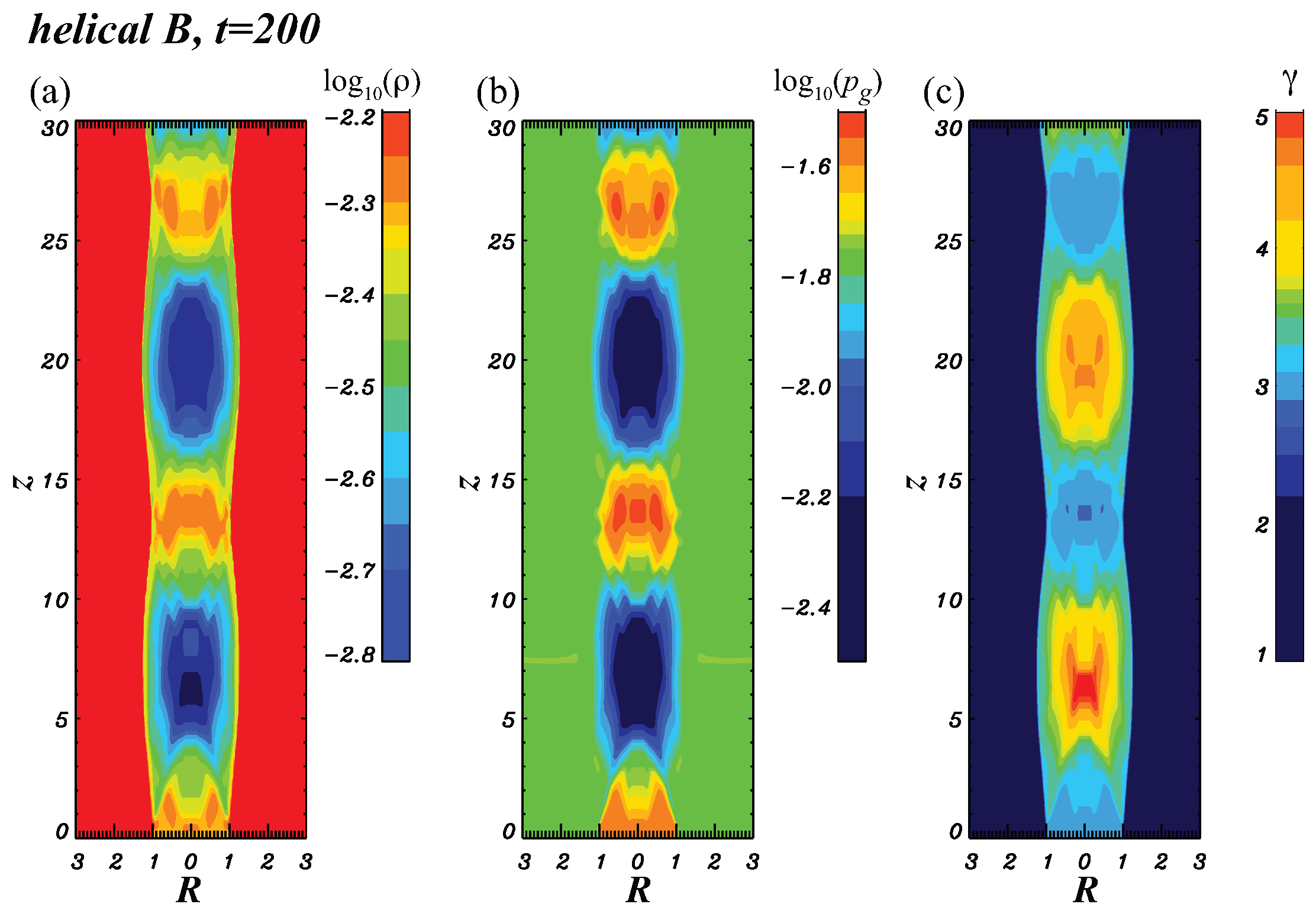
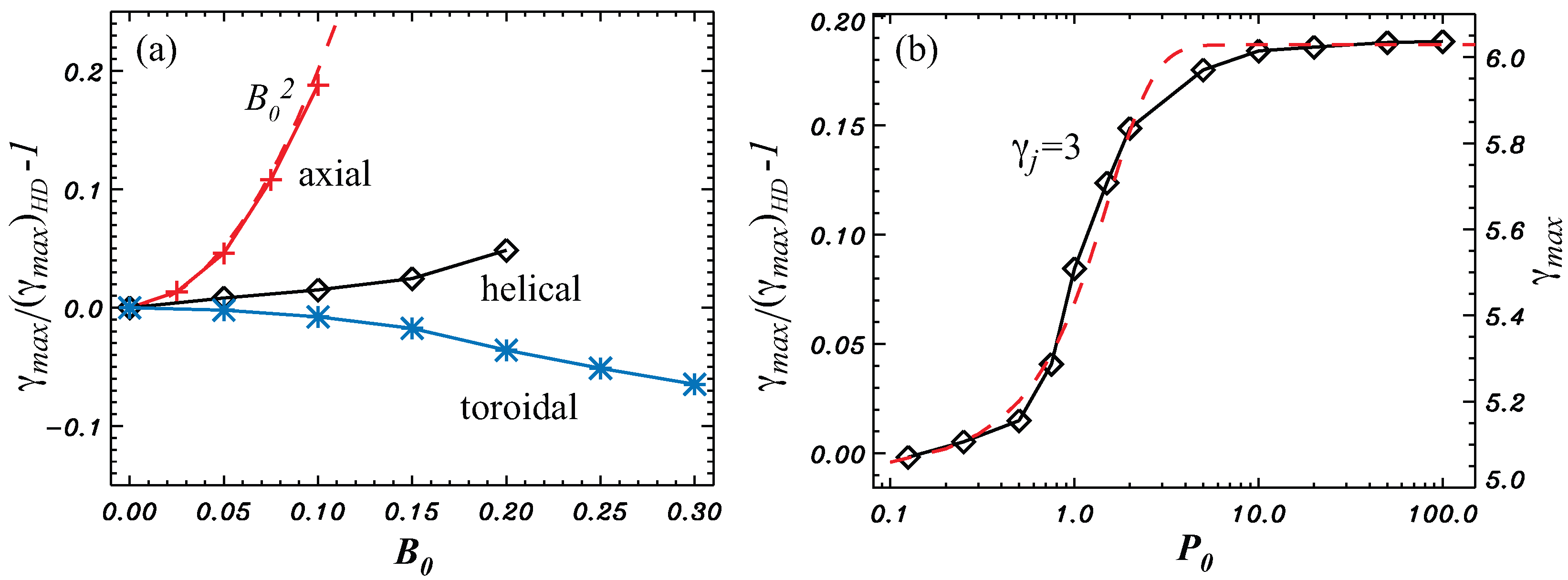
3. Recollimation Shock
4. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Blandford, R.D.; Payne, D.G. Hydromagnetic flows from accretion discs and the production of radio jets. Mon. Not. R. Astron. Soc. 1982, 199, 883–903. [Google Scholar] [CrossRef]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- McKinney, J.C. General relativistic magnetohydrodynamic simulations of the jet formation and large-scale propagation from black hole accretion systems. Mon. Not. R. Astron. Soc. 2006, 368, 1561–1582. [Google Scholar] [CrossRef]
- McKinney, J.C.; Blandford, R.D. Stability of relativistic jets from rotating, accreting black holes via fully three-dimensional magnetohydrodynamic simulations. Mon. Not. R. Astron. Soc. 2009, 39, L126–L130. [Google Scholar] [CrossRef]
- Balbus, S.A.; Hawley, J.F. Instability, turbulence, and enhanced transport in accretion disks. Rev. Mod. Phys. 1998, 70, 1–53. [Google Scholar] [CrossRef]
- Beskin, V.S.; Nokhrina, E.E. The effective acceleration of plasma outflow in the paraboloidal magnetic field. Mon. Not. R. Astron. Soc. 2006, 367, 375–386. [Google Scholar] [CrossRef]
- Lyubarsky, Y. Asymptotic Structure of Poynting-Dominated Jets. Astrophys. J. 2009, 698, 1570–1589. [Google Scholar] [CrossRef]
- Lyubarsky, Y.E. Transformation of the Poynting flux into kinetic energy in relativistic jets. Mon. Not. R. Astron. Soc. 2010, 402, 353–361. [Google Scholar] [CrossRef]
- McKinney, J.C.; Uzdensky, D.A. A reconnection switch to trigger gamma-ray burst jet dissipation. Mon. Not. R. Astron. Soc. 2012, 419, 573–607. [Google Scholar] [CrossRef]
- Begelman, M.C. Instability of Toroidal Magnetic Field in Jets and Plerions. Astrophys. J. 1998, 493, 291–300. [Google Scholar] [CrossRef]
- Giannios, D.; Spruit, H.C. The role of kink instability in Poynting-flux dominated jets. Astron. Astrophys. 2006, 450, 887–898. [Google Scholar] [CrossRef]
- Sikora, M.; Begelman, M.C.; Madejski, G.M.; Lasota, J.-P. Are Quasar Jets Dominated by Poynting Flux? Astrophys. J. 2005, 625, 72–77. [Google Scholar] [CrossRef]
- Begelman, M.C.; Fabian, A.C.; Rees, M.J. Implications of very rapid TeV variability in blazars. Mon. Not. R. Astron. Soc. 2008, 384, L19–L23. [Google Scholar] [CrossRef]
- Giannios, D.; Uzdensky, D.A.; Begelman, M.C. Fast TeV variability in blazars: Jets in a jet. Mon. Not. R. Astron. Soc. 2009, 395, L29–L33. [Google Scholar] [CrossRef]
- Tavecchio, F.; Ghisellini, G.; Bonnoli, G.; Ghirlanda, G. Constraining the location of the emitting region in Fermi blazars through rapid γ-ray variability. Mon. Not. R. Astron. Soc. 2010, 405, L94–L98. [Google Scholar] [CrossRef]
- Marscher, A.P.; Jorstad, S.G.; Larionov, V.M.; Aller, M.F.; Aller, H.D.; Lähteenmäki, A.; Agudo, I.; Smith, P.S.; Gurwell, M.; Hagen-Thorn, V.A.; et al. Probing the Inner Jet of the Quasar PKS 1510-089 with Multi-Waveband Monitoring During Strong Gamma-Ray Activity. Astrophys. J. Lett. 2010, 710, L126–L131. [Google Scholar] [CrossRef]
- Agudo, I.; Jorstad, S.G.; Marscher, A.P.; Larionov, V.M.; Gómez, J.L.; Lähteenmäki, A.; Gurwell, M.; Smith, P.S.; Wiesemeyer, H.; Thum, C.; et al. Location of γ-ray Flare Emission in the Jet of the BL Lacertae Object OJ287 More than 14 pc from the Central Engine. Astrophys. J. Lett. 2011, 726, L13. [Google Scholar] [CrossRef]
- Gómez, J.L.; Martí, J.M.A.; Marscher, A.P.; Ibáñez, J.M.A.; Marcaide, J.M. Parsec-Scale Synchrotron Emission from Hydrodynamic Relativistic Jets in Active Galactic Nuclei. Astrophys. J. Lett. 1995, 449, L19–L21. [Google Scholar] [CrossRef]
- Gómez, J.L.; Martí, J.M.; Marscher, A.P.; Ibáñez, J.M.; Alberdi, A. Hydrodynamical Models of Superluminal Sources. Astrophys. J. Lett. 1997, 482, L33–L36. [Google Scholar] [CrossRef]
- Istomin, Y.N.; Pariev, V.I. Stability of a relativistic rotating electron-positron jet: Non-axisymmetric perturbations. Mon. Not. R. Astron. Soc. 1996, 281, 1–26. [Google Scholar] [CrossRef]
- Lyubarskii, Y.E. Kink instability of relativistic force-free jets. Mon. Not. R. Astron. Soc. 1999, 308, 1006–1010. [Google Scholar] [CrossRef]
- Mizuno, Y.; Lyubarsky, Y.; Nishikawa, K.-I.; Hardee, P.E. Three-Dimensional Relativistic Magnetohydrodynamic Simulations of Current-Driven Instability. I. Instability of a Static Column. Astrophys. J. 2009, 700, 684–693. [Google Scholar] [CrossRef]
- Mizuno, Y.; Hardee, P.E.; Nishikawa, K.-I. Three-dimensional Relativistic Magnetohydrodynamic Simulations of Current-driven Instability with a Sub-Alfvénic Jet: Temporal Properties. Astrophys. J. 2011, 734, 19. [Google Scholar] [CrossRef]
- Mizuno, Y.; Lyubarsky, Y.; Nishikawa, K.-I.; Hardee, P.E. Three-dimensional Relativistic Magnetohydrodynamic Simulations of Current-driven Instability. III. Rotating Relativistic Jets. Astrophys. J. 2012, 757, 16. [Google Scholar] [CrossRef]
- Singh, C.B.; Mizuno, Y.; de Gouveia Dal Pino, E.M. Spatial Growth of Current-driven Instability in Relativistic Rotating Jets and the Search for Magnetic Reconnection. Astrophys. J. 2016, 824, 48. [Google Scholar] [CrossRef]
- Mizuno, Y.; Hardee, P.E.; Nishikawa, K.-I. Spatial Growth of the Current-driven Instability in Relativistic Jets. Astrophys. J. 2014, 784, 167. [Google Scholar] [CrossRef]
- Kowal, G.; de Gouveia Dal Pino, E.M.; Lazarian, A. Particle Acceleration in Turbulence and Weakly Stochastic Reconnection. Phys. Rev. Lett. 2012, 108, 241102. [Google Scholar] [CrossRef] [PubMed]
- Takamoto, M.; Inoue, T.; Lazarian, A. Turbulent Reconnection in Relativistic Plasmas and Effects of Compressibility. Astrophys. J. 2015, 815, 16. [Google Scholar] [CrossRef]
- Kowal, G.; Lazarian, A.; Vishniac, E.T.; Otmianowska-Mazur, K. Numerical Tests of Fast Reconnection in Weakly Stochastic Magnetic Fields. Astrophys. J. 2009, 700, 63–85. [Google Scholar] [CrossRef]
- De Gouveia Dal Pino, E.M.; Kowal, G. Particle Acceleration by Magnetic Reconnection. In Magnetic Fields in Diffuse Media; Lazarian, A., de Gouveia Dal Pino, E.M., Melioli, C., Eds.; Astrophysics and Space Science Library; Springer: Berlin/Heidelberg, Germany, 2015; pp. 373–396. [Google Scholar]
- Cohen, M.H.; Meier, D.L.; Arshakian, T.G.; Homan, D.C.; Hovatta, T.; Kovalev, Y.Y.; Lister, M.L.; Pushkarev, A.B.; Richards, J.L.; Savolainen, T. Studies of the Jet in Bl Lacertae. I. Recollimation Shock and Moving Emission Features. Astrophys. J. 2014, 787, 151. [Google Scholar] [CrossRef]
- Asada, K.; Nakamura, M. The Structure of the M87 Jet: A Transition from Parabolic to Conical Streamlines. Astrophys. J. Lett. 2012, 745, L28. [Google Scholar] [CrossRef]
- Aloy, M.A.; Rezzolla, L. A Powerful Hydrodynamic Booster for Relativistic Jets. Astrophys. J. Lett. 2006, 640, L115–L118. [Google Scholar] [CrossRef]
- Mizuno, Y.; Hardee, P.; Hartmann, D.H.; Nishikawa, K.-I.; Zhang, B. A Magnetohydrodynamic Boost for Relativistic Jets. Astrophys. J. 2008, 672, 72–82. [Google Scholar] [CrossRef]
- Mizuno, Y.; Gómez, J.L.; Nishikawa, K.-I.; Meli, A.; Hardee, P.E.; Rezzolla, L. Recollimation Shocks in Magnetized Relativistic Jets. Astrophys. J. 2015, 809, 38. [Google Scholar] [CrossRef]
- Krichbaum, T.P.; Roy, A.; Wagner, J.; Rottmann, H.; Hodgson, J.A.; Bertarini, A.; Alef, W.; Zensus, J.A.; Marscher, A.; Jorstad, S.G.; et al. Zooming towards the Event Horizon - mm-VLBI Today and Tomorrow. In Proceedings of the 11th EVN Symposium 055; Available online: http://pos.sissa.it/archive/conferences/178/055/11th%20EVN%20Symposium_055.pdf (accessed on 20 September 2016).
- Fish, V.L.; Johnson, M.D.; Lu, R.-S.; Doeleman, S.S.; Bouman, K.L.; Zoran, D.; Freeman, W.T.; Psaltis, D.; Narayan, R.; Pankratius, V.; et al. Imaging an Event Horizon: Mitigation of Scattering toward Sagittarius A*. Astrophys. J. 2014, 795, 134. [Google Scholar] [CrossRef]
- Goddi, C.; Falcke, H.; Kramer, M.; Rezzolla, L.; Brinkerink, C.; Bronzwaer, T.; Deane, R.; De Laurentis, M.; Desvignes, G.; Davelaar, J.R.J.; et al. BlackHoleCam: Fundamental physics of the Galactic center. Int. J. Mod. Phys. D 2016. submitted. [Google Scholar] [CrossRef]
- Gomez, J.L.; Lobanov, A.P.; Bruni, G.; Kovalev, Y.Y.; Marscher, A.P.; Jorstad, S.G.; Mizuno, Y.; Bach, U.; Sokolovsky, K.V.; Anderson, J.M.; et al. Probing the Innermost Regions of AGN Jets and Their Magnetic Fields with RadioAstron. I. Imaging BL Lacertae at 21 Microarcsecond Resolution. Astrophys. J. 2016, 817, 96. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mizuno, Y.; Gómez, J.L.; Nishikawa, K.-I.; Meli, A.; Hardee, P.E.; Rezzolla, L.; Singh, C.B.; Pino, E.M.d.G.D. Magnetic Dissipation in Relativistic Jets. Galaxies 2016, 4, 40. https://doi.org/10.3390/galaxies4040040
Mizuno Y, Gómez JL, Nishikawa K-I, Meli A, Hardee PE, Rezzolla L, Singh CB, Pino EMdGD. Magnetic Dissipation in Relativistic Jets. Galaxies. 2016; 4(4):40. https://doi.org/10.3390/galaxies4040040
Chicago/Turabian StyleMizuno, Yosuke, Jose L. Gómez, Ken-Ichi Nishikawa, Athina Meli, Philip E. Hardee, Luciano Rezzolla, Chandra B. Singh, and Elisabete M. de Gouveia Dal Pino. 2016. "Magnetic Dissipation in Relativistic Jets" Galaxies 4, no. 4: 40. https://doi.org/10.3390/galaxies4040040
APA StyleMizuno, Y., Gómez, J. L., Nishikawa, K.-I., Meli, A., Hardee, P. E., Rezzolla, L., Singh, C. B., & Pino, E. M. d. G. D. (2016). Magnetic Dissipation in Relativistic Jets. Galaxies, 4(4), 40. https://doi.org/10.3390/galaxies4040040





