Self-Gravitating Bose-Einstein Condensates and the Thomas-Fermi Approximation
Abstract
:1. Introduction
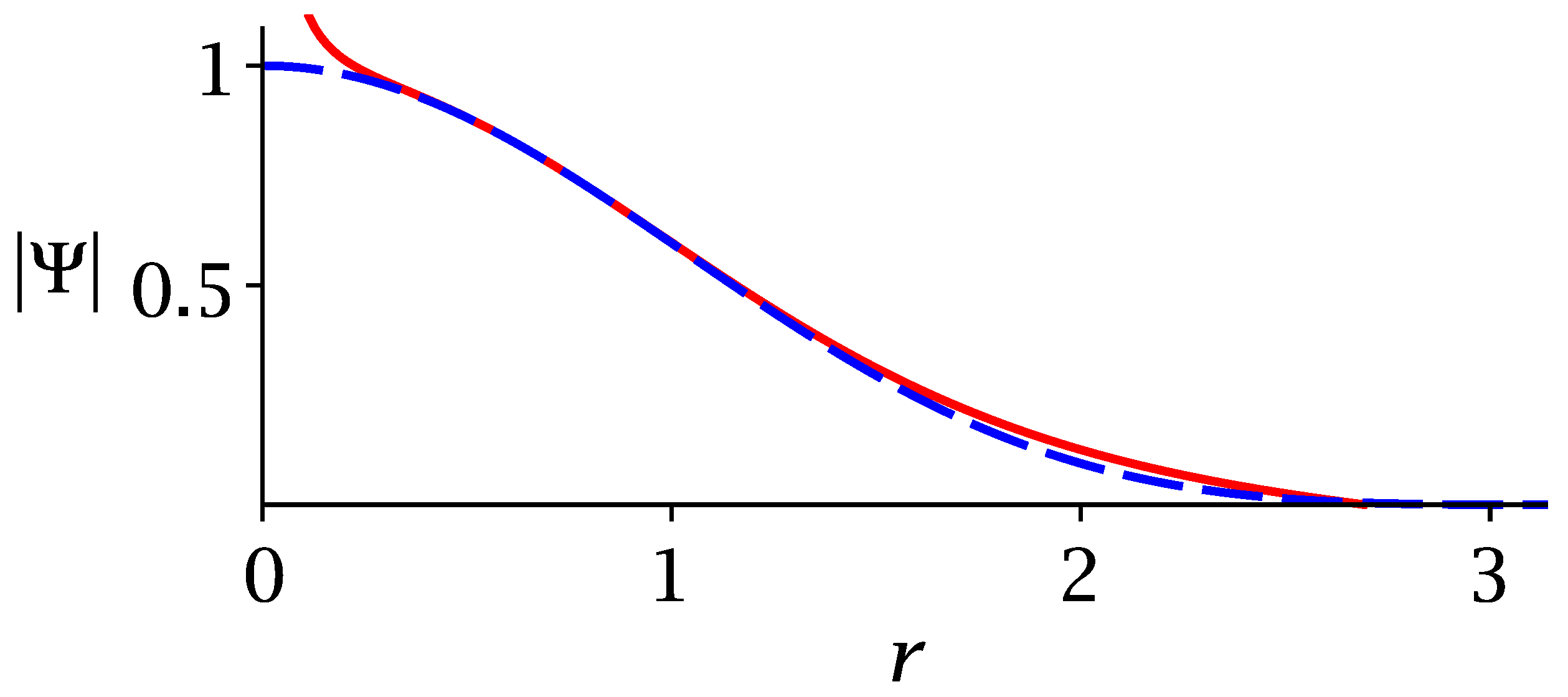
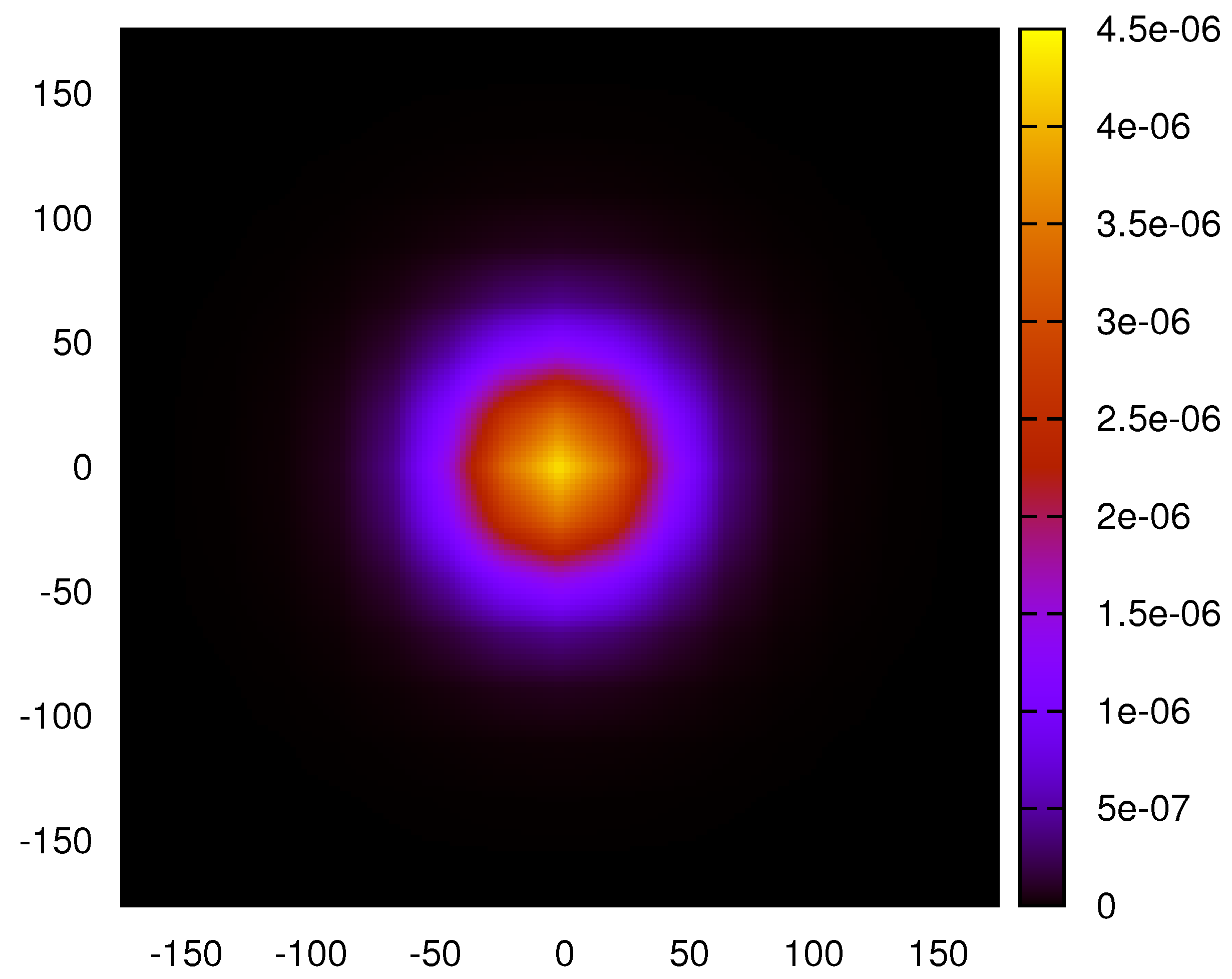
2. Discussion
3. Conclusions
Acknowledgments
Conflicts of Interest
References
- Kaup, D.J. Klein-Gordon Geon. Phys. Rev. 1968, 172, 1331–1342. [Google Scholar] [CrossRef]
- Ruffini, R.; Bonazzola, S. Systems of self-gravitating particles in general relativity and the concept of an equation of state. Phys. Rev. 1969, 187, 1767–1783. [Google Scholar] [CrossRef]
- Colpi, M.; Shapiro, S.L.; Wasserman, I. Boson stars—Gravitational equilibria of self-interacting scalar fields. Phys. Rev. Lett. 1986, 57, 2485–2488. [Google Scholar] [CrossRef] [PubMed]
- Chavanis, P.H.; Harko, T. Bose-Einstein condensate general relativistic stars. Phys. Rev. D 2012, 86, 064011. [Google Scholar] [CrossRef]
- Lee, J.W.; Koh, I.G. Galactic halos as boson stars. Phys. Rev. D 1996, 53, 2236–2239. [Google Scholar] [CrossRef]
- Böhmer, C.G.; Harko, T. Can dark matter be a Bose Einstein condensate? J. Cosmol. Astropart. Phys. 2007, 2007, 025. [Google Scholar] [CrossRef]
- Chavanis, P.H. Mass-radius relation of Newtonian self-gravitating Bose-Einstein condensates with short-range interactions. I. Analytical results. Phys. Rev. D 2011, 84, 043531. [Google Scholar] [CrossRef]
- Chavanis, P.H.; Delfini, L. Mass-radius relation of Newtonian self-gravitating Bose-Einstein condensates with short-range interactions. II. Numerical results. Phys. Rev. D 2011, 84, 043532. [Google Scholar] [CrossRef]
- Goodman, J. Repulsive dark matter. New Astron. 2000, 5, 103–107. [Google Scholar] [CrossRef]
- Arbey, A.; Lesgourgues, J.; Salati, P. Galactic halos of fluid dark matter. Phys. Rev. D 2003, 68, 023511. [Google Scholar] [CrossRef]
- Suárez, A.; Robles, V.; Matos, T. A Review on the Scalar Field/Bose-Einstein Condensate Dark Matter Model. In Accelerated Cosmic Expansion; Springer: Berlin, Germany, 2013; pp. 107–142. [Google Scholar]
- Schroven, K.; List, M.; Lämmerzahl, C. Stability of self-gravitating Bose-Einstein condensates. Phys. Rev. D 2015, 92, 124008. [Google Scholar] [CrossRef]
- Kühnel, F.; Rampf, C. Astrophysical Bose-Einstein condensates and superradiance. Phys. Rev. D 2014, 90, 103526. [Google Scholar] [CrossRef]
- Bahrami, M.; Großardt, A.; Donadi, S.; Bassi, A. The Schrödinger-Newton equation and its foundations. New J. Phys. 2014, 16, 115007. [Google Scholar] [CrossRef]
- Giulini, D.; Großardt, A. Centre-of-mass motion in multi-particle Schrödinger-Newton dynamics. New J. Phys. 2014, 16, 075005. [Google Scholar] [CrossRef]
- Guzmán, F.S.; Lora-Clavijo, F.D.; González-Avilés, J.J.; Rivera-Paleo, F.J. Stability of BEC galactic dark matter halos. J. Cosmol. Astropart. Phys. 2013, 2013, 034. [Google Scholar] [CrossRef]
- Dalfovo, F.; Pitaevskii, L.P.; Stringari, S. The condensate wave function of a trapped atomic gas. J. Res. Natl. Inst. Stand. Tech. 1996, 101, 537–544. [Google Scholar] [CrossRef]
- Pethick, C.J.; Smith, H. Bose-Einstein Condensation in Dilute Gases, 2nd ed.; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Wang, X.Z. Cold Bose stars: Self-gravitating Bose-Einstein condensates. Phys. Rev. D 2001, 64, 124009. [Google Scholar] [CrossRef]
- Madarassy, E.J.M.; Toth, V.T. Numerical simulation code for self-gravitating Bose–Einstein condensates. Comput. Phys. Commun. 2013, 184, 1339–1343. [Google Scholar] [CrossRef]
- Madarassy, E.J.M.; Toth, V.T. Evolution and dynamical properties of Bose-Einstein condensate dark matter stars. Phys. Rev. D 2015, 91, 044041. [Google Scholar] [CrossRef]
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toth, V.T. Self-Gravitating Bose-Einstein Condensates and the Thomas-Fermi Approximation. Galaxies 2016, 4, 9. https://doi.org/10.3390/galaxies4030009
Toth VT. Self-Gravitating Bose-Einstein Condensates and the Thomas-Fermi Approximation. Galaxies. 2016; 4(3):9. https://doi.org/10.3390/galaxies4030009
Chicago/Turabian StyleToth, Viktor T. 2016. "Self-Gravitating Bose-Einstein Condensates and the Thomas-Fermi Approximation" Galaxies 4, no. 3: 9. https://doi.org/10.3390/galaxies4030009
APA StyleToth, V. T. (2016). Self-Gravitating Bose-Einstein Condensates and the Thomas-Fermi Approximation. Galaxies, 4(3), 9. https://doi.org/10.3390/galaxies4030009




