Gamma-Ray Variability Induced by Microlensing on Intermediate Size Structures in Lensed Blazars
Abstract
:1. Introduction
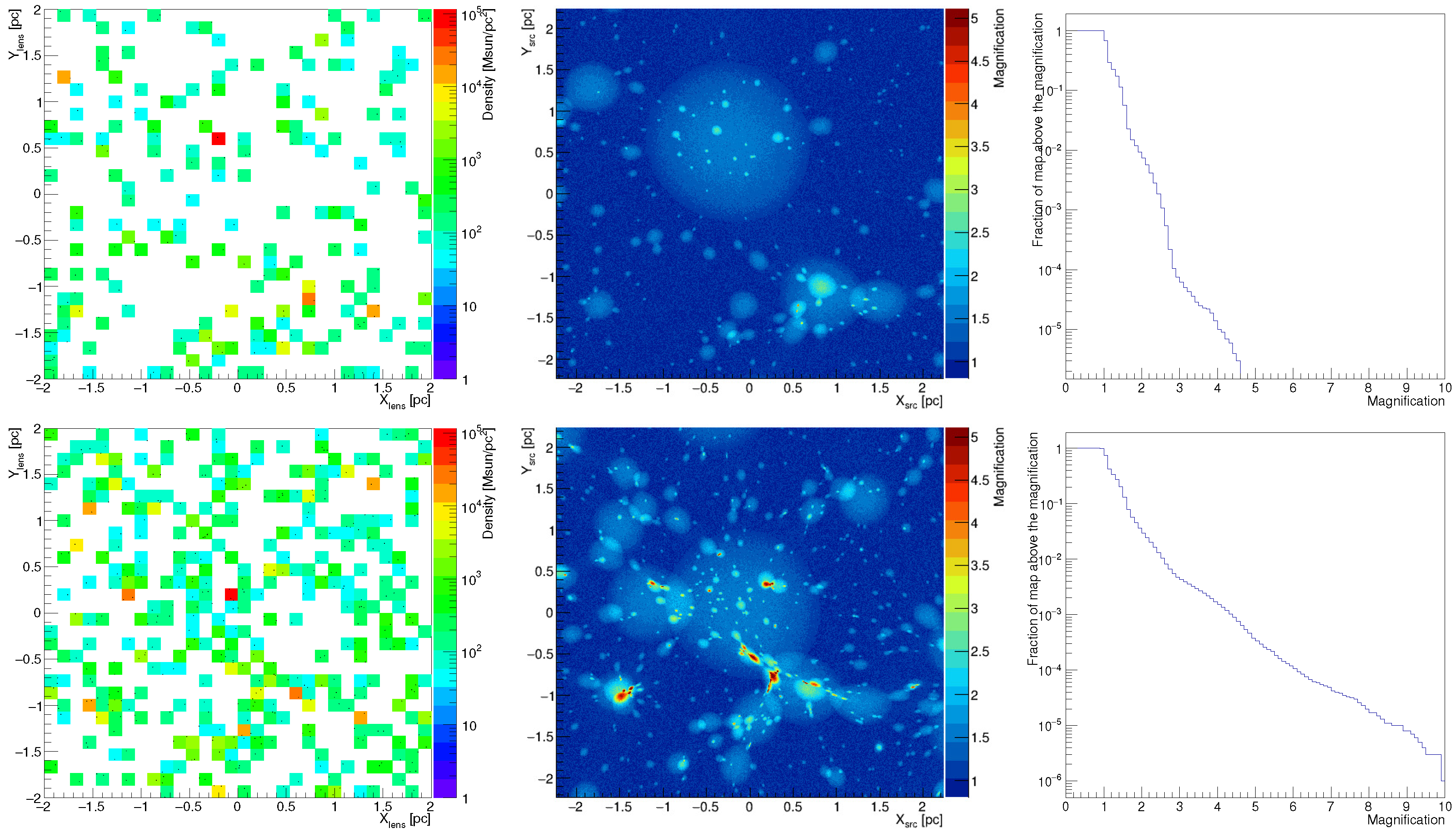
2. Experimental Section
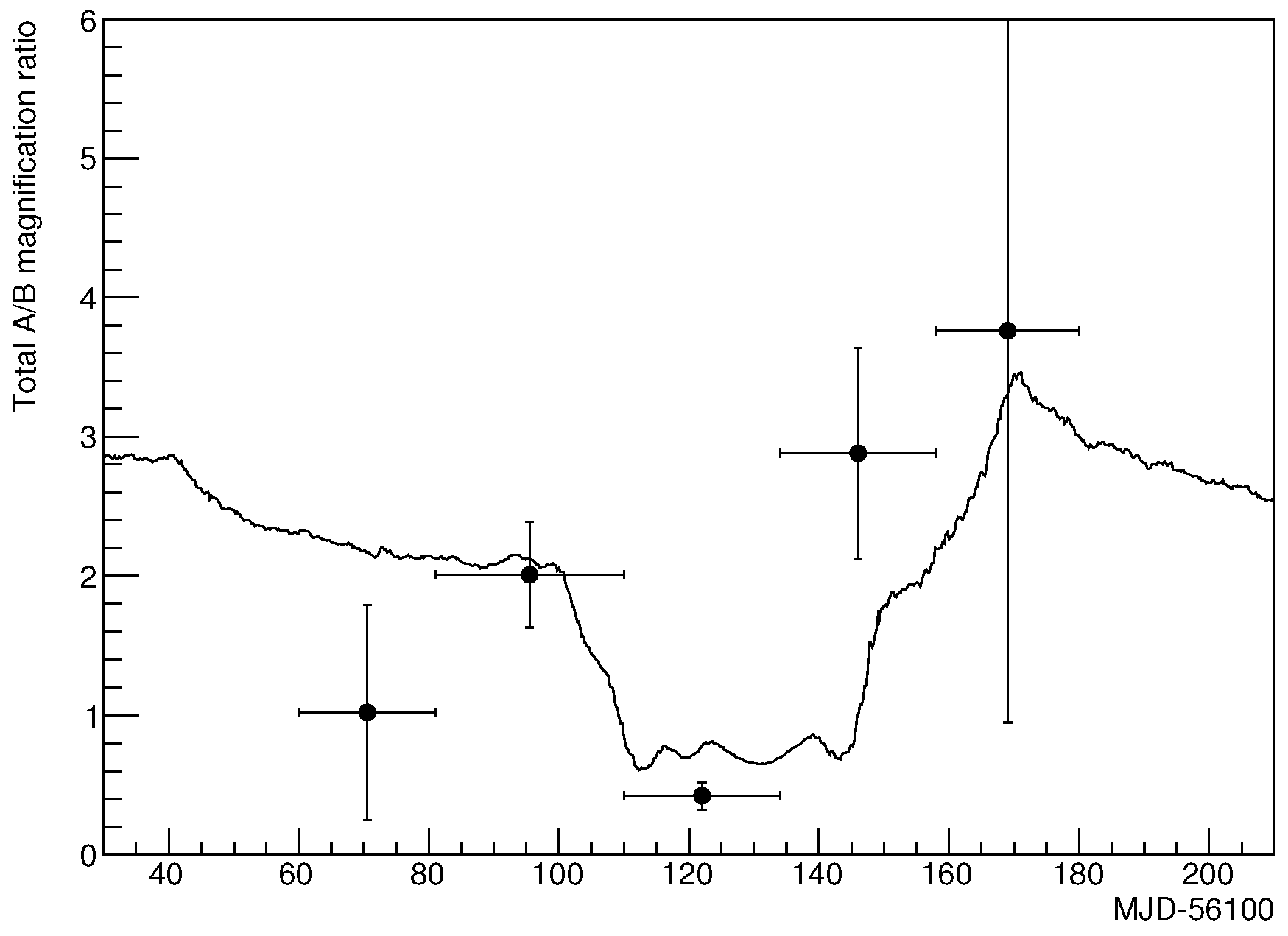
3. Results
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Schneider, P.; Kochanek, C.; Wambsganss, J. Gravitational Lensing: Strong, Weak & Micro; Meylan, G., Jetzer, P., North, P., Eds.; Springer-Verlag: Berlin, Germany, 2006; p. 457. [Google Scholar]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Allafort, A.; Amin, M.A.; Baldini, L.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; et al. Gamma-Ray Flaring Activity from the Gravitationally Lensed Blazar PKS 1830-211 Observed by Fermi LAT. Astrophys. J. 2015, 799, 143. [Google Scholar] [CrossRef]
- Neronov, A.; Vovk, I.; Malyshev, D. Central engine of a gamma-ray blazar resolved through the magnifying glass of gravitational microlensing. Nat. Phys. 2016, 11, 664–667. [Google Scholar] [CrossRef]
- Vovk, I.; Neronov, A. Microlensing constraints on the size of the gamma-ray emission region in blazar B0218+357. Astron. Astrophys. 2016, 586, A150. [Google Scholar] [CrossRef]
- Cohen, J.G.; Lawrence, C.R.; Blandford, R.D. The Redshift of the Lensed Object in the Einstein Ring B0218+357. Astrophys. J. 2003, 583, 67–69. [Google Scholar] [CrossRef]
- CASTLES Survey. Available online: https://www.cfa.harvard.edu/castles/ (accessed on 20 August 2016).
- Browne, I.W.A.; Patnaik, A.R.; Walsh, D.; Wilkinson, P.N. The Redshift of the Lensing Galaxy in the Gravitationally Lensed System B0218+35.7. Mon. Not. R. Astron. Soc. 1993, 263, L32–L36. [Google Scholar] [CrossRef]
- O’Dea, C.P.; Baum, S.A.; Stanghellini, C.; Dey, A.; van Breugel, W.; Deustua, S. Radio and optical observations of 0218+357—The smallest Einstein ring? Astrophys. J. 1992, 104, 1320–1330. [Google Scholar] [CrossRef]
- Biggs, A.D.; Browne, I.W.A.; Helbig, P.; Koopmans, L.V.E.; Wilkinson, P.N.; Perley, R.A. Time delay for the gravitational lens system B0218+357. Mon. Not. R. Astron. Soc. 1999, 304, 349–358. [Google Scholar] [CrossRef]
- Cohen, A.S.; Hewitt, J.N.; Moore, C.B.; Haarsma, D.B. Further Investigation of the Time Delay, Magnification Ratios, and Variability in the Gravitational Lens 0218+357. Astrophys. J. 2000, 545, 578. [Google Scholar] [CrossRef]
- Mittal, R.; Porcas, R.; Wucknitz, O.; Biggs, A.; Browne, I. VLBI phase-reference observations of the gravitational lens JVAS B0218+357. Astron. Astrophys. 2006, 447, 515–524. [Google Scholar] [CrossRef]
- Mittal, R.; Porcas, R.; Wucknitz, O. Free-free absorption in the gravitational lens JVAS B0218+357. Astron. Astrophys. 2007, 465, 405–415. [Google Scholar] [CrossRef]
- Martí-Vidal, I.; Muller, S. Using gravitationally lensed images to investigate the intrinsic AGN variability. Astron. Astrophys. 2016, 590, A83. [Google Scholar] [CrossRef]
- Cheung, C.C.; Larsson, S.; Scargle, J.D.; Amin, M.A.; Blandford, R.D.; Bulmash, D.; Chiang, J.; Ciprini, S.; Corbet, R.H.D.; Falco, E.E.; et al. Fermi Large Area Telescope Detection of Gravitational Lens Delayed γ-Ray Flares from Blazar B0218+357. Astrophys. J. Lett. 2014, 782, L14. [Google Scholar] [CrossRef]
- Sitarek, J.; Bednarek, W. Variability of GeV gamma-ray emission in QSO B0218+357 due to microlensing on intermediate size structures. Mon. Not. R. Astron. Soc. 2016, 459, 1959–1967. [Google Scholar] [CrossRef]
- Blitz, L. Giant molecular clouds. In Protostars and Planets III; University of Arizona Press: Tucson, AZ, USA, 1993. [Google Scholar]
- Murray, N. Star Formation Efficiencies and Lifetimes of Giant Molecular Clouds in the Milky Way. Astrophys. J. 2011, 729, 133. [Google Scholar] [CrossRef]
- Williams, J.P.; Blitz, L.; McKee, C.F. The Structure and Evolution of Molecular Clouds: From Clumps to Cores to the IMF. In Protostars and Planets IV; University of Arizona Press: Tucson, AZ, USA, 2000. [Google Scholar]
- Sanders, D.B.; Solomon, P.M.; Scoville, N.Z. Giant molecular clouds in the Galaxy. I—The axisymmetric distribution of H2. Astrophys. J. 1984, 276, 182–203. [Google Scholar] [CrossRef]
- Falco, E.E.; Impey, C.D.; Kochanek, C.S.; Lehár, J.; McLeod, B.A.; Rix, H.-W.; Keeton, C.R.; Muñoz, J.A.; Peng, C.Y. Dust and Extinction Curves in Galaxies with z > 0: The Interstellar Medium of Gravitational Lens Galaxies. Astrophys. J. 1999, 523, 617–632. [Google Scholar] [CrossRef]
- Menten, K.M.; Reid, M.J. Formaldehyde Absorption at z = 0.685 toward the “Einstein Ring” B0218+357. Astrophys. J. 1996, 465, L99–L102. [Google Scholar] [CrossRef]
- Wiklind, T.; Combes, F. The redshift of the gravitational lens of PKS1830-211 determined from molecular absorption lines. Nature 1996, 379, 139–141. [Google Scholar] [CrossRef]
- Schneider, P.; Weiss, A. The two-point-mass lens—Detailed investigation of a special asymmetric gravitational lens. Astron. Astrophys. 1986, 164, 237–259. [Google Scholar]
- Stutzki, J.; Guesten, R. High spatial resolution isotopic CO and CS observations of M17 SW—The clumpy structure of the molecular cloud core. Astrophys. J. 1990, 356, 513–533. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sitarek, J.; Bednarek, W. Gamma-Ray Variability Induced by Microlensing on Intermediate Size Structures in Lensed Blazars. Galaxies 2016, 4, 20. https://doi.org/10.3390/galaxies4030020
Sitarek J, Bednarek W. Gamma-Ray Variability Induced by Microlensing on Intermediate Size Structures in Lensed Blazars. Galaxies. 2016; 4(3):20. https://doi.org/10.3390/galaxies4030020
Chicago/Turabian StyleSitarek, Julian, and Włodek Bednarek. 2016. "Gamma-Ray Variability Induced by Microlensing on Intermediate Size Structures in Lensed Blazars" Galaxies 4, no. 3: 20. https://doi.org/10.3390/galaxies4030020
APA StyleSitarek, J., & Bednarek, W. (2016). Gamma-Ray Variability Induced by Microlensing on Intermediate Size Structures in Lensed Blazars. Galaxies, 4(3), 20. https://doi.org/10.3390/galaxies4030020





