The Classifications and Some Correlations for Fermi Blazars
Abstract
:1. Introduction
2. Sample and Classifications
- for LSPs,
- for ISPs, and
- for HSPs.
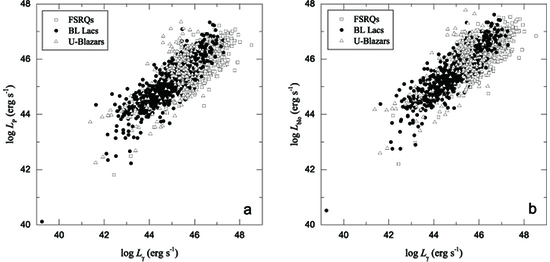
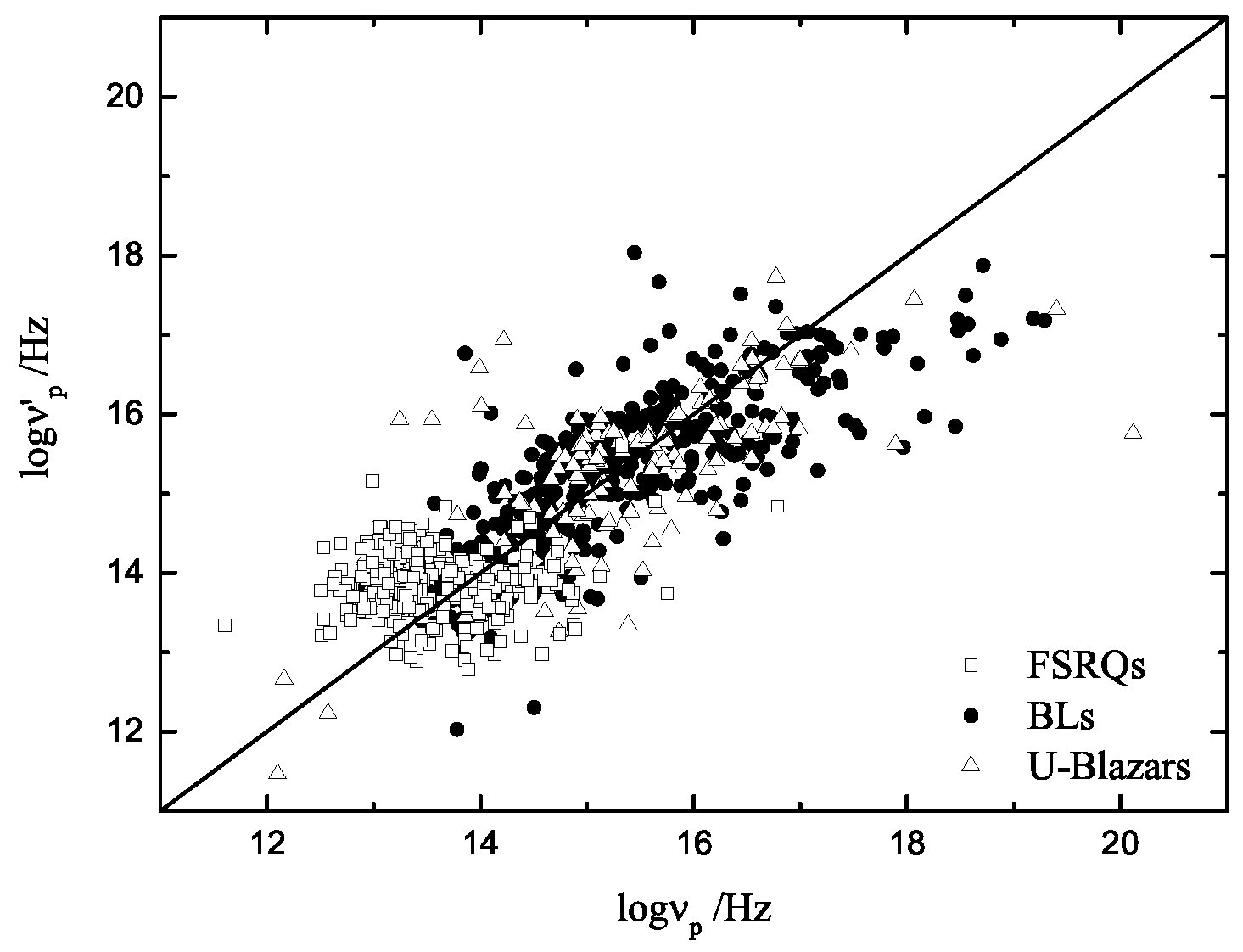
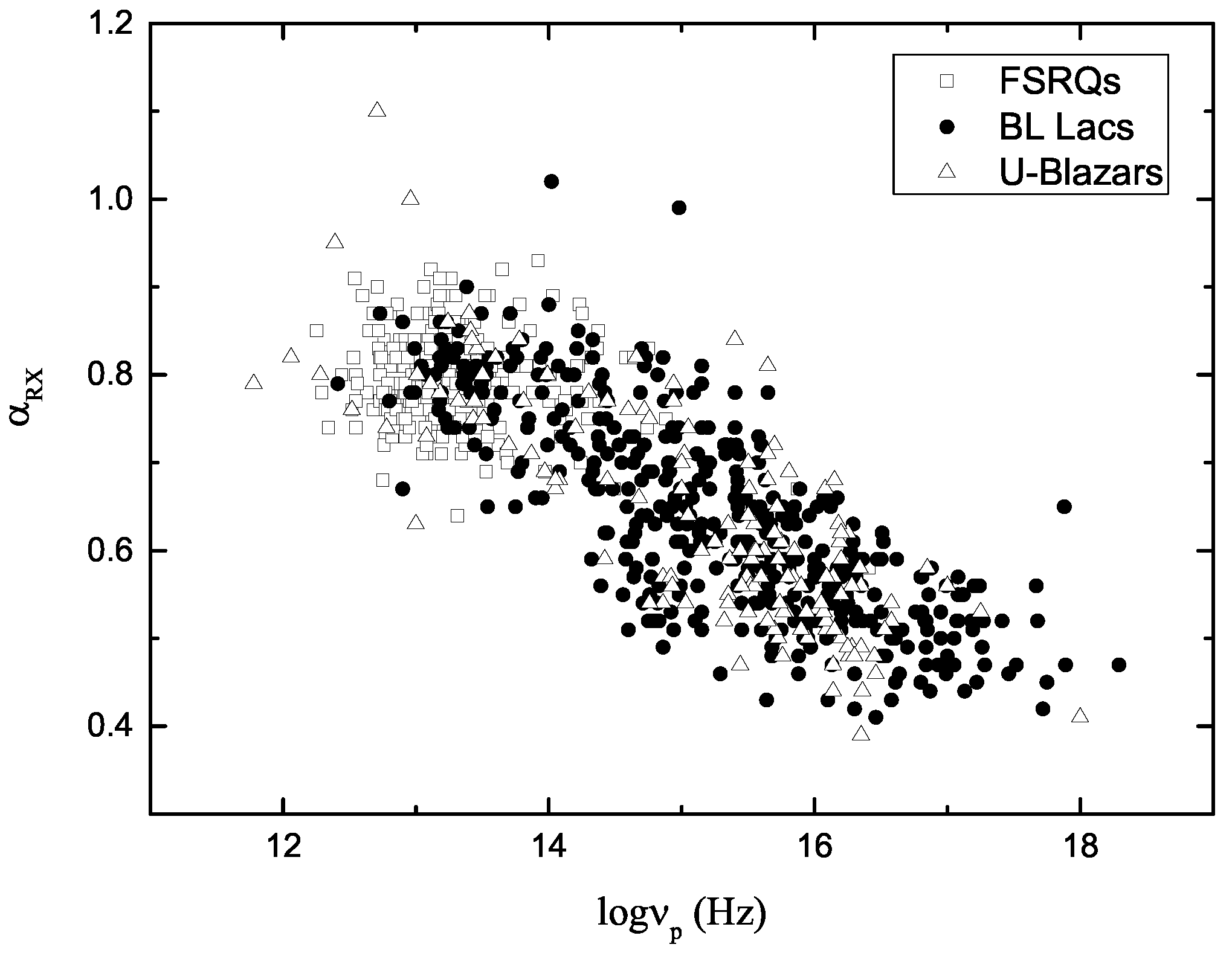
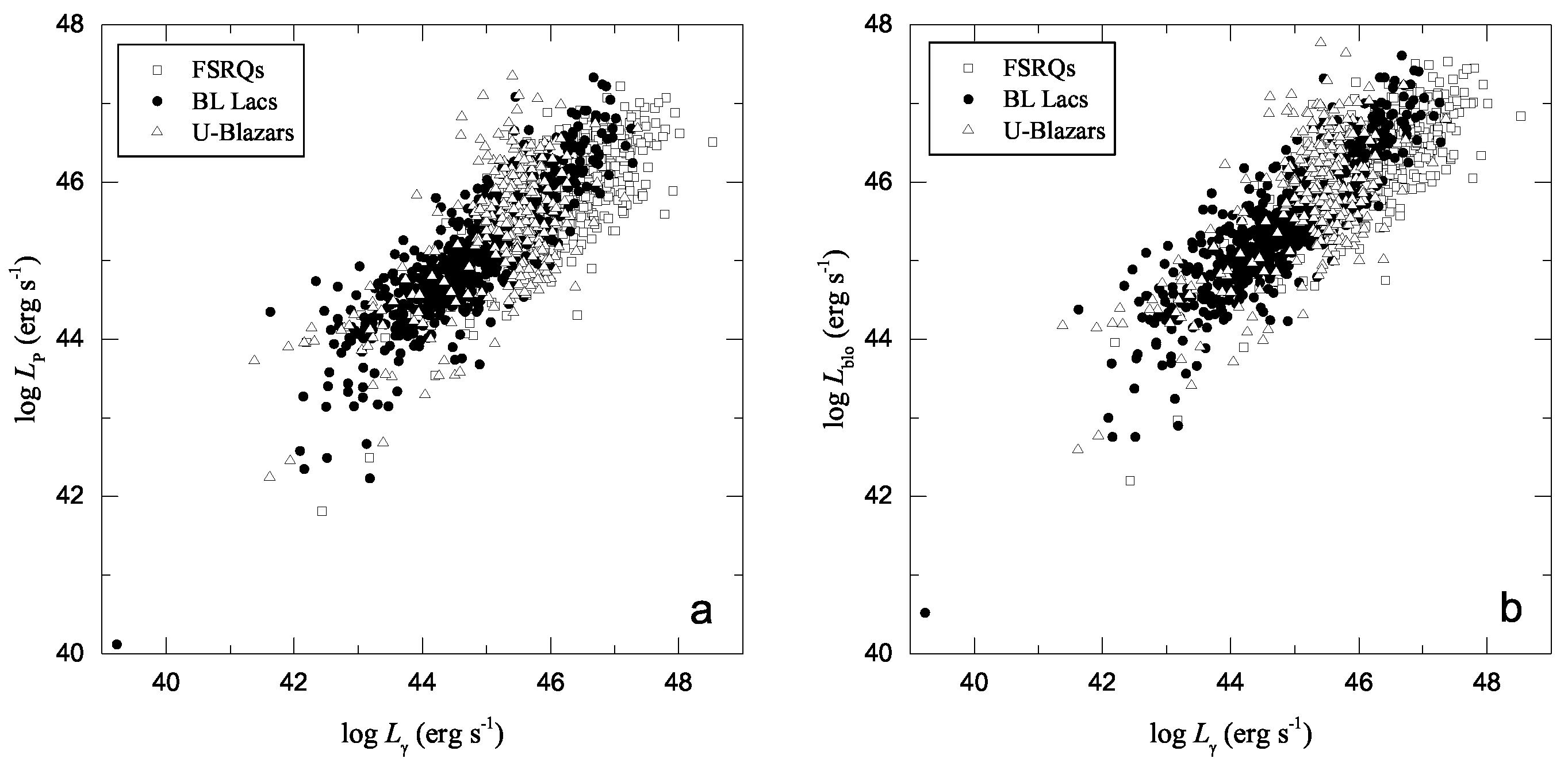
3. Correlations
4. Discussion and Conclusions
- (1)
- There are only three subclasses of Fermi blazars (LSPs, ISPs, and HSPs), and there is no extreme high peak frequency component for blazars. On the contrary, there are extreme blazars not detected by Fermi but detected by Cherenkov telescope;
- (2)
- There is an anti-correlation between broad band spectral index () and peak frequency;
- (3)
- Peak frequency can be estimated using the broad band spectral indexes;
- (4)
- The peak/bolometric luminosity can be estimated using γ/optical luminosity;
- (5)
- There is a very significant correlation between peak and bolometric luminosity.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Acero, F.; Ackermann, M.; Ajello, M.; Albert, A.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; et al. Fermi Large Area Telescope Third Source Catalog. Astrophys. J. Suppl. Ser. 2015, 218, 23–63. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Gonzalez, J.B.; Bellazzini, R.; Bissaldi, E.; et al. The Third Catalog of Active Galactic Nuclei Detected by the Fermi Large Area Telescope. Astrophys. J. 2015, 810, 14–47. [Google Scholar] [CrossRef]
- Aller, M.F.; Aller, H.D.; Hughes, P.A. Radio Band Observations of Blazar Variability. J. Astrophys. Astron. 2011, 32, 5–11. [Google Scholar] [CrossRef]
- Bai, J.M.; Xie, G.Z.; Li, K.H.; Zhang, X.; Liu, W.W. The intraday variability in the radio-selected and X-ray-selected BL Lacertae objects. Astron. Astrophys. Suppl. Ser. 1998, 132, 83–92. [Google Scholar] [CrossRef]
- Bastieri, D.; Ciprini, S.; Gasparrini, D. Fermi-LAT View of Bright Flaring Gamma-Ray Blazars. J. Astrophys. Astron. 2011, 32, 169–172. [Google Scholar] [CrossRef]
- Fan, J.H.; Xie, G.Z. The properties of BL Lacertae objects. Astrophys. Astron. 1996, 306, 55–60. [Google Scholar]
- Fan, J.H.; Yang, J.H.; Liu, Y.; Zhang, J.Y. The gamma-ray Doppler factor determinations for a Fermi blazar sample. Res. Astron. Astrophys. 2013, 13, 259–269. [Google Scholar] [CrossRef]
- Fan, J.H.; Bastieri, D.; Yang, J.H.; Liu, Y.; Hua, T.-X.; Yuan, Y.-H.; Wu, D.-X. The lower limit of the Doppler factor for a Fermi blazar sample. Res. Astron. Astrophys. 2014, 14, 1135–1145. [Google Scholar] [CrossRef]
- Gu, M.F.; Li, S.L. The ultraviolet/optical variability of steep-spectrum radio quasars: The change in accretion rate? Astron. Astrophys. 2013, 554, A51. [Google Scholar] [CrossRef]
- Gu, M.F. Spectral Variability in Radio-Loud Quasars. J. Astrophys. Astron. 2014, 35, 369–372. [Google Scholar] [CrossRef]
- Gupta, A.C. UV and X-ray Variability of Blazars. J. Astrophys. Astron. 2011, 32, 155–161. [Google Scholar] [CrossRef]
- Gupta, A.C.; Krichbaum, T.P.; Wiita, P.J.; Rani, B.; Sokolovsky, K.V.; Mohan, P.; Mangalam, A.; Marchili, N.; Fuhrmann, L.; Agudo, I.; et al. Multiwavelength intraday variability of the BL Lacertae S5 0716+714. Mon. Not. R. Astron. Soc. 2012, 425, 1357–1370. [Google Scholar] [CrossRef]
- Hu, S.M.; Zhao, G.; Guo, H.Y.; Zhang, X.; Zheng, Y.G. The optical spectral slope variability of 17 blazars. Mon. Not. R. Astron. Soc. 2006, 371, 1243–1250. [Google Scholar] [CrossRef]
- Lin, C.; Fan, J.H. Comparison between TeV and non-TeV BL Lac Objects. Res. Astrophys. Astron. 2016, 16, 88. [Google Scholar] [CrossRef]
- Romero, G.E.; Cellone, S.A.; Combi, J.A.; Andruchow, I. Optical microvariability of EGRET blazars. Astron. Astrophys. 2002, 390, 431–438. [Google Scholar] [CrossRef]
- Urry, M. Gamma-Ray and Multiwavelength Emission from Blazars. J. Astrophys. Astron. 2011, 32, 139–145. [Google Scholar] [CrossRef]
- Wehrle, A. Multi-wavelength studies of blazars BL Lac and 3C454.3. In Proceedings of the Blazars through Sharp Multi-Wavelength Eyes, Malaga, Spain, 30 May–3 June 2016.
- Wills, B.J.; Wills, D.; Breger, M.; Antonucci, R.R.J.; Barvainis, R. A survey for high optical polarization in quasars with core-dominant radio structure—Is there a beamed optical continuum? Astrophys. J. 1992, 398, 454–475. [Google Scholar] [CrossRef]
- Wu, Q.W.; Yuan, F.; Cao, X.W. On the Origin of X-Ray Emission in Some FR I Galaxies: ADAF or Jet? Astrophys. J. 2007, 669, 96–105. [Google Scholar] [CrossRef]
- Yang, J.H.; Fan, J.H.; Yang, R.S. The line emissions and polarization in blazars. Sci. China Phys. Mech. Astron. 2010, 53, 1162–1168. [Google Scholar] [CrossRef]
- Yang, J.H.; Fan, J.H. The central black hole masses for the γ-ray loud blazars. Sci. China Phys. Mech. Astron. 2010, 53, 1921–1927. [Google Scholar] [CrossRef]
- Yang, J.H.; Fan, J.H.; Yuan, Y.H. Lorentz factor estimation for radio sources. Sci. China Phys. Mech. Astron. 2012, 55, 1510–1514. [Google Scholar] [CrossRef]
- Yang, J.H.; Fan, J.H.; Nie, J.J.; Yang, R.S. The gamma-ray spectral index changes for blazars. Sci. China Phys. Mech. Astron. 2012, 55, 2179–2185. [Google Scholar] [CrossRef]
- Yang, J.H.; Fan, J.H.; Hua, T.X.; Wu, D.X. The γ-ray emission mechanism for Fermi Blazars. Astrophys. Space Sci. 2014, 352, 819–824. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Agudo, I.; Ajello, M.; Aller, H.D.; Aller, M.F.; Angelakis, E.; Arkharov, A.A.; Axelsson, M.; Bach, U.; et al. The Spectral Energy Distribution of Fermi Bright Blazars. Astrophysi. J. 2010, 716, 30–70. [Google Scholar] [CrossRef]
- Fan, J.H.; Yang, J.H.; Liu, Y.; Luo, G.Y.; Lin, C.; Yuan, Y.H.; Xiao, H.B.; Zhou, A.Y.; Hua, T.X.; Pei, Z.Y. The Spectral Energy Distributions of Fermi Blazars. Astrophys. J. Suppl. Ser. 2016, in press. [Google Scholar]
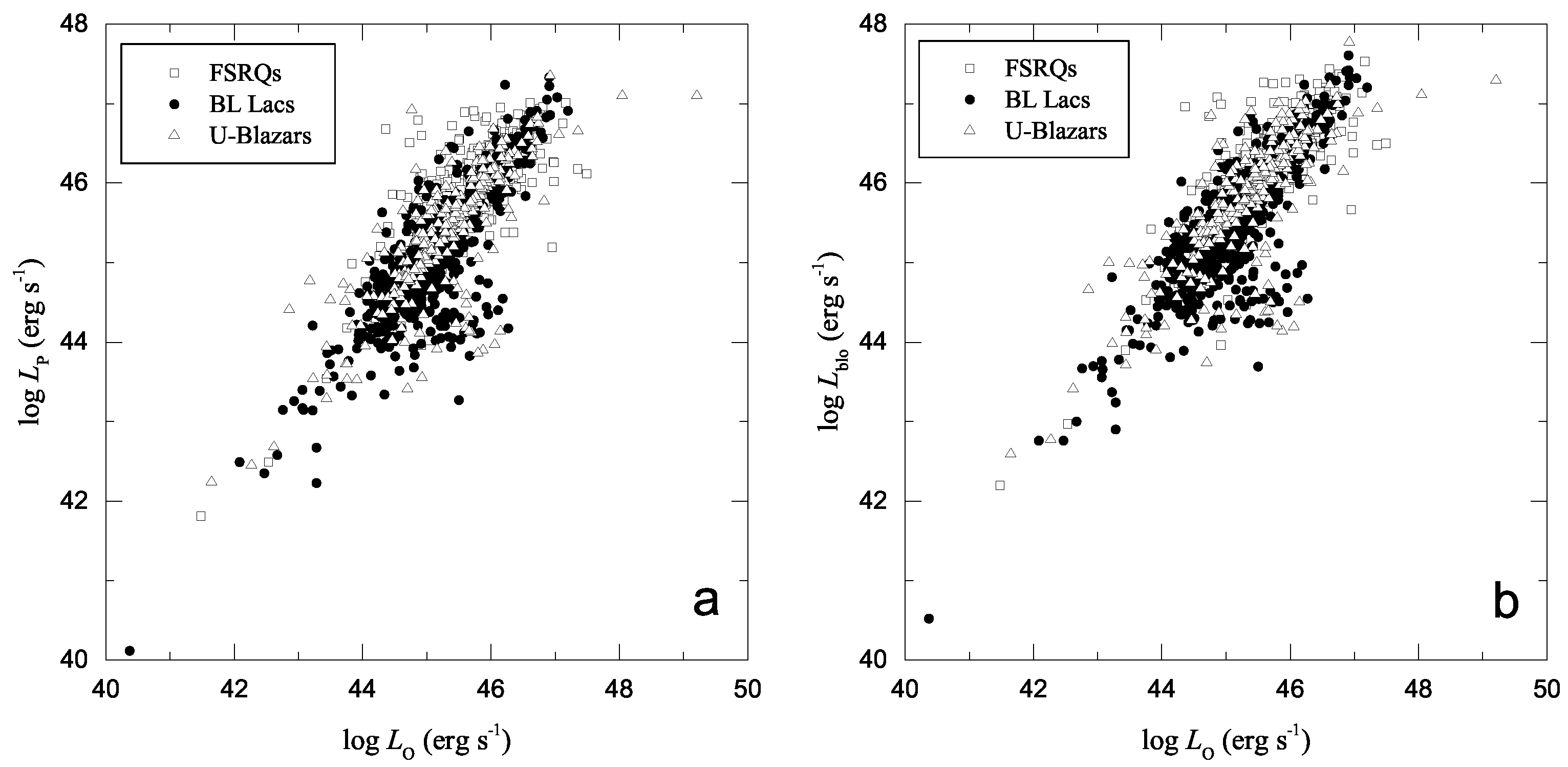
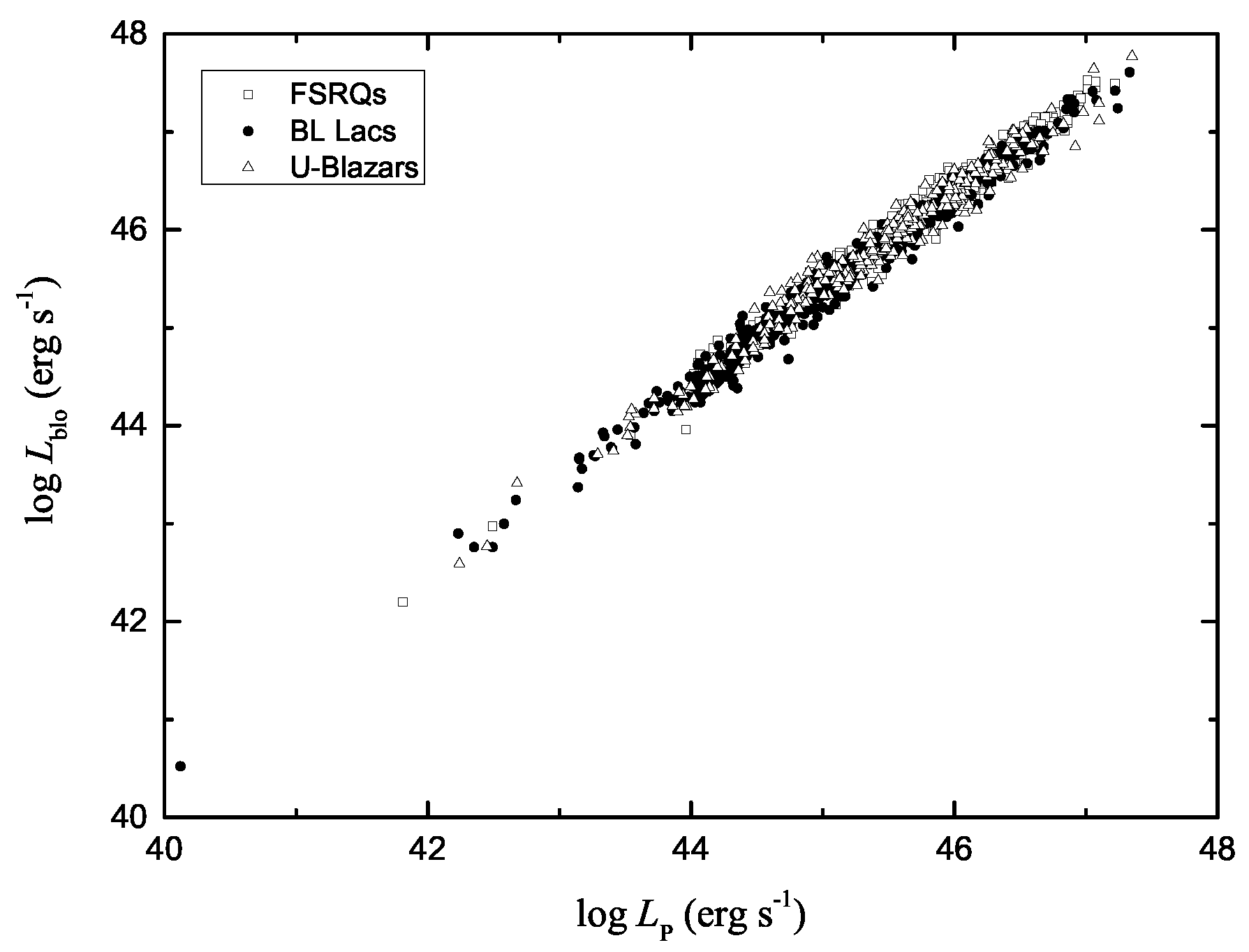
| y vs. x | Sample | a a | b b | r | N | p |
|---|---|---|---|---|---|---|
| vs. | All Blazars | −0.078 ± 0.002 | 1.822 ± 0.026 | 0.837 | 853 | |
| FSRQs | −0.017 ± 0.006 | 1.025 ± 0.077 | 0.174 | 283 | 0.33% | |
| BL Lacs | −0.079 ± 0.003 | 1.836 ± 0.046 | 0.787 | 428 | ||
| HBLs | −0.039 ± 0.006 | 1.178 ± 0.090 | 0.473 | 176 | ||
| IBLs | −0.071 ± 0.005 | 1.740 ± 0.076 | 0.663 | 244 | ||
| LBLs | 0.018 ± 0.038 | 0.567 ± 0.497 | 0.195 | 8 | 64.31% | |
| vs. | All Blazars | 0.866 ± 0.016 | 6.145 ± 0.747 | 0.818 | 1360 | |
| FSRQs | 0.765 ± 0.028 | 10.921 ± 1.275 | 0.792 | 447 | ||
| BL Lacs | 0.886 ± 0.025 | 5.086 ± 1.110 | 0.824 | 614 | ||
| HBLs | 0.818 ± 0.042 | 8.140 ± 1.875 | 0.811 | 202 | ||
| IBLs | 0.933 ± 0.032 | 2.921 ± 1.458 | 0.841 | 347 | ||
| LBLs | 0.871 ± 0.068 | 6.141 ± 3.076 | 0.849 | 65 | ||
| vs. | All Blazars | 0.851 ± 0.016 | 7.212 ± 0.735 | 0.818 | 1360 | |
| FSRQs | 0.775 ± 0.026 | 10.870 ± 1.163 | 0.821 | 447 | ||
| BL Lacs | 0.859 ± 0.025 | 6.696 ± 1.112 | 0.816 | 614 | ||
| HBLs | 0.791 ± 0.042 | 9.837 ± 1.907 | 0.797 | 202 | ||
| IBLs | 0.913 ± 0.033 | 4.183 ± 1.483 | 0.832 | 347 | ||
| LBLs | 0.851 ± 0.069 | 7.287 ± 3.123 | 0.840 | 65 | ||
| vs. | All Blazars | 0.973 ± 0.004 | 1.601 ± 0.169 | 0.990 | 1392 | |
| FSRQs | 0.962 ± 0.008 | 2.136 ± 0.354 | 0.986 | 461 | ||
| BL Lacs | 0.970 ± 0.005 | 1.728 ± 0.237 | 0.991 | 620 | ||
| HBLs | 0.978 ± 0.007 | 1.459 ± 0.299 | 0.995 | 207 | ||
| IBLs | 0.984 ± 0.006 | 1.072 ± 0.248 | 0.995 | 348 | ||
| LBLs | 0.975 ± 0.020 | 1.376 ± 0.904 | 0.987 | 65 | ||
| vs. | All Blazars | 0.595 ± 0.012 | 18.384 ± 0.525 | 0.810 | 1392 | |
| FSRQs | 0.584 ± 0.023 | 18.806 ± 1.060 | 0.765 | 461 | ||
| BL Lacs | 0.675 ± 0.016 | 14.835 ± 0.723 | 0.860 | 620 | ||
| HBLs | 0.701 ± 0.037 | 13.754 ± 1.644 | 0.798 | 207 | ||
| IBLs | 0.705 ± 0.018 | 13.419 ± 0.807 | 0.904 | 348 | ||
| LBLs | 0.572 ± 0.059 | 19.498 ± 2.663 | 0.775 | 65 | ||
| vs. | All Blazars | 0.597 ± 0.011 | 18.717 ± 0.497 | 0.825 | 1392 | |
| FSRQs | 0.583 ± 0.022 | 19.277 ± 1.002 | 0.782 | 461 | ||
| BL Lacs | 0.670 ± 0.015 | 15.449 ± 0.679 | 0.872 | 620 | ||
| HBLs | 0.699 ± 0.035 | 14.311 ± 1.572 | 0.810 | 207 | ||
| IBLs | 0.712 ± 0.016 | 13.478 ± 0.722 | 0.922 | 348 | ||
| LBLs | 0.619 ± 0.049 | 17.631 ± 2.203 | 0.848 | 65 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, J.; Liu, Y.; Yang, J.; Lin, C.; Hao, J.; Xiao, H. The Classifications and Some Correlations for Fermi Blazars. Galaxies 2016, 4, 16. https://doi.org/10.3390/galaxies4030016
Fan J, Liu Y, Yang J, Lin C, Hao J, Xiao H. The Classifications and Some Correlations for Fermi Blazars. Galaxies. 2016; 4(3):16. https://doi.org/10.3390/galaxies4030016
Chicago/Turabian StyleFan, Junhui, Yi Liu, Jianghe Yang, Chao Lin, Jingmeng Hao, and Hubing Xiao. 2016. "The Classifications and Some Correlations for Fermi Blazars" Galaxies 4, no. 3: 16. https://doi.org/10.3390/galaxies4030016
APA StyleFan, J., Liu, Y., Yang, J., Lin, C., Hao, J., & Xiao, H. (2016). The Classifications and Some Correlations for Fermi Blazars. Galaxies, 4(3), 16. https://doi.org/10.3390/galaxies4030016