On the Number of Galaxies at High Redshift
Abstract
:1. Introduction
2. Basic Formulae
2.1. Magnitude System

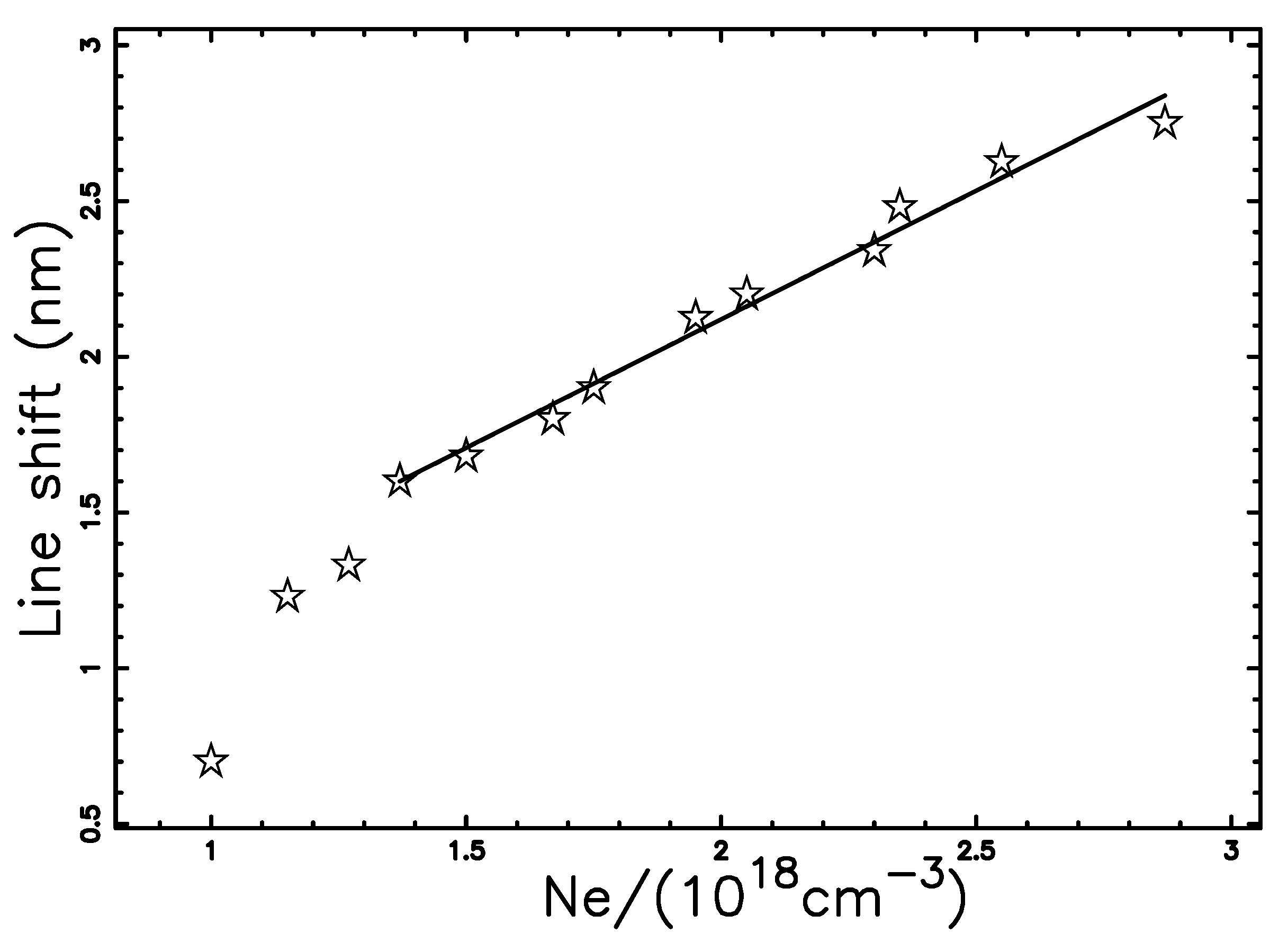
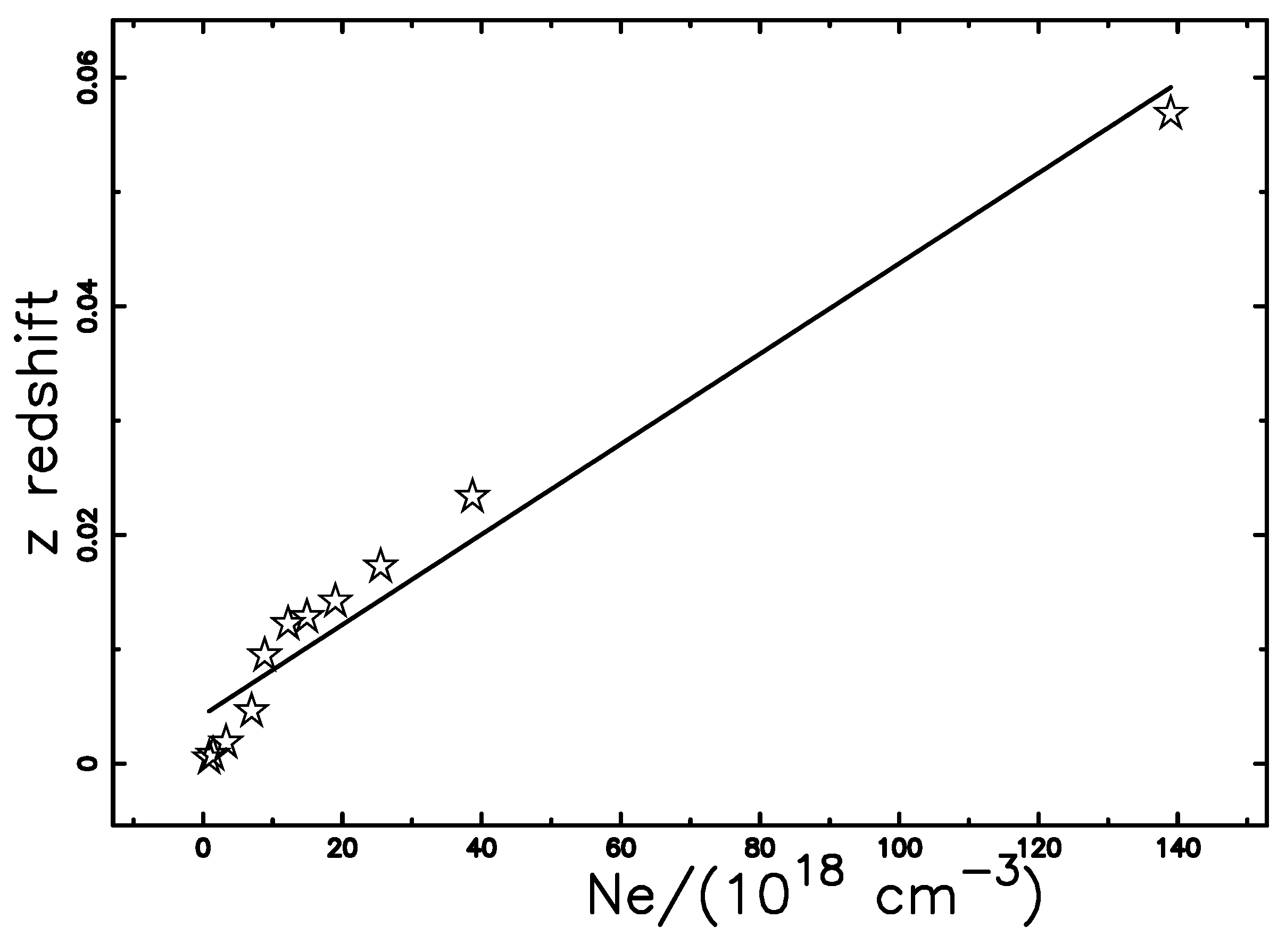
2.2. Tired Light
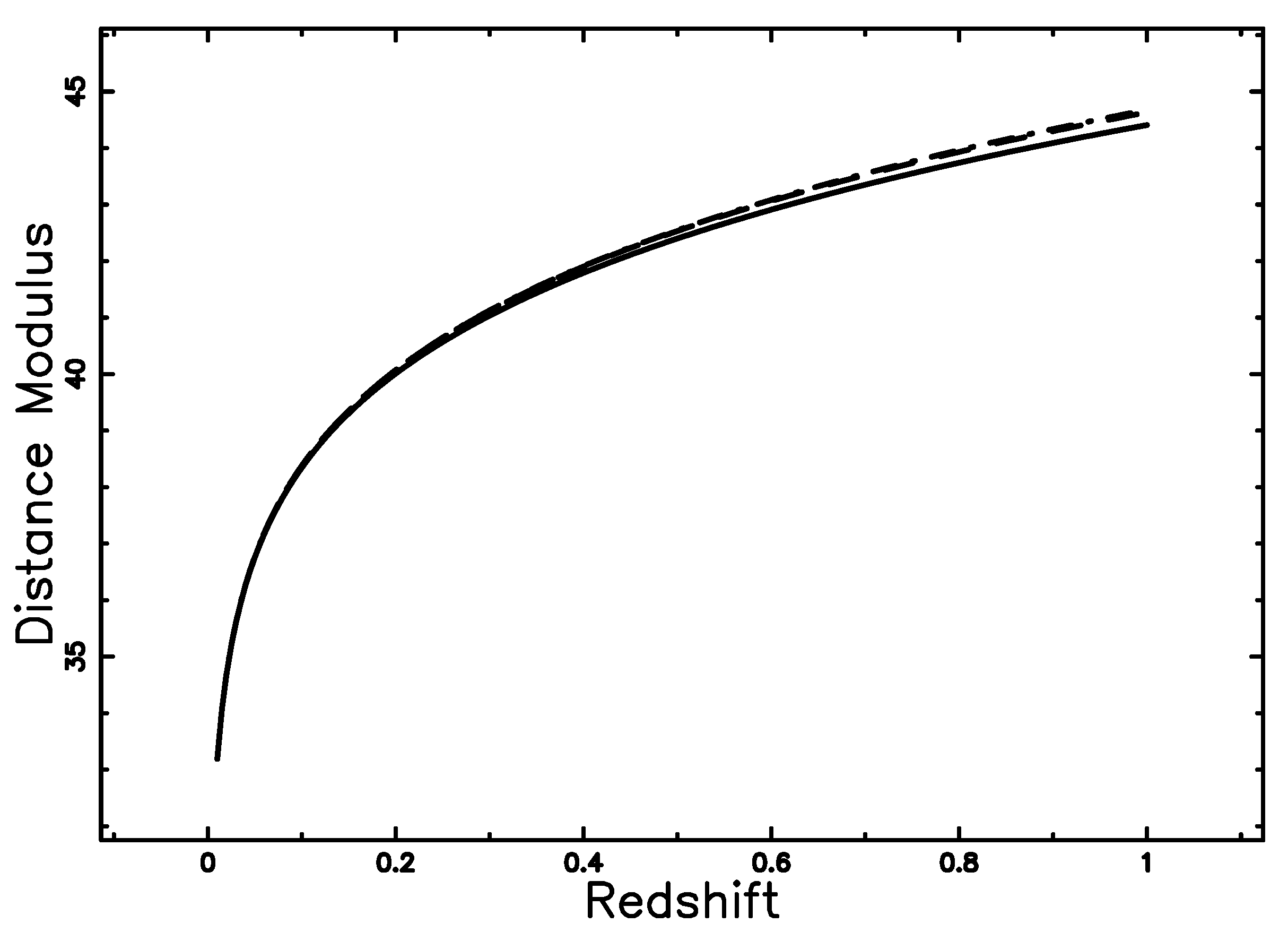
2.3. The Luminosity Function
3. N–z Relation
3.1. The Linear Case
3.2. The Nonlinear Case
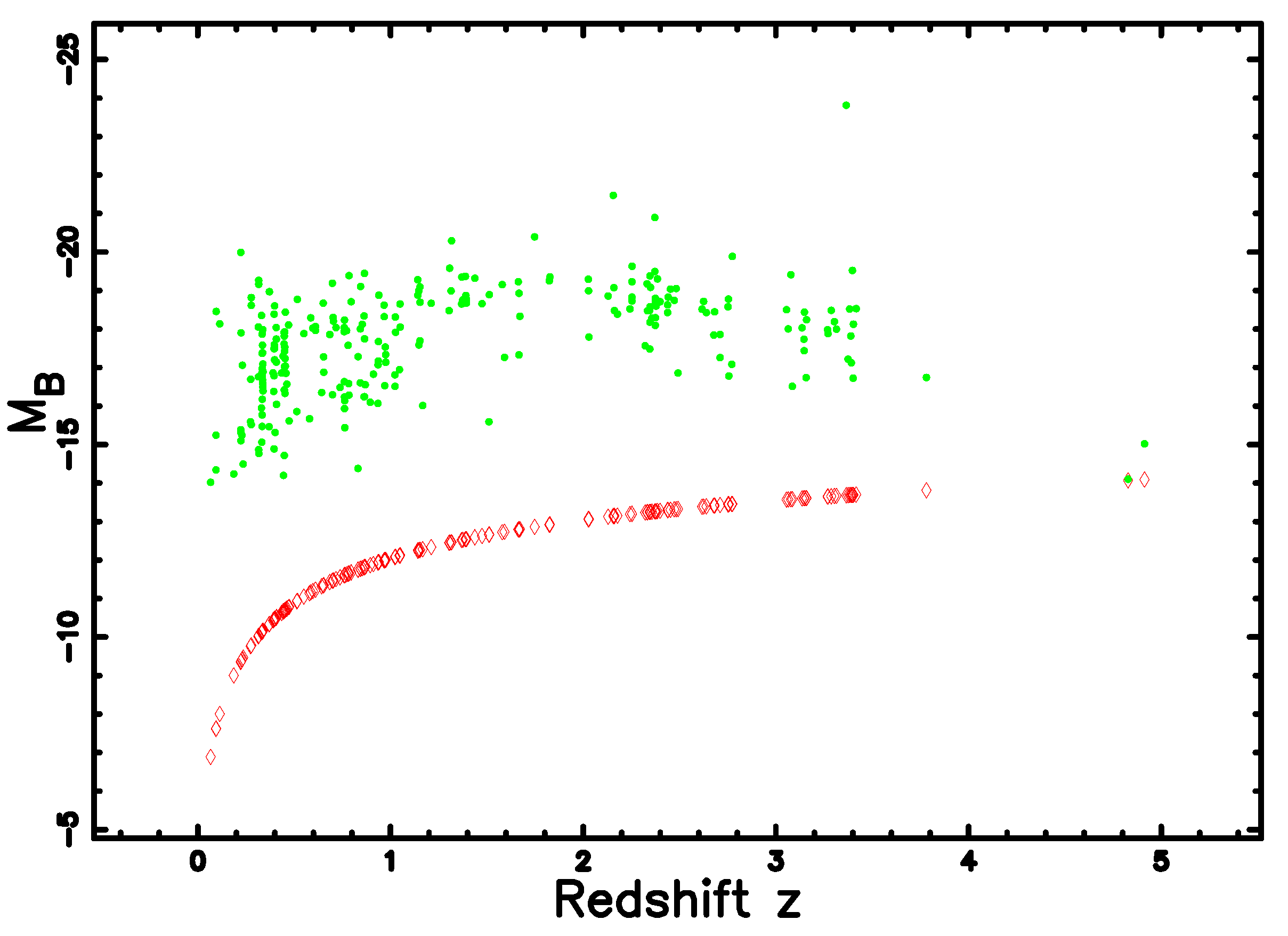
4. Astrophysical Applications
- (1)
- A window in apparent magnitude or flux is chosen around m or f.
- (2)
- All the galaxies which fall in the window are selected.
- (3)
- The mean value in redshift of N selected galaxies is and the uncertainty in the mean, , is where s is the standard deviation, see formula (4.14) in [34].
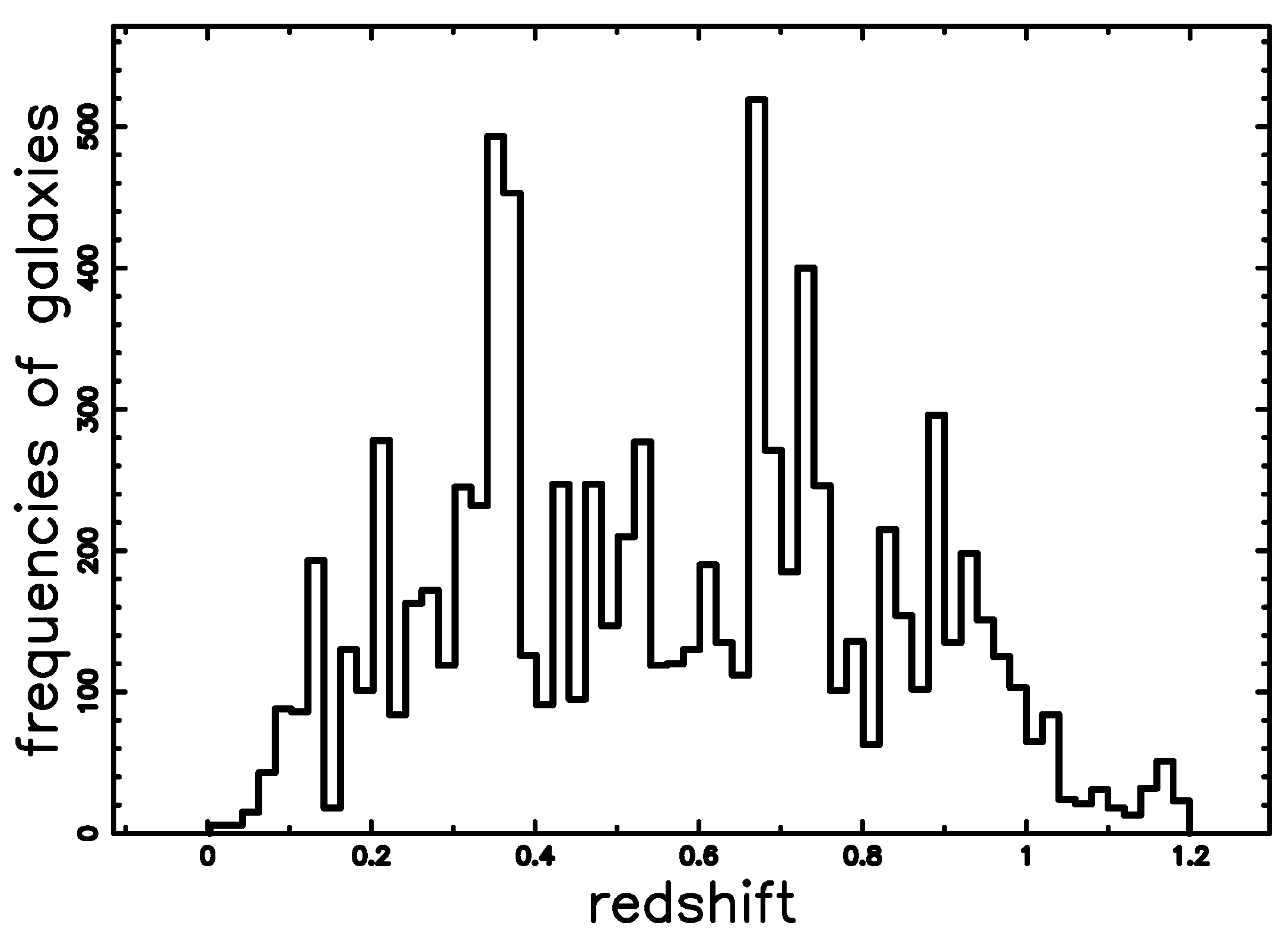
4.1. The FDF Catalog


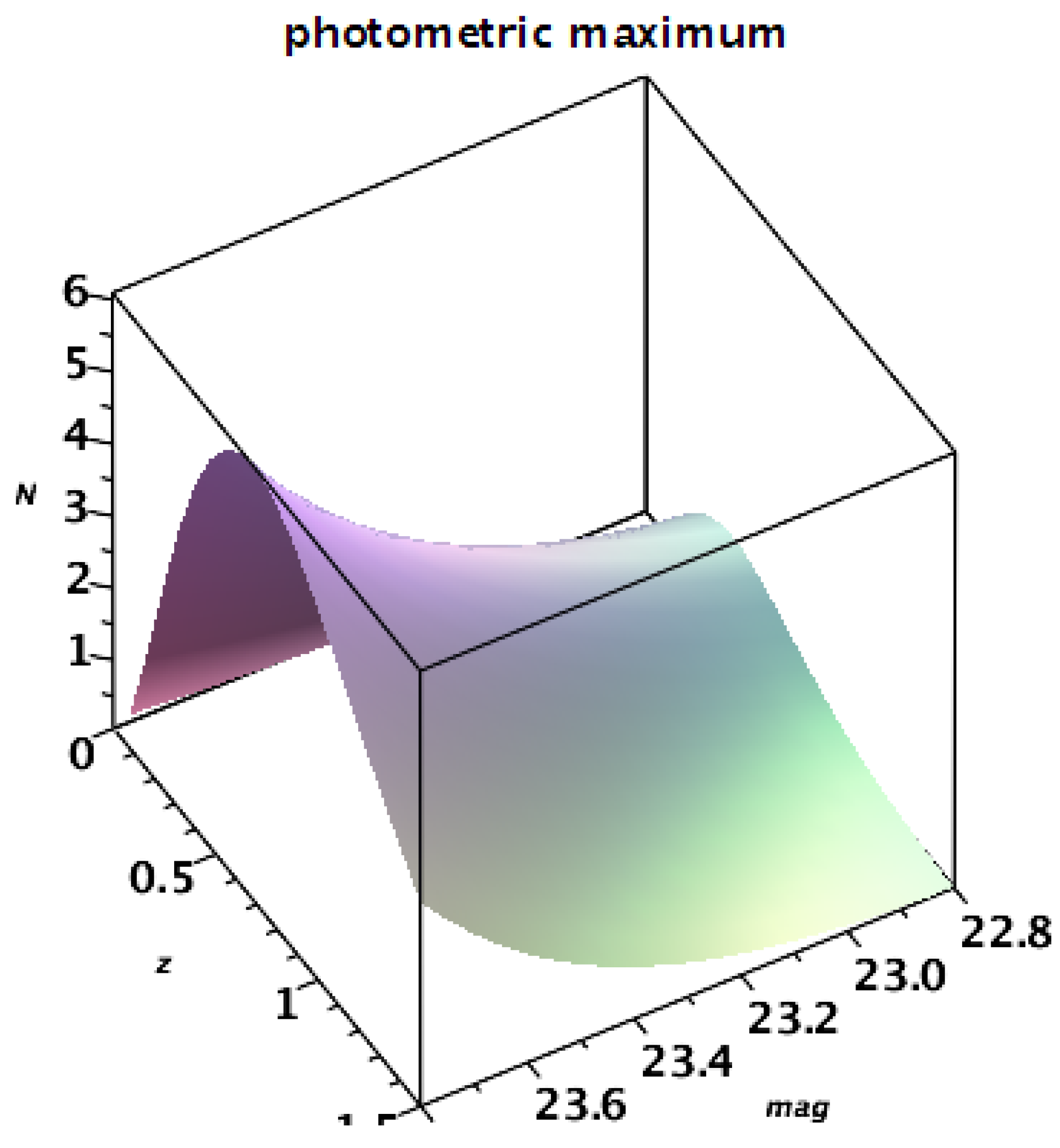
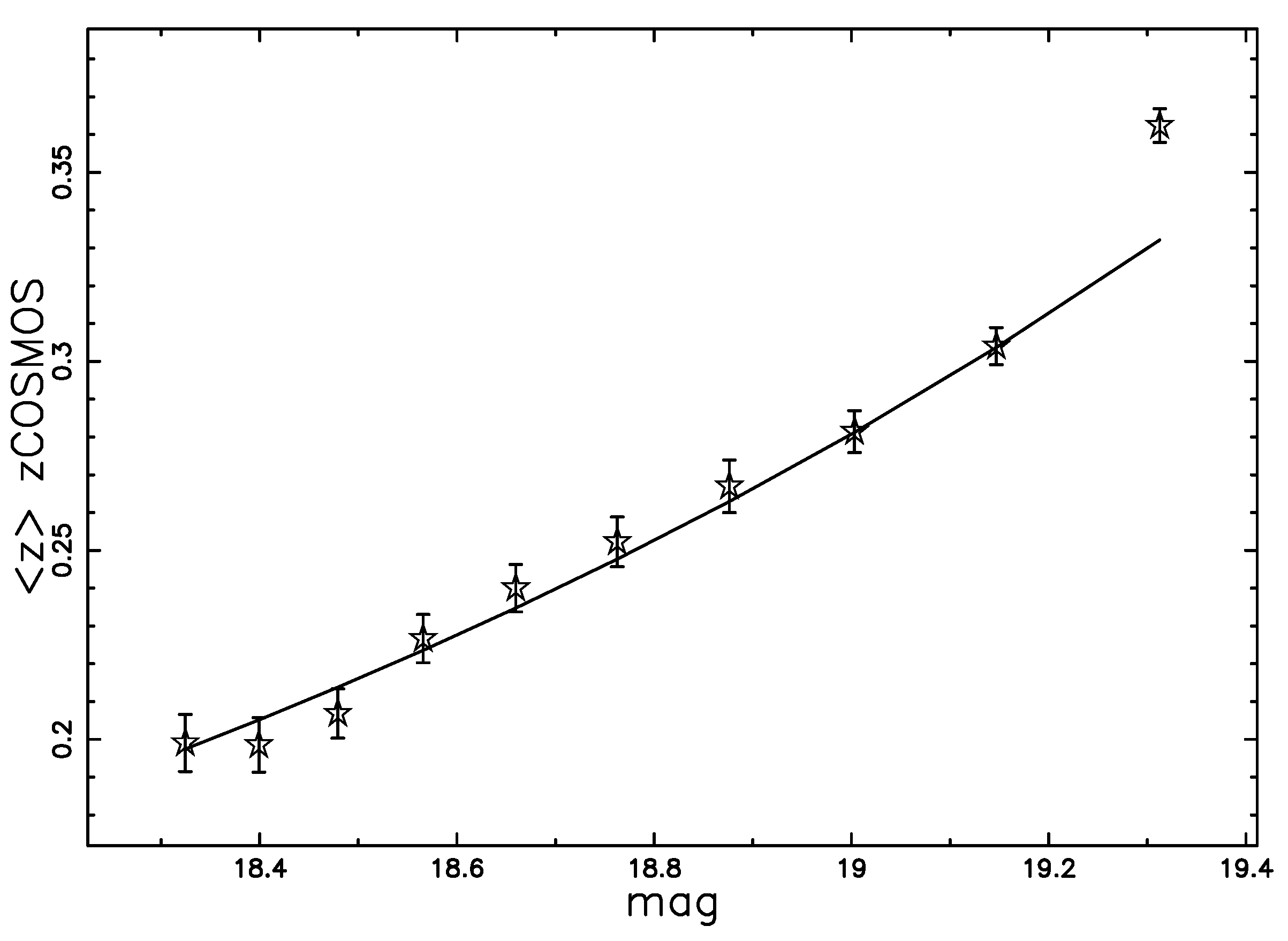
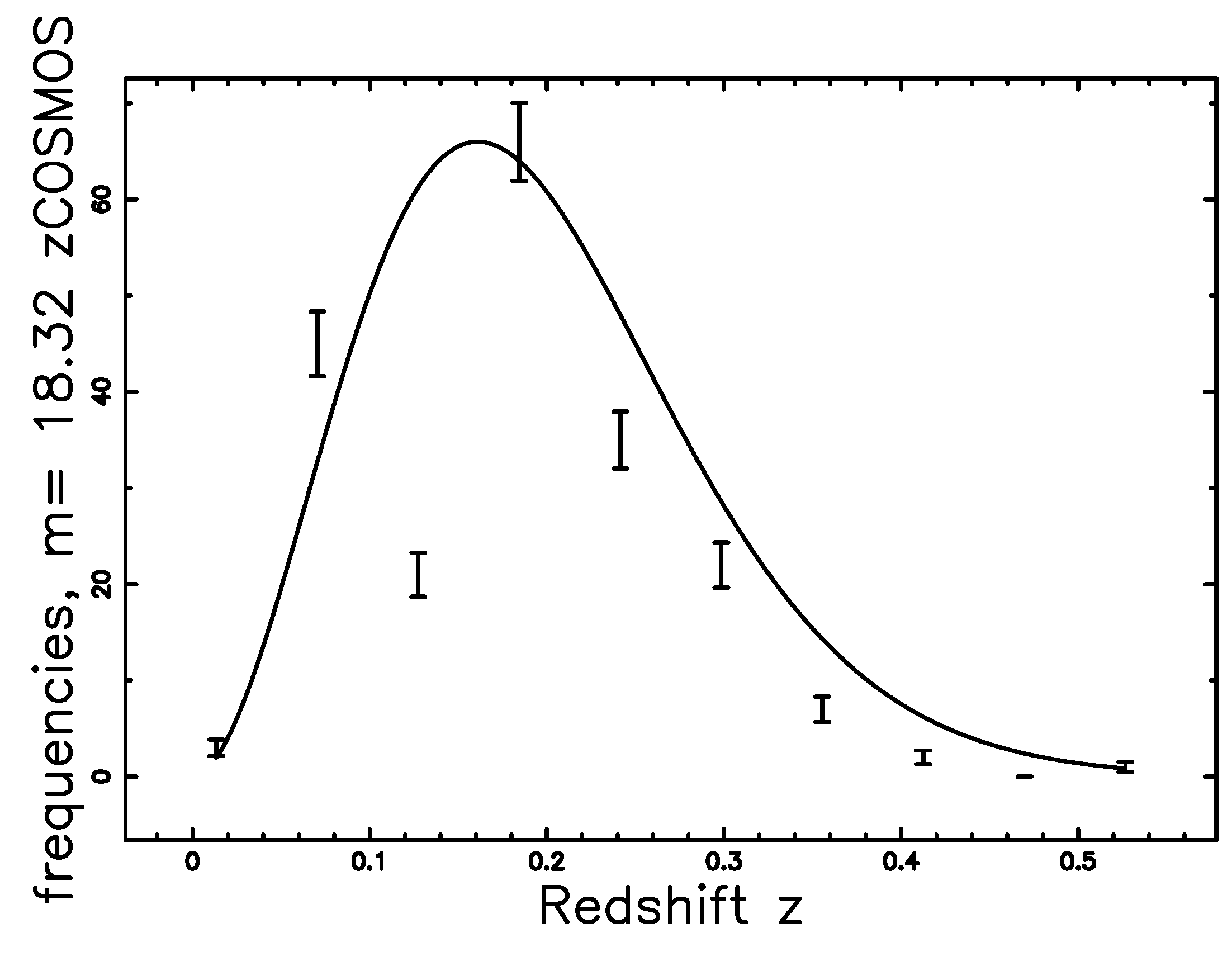
4.2. The zCOSMOS Catalog
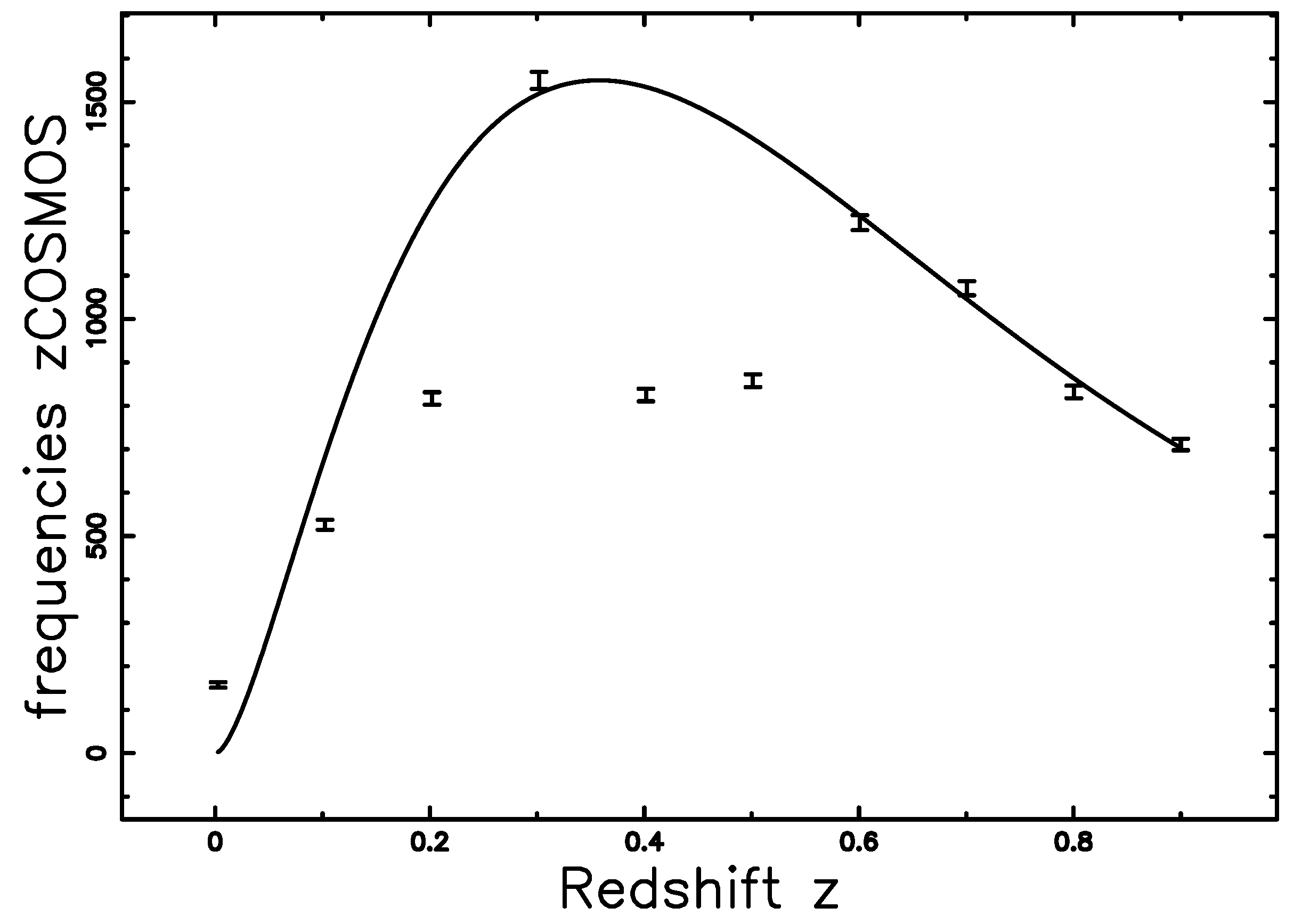
5. The Relativistic Case
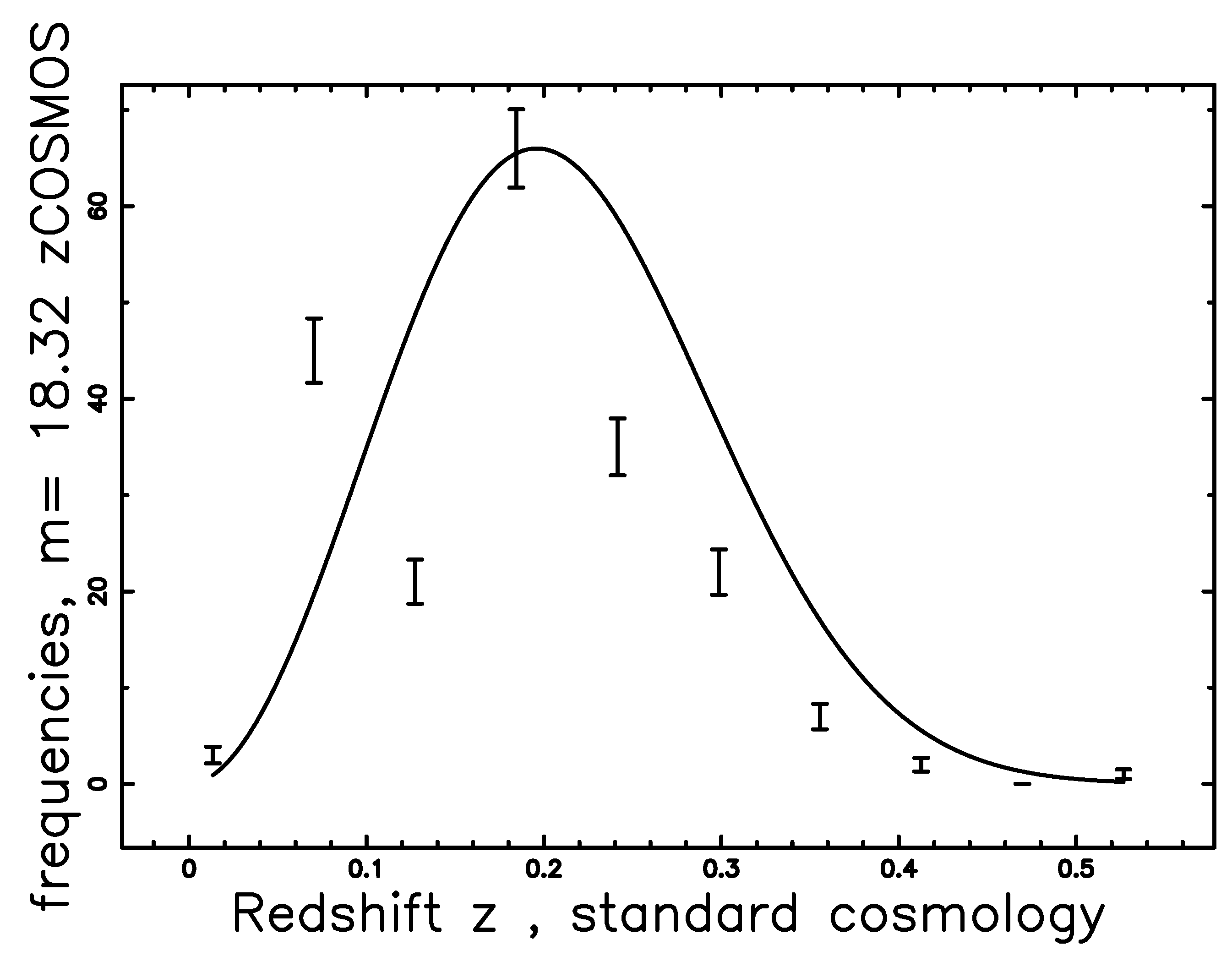

6. Evolutionary Effects
- (1)
- A value for the redshift is fixed, z, as well as the thickness of the layer, .
- (2)
- All the galaxies comprised between z and are selected.
- (3)
- The absolute magnitude can be computed from Equation (28) which represents the distance modulus for tired light.
- (4)
- The distribution in magnitude is organized in frequencies versus absolute magnitude.
- (5)
- The frequencies are divided by the volume, which is , where r is the considered radius, is the thickness of the radius, and Ω is the solid angle of ZCOSMOS.
- (6)
- The error in the observed LF is obtained as the square root of the frequencies divided by the volume.
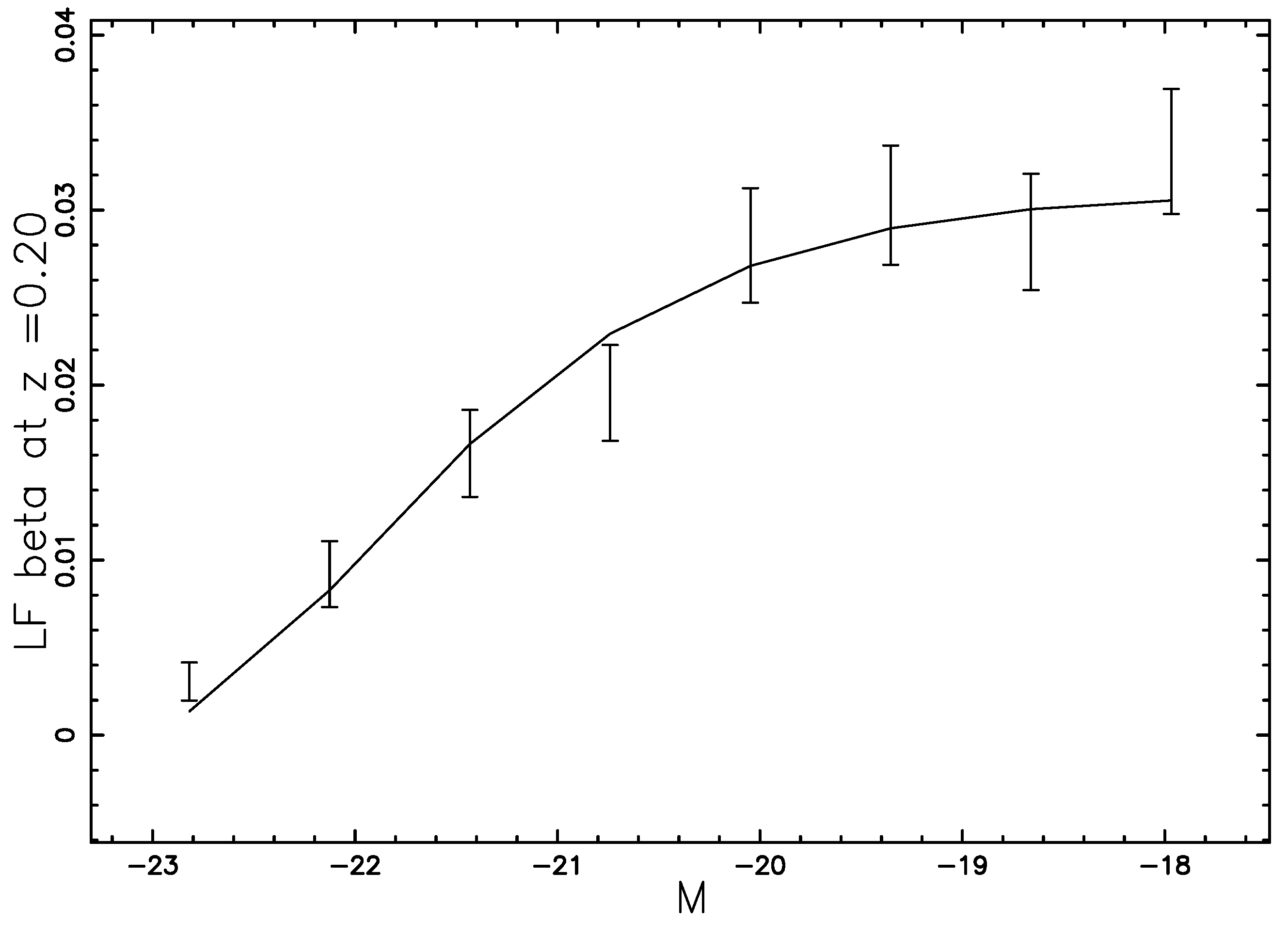
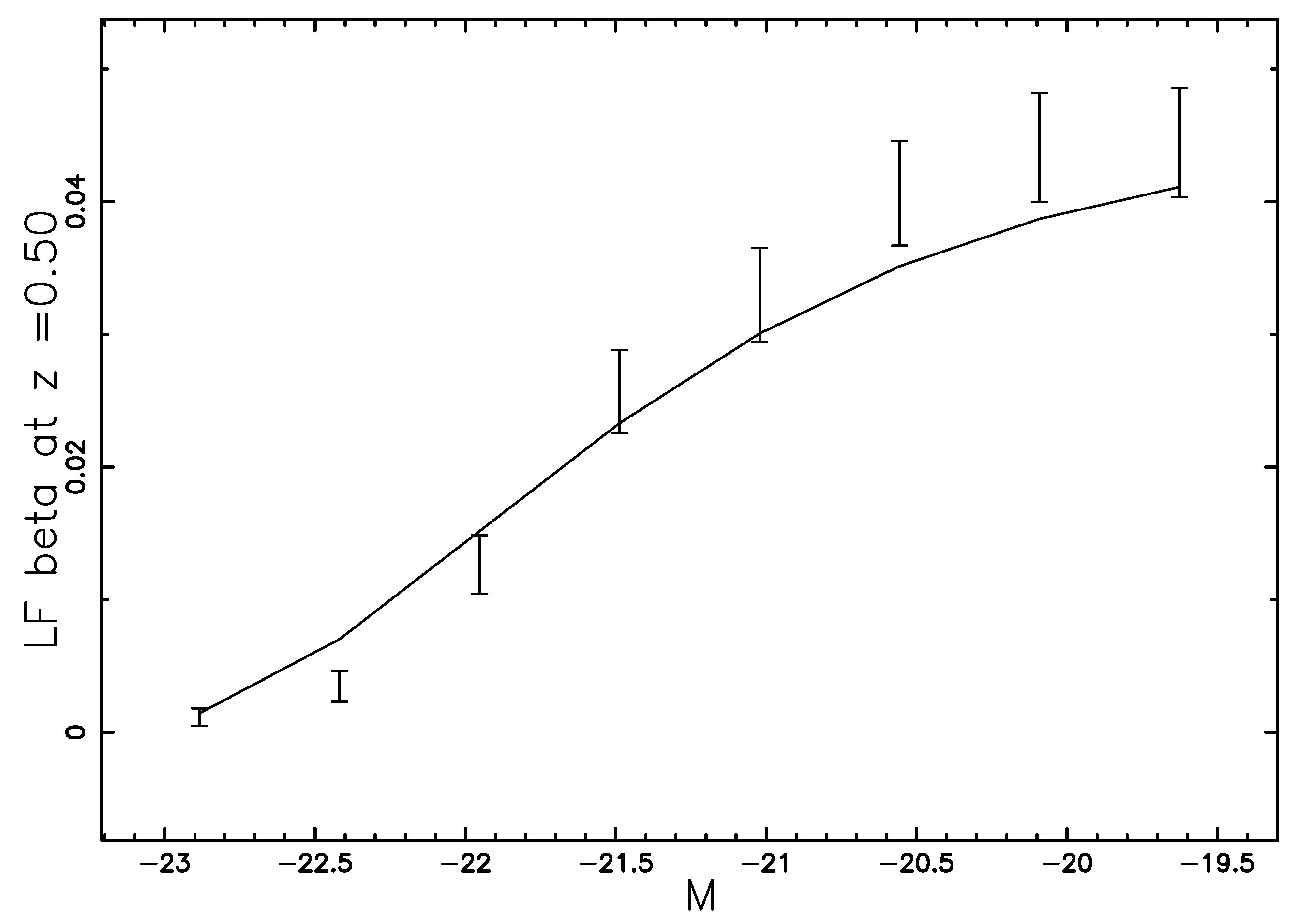
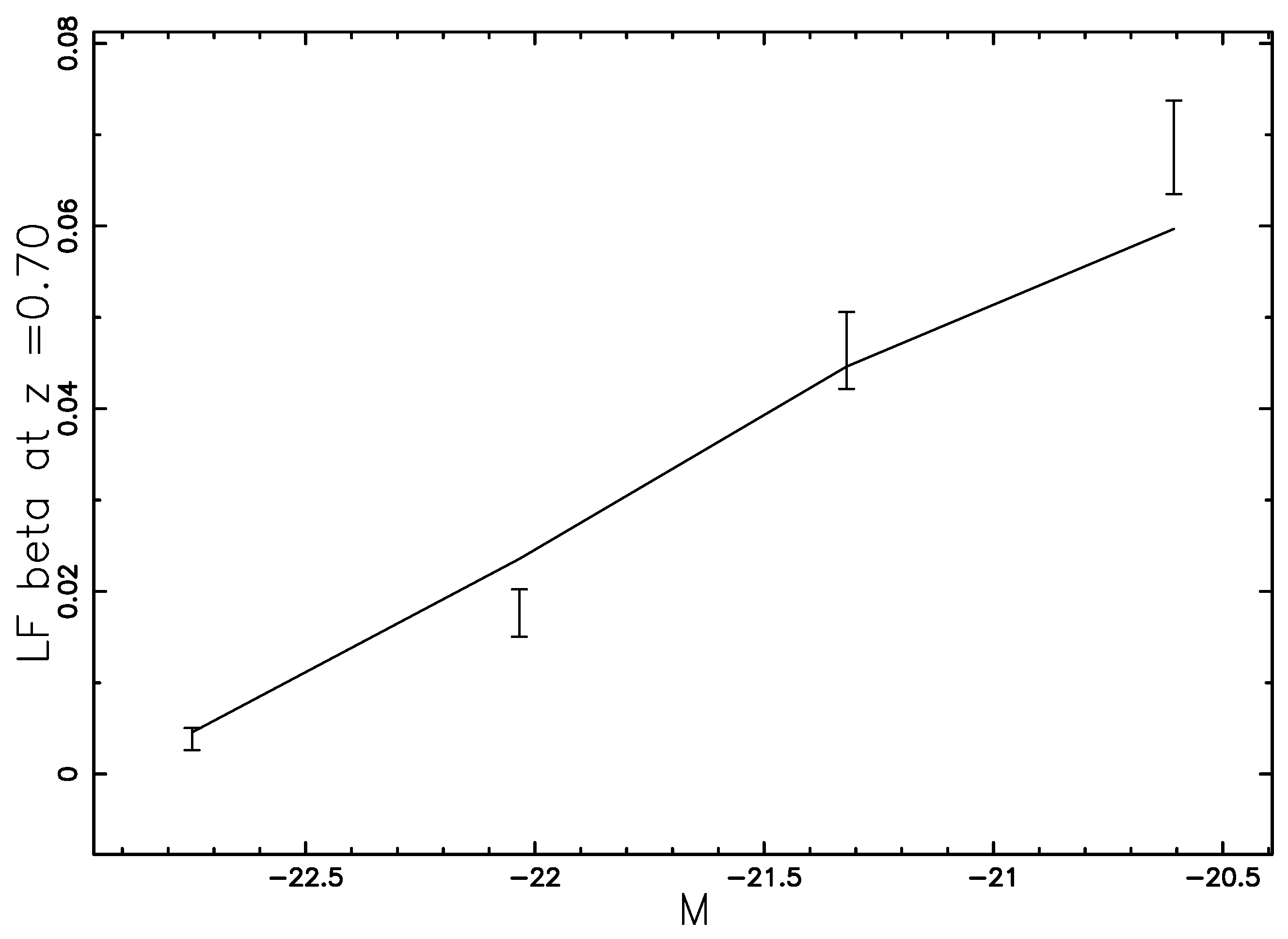

7. Conclusions
7.1. Results
7.2. Generalizated Tired Light
7.3. Tired Light versus GR
7.4. The Cells
Acknowledgments
Conflicts of Interest
References
- Mohr, P.J.; Taylor, B.N.; Newell, D.B. CODATA recommended values of the fundamental physical constants: 2010. Rev. Mod. Phys. 2012, 84, 1527–1605. [Google Scholar] [CrossRef]
- Kaiser, N. Astronomical redshifts and the expansion of space. Mon. Not. R. Astron. Soc. 2014, 438, 2456–2465. [Google Scholar] [CrossRef]
- Brynjolfsson, A. Redshift of Photons Penetrating a Hot Plasma; Cornell University: Ithaca, NY, USA, 2004. [Google Scholar]
- Ashmore, L. Recoil Between Photons and Electrons Leading to the Hubble Constant and CMB. Galilean Electrodyn. 2006, 17, 53–57. [Google Scholar]
- Crawford, D.F. Observational Evidence Favors a Static Universe (Part I). J. Cosmol. 2011, 13, 3875–3946. [Google Scholar]
- Marmet, L. Survey of Redshift Relationships for the Proposed Mechanisms at the 2nd Crisis in Cosmology Conference, Proceedings of the 2nd Crisis in Cosmology Conference, Port Angeles, WA, USA, 7–11 September 2008; Potter, F., Ed.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2009; Volume 413, pp. 315–335.
- Bennett, C.L.; Larson, D.; Weiland, J.L.; Hinshaw, G. The 1% Concordance Hubble Constant. Astrophys. J. 2014, 794, 135. [Google Scholar] [CrossRef]
- Friedmann, A. Über die Krümmung des Raumes. Z. Phys. 1922, 10, 377–386. [Google Scholar] [CrossRef]
- Friedmann, A. Über die Möglichkeit einer Welt mit konstanter negativer Krümmung des Raumes. Z. Phys. 1924, 21, 326–332. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A. Measurements of Omega and Lambda from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Gabasch, A.; Bender, R.; Seitz, S.; Hopp, U.; Saglia, R.P.; Feulner, G.; Snigula, J.; Drory, N.; Appenzeller, I.; Heidt, J.; et al. The evolution of the luminosity functions in the FORS Deep Field from low to high redshift. I. The blue bands. Astron. Astrophys. 2004, 421, 41–58. [Google Scholar] [CrossRef]
- Appenzeller, I.; Bender, R.; Böhm, A.; Frank, S.; Fricke, K.; Gabasch, A.; Heidt, J.; Hopp, U.; Jäger, K.; Mehlert, D.; et al. Exploring Cosmic Evolution with the FORS Deep Field. Messenger 2004, 116, 18–24. [Google Scholar]
- Lilly, S.J.; Le Brun, V.; Maier, C.; Mainieri, V. The zCOSMOS 10k-Bright Spectroscopic Sample. Astrophys. J. Suppl. Ser. 2009, 184, 218–229. [Google Scholar] [CrossRef]
- Zwicky, F. On the Red Shift of Spectral Lines through Interstellar Space. Proc. Natl. Acad. Sci. 1929, 15, 773–779. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.S.; Zhou, X.L.; Man, B.Y.; Zhang, Y.Q.; Guo, J. Investigation of the mechanism of spectral emission and redshifts of atomic line in laser-induced plasmas. Optik 2009, 120, 473–478. [Google Scholar] [CrossRef]
- Nguyen, H.; Koenig, M.; Benredjem, D.; Caby, M.; Coulaud, G. Atomic structure and polarization line shift in dense and hot plasmas. Phys. Rev. A 1986, 33, 1279–1290. [Google Scholar] [CrossRef] [PubMed]
- Leng, Y.; Goldhar, J.; Griem, H.R.; Lee, R.W. C vi Lyman line profiles from 10-ps KrF-laser-produced plasmas. Phys. Rev. E 1995, 52, 4328–4337. [Google Scholar] [CrossRef]
- Saemann, A.; Eidmann, K.; Golovkin, I.E. Isochoric heating of solid aluminum by ultrashort laser pulses focused on a tamped target. Phys. Rev. Lett. 1999, 82, 4843–4846. [Google Scholar] [CrossRef]
- Zhidkov, A.G.; Sasaki, A.; Tajima, T. Direct spectroscopic observation of multiple-charged-ion acceleration by an intense femtosecond-pulse laser. Phys. Rev. E 1999, 60, 3273–3278. [Google Scholar] [CrossRef]
- Wang, H.; Yang, X.; Li, X. Ground-State Energy Shifts of H-Like Ti Under Dense and Hot Plasma Conditions. Plasma Sci. Technol. 2007, 9, 128–132. [Google Scholar]
- Ashmore, L. Intrinsic Plasma Redshifts Now Reproduced In the Laboratory—A Discussion in Terms of New Tired Light; Cornell University: Ithaca, NY, USA, 2011. [Google Scholar]
- Kielkopf, J.F.; Allard, N.F. Shift and width of the Balmer series Halpha line at high electron density in a laser-produced plasma. J. Phys. B 2014, 47, 155701. [Google Scholar] [CrossRef]
- Malmquist, K. A study of the stars of spectral type A. Lund Medd. Ser. II 1920, 22, 1–10. [Google Scholar]
- Malmquist, K. On some relations in stellar statistics. Lund Medd. Ser. I 1922, 100, 1–10. [Google Scholar]
- Behr, A. Zur Entfernungsskala der extragalaktischen Nebel. Astron. Nachr. 1951, 279, 97–107. [Google Scholar] [CrossRef]
- Brynjolfsson, A. Magnitude-Redshift Relation for SNe Ia, Time Dilation, and Plasma Redshift; Cornell University: Ithaca, NY, USA, 2006. [Google Scholar]
- Sandage, A. The Ability of the 200-INCH Telescope to Discriminate Between Selected World Models. Astrophys. J. 1961, 133, 355. [Google Scholar] [CrossRef]
- Hoyle, F.; Sandage, A. The Second-Order Term in the Redshift-Magnitude Relation. Publ. Astron. Soc. Pac. 1956, 68, 301–307. [Google Scholar] [CrossRef]
- Schechter, P. An analytic expression for the luminosity function for galaxies. Astrophys. J. 1976, 203, 297–306. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Principles of Physical Cosmology; Princeton University Press: Princeton, NJ, USA, 1993. [Google Scholar]
- Padmanabhan, T. Cosmology and Astrophysics through Problems; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Padmanabhan, P. Theoretical Astrophysics. Volume III: Galaxies and Cosmology; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Bevington, P.R.; Robinson, D. K. Data Reduction and Error Analysis for the Physical Sciences; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]
- Aggarwal, R.; Caldwell, A. Error bars for distributions of numbers of events. Eur. Phys. J. Plus 2012, 127, 1–8. [Google Scholar] [CrossRef]
- Binney, J.; Merrifield, M. Galactic Astronomy; Princeton University Press: Princeton, NJ, USA, 1998. [Google Scholar]
- Hogg, D.W. Distance Measures in Cosmology; Cornell University: Ithaca, NY, USA, 1999. [Google Scholar]
- Bertacca, D.; Maartens, R.; Clarkson, C. Observed galaxy number counts on the lightcone up to second order: I. Main result. J. Cosmol. Astropart. Phys. 2014, 9, 37. [Google Scholar] [CrossRef]
- Bertacca, D.; Maartens, R.; Clarkson, C. Observed galaxy number counts on the lightcone up to second order: II. Derivation. J. Cosmol. Astropart. Phys. 2014, 11, 13. [Google Scholar] [CrossRef]
- Zaninetti, L. The initial mass function modeled by a left truncated beta distribution. Astrophys. J. 2013, 765, 128–135. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Dover: New York, NJ, USA, 1965. [Google Scholar]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Zaninetti, L. The Luminosity Function of Galaxies as Modeled by a Left Truncated Beta Distribution. Int. J. Astron. Astrophys. 2014, 4, 145–154. [Google Scholar] [CrossRef]
- Adachi, M.; Kasai, M. An Analytical Approximation of the Luminosity Distance in Flat Cosmologies with a Cosmological Constant. Prog. Theor. Phys. 2012, 127, 145–152. [Google Scholar] [CrossRef]
- Wei, H.; Yan, X.P.; Zhou, Y.N. Cosmological applications of Pade approximant. J. Cosmol. Astropart. Phys. 2014, 1, 45. [Google Scholar] [CrossRef]
- Bagla, J.S.; Yadav, J.; Seshadri, T.R. Fractal dimensions of a weakly clustered distribution and the scale of homogeneity. Mon. Not. R. Astron. Soc. 2008, 390, 829–838. [Google Scholar] [CrossRef]
- Alonso, D.; Salvador, A.I.; Sánchez, F.J.; Bilicki, M.; García-Bellido, J.; Sánchez, E. Homogeneity and isotropy in the Two Micron All Sky Survey Photometric Redshift catalogue. Mon. Not. R. Astron. Soc. 2015, 449, 670–684. [Google Scholar] [CrossRef]
- Zaninetti, L. Revisiting the Cosmological Principle in a Cellular Framework. J. Astrophys. Astron. 2012, 33, 399–416. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaninetti, L. On the Number of Galaxies at High Redshift. Galaxies 2015, 3, 129-155. https://doi.org/10.3390/galaxies3030129
Zaninetti L. On the Number of Galaxies at High Redshift. Galaxies. 2015; 3(3):129-155. https://doi.org/10.3390/galaxies3030129
Chicago/Turabian StyleZaninetti, Lorenzo. 2015. "On the Number of Galaxies at High Redshift" Galaxies 3, no. 3: 129-155. https://doi.org/10.3390/galaxies3030129
APA StyleZaninetti, L. (2015). On the Number of Galaxies at High Redshift. Galaxies, 3(3), 129-155. https://doi.org/10.3390/galaxies3030129