Light Variability from UV to Near-Infrared in the Ap Star CU Vir Induced by Chemical Spots
Abstract
1. Introduction
2. Observational Data
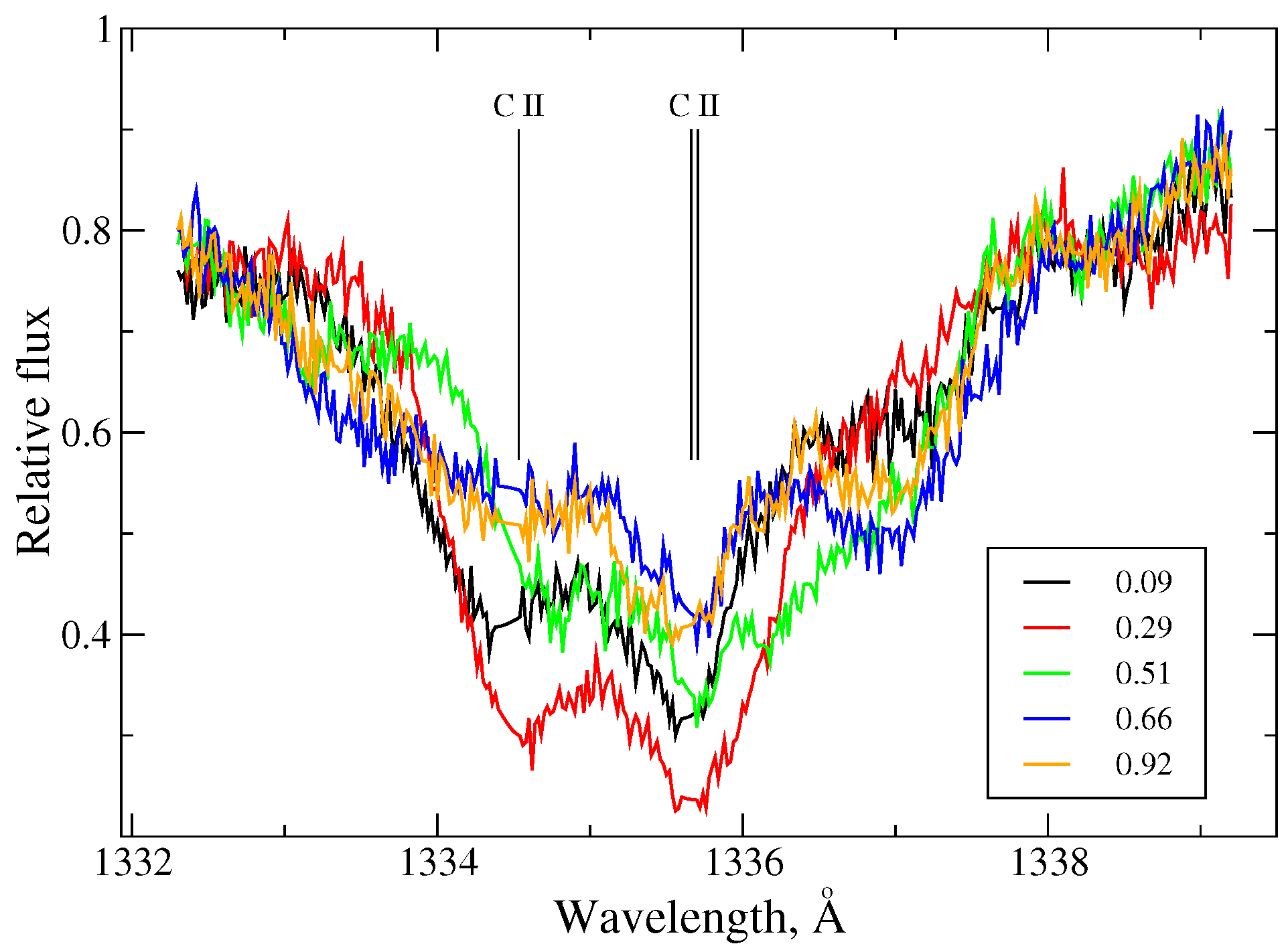
2.1. Doppler Imaging
2.2. Photometry
3. Period Changes in CU Vir and Ephemeris
| Years | Range, Days | Band | Reference | |
|---|---|---|---|---|
| 1955 | 99 | 54 | UBV | Hardie [13] |
| 1964–1966 | 836 | 235 | UBV | Abuladze [31] |
| 1980–1983 | 1139 | 23 | Pyper and Adelman [27] | |
| 1987–1989 | 796 | 354 | UBV | Adelman et al. [28] |
| 1990–1993 | 1068 | 79 | Hoeg et al. [29] | |
| 2003–2010 | 2885 | 11,990 | SMEI (4500–9500 Å) | Krtička et al. [22] |
| 2011–2017 | 2016/2028 | 1059/995 | B/V | Krtička et al. [22] |
| 1991–2012 | 7710 | 2820 | Pyper et al. [15] | |
| 2022 | 26 | 14,264 | TESS (5800–11,000 Å) | MAST * |
| Literature values | ||||
| 1966 | 3 | 18 | B | Hardie et al. [32] |
| 1968 | 120 | 85–105 | UBV | Blanco and Catalano [33] |
4. Light Curve Modelling
4.1. Calculation of Intensity Map
4.2. Synthetic Photometry Technique
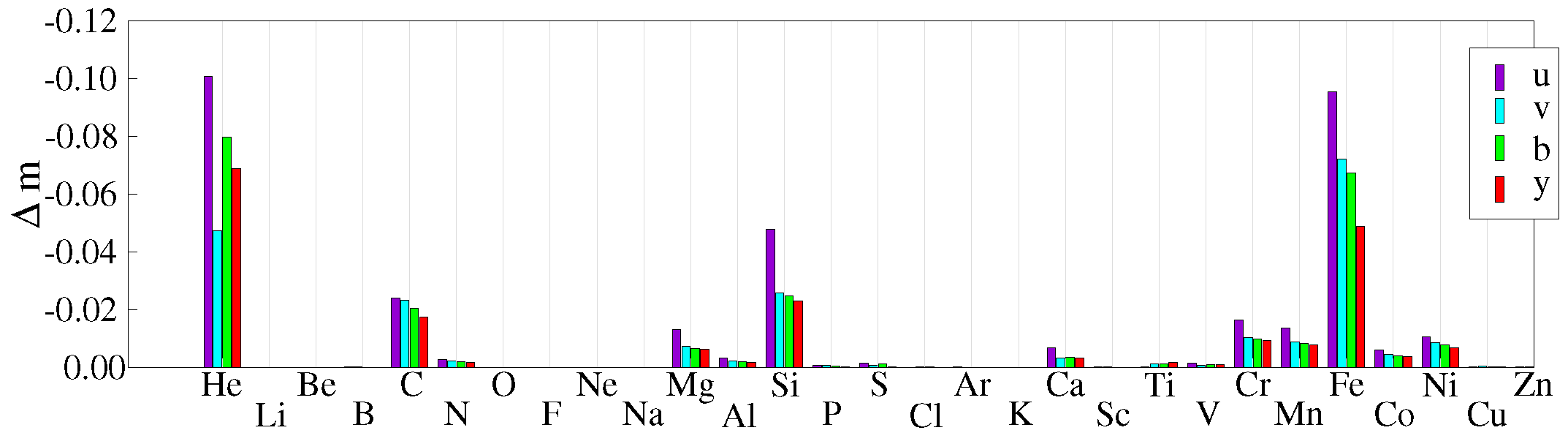
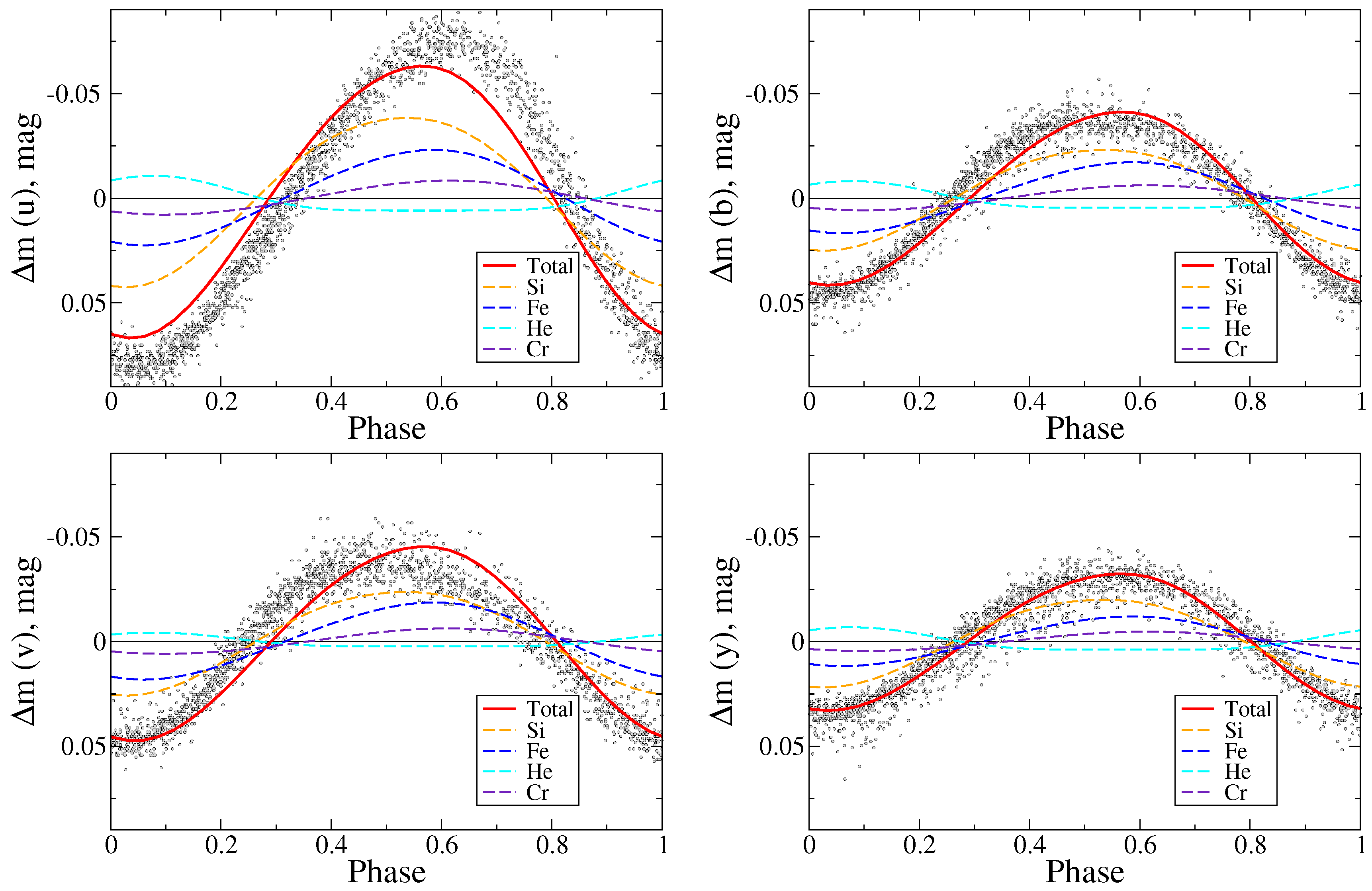
4.3. Contribution of Different Elements to Light Variability
5. Results
5.1. Visual Light Curve
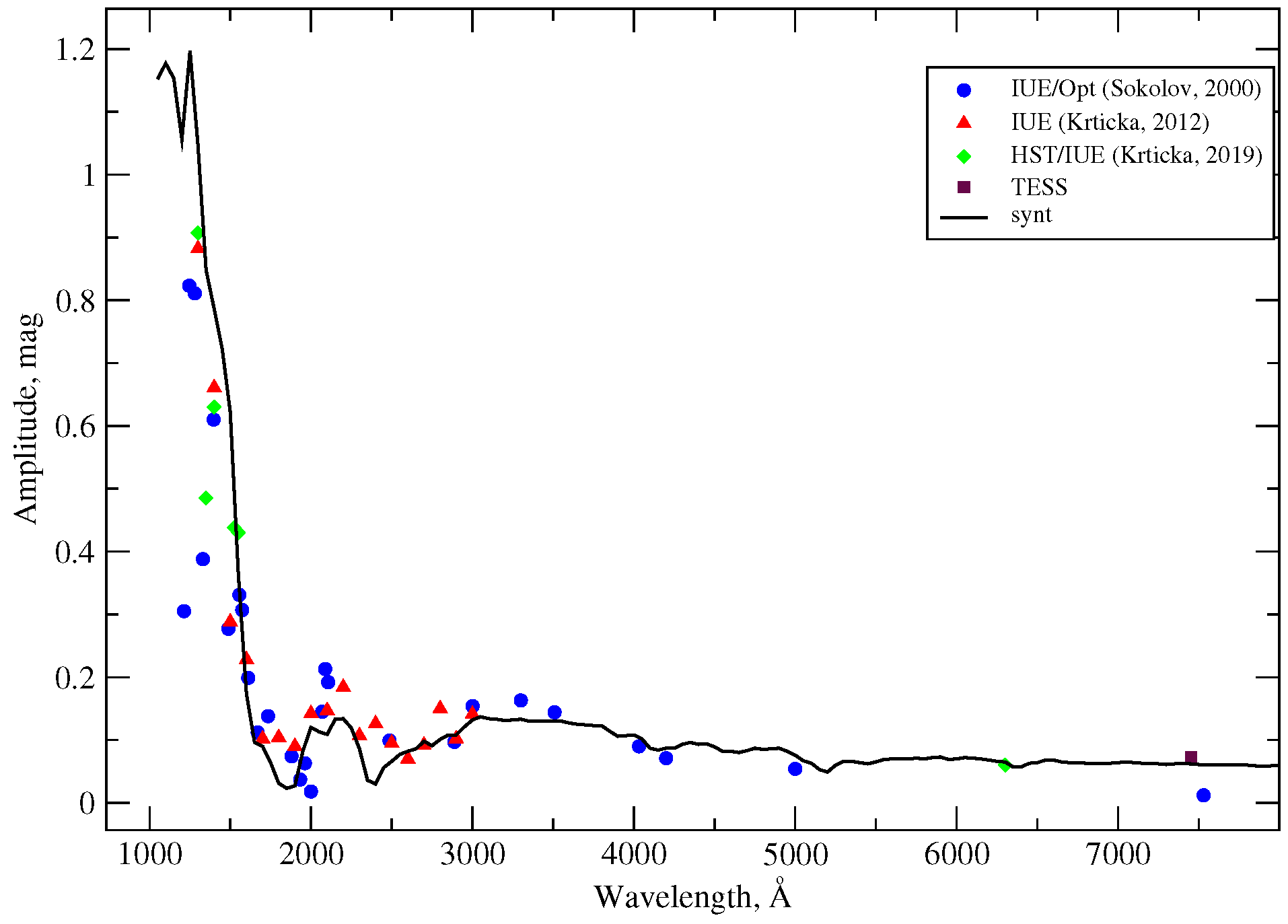
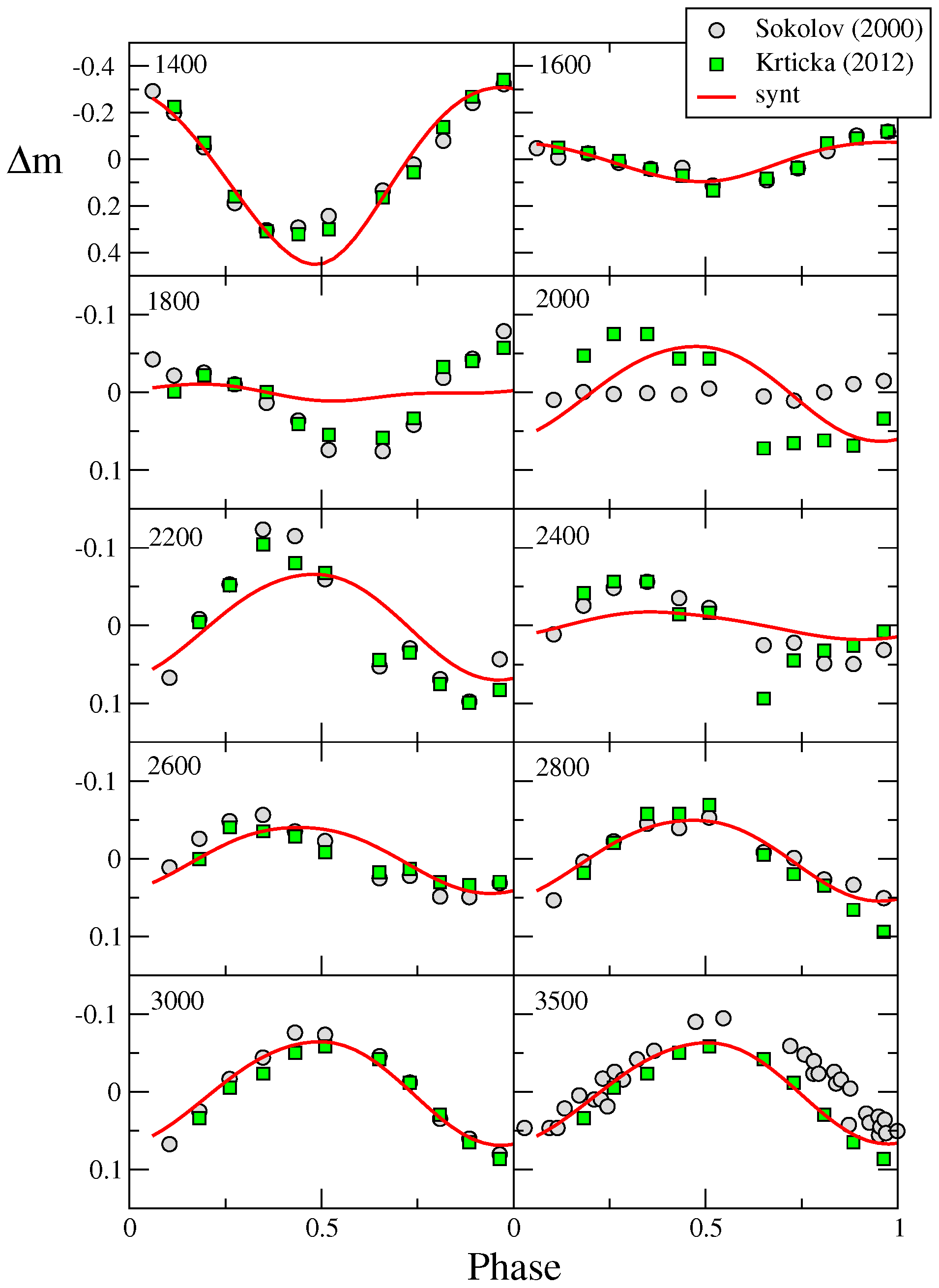
5.2. UV Variations
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DI | Doppler Imaging |
| LTE | Local Thermodynamic Equilibrum |
| IUE | International Ultraviolet Explorer |
| HST | Hubble Space Telescope |
| TESS | Transiting Exoplanet Survey Satellite |
| MAST | Mikulski Archive for Space Telescopes |
| SMEI | Solar Mass Ejection Imager |
| FCATP | Four College Automated Photometric Telescope |
| UV | Ultraviolet |
| IR | Infrared |
| NIR | Near infrared |
| BIC | Bayesian information criterion |
| RMS | Root mean square |
| MHD | Magnetohydrodynamics |
Appendix A. Bayesian Information Criterion
References
- Stibbs, D.W.N. A study of the spectrum and magnetic variable star HD 125248. Mon. Not. R. Astron. Soc. 1950, 110, 395. [Google Scholar] [CrossRef]
- Michaud, G. Diffusion Processes in Peculiar a Stars. Astrophys. J. 1970, 160, 641. [Google Scholar] [CrossRef]
- Michaud, G.; Alecian, G.; Richer, J. Atomic Diffusion in Stars; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Khan, S.A.; Shulyak, D.V. Theoretical analysis of the atmospheres of CP stars. Effects of the individual abundance patterns. Astron. Astrophys. 2007, 469, 1083–1100. [Google Scholar] [CrossRef]
- Krivoseina, A.A.; Ryabchikova, T.A.; Khokhlova, V.L. Distribution of SI on the Surface of the Silicon Ap-Star Cu-Virginis and Interpretation of the Lightcurves in the Vby Bands. Nauchnye Informatsii 1980, 43, 70. [Google Scholar]
- Krtička, J.; Mikulášek, Z.; Zverko, J.; Žižńovský, J. The light variability of the helium strong star HD 37776 as a result of its inhomogeneous elemental surface distribution. Astron. Astrophys. 2007, 470, 1089–1098. [Google Scholar] [CrossRef]
- Shulyak, D.; Krtička, J.; Mikulášek, Z.; Kochukhov, O.; Lüftinger, T. Modelling the light variability of the Ap star ε Ursae Majoris. Astron. Astrophys. 2010, 524, A66. [Google Scholar] [CrossRef]
- Krtička, J.; Mikulášek, Z.; Lüftinger, T.; Shulyak, D.; Zverko, J.; Žižňovský, J.; Sokolov, N.A. Modelling of the ultraviolet and visual SED variability in the hot magnetic Ap star CU Virginis. Astron. Astrophys. 2012, 537, A14. [Google Scholar] [CrossRef]
- Pakhomov, Y.; Potravnov, I.; Romanovskaya, A.; Ryabchikova, T. Modeling the TESS Light Curve of Ap Si Star MX TrA. Universe 2024, 10, 341. [Google Scholar] [CrossRef]
- Prvák, M.; Krtička, J.; Korhonen, H. The nature of the photometric variability of HgMn stars: A test of simulated light curves of φ Phe against the TESS data. Mon. Not. R. Astron. Soc. 2020, 492, 1834–1840. [Google Scholar] [CrossRef]
- Pyper, D.M.; Adelman, S.J. Light Curve Changes and Possible Precession in mCP Stars. Publ. Astron. Soc. Pacific 2021, 133, 084203. [Google Scholar] [CrossRef]
- Deutsch, A.J. A New Spectrum Variable of Short Period, HD 124224. Astrophys. J. 1952, 116, 536. [Google Scholar] [CrossRef]
- Hardie, R. Light-Variation of the Spectrum Variable HD 124224. Astrophys. J. 1958, 127, 620. [Google Scholar] [CrossRef]
- Pyper, D.M.; Ryabchikova, T.; Malanushenko, V.; Kuschnig, R.; Plachinda, S.; Savanov, I. An abrupt decrease in the rotational period of the chemically peculiar magnetic star CU Virginis. Astron. Astrophys. 1998, 339, 822–830. [Google Scholar]
- Pyper, D.M.; Stevens, I.R.; Adelman, S.J. An update on the rotational period of the magnetic chemically peculiar star CU Virginis. Mon. Not. R. Astron. Soc. 2013, 431, 2106–2110. [Google Scholar] [CrossRef]
- Pyper, D.M.; Adelman, S.J. Newly Discovered Period Changes in Two mCP Stars and Updates for Previously Published Stars. Publ. Astron. Soc. Pacific 2020, 132, 024201. [Google Scholar] [CrossRef]
- Mikulášek, Z.; Krtička, J.; Henry, G.W.; Janík, J.; Zverko, J.; Žižňovský, J.; Zejda, M.; Liška, J.; Zvěřina, P.; Kudrjavtsev, D.O.; et al. Surprising variations in the rotation of the chemically peculiar stars CU Virginis and V901 Orionis. Astron. Astrophys. 2011, 534, L5. [Google Scholar] [CrossRef]
- Mikulášek, Z.; Krtička, J.; Henry, G.W.; Janík, J.; Pigulski, A. Towards Comprehension of the Variability of the mCP Star CU Virginis. In Proceedings of the Physics of Magnetic Stars, Nizhny Arkhyz, Russia, 1–5 October 2018; Volume 518, p. 125. [Google Scholar] [CrossRef]
- Kuschnig, R.; Ryabchikova, T.A.; Piskunov, N.E.; Weiss, W.W.; Gelbmann, M.J. Multi element Doppler imaging of AP stars. I. He, Mg, Si, CR and Fe surface distribution for CU Virginis. Astron. Astrophys. 1999, 348, 924–932. [Google Scholar]
- Kochukhov, O.; Lüftinger, T.; Neiner, C.; Alecian, E.; MiMeS Collaboration. Magnetic field topology of the unique chemically peculiar star CU Virginis. Astron. Astrophys. 2014, 565, A83. [Google Scholar] [CrossRef]
- Aurière, M. Stellar Polarimetry with NARVAL. In Setting a New Standard in the Analysis of Binary Stars; European Astronomical Society Publications Series; Arnaud, J., Meunier, N., Eds.; Cambridge University Press: Cambridge, UK, 2003; Volume 9, p. 105. [Google Scholar]
- Krtička, J.; Mikulášek, Z.; Henry, G.W.; Janík, J.; Kochukhov, O.; Pigulski, A.; Leto, P.; Trigilio, C.; Krtičková, I.; Lüftinger, T.; et al. HST/STIS analysis of the first main sequence pulsar CU Virginis. Astron. Astrophys. 2019, 625, A34. [Google Scholar] [CrossRef]
- Ricker, G.R.; Winn, J.N.; Vanderspek, R.; Latham, D.W.; Bakos, G.Á.; Bean, J.L.; Berta-Thompson, Z.K.; Brown, T.M.; Buchhave, L.; Butler, N.R.; et al. Transiting Exoplanet Survey Satellite (TESS). J. Astron. Telesc. Instruments Syst. 2015, 1, 014003. [Google Scholar] [CrossRef]
- Potravnov, I.; Ryabchikova, T.; Kitchatinov, L.; Pakhomov, Y. Long-term stability of chemical spots and reasons for the period variations in Ap star CU Vir. Galaxies 2025, 13, 90. [Google Scholar] [CrossRef]
- Sokolov, N.A. Spectrophotometric behavior of CU Virginis. Astron. Astrophys. 2000, 353, 707–714. [Google Scholar]
- Kuschnig, R.; Ryabchikova, T.; Piskunov, N.E.; Weiss, W.W. Ap-star mapping: He, Mg, Si, and Fe surface distributions on the CP2 star CU Virginis. In Proceedings of the IAU Symposium, Vienna, Austria, 9–13 October 1995; Volume 176, p. 135. [Google Scholar]
- Pyper, D.M.; Adelman, S.J. Spectrophotometry of peculiar B and A stars. XVII. 63 Andromedae, HD 34452, epsilon Ursae Majoris, CQ Ursae Majoris, CU Virginis, CS Virginis and beta Coronae Borealis. Astron. Astrophys Suppl. Ser. 1985, 59, 369–397. [Google Scholar]
- Adelman, S.J.; Dukes, R.J., Jr.; Pyper, D.M. Photometry of eight Magnetic Peculiar A Stars. Astron. J. 1992, 104, 314. [Google Scholar] [CrossRef]
- Hoeg, E.; Bässgen, G.; Bastian, U.; Egret, D.; Fabricius, C.; Großmann, V.; Halbwachs, J.L.; Makarov, V.V.; Perryman, M.A.C.; Schwekendiek, P.; et al. The TYCHO Catalogue. Astron. Astrophys. 1997, 323, L57–L60. [Google Scholar]
- Zechmeister, M.; Kürster, M. The generalised Lomb-Scargle periodogram. A new formalism for the floating-mean and Keplerian periodograms. Astron. Astrophys. 2009, 496, 577–584. [Google Scholar] [CrossRef]
- Abuladze, O.P. Photoelectric observations of spectral binary variable star CU Vir. Abastumanskaia Astrofiz. Obs. Byulleten 1968, 36, 43–50. [Google Scholar]
- Hardie, R.H.; Lieberman, L.; Reichmann, E. On the Period of HD 124224. Publ. Astron. Soc. Pacific 1967, 79, 74. [Google Scholar] [CrossRef]
- Blanco, C.; Catalano, F.A. Photoelectric observations of magnetic stars. III. HD 124224, HD 140160, and HD 224801. Astron. J. 1971, 76, 630–633. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Shulyak, D.; Tsymbal, V.; Ryabchikova, T.; Stütz, C.; Weiss, W.W. Line-by-line opacity stellar model atmospheres. Astron. Astrophys. 2004, 428, 993–1000. [Google Scholar] [CrossRef]
- Kurucz, R.L. ATLAS12, SYNTHE, ATLAS9, WIDTH9, et cetera. Mem. Della Soc. Astron. Ital. Suppl. 2005, 8, 14. [Google Scholar]
- Kurucz, R.L. ATLAS12: Opacity Sampling Model Atmosphere Program; Record ascl:1303.024; Astrophysics Source Code Library: College Park, MD, USA, 2013. [Google Scholar]
- Piskunov, N.E.; Kupka, F.; Ryabchikova, T.A.; Weiss, W.W.; Jeffery, C.S. VALD: The Vienna Atomic Line Data Base. Astron. Astrophys Suppl. Ser. 1995, 112, 525. [Google Scholar]
- Ryabchikova, T.; Piskunov, N.; Kurucz, R.L.; Stempels, H.C.; Heiter, U.; Pakhomov, Y.; Barklem, P.S. A major upgrade of the VALD database. Physica Scripta 2015, 90, 054005. [Google Scholar] [CrossRef]
- Crawford, D.L.; Barnes, J.V. Standard stars for uvby photometry. Astron. J. 1970, 75, 978–998. [Google Scholar] [CrossRef]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Strom, S.E.; Strom, K.M. Effect of Silicon Opacity on b- and A-Star Atmospheres. Astrophys. J. 1969, 155, 17. [Google Scholar] [CrossRef]
- Romanovskaya, A.; Ryabchikova, T.; Pakhomov, Y.; Potravnov, I.; Sitnova, T. Abundance and stratification analysis of slowly-rotating Si-star BD+00°1659 as a benchmark for ApSi-stars studies. Galaxies, 2024; in preparation. [Google Scholar]
- Krtička, J.; Mikulášek, Z.; Henry, G.W.; Kurfürst, P.; Karlický, M. Torsional oscillations and observed rotational period variations in early-type stars. Mon. Not. R. Astron. Soc. 2017, 464, 933–939. [Google Scholar] [CrossRef]
- Takahashi, K.; Langer, N. Standing torsional Alfvén waves as the source of the rotational period variation in magnetic early-type stars. Astron. Astrophys. 2025, 696, A129. [Google Scholar] [CrossRef]
- Potravnov, I.S.; Kitchatinov, L.L. Tayler instability as possible reason for the period changes in Ap star 56 Ari. arXiv 2025, arXiv:2504.08447. [Google Scholar] [CrossRef]
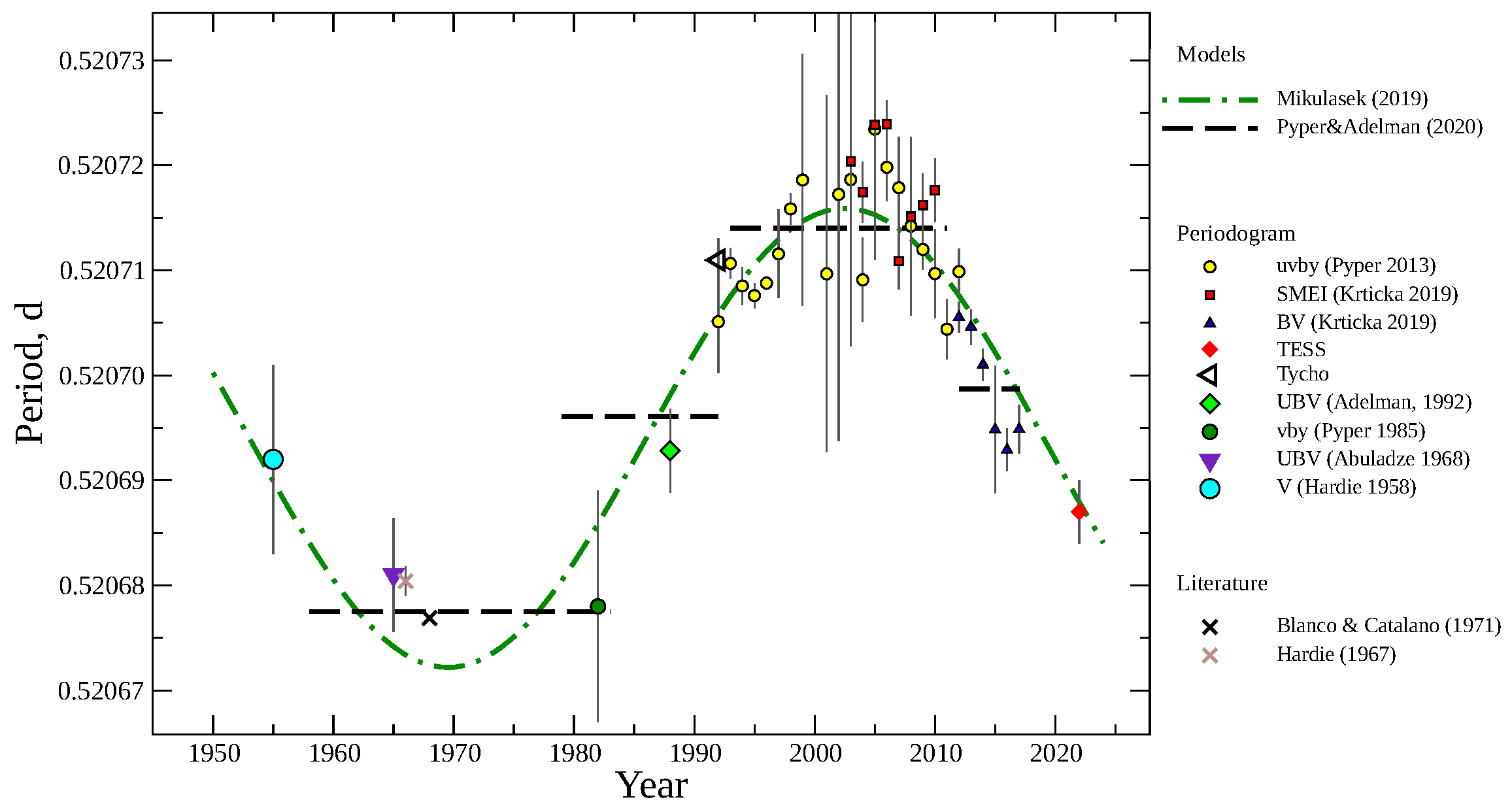

| Period | P20 | M19 | ||
|---|---|---|---|---|
| RMS | BIC | RMS | BIC | |
| 1955–1983 | 6.62×10−6 | −309.8 | 8.45×10−6 | −291.6 |
| 1983–1992 ∗ | 1.46×10−5 | −56.1 | 1.28×10−5 | −52.5 |
| 1992–2012 | 5.73×10−6 | −1780.4 | 4.33×10−6 | −1809.8 |
| 2012–2022 | 5.34×10−6 | −231.1 | 2.82×10−6 | −235.5 |
| Element | [X/H] |
|---|---|
| Si | −6.5 −5.3 −4.1 −2.9 −1.7 |
| Fe | −5.5 −4.5 −3.5 −2.5 |
| He | −3.4 −1.8 −0.2 |
| Cr | −6.4 −4.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pakhomov, Y.; Potravnov, I.; Ryabchikova, T. Light Variability from UV to Near-Infrared in the Ap Star CU Vir Induced by Chemical Spots. Galaxies 2025, 13, 97. https://doi.org/10.3390/galaxies13040097
Pakhomov Y, Potravnov I, Ryabchikova T. Light Variability from UV to Near-Infrared in the Ap Star CU Vir Induced by Chemical Spots. Galaxies. 2025; 13(4):97. https://doi.org/10.3390/galaxies13040097
Chicago/Turabian StylePakhomov, Yury, Ilya Potravnov, and Tatiana Ryabchikova. 2025. "Light Variability from UV to Near-Infrared in the Ap Star CU Vir Induced by Chemical Spots" Galaxies 13, no. 4: 97. https://doi.org/10.3390/galaxies13040097
APA StylePakhomov, Y., Potravnov, I., & Ryabchikova, T. (2025). Light Variability from UV to Near-Infrared in the Ap Star CU Vir Induced by Chemical Spots. Galaxies, 13(4), 97. https://doi.org/10.3390/galaxies13040097







