Universal Relations for Non-Rotating Objects Made of Dark Energy
Abstract
1. Introduction
2. Formalism: Structure Equations and Tidal Deformability
2.1. Hydrostatic Equilibrium
2.2. Gravito-Electric Tidal Love Numbers
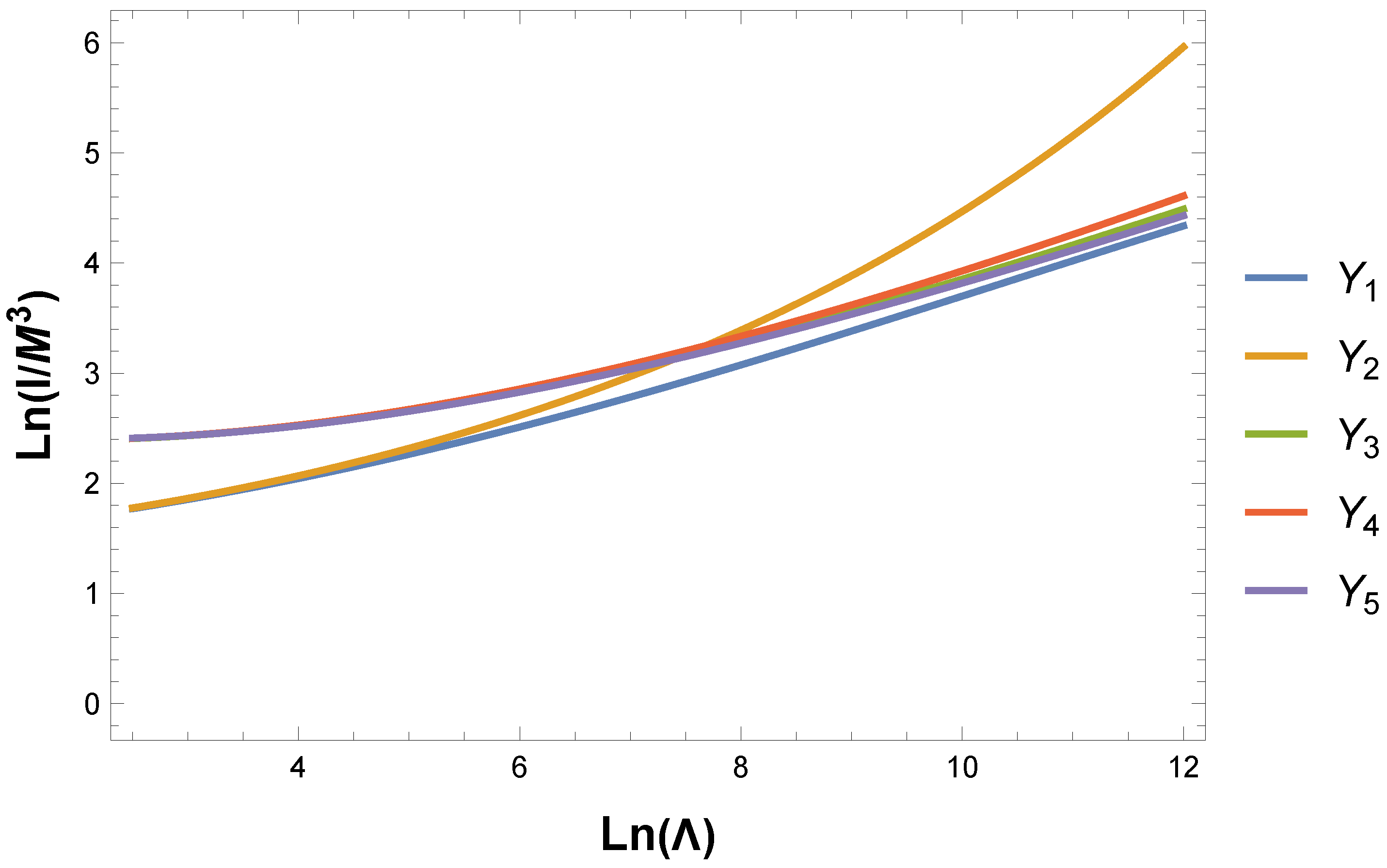
3. Numerical Analysis and Main Results
4. Discussion and Summary
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shapiro, S.L.; Teukolsky, S.A. Black holes, white dwarfs, and neutron stars: The physics of compact objects. Phys. Today 1983, 36, 89–90. [Google Scholar] [CrossRef]
- Schaffner-Bielich, J. Compact Star Physics; Cambridge University Press: Cambridge, UK, 2020; ISBN 978-1-316-84835-7/978-1-107-18089-5. [Google Scholar]
- Chadwick, J. Possible Existence of a Neutron. Nature 1932, 129, 312. [Google Scholar] [CrossRef]
- Chadwick, J. The Existence of a Neutron. Proc. R. Soc. Lond. A 1932, 136, 692–708. [Google Scholar]
- Baade, W.; Zwicky, F. Remarks on Super-Novae and Cosmic Rays. Phys. Rev. 1934, 46, 76. [Google Scholar] [CrossRef]
- Hewish, A.; Bell, S.J.; Pilkington, J.D.H.; Scott, P.F.; Collins, R.A. Observation of a rapidly pulsating radio source. Nature 1968, 217, 709–713. [Google Scholar] [CrossRef]
- Safi-Harb, S. Neutron stars: Observational diversity and evolution. J. Phys. Conf. Ser. 2017, 932, 012005. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. The physics of neutron stars. Science 2004, 304, 536–542. [Google Scholar] [CrossRef]
- Haensel, P.; Zdunik, J.L.; Schaeffer, R. Strange quark stars. Astron. Astrophys. 1986, 160, 121–128. [Google Scholar]
- Itoh, N. Hydrostatic Equilibrium of Hypothetical Quark Stars. Prog. Theor. Phys. 1970, 44, 291. [Google Scholar] [CrossRef]
- Collins, J.C.; Perry, M.J. Superdense Matter: Neutrons Or Asymptotically Free Quarks? Phys. Rev. Lett. 1975, 34, 1353. [Google Scholar] [CrossRef]
- Madsen, J. Physics and astrophysics of strange quark matter. Lect. Notes Phys. 1999, 516, 162–203. [Google Scholar]
- Witten, E. Cosmic Separation of Phases. Phys. Rev. D 1984, 30, 272–285. [Google Scholar] [CrossRef]
- Farhi, E.; Jaffe, R.L. Strange Matter. Phys. Rev. D 1984, 30, 2379. [Google Scholar] [CrossRef]
- Ofek, E.O.; Cameron, P.B.; Kasliwal, M.M.; Gal-Yam, A.; Rau, A.; Kulkarni, S.R.; Frail, D.A.; Chandra, P.; Cenko, S.B.; Soderberg, A.M.; et al. SN 2006gy: An extremely luminous supernova in the early-type galaxy NGC 1260. Astrophys. J. Lett. 2007, 659, L13–L16. [Google Scholar] [CrossRef]
- Ouyed, R.; Leahy, D.; Jaikumar, P. Predictions for signatures of the quark-nova in superluminous supernovae. arXiv 2009, arXiv:0911.5424. [Google Scholar]
- Henderson, J.A.; Page, D. RX J1856.5-3754 as a possible Strange Star candidate. Astrophys. Space Sci. 2007, 308, 513–517. [Google Scholar] [CrossRef]
- Li, A.; Peng, G.X.; Lu, J.F. Strange star candidates revised within a quark model with chiral mass scaling. Res. Astron. Astrophys. 2011, 11, 482–490. [Google Scholar] [CrossRef]
- Aziz, A.; Ray, S.; Rahaman, F.; Khlopov, M.; Guha, B.K. Constraining values of bag constant for strange star candidates. Int. J. Mod. Phys. D 2019, 28, 1941006. [Google Scholar] [CrossRef]
- Weber, F. Strange quark matter and compact stars. Prog. Part. Nucl. Phys. 2005, 54, 193–288. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gillil, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Freedman, W.L.; Turner, M.S. Measuring and understanding the universe. Rev. Mod. Phys. 2003, 75, 1433–1447. [Google Scholar] [CrossRef]
- Singh, K.N.; Ali, A.; Rahaman, F.; Nasri, S. Compact stars with exotic matter. Phys. Dark Univ. 2020, 29, 100575. [Google Scholar] [CrossRef]
- Tello-Ortiz, F.; Malaver, M.; Rincón, Á.; Gomez-Leyton, Y. Relativistic anisotropic fluid spheres satisfying a non-linear equation of state. Eur. Phys. J. C 2020, 80, 371. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Rincón, Á.; Lopes, I. Radial oscillations and tidal Love numbers of dark energy stars. Eur. Phys. J. Plus 2020, 135, 856. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Rincón, Á.; Lopes, I. Slowly rotating dark energy stars. Phys. Dark Univ. 2021, 34, 100885. [Google Scholar] [CrossRef]
- Rincón, Á.; Panotopoulos, G.; Lopes, I. Anisotropic stars made of exotic matter within the complexity factor formalism. Eur. Phys. J. C 2023, 83, 116. [Google Scholar] [CrossRef]
- Pourhassan, B.; Kahya, E.O. Extended Chaplygin gas model. Results Phys. 2014, 4, 101–102. [Google Scholar] [CrossRef]
- Pourhassan, B.; Kahya, E.O. FRW cosmology with the extended Chaplygin gas. Adv. High Energy Phys. 2014, 2014, 231452. [Google Scholar] [CrossRef]
- Kamenshchik, A.Y.; Moschella, U.; Pasquier, V. An Alternative to quintessence. Phys. Lett. B 2001, 511, 265–268. [Google Scholar] [CrossRef]
- Bento, M.C.; Bertolami, O.; Sen, A.A. Generalized Chaplygin gas, accelerated expansion and dark energy matter unification. Phys. Rev. D 2002, 66, 043507. [Google Scholar] [CrossRef]
- Love, A.E.H. The Yielding of the Earth to Disturbing Forces. Proc. R. Soc. A 1909, 82, 73. [Google Scholar] [CrossRef]
- Love, A.E.H. Some Problems of Geodynamics; Cornell University Library: Ithaca, NY, USA, 1911. [Google Scholar]
- Flanagan, E.E.; Hinderer, T. Constraining neutron star tidal Love numbers with gravitational wave detectors. Phys. Rev. D 2008, 77, 021502. [Google Scholar] [CrossRef]
- Hinderer, T. Tidal Love numbers of neutron stars. Astrophys. J. 2008, 677, 1216. [Google Scholar] [CrossRef]
- Damour, T.; Nagar, A. Relativistic tidal properties of neutron stars. Phys. Rev. D 2009, 80, 084035. [Google Scholar] [CrossRef]
- Postnikov, S.; Prakash, M.; Lattimer, J.M. Tidal Love Numbers of Neutron and Self-Bound Quark Stars. Phys. Rev. D 2010, 82, 024016. [Google Scholar] [CrossRef]
- Binnington, T.; Poisson, E. Relativistic theory of tidal Love numbers. Phys. Rev. D 2009, 80, 084018. [Google Scholar] [CrossRef]
- DeDeo, S.; Psaltis, D. Towards New Tests of Strong-field Gravity with Measurements of Surface Atomic Line Redshifts from Neutron Stars. Phys. Rev. Lett. 2003, 90, 141101. [Google Scholar] [CrossRef]
- Ekşi, K.Y.; Güngör, C.; Türkoğlu, M.M. What does a measurement of mass and/or radius of a neutron star constrain: Equation of state or gravity? Phys. Rev. D 2014, 89, 063003. [Google Scholar] [CrossRef]
- Bejger, M.; Haensel, P. Moments of inertia for neutron and strange stars: Limits derived for the Crab pulsar. Astron. Astrophys. 2002, 396, 917. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Schutz, B.F. Constraining the equation of state with moment of inertia measurements. Astrophys. J. 2005, 629, 979–984. [Google Scholar] [CrossRef]
- Maselli, A.; Pappas, G.; Pani, P.; Gualtieri, L.; Motta, S.; Ferrari, V.; Stella, L. A new method to constrain neutron star structure from quasi-periodic oscillations. Astrophys. J. 2020, 899, 139. [Google Scholar] [CrossRef]
- Tews, I.; Margueron, J.; Reddy, S. Critical examination of constraints on the equation of state of dense matter obtained from GW170817. Phys. Rev. C 2018, 98, 045804. [Google Scholar] [CrossRef]
- Weih, L.R.; Most, E.R.; Rezzolla, L. Optimal Neutron-star Mass Ranges to Constrain the Equation of State of Nuclear Matter with Electromagnetic and Gravitational-wave Observations. Astrophys. J. 2019, 881, 73. [Google Scholar] [CrossRef]
- Yagi, K.; Yunes, N. I-Love-Q. Science 2013, 341, 365–368. [Google Scholar] [CrossRef] [PubMed]
- Yagi, K.; Yunes, N. I-Love-Q Relations in Neutron Stars and their Applications to Astrophysics, Gravitational Waves and Fundamental Physics. Phys. Rev. D 2013, 88, 023009. [Google Scholar] [CrossRef]
- Doneva, D.D.; Yazadjiev, S.S.; Staykov, K.V.; Kokkotas, K.D. Universal I-Q relations for rapidly rotating neutron and strange stars in scalar-tensor theories. Phys. Rev. D 2014, 90, 104021. [Google Scholar] [CrossRef]
- Chan, T.K.; Sham, Y.H.; Leung, P.T.; Lin, L.M. Multipolar universal relations between f-mode frequency and tidal deformability of compact stars. Phys. Rev. D 2014, 90, 124023. [Google Scholar] [CrossRef]
- Chirenti, C.; de Souza, G.H.; Kastaun, W. Fundamental oscillation modes of neutron stars: Validity of universal relations. Phys. Rev. D 2015, 91, 044034. [Google Scholar] [CrossRef]
- Yagi, K.; Yunes, N. I-Love-Q anisotropically: Universal relations for compact stars with scalar pressure anisotropy. Phys. Rev. D 2015, 91, 123008. [Google Scholar] [CrossRef]
- Staykov, K.V.; Doneva, D.D.; Yazadjiev, S.S. Moment-of-inertia–compactness universal relations in scalar-tensor theories and R2 gravity. Phys. Rev. D 2016, 93, 084010. [Google Scholar] [CrossRef]
- Doneva, D.D.; Yazadjiev, S.S. Rapidly rotating neutron stars with a massive scalar field—Structure and universal relations. J. Cosmol. Astropart. Phys. 2016, 11, 19. [Google Scholar] [CrossRef]
- Doneva, D.D.; Pappas, G. Universal Relations and Alternative Gravity Theories. Astrophys. Space Sci. Libr. 2018, 457, 737–806. [Google Scholar]
- Blázquez-Salcedo, J.L.; Eickhoff, K. Axial quasinormal modes of static neutron stars in the nonminimal derivative coupling sector of Horndeski gravity: Spectrum and universal relations for realistic equations of state. Phys. Rev. D 2018, 97, 104002. [Google Scholar] [CrossRef]
- Wei, J.B.; Figura, A.; Burgio, G.F.; Chen, H.; Schulze, H.J. Neutron star universal relations with microscopic equations of state. J. Phys. G 2019, 46, 034001. [Google Scholar] [CrossRef]
- Popchev, D.; Staykov, K.V.; Doneva, D.D.; Yazadjiev, S.S. Moment of inertia–mass universal relations for neutron stars in scalar-tensor theory with self-interacting massive scalar field. Eur. Phys. J. C 2019, 79, 178. [Google Scholar] [CrossRef]
- Pappas, G.; Doneva, D.D.; Sotiriou, T.P.; Yazadjiev, S.S.; Kokkotas, K.D. Multipole moments and universal relations for scalarized neutron stars. Phys. Rev. D 2019, 99, 104014. [Google Scholar] [CrossRef]
- Kumar, B.; Landry, P. Inferring neutron star properties from GW170817 with universal relations. Phys. Rev. D 2019, 99, 123026. [Google Scholar] [CrossRef]
- Bozzola, G.; Espino, P.L.; Lewin, C.D.; Paschalidis, V. Maximum mass and universal relations of rotating relativistic hybrid hadron-quark stars. Eur. Phys. J. A 2019, 55, 149. [Google Scholar] [CrossRef]
- Benitez, E.; Weller, J.; Guedes, V.; Chirenti, C.; Miller, M.C. Investigating the I-Love-Q and w-mode Universal Relations Using Piecewise Polytropes. Phys. Rev. D 2021, 103, 023007. [Google Scholar] [CrossRef]
- Danchev, V.I.; Doneva, D.D. Constraining the equation of state in modified gravity via universal relations. Phys. Rev. D 2021, 103, 024049. [Google Scholar] [CrossRef]
- Adam, C.; Mourelle, J.C.; Filho, E.d.S.C.; Herdeiro, C.A.R.; Wereszczynski, A. Universal relations for rotating scalar and vector boson stars. Phys. Rev. D 2024, 110, 084017. [Google Scholar] [CrossRef]
- Pretel, J.M.Z.; Zhang, C. Universal relations for anisotropic interacting quark stars. J. Cosmol. Astropart. Phys. 2024, 10, 032. [Google Scholar] [CrossRef]
- Einstein, A. The Field Equations of Gravitation. Sitzungsber. Preuss. Akad. Wiss. Berlin (Math. Phys.) 1915, 1915, 844–847. [Google Scholar]
- Tolman, R.C. Static solutions of Einstein’s field equations for spheres of fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On massive neutron cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Schwarzschild, K. On the gravitational field of a mass point according to Einstein’s theory. Sitzungsber. Preuss. Akad. Wiss. Berlin (Math. Phys.) 1916, 1916, 189–196. [Google Scholar]
- Hinderer, T.; Lackey, B.D.; Lang, R.N.; Read, J.S. Tidal deformability of neutron stars with realistic equations of state and their gravitational wave signatures in binary inspiral. Phys. Rev. D 2010, 81, 123016. [Google Scholar] [CrossRef]
- Iacovelli, F.; Mancarella, M.; Mondal, C.; Puecher, A.; Dietrich, T.; Gulminelli, F.; Maggiore, M.; Oertel, M. Nuclear physics constraints from binary neutron star mergers in the Einstein Telescope era. Phys. Rev. D 2023, 108, 122006. [Google Scholar] [CrossRef]
- Piovano, G.A.; Maselli, A.; Pani, P. Constraining the tidal deformability of supermassive objects with extreme mass ratio inspirals and semianalytical frequency-domain waveforms. Phys. Rev. D 2023, 107, 024021. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Lopes, I. Millisecond pulsars modeled as strange quark stars admixed with condensed dark matter. Int. J. Mod. Phys. D 2018, 27, 1850093. [Google Scholar] [CrossRef]
- Staykov, K.V.; Doneva, D.D.; Yazadjiev, S.S.; Kokkotas, K.D. Slowly rotating neutron and strange stars in R2 gravity. J. Cosmol. Astropart. Phys. 2014, 10, 6. [Google Scholar] [CrossRef]
- Murshid, M.; Kalam, M. Neutron stars in f(R,T) theory: Slow rotation approximation. J. Cosmol. Astropart. Phys. 2024, 9, 30. [Google Scholar] [CrossRef]
- Yagi, K.; Yunes, N. Approximate Universal Relations for Neutron Stars and Quark Stars. Phys. Rep. 2017, 681, 1–72. [Google Scholar] [CrossRef]
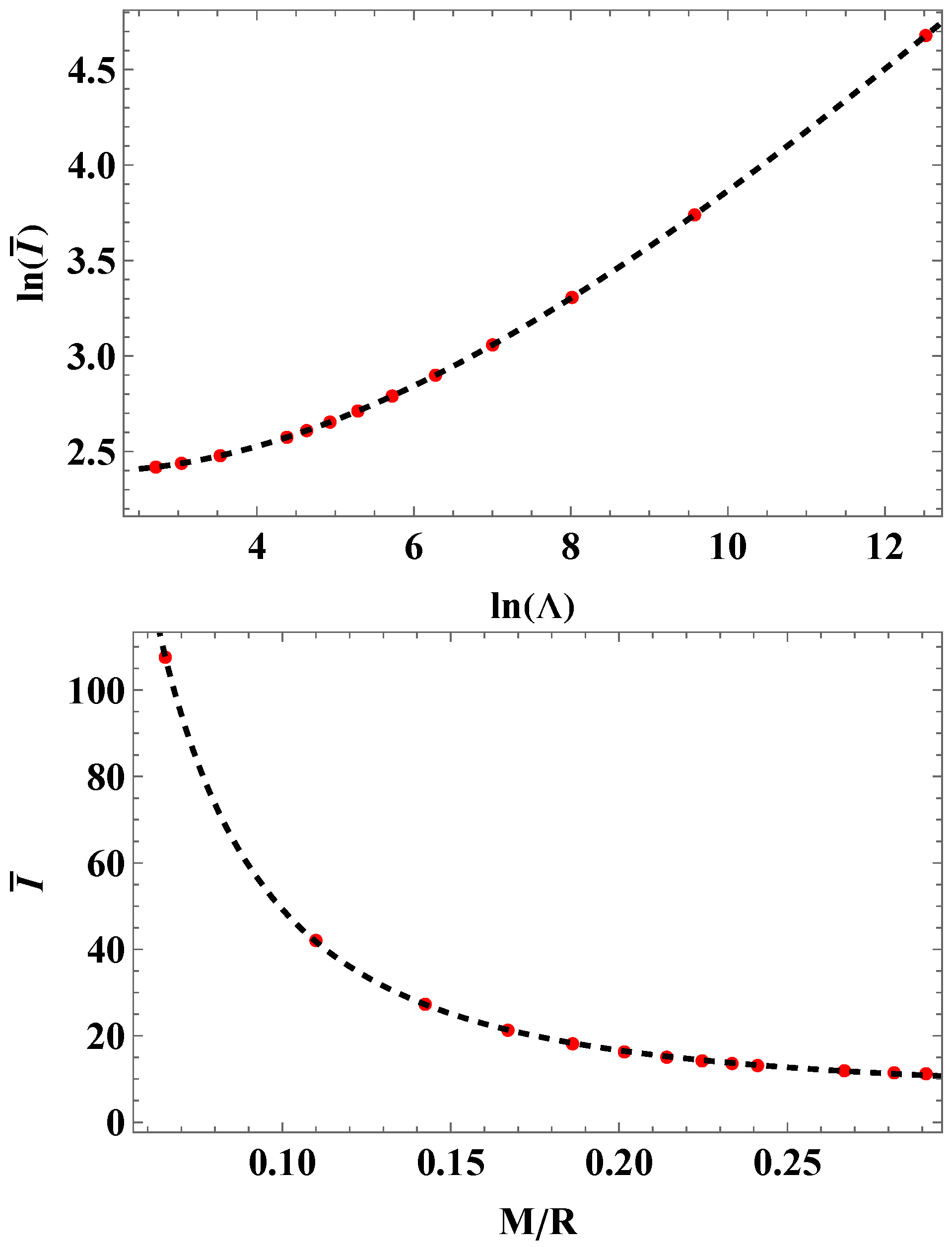

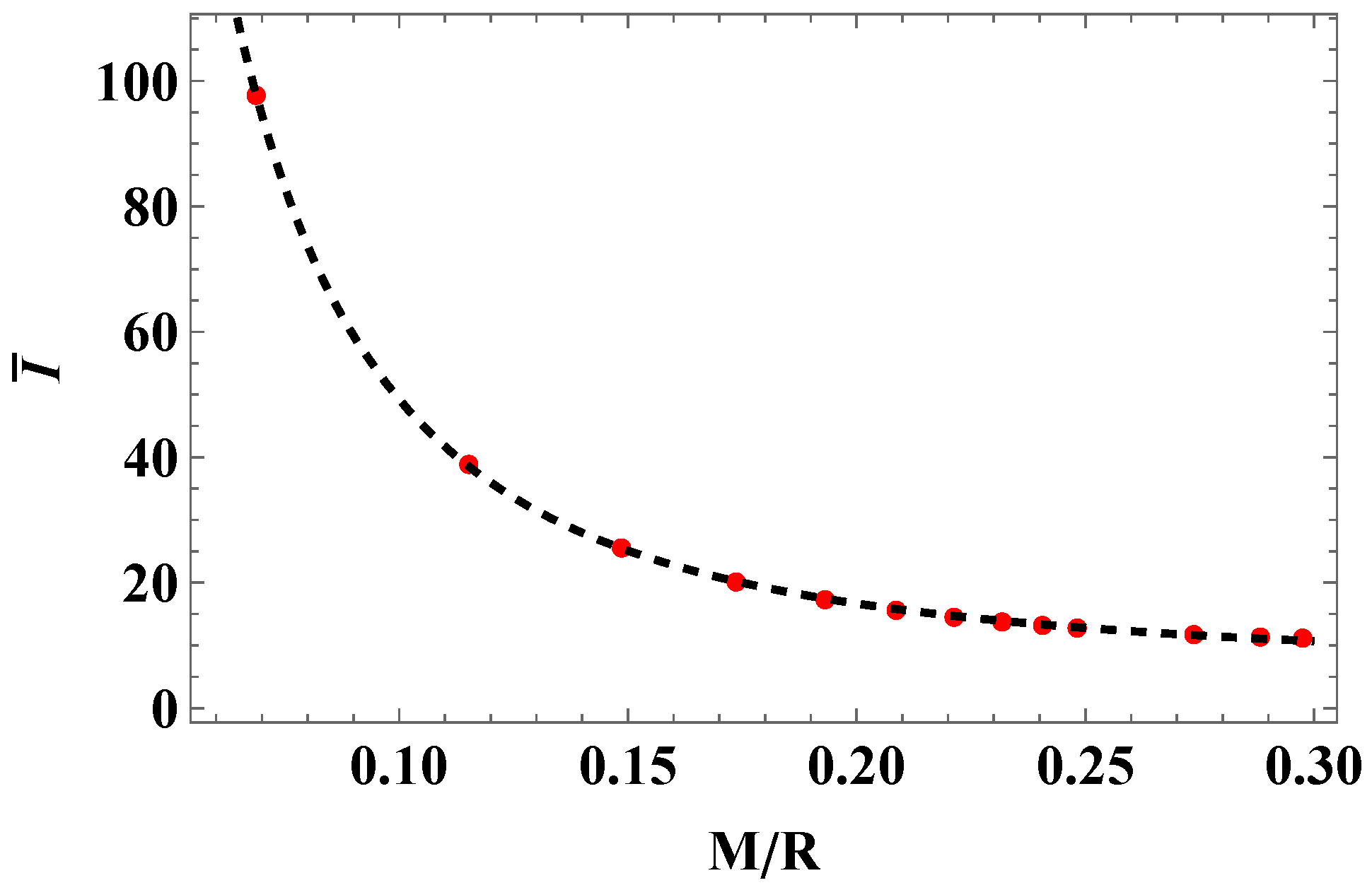
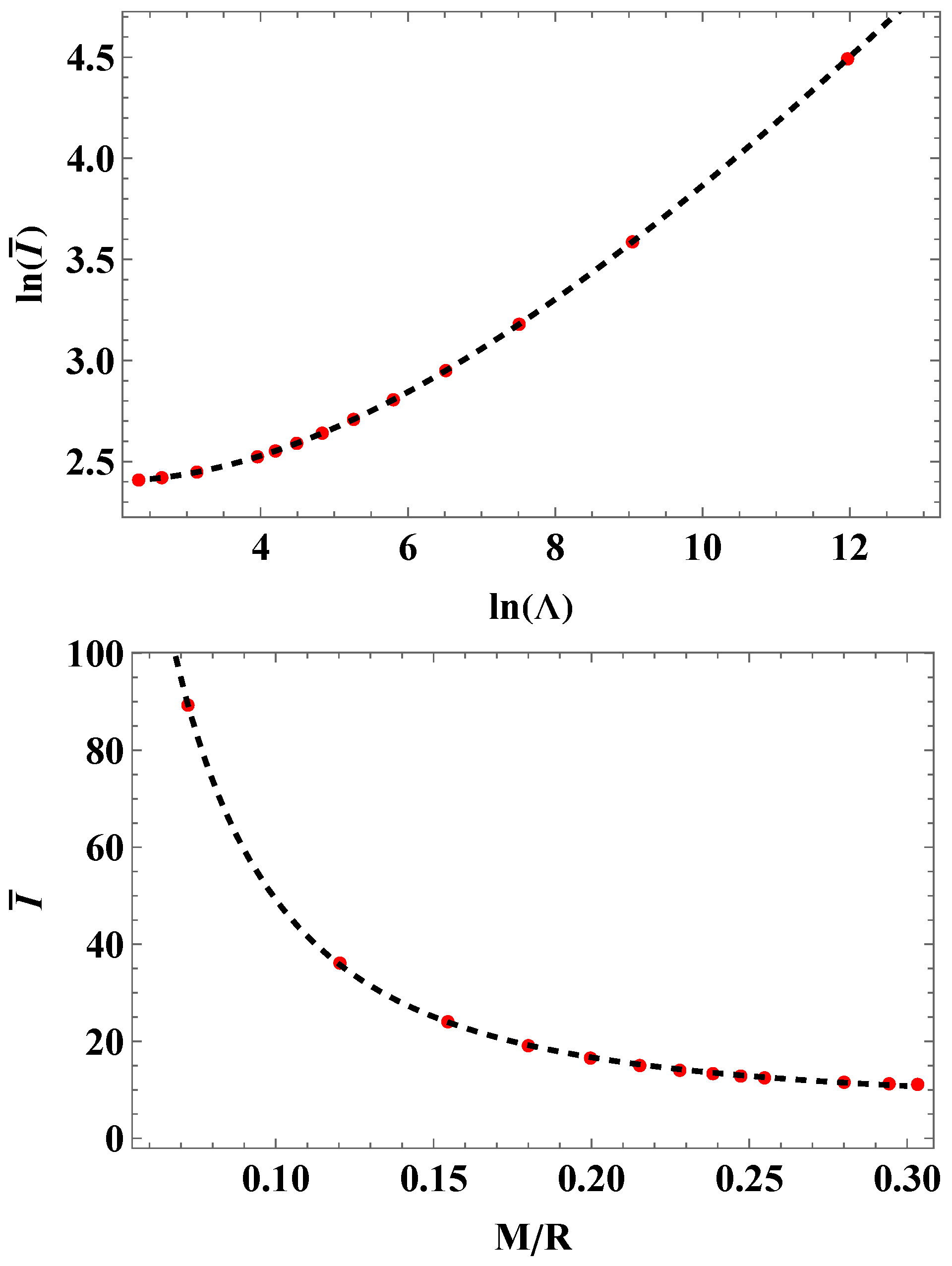
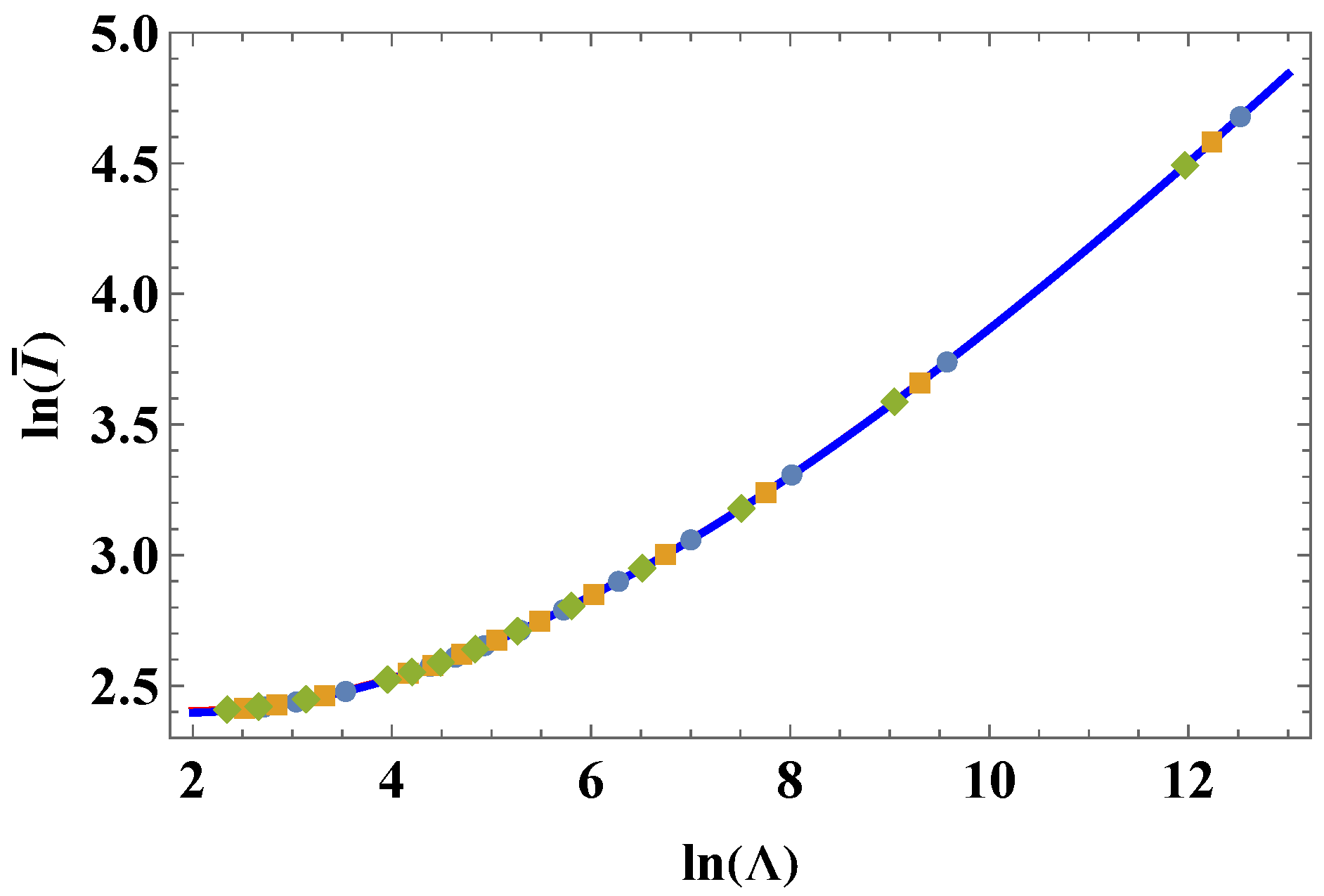

| Model | A | B |
|---|---|---|
| 1 | 0.23 × 0.001 km−2 | |
| 2 | 0.215 × 0.001 km−2 | |
| 3 | 0.2 × 0.001 km−2 |
| Coefficient | a | b | c | d | e |
|---|---|---|---|---|---|
| Model 1 | 2.506 | −0.124 | 0.037 | −0.0013 | |
| Model 2 | 2.515 | −0.128 | 0.038 | −0.0013 | |
| Model 3 | 2.522 | −0.131 | 0.038 | −0.0014 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panotopoulos, G. Universal Relations for Non-Rotating Objects Made of Dark Energy. Galaxies 2025, 13, 13. https://doi.org/10.3390/galaxies13010013
Panotopoulos G. Universal Relations for Non-Rotating Objects Made of Dark Energy. Galaxies. 2025; 13(1):13. https://doi.org/10.3390/galaxies13010013
Chicago/Turabian StylePanotopoulos, Grigoris. 2025. "Universal Relations for Non-Rotating Objects Made of Dark Energy" Galaxies 13, no. 1: 13. https://doi.org/10.3390/galaxies13010013
APA StylePanotopoulos, G. (2025). Universal Relations for Non-Rotating Objects Made of Dark Energy. Galaxies, 13(1), 13. https://doi.org/10.3390/galaxies13010013






