Kinematics of the Milky Way from the Statistical Analysis of the Gaia Data Release 3
Abstract
1. Introduction
2. Methodology and Definitions
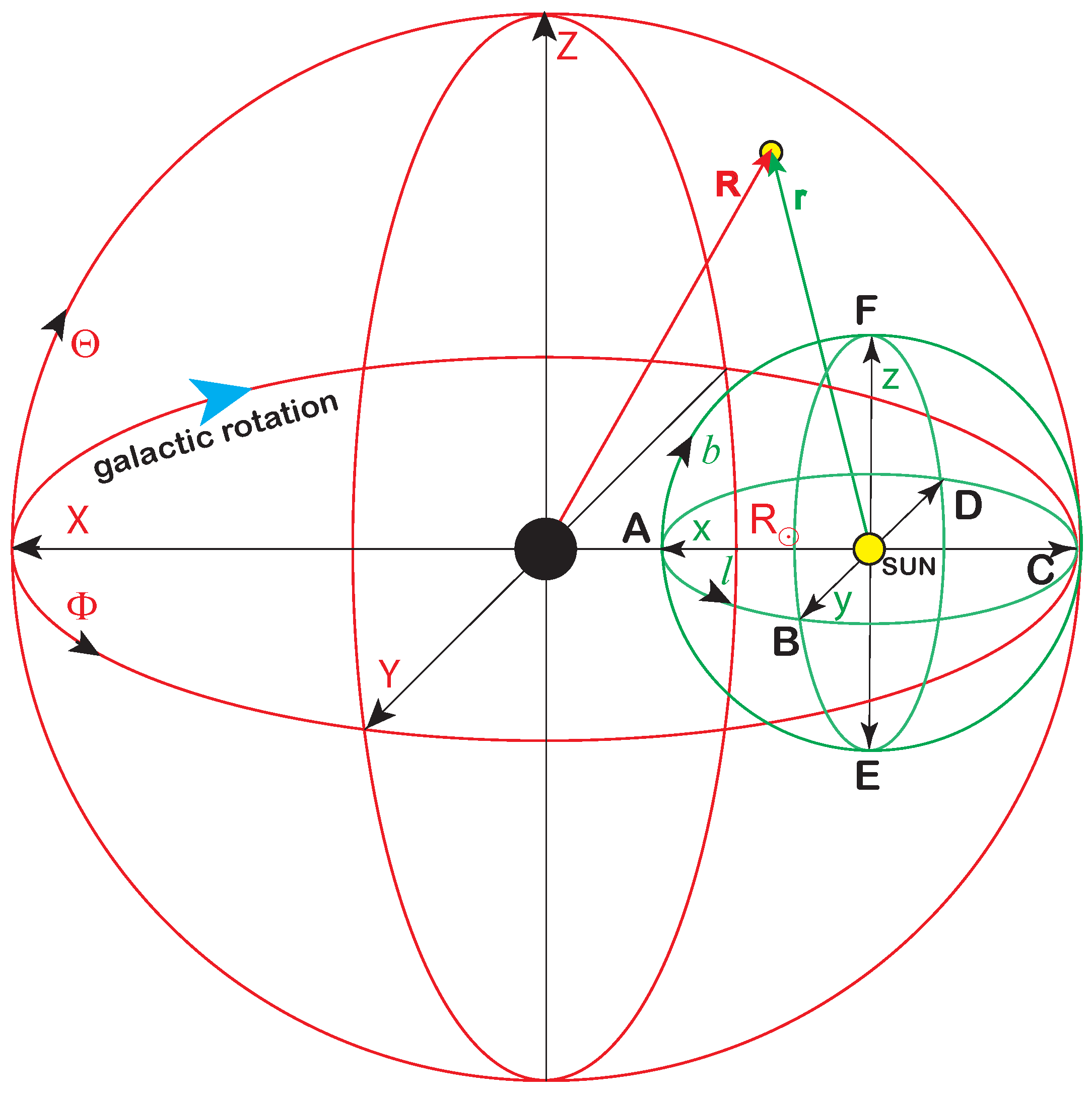
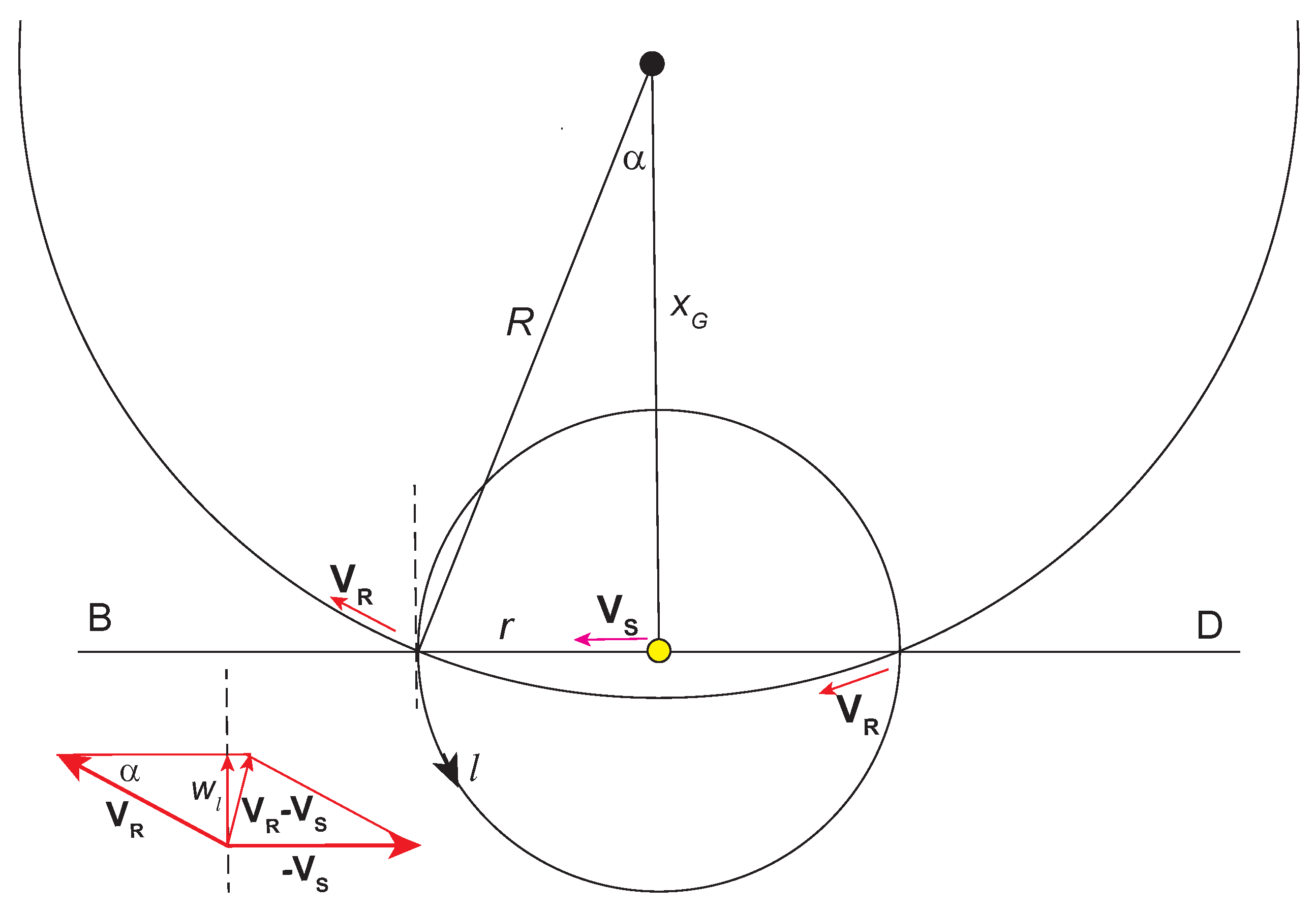
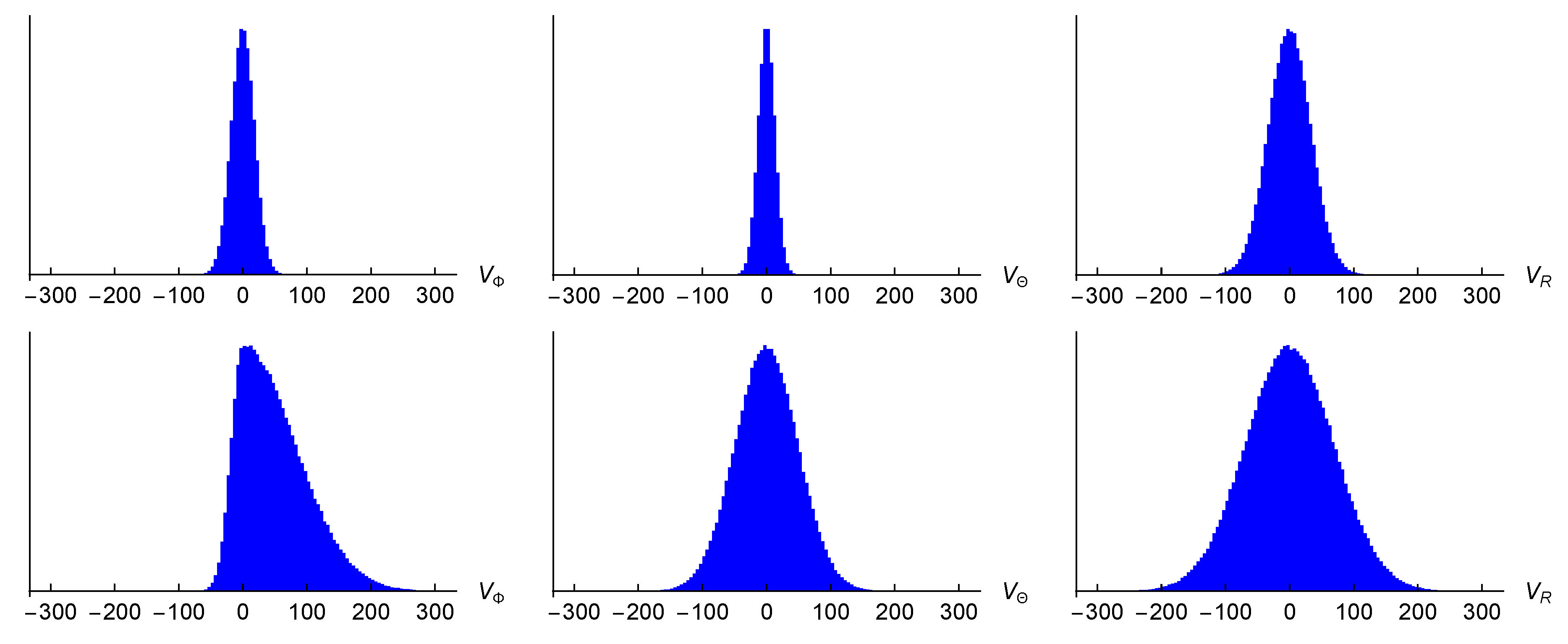
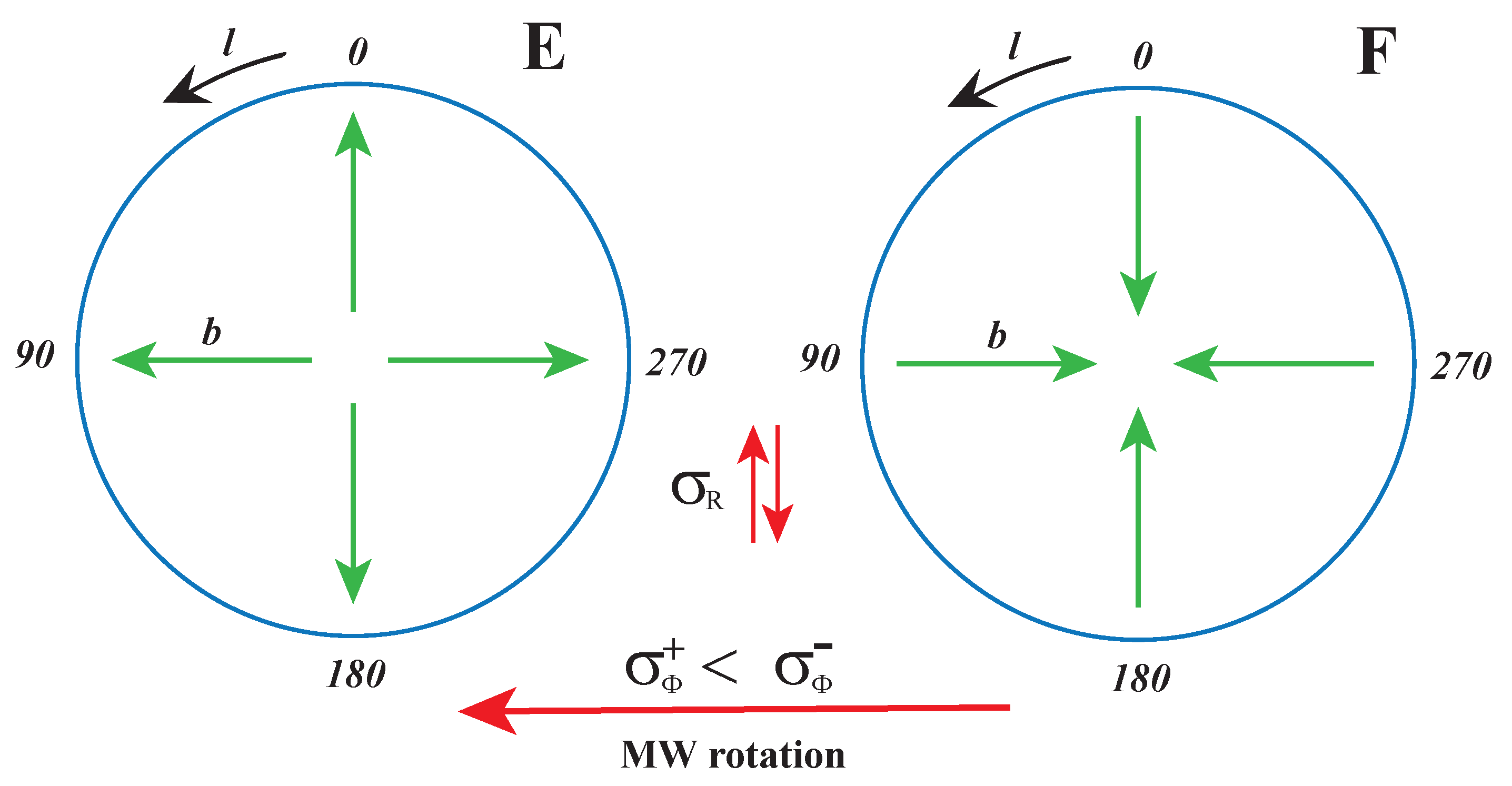
2.1. Reference Frames
2.2. Simulation Model of Stellar Velocities
2.3. Data Set
3. Methods and Results
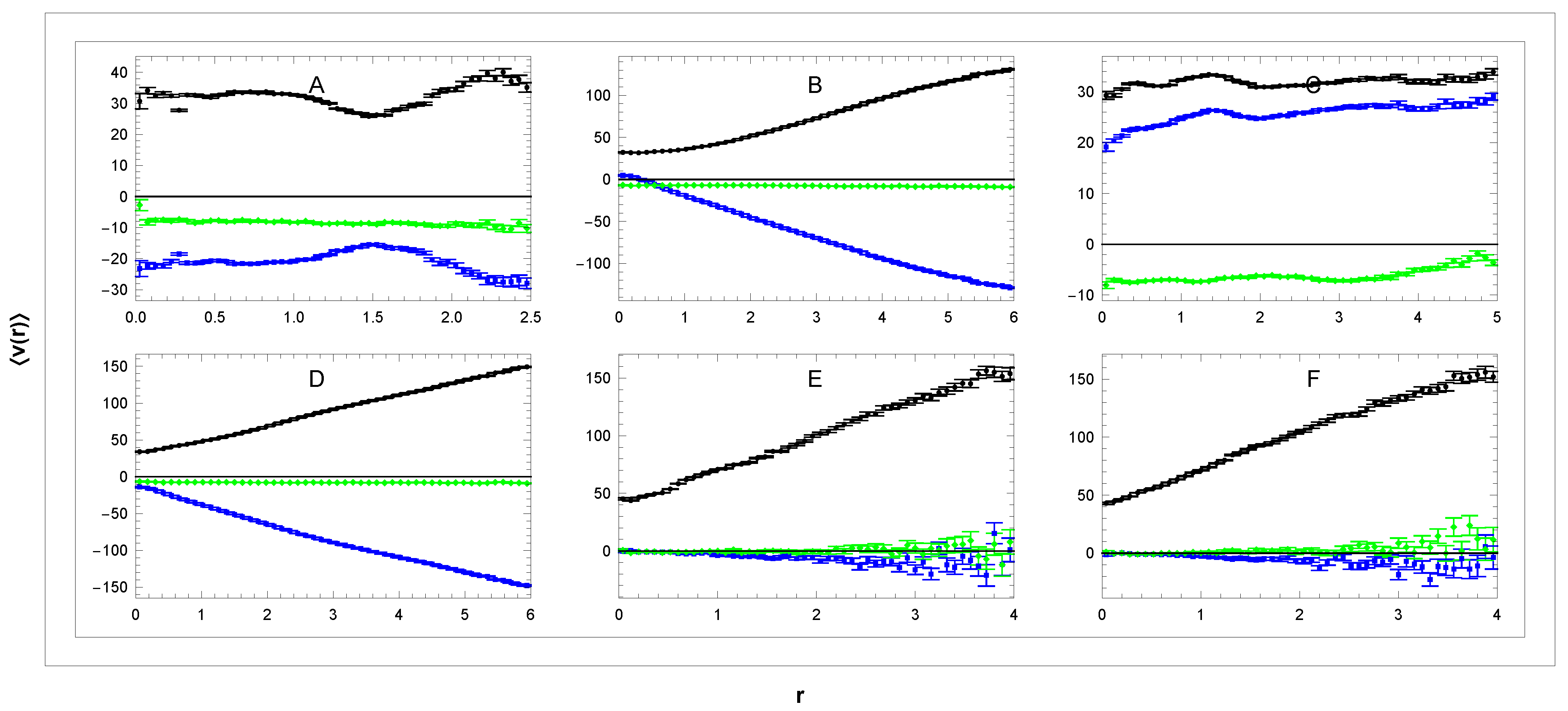
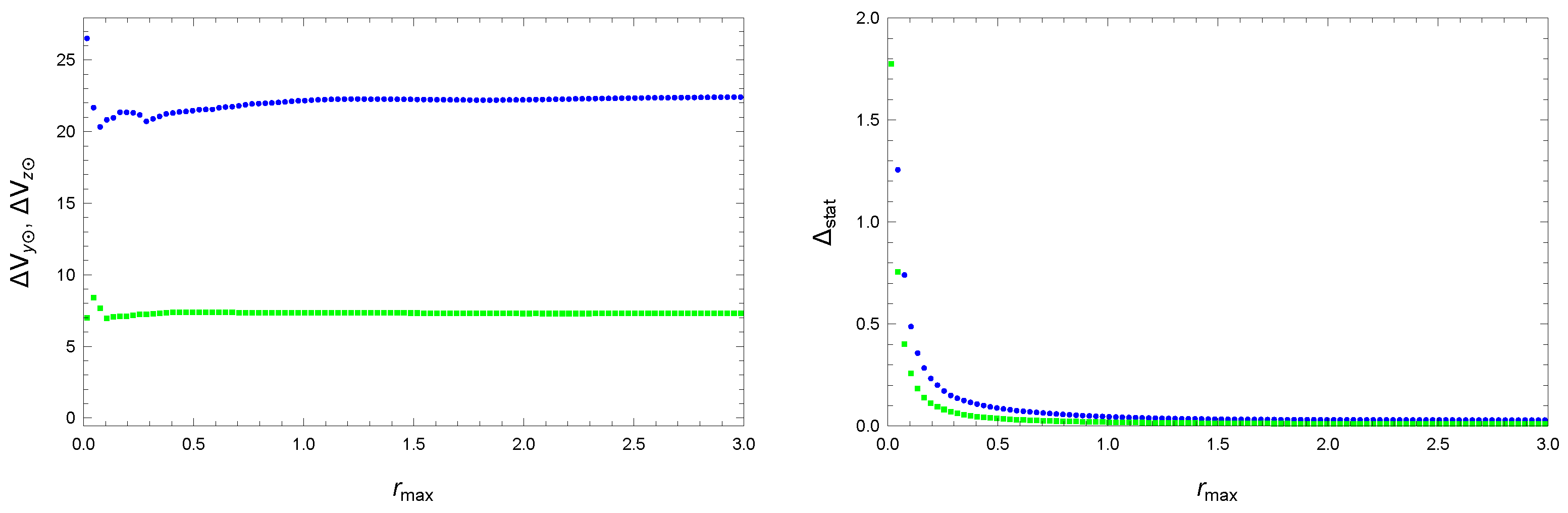
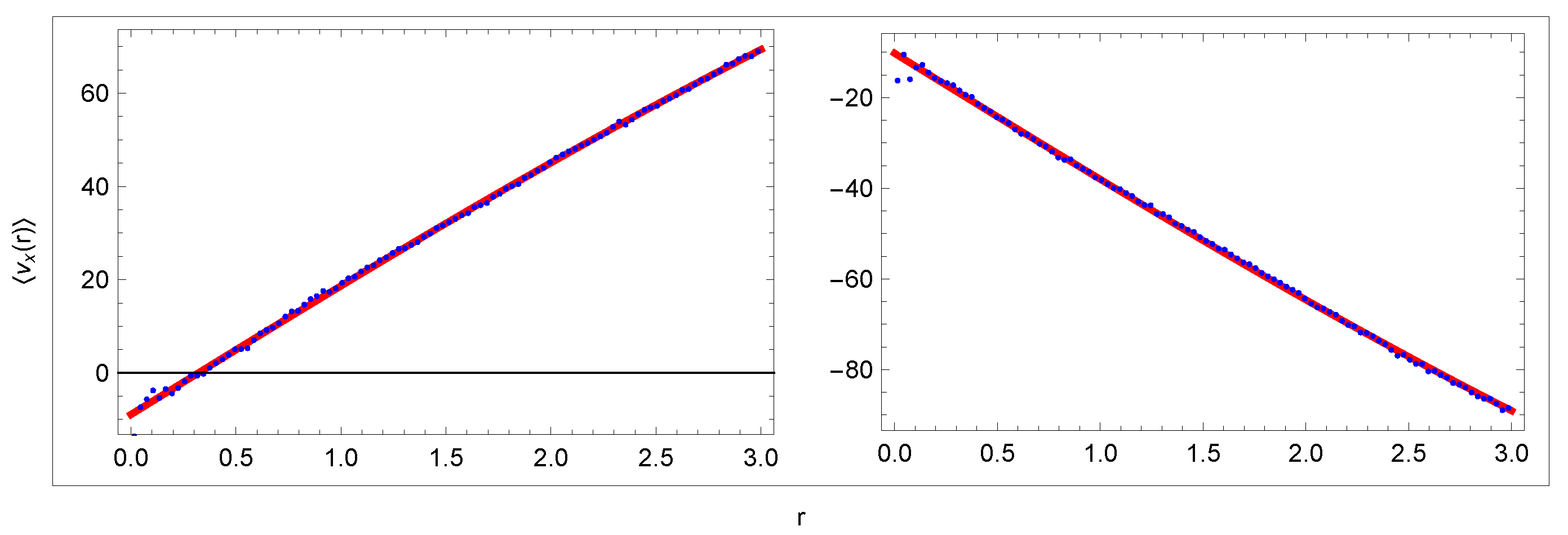
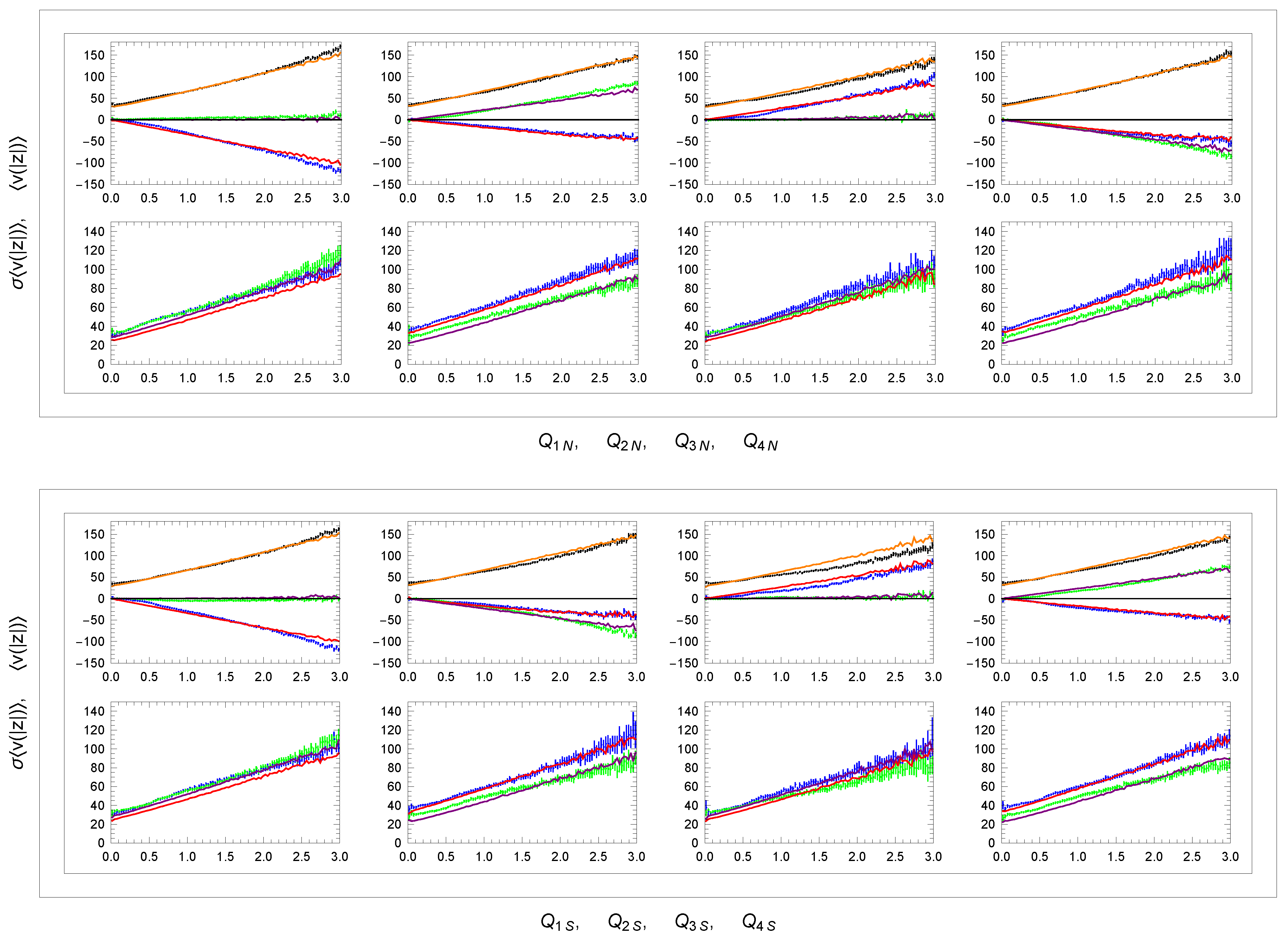
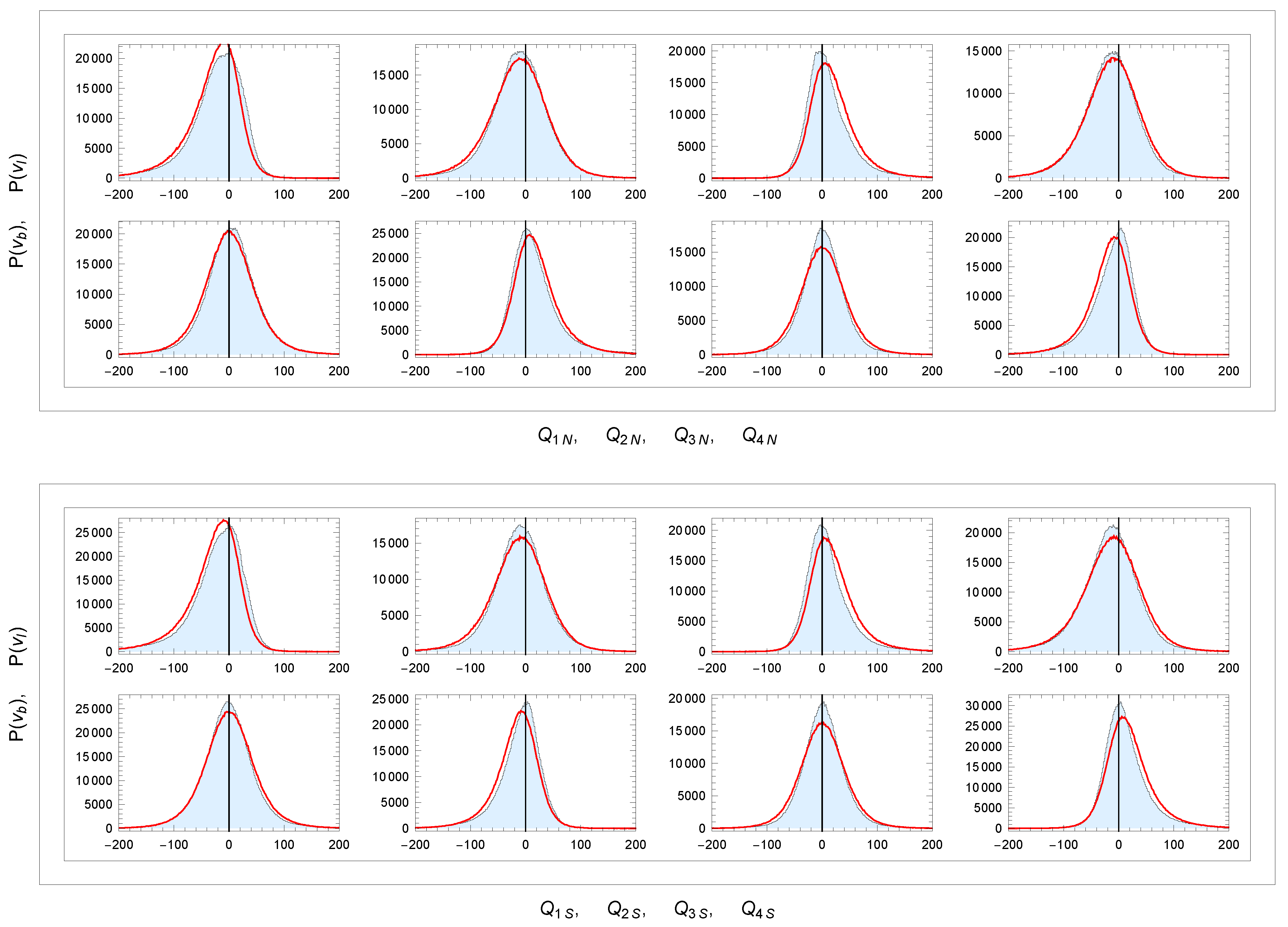
3.1. Velocity of the Sun
- (1)
- in the sectors A–D
- (2)
- in the sectors A and C
- (3)
- and in the sectors B and D
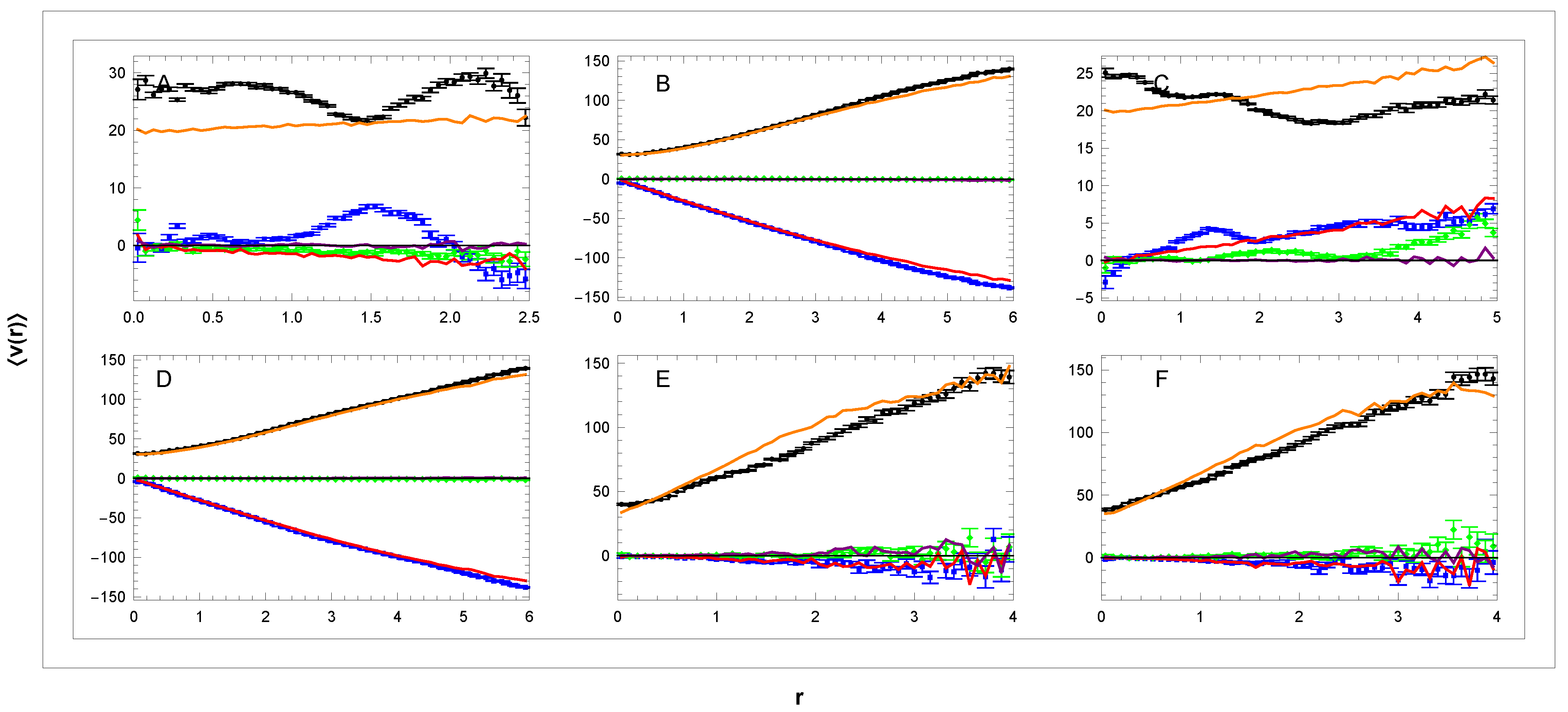
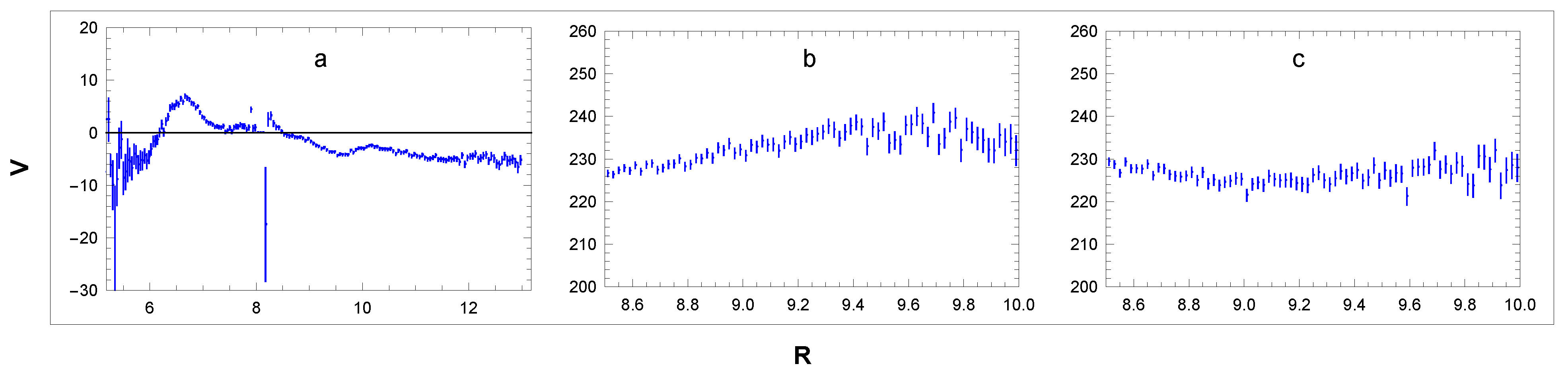
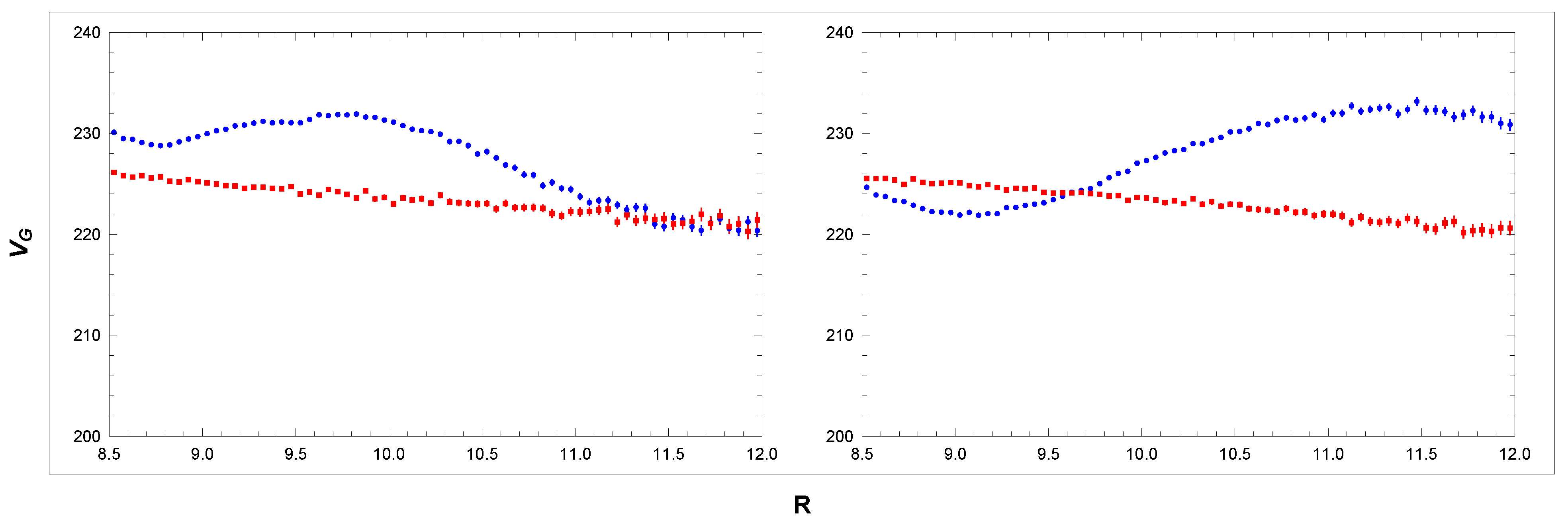
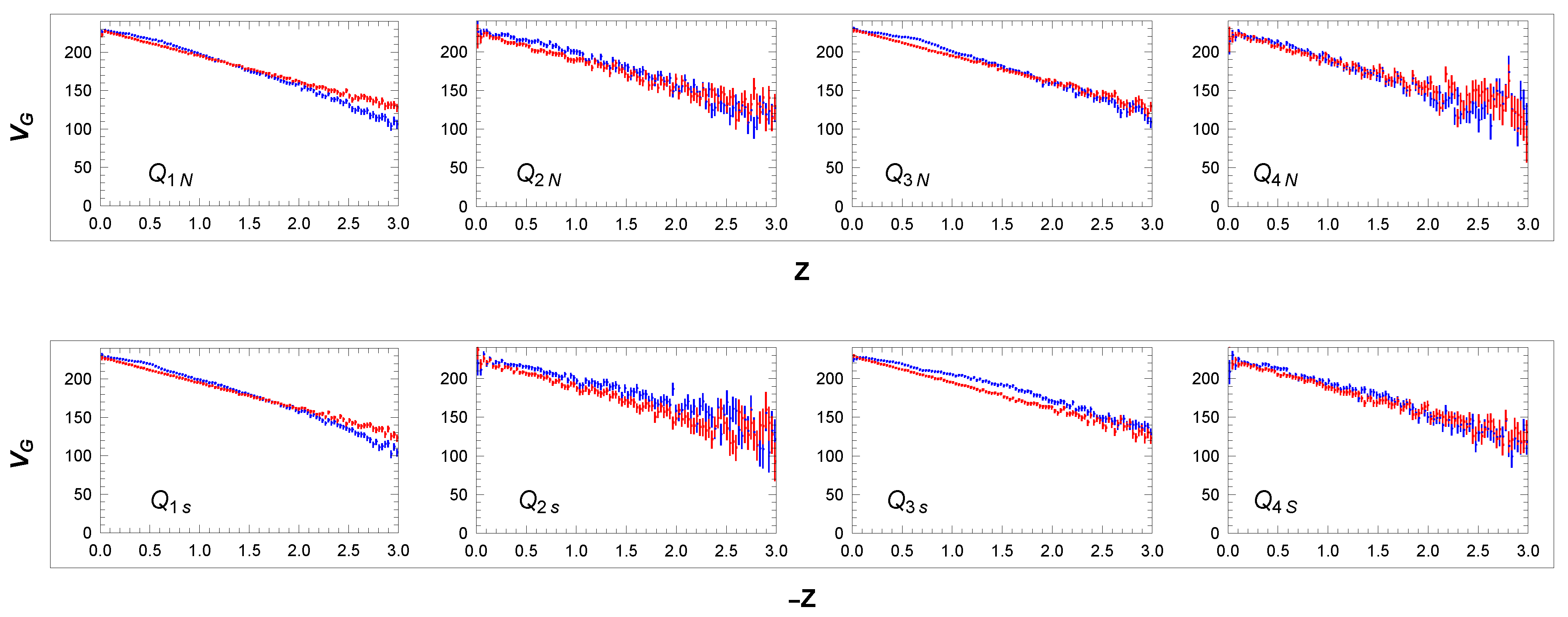
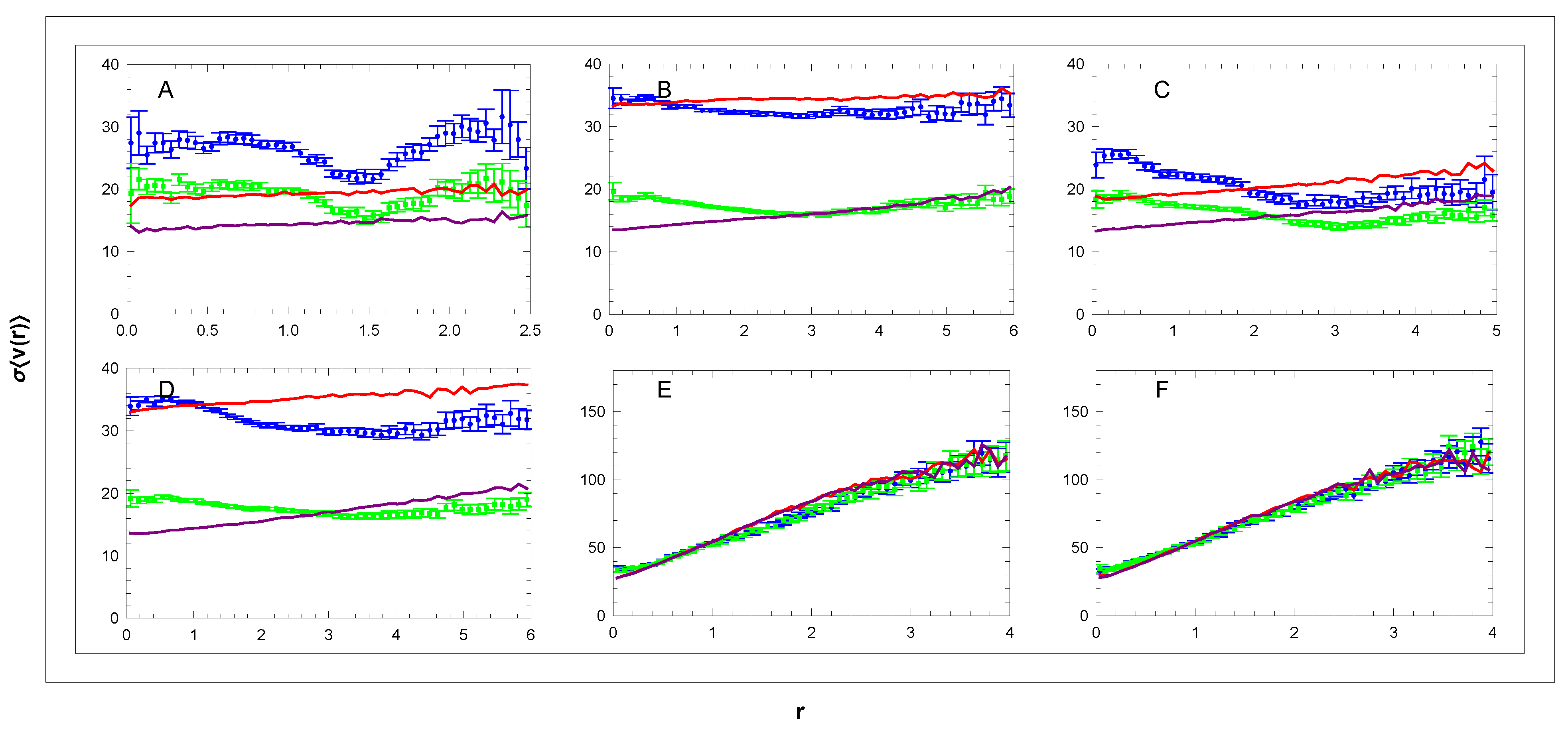
3.2. Rotation Curves
3.3. Six Parameters of the MW Collective Rotation
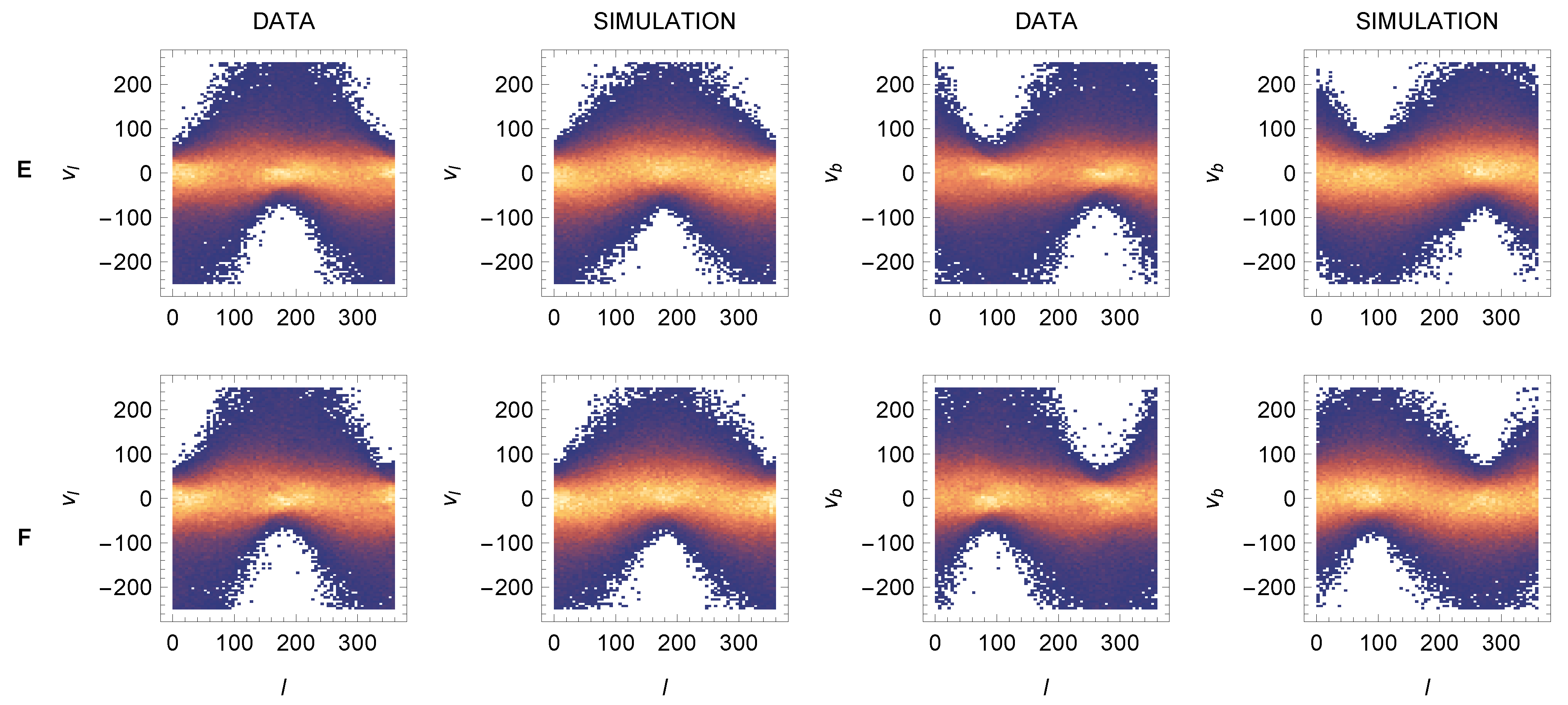
3.4. Comparison of Simulation Model with Data
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vallenari, A.; Brown, A.G.; Prusti, T.; De Bruijne, J.H.; Arenou, F.; Babusiaux, C.; Biermann, M.; Creevey, O.L.; Ducourant, C.; Evans, D.W.; et al. Gaia Data Release 3: Summary of the content and survey properties. Astron. Astrophys. 2023, 674, A1. [Google Scholar]
- Zavada, P.; Píška, K. Catalog of Wide Binary, Trinary and Quaternary Candidates from the Gaia Data Release 2. Astrophys. J. 2022, 163, 33. [Google Scholar] [CrossRef]
- Antoja, T.; Roca-Fàbrega, S.; De Bruijne, J.; Prusti, T. Kinematics of symmetric Galactic longitudes to probe the spiral arms of the Milky Way with Gaia. Astron. Astrophys. 2016, 589, A13. [Google Scholar] [CrossRef]
- Antoja, T.; Helmi, A.; Romero-Gómez, M.; Katz, D.; Babusiaux, C.; Drimmel, R.; Evans, D.W.; Figueras, F.; Poggio, E.; Reylé, C.; et al. A dynamically young and perturbed Milky Way disk. Nature 2018, 561, 360. [Google Scholar] [CrossRef]
- Bhattacharjee, P.; Chaudhury, S.; Kundu, S. Rotation Curve of the Milky Way out to 200 kpc. Astrophys. J. 2014, 785, 63. [Google Scholar] [CrossRef]
- Eilers, A.C.; Hogg, D.W.; Rix, H.W.; Ness, M.K. The Circular Velocity Curve of the Milky Way from 5 to 25 kpc. Astrophys. J. 2019, 871, 120. [Google Scholar] [CrossRef]
- Mróz, P.; Udalski, A.; Skowron, D.M.; Skowron, J.; Soszyński, I.; Pietrukowicz, P.; Szymański, M.K.; Poleski, R.; Kozłowski, S.; Ulaczyk, K. Rotation Curve of the Milky Way from Classical Cepheids. Astrophys. J. Lett. 2019, 870, 10. [Google Scholar] [CrossRef]
- Reid, M.J.; Menten, K.M.; Brunthaler, A.; Zheng, X.W.; Dame, T.M.; Xu, Y.; Wu, Y.; Zhang, B.; Sanna, A.; Sato, M.; et al. Trigonometric Parallaxes of High Mass Star Forming Regions. Astrophys. J. 2014, 783, 130. [Google Scholar] [CrossRef]
- Burch, B.; Cowsik, R. Properties of Galactic Dark Matter: Constraints from Astronomical Observations. Astrophys. J. 2013, 779, 35. [Google Scholar] [CrossRef]
- Chrobáková, Ž.; López-Corredoira, M.; Labini, F.S.; Wang, H.F.; Nagy, R. Gaia-DR2 extended kinematical maps: III. Rotation curves analysis, dark matter, and MOND tests. Astron. Astrophys. 2020, 642, A95. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, X.W.; Yuan, H.B.; Xiang, M.S.; Zhang, H.W.; Chen, B.Q.; Ren, J.J.; Wang, C.; Zhang, Y.; Hou, Y.H.; et al. The Milky Way’s rotation curve out to 100 kpc and its constraint on the Galactic mass. Mon. Not. R. Astron. Soc. 2016, 463, 2623. [Google Scholar] [CrossRef]
- Jiao, Y.; Hammer, F.; Wang, J.L.; Yang, Y.B. Which Milky Way masses are consistent with the slightly declining 5–25 kpc rotation curve? Astron. Astrophys. 2021, 654, A25. [Google Scholar] [CrossRef]
- Wegg, C.; Gerhard, O.; Bieth, M. The gravitational force field of the Galaxy measured from the kinematics of RR Lyrae in Gaia. Mon. Not. R. Astron. Soc. 2019, 485, 3296. [Google Scholar] [CrossRef]
- Ablimit, I.; Zhao, G. The Milky Way’s Circular Velocity Curve and Its Constraint on the Galactic Mass with RR Lyrae Stars. Astrophys. J. 2017, 846, 10. [Google Scholar] [CrossRef]
- Sofue, Y. Rotation Curve of the Milky Way and the Dark Matter Density. Galaxies 2020, 8, 37. [Google Scholar] [CrossRef]
- Drimmel, R.; Romero-Gómez, M.; Chemin, L.; Ramos, P.; Poggio, E.; Ripepi, V.; Andrae, R.; Blomme, R.; Cantat-Gaudin, T.; Castro-Ginard, A.; et al. Gaia Data Release 3: Mapping the asymmetric disc of the Milky Way. Astron. Astrophys. 2023, 674, A37. [Google Scholar]
- Katz, D.; Antoja, T.; Romero-Gómez, M.; Drimmel, R.; Reylé, C.; Seabroke, G.M.; Soubiran, C.; Babusiaux, C.; Di Matteo, P.; Figueras, F.; et al. Gaia Data Release 2: Mapping the Milky Way disc kinematics. Astron. Astrophys. 2018, 616, A11. [Google Scholar]
- Kawata, D.; Baba, J.; Ciucă, I.; Cropper, M.; Grand, R.J.; Hunt, J.A.; Seabroke, G. Radial distribution of stellar motions in Gaia DR2. MNRAS Lett. 2018, 479, 108. [Google Scholar] [CrossRef]
- López-Corredoira, M.; Sylos Labini, F. Gaia-DR2 extended kinematical maps. Astron. Astrophys. 2019, 621, A48. [Google Scholar] [CrossRef]
- Ramos, P.; Antoja, T.; Figueras, F. Riding the kinematic waves in the Milky Way disk with Gaia. Astron. Astrophys. 2018, 619, A72. [Google Scholar] [CrossRef]
- Wang, H.F.; Chrobáková, Ž.; López-Corredoira, M.; Labini, F.S. Mapping the Milky Way Disk with Gaia DR3. Astrophys. J. 2023, 942, 12. [Google Scholar] [CrossRef]
- Wang, H.F.; López-Corredoira, M.; Huang, Y.; Carlin, J.L.; Chen, B.Q.; Wang, C.; Chang, J.; Zhang, H.W.; Xiang, M.S.; Yuan, H.B.; et al. Mapping the Galactic disc with the LAMOST and Gaia red clump sample: II. 3D asymmetrical kinematics of mono-age populations in the disc between 6–14 kpc. Mon. Not. R. Astron. Soc. 2020, 491, 2104. [Google Scholar] [CrossRef]
- Kushniruk, I.; Schirmer, T.; Bensby, T. Kinematic structures of the solar neighbourhood revealed by Gaia DR1/TGAS and RAVE. Astron. Astrophys. 2017, 608, A73. [Google Scholar] [CrossRef]
- Kawata, D.; Bovy, J.; Matsunaga, N.; Baba, J. Galactic rotation from Cepheids with Gaia DR2 and effects of non-axisymmetry. Mon. Not. R. Astron. Soc. 2019, 482, 40. [Google Scholar] [CrossRef]
- Tian, H.J.; Liu, C.; Wan, J.C.; Wang, Y.G.; Wang, Q.; Deng, L.C.; Cao, Z.H.; Hou, Y.H.; Wang, Y.F.; Wu, Y.; et al. Peculiar in-plane velocities in the outer disc of the Milky Way. Res. Astron. Astrophys. 2017, 17, 114. [Google Scholar] [CrossRef]
- Bland-Hawthorn, J.; Gerhard, O. The Galaxy in Context: Structural, Kinematic, and Integrated Properties. Annu. Rev. Astron. Astrophys. 2016, 54, 529. [Google Scholar] [CrossRef]
- Antoja, T.; De Bruijne, J.; Figueras, F.; Mor, R.; Prusti, T.; Roca-Fàbrega, S. The intricate Galaxy disk: Velocity asymmetries in Gaia-TGAS. Astron. Astrophys. 2017, 602, L13. [Google Scholar] [CrossRef][Green Version]
- Mikkola, D.; Paul, J.; McMillan, P.; Hobbs, D. New stellar velocity substructures from Gaia DR3 proper motions. Mon. Not. R. Astron. Soc. 2023, 519, 1989. [Google Scholar] [CrossRef]
- Abuter, R.; Amorim, A.; Bauböck, M.; Berger, J.P.; Bonnet, H.; Brandner, W.; Clénet, Y.; Du Foresto, V.C.; De Zeeuw, P.T.; Dexter, J.; et al. A geometric distance measurement to the Galactic center black hole with 0.3% uncertainty. Astron. Astrophys. 2019, 625, L10. [Google Scholar]
- Bennet, M.; Bovy, J. Vertical waves in the solar neighbourhood in Gaia DR2. Mon. Not. R. Astron. Soc. 2019, 482, 1417. [Google Scholar] [CrossRef]
- Schönrich, R.; Binney, J.; Dehnen, W. Local kinematics and the local standard of rest. Mon. Not. R. Astron. Soc. 2010, 403, 1829. [Google Scholar] [CrossRef]
- Gaia Data Processing and Analysis Consortium 2023, Gaia Data Release 3, Documentation Release 1.3. Available online: https://gea.esac.esa.int/archive/documentation/GDR3/ (accessed on 20 January 2025).
- Antoja, T.; McMillan, P.J.; Kordopatis, G.; Ramos, P.; Helmi, A.; Balbinot, E.; Cantat-Gaudin, T.; Chemin, L.; Figueras, F.; Jordi, C.; et al. Gaia Early Data Release 3: The Galactic anticentre. Astron. Astrophys. 2021, 649, A8. [Google Scholar]
- Bailer-Jones, C.A.L. Estimating Distances from Parallaxes. Publ. Astron. Soc. Pac. 2015, 127, 994–1009. [Google Scholar] [CrossRef]
- Gaia Collaboration: Luri, X.; Brown, A.G.A.; Sarro, L.M. Gaia Data Release 2: Using Gaia parallaxes. Astron. Astrophys. 2018, 616, A9. [Google Scholar] [CrossRef]
- Lindegren, L.; Bastian, U.; Biermann, M.; Bombrun, A.; De Torres, A.; Gerlach, E.; Geyer, R.; Hernández, J.; Hilger, T.; Hobbs, D.; et al. Gaia Early Data Release 3: Parallax bias versus magnitude, colour, and position. Astron. Astrophys. 2021, 649, A4. [Google Scholar] [CrossRef]
- Jeans, J.H. On the theory of star-streaming and the structure of the universe. Mon. Not. R. Astron. Soc. 1915, 76, 70. [Google Scholar] [CrossRef]
- Bovy, J. Dynamics and Astrophysics of Galaxies; Princeton University Press: Princeton, NJ, USA, 2024; (in preparation). Available online: https://galaxiesbook.org/index.html (accessed on 20 January 2025).
- Li, X.; Yang, P.; Wang, H.F.; Li, Q.; Luo, Y.P.; Luo, Z.Q.; Wang, G.Y. Asymmetric Drift Map of the Milky Way disk Populations between 8–16 kpc with LAMOST and Gaia datasets. arXiv 2023, arXiv:2310.01311. [Google Scholar] [CrossRef]
- Bobylev, V.V.; Bajkova, A.T. Kinematic Analysis of Solar-Neighborhood Stars Based on RAVE4 Data. Astron. Lett. 2016, 42, 90. [Google Scholar] [CrossRef]
- Tian, H.J.; Liu, C.; Carlin, J.L.; Zhao, Y.H.; Chen, X.L.; Wu, Y.; Li, G.W.; Hou, Y.H.; Zhang, Y. The Stellar Kinematics in the Solar Neighborhood from LAMOST Data. Astrophys. J. 2015, 809, 145. [Google Scholar] [CrossRef]
- Dehnen, W.; James, J. Binney, J.J. Local stellar kinematics from Hipparcos data. Mon. Not. R. Astron. Soc. 1998, 298, 387. [Google Scholar] [CrossRef]
- Bovy, J.; Prieto, C.A.; Beers, T.C.; Bizyaev, D.; Da Costa, L.N.; Cunha, K.; Ebelke, G.L.; Eisenstein, D.J.; Frinchaboy, P.M.; Pérez, A.E.; et al. The Milky Way’s circular velocity curve between 4 and 14 kpc from APOGEE data. Astrophys. J. 2012, 759, 131. [Google Scholar] [CrossRef]
- Bovy, J.; Bird, J.C.; Pérez, A.E.; Majewski, S.R.; Nidever, D.L.; Zasowski, G. The Power Spectrum of the Milky Way: Velocity Fluctuations in the Galactic Disk. Astrophys. J. 2015, 800, 83. [Google Scholar] [CrossRef]
- Schönrich, R. Galactic rotation and solar motion from stellar kinematics. Mon. Not. R. Astron. Soc. 2012, 427, 274. [Google Scholar] [CrossRef]
- Koposov, S.E.; Rix, H.-W.; Hogg, D.W. Constraining the Milky Way potential with a 6-D phase-space map of the GD-1 stellar stream. Astrophys. J. 2010, 712, 260. [Google Scholar] [CrossRef]
- Hayes, C.R.; Law, D.R.; Majewski, S.R. Constraining the Solar Galactic Reflex Velocity using Gaia Observations of the Sagittarius. Astrophys. J. Lett. 2018, 867, L20. [Google Scholar] [CrossRef]
- Anguiano, B.; Majewski, S.R.; Hayes, C.R.; Prieto, C.A.; Cheng, X.; Bidin, C.M.; Beaton, R.L.; Beers, T.C.; Minniti, D. The Stellar Velocity Distribution Function in the Milky Way Galaxy. Astron. J. 2020, 160, 43. [Google Scholar] [CrossRef]
- Vieira, K.; Carraro, G.; Korchagin, V.; Lutsenko, A.; Girard, T.M.; van Altena, W. Milky Way Thin and Thick Disk Kinematics with Gaia EDR3 and RAVE DR5. Astrophys. J. 2022, 932, 28. [Google Scholar] [CrossRef]
- Bienaymé, O.; Leca, J.; Robin, A.C. A new dynamically self-consistent version of the Besançon Galaxy model. Astron. Astrophys. 2018, 620, A103. [Google Scholar] [CrossRef]


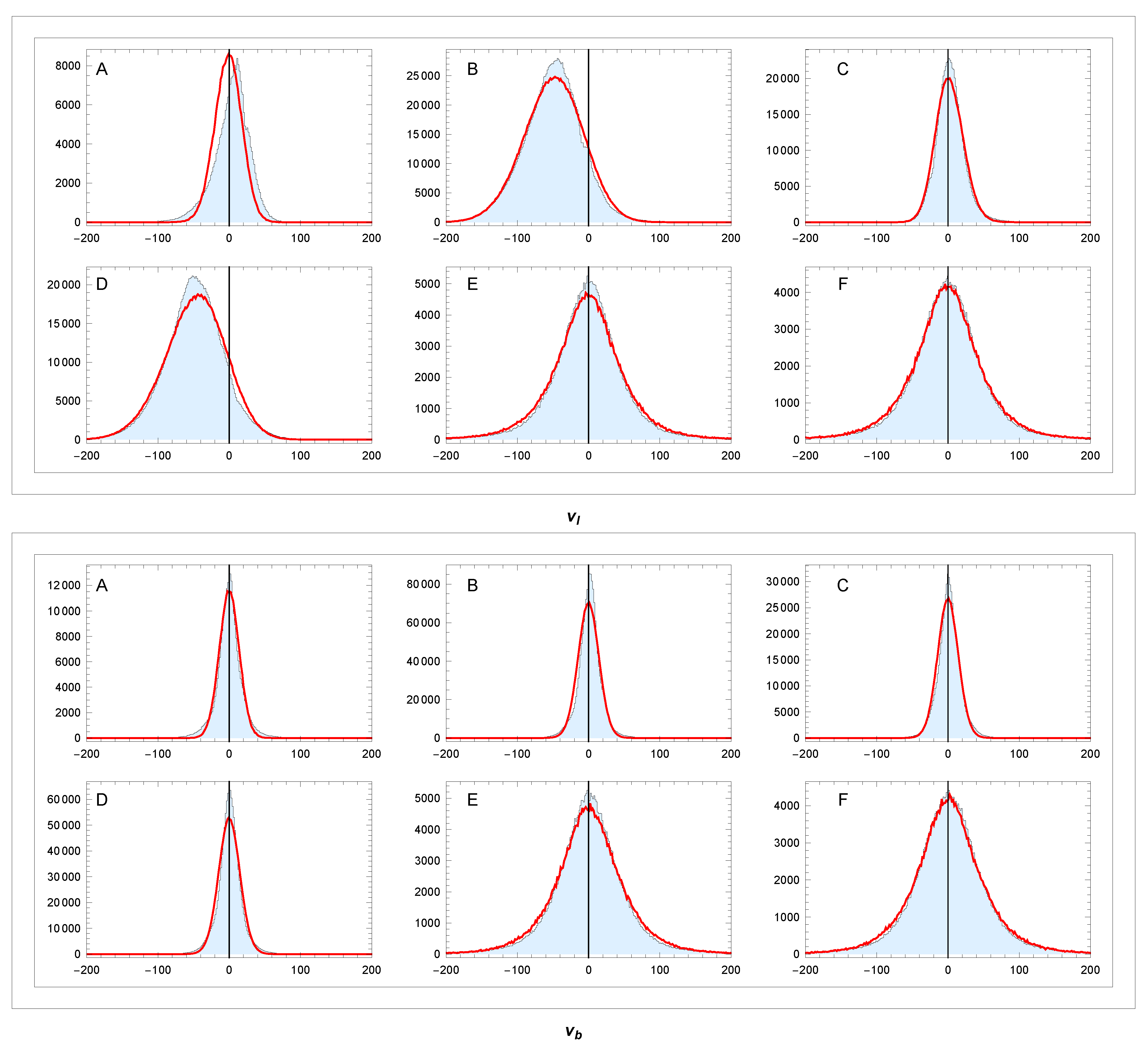

| A | B | C | D | E | F | |||
| 1.02 | 1.89 | 1.63 | 1.84 | 0.90 | 0.93 | 1.93 | 2.08 | |
| 253,546 | 1,612,100 | 609,593 | 1,233,495 | 314,515 | 283,906 | 18,968,282 | 24,584,392 | |
| 22,704,200 | 6,646,423 | 2,498,909 | 5,422,928 | 573,436 | 540,330 | 70,260,517 | 85,849,109 | |
| H | ||||||||
| 0.89 | 0.75 | 0.72 | 0.87 | 0.89 | 0.87 | 0.74 | 0.79 | |
| 1,646,264 | 1,161,311 | 995,955 | 1,475,289 | 1,378,017 | 1,337,495 | 977,358 | 1,052,616 | |
| 3,331,201 | 2,164,099 | 1,716,957 | 2,640,374 | 2,973,013 | 2,259,886 | 1,688,028 | 2,153,065 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zavada, P.; Píška, K. Kinematics of the Milky Way from the Statistical Analysis of the Gaia Data Release 3. Galaxies 2025, 13, 10. https://doi.org/10.3390/galaxies13010010
Zavada P, Píška K. Kinematics of the Milky Way from the Statistical Analysis of the Gaia Data Release 3. Galaxies. 2025; 13(1):10. https://doi.org/10.3390/galaxies13010010
Chicago/Turabian StyleZavada, Petr, and Karel Píška. 2025. "Kinematics of the Milky Way from the Statistical Analysis of the Gaia Data Release 3" Galaxies 13, no. 1: 10. https://doi.org/10.3390/galaxies13010010
APA StyleZavada, P., & Píška, K. (2025). Kinematics of the Milky Way from the Statistical Analysis of the Gaia Data Release 3. Galaxies, 13(1), 10. https://doi.org/10.3390/galaxies13010010





