Abstract
While the dominant radiation mechanism of gamma-ray bursts (GRBs) remains a question of debate, synchrotron emission is one of the foremost candidates to describe the multi-wavelength afterglow observations. As such, it is expected that GRBs should present some degree of polarization across their evolution—presenting a feasible means of probing these bursts’ energetic and angular properties. Although obtaining polarization data is difficult due to the inherent complexities regarding GRB observations, advances are being made, and theoretical modeling of synchrotron polarization is now more relevant than ever. In this manuscript, we present the polarization for a fiduciary model, where the synchrotron FS emission evolving in the radiative–adiabatic regime is described by a radially stratified off-axis outflow. This is parameterized with a power-law velocity distribution and decelerated in a constant-density and wind-like external environment. We apply this theoretical polarization model for two select GRBs, presenting upper limits in their polarization—GRB 170817A, a known off-axis GRB with radio polarization upper limits, and GRB 190014C, an on-axis case, where the burst was seen from within the half-opening angle of the jet, with observed optical polarization—in an attempt to constrain their magnetic field geometry in the emitting region.
1. Introduction
Gamma-ray Bursts (GRBs) are the most luminescent phenomena in the universe. They result from the deaths of massive stars [1,2,3,4] or the merger of two compact objects, such as neutron stars (NSs; [5,6,7,8]) or a NS with a black hole (BH, [9]). GRBs are evaluated based on the phenomenology seen during their early and late phases and are often characterized by the fireball model [10] to distinguish their various sources. The principal and earliest emission, known as the “prompt emission”, is detected from hard X-rays to -rays. This phase can be explained by the interactions of internal shells of material launched forcefully from the central engine at various speeds [11,12], photospheric emission from the fireball [13,14,15] or discharges from a Poynting-flux-dominated ejecta [16,17,18,19]. Later emission, known as “afterglow”, (e.g., [10,20,21,22,23,24,25,26,27,28]) is a long-lasting multi-wavelength emission detectable in gamma-rays, X-rays, optical, and radio. It is modeled using synchrotron radiation produced when the external environment decelerates the relativistic outflow, and a significant portion of its energy is transferred. Long GRBs (lGRBs) and short GRBs (sGRBs) are categorized based on their duration:1 or ,2 respectively [30,31].
Synchrotron radiation is the fundamental emission mechanism in GRB afterglows in a forward-shock (FS) scenario [32,33]. Nevertheless, synchrotron is contingent on the existence of magnetic fields. The origin and arrangement of these magnetic fields behind the shock remain debatable. They can originate from the compression of an existing magnetic field within the interstellar medium (ISM; [34,35]) and shock-generated two-stream instabilities [36,37]. The magnetic field generated by these plasma instabilities is random in orientation but mostly confined to the plane of the shock [38]. Modeling the source and arrangement of those fields and other physical properties of GRBs presents a challenging task. This has necessitated the development of other methods for investigating these complicated systems. Among these techniques is linear polarization. Linear polarization () has been measured, up to a few percent, from the afterglow of several GRBs. Some examples include GRB 191221B (; [39]) at the late afterglow, GRB 190114C (; [40]) on the radio band, and the upper limit determinations of GRB 991216 (yielding ; [41]) and GRB 170817A (yielding , on the 2.8 GHz radio band [42]). Meanwhile, for the prompt phase, polarization has been observed in several bursts, with significant higher polarization degree, such as GRB 021206 ( [43]), GRB 041219A ( [44]), GRB 120308A ( [45]), GRB 160821A ( [46]), and many more. The high value of polarization observed in the prompt phase would be a strong indicator of synchrotron emission as the mechanism for the prompt emission, as the high polarization is a characteristic of this emission mechanism, and the polarization obtained from a Comptonized spectrum would be smaller, [47,48,49]. However, reaching a conclusive result from the current data is problematic, as much of it has low statistical significance. Previous works, including [35,50,51,52,53,54,55,56], have already investigated the practicality of utilizing polarization models to acquire source-related information, both in the prompt and afterglow phases. Due to the unfortunately low number of orbital polarimeters, the brightness of the events, sensitivity, and response time limitations, collecting polarization data both at the prompt and aftergflow phase has been one of the most significant impediments towards advancement of the field. Despite this, progress has been made in the field as a result of multiple global initiatives, and it is anticipated that we will have abundant data with higher statistical significance to test various models in the coming years.
This study expands the analytical synchrotron afterglow scenario of the off-axis homogeneous jet in a stratified environment, which was required to characterize the multi-wavelength data of GRB 170817A [57] and a sample of GRBs exhibiting off-axis emission.3 The phenomenological model is extended from the adiabatic to the radiative regime, including the self-absorption synchrotron phase and the dimensionless factor, which provides information on the equal arrival time surface (EATS). We show the temporal development of polarization from the synchrotron afterglow stratification model and compute the expected polarization for GRB 170817A [59,60,61,62,63] and GRB 190114C [40,64,65,66]. For GRB 170817A we employ the available polarimetric upper limits from [42], and for GRB 190114C the optical polarization data from [40]. Keeping this in mind, the structure of the paper is as follows: In Section 2, we briefly describe the off-axis jet synchrotron model derived in [57] with the extension. In Section 3, we introduce the polarization model used in this paper. In Section 4, we compute the assumed polarization and give the outcomes for our chosen afterglow-emitting bursts. Finally, in Section 5, we present the conclusion and provide closing thoughts.
2. Synchrotron Forward-Shock Model from a Radially Stratified Off-Axis Jet
The multi-wavelength afterglow observations of GRB 170817A are consistent with the synchrotron FS scenario in the fully adiabatic regime from a radially stratified off-axis outflow decelerated in a homogeneous medium [67,68,69]. Ref. [57] extended the synchrotron FS approach to a stratified environment based on the immediate vicinity of a binary NS merger proposed to explain the gamma-ray flux in GRB 150101B. Additionally, Ref. [57] successfully explained the multi-wavelength afterglow observations in GRB 080503, GRB 140903A, and GRB 160821B using the synchrotron off-axis model.
In order to present a polarization model and perform a fully time-evolving analysis, we extend the synchrotron scenario described in [57,67] from adiabatic to radiative regime including the self-absorption phase and the dimensionless factor which provides information on the EATS [70,71].
2.1. Synchrotron Scenario
Relativistic electrons are accelerated in the FS and cooled down mainly via synchrotron emission in the presence of a comoving magnetic field , where e is the energy density and the fraction of magnetic energy given in the FS. Hereafter, we use the prime and unprimed quantities to refer them in the comoving and observer frames, respectively. The acceleration process leads to electrons with Lorentz factors () coming via a distribution of the form with p as the electron power index. We consider a radially off-axis jet with an equivalent kinetic energy given by the following:
where is the characteristic energy, corresponds to the viewing angle () and the half-opening angle of the jet () and is the bulk Lorentz factor, and is a mathematical parameter whose value is , introduced to give a power-law profile to the kinetic energy. We consider that the circumburst medium can be constant (n) or stratified (with a profile given by the stellar wind with as the density parameter).
2.1.1. Constant-Density Medium
We assume an evolution of the FS with an isotropic equivalent-kinetic energy (Blandford–McKee solution; [72]), where corresponds to the adiabatic regime and to the fully radiative one [73,74,75], and a radial distance with c the speed of light, is the proton mass and z is the redshift. Therefore, the evolution of the bulk Lorentz factor is given by the following:
with . Using the bulk Lorentz factor (Equation (2)) and the synchrotron afterglow theory introduced in [10] for the fully adiabatic regime, we derive in this formalism the relevant quantities of synchrotron emission that originated from the FS. The minimum and cooling electron Lorentz factors can be written as follows:
respectively. Here, Y is the Compton parameter, whereas is the fraction of energy given to accelerate the electron population. Using the electron Lorentz factors (Equation (4)), the characteristic and cooling spectral breaks for synchrotron radiation are
respectively. Considering the maximum emissivity, the total number of radiating electrons and the luminosity distance , the maximum flux emitted by synchrotron radiation is given by
The synchrotron spectral breaks in the self-absorption regime are derived from , and with the optical depths given by and .
The light curves in the fast cooling regime are as follows:
and in the slow cooling regime they are as follows:
2.1.2. Stellar-Wind Medium
In the case of a stratified stellar-wind-like medium, the number density is given by where , with the mass-loss rate and v the velocity of the outflow (e.g., see [76]). Taking into account the Blandford–McKee solution for a stratified stellar-wind-like medium, the bulk Lorentz factor derived through the adiabatic evolution [72,77] is given by
with the characteristic energy given by . Using the bulk Lorentz factor (Equation (11)) and the synchrotron afterglow theory for a wind-like medium [71,78], we derive the relevant quantities of synchrotron emission for our model in the fully adiabatic regime. The minimum and cooling electron Lorentz factors are given by
The characteristic and cooling spectral breaks for synchrotron emission are
respectively. Given the maximum emissivity in a stratified stellar-wind-like medium, the maximum flux radiated by synchrotron emission is given by
The synchrotron spectral breaks in the self-absorption regime are derived from , and with the optical depths given by and .
The light curves in the fast cooling regime are
whereas in the slow cooling regime they are
3. Polarization Model
GRB afterglows are expected to be intrinsically polarized, due to their non-thermal emission mechanisms. Polarization is commonly attributed to synchrotron radiation behind shock waves. This makes it dependent on the magnetic field configuration and the geometry of the shock, as they will define the polarization degree (PD) on each point and its integration over the whole image [51]. The Stokes parameters (I, Q, U, and V) control the approach to polarization calculation, and normally only linear polarization is considered. From this point on, we refer to the observer and comoving frames as unprimed and primed, respectively. The stokes parameters are expressed as
where is the polarization angle. The measured stokes parameters are the sum over the flux [79], so
The relationship —where is the spectral luminosity and is the element of the solid angle of the fluid element in relation to the source—allows the introduction of the factors regarding the geometry of the magnetic field and outflow by using [80]
For this work, we consider and , with as the spectral index, which we obtain with the electron power-law index p; i.e., [79]. The parameter is the angle between the local magnetic field and the particle’s direction of motion, and due to the highly beamed nature of synchrotron emission, this angle is also the pitch angle. The geometrical considerations of polarization can then be taken by averaging this factor over the local probability distribution of the magnetic field (see Equation (15) of [51]),
One of the still-unsolved mysteries of GRBs is the configuration of the magnetic field present at different regions of emission. The considerations regarding the magnetic field geometry are varied based on the GRB epoch of relevance. For a scenario where the afterglow is described by an FS, two of the most suitable configurations are a random perpendicular configuration—where the anisotropy factor is confined to the shock plane; and an ordered configuration parallel to the velocity vector, where . More complex configurations with multi-component magnetic fields, where the anisotropy is , have been conducted [35,38,42,55]. As it is warranted and needed, however, for the purposes of this paper, we limit ourselves to the two following cases.
- Random magnetic field ()
In this scenario, the symmetry of the random magnetic field configuration, perpendicular to the shock plane, causes the polarization over the image to disappear when the beaming cone is wholly contained within the jet aperture or if it is seen along the axis (). To break the symmetry, the jet must be viewed close to its edge (), where the missing emission (from ) results only in partial cancellation [81]. The equation necessary to calculate this polarization is explicitly laid out as Equation (5) in [79].
- Ordered magnetic field ()
For the ordered magnetic field, a configuration parallel to the velocity vector, the same symmetry observations hold true and the calculation follows [51,79], with .
By substituting the following integration limits
with an appropriate prescription of the bulk Lorentz factor , the evolution of the opening angle of the jet , and the parameters required to describe these expressions as described in Section 2 and [57], we can obtain the temporal evolution of polarization.
Polarization Evolution for a Forward-Shock
Figure 1 and Figure 2 show the temporal evolution of polarization degree for our chosen magnetic field configurations in two distinct scenarios regarding the density of the circumburst medium—here considered to be a constant density and a wind-like medium. Each column of these figures represents a chosen combination of the and parameters. Table 1 shows the values required to generate Figure 1 and Figure 2. We highlight that the generic values were determined based on the typical range reported for each parameter in the GRB synchrotron literature (for reviews, see [32,82]). The values of the observation angle are varied over a range between 8 and .4 This range of values is shown in these figures with different colored lines, each one standing for a value of , the ratio between the observation angle and initial opening angle of the jet.
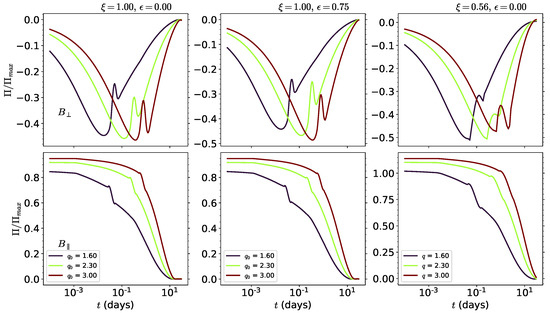
Figure 1.
Polarization curves for our fiducial model, considering a constant medium. The top row shows the perpendicular magnetic field configuration, the bottom row shows the parallel one. Each column represent a different pairing and .
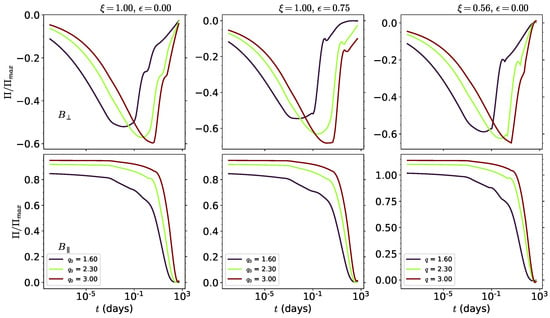
Figure 2.
Same as Figure 1, but for a wind-like medium.

Table 1.
Parameters used to calculate the polarization curves for the fiducial model.
The equivalent kinetic energy presented in Equation (1), which is parameterized with a power-law velocity distribution, can be visualized as the superposition of a traditional homogeneous (‘top-hat’) jet and a quasi-spherical component . The homogeneous jet case has been studied by a few works now, such as [83,84,85,86] now. Comparing results with the leftmost column of Figure 1, we see the typical double peak behavior for a homogeneous jet, reported by [85] for , is present for us as well. Some discrepancies are shown, with our polarization being initially higher at earlier times (increasingly so as ) and overall in the magnitude of the peaks. The highest likelihood culprit for these differences is the choice of synchrotron model and parameter values. The center column of Figure 1 presents the case for a partially radiative scenario, and it behaves quite similarly to the adiabatic case, with only a change in the magnitude of the peaks being observable. The deceleration of the relativistic outflow by the circumburst medium is faster when it lies in the radiative regime rather than adiabatic one, and the temporal evolution of polarization is modified [87,88]. For our model, this has resulted in an enhancement of the increase in polarization as grows, but smaller second peaks. The rightmost side of Figure 1 displays the case for an adiabatic regime with [71]. The variation on causes the emission to arrive earlier or later, and this produces a difference in the magnitudes of the peaks, as observed in Figure 1 [70,71,89]. The polarization behavior flips in comparison with , with the peak increasing as ; comparatively, the second peak remains mostly the same. The parallel case presents similar behavior for all three considered cases. A small change is observed in the sharpness of the decline of polarization at jet-break (where the synchrotron model, the bulk Lorentz factor, changes regime to follow the on-axis calculations presented by [57]) and post-break, with a sharper decline happening with a decreasing value of . Figure 2 shows the polarization evolution for the wind-like medium. Ref. [90] expected that the polarization evolved slower for a wind-like medium, as the relationship between afterglow timescale and density was ([32,91] and with for a wind-like medium), and this is observed here too. For the convenience of observation, the limits of the timescale have been expanded. Ref. [92] also calculated the polarization for stratified media in a fully adiabatic case, with the inclusion of the reverse-shock contributions as well as EATS integration, as a continuation of their previous works in polarization [93,94,95]. When analyzing their FS case, we find that their results also agree with the slower evolution in a wind-like medium, similarly to [90]. However, we find a discrepancy in the fact that their model expects the peaks of the forward shock to appear earlier in a wind-like medium by a more substantial margin when compared to a constant-density medium, while our work sees the second peak appearing at similar times for ( days) and (∼0.1 days) and later for (∼0.4 and ∼2.0 days). Other significant differences between the constant-density medium and this scenario are the higher initial polarization peak and lower magnitude of the second peak, which is in all likelihood due to the lower value of the bulk Lorentz factor at later times. Between the chosen values of and , we see that a lower value of increases the magnitude of the first peak while decreasing the magnitude of the second one. This is similar to the constant-density medium case, with the addendum that the second peak is reduced further when compared to . For the partially radiative case, the first polarization peak is similar to the adiabatic case with higher magnitude, but the second polarization peak is further reduced.
4. Modeling the Polarization of Observed Bursts
In this section, we describe the polarization for two distinct bursts: GRB 170817A and GRB 190114C. These bursts are expected to be completely different in nature, with GRB 170817A being a sGRB viewed off-axis, and 190114C a lGRB viewed on-axis (from within the half-opening angle of the jet). This choice of bursts with polarization data allows us to observe two distinct cases for our model. We use the parameter values obtained by [57,65] via Markov Chain Monte Carlo (MCMC) simulations to calculate the polarization. For this section, we will adopt the notation to show the polarization for each value of present.
- GRB 170817A
Figure 3 shows the expected polarization, calculated with our model, for the different configurations of magnetic fields. GRB 170817A has been modeled by a variety of different synchrotron scenarios; while the more traditional top-hat off-axis jet has fallen out of favour, other models such as radially stratified ejecta [62,67,96], structured jets [59,60,97], or the sum of multiple components [98], can properly describe the multi-wavelength afterglow observations. One thing to note is that for the period starting two weeks after the burst, the flux can be described solely by a relativistic collimated jet (see references above and [63]). As such, the angular structure of the jet is less relevant to describe the late afterglow. We use the phenomenological model presented in this paper for a constant-density medium with and to obtain the polarization. These conditions reduce our model to the one used in [67], where the authors have fitted the synchrotron light curves. We have used the values reported in Table 2 to generate the polarization curves. For the perpendicular configuration of magnetic field, we observe an initial polarization for all values of . Then, the polarization begins its evolution towards a first peak of at days, with a second peak of at days. The parallel configuration has an initially high degree of polarization across the board and low influence of , with , and at the break. The blue inverted triangles in Figure 3 show the upper limits, of at days (derived by [42]). The upper limits are broken by the polarization curves, with and . This indicates that the chosen configurations cannot successfully describe the polarization observed for GRB 170817A. This result is expected in accordance with previous investigations of GRB 170817A’s polarization (e.g., see [35,38,55,86,99]). Multiple models, ranging from a traditional top-hat jet to a more complex structured jet, were used in an attempt to describe the polarization upper limits. However, all works have found that the usage of a anisotropic magnetic field, be it a random field generated at the shock front or a globally ordered configuration, breaks the upper limits imposed. The single exception is the case of a wide-angled quasi-spherical outflow [99], which does not break the upper limits. However, this particular model is not favored for describing the afterglow flux of the burst. It is required, then, that the magnetic field at the emitting region must not be anisotropic. Refs. [35,38] have constrained the anisotropy of the magnetic fields to a dominant perpendicular component with a sub-dominant parallel component ( and , for each paper, respectively). When [100] modeled the polarization of this burst, they discovered a more general 3D mixed magnetic field in the RS region of the jet and a 2D field in the FS region. Their model successfully describes the polarization upper limits imposed to this burst, with a early time peak arising due to the off-axis FS observation, with the mixed magnetic field of the RS region maintaining a roughly constant polarization degree (∼10%) at the upper limit times. Their model predict a constraint of . More observations on a shorter post-burst period would be needed to constrain the magnetic field configuration further, and proper modeling of the afterglow light curve is necessary for breaking the degeneracy between models. Unfortunately, there were no polarization observations at any other frequency and time [42].
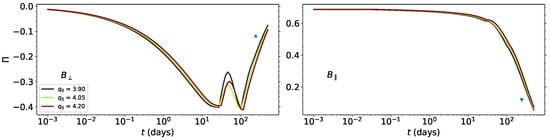
Figure 3.
Expected temporal evolution of the polarization for GRB 170817A for two configurations of magnetic fields—Perpendicular () and Parallel (). These polarization curves were calculated using the best fit values presented in Table 2. For , we have used the range of deg with three values linearly spaced between the limits. The inverted triangles represent the polarization upper limits (derived by [42]).

Table 2.
Posterior distribution for the parameters used to calculate the polarization the observed GRBs.
- GRB 190114C
Figure 4 shows the expected polarization, calculated with our model, for the different configurations of magnetic fields. Unlike the previous shown cases, this burst was expected to be seen on-axis (, ). To reduce the model presented in this work to one equivalent to the one used in [65,101] we use , , and . This reduces Equation (1) to and the bulk Lorentz factor becomes for a homogeneous medium, and for a wind-like one. GRB 190114C has plenty of available polarization data; for this work we limit ourselves to the observations of RINGO3 at the R Band (see [102]). The authors find polarization data ranging from 500 to the 3000s mark. A general agreement regarding GRB 190114C is that this burst show a clear combination of FS and reverse shock (RS) components, dominating at different times (see; [40,64,65,66]). As such, verifying the origin of this polarization is important. Refs. [40]5 and [65] expect that the optical flux is dominated by the RS component at times <500s, while the FS dominates past that time. We argue then, that the majority of the optical polarization observations from RINGO3 were of synchrotron origin in a FS scenario, in concordance with the findings of [103]. However, due to the contention regarding a more precise time where the dominance of the emission shifts from a RS to a FS case, the point observed at ∼500s is of dubious origin, as there is no clear dominance of either component in this specific time. We include this point in Figure 4, under different coloration, but ignore it to discriminate the wellness of the fit. Furthermore, Ref. [65] expect that the FS is dominated by a constant medium density, and we take the same assumptions for the polarization calculations. Modeling of this burst’s light curve indicates that it was viewed on-axis (), and this is further strengthened by the polarization observed. For both chosen magnetic field configurations, the values of are ruled out. The value of returns a better fit to the low polarization observed at days in both configurations, but the upper limit at is broken in the parallel case. This can, in theory, be remedied by a smaller value of , as it would reduce the total polarization, without effecting the on-axis flux fitting. However, the polarization would return a worse fit to the observed data point. With this in mind, we rule out the parallel configuration in the FS as a possibility, with the parameters chosen by [65]. The polarization values found stayed roughly at for the perpendicular configuration at all times. Ref. [40] analyzed a different set of polarization data, at the radio band, observed at days. The author’s flux fitting indicates that this emission was associated with the RS, and as such, so is the radio polarization. Nonetheless, the authors found that any off-axis () scenario breaks the polarization data independent of field configuration as well, with further considerations to the reverse-shock emission.
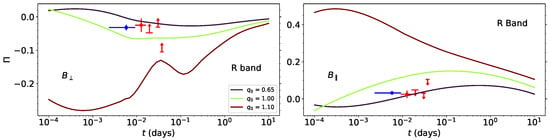
Figure 4.
Expected temporal evolution of the polarization for GRB 190114C for two configurations of magnetic fields—Perpendicular () and Parallel (). These polarization curves were calculated using the best fit values presented in Table 2. For , we have used the range of . Polarization data and upper limits are obtained from [102].
5. Conclusions
We have introduced a polarization phenomenological model as an extension of the analytical synchrotron afterglow off-axis scenario presented in [57,91,98,104]. This synchrotron model can describe the multi-wavelength afterglow observations for both a constant-density and wind-like medium. We have shown the expected temporal evolution of polarization with a dependency on the physical parameters associated with afterglow GRB emission for two configurations of a magnetic field. Regarding our fiducial model, the calculated polarization took into consideration a broad set of parameters constrained within the typical values observed for off-axis GRBs. We were able to see the differences in possible polarization caused by the two different ambient media and the chosen synchrotron model. We showed that our fiducial model generally agrees with previously found results for a homogeneous sideways expanding jet for the conditions of a constant-density medium and an adiabatic case with [84,85]. We have expanded the scenarios for a partially radiative regime and a case where . We expect that the variation of these parameters presents modifications on the temporal evolution of polarization. A partially radiative regime hastens the deceleration of the relativist outflow by the circumburst medium [87,88], and this has exacerbated the baseline () profile of polarization—with peak increasing further as grows, but the second bump decreasing slightly. On the other hand, changing alters the arrival time of the emission [70,71,89] and our chosen value of [71] has caused the polarization behavior regarding to flip, with the magnitude of the peaks now decreasing as increases. Furthermore, we have calculated the same polarization for a wind-like medium to verify the possible differences. For the change in circumburst medium, we have found that the polarization evolves slower in time and changes in the magnitude of polarization compared to the constant-density medium, in agreement with [90]. In particular, we have used the available polarimetric upper limits of GRB 170817A; at 2.8 GHz and days [42] to rule out our chosen magnetic field configurations of anisotropy factors and . The peaks of polarization also roughly coincide with the afterglow flux peak in time (see [57,98] for the flux fitting), which is a result that agrees with the literature [35,50,83,85]. A similar analysis was extended to GRB 190114C, using the data obtained by RINGO3 [102] to eliminate the possibility of an off-axis observation and introduce the requirement that , based on the parameters of [65]. The requirement of an on-axis observation is also in concordance with previous analysis of the burst’s light curve and [40] analysis of the RS radio polarization observed by ALMA. More observations, from seconds after the trigger to months and years, are needed to infer tighter constraints on polarization and adequate fitting of the light curves is necessary to obtain adequate parameter values and break degeneracy between synchrotron models.
Author Contributions
A.C.C.d.E.S.P. wrote the original draft of this paper. A.C.C.d.E.S.P. and N.F. conceptualized this manuscript. N.F., A.G.-G., B.B.K., S.D., M.G.D., R.L.B. and P.V. further contributed to the final version. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by UNAM-DGAPA-PAPIIT grants number IN106521, IG100820, and IN105921. A.C.C.d.E.S.P. acknowledges financial support from CONACyT’s doctoral fellowship.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The polarization data and upper limits used in this work can be obtained by the sources cited in text.
Acknowledgments
We thank Walas Oliveira, Rodolfo Barniol Duran, Tanmoy Laskar, Paz Beniamini and Bing Zhang for useful discussions.
Conflicts of Interest
The authors declare no conflicts of interest.
Notes
| 1 | For a debate of controversial situations, see [29]. |
| 2 | is the time over which a GRB releases from to of the total measured counts. |
| 3 | We use the values of the cosmological constants , and [58], which correspond to a spatially flat universe CDM model. |
| 4 | Over the course of this manuscript we will be using deg as the abbreviation of degree. |
| 5 | The authors also observe a polarization reading in the radio band and attribute the emission to the RS component. |
References
- Woosley, S.E. Gamma-Ray Bursts from Stellar Mass Accretion Disks around Black Holes. Astrophys. J. 1993, 405, 273. [Google Scholar] [CrossRef]
- Paczyński, B. Are Gamma-Ray Bursts in Star-Forming Regions? Astrophys. J. 1998, 494, L45–L48. [Google Scholar] [CrossRef]
- Woosley, S.E.; Bloom, J.S. The Supernova Gamma-Ray Burst Connection. Annu. Rev. Astron. Astrophys. 2006, 44, 507–556. [Google Scholar] [CrossRef]
- Cano, Z.; Wang, S.Q.; Dai, Z.G.; Wu, X.F. The Observer’s Guide to the Gamma-Ray Burst Supernova Connection. Adv. Astron. 2017, 2017, 8929054. [Google Scholar] [CrossRef]
- Duncan, R.C.; Thompson, C. Formation of Very Strongly Magnetized Neutron Stars: Implications for Gamma-Ray Bursts. Astrophys. J. Lett. 1992, 392, L9. [Google Scholar] [CrossRef]
- Usov, V.V. Millisecond pulsars with extremely strong magnetic fields as a cosmological source of gamma-ray bursts. Nature 1992, 357, 472–474. [Google Scholar] [CrossRef]
- Thompson, C. A Model of Gamma-Ray Bursts. Mon. Not. R. Astron. Soc. 1994, 270, 480. [Google Scholar] [CrossRef]
- Metzger, B.D.; Giannios, D.; Thompson, T.A.; Bucciantini, N.; Quataert, E. The protomagnetar model for gamma-ray bursts. Mon. Not. R. Astron. Soc. 2011, 413, 2031–2056. [Google Scholar] [CrossRef]
- Narayan, R.; Paczynski, B.; Piran, T. Gamma-ray bursts as the death throes of massive binary stars. Astrophys. J. Lett. 1992, 395, L83–L86. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T.; Narayan, R. Spectra and Light Curves of Gamma-Ray Burst Afterglows. Astrophys. J. Lett. 1998, 497, L17–L20. [Google Scholar] [CrossRef]
- Rees, M.J.; Meszaros, P. Unsteady outflow models for cosmological gamma-ray bursts. Astrophys. J. Lett. 1994, 430, L93–L96. [Google Scholar] [CrossRef]
- Paczynski, B.; Xu, G. Neutrino Bursts from Gamma-Ray Bursts. Astrophys. J. 1994, 427, 708. [Google Scholar] [CrossRef]
- Thompson, C.; Mészáros, P.; Rees, M.J. Thermalization in Relativistic Outflows and the Correlation between Spectral Hardness and Apparent Luminosity in Gamma-Ray Bursts. Astrophys. J. 2007, 666, 1012–1023. [Google Scholar] [CrossRef]
- Lazzati, D.; Morsony, B.J.; Margutti, R.; Begelman, M.C. Photospheric Emission as the Dominant Radiation Mechanism in Long-duration Gamma-Ray Bursts. Astrophys. J. 2013, 765, 103. [Google Scholar] [CrossRef]
- Mizuta, A.; Nagataki, S.; Aoi, J. Thermal Radiation from Gamma-ray Burst Jets. Astrophys. J. 2011, 732, 26. [Google Scholar] [CrossRef]
- Giannios, D. Prompt GRB emission from gradual energy dissipation. Astron. Astrophys. 2008, 480, 305–312. [Google Scholar] [CrossRef]
- Beniamini, P.; Granot, J. Properties of GRB light curves from magnetic reconnection. Mon. Not. R. Astron. Soc. 2016, 459, 3635–3658. [Google Scholar] [CrossRef]
- Kumar, P.; Crumley, P. Radiation from a relativistic Poynting jet: Some general considerations. Mon. Not. R. Astron. Soc. 2015, 453, 1820–1828. [Google Scholar] [CrossRef]
- Zhang, B.; Yan, H. The Internal-collision-induced Magnetic Reconnection and Turbulence (ICMART) Model of Gamma-ray Bursts. Astrophys. J. 2011, 726, 90. [Google Scholar] [CrossRef]
- Costa, E.; Frontera, F.; Heise, J.; Feroci, M.; in’t Zand, J.; Fiore, F.; Cinti, M.N.; Dal Fiume, D.; Nicastro, L.; Orlandini, M.; et al. Discovery of an X-ray afterglow associated with the γ-ray burst of 28 February 1997. Nature 1997, 387, 783–785. [Google Scholar] [CrossRef]
- Granot, J.; Sari, R. The Shape of Spectral Breaks in Gamma-Ray Burst Afterglows. Astrophys. J. 2002, 568, 820–829. [Google Scholar] [CrossRef]
- van Paradijs, J.; Groot, P.J.; Galama, T.; Kouveliotou, C.; Strom, R.G.; Telting, J.; Rutten, R.G.M.; Fishman, G.J.; Meegan, C.A.; Pettini, M.; et al. Transient optical emission from the error box of the γ-ray burst of 28 February 1997. Nature 1997, 386, 686–689. [Google Scholar] [CrossRef]
- Piro, L.; Amati, L.; Antonelli, L.A.; Butler, R.C.; Costa, E.; Cusumano, G.; Feroci, M.; Frontera, F.; Heise, J.; in ’t Zand, J.J.M.; et al. Evidence for a late-time outburst of the X-ray afterglow of GB970508 from BeppoSAX. Astron. Astrophys. 1998, 331, L41–L44. [Google Scholar]
- Gehrels, N.; Ramirez-Ruiz, E.; Fox, D.B. Gamma-Ray Bursts in the Swift Era. Annu. Rev. Astron. Astrophys. 2009, 47, 567–617. [Google Scholar] [CrossRef]
- Wang, X.G.; Zhang, B.; Liang, E.W.; Gao, H.; Li, L.; Deng, C.M.; Qin, S.M.; Tang, Q.W.; Kann, D.A.; Ryde, F.; et al. How Bad or Good Are the External Forward Shock Afterglow Models of Gamma-Ray Bursts? Astrophys. J. Suppl. Ser. 2015, 219, 9. [Google Scholar] [CrossRef]
- Fraija, N.; Dichiara, S.; Pedreira, A.C.C.d.E.S.; Galvan-Gamez, A.; Becerra, R.L.; Montalvo, A.; Montero, J.; Betancourt Kamenetskaia, B.; Zhang, B.B. Modeling the Observations of GRB 180720B: From Radio to Sub-TeV Gamma-Rays. Astrophys. J. 2019, 885, 29. [Google Scholar] [CrossRef]
- Fraija, N.; Dainotti, M.G.; Betancourt Kamenetskaia, B.; Galván-Gámez, A.; Aguilar-Ruiz, E. Microphysical parameter variation in gamma-ray burst stratified afterglows and closure relations: From sub-GeV to TeV observations. Mon. Not. R. Astron. Soc. 2024, 527, 1884–1909. [Google Scholar] [CrossRef]
- Fraija, N.; Betancourt Kamenetskaia, B.; Galván-Gámez, A.; Veres, P.; Becerra, R.L.; Dichiara, S.; Dainotti, M.G.; Lizcano, F.; Aguilar-Ruiz, E. An explanation of GRB Fermi-LAT flares and high-energy photons in stratified afterglows. Mon. Not. R. Astron. Soc. 2024, 527, 1674–1704. [Google Scholar] [CrossRef]
- Kann, D.A.; Klose, S.; Zhang, B.; Covino, S.; Butler, N.R.; Malesani, D.; Nakar, E.; Wilson, A.C.; Antonelli, L.A.; Chincarini, G.; et al. The Afterglows of Swift-era Gamma-Ray Bursts. II. Type I GRB versus Type II GRB Optical Afterglows. Astrophys. J. 2011, 734, 96. [Google Scholar] [CrossRef]
- Mazets, E.; Golenetskii, S.; Il’Inskii, V.; Panov, V.; Aptekar, R.; Gur’Yan, Y.A.; Proskura, M.; Sokolov, I.; Sokolova, Z.Y.; Kharitonova, T.; et al. Catalog of cosmic gamma-ray bursts from the KONUS experiment data. Astrophys. Space Sci. 1981, 80, 3–83. [Google Scholar] [CrossRef]
- Kouveliotou, C.; Meegan, C.A.; Fishman, G.J.; Bhat, N.P.; Briggs, M.S.; Koshut, T.M.; Paciesas, W.S.; Pendleton, G.N. Identification of two classes of gamma-ray bursts. Astrophys. J. 1993, 413, L101–L104. [Google Scholar] [CrossRef]
- Kumar, P.; Zhang, B. The physics of gamma-ray bursts & relativistic jets. Phys. Rep. 2015, 561, 1–109. [Google Scholar] [CrossRef]
- Mészáros, P.; Rees, M.J. Optical and Long-Wavelength Afterglow from Gamma-Ray Bursts. Astrophys. J. 1997, 476, 232–237. [Google Scholar] [CrossRef]
- Laing, R.A. A model for the magnetic-field structure in extended radio sources. Mon. Not. R. Astron. Soc. 1980, 193, 439–449. [Google Scholar] [CrossRef]
- Teboul, O.; Shaviv, N.J. Impact of the ISM magnetic field on GRB afterglow polarization. Mon. Not. R. Astron. Soc. 2021, 507, 5340–5347. [Google Scholar] [CrossRef]
- Weibel, E.S. Spontaneously Growing Transverse Waves in a Plasma Due to an Anisotropic Velocity Distribution. Phys. Rev. Lett. 1959, 2, 83–84. [Google Scholar] [CrossRef]
- Medvedev, M.V.; Loeb, A. Generation of Magnetic Fields in the Relativistic Shock of Gamma-Ray Burst Sources. Astrophys. J. 1999, 526, 697–706. [Google Scholar] [CrossRef]
- Gill, R.; Granot, J. Constraining the magnetic field structure in collisionless relativistic shocks with a radio afterglow polarization upper limit in GW 170817. Mon. Not. R. Astron. Soc. 2020, 491, 5815–5825. [Google Scholar] [CrossRef]
- Buckley, D.A.H.; Bagnulo, S.; Britto, R.J.; Mao, J.; Kann, D.A.; Cooper, J.; Lipunov, V.; Hewitt, D.M.; Razzaque, S.; Kuin, N.P.M.; et al. Spectropolarimetry and photometry of the early afterglow of the gamma-ray burst GRB 191221B. Mon. Not. R. Astron. Soc. 2021, 506, 4621–4631. [Google Scholar] [CrossRef]
- Laskar, T.; Alexander, K.D.; Gill, R.; Granot, J.; Berger, E.; Mundell, C.G.; Barniol Duran, R.; Bolmer, J.; Duffell, P.; van Eerten, H.; et al. ALMA Detection of a Linearly Polarized Reverse Shock in GRB 190114C. Astrophys. J. Lett. 2019, 878, L26. [Google Scholar] [CrossRef]
- Granot, J.; Taylor, G.B. Radio Flares and the Magnetic Field Structure in Gamma-Ray Burst Outflows. Astrophys. J. 2005, 625, 263–270. [Google Scholar] [CrossRef]
- Corsi, A.; Hallinan, G.W.; Lazzati, D.; Mooley, K.P.; Murphy, E.J.; Frail, D.A.; Carbone, D.; Kaplan, D.L.; Murphy, T.; Kulkarni, S.R.; et al. An Upper Limit on the Linear Polarization Fraction of the GW170817 Radio Continuum. Astrophys. J. Lett. 2018, 861, L10. [Google Scholar] [CrossRef]
- Coburn, W.; Boggs, S.E. Polarization of the prompt γ-ray emission from the γ-ray burst of 6 December 2002. Nature 2003, 423, 415–417. [Google Scholar] [CrossRef] [PubMed]
- Kalemci, E.; Boggs, S.E.; Kouveliotou, C.; Finger, M.; Baring, M.G. Search for Polarization from the Prompt Gamma-Ray Emission of GRB 041219a with SPI on INTEGRAL. Astrophys. J. Suppl. Ser. 2007, 169, 75–82. [Google Scholar] [CrossRef]
- Mundell, C.G.; Kopač, D.; Arnold, D.M.; Steele, I.A.; Gomboc, A.; Kobayashi, S.; Harrison, R.M.; Smith, R.J.; Guidorzi, C.; Virgili, F.J.; et al. Highly polarized light from stable ordered magnetic fields in GRB 120308A. Nature 2013, 504, 119–121. [Google Scholar] [CrossRef] [PubMed]
- Chattopadhyay, T.; Vadawale, S.V.; Aarthy, E.; Mithun, N.P.S.; Chand, V.; Ratheesh, A.; Basak, R.; Rao, A.R.; Bhalerao, V.; Mate, S.; et al. Prompt Emission Polarimetry of Gamma-Ray Bursts with the AstroSat CZT Imager. Astrophys. J. 2019, 884, 123. [Google Scholar] [CrossRef]
- Ito, H.; Nagataki, S.; Matsumoto, J.; Lee, S.H.; Tolstov, A.; Mao, J.; Dainotti, M.; Mizuta, A. Spectral and Polarization Properties of Photospheric Emission from Stratified Jets. Astrophys. J. 2014, 789, 159. [Google Scholar] [CrossRef]
- Parsotan, T.; López-Cámara, D.; Lazzati, D. Photospheric Polarization Signatures from Long Gamma-Ray Burst Simulations. Astrophys. J. 2020, 896, 139. [Google Scholar] [CrossRef]
- Gill, R.; Granot, J. Temporal evolution of prompt GRB polarization. Mon. Not. R. Astron. Soc. 2021, 504, 1939–1958. [Google Scholar] [CrossRef]
- Granot, J.; Königl, A. Linear Polarization in Gamma-Ray Bursts: The Case for an Ordered Magnetic Field. Astrophys. J. Lett. 2003, 594, L83–L87. [Google Scholar] [CrossRef]
- Gill, R.; Granot, J.; Kumar, P. Linear polarization in gamma-ray burst prompt emission. Mon. Not. R. Astron. Soc. 2020, 491, 3343–3373. [Google Scholar] [CrossRef]
- Rutledge, R.E.; Fox, D.B. Re-analysis of polarization in the γ-ray flux of GRB 021206. Mon. Not. R. Astron. Soc. 2004, 350, 1288–1300. [Google Scholar] [CrossRef]
- Lyutikov, M.; Pariev, V.I.; Blandford, R.D. Polarization of Prompt Gamma-Ray Burst Emission: Evidence for Electromagnetically Dominated Outflow. Astrophys. J. 2003, 597, 998–1009. [Google Scholar] [CrossRef]
- Nakar, E.; Piran, T.; Waxman, E. Implications of the γ-ray polarization of GRB 021206. J. Cosmol. Astropart. Phys. 2003, 2003, 005. [Google Scholar] [CrossRef]
- Stringer, E.; Lazzati, D. Polarization Constraints on the Geometry of the Magnetic Field in the External Shock of Gamma-Ray Bursts. Astrophys. J. 2020, 892, 131. [Google Scholar] [CrossRef]
- Medina Covarrubias, R.; De Colle, F.; Urrutia, G.; Vargas, F. Numerical simulations of polarization in gamma-ray burst afterglows. Mon. Not. R. Astron. Soc. 2023, 523, 4583–4592. [Google Scholar] [CrossRef]
- Fraija, N.; De Colle, F.; Veres, P.; Dichiara, S.; Barniol Duran, R.; Pedreira, A.C.C.d.E.S.; Galvan-Gamez, A.; Betancourt Kamenetskaia, B. Description of atypical bursts seen slightly off-axis. arXiv 2019, arXiv:1906.00502. [Google Scholar] [CrossRef]
- Ade, P.A.R. et al. [Planck Collaboration] Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Kasliwal, M.M.; Nakar, E.; Singer, L.P.; Kaplan, D.L.; Cook, D.O.; Van Sistine, A.; Lau, R.M.; Fremling, C.; Gottlieb, O.; Jencson, J.E.; et al. Illuminating gravitational waves: A concordant picture of photons from a neutron star merger. Science 2017, 358, 1559–1565. [Google Scholar] [CrossRef]
- Lamb, G.P.; Kobayashi, S. Electromagnetic counterparts to structured jets from gravitational wave detected mergers. Mon. Not. R. Astron. Soc. 2017, 472, 4953–4964. [Google Scholar] [CrossRef]
- Mooley, K.P.; Deller, A.T.; Gottlieb, O.; Nakar, E.; Hallinan, G.; Bourke, S.; Frail, D.A.; Horesh, A.; Corsi, A.; Hotokezaka, K. Superluminal motion of a relativistic jet in the neutron-star merger GW170817. Nature 2018, 561, 355–359. [Google Scholar] [CrossRef]
- Hotokezaka, K.; Kiuchi, K.; Shibata, M.; Nakar, E.; Piran, T. Synchrotron Radiation from the Fast Tail of Dynamical Ejecta of Neutron Star Mergers. Astrophys. J. 2018, 867, 95. [Google Scholar] [CrossRef]
- Fraija, N.; Lopez-Camara, D.; Pedreira, A.C.C.d.E.S.; Betancourt Kamenetskaia, B.; Veres, P.; Dichiara, S. Signatures from a Quasi-spherical Outflow and an Off-axis Top-hat Jet Launched in a Merger of Compact Objects: An Analytical Approach. Astrophys. J. 2019, 884, 71. [Google Scholar] [CrossRef]
- Acciari, V.A. et al. [MAGIC Collaboration] Observation of inverse Compton emission from a long γ-ray burst. Nature 2019, 575, 459–463. [Google Scholar] [CrossRef]
- Fraija, N.; Dichiara, S.; Pedreira, A.C.C.d.E.S.; Galvan-Gamez, A.; Becerra, R.L.; Barniol Duran, R.; Zhang, B.B. Analysis and Modeling of the Multi-wavelength Observations of the Luminous GRB 190114C. Astrophys. J. Lett. 2019, 879, L26. [Google Scholar] [CrossRef]
- Wang, X.Y.; Liu, R.Y.; Zhang, H.M.; Xi, S.Q.; Zhang, B. Synchrotron Self-Compton Emission from External Shocks as the Origin of the Sub-TeV Emission in GRB 180720B and GRB 190114C. Astrophys. J. 2019, 884, 117. [Google Scholar] [CrossRef]
- Fraija, N.; De Colle, F.; Veres, P.; Dichiara, S.; Barniol Duran, R.; Galvan-Gamez, A.; Pedreira, A.C.C.d.E.S. The Short GRB 170817A: Modeling the Off-axis Emission and Implications on the Ejecta Magnetization. Astrophys. J. 2019, 871, 123. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Lenart, A.Ł.; Fraija, N.; Nagataki, S.; Warren, D.C.; De Simone, B.; Srinivasaragavan, G.; Mata, A. Closure relations during the plateau emission of Swift GRBs and the fundamental plane. Publ. Astron. Soc. Jpn. 2021, 73, 970–1000. [Google Scholar] [CrossRef]
- Dainotti, M.; Levine, D.; Fraija, N.; Warren, D.; Veres, P.; Sourav, S. The Closure Relations in High-Energy Gamma-ray Bursts Detected by Fermi-LAT. Galaxies 2023, 11, 25. [Google Scholar] [CrossRef]
- Panaitescu, A.; Mészáros, P. Rings in Fireball Afterglows. Astrophys. J. Lett. 1998, 493, L31–L34. [Google Scholar] [CrossRef][Green Version]
- Chevalier, R.A.; Li, Z.Y. Wind Interaction Models for Gamma-Ray Burst Afterglows: The Case for Two Types of Progenitors. Astrophys. J. 2000, 536, 195–212. [Google Scholar] [CrossRef]
- Blandford, R.D.; McKee, C.F. Fluid dynamics of relativistic blast waves. Phys. Fluids 1976, 19, 1130–1138. [Google Scholar] [CrossRef]
- Fraija, N.; Dainotti, M.G.; Ugale, S.; Jyoti, D.; Warren, D.C. Synchrotron Self-Compton Afterglow Closure Relations and Fermi-LAT-detected Gamma-Ray Bursts. Astrophys. J. 2022, 934, 188. [Google Scholar] [CrossRef]
- Fraija, N.; Veres, P.; Betancourt Kamenetskaia, B.; Galvan-Gamez, A.; Dainotti, M.G.; Dichiara, S.; Becerra, R.L. Synchrotron self-Compton in a radiative-adiabatic fireball scenario: Modelling the multiwavelength observations in some Fermi/LAT bursts. arXiv 2024, arXiv:2409.12166. [Google Scholar] [CrossRef]
- Fraija, N.; Dainotti, M.G.; Kamenetskaia, B.B.; Levine, D.; Galvan-Gamez, A. Closure relations of synchrotron self-compton in afterglow-stratified medium and Fermi-LAT detected gamma-ray bursts. Mon. Not. R. Astron. Soc. 2023, 525, 1630–1640. [Google Scholar] [CrossRef]
- Fraija, N.; Lee, W.; Veres, P. Modeling the Early Multiwavelength Emission in GRB130427A. Astrophys. J. 2016, 818, 190. [Google Scholar] [CrossRef]
- Sari, R. Hydrodynamics of Gamma-Ray Burst Afterglow. Astrophys. J. Lett. 1997, 489, L37–L40. [Google Scholar] [CrossRef]
- Panaitescu, A.; Kumar, P. Analytic Light Curves of Gamma-Ray Burst Afterglows: Homogeneous versus Wind External Media. Astrophys. J. 2000, 543, 66–76. [Google Scholar] [CrossRef]
- Granot, J. The Most Probable Cause for the High Gamma-Ray Polarization in GRB 021206. Astrophys. J. Lett. 2003, 596, L17–L21. [Google Scholar] [CrossRef]
- Rybicki, G.B.; Lightman, A.P. Radiative Processes in Astrophysics; John Wiley & Sons: Hoboken, NJ, USA, 1979. [Google Scholar]
- Waxman, E. Astronomy: New direction for γ-rays. Nature 2003, 423, 388–389. [Google Scholar] [CrossRef] [PubMed]
- Berger, E. Short-Duration Gamma-Ray Bursts. Annu. Rev. Astron. Astrophys. 2014, 52, 43–105. [Google Scholar] [CrossRef]
- Ghisellini, G.; Lazzati, D. Polarization light curves and position angle variation of beamed gamma-ray bursts. Mon. Not. R. Astron. Soc. 1999, 309, L7–L11. [Google Scholar] [CrossRef]
- Granot, J.; Panaitescu, A.; Kumar, P.; Woosley, S.E. Off-Axis Afterglow Emission from Jetted Gamma-Ray Bursts. Astrophys. J. Lett. 2002, 570, L61–L64. [Google Scholar] [CrossRef]
- Rossi, E.M.; Lazzati, D.; Salmonson, J.D.; Ghisellini, G. The polarization of afterglow emission reveals γ-ray bursts jet structure. Mon. Not. R. Astron. Soc. 2004, 354, 86–100. [Google Scholar] [CrossRef]
- Caligula, A.C.d.E.S.P.; Fraija, N.; Galvan-Gamez, A.; Kamenetskaia, B.B.; Veres, P.; Dainotti, M.G.; Dichiara, S.; Becerra, R.L. Afterglow Polarization from Off-axis Gamma-Ray Burst Jets. Astrophys. J. 2023, 942, 81. [Google Scholar] [CrossRef]
- Böttcher, M.; Dermer, C.D. Early Gamma-Ray Burst Afterglows from Relativistic Blast Waves in General Radiative Regimes. Astrophys. J. 2000, 532, 281–285. [Google Scholar] [CrossRef][Green Version]
- Wu, X.F.; Dai, Z.G.; Huang, Y.F.; Lu, T. Analytical Light Curves in the Realistic Model for Gamma-Ray Burst Afterglows. Astrophys. J. 2005, 619, 968–982. [Google Scholar] [CrossRef]
- Waxman, E. Angular Size and Emission Timescales of Relativistic Fireballs. Astrophys. J. Lett. 1997, 491, L19–L22. [Google Scholar] [CrossRef]
- Lazzati, D.; Covino, S.; Gorosabel, J.; Rossi, E.; Ghisellini, G.; Rol, E.; Castro Cerón, J.M.; Castro-Tirado, A.J.; Della Valle, M.; di Serego Alighieri, S.; et al. On the jet structure and magnetic field configuration of GRB 020813. Astron. Astrophys. 2004, 422, 121–128. [Google Scholar] [CrossRef]
- Fraija, N.; Galvan-Gamez, A.; Betancourt Kamenetskaia, B.; Dainotti, M.G.; Dichiara, S.; Veres, P.; Becerra, R.L.; do E. S. Pedreira, A.C.C. Modeling Gamma-Ray Burst Afterglow Observations with an Off-axis Jet Emission. Astrophys. J. 2022, 940, 189. [Google Scholar] [CrossRef]
- Lan, M.X.; Wu, X.F.; Dai, Z.G. Afterglow Polarizations in a Stratified Medium with Effect of the Equal Arrival Time Surface. Astrophys. J. 2023, 952, 31. [Google Scholar] [CrossRef]
- Lan, M.X.; Wu, X.F.; Dai, Z.G. Polarization Evolution of Early Optical Afterglows of Gamma-Ray Bursts. Astrophys. J. 2016, 816, 73. [Google Scholar] [CrossRef]
- Lan, M.X.; Wu, X.F.; Dai, Z.G. Gamma-Ray Burst Optical Afterglows with Two-component Jets: Polarization Evolution Revisited. Astrophys. J. 2018, 860, 44. [Google Scholar] [CrossRef]
- Lan, M.X.; Dai, Z.G. Time-resolved and Energy-resolved Polarizations of GRB Prompt Emission. Astrophys. J. 2020, 892, 141. [Google Scholar] [CrossRef]
- Mooley, K.P.; Nakar, E.; Hotokezaka, K.; Hallinan, G.; Corsi, A.; Frail, D.A.; Horesh, A.; Murphy, T.; Lenc, E.; Kaplan, D.L.; et al. A mildly relativistic wide-angle outflow in the neutron-star merger event GW170817. Nature 2018, 554, 207–210. [Google Scholar] [CrossRef]
- Lazzati, D.; Perna, R.; Morsony, B.J.; Lopez-Camara, D.; Cantiello, M.; Ciolfi, R.; Giacomazzo, B.; Workman, J.C. Late Time Afterglow Observations Reveal a Collimated Relativistic Jet in the Ejecta of the Binary Neutron Star Merger GW170817. Phys. Rev. Lett. 2018, 120, 241103. [Google Scholar] [CrossRef]
- Fraija, N.; Pedreira, A.C.C.d.E.S.; Veres, P. Light Curves of a Shock-breakout Material and a Relativistic Off-axis Jet from a Binary Neutron Star System. Astrophys. J. 2019, 871, 200. [Google Scholar] [CrossRef]
- Gill, R.; Granot, J. Afterglow imaging and polarization of misaligned structured GRB jets and cocoons: Breaking the degeneracy in GRB 170817A. Mon. Not. R. Astron. Soc. 2018, 478, 4128–4141. [Google Scholar] [CrossRef]
- Lan, M.X.; Geng, J.J.; Wu, X.F.; Dai, Z.G. Polarization with a Three-dimensional Mixed Magnetic Field and Its Application to GRB 170817A. Astrophys. J. 2019, 870, 96. [Google Scholar] [CrossRef]
- Fraija, N.; Barniol Duran, R.; Dichiara, S.; Beniamini, P. Synchrotron Self-Compton as a Likely Mechanism of Photons beyond the Synchrotron Limit in GRB 190114C. Astrophys. J. 2019, 883, 162. [Google Scholar] [CrossRef]
- Shrestha, M.; Steele, I.A.; Kobayashi, S.; Smith, R.J.; Guidorzi, C.; Jordana-Mitjans, N.; Jermak, H.; Arnold, D.; Mundell, C.G.; Gomboc, A. Polarimetry and photometry of gamma-ray bursts afterglows with RINGO3. Mon. Not. R. Astron. Soc. 2022, 516, 1584–1600. [Google Scholar] [CrossRef]
- Jordana-Mitjans, N.; Mundell, C.G.; Kobayashi, S.; Smith, R.J.; Guidorzi, C.; Steele, I.A.; Shrestha, M.; Gomboc, A.; Marongiu, M.; Martone, R.; et al. Lowly Polarized Light from a Highly Magnetized Jet of GRB 190114C. Astrophys. J. 2020, 892, 97. [Google Scholar] [CrossRef]
- Fraija, N.; Dainotti, M.G.; Levine, D.; Kamenetskaia, B.B.; Galvan-Gamez, A. Off-axis Afterglow Closure Relations and Fermi-LAT Detected Gamma-Ray Bursts. Astrophys. J. 2023, 958, 126. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).