Vertical Structure of the Milky Way Disk with Gaia DR3
Abstract
1. Introduction
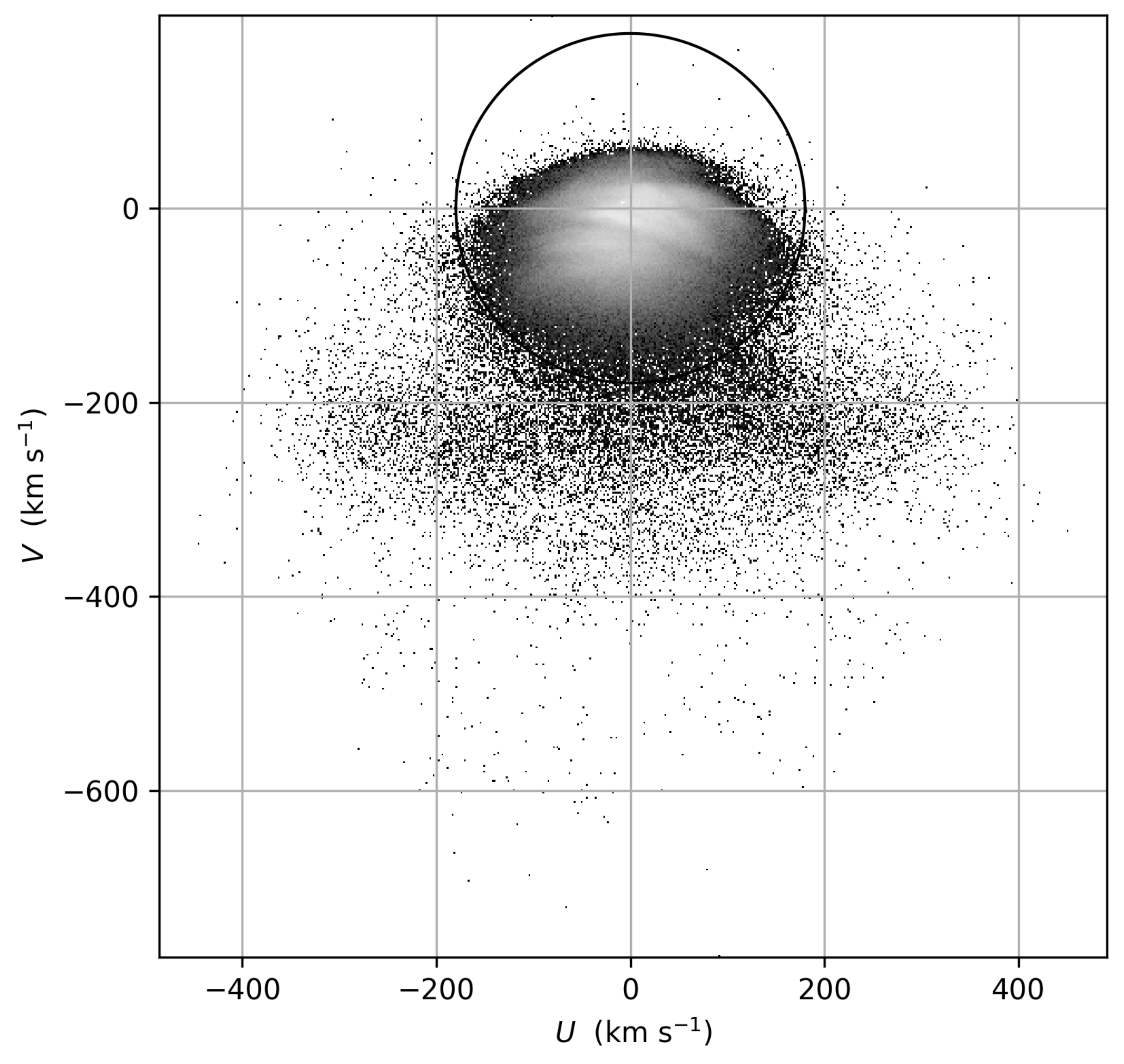
2. Data Selection and Completeness
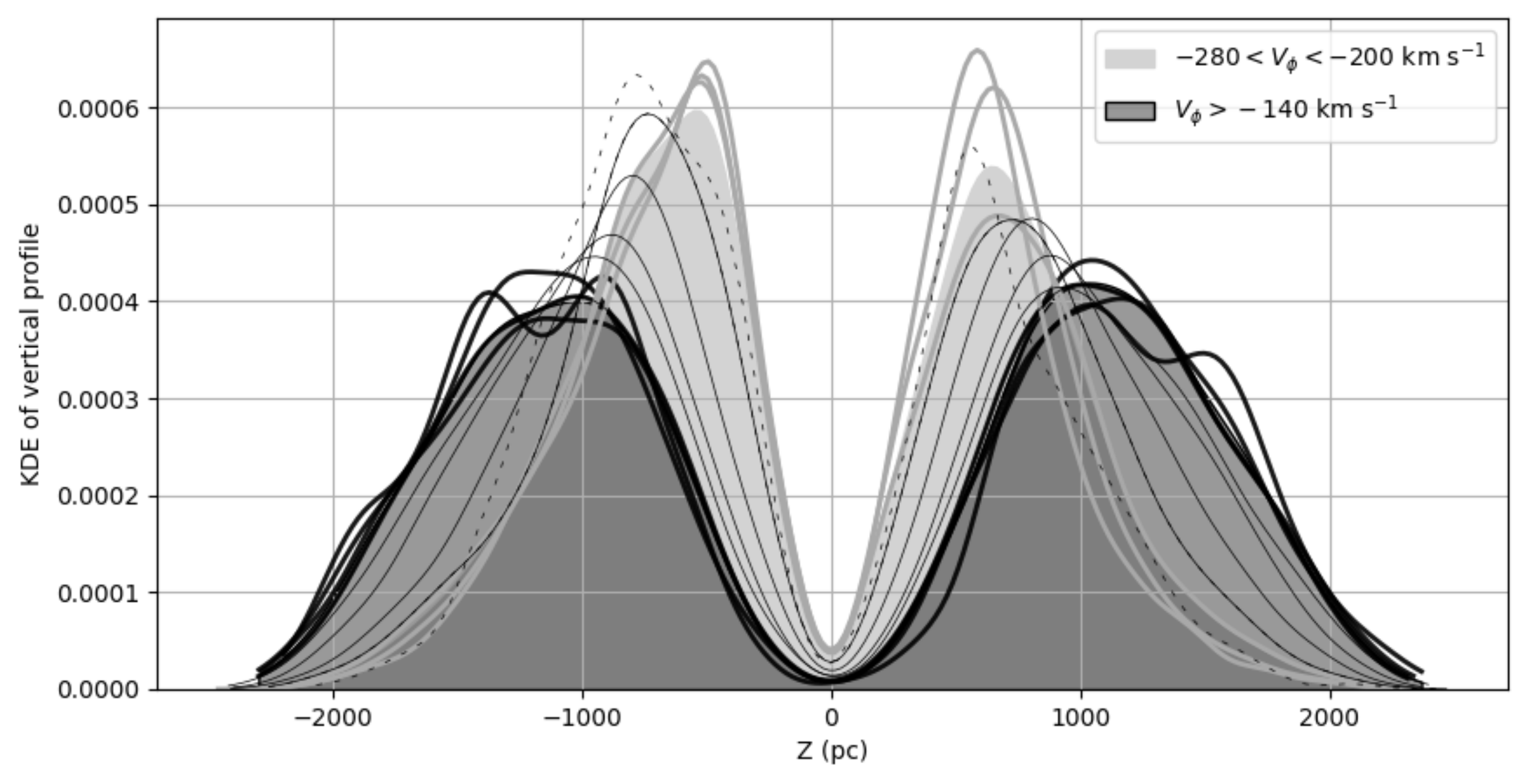
3. Vertical Distribution for Different Populations
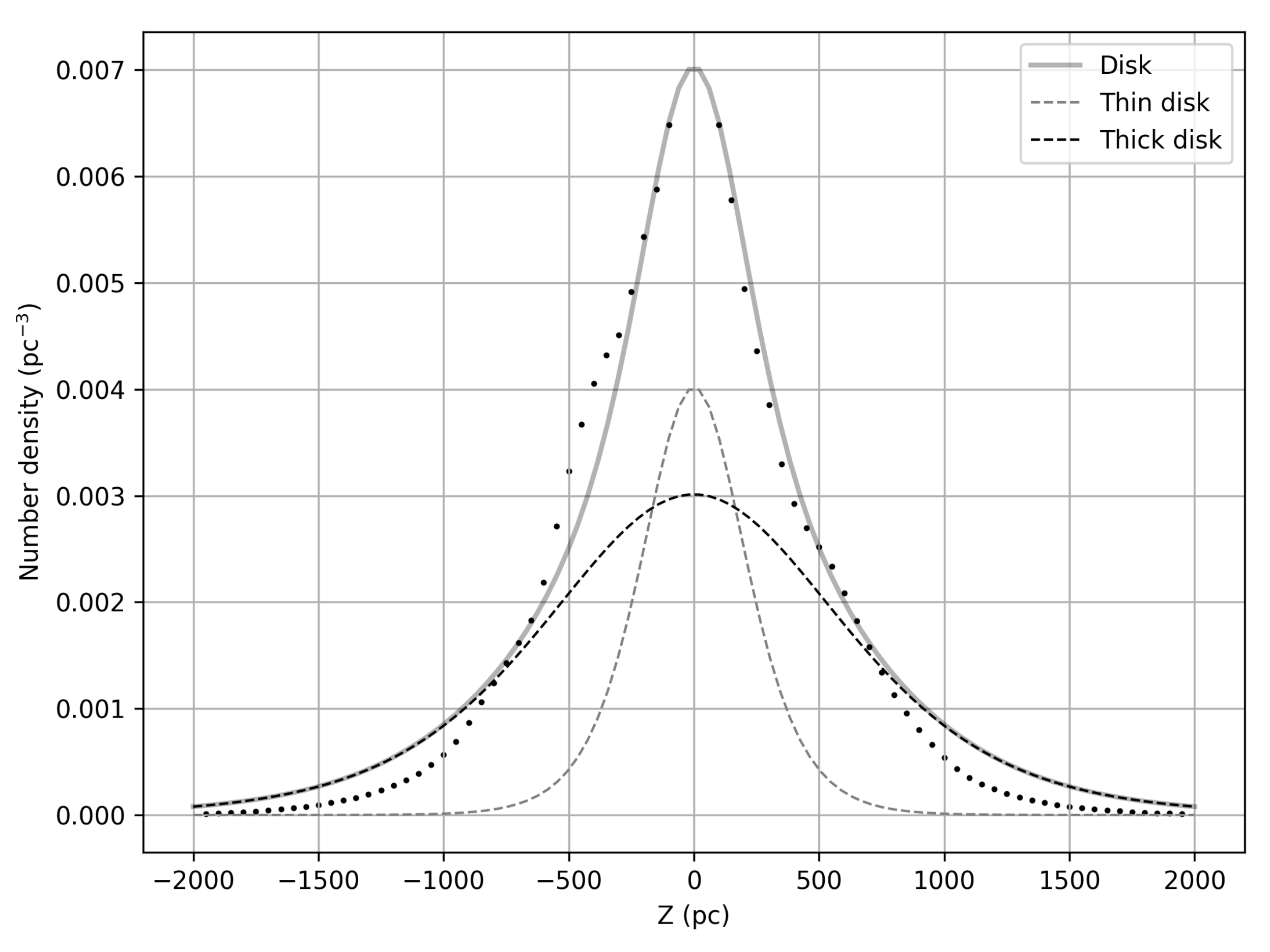
4. Results: Scale Heights and Number Density Ratio
4.1. Thick Disk Vertical Scale Height
4.2. Thin Disk Vertical Scale Height
4.3. Thick-to-Thin Number Density Ratio
- Assuming and estimating and ;
- Assuming and estimating and ;
- Estimating all parameters and .
5. Comparison with Previous Work by the Authors
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| 1 | A procedure to smooth a histogram in which each discrete point contributing to a bin is replaced by an extended probability distribution, called a kernel, and the probability density at any given point in the space is then estimated to be the sum of the kernels at the chosen point, over all of the discrete points, after proper normalization. |
References
- Gilmore, G.; Reid, N. New light on faint stars—III. Galactic structure towards the South Pole and the Galactic thick disc. Mon. Not. R. Astron. Soc. 1983, 202, 1025–1047. [Google Scholar] [CrossRef]
- Kuijken, K.; Gilmore, G. The mass distribution in the galactic disc—II. Determination of the surface mass density of the galactic disc near the Sun. Mon. Not. R. Astron. Soc. 1989, 239, 605–649. [Google Scholar] [CrossRef]
- Bilir, S.; Karaali, S.; Ak, S.; Yaz, E.; Hamzaoğlu, E. Galactic longitude dependent galactic model parameters. New Astron. 2006, 12, 234–245. [Google Scholar] [CrossRef]
- Jurić, M.; Ivezić, Ž.; Brooks, A.; Lupton, R.H.; Schlegel, D.; Finkbeiner, D.; Padmanabhan, N.; Bond, N.; Sesar, B.; Rockosi, C.M.; et al. The Milky Way Tomography with SDSS. I. Stellar Number Density Distribution. Astrophys. J. 2008, 673, 864–914. [Google Scholar] [CrossRef]
- Ak, T.; Bilir, S.; Ak, S.; Eker, Z. Spatial distribution and galactic model parameters of cataclysmic variables. New Astron. 2008, 13, 133–143. [Google Scholar] [CrossRef]
- De Jong, J.T.A.; Yanny, B.; Rix, H.W.; Dolphin, A.E.; Martin, N.F.; Beers, T.C. Mapping the Stellar Structure of the Milky Way Thick Disk and Halo Using SEGUE Photometry. Astrophys. J. 2010, 714, 663–674. [Google Scholar] [CrossRef]
- Ferguson, D.; Gardner, S.; Yanny, B. Milky Way Tomography with K and M Dwarf Stars: The Vertical Structure of the Galactic Disk. Astrophys. J. 2017, 843, 141. [Google Scholar] [CrossRef]
- Mateu, C.; Vivas, A.K. The Galactic thick disc density profile traced with RR Lyrae stars. Mon. Not. R. Astron. Soc. 2018, 479, 211–227. [Google Scholar] [CrossRef]
- Dobbie, P.S.; Warren, S.J. A Bayesian Approach to the Vertical Structure of the Disk of the Milky Way. Open J. Astrophys. 2020, 3, 5. [Google Scholar] [CrossRef]
- Everall, A.; Belokurov, V.; Evans, N.W.; Boubert, D.; Grand, R.J.J. The photo-astrometric vertical tracer density of the Milky Way—II. Results from Gaia. Mon. Not. R. Astron. Soc. 2022, 511, 3863–3880. [Google Scholar] [CrossRef]
- Everall, A.; Evans, N.W.; Belokurov, V.; Boubert, D.; Grand, R.J.J. The Photo-Astrometric vertical tracer density of the Milky Way—I. The method. Mon. Not. R. Astron. Soc. 2022, 511, 2390–2404. [Google Scholar] [CrossRef]
- Spitzer, L., Jr.; Schwarzschild, M. The Possible Influence of Interstellar Clouds on Stellar Velocities. Astrophys. J. 1951, 114, 385. [Google Scholar] [CrossRef]
- Sellwood, J.; Carlberg, R. Spiral instabilities provoked by accretion and star formation. Astrophys. J. 1984, 282, 61–74. [Google Scholar] [CrossRef]
- Quinn, P.; Hernquist, L.; Fullagar, D. Heating of galactic disks by mergers. Astrophys. J. 1993, 403, 74–93. [Google Scholar] [CrossRef]
- Roškar, R.; Debattista, V.P.; Quinn, T.R.; Stinson, G.S.; Wadsley, J. Riding the spiral waves: Implications of stellar migration for the properties of galactic disks. Astrophys. J. Lett. 2008, 684, L79. [Google Scholar] [CrossRef]
- Schönrich, R.; Binney, J. Chemical evolution with radial mixing. Mon. Not. R. Astron. Soc. 2009, 396, 203–222. [Google Scholar] [CrossRef]
- Abadi, M.G.; Navarro, J.F.; Steinmetz, M.; Eke, V.R. Simulations of galaxy formation in a Λ cold dark matter universe. I. Dynamical and photometric properties of a simulated disk galaxy. Astrophys. J. 2003, 591, 499. [Google Scholar] [CrossRef]
- Bovy, J.; Rix, H.W.; Hogg, D.W.; Beers, T.C.; Lee, Y.S.; Zhang, L. The Vertical Motions of Mono-abundance Sub-populations in the Milky Way Disk. Astrophys. J. 2012, 755, 115. [Google Scholar] [CrossRef]
- Rix, H.W.; Bovy, J. The Milky Way’s stellar disk. Mapping and modeling the Galactic disk. Astron. Astrophys. Rev. 2013, 21, 61. [Google Scholar] [CrossRef]
- Bird, J.C.; Kazantzidis, S.; Weinberg, D.H. Radial mixing in galactic discs: The effects of disc structure and satellite bombardment. Mon. Not. R. Astron. Soc. 2012, 420, 913–925. [Google Scholar] [CrossRef]
- Bird, J.C.; Kazantzidis, S.; Weinberg, D.H.; Guedes, J.; Callegari, S.; Mayer, L.; Madau, P. Inside out and Upside down: Tracing the Assembly of a Simulated Disk Galaxy Using Mono-age Stellar Populations. Astrophys. J. 2013, 773, 43. [Google Scholar] [CrossRef]
- Fuhrmann, K. The Deep Thick Disk as Seen by UVES. In Proceedings of the from Extrasolar Planets to Cosmology: The VLT Opening Symposium; Springer: Berlin, Germany, 2000; pp. 351–356. [Google Scholar] [CrossRef]
- Girard, P.; Soubiran, C. Abundances and ages of the deconvolved thin/thick disks of the Galaxy. In Chemical Abundances and Mixing in Stars in the Milky Way and its Satellites; Springer: Berlin, Germany, 2006; pp. 56–57. [Google Scholar] [CrossRef]
- Kordopatis, G.; Recio-Blanco, A.; De Laverny, P.; Gilmore, G.; Hill, V.; Wyse, R.; Helmi, A.; Bijaoui, A.; Zoccali, M.; Bienaymé, O. A spectroscopic survey of thick disc stars outside the solar neighbourhood. Astron. Astrophys. 2011, 535, A107. [Google Scholar] [CrossRef]
- Girard, T.M.; Korchagin, V.I.; Casetti-Dinescu, D.I.; van Altena, W.F.; López, C.E.; Monet, D.G. Velocity Shear of the Thick Disk from SPM3 Proper Motions at the South Galactic Pole. Astron. J. 2006, 132, 1768–1782. [Google Scholar] [CrossRef]
- Gaia Collaboration; Vallenari, A.; Brown, A.G.A.; Prusti, T.; de Bruijne, J.H.J.; Arenou, F.; Babusiaux, C.; Biermann, M.; Creevey, O.L.; Ducourant, C.; et al. Gaia Data Release 3: Summary of the content and survey properties. arXiv 2022, arXiv:2208.00211. [Google Scholar]
- Lindegren, L.; Bastian, U.; Biermann, M.; Bombrun, A.; de Torres, A.; Gerlach, E.; Geyer, R.; Hernández, J.; Hilger, T.; Hobbs, D.; et al. Gaia Early Data Release 3. Parallax bias versus magnitude, colour, and position. Astron. Astrophys. 2021, 649, A4. [Google Scholar] [CrossRef]
- Schönrich, R.; Binney, J.; Dehnen, W. Local kinematics and the local standard of rest. Mon. Not. R. Astron. Soc. 2010, 403, 1829–1833. [Google Scholar] [CrossRef]
- Gaia Collaboration; Brown, A.G.A.; Vallenari, A.; Prusti, T.; de Bruijne, J.H.J.; Babusiaux, C.; Biermann, M.; Creevey, O.L.; Evans, D.W.; Eyer, L.; et al. Gaia Early Data Release 3. Summary of the contents and survey properties. Astron. Astrophys. 2021, 649, A1. [Google Scholar] [CrossRef]
- Vieira, K.; Carraro, G.; Korchagin, V.; Lutsenko, A.; Girard, T.M.; van Altena, W. Milky Way Thin and Thick Disk Kinematics with Gaia EDR3 and RAVE DR5. Astrophys. J. 2022, 932, 28. [Google Scholar] [CrossRef]
- Park, M.J.; Yi, S.K.; Peirani, S.; Pichon, C.; Dubois, Y.; Choi, H.; Devriendt, J.; Kaviraj, S.; Kimm, T.; Kraljic, K.; et al. Exploring the Origin of Thick Disks Using the NewHorizon and Galactica Simulations. Astrophys. J. Suppl. Ser. 2021, 254, 2. [Google Scholar] [CrossRef]
- Obreja, A.; Macciò, A.V.; Moster, B.; Dutton, A.A.; Buck, T.; Stinson, G.S.; Wang, L. Introducing galactic structure finder: The multiple stellar kinematic structures of a simulated Milky Way mass galaxy. Mon. Not. R. Astron. Soc. 2018, 477, 4915–4930. [Google Scholar] [CrossRef]
- Kasparova, A.V.; Katkov, I.Y.; Chilingarian, I.V. An excessively massive thick disc of the enormous edge-on lenticular galaxy NGC 7572. Mon. Not. R. Astron. Soc. 2020, 493, 5464–5478. [Google Scholar] [CrossRef]




| (pc) | (pc) | (pc−3) | (pc−3) | |
|---|---|---|---|---|
| 279.76 | 797.23 | |||
| ±12.49 | ±12.34 | |||
| 5% | 2% | 5% | 4% | 6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vieira, K.; Korchagin, V.; Carraro, G.; Lutsenko, A. Vertical Structure of the Milky Way Disk with Gaia DR3. Galaxies 2023, 11, 77. https://doi.org/10.3390/galaxies11030077
Vieira K, Korchagin V, Carraro G, Lutsenko A. Vertical Structure of the Milky Way Disk with Gaia DR3. Galaxies. 2023; 11(3):77. https://doi.org/10.3390/galaxies11030077
Chicago/Turabian StyleVieira, Katherine, Vladimir Korchagin, Giovanni Carraro, and Artem Lutsenko. 2023. "Vertical Structure of the Milky Way Disk with Gaia DR3" Galaxies 11, no. 3: 77. https://doi.org/10.3390/galaxies11030077
APA StyleVieira, K., Korchagin, V., Carraro, G., & Lutsenko, A. (2023). Vertical Structure of the Milky Way Disk with Gaia DR3. Galaxies, 11(3), 77. https://doi.org/10.3390/galaxies11030077






