The Effect of the LMC on the Milky Way System
Abstract
1. Introduction
2. Introducing the Participants
2.1. Milky Way

2.2. LMC
2.2.1. Mass
- Cosmological stellar mass–halo mass relation.
- Mass modelling from internal kinematics.
- Census of its satellites.
- Interaction with the SMC.
- Dynamical perturbation of stellar streams.
- Kinematic and spatial distortions in the Milky Way halo.
- Hubble flow in the Local Universe.
2.2.2. Satellites
2.3. SMC
| Galaxy | J16 | S17 | K18 | E20 | P20 | B22 | C22 |
|---|---|---|---|---|---|---|---|
| Carina | – | – | ? | – | |||
| Carina II | + | + | + | + | + | ||
| Carina III | + | + | + | + | + | ||
| Delve 2 | (?) | ||||||
| Eridanus III | (?) | (?) | (?) | ||||
| Grus I | ? | ? | – | – | – | – | |
| Grus II | (?) | (–) | c | c | |||
| Horologium I | + | + | + | + | + | + | + |
| Horologium II | (+) | (?) | (–) | ? | ? | ||
| Hydrus I | + | + | + | + | + | ||
| Pictor I | (?) | (–) | (–) | ||||
| Pictor II | (?) | ||||||
| Phoenix II | (+) | (?) | (?) | + | c | + | + |
| Reticulum II | + | ? | – | + | c | + | ? |
| Reticulum III | (?) | (?) | (–) | – | – | ||
| SMC | + | + | |||||
| Tucana II | + | ? | – | – | – | – | |
| Tucana III | (?) | – | – | – | – | – | |
| Tucana IV | (+) | (?) | (–) | ? | c | ||
| Tucana V | (+) | (?) | – | – |
2.4. Magellanic Stream, Bridge, and Other Structures
3. Orbit of the LMC
3.1. Present-Day Position and Velocity
- Vigorous ongoing star formation without signs of quenching indicates an ample reservoir of gas, while it is expected that a satellite galaxy would be stripped of its gas shortly after infall into the main halo. The star formation rate of the LMC has been unusually low until a recent burst starting ∼3–4 Gyr ago [80,81,82,83], which might have been triggered by the compression of gas as it experiences a bow shock upon entering the Milky Way gas corona, although the interaction with the SMC is another possible explanation. A lack of evidence for an earlier episode of elevated star formation rate (excluding the time shortly after the Big Bang) may be seen as the argument against a previous pericentre passage.
- Absence of a large-scale stellar tidal stream like that of the Sagittarius Galaxy, which has completed several orbits around the Milky Way. Signs of tidal perturbation in the outer disc [50,75,77] can be attributed to the interaction between the LMC and SMC. There is a prominent gas stream [63] that roughly matches the past orbit of the Magellanic Clouds over in the sky; however, it is also better explained by the interaction between the two Clouds [64,84].
- LMC satellites, including the SMC, would have been tidally stripped from it if it had a similarly close pericentre passage around the Milky Way in the past.
3.2. Past Orbit
- bulge: ;
- disc: ;
- halo: .
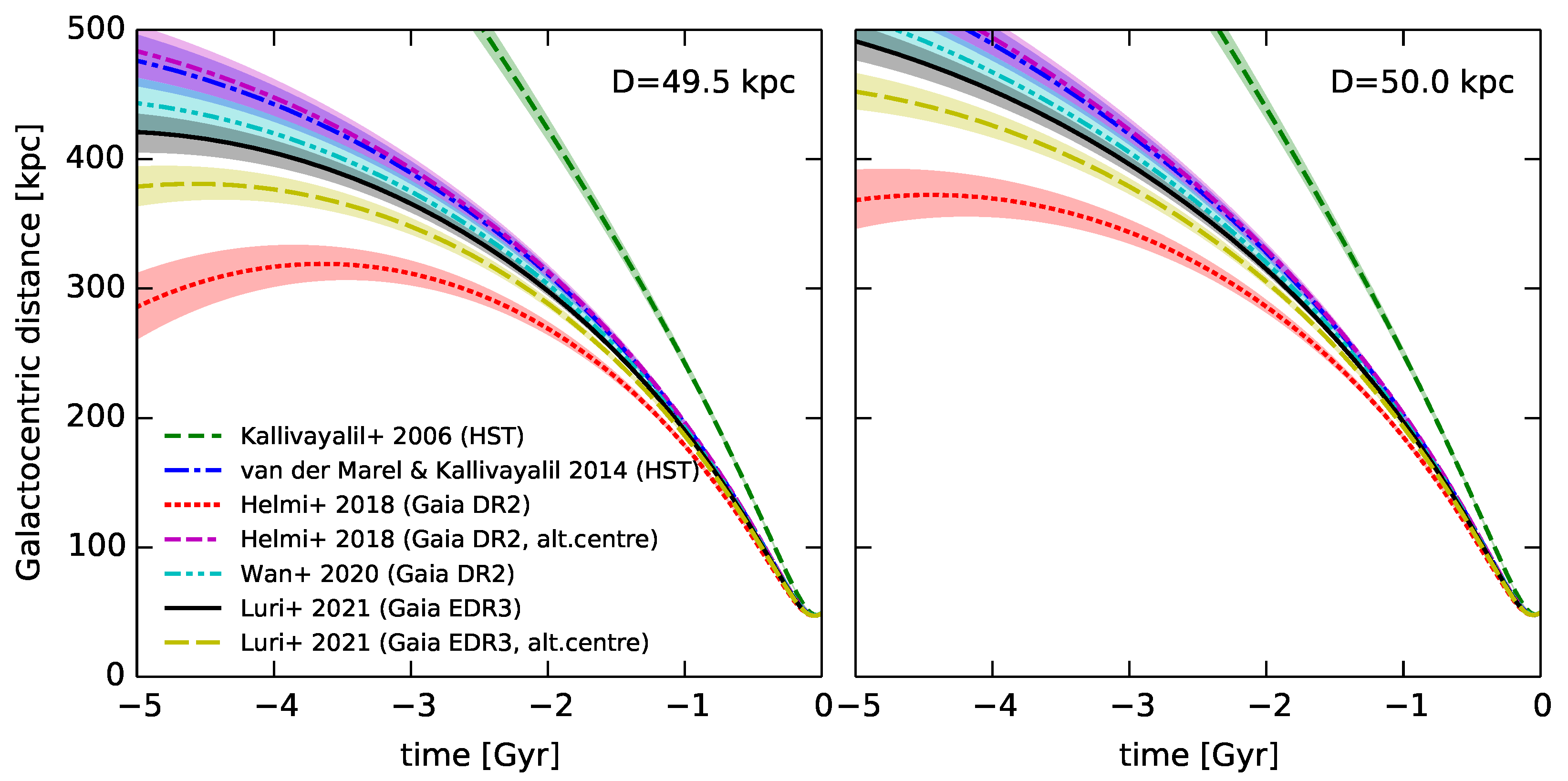

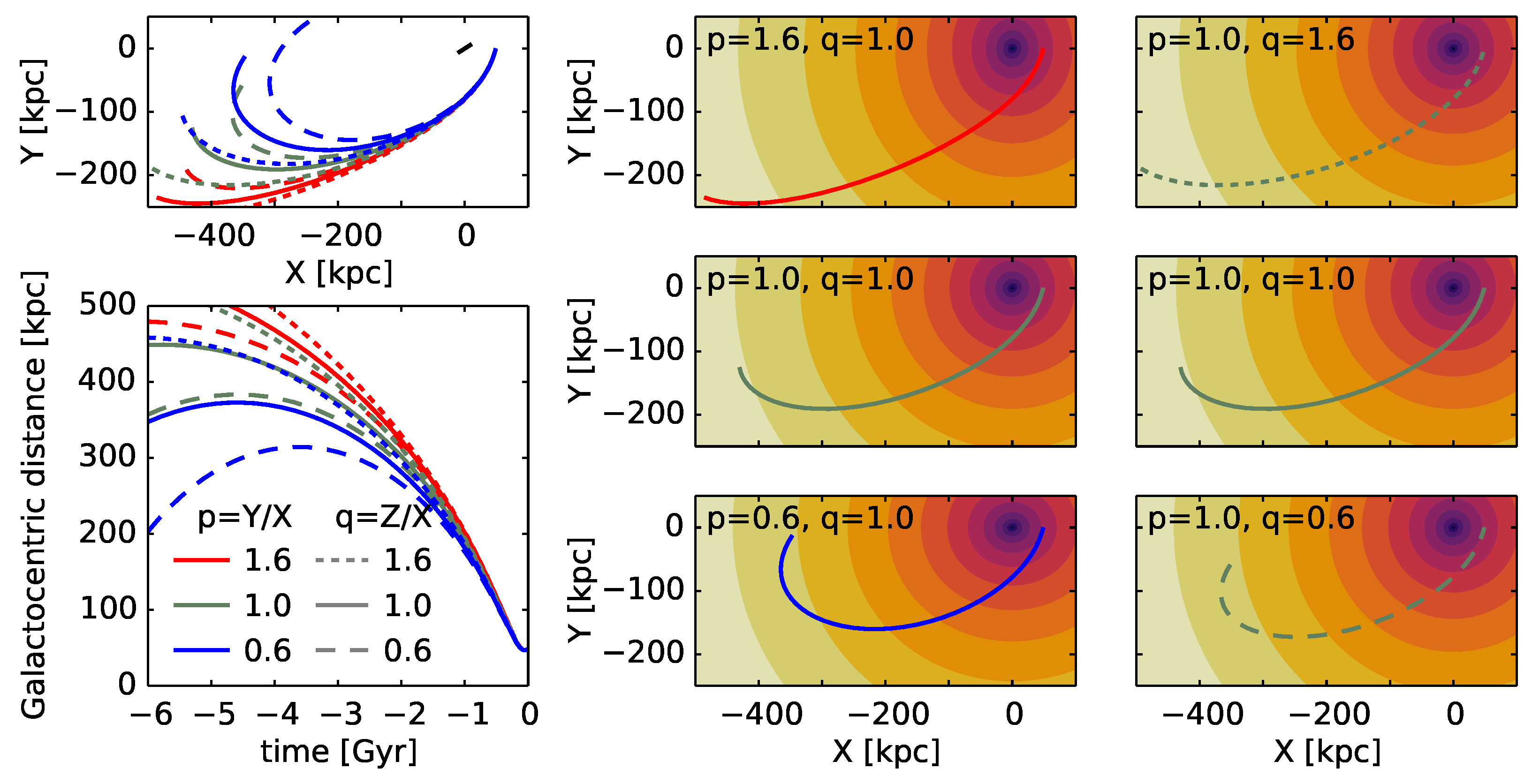
4. Dynamical Implications
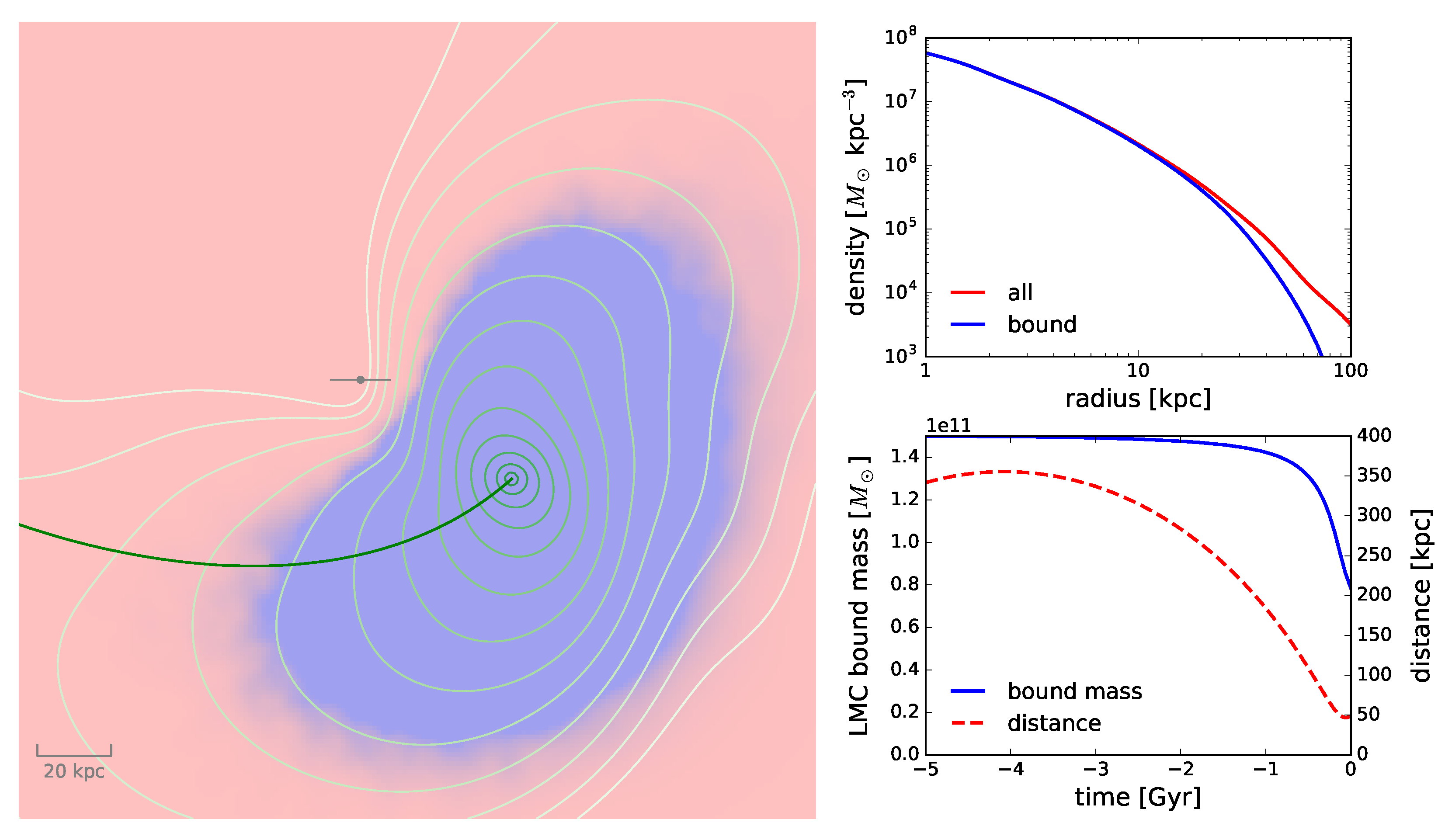
4.1. Local Effects
4.2. Global Effects on the Milky Way
4.2.1. Theory
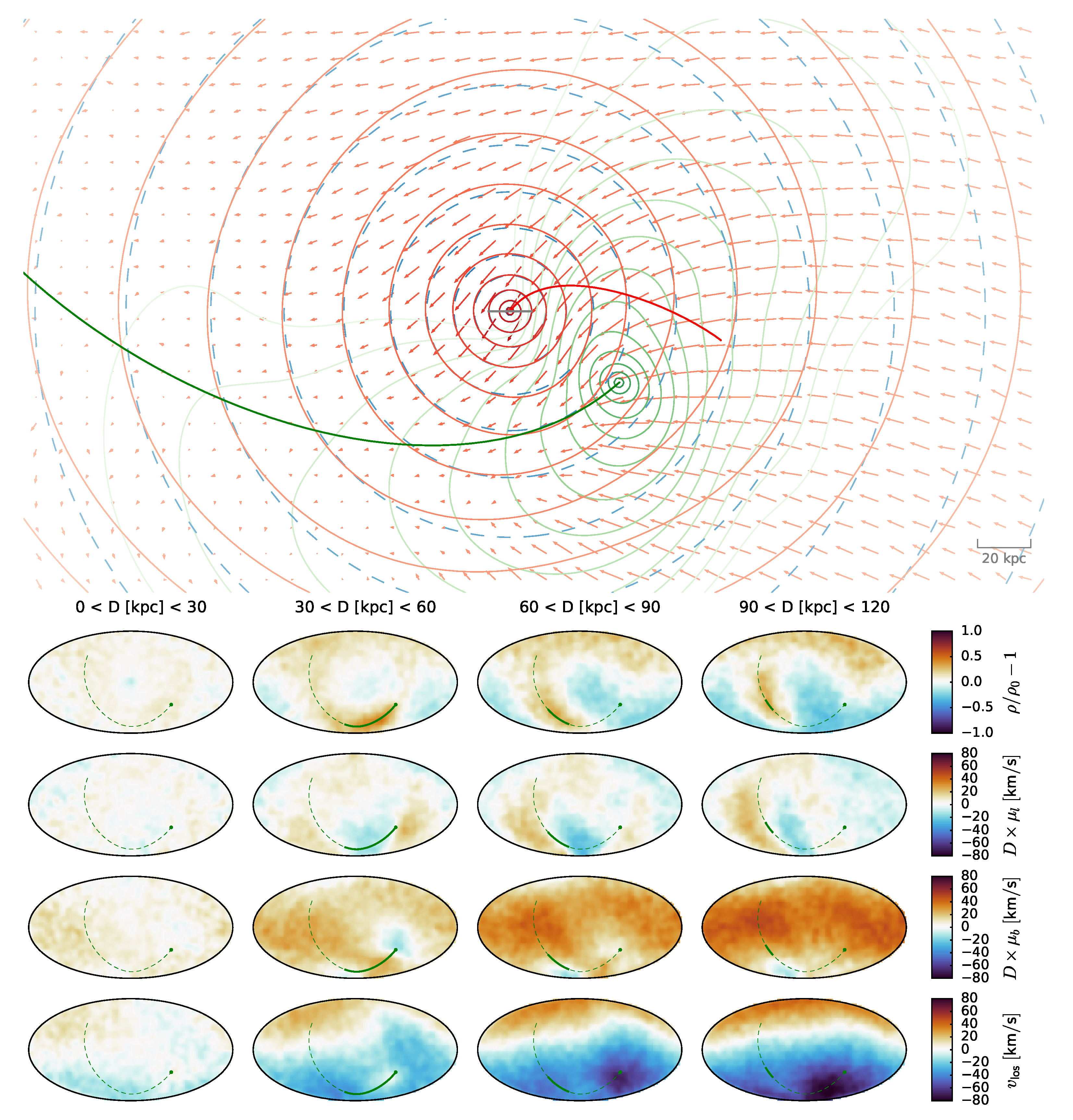

4.2.2. Observations
4.2.3. Implications for the Milky Way Dynamics
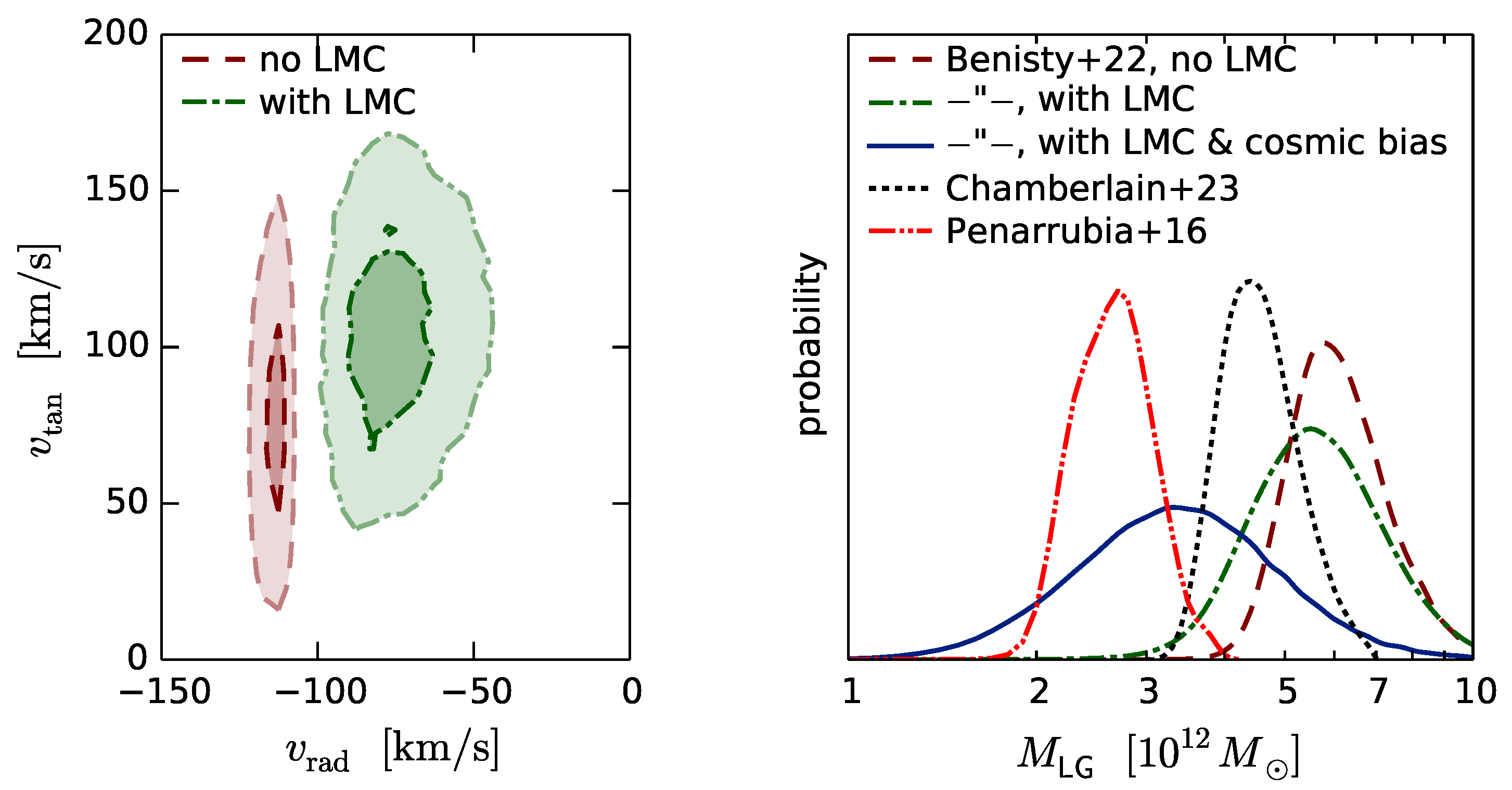
4.3. Effects on the Local Group
5. Conclusions
- The total pre-infall mass of the LMC is likely to be (1–2), i.e., only 5–10 times smaller than the Milky Way mass. This estimate is supported by a number of empirical arguments reviewed in Section 2.2.1, and the dynamical effects of the LMC on the Milky Way discussed in Section 4 are best explained by a similar mass range. If the LMC is on its first passage around the Galaxy, its dark halo becomes deformed, but is still almost entirely brought within 100 kpc from the Milky Way centre.
- Despite the increasing precision of PM measurements, there remains a considerable uncertainty in the orbital period and apocentre distance of the LMC (Section 3.2). This is largely due to the orbit being only marginally (if at all) bound to the Milky Way. Likewise, these parameters depend strongly on the Milky Way mass profile. The evidence for the first-passage scenario is less strong now than it was 15 years ago [5], since the most recent PM measurements reduce the tangential velocity by a few tens of kms. The orbital period most likely exceeds 5 Gyr, unless the Milky Way is significantly more massive than (which is disfavoured by current models), but an earlier pericentre passage at a distance of ∼100 kpc cannot be ruled out with certainty. The implications of this alternative second-passage scenario for the LMC satellites, the Magellanic Stream, and the Milky Way itself are poorly studied.
- The most obvious dynamical consequences of the massive LMC are local perturbations to objects that pass in its vicinity (Section 4.1), but equally, if not more important, is its global effect on the Milky Way (Section 4.2). It is often associated with the reflex motion of the Galaxy about the common centre of mass of the Milky Way–LMC system, but this is only part of the story. Stars and other objects in the outer halo of the Milky Way (roughly beyond 30 kpc) are not displaced by the LMC in the same way as the inner Galaxy; in other words, the differential perturbation causes a deformation of the Milky Way both in space and in kinematics. This phenomenon only began to be appreciated in the last few years, and is now clearly seen both in simulations and in observations.
- The LMC-induced reflex motion of the Milky Way leads to an overall reduction of its inferred past orbital period in the case of a more massive LMC compared to a test-particle orbit. This counteracts the more well-known effect of dynamical friction, and has not been accounted for in many earlier studies.
- As already mentioned, the reconstruction of the past orbit of the LMC is still uncertain and very sensitive to variations in its present-day phase-space coordinates, parameters of the Milky Way potential and other factors.
- Connected to the previous point, any modelling effort that aims at exploring the dependence of the past LMC orbit on its mass or on the Milky Way potential must match the present-day position and velocity of the LMC with very high accuracy (better than 1 kpc and a few kms) to ensure a meaningful comparison between different cases. This is nearly impossible to achieve in large-volume cosmological simulations and is very difficult even in dedicated simulations of the Milky Way–LMC[–SMC] system; this level of precision was rarely attained or even mandated in previous studies. On the other hand, the LMC trajectory in the last few hundred Myr (up to 100–150 kpc from the Galactic centre) is only weakly sensitive to its current velocity or the Galactic potential, so most of the dynamical effects on the Milky Way do not strongly depend on these factors (but do scale with the LMC mass).
- Given that full N-body simulations of the Milky Way–LMC interaction are expensive and difficult to conduct with sufficient precision, alternative computationally cheaper methods need to be more accurate and sophisticated. The classical dynamical friction expression poorly describes the orbital evolution of massive satellites [143] even after the manual tuning of the Coulomb logarithm, and the distortions in the gravitational potential of both galaxies have non-negligible dynamical effects [98]; these factors are ignored in the popular approximation of orbital evolution of two extended but non-deforming bodies.
- The analysis of the perturbations is hampered by the scarcity of available kinematic tracers: existing major spectroscopic surveys, with the exception of SEGUE [9], contain very few stars beyond 50 kpc. Fortunately, the sample will expand significantly in the coming years with the public data releases from DESI [144], WEAVE [145], and H3 [146] surveys.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tremaine, S.D. The effect of dynamical friction on the orbit of the Magellanic Clouds. Astrophys. J. 1976, 203, 72–74. [Google Scholar] [CrossRef]
- Murai, T.; Fujimoto, M. The Magellanic stream and the galaxy with a massive halo. Publ. Soc. Jpn. 1980, 32, 581–603. [Google Scholar]
- Lin, D.N.C.; Lynden-Bell, D. On the proper motion of the Magellanic Clouds and the halo mass of our galaxy. Mon. Not. R. Astron. Soc. 1982, 198, 707–721. [Google Scholar] [CrossRef]
- Gardiner, L.T.; Sawa, T.; Fujimoto, M. Numerical simulations of the Magellanic system—I. Orbits of the Magellanic Cloufs and the global gas distribution. Mon. Not. R. Astron. Soc. 1994, 266, 567–582. [Google Scholar] [CrossRef]
- Besla, G.; Kallivayalil, N.; Hernquist, L.; Robertson, B.; Cox, T.J.; van der Marel, R.P.; Alcock, C. Are the Magellanic Clouds on Their First Passage about the Milky Way? Astrophys. J. 2007, 668, 949–967. [Google Scholar] [CrossRef]
- Kallivayalil, N.; van der Marel, R.P.; Alcock, C.; Axelrod, T.; Cook, K.H.; Drake, A.J.; Geha, M. The Proper Motion of the Large Magellanic Cloud Using HST. Astrophys. J. 2006, 638, 772–785. [Google Scholar] [CrossRef]
- Kallivayalil, N.; van der Marel, R.P.; Besla, G.; Anderson, J.; Alcock, C. Third-epoch Magellanic Cloud Proper Motions. I. Hubble Space Telescope/WFC3 Data and Orbit Implications. Astrophys. J. 2013, 764, 161. [Google Scholar] [CrossRef]
- Avner, E.S.; King, I.R. The influence of the Magellanic Clouds on the Milky Way. Astron. J. 1967, 72, 650. [Google Scholar] [CrossRef]
- Yanny, B.; Rockosi, C.; Newberg, H.J.; Knapp, G.R.; Adelman-McCarthy, J.K.; Alcorn, B.; Allam, S.; Allende Prieto, C.; An, D.; Anderson, K.S.J.; et al. SEGUE: A Spectroscopic Survey of 240,000 Stars with g = 14–20. Astron. J. 2009, 137, 4377–4399. [Google Scholar] [CrossRef]
- Majewski, S.R.; Schiavon, R.P.; Frinchaboy, P.M.; Allende Prieto, C.; Barkhouser, R.; Bizyaev, D.; Blank, B.; Brunner, S.; Burton, A.; Carrera, R.; et al. The Apache Point Observatory Galactic Evolution Experiment (APOGEE). Astron. J. 2017, 154, 94. [Google Scholar] [CrossRef]
- Zhao, G.; Zhao, Y.H.; Chu, Y.Q.; Jing, Y.P.; Deng, L.C. LAMOST spectral survey—An overview. Res. Astron. Astrophys. 2012, 12, 723–734. [Google Scholar] [CrossRef]
- Gaia Collaboration. Gaia Data Release 2. Summary of the contents and survey properties. Astron. Astrophys. 2018, 616, A1. [Google Scholar] [CrossRef]
- Gaia Collaboration. Gaia Early Data Release 3. Summary of the contents and survey properties. Astron. Astrophys. 2021, 649, A1. [Google Scholar] [CrossRef]
- Gaia Collaboration. Gaia Data Release 3: Summary of the content and survey properties. arXiv 2022, arXiv:2208.00211. [Google Scholar] [CrossRef]
- Antoja, T.; Helmi, A.; Romero-Gómez, M.; Katz, D.; Babusiaux, C.; Drimmel, R.; Evans, D.W.; Figueras, F.; Poggio, E.; Reylé, C.; et al. A dynamically young and perturbed Milky Way disk. Nature 2018, 561, 360–362. [Google Scholar] [CrossRef] [PubMed]
- Widrow, L.M.; Gardner, S.; Yanny, B.; Dodelson, S.; Chen, H.Y. Galactoseismology: Discovery of Vertical Waves in the Galactic Disk. Astrophys. Lett. 2012, 750, L41. [Google Scholar] [CrossRef]
- Laporte, C.F.P.; Johnston, K.V.; Gómez, F.A.; Garavito-Camargo, N.; Besla, G. The influence of Sagittarius and the Large Magellanic Cloud on the stellar disc of the Milky Way Galaxy. Mon. Not. R. Astron. Soc. 2018, 481, 286–306. [Google Scholar] [CrossRef]
- Eyre, A.; Binney, J. The mechanics of tidal streams. Mon. Not. R. Astron. Soc. 2011, 413, 1852–1874. [Google Scholar] [CrossRef]
- Sanders, J.L.; Binney, J. Stream-orbit misalignment—I. The dangers of orbit-fitting. Mon. Not. R. Astron. Soc. 2013, 433, 1813–1825. [Google Scholar] [CrossRef]
- Bovy, J. Dynamical Modeling of Tidal Streams. Astrophys. J. 2014, 795, 95. [Google Scholar] [CrossRef]
- Gibbons, S.L.J.; Belokurov, V.; Evans, N.W. ‘Skinny Milky Way please’, says Sagittarius. Mon. Not. R. Astron. Soc. 2014, 445, 3788–3802. [Google Scholar] [CrossRef]
- Mateu, C. galstreams: A library of Milky Way stellar stream footprints and tracks. Mon. Not. R. Astron. Soc. 2023, 520, 5225–5258. [Google Scholar] [CrossRef]
- Majewski, S.R.; Skrutskie, M.F.; Weinberg, M.D.; Ostheimer, J.C. A Two Micron All Sky Survey View of the Sagittarius Dwarf Galaxy. I. Morphology of the Sagittarius Core and Tidal Arms. Astrophys. J. 2003, 599, 1082–1115. [Google Scholar] [CrossRef]
- Grillmair, C.J. Detection of a 60°-long Dwarf Galaxy Debris Stream. Astrophys. Lett. 2006, 645, L37–L40. [Google Scholar] [CrossRef]
- Belokurov, V.; Evans, N.W.; Irwin, M.J.; Lynden-Bell, D.; Yanny, B.; Vidrih, S.; Gilmore, G.; Seabroke, G.; Zucker, D.B.; Wilkinson, M.I.; et al. An Orphan in the “Field of Streams”. Astrophys. J. 2007, 658, 337–344. [Google Scholar] [CrossRef]
- Shipp, N.; Drlica-Wagner, A.; Balbinot, E.; Ferguson, P.; Erkal, D.; Li, T.S.; Bechtol, K.; Belokurov, V.; Buncher, B.; Carollo, D.; et al. Stellar Streams Discovered in the Dark Energy Survey. Astrophys. J. 2018, 862, 114. [Google Scholar] [CrossRef]
- Koposov, S.E.; Belokurov, V.; Li, T.S.; Mateu, C.; Erkal, D.; Grillmair, C.J.; Hendel, D.; Price-Whelan, A.M.; Laporte, C.F.P.; Hawkins, K.; et al. Piercing the Milky Way: An all-sky view of the Orphan Stream. Mon. Not. R. Astron. Soc. 2019, 485, 4726–4742. [Google Scholar] [CrossRef]
- Johnston, K.V.; Zhao, H.; Spergel, D.N.; Hernquist, L. Tidal Streams as Probes of the Galactic Potential. Astrophys. Lett. 1999, 512, L109–L112. [Google Scholar] [CrossRef]
- Bonaca, A.; Hogg, D.W. The Information Content in Cold Stellar Streams. Astrophys. J. 2018, 867, 101. [Google Scholar] [CrossRef]
- Bland-Hawthorn, J.; Gerhard, O. The Galaxy in Context: Structural, Kinematic, and Integrated Properties. Annu. Rev. Astron. Astrophys. 2016, 54, 529–596. [Google Scholar] [CrossRef]
- Wang, W.; Han, J.; Cautun, M.; Li, Z.; Ishigaki, M.N. The mass of our Milky Way. Sci. China Phys. Mech. Astron. 2020, 63, 109801. [Google Scholar] [CrossRef]
- Peñarrubia, J.; Gómez, F.A.; Besla, G.; Erkal, D.; Ma, Y.Z. A timing constraint on the (total) mass of the Large Magellanic Cloud. Mon. Not. R. Astron. Soc. 2016, 456, L54–L58. [Google Scholar] [CrossRef]
- Erkal, D.; Belokurov, V.; Laporte, C.F.P.; Koposov, S.E.; Li, T.S.; Grillmair, C.J.; Kallivayalil, N.; Price-Whelan, A.M.; Evans, N.W.; Hawkins, K.; et al. The total mass of the Large Magellanic Cloud from its perturbation on the Orphan stream. Mon. Not. R. Astron. Soc. 2019, 487, 2685–2700. [Google Scholar] [CrossRef]
- Erkal, D.; Belokurov, V.A. Limit on the LMC mass from a census of its satellites. Mon. Not. R. Astron. Soc. 2020, 495, 2554–2563. [Google Scholar] [CrossRef]
- Vasiliev, E.; Belokurov, V.; Erkal, D. Tango for three: Sagittarius, LMC, and the Milky Way. Mon. Not. R. Astron. Soc. 2021, 501, 2279–2304. [Google Scholar] [CrossRef]
- Shipp, N.; Erkal, D.; Drlica-Wagner, A.; Li, T.S.; Pace, A.B.; Koposov, S.E.; Cullinane, L.R.; Da Costa, G.S.; Ji, A.P.; Kuehn, K.; et al. Measuring the Mass of the Large Magellanic Cloud with Stellar Streams Observed by S 5. Astrophys. J. 2021, 923, 149. [Google Scholar] [CrossRef]
- Correa Magnus, L.; Vasiliev, E. Measuring the Milky Way mass distribution in the presence of the LMC. Mon. Not. R. Astron. Soc. 2022, 511, 2610–2630. [Google Scholar] [CrossRef]
- Koposov, S.E.; Erkal, D.; Li, T.S.; Da Costa, G.S.; Cullinane, L.R.; Ji, A.P.; Kuehn, K.; Lewis, G.F.; Pace, A.B.; Shipp, N.; et al. S 5: Probing the Milky Way and Magellanic Clouds potentials with the 6-D map of the Orphan-Chenab stream. Mon. Not. R. Astron. Soc. 2023. [Google Scholar] [CrossRef]
- van der Marel, R.P.; Alves, D.R.; Hardy, E.; Suntzeff, N.B. New Understanding of Large Magellanic Cloud Structure, Dynamics, and Orbit from Carbon Star Kinematics. Astron. J. 2002, 124, 2639–2663. [Google Scholar] [CrossRef]
- Fox, A.J.; Wakker, B.P.; Barger, K.A.; Hernandez, A.K.; Richter, P.; Lehner, N.; Bland-Hawthorn, J.; Charlton, J.C.; Westmeier, T.; Thom, C.; et al. The COS/UVES Absorption Survey of the Magellanic Stream. III. Ionization, Total Mass, and Inflow Rate onto the Milky Way. Astrophys. J. 2014, 787, 147. [Google Scholar] [CrossRef]
- Moster, B.P.; Naab, T.; White, S.D.M. Galactic star formation and accretion histories from matching galaxies to dark matter haloes. Mon. Not. R. Astron. Soc. 2013, 428, 3121–3138. [Google Scholar] [CrossRef]
- Read, J.I.; Erkal, D. Abundance matching with the mean star formation rate: There is no missing satellites problem in the Milky Way above M200 ∼109 M⊙. Mon. Not. R. Astron. Soc. 2019, 487, 5799–5812. [Google Scholar] [CrossRef]
- Vasiliev, E.; Belokurov, V. The last breath of the Sagittarius dSph. Mon. Not. R. Astron. Soc. 2020, 497, 4162–4182. [Google Scholar] [CrossRef]
- van der Marel, R.P.; Kallivayalil, N. Third-epoch Magellanic Cloud Proper Motions. II. The Large Magellanic Cloud Rotation Field in Three Dimensions. Astrophys. J. 2014, 781, 121. [Google Scholar] [CrossRef]
- Vasiliev, E. Internal dynamics of the Large Magellanic Cloud from Gaia DR2. Mon. Not. R. Astron. Soc. 2018, 481, L100–L104. [Google Scholar] [CrossRef]
- Wan, Z.; Guglielmo, M.; Lewis, G.F.; Mackey, D.; Ibata, R.A. A SkyMapper view of the Large Magellanic Cloud: The dynamics of stellar populations. Mon. Not. R. Astron. Soc. 2020, 492, 782–795. [Google Scholar] [CrossRef]
- Luri, X.; Chemin, L.; Clementini, G.; Delgado, H.E.; McMillan, P.J.; Romero-Gómez, M.; Balbinot, E.; Castro-Ginard, A.; Mor, R.; Ripepi, V.; et al. Gaia Early Data Release 3. Structure and properties of the Magellanic Clouds. Astron. Astrophys. 2021, 649, A7. [Google Scholar] [CrossRef]
- Jiménez-Arranz, Ó.; Romero-Gómez, M.; Luri, X.; McMillan, P.J.; Antoja, T.; Chemin, L.; Roca-Fàbrega, S.; Masana, E.; Muros, A. Kinematic analysis of the Large Magellanic Cloud using Gaia DR3. Astron. Astrophys. 2023, 669, A91. [Google Scholar] [CrossRef]
- Choi, Y.; Olsen, K.A.G.; Besla, G.; van der Marel, R.P.; Zivick, P.; Kallivayalil, N.; Nidever, D.L. The Recent LMC-SMC Collision: Timing and Impact Parameter Constraints from Comparison of Gaia LMC Disk Kinematics and N-body Simulations. Astrophys. J. 2022, 927, 153. [Google Scholar] [CrossRef]
- Cullinane, L.R.; Mackey, A.D.; Da Costa, G.S.; Erkal, D.; Koposov, S.E.; Belokurov, V. The Magellanic Edges Survey - III. Kinematics of the disturbed LMC outskirts. Mon. Not. R. Astron. Soc. 2022, 512, 4798–4818. [Google Scholar] [CrossRef]
- Katz, H.; Desmond, H.; McGaugh, S.; Lelli, F. The tight empirical relation between dark matter halo mass and flat rotation velocity for late-type galaxies. Mon. Not. R. Astron. Soc. 2019, 483, L98–L103. [Google Scholar] [CrossRef]
- Koposov, S.E.; Belokurov, V.; Torrealba, G.; Evans, N.W. Beasts of the Southern Wild: Discovery of Nine Ultra Faint Satellites in the Vicinity of the Magellanic Clouds. Astrophys. J. 2015, 805, 130. [Google Scholar] [CrossRef]
- Bechtol, K.; Drlica-Wagner, A.; Balbinot, E.; Pieres, A.; Simon, J.D.; Yanny, B.; Santiago, B.; Wechsler, R.H.; Frieman, J.; Walker, A.R.; et al. Eight New Milky Way Companions Discovered in First-year Dark Energy Survey Data. Astrophys. J. 2015, 807, 50. [Google Scholar] [CrossRef]
- Drlica-Wagner, A.; Bechtol, K.; Rykoff, E.S.; Luque, E.; Queiroz, A.; Mao, Y.Y.; Wechsler, R.H.; Simon, J.D.; Santiago, B.; Yanny, B.; et al. Eight Ultra-faint Galaxy Candidates Discovered in Year Two of the Dark Energy Survey. Astrophys. J. 2015, 813, 109. [Google Scholar] [CrossRef]
- Jethwa, P.; Erkal, D.; Belokurov, V. A Magellanic origin of the DES dwarfs. Mon. Not. R. Astron. Soc. 2016, 461, 2212–2233. [Google Scholar] [CrossRef]
- Tatton, B.L.; van Loon, J.T.; Cioni, M.R.L.; Bekki, K.; Bell, C.P.M.; Choudhury, S.; de Grijs, R.; Groenewegen, M.A.T.; Ivanov, V.D.; Marconi, M.; et al. The VMC Survey-XL. Three-dimensional structure of the Small Magellanic Cloud as derived from red clump stars. Mon. Not. R. Astron. Soc. 2021, 504, 2983–2997. [Google Scholar] [CrossRef]
- Besla, G.; Kallivayalil, N.; Hernquist, L.; van der Marel, R.P.; Cox, T.J.; Kereš, D. The role of dwarf galaxy interactions in shaping the Magellanic System and implications for Magellanic Irregulars. Mon. Not. R. Astron. Soc. 2012, 421, 2109–2138. [Google Scholar] [CrossRef]
- Zivick, P.; Kallivayalil, N.; van der Marel, R.P.; Besla, G.; Linden, S.T.; Kozłowski, S.; Fritz, T.K.; Kochanek, C.S.; Anderson, J.; Sohn, S.T.; et al. The Proper Motion Field of the Small Magellanic Cloud: Kinematic Evidence for Its Tidal Disruption. Astrophys. J. 2018, 864, 55. [Google Scholar] [CrossRef]
- Sales, L.V.; Navarro, J.F.; Kallivayalil, N.; Frenk, C.S. Identifying true satellites of the Magellanic Clouds. Mon. Not. R. Astron. Soc. 2017, 465, 1879–1888. [Google Scholar] [CrossRef]
- Kallivayalil, N.; Sales, L.V.; Zivick, P.; Fritz, T.K.; Del Pino, A.; Sohn, S.T.; Besla, G.; van der Marel, R.P.; Navarro, J.F.; Sacchi, E. The Missing Satellites of the Magellanic Clouds? Gaia Proper Motions of the Recently Discovered Ultra-faint Galaxies. Astrophys. J. 2018, 867, 19. [Google Scholar] [CrossRef]
- Patel, E.; Kallivayalil, N.; Garavito-Camargo, N.; Besla, G.; Weisz, D.R.; van der Marel, R.P.; Boylan-Kolchin, M.; Pawlowski, M.S.; Gómez, F.A. The Orbital Histories of Magellanic Satellites Using Gaia DR2 Proper Motions. Astrophys. J. 2020, 893, 121. [Google Scholar] [CrossRef]
- Battaglia, G.; Taibi, S.; Thomas, G.F.; Fritz, T.K. Gaia early DR3 systemic motions of Local Group dwarf galaxies and orbital properties with a massive Large Magellanic Cloud. Astron. Astrophys. 2022, 657, A54. [Google Scholar] [CrossRef]
- Mathewson, D.S.; Cleary, M.N.; Murray, J.D. The Magellanic Stream. Astrophys. J. 1974, 190, 291–296. [Google Scholar] [CrossRef]
- Besla, G.; Kallivayalil, N.; Hernquist, L.; van der Marel, R.P.; Cox, T.J.; Kereš, D. Simulations of the Magellanic Stream in a First Infall Scenario. Astrophys. Lett. 2010, 721, L97–L101. [Google Scholar] [CrossRef]
- Tepper-García, T.; Bland-Hawthorn, J.; Pawlowski, M.S.; Fritz, T.K. The Magellanic System: The puzzle of the leading gas stream. Mon. Not. R. Astron. Soc. 2019, 488, 918–938. [Google Scholar] [CrossRef]
- Lucchini, S.; D’Onghia, E.; Fox, A.J.; Bustard, C.; Bland-Hawthorn, J.; Zweibel, E. The Magellanic Corona as the key to the formation of the Magellanic Stream. Nature 2020, 585, 203–206. [Google Scholar] [CrossRef]
- D’Onghia, E.; Fox, A.J. The Magellanic Stream: Circumnavigating the Galaxy. Annu. Rev. Astron. Astrophys. 2016, 54, 363–400. [Google Scholar] [CrossRef]
- Zaritsky, D.; Conroy, C.; Naidu, R.P.; Cargile, P.A.; Putman, M.; Besla, G.; Bonaca, A.; Caldwell, N.; Han, J.J.; Johnson, B.D.; et al. Discovery of Magellanic Stellar Debris in the H3 Survey. Astrophys. Lett. 2020, 905, L3. [Google Scholar] [CrossRef]
- Petersen, M.S.; Peñarrubia, J.; Jones, E. Tidally stripped halo stars from the Large Magellanic Cloud in the Galactic North. Mon. Not. R. Astron. Soc. 2022, 514, 1266–1273. [Google Scholar] [CrossRef]
- Besla, G.; Hernquist, L.; Loeb, A. The origin of the microlensing events observed towards the LMC and the stellar counterpart of the Magellanic stream. Mon. Not. R. Astron. Soc. 2013, 428, 2342–2365. [Google Scholar] [CrossRef]
- Price-Whelan, A.M.; Nidever, D.L.; Choi, Y.; Schlafly, E.F.; Morton, T.; Koposov, S.E.; Belokurov, V. Discovery of a Disrupting Open Cluster Far into the Milky Way Halo: A Recent Star Formation Event in the Leading Arm of the Magellanic Stream? Astrophys. J. 2019, 887, 19. [Google Scholar] [CrossRef]
- Nidever, D.L.; Price-Whelan, A.M.; Choi, Y.; Beaton, R.L.; Hansen, T.T.; Boubert, D.; Aguado, D.; Ezzeddine, R.; Oh, S.; Evans, N.W. Spectroscopy of the Young Stellar Association Price-Whelan 1: Origin in the Magellanic Leading Arm and Constraints on the Milky Way Hot Halo. Astrophys. J. 2019, 887, 115. [Google Scholar] [CrossRef]
- Bellazzini, M.; Ibata, R.A.; Martin, N.; Malhan, K.; Marasco, A.; Famaey, B. Young stars raining through the galactic halo: The nature and orbit of price-whelan 1. Mon. Not. R. Astron. Soc. 2019, 490, 2588–2598. [Google Scholar] [CrossRef]
- Belokurov, V.; Erkal, D.; Deason, A.J.; Koposov, S.E.; De Angeli, F.; Evans, D.W.; Fraternali, F.; Mackey, D. Clouds, Streams and Bridges. Redrawing the blueprint of the Magellanic System with Gaia DR1. Mon. Not. R. Astron. Soc. 2017, 466, 4711–4730. [Google Scholar] [CrossRef]
- Belokurov, V.A.; Erkal, D. Clouds in arms. Mon. Not. R. Astron. Soc. 2019, 482, L9–L13. [Google Scholar] [CrossRef]
- Zivick, P.; Kallivayalil, N.; Besla, G.; Sohn, S.T.; van der Marel, R.P.; del Pino, A.; Linden, S.T.; Fritz, T.K.; Anderson, J. The Proper-motion Field along the Magellanic Bridge: A New Probe of the LMC-SMC Interaction. Astrophys. J. 2019, 874, 78. [Google Scholar] [CrossRef]
- Mackey, A.D.; Koposov, S.E.; Erkal, D.; Belokurov, V.; Da Costa, G.S.; Gómez, F.A. A 10 kpc stellar substructure at the edge of the Large Magellanic Cloud: Perturbed outer disc or evidence for tidal stripping? Mon. Not. R. Astron. Soc. 2016, 459, 239–255. [Google Scholar] [CrossRef]
- Pietrzyński, G.; Graczyk, D.; Gallenne, A.; Gieren, W.; Thompson, I.B.; Pilecki, B.; Karczmarek, P.; Górski, M.; Suchomska, K.; Taormina, M.; et al. A distance to the Large Magellanic Cloud that is precise to one per cent. Nature 2019, 567, 200–203. [Google Scholar] [CrossRef]
- Helmi, A.; van Leeuwen, F.; McMillan, P.J.; Massari, D.; Antoja, T.; Robin, A.C.; Lindegren, L.; Bastian, U.; Arenou, F.; Babusiaux, C.; et al. Gaia Data Release 2. Kinematics of globular clusters and dwarf galaxies around the Milky Way. Astron. Astrophys. 2018, 616, A12. [Google Scholar] [CrossRef]
- Harris, J.; Zaritsky, D. The Star Formation History of the Large Magellanic Cloud. Astron. J. 2009, 138, 1243–1260. [Google Scholar] [CrossRef]
- Meschin, I.; Gallart, C.; Aparicio, A.; Hidalgo, S.L.; Monelli, M.; Stetson, P.B.; Carrera, R. Spatially resolved LMC star formation history - I. Outside in evolution of the outer LMC disc. Mon. Not. R. Astron. Soc. 2014, 438, 1067–1080. [Google Scholar] [CrossRef]
- Hasselquist, S.; Hayes, C.R.; Lian, J.; Weinberg, D.H.; Zasowski, G.; Horta, D.; Beaton, R.; Feuillet, D.K.; Garro, E.R.; Gallart, C.; et al. APOGEE Chemical Abundance Patterns of the Massive Milky Way Satellites. Astrophys. J. 2021, 923, 172. [Google Scholar] [CrossRef]
- Massana, P.; Ruiz-Lara, T.; Noël, N.E.D.; Gallart, C.; Nidever, D.L.; Choi, Y.; Sakowska, J.D.; Besla, G.; Olsen, K.A.G.; Monelli, M.; et al. The synchronized dance of the magellanic clouds’ star formation history. Mon. Not. R. Astron. Soc. 2022, 513, L40–L45. [Google Scholar] [CrossRef]
- Diaz, J.D.; Bekki, K. The Tidal Origin of the Magellanic Stream and the Possibility of a Stellar Counterpart. Astrophys. J. 2012, 750, 36. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Dynamical Friction. I. General Considerations: The Coefficient of Dynamical Friction. Astrophys. J. 1943, 97, 255. [Google Scholar] [CrossRef]
- Hashimoto, Y.; Funato, Y.; Makino, J. To Circularize or Not To Circularize? Orbital Evolution of Satellite Galaxies. Astrophys. J. 2003, 582, 196–201. [Google Scholar] [CrossRef]
- Just, A.; Peñarrubia, J. Large scale inhomogeneity and local dynamical friction. Astron. Astrophys. 2005, 431, 861–877. [Google Scholar] [CrossRef]
- Besla, G. The Orbits of the Magellanic Clouds. In Lessons from the Local Group: A Conference in honor of David Block and Bruce Elmegreen; Springer: Cham, Switzerland, 2015; p. 311. [Google Scholar] [CrossRef]
- Gómez, F.A.; Besla, G.; Carpintero, D.D.; Villalobos, Á.; O’Shea, B.W.; Bell, E.F. And Yet it Moves: The Dangers of Artificially Fixing the Milky Way Center of Mass in the Presence of a Massive Large Magellanic Cloud. Astrophys. J. 2015, 802, 128. [Google Scholar] [CrossRef]
- Patel, E.; Besla, G.; Sohn, S.T. Orbits of massive satellite galaxies - I. A close look at the Large Magellanic Cloud and a new orbital history for M33. Mon. Not. R. Astron. Soc. 2017, 464, 3825–3849. [Google Scholar] [CrossRef]
- Hammer, F.; Yang, Y.B.; Flores, H.; Puech, M.; Fouquet, S. The Magellanic Stream System. I. Ram-Pressure Tails and the Relics of the Collision Between the Magellanic Clouds. Astrophys. J. 2015, 813, 110. [Google Scholar] [CrossRef]
- Wang, J.; Hammer, F.; Yang, Y.; Ripepi, V.; Cioni, M.R.L.; Puech, M.; Flores, H. Towards a complete understanding of the Magellanic Stream Formation. Mon. Not. R. Astron. Soc. 2019, 486, 5907–5916. [Google Scholar] [CrossRef]
- Guglielmo, M.; Lewis, G.F.; Bland-Hawthorn, J. A genetic approach to the history of the Magellanic Clouds. Mon. Not. R. Astron. Soc. 2014, 444, 1759–1774. [Google Scholar] [CrossRef]
- Belokurov, V.; Deason, A.J.; Erkal, D.; Koposov, S.E.; Carballo-Bello, J.A.; Smith, M.C.; Jethwa, P.; Navarrete, C. The Pisces Plume and the Magellanic wake. Mon. Not. R. Astron. Soc. 2019, 488, L47–L52. [Google Scholar] [CrossRef]
- Garavito-Camargo, N.; Besla, G.; Laporte, C.F.P.; Johnston, K.V.; Gómez, F.A.; Watkins, L.L. Hunting for the Dark Matter Wake Induced by the Large Magellanic Cloud. Astrophys. J. 2019, 884, 51. [Google Scholar] [CrossRef]
- Simon, J.D.; Li, T.S.; Erkal, D.; Pace, A.B.; Drlica-Wagner, A.; James, D.J.; Marshall, J.L.; Bechtol, K.; Hansen, T.; Kuehn, K.; et al. Birds of a Feather? Magellan/IMACS Spectroscopy of the Ultra-faint Satellites Grus II, Tucana IV, and Tucana V. Astrophys. J. 2020, 892, 137. [Google Scholar] [CrossRef]
- Dillamore, A.M.; Belokurov, V.; Evans, N.W.; Price-Whelan, A.M. The impact of a massive Sagittarius dSph on GD-1-like streams. Mon. Not. R. Astron. Soc. 2022, 516, 1685–1703. [Google Scholar] [CrossRef]
- Lilleengen, S.; Petersen, M.S.; Erkal, D.; Peñarrubia, J.; Koposov, S.E.; Li, T.S.; Cullinane, L.R.; Ji, A.P.; Kuehn, K.; Lewis, G.F.; et al. The effect of the deforming dark matter haloes of the Milky Way and the Large Magellanic Cloud on the Orphan-Chenab stream. Mon. Not. R. Astron. Soc. 2023, 518, 774–790. [Google Scholar] [CrossRef]
- Valluri, M.; Price-Whelan, A.M.; Snyder, S.J. Detecting the Figure Rotation of Dark Matter Halos with Tidal Streams. Astrophys. J. 2021, 910, 150. [Google Scholar] [CrossRef]
- Erkal, D.; Li, T.S.; Koposov, S.E.; Belokurov, V.; Balbinot, E.; Bechtol, K.; Buncher, B.; Drlica-Wagner, A.; Kuehn, K.; Marshall, J.L.; et al. Modelling the Tucana III stream—A close passage with the LMC. Mon. Not. R. Astron. Soc. 2018, 481, 3148–3159. [Google Scholar] [CrossRef]
- Shipp, N.; Li, T.S.; Pace, A.B.; Erkal, D.; Drlica-Wagner, A.; Yanny, B.; Belokurov, V.; Wester, W.; Koposov, S.E.; Kuehn, K.; et al. Proper Motions of Stellar Streams Discovered in the Dark Energy Survey. Astrophys. J. 2019, 885, 3. [Google Scholar] [CrossRef]
- Fardal, M.A.; van der Marel, R.P.; Sohn, S.T.; del Pino Molina, A. The course of the Orphan Stream in the Northern Galactic hemisphere traced with Gaia DR2. Mon. Not. R. Astron. Soc. 2019, 486, 936–949. [Google Scholar] [CrossRef]
- Besla, G.; Peter, A.H.G.; Garavito-Camargo, N. The highest-speed local dark matter particles come from the Large Magellanic Cloud. J. Cosmol. Astropart. Phys. 2019, 2019, 13. [Google Scholar] [CrossRef]
- Donaldson, K.; Petersen, M.S.; Peñarrubia, J. Effects on the local dark matter distribution due to the large magellanic cloud. Mon. Not. R. Astron. Soc. 2022, 513, 46–51. [Google Scholar] [CrossRef]
- Smith-Orlik, A.; Ronaghi, N.; Bozorgnia, N.; Cautun, M.; Fattahi, A.; Besla, G.; Frenk, C.S.; Garavito-Camargo, N.; Gómez, F.A.; Grand, R.J.J.; et al. The impact of the Large Magellanic Cloud on dark matter direct detection signals. arXiv 2023, arXiv:2302.04281. [Google Scholar]
- Weinberg, M.D. Production of Milky Way Structure by the Magellanic Clouds. Astrophys. Lett. 1995, 455, L31. [Google Scholar] [CrossRef]
- Garavito-Camargo, N.; Besla, G.; Laporte, C.F.P.; Price-Whelan, A.M.; Cunningham, E.C.; Johnston, K.V.; Weinberg, M.; Gómez, F.A. Quantifying the Impact of the Large Magellanic Cloud on the Structure of the Milky Way’s Dark Matter Halo Using Basis Function Expansions. Astrophys. J. 2021, 919, 109. [Google Scholar] [CrossRef]
- Erkal, D.; Belokurov, V.A.; Parkin, D.L. Equilibrium models of the Milky Way mass are biased high by the LMC. Mon. Not. R. Astron. Soc. 2020, 498, 5574–5580. [Google Scholar] [CrossRef]
- Petersen, M.S.; Peñarrubia, J. Reflex motion in the Milky Way stellar halo resulting from the Large Magellanic Cloud infall. Mon. Not. R. Astron. Soc. 2020, 494, L11–L16. [Google Scholar] [CrossRef]
- Cunningham, E.C.; Garavito-Camargo, N.; Deason, A.J.; Johnston, K.V.; Erkal, D.; Laporte, C.F.P.; Besla, G.; Luger, R.; Sanderson, R.E. Quantifying the Stellar Halo’s Response to the LMC’s Infall with Spherical Harmonics. Astrophys. J. 2020, 898, 4. [Google Scholar] [CrossRef]
- Makarov, D.; Khoperskov, S.; Makarov, D.; Makarova, L.; Libeskind, N.; Salomon, J.B. The LMC impact on the kinematics of the Milky Way satellites: Clues from the running solar apex. Mon. Not. R. Astron. Soc. 2023, in press. [CrossRef]
- Laporte, C.F.P.; Gómez, F.A.; Besla, G.; Johnston, K.V.; Garavito-Camargo, N. Response of the Milky Way’s disc to the Large Magellanic Cloud in a first infall scenario. Mon. Not. R. Astron. Soc. 2018, 473, 1218–1230. [Google Scholar] [CrossRef]
- Fritz, T.K.; Battaglia, G.; Pawlowski, M.S.; Kallivayalil, N.; van der Marel, R.; Sohn, S.T.; Brook, C.; Besla, G. Gaia DR2 proper motions of dwarf galaxies within 420 kpc. Orbits, Milky Way mass, tidal influences, planar alignments, and group infall. Astron. Astrophys. 2018, 619, A103. [Google Scholar] [CrossRef]
- Petersen, M.S.; Peñarrubia, J. Detection of the Milky Way reflex motion due to the Large Magellanic Cloud infall. Nature Astronomy 2021, 5, 251–255. [Google Scholar] [CrossRef]
- Erkal, D.; Deason, A.J.; Belokurov, V.; Xue, X.X.; Koposov, S.E.; Bird, S.A.; Liu, C.; Simion, I.T.; Yang, C.; Zhang, L.; et al. Detection of the LMC-induced sloshing of the Galactic halo. Mon. Not. R. Astron. Soc. 2021, 506, 2677–2684. [Google Scholar] [CrossRef]
- Xue, X.X.; Rix, H.W.; Yanny, B.; Beers, T.C.; Bell, E.F.; Zhao, G.; Bullock, J.S.; Johnston, K.V.; Morrison, H.; Rockosi, C.; et al. Quantifying Kinematic Substructure in the Milky Way’s Stellar Halo. Astrophys. J. 2011, 738, 79. [Google Scholar] [CrossRef]
- Xue, X.X.; Ma, Z.; Rix, H.W.; Morrison, H.L.; Harding, P.; Beers, T.C.; Ivans, I.I.; Jacobson, H.R.; Johnson, J.; Lee, Y.S.; et al. The SEGUE K Giant Survey. II. A Catalog of Distance Determinations for the SEGUE K Giants in the Galactic Halo. Astrophys. J. 2014, 784, 170. [Google Scholar] [CrossRef]
- Boubert, D.; Everall, A. Completeness of the Gaia verse II: What are the odds that a star is missing from Gaia DR2? Mon. Not. R. Astron. Soc. 2020, 497, 4246–4261. [Google Scholar] [CrossRef]
- Cantat-Gaudin, T.; Fouesneau, M.; Rix, H.W.; Brown, A.G.A.; Castro-Ginard, A.; Kostrzewa-Rutkowska, Z.; Drimmel, R.; Hogg, D.W.; Casey, A.R.; Khanna, S.; et al. An empirical model of the Gaia DR3 selection function. Astron. Astrophys. 2023, 669, A55. [Google Scholar] [CrossRef]
- Conroy, C.; Naidu, R.P.; Garavito-Camargo, N.; Besla, G.; Zaritsky, D.; Bonaca, A.; Johnson, B.D. All-sky dynamical response of the Galactic halo to the Large Magellanic Cloud. Nature 2021, 592, 534–536. [Google Scholar] [CrossRef]
- Chandra, V.; Naidu, R.P.; Conroy, C.; Ji, A.P.; Rix, H.W.; Bonaca, A.; Cargile, P.; Han, J.J.; Johnson, B.D.; Ting, Y.S.; et al. Distant Echoes of the Milky Way’s Last Major Merger. arXiv 2022, arXiv:2212.00806. [Google Scholar] [CrossRef]
- Rozier, S.; Famaey, B.; Siebert, A.; Monari, G.; Pichon, C.; Ibata, R. Constraining the Milky Way Halo Kinematics via Its Linear Response to the Large Magellanic Cloud. Astrophys. J. 2022, 933, 113. [Google Scholar] [CrossRef]
- Law, D.R.; Majewski, S.R. The Sagittarius Dwarf Galaxy: A Model for Evolution in a Triaxial Milky Way Halo. Astrophys. J. 2010, 714, 229–254. [Google Scholar] [CrossRef]
- Vera-Ciro, C.; Helmi, A. Constraints on the Shape of the Milky Way Dark Matter Halo from the Sagittarius Stream. Astrophys. Lett. 2013, 773, L4. [Google Scholar] [CrossRef]
- Boubert, D.; Erkal, D.; Gualandris, A. Deflection of the hypervelocity stars by the pull of the Large Magellanic Cloud on the Milky Way. Mon. Not. R. Astron. Soc. 2020, 497, 2930–2940. [Google Scholar] [CrossRef]
- Watkins, L.L.; Evans, N.W.; An, J.H. The masses of the Milky Way and Andromeda galaxies. Mon. Not. R. Astron. Soc. 2010, 406, 264–278. [Google Scholar] [CrossRef]
- Deason, A.J.; Erkal, D.; Belokurov, V.; Fattahi, A.; Gómez, F.A.; Grand, R.J.J.; Pakmor, R.; Xue, X.X.; Liu, C.; Yang, C.; et al. The mass of the Milky Way out to 100 kpc using halo stars. Mon. Not. R. Astron. Soc. 2021, 501, 5964–5972. [Google Scholar] [CrossRef]
- Fritz, T.K.; Carrera, R.; Battaglia, G.; Taibi, S. Gaia DR 2 and VLT/FLAMES search for new satellites of the LMC. Astron. Astrophys. 2019, 623, A129. [Google Scholar] [CrossRef]
- D’Souza, R.; Bell, E.F. Uncertainties associated with the backward integration of dwarf satellites using simple parametric potentials. Mon. Not. R. Astron. Soc. 2022, 512, 739–760. [Google Scholar] [CrossRef]
- Kroupa, P.; Theis, C.; Boily, C.M. The great disk of Milky-Way satellites and cosmological sub-structures. Astron. Astrophys. 2005, 431, 517–521. [Google Scholar] [CrossRef]
- Pawlowski, M.S.; Pflamm-Altenburg, J.; Kroupa, P. The VPOS: A vast polar structure of satellite galaxies, globular clusters and streams around the Milky Way. Mon. Not. R. Astron. Soc. 2012, 423, 1109–1126. [Google Scholar] [CrossRef]
- Pawlowski, M.S.; Kroupa, P. The Milky Way’s disc of classical satellite galaxies in light of Gaia DR2. Mon. Not. R. Astron. Soc. 2020, 491, 3042–3059. [Google Scholar] [CrossRef]
- Garavito-Camargo, N.; Patel, E.; Besla, G.; Price-Whelan, A.M.; Gómez, F.A.; Laporte, C.F.P.; Johnston, K.V. The Clustering of Orbital Poles Induced by the LMC: Hints for the Origin of Planes of Satellites. Astrophys. J. 2021, 923, 140. [Google Scholar] [CrossRef]
- Pawlowski, M.S.; Oria, P.A.; Taibi, S.; Famaey, B.; Ibata, R. On the Effect of the Large Magellanic Cloud on the Orbital Poles of Milky Way Satellite Galaxies. Astrophys. J. 2022, 932, 70. [Google Scholar] [CrossRef]
- Kahn, F.D.; Woltjer, L. Intergalactic Matter and the Galaxy. Astrophys. J. 1959, 130, 705. [Google Scholar] [CrossRef]
- Salomon, J.B.; Ibata, R.; Reylé, C.; Famaey, B.; Libeskind, N.I.; McConnachie, A.W.; Hoffman, Y. The proper motion of Andromeda from Gaia EDR3: Confirming a nearly radial orbit. Mon. Not. R. Astron. Soc. 2021, 507, 2592–2601. [Google Scholar] [CrossRef]
- van der Marel, R.P.; Fardal, M.A.; Sohn, S.T.; Patel, E.; Besla, G.; del Pino, A.; Sahlmann, J.; Watkins, L.L. First Gaia Dynamics of the Andromeda System: DR2 Proper Motions, Orbits, and Rotation of M31 and M33. Astrophys. J. 2019, 872, 24. [Google Scholar] [CrossRef]
- Peñarrubia, J.; Ma, Y.Z.; Walker, M.G.; McConnachie, A. A dynamical model of the local cosmic expansion. Mon. Not. R. Astron. Soc. 2014, 443, 2204–2222. [Google Scholar] [CrossRef]
- Benisty, D.; Vasiliev, E.; Evans, N.W.; Davis, A.C.; Hartl, O.V.; Strigari, L.E. The Local Group Mass in the Light of Gaia. Astrophys. Lett. 2022, 928, L5. [Google Scholar] [CrossRef]
- Chamberlain, K.; Price-Whelan, A.M.; Besla, G.; Cunningham, E.C.; Garavito-Camargo, N.; Peñarrubia, J.; Petersen, M.S. Implications of the Milky Way Travel Velocity for Dynamical Mass Estimates of the Local Group. Astrophys. J. 2023, 942, 18. [Google Scholar] [CrossRef]
- Liu, L.; Gerke, B.F.; Wechsler, R.H.; Behroozi, P.S.; Busha, M.T. How Common are the Magellanic Clouds? Astrophys. J. 2011, 733, 62. [Google Scholar] [CrossRef]
- Tollerud, E.J.; Boylan-Kolchin, M.; Barton, E.J.; Bullock, J.S.; Trinh, C.Q. Small-scale Structure in the Sloan Digital Sky Survey and ΛCDM: Isolated L* Galaxies with Bright Satellites. Astrophys. J. 2011, 738, 102. [Google Scholar] [CrossRef]
- Vasiliev, E.; Belokurov, V.; Evans, N.W. Radialization of Satellite Orbits in Galaxy Mergers. Astrophys. J. 2022, 926, 203. [Google Scholar] [CrossRef]
- Cooper, A.P.; Koposov, S.E.; Allende Prieto, C.; Manser, C.J.; Kizhuprakkat, N.; Myers, A.D.; Dey, A.; Gaensicke, B.T.; Li, T.S.; Rockosi, C.; et al. Overview of the DESI Milky Way Survey. Astrophys. J. 2023, in press. arXiv:2208.08514. [Google Scholar] [CrossRef]
- Jin, S.; Trager, S.C.; Dalton, G.B.; Aguerri, J.A.L.; Drew, J.E.; Falcón-Barroso, J.; Gänsicke, B.T.; Hill, V.; Iovino, A.; Pieri, M.M.; et al. The wide-field, multiplexed, spectroscopic facility WEAVE: Survey design, overview, and simulated implementation. Mon. Not. R. Astron. Soc. 2023. [Google Scholar] [CrossRef]
- Conroy, C.; Bonaca, A.; Cargile, P.; Johnson, B.D.; Caldwell, N.; Naidu, R.P.; Zaritsky, D.; Fabricant, D.; Moran, S.; Rhee, J.; et al. Mapping the Stellar Halo with the H3 Spectroscopic Survey. Astrophys. J. 2019, 883, 107. [Google Scholar] [CrossRef]
- Cautun, M.; Deason, A.J.; Frenk, C.S.; McAlpine, S. The aftermath of the Great Collision between our Galaxy and the Large Magellanic Cloud. Mon. Not. R. Astron. Soc. 2019, 483, 2185–2196. [Google Scholar] [CrossRef]
| Reference | ||||
|---|---|---|---|---|
| Kallivayalil et al. [6] | () | () | ||
| van der Marel and Kallivayalil [44] | ||||
| Helmi et al. [79] | () | () | ||
| — (alt.centre) | () | () | ||
| Wan et al. [46] | ||||
| Luri et al. [47] | () | () | ||
| — (alt.centre) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasiliev, E. The Effect of the LMC on the Milky Way System. Galaxies 2023, 11, 59. https://doi.org/10.3390/galaxies11020059
Vasiliev E. The Effect of the LMC on the Milky Way System. Galaxies. 2023; 11(2):59. https://doi.org/10.3390/galaxies11020059
Chicago/Turabian StyleVasiliev, Eugene. 2023. "The Effect of the LMC on the Milky Way System" Galaxies 11, no. 2: 59. https://doi.org/10.3390/galaxies11020059
APA StyleVasiliev, E. (2023). The Effect of the LMC on the Milky Way System. Galaxies, 11(2), 59. https://doi.org/10.3390/galaxies11020059






