Primordial Black Hole Formation in Non-Standard Post-Inflationary Epochs
Abstract
1. Introduction
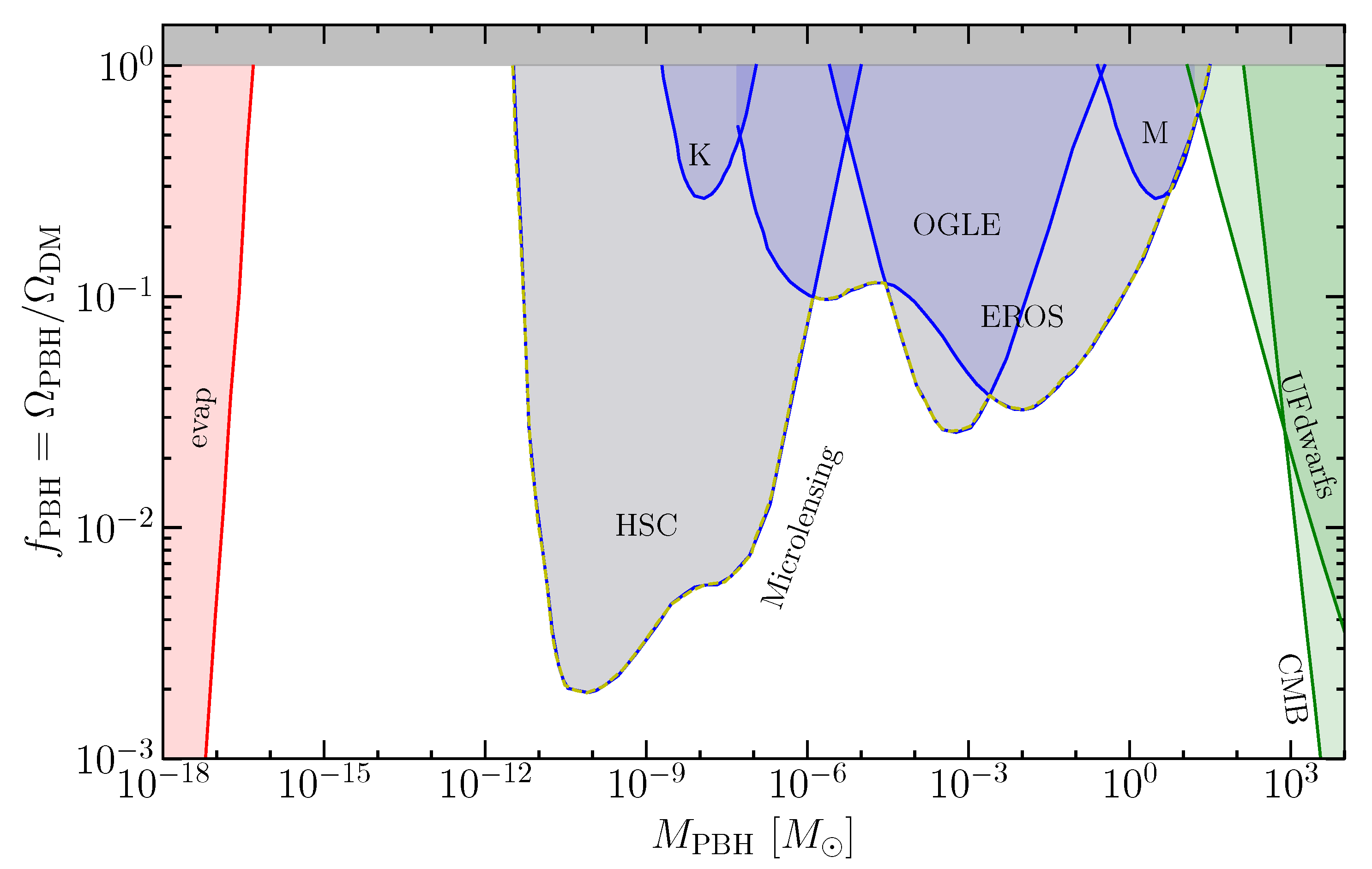
2. Importance in Current Phenomenology
3. Non-Standard Epochs after Inflation
3.1. Reheating
3.2. General W-Dominated Epoch
4. Primordial Fluctuations
5. Formation of PBH: Analysis
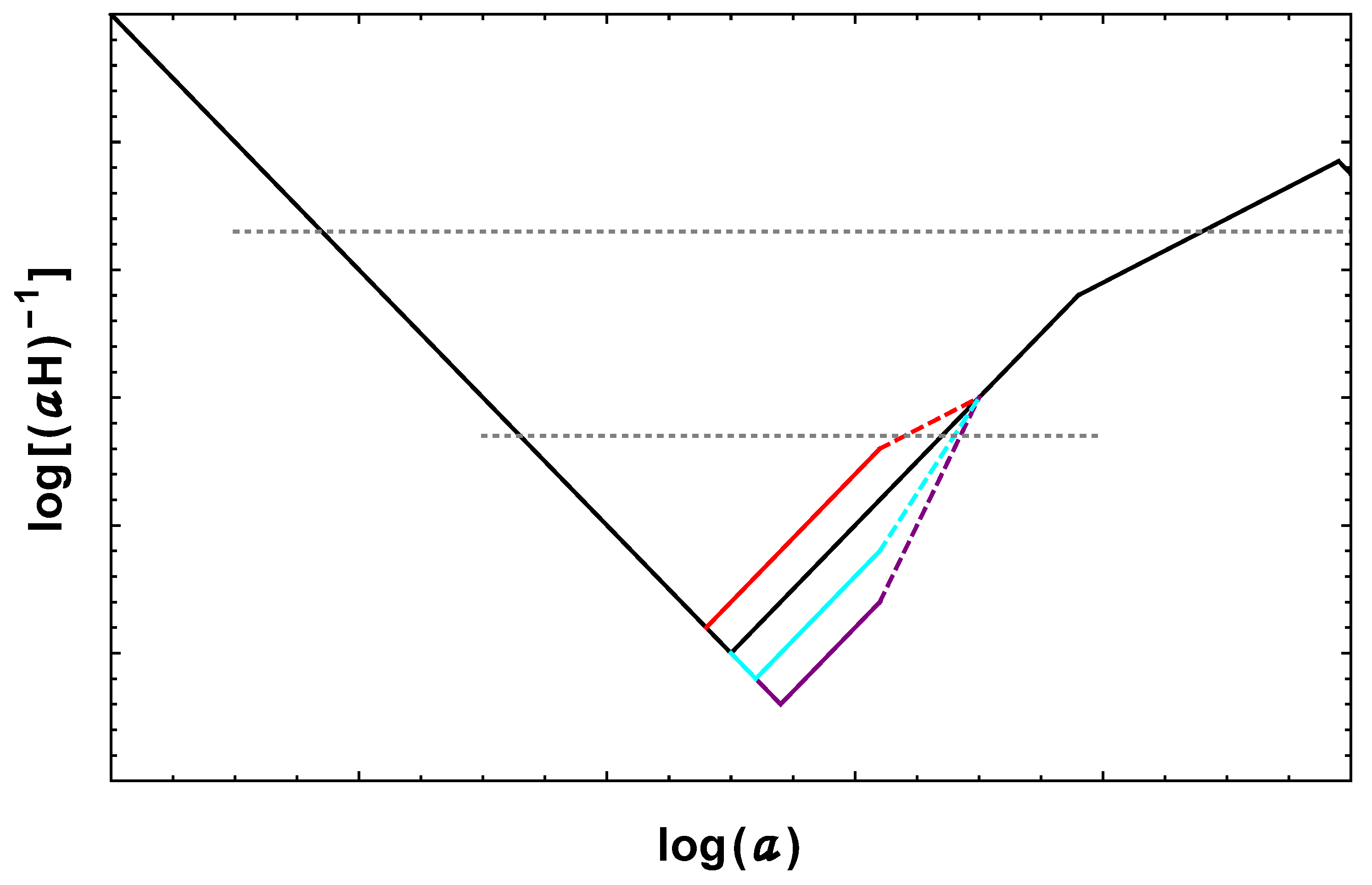
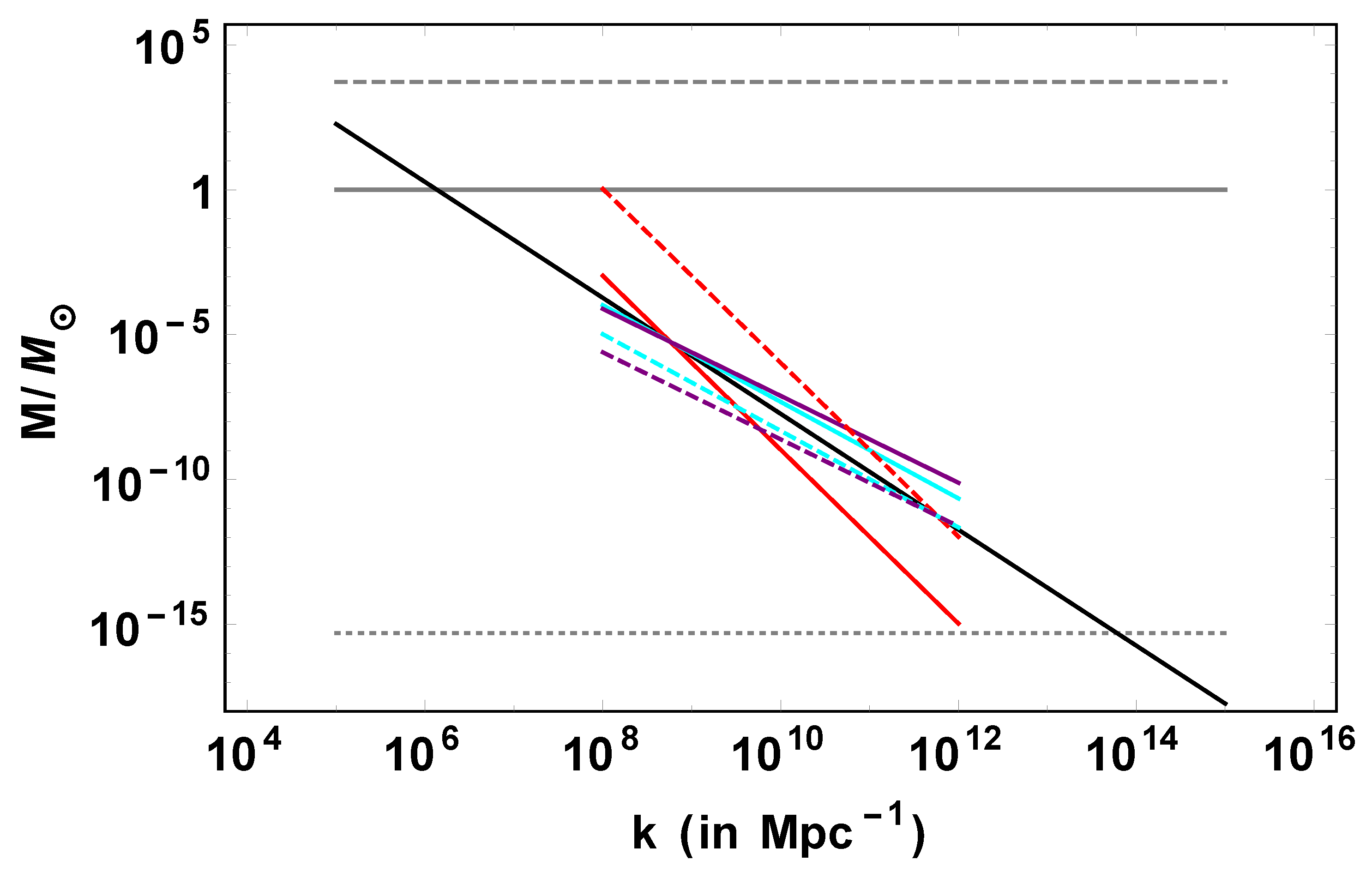
5.1. Length Scale and PBH Mass
5.2. Formation in a w-Dominated Epoch
5.3. Formation in a Matter Dominated Epoch
5.4. Understanding the Contributions
5.4.1. Critical Overdensity
5.4.2. Density Distribution
5.4.3. Various Methods to Calculate
5.4.4. Constant w
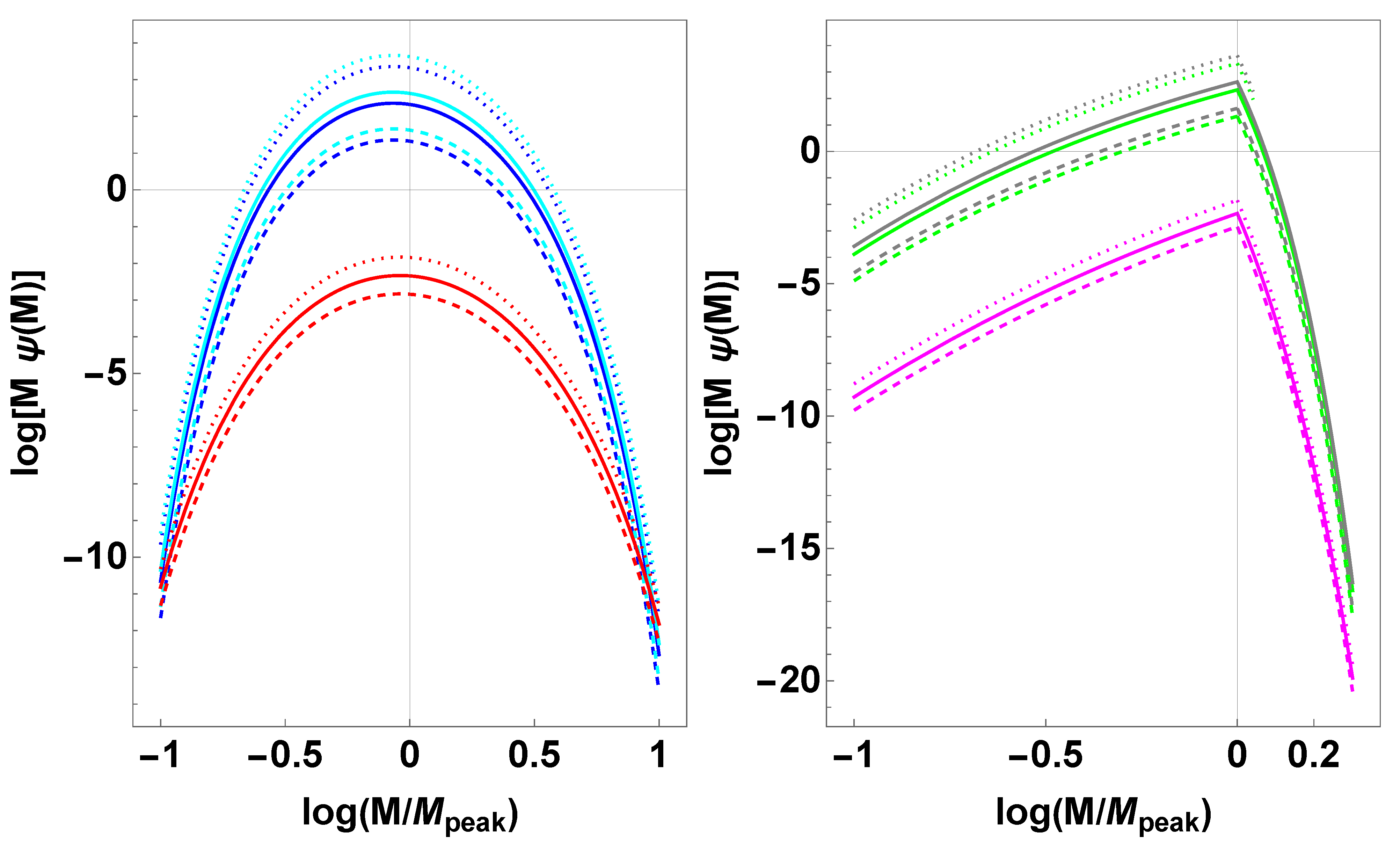
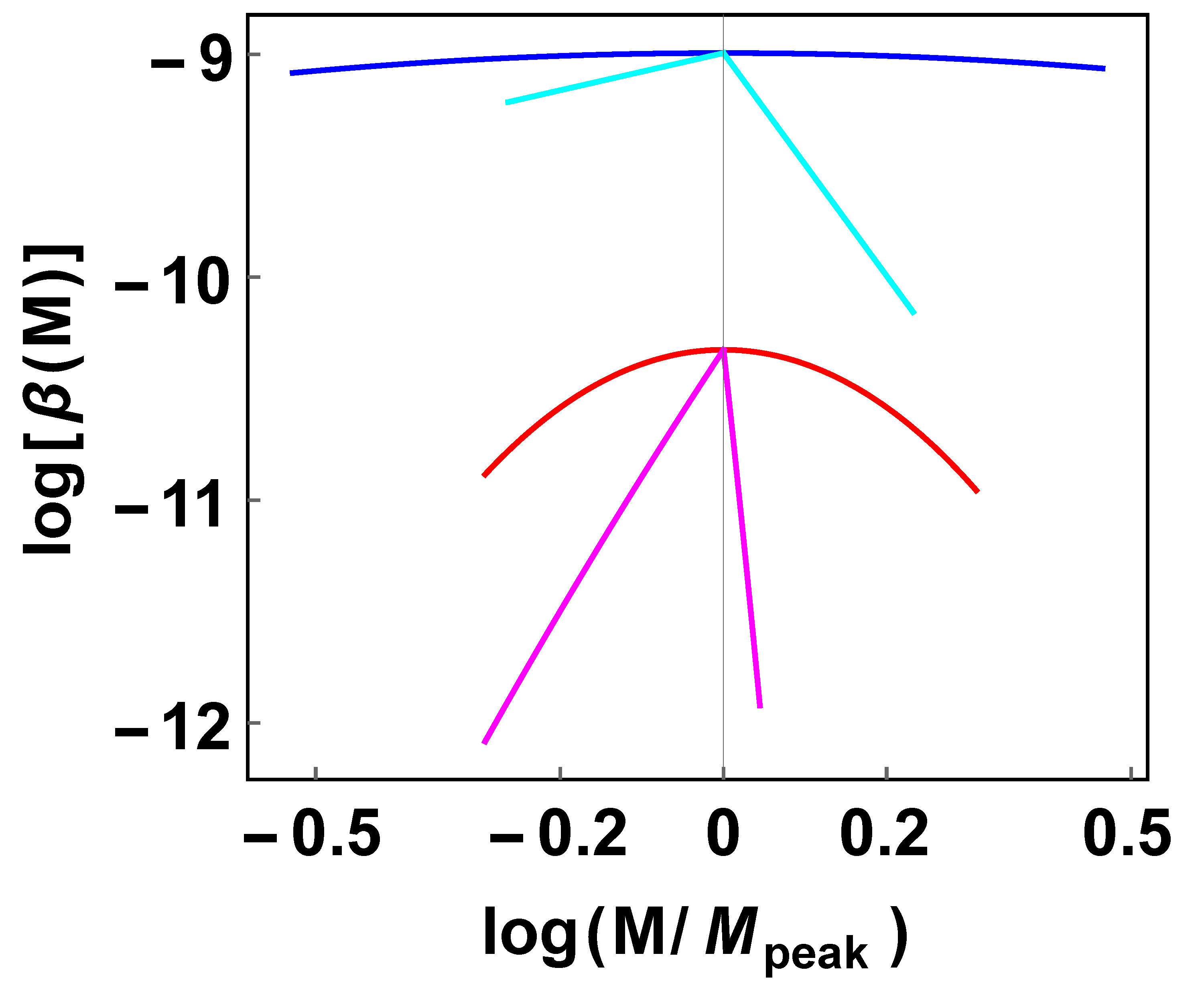
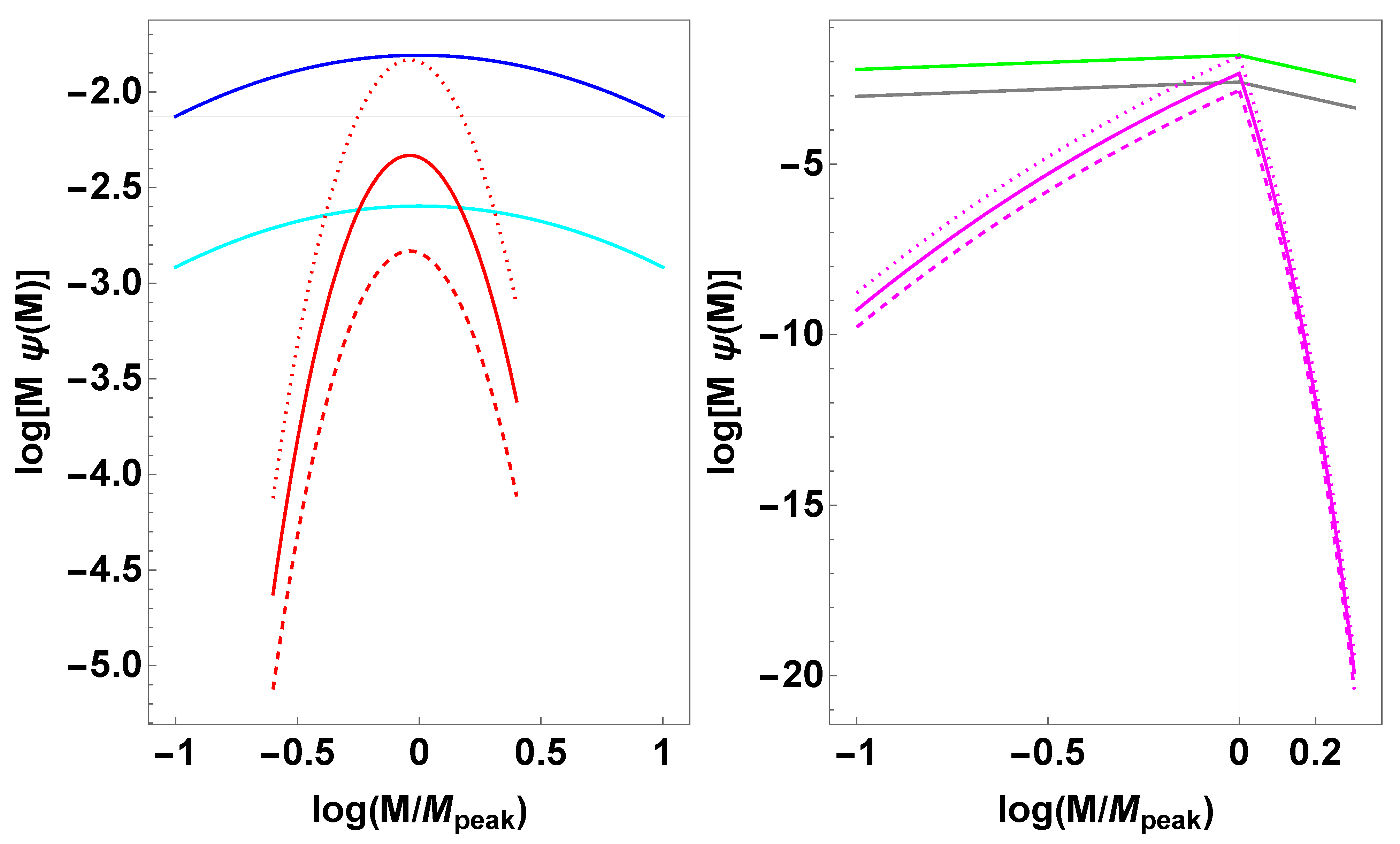
6. Results for Specific Cases
6.1. Gaussian Power Spectrum
6.2. Broken Power Law Power Spectrum
6.3. Kinetic Energy Dominated Epoch
6.4. Early Matter Dominated Epoch
| for RD | for KD | for mD | ||
|---|---|---|---|---|
6.5. QCD Epoch
7. Discussions and Future Prospects
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | does not affect PBH formation when we assume that the formation process begins during the w-dominated epoch, since the energy fraction contained in PBH at the time of formation depends only on the temperature at formation. |
| 2 | |
| 3 | Here, we will use the uniform density curvature perturbation and comoving curvature perturbation interchangeably, since at the superhorizon scales. |
| 4 | This is a simplified assumption, since light PBHs of mass ≳ gm have a significant mass loss due to radiation, whereas heavier PBHs of near solar mass tend to accrete and merge. |
| 5 | This fraction depends on the separation between horizon re-entry of the mode k and the time of maximum expansion, which for the case of RD is very small due to logarithmic growth of perturbations. Therefore, for RD formation of PBH, , typically assumed to be . |
| 6 | Here, we neglect the formation of PBHs of mass M via collapse or accretion anytime after the primordial formation. The recent epoch of dark energy domination can be neglected as well since it started dominating at around redshift . |
| 7 | MeV corresponds to TeV. |
| 8 | See https://www.ligo.caltech.edu/MIT/image/ligo20211107a (accessed on 12 February 2023). |
References
- Hawking, S. Gravitationally collapsed objects of very low mass. Mon. Not. Roy. Astron. Soc. 1971, 152, 75. [Google Scholar] [CrossRef]
- Carr, B.J.; Hawking, S. Black holes in the early Universe. Mon. Not. Roy. Astron. Soc. 1974, 168, 399–415. [Google Scholar] [CrossRef]
- Carr, B.J. The Primordial black hole mass spectrum. Astrophys. J. 1975, 201, 1–19. [Google Scholar] [CrossRef]
- Carr, B.; Kuhnel, F. Primordial black holes as dark matter candidates. SciPost Phys. Lect. Notes 2022, 48, 1. [Google Scholar] [CrossRef]
- Carr, B.; Kuhnel, F. Primordial Black Holes as Dark Matter: Recent Developments. Ann. Rev. Nucl. Part. Sci. 2020, 70, 355–394. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [LIGO Scientific Collaboration and Virgo Collaboration]. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [LIGO Scientific Collaboration and Virgo Collaboration]. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P. et al. [LIGO Scientific Collaboration and Virgo Collaboration]. Binary Black Hole Mergers in the first Advanced LIGO Observing Run. Phys. Rev. X 2016, 6, 041015. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [LIGO Scientific Collaboration and Virgo Collaboration]. The basic physics of the binary black hole merger GW150914. Annalen Phys. 2017, 529, 1600209. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [LIGO Scientific Collaboration and Virgo Collaboration]. GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2. Phys. Rev. Lett. 2017, 118, 221101. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [LIGO Scientific Collaboration and Virgo Collaboration]. GW170608: Observation of a 19-solar-mass Binary Black Hole Coalescence. Astrophys. J. Lett. 2017, 851, L35. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [LIGO Scientific Collaboration and Virgo Collaboration]. GW170814: A Three-Detector Observation of Gravitational Waves from a Binary Black Hole Coalescence. Phys. Rev. Lett. 2017, 119, 141101. [Google Scholar] [CrossRef] [PubMed]
- Fernandez, N.; Profumo, S. Unraveling the origin of black holes from effective spin measurements with LIGO-Virgo. JCAP 2019, 08, 022. [Google Scholar] [CrossRef]
- Carr, B.; Kohri, K.; Sendouda, Y.; Yokoyama, J. Constraints on Primordial Black Holes. Rep. Prog. Phys. 2020, 84, 116902. [Google Scholar] [CrossRef] [PubMed]
- Green, A.M.; Kavanagh, B.J. Primordial Black Holes as a dark matter candidate. J. Phys. G 2021, 48, 043001. [Google Scholar] [CrossRef]
- Green, A.M. Primordial Black Holes: Sirens of the early Universe. Fundam. Theor. Phys. 2015, 178, 129–149. [Google Scholar] [CrossRef]
- Young, S.; Byrnes, C.T.; Sasaki, M. Calculating the mass fraction of primordial black holes. JCAP 2014, 7, 45. [Google Scholar] [CrossRef]
- Bloomfield, J.; Bulhosa, D.; Face, S. Formalism for Primordial Black Hole Formation in Spherical Symmetry. arXiv 2015, arXiv:1504.02071. [Google Scholar]
- Kühnel, F.; Rampf, C.; Sandstad, M. Effects of Critical Collapse on Primordial Black-Hole Mass Spectra. Eur. Phys. J. C 2016, 76, 93. [Google Scholar] [CrossRef]
- Georg, J.; Şengör, G.; Watson, S. Nonthermal WIMPs and primordial black holes. Phys. Rev. D 2016, 93, 123523. [Google Scholar] [CrossRef]
- Young, S. Constraining the Early Universe with Primordial Black Holes. Ph.D. Thesis, Sussex University, Brighton, UK, 2016. [Google Scholar]
- Young, S.; Musco, I.; Byrnes, C.T. Primordial black hole formation and abundance: Contribution from the nonlinear relation between the density and curvature perturbation. JCAP 2019, 11, 012. [Google Scholar] [CrossRef]
- Villanueva-Domingo, P.; Mena, O.; Palomares-Ruiz, S. A brief review on primordial black holes as dark matter. Front. Astron. Space Sci. 2021, 8, 87. [Google Scholar] [CrossRef]
- Gow, A.D. A History of the Universe in Primordial Black Holes. Ph.D. Thesis, Sussex University, Brighton, UK, 2021. [Google Scholar]
- Ivanov, P.; Naselsky, P.; Novikov, I. Inflation and primordial black holes as dark matter. Phys. Rev. D 1994, 50, 7173–7178. [Google Scholar] [CrossRef] [PubMed]
- Yokoyama, J. Chaotic new inflation and formation of primordial black holes. Phys. Rev. D 1998, 58, 083510. [Google Scholar] [CrossRef]
- Garcia-Bellido, J.; Ruiz Morales, E. Primordial black holes from single field models of inflation. Phys. Dark Univ. 2017, 18, 47–54. [Google Scholar] [CrossRef]
- Ballesteros, G.; Taoso, M. Primordial black hole dark matter from single field inflation. Phys. Rev. D 2018, 97, 023501. [Google Scholar] [CrossRef]
- Hertzberg, M.P.; Yamada, M. Primordial Black Holes from Polynomial Potentials in Single Field Inflation. Phys. Rev. D 2018, 97, 083509. [Google Scholar] [CrossRef]
- Kinney, W.H. Horizon crossing and inflation with large eta. Phys. Rev. D 2005, 72, 023515. [Google Scholar] [CrossRef]
- Germani, C.; Prokopec, T. On primordial black holes from an inflection point. Phys. Dark Univ. 2017, 18, 6–10. [Google Scholar] [CrossRef]
- Pattison, C.; Vennin, V.; Assadullahi, H.; Wands, D. Quantum diffusion during inflation and primordial black holes. JCAP 2017, 10, 046. [Google Scholar] [CrossRef]
- Ezquiaga, J.M.; García-Bellido, J. Quantum diffusion beyond slow-roll: Implications for primordial black-hole production. JCAP 2018, 8, 18. [Google Scholar] [CrossRef]
- Biagetti, M.; Franciolini, G.; Kehagias, A.; Riotto, A. Primordial Black Holes from Inflation and Quantum Diffusion. JCAP 2018, 7, 32. [Google Scholar] [CrossRef]
- Stewart, E.D. Flattening the inflaton’s potential with quantum corrections. 2. Phys. Rev. D 1997, 56, 2019–2023. [Google Scholar] [CrossRef]
- Kohri, K.; Lyth, D.H.; Melchiorri, A. Black hole formation and slow-roll inflation. JCAP 2008, 4, 38. [Google Scholar] [CrossRef]
- Alabidi, L.; Kohri, K. Generating Primordial Black Holes Via Hilltop-Type Inflation Models. Phys. Rev. D 2009, 80, 063511. [Google Scholar] [CrossRef]
- Randall, L.; Soljacic, M.; Guth, A.H. Supernatural inflation: Inflation from supersymmetry with no (very) small parameters. Nucl. Phys. B 1996, 472, 377–408. [Google Scholar] [CrossRef]
- Garcia-Bellido, J.; Linde, A.D.; Wands, D. Density perturbations and black hole formation in hybrid inflation. Phys. Rev. D 1996, 54, 6040–6058. [Google Scholar] [CrossRef] [PubMed]
- Kawasaki, M.; Sugiyama, N.; Yanagida, T. Primordial black hole formation in a double inflation model in supergravity. Phys. Rev. D 1998, 57, 6050–6056. [Google Scholar] [CrossRef]
- Clesse, S.; García-Bellido, J. Massive Primordial Black Holes from Hybrid Inflation as Dark Matter and the seeds of Galaxies. Phys. Rev. D 2015, 92, 023524. [Google Scholar] [CrossRef]
- Lyth, D.H.; Wands, D. Generating the curvature perturbation without an inflaton. Phys. Lett. B 2002, 524, 5–14. [Google Scholar] [CrossRef]
- Kawasaki, M.; Kitajima, N.; Yanagida, T.T. Primordial black hole formation from an axionlike curvaton model. Phys. Rev. D 2013, 87, 063519. [Google Scholar] [CrossRef]
- Kohri, K.; Lin, C.M.; Matsuda, T. Primordial black holes from the inflating curvaton. Phys. Rev. D 2013, 87, 103527. [Google Scholar] [CrossRef]
- Yokoyama, J. Formation of MACHO primordial black holes in inflationary cosmology. Astron. Astrophys. 1997, 318, 673. [Google Scholar]
- Bhattacharya, S.; Zavala, I. Sharp turns in axion monodromy: Primordial black holes and gravitational waves. arXiv 2022, arXiv:2205.06065. [Google Scholar]
- Crawford, M.; Schramm, D.N. Spontaneous Generation of Density Perturbations in the Early Universe. Nature 1982, 298, 538–540. [Google Scholar] [CrossRef]
- Hawking, S.W.; Moss, I.G.; Stewart, J.M. Bubble Collisions in the Very Early Universe. Phys. Rev. D 1982, 26, 2681. [Google Scholar] [CrossRef]
- La, D.; Steinhardt, P.J. Bubble Percolation in Extended Inflationary Models. Phys. Lett. B 1989, 220, 375–378. [Google Scholar] [CrossRef]
- Moss, I.G. Singularity formation from colliding bubbles. Phys. Rev. D 1994, 50, 676–681. [Google Scholar] [CrossRef]
- Konoplich, R.V.; Rubin, S.G.; Sakharov, A.S.; Khlopov, M.Y. Formation of black holes in first-order phase transitions as a cosmological test of symmetry-breaking mechanisms. Phys. Atom. Nucl. 1999, 62, 1593–1600. [Google Scholar]
- Konoplich, R.V.; Rubin, S.G.; Sakharov, A.S.; Khlopov, M.Y. Formation of black holes in first-order phase transitions in the Universe. Astron. Lett. 1998, 24, 413–417. [Google Scholar]
- Sato, K. First Order Phase Transition of a Vacuum and Expansion of the Universe. Mon. Not. Roy. Astron. Soc. 1981, 195, 467–479. [Google Scholar] [CrossRef]
- Guth, A.H. The Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 results. XXV. Searches for cosmic strings and other topological defects. Astron. Astrophys. 2014, 571, A25. [Google Scholar] [CrossRef]
- Blanco-Pillado, J.J.; Olum, K.D.; Siemens, X. New limits on cosmic strings from gravitational wave observation. Phys. Lett. B 2018, 778, 392–396. [Google Scholar] [CrossRef]
- Hawking, S.W. Black Holes From Cosmic Strings. Phys. Lett. B 1989, 231, 237–239. [Google Scholar] [CrossRef]
- Polnarev, A.; Zembowicz, R. Formation of Primordial Black Holes by Cosmic Strings. Phys. Rev. D 1991, 43, 1106–1109. [Google Scholar] [CrossRef]
- Hansen, R.N.; Christensen, M.; Larsen, A.L. Cosmic string loops collapsing to black holes. Int. J. Mod. Phys. A 2000, 15, 4433–4446. [Google Scholar] [CrossRef]
- Hogan, C.J. Massive black holes generated by cosmic strings. Phys. Lett. B 1984, 143, 87–91. [Google Scholar] [CrossRef]
- Nagasawa, M. Primordial black hole formation by stabilized embedded strings in the early universe. Gen. Rel. Grav. 2005, 37, 1635–1649. [Google Scholar] [CrossRef]
- James-Turner, C.; Weil, D.P.B.; Green, A.M.; Copeland, E.J. Constraints on the cosmic string loop collapse fraction from primordial black holes. Phys. Rev. D 2020, 101, 123526. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Allen, B. Cosmological constraints on cosmic string gravitational radiation. Phys. Rev. D 1992, 45, 3447–3468. [Google Scholar] [CrossRef]
- MacGibbon, J.H.; Brandenberger, R.H.; Wichoski, U.F. Limits on black hole formation from cosmic string loops. Phys. Rev. D 1998, 57, 2158–2165. [Google Scholar] [CrossRef]
- Jenkins, A.C.; Sakellariadou, M. Primordial black holes from cusp collapse on cosmic strings. arXiv 2020, arXiv:2006.16249. [Google Scholar]
- Helfer, T.; Aurrekoetxea, J.C.; Lim, E.A. Cosmic String Loop Collapse in Full General Relativity. Phys. Rev. D 2019, 99, 104028. [Google Scholar] [CrossRef]
- Matsuda, T. Primordial black holes from cosmic necklaces. JHEP 2006, 4, 17. [Google Scholar] [CrossRef]
- Lake, M.; Thomas, S.; Ward, J. String Necklaces and Primordial Black Holes from Type IIB Strings. JHEP 2009, 12, 033. [Google Scholar] [CrossRef]
- Rubin, S.G.; Sakharov, A.S.; Khlopov, M.Y. The Formation of primary galactic nuclei during phase transitions in the early universe. J. Exp. Theor. Phys. 2001, 91, 921–929. [Google Scholar] [CrossRef]
- Dokuchaev, V.; Eroshenko, Y.; Rubin, S. Quasars formation around clusters of primordial black holes. Grav. Cosmol. 2005, 11, 99–104. [Google Scholar]
- Khlopov, M.Y.; Konoplich, R.V.; Rubin, S.G.; Sakharov, A.S. First-order phase transitions as a source of black holes in the early universe. Grav. Cosmol. 2000, 6, 153–156. [Google Scholar]
- Ge, S. Sublunar-Mass Primordial Black Holes from Closed Axion Domain Walls. Phys. Dark Univ. 2020, 27, 100440. [Google Scholar] [CrossRef]
- Garriga, J.; Vilenkin, A.; Zhang, J. Black holes and the multiverse. JCAP 2016, 2, 64. [Google Scholar] [CrossRef]
- Deng, H.; Garriga, J.; Vilenkin, A. Primordial black hole and wormhole formation by domain walls. JCAP 2017, 4, 50. [Google Scholar] [CrossRef]
- Deng, H.; Vilenkin, A. Primordial black hole formation by vacuum bubbles. JCAP 2017, 12, 044. [Google Scholar] [CrossRef]
- Liu, J.; Guo, Z.K.; Cai, R.G. Primordial Black Holes from Cosmic Domain Walls. Phys. Rev. D 2020, 101, 023513. [Google Scholar] [CrossRef]
- Kopp, M.; Hofmann, S.; Weller, J. Separate Universes Do Not Constrain Primordial Black Hole Formation. Phys. Rev. D 2011, 83, 124025. [Google Scholar] [CrossRef]
- Harada, T.; Carr, B.J. Upper limits on the size of a primordial black hole. Phys. Rev. D 2005, 71, 104009. [Google Scholar] [CrossRef]
- Cotner, E.; Kusenko, A. Primordial black holes from supersymmetry in the early universe. Phys. Rev. Lett. 2017, 119, 031103. [Google Scholar] [CrossRef] [PubMed]
- Cotner, E.; Kusenko, A. Primordial black holes from scalar field evolution in the early universe. Phys. Rev. D 2017, 96, 103002. [Google Scholar] [CrossRef]
- Cotner, E.; Kusenko, A.; Takhistov, V. Primordial Black Holes from Inflaton Fragmentation into Oscillons. Phys. Rev. D 2018, 98, 083513. [Google Scholar] [CrossRef]
- Cotner, E.; Kusenko, A.; Sasaki, M.; Takhistov, V. Analytic Description of Primordial Black Hole Formation from Scalar Field Fragmentation. JCAP 2019, 10, 077. [Google Scholar] [CrossRef]
- Bassett, B.A.; Tsujikawa, S.; Wands, D. Inflation dynamics and reheating. Rev. Mod. Phys. 2006, 78, 537–589. [Google Scholar] [CrossRef]
- Frolov, A.V. Nonlinear Dynamics and Primordial Curvature Perturbations from Preheating. Class. Quant. Grav. 2010, 27, 124006. [Google Scholar] [CrossRef]
- Allahverdi, R.; Brandenberger, R.; Cyr-Racine, F.Y.; Mazumdar, A. Reheating in Inflationary Cosmology: Theory and Applications. Ann. Rev. Nucl. Part. Sci. 2010, 60, 27–51. [Google Scholar] [CrossRef]
- Amin, M.A.; Hertzberg, M.P.; Kaiser, D.I.; Karouby, J. Nonperturbative Dynamics Of Reheating After Inflation: A Review. Int. J. Mod. Phys. D 2014, 24, 1530003. [Google Scholar] [CrossRef]
- Lozanov, K.D. Lectures on Reheating after Inflation. arXiv 2019, arXiv:1907.04402. [Google Scholar]
- Allahverdi, R.; Amin, M.A.; Berlin, A.; Bernal, N.; Byrnes, C.T.; Delos, M.S.; Erickcek, A.L.; Escudero, M.; Figueroa, D.G.; Freese, K.; et al. The First Three Seconds: A Review of Possible Expansion Histories of the Early Universe. arXiv 2020, arXiv:2006.16182. [Google Scholar] [CrossRef]
- Carr, B.; Dimopoulos, K.; Owen, C.; Tenkanen, T. Primordial Black Hole Formation During Slow Reheating After Inflation. Phys. Rev. 2018, D97, 123535. [Google Scholar] [CrossRef]
- Hawking, S. Black hole explosions. Nature 1974, 248, 30–31. [Google Scholar] [CrossRef]
- Churazov, E.; Sazonov, S.; Tsygankov, S.; Sunyaev, R.; Varshalovich, D. Positron annihilation spectrum from the Galactic Centre region observed by SPI/INTEGRAL, revisited: Annihilation in a cooling ISM? Mon. Not. Roy. Astron. Soc. 2011, 411, 1727. [Google Scholar] [CrossRef]
- Siegert, T.; Diehl, R.; Vincent, A.C.; Guglielmetti, F.; Krause, M.G.; Boehm, C. Search for 511 keV Emission in Satellite Galaxies of the Milky Way with INTEGRAL/SPI. Astron. Astrophys. 2016, 595, A25. [Google Scholar] [CrossRef]
- Laha, R. Primordial Black Holes as a Dark Matter Candidate Are Severely Constrained by the Galactic Center 511 keV γ-Ray Line. Phys. Rev. Lett. 2019, 123, 251101. [Google Scholar] [CrossRef] [PubMed]
- Bays, K.; Iida, T.; Abe, K.; Hayato, Y.; Iyogi, K.; Kameda, J.; Koshio, Y.; Marti, L.; Miura, M.; Moriyama, S.; et al. Supernova Relic Neutrino Search at Super-Kamiokande. Phys. Rev. D 2012, 85, 052007. [Google Scholar] [CrossRef]
- Gando, A. et al. [The Super-Kamiokande Collaboration]. A study of extraterrestrial antineutrino sources with the KamLAND detector. Astrophys. J. 2012, 745, 193. [Google Scholar] [CrossRef]
- Agostini, M.; Altenmüller, K.; Appel, S.; Atroshchenko, V.; Bagdasarian, Z.; Basilico, D.; Bellini, G.; Benziger, J.; Bick, D.; Bonfini, G.; et al. Search for low-energy neutrinos from astrophysical sources with Borexino. Astropart. Phys. 2021, 125, 102509. [Google Scholar] [CrossRef]
- Dasgupta, B.; Laha, R.; Ray, A. Neutrino and positron constraints on spinning primordial black hole dark matter. Phys. Rev. Lett. 2020, 125, 101101. [Google Scholar] [CrossRef]
- Laha, R.; Muñoz, J.B.; Slatyer, T.R. INTEGRAL constraints on primordial black holes and particle dark matter. Phys. Rev. D 2020, 101, 123514. [Google Scholar] [CrossRef]
- Acharya, S.K.; Khatri, R. CMB and BBN constraints on evaporating primordial black holes revisited. JCAP 2020, 6, 18. [Google Scholar] [CrossRef]
- Smyth, N.; Profumo, S.; English, S.; Jeltema, T.; McKinnon, K.; Guhathakurta, P. Updated Constraints on Asteroid-Mass Primordial Black Holes as Dark Matter. Phys. Rev. D 2020, 101, 063005. [Google Scholar] [CrossRef]
- Tisserand, P. et al. [The EROS-2 Collaboration]. Limits on the Macho Content of the Galactic Halo from the EROS-2 Survey of the Magellanic Clouds. Astron. Astrophys. 2007, 469, 387–404. [Google Scholar] [CrossRef]
- Niikura, H.; Takada, M.; Yasuda, N.; Lupton, R.H.; Sumi, T.; More, S.; Kurita, T.; Sugiyama, S.; More, A.; Oguri, M.; et al. Microlensing constraints on primordial black holes with Subaru/HSC Andromeda observations. Nature Astron. 2019, 3, 524–534. [Google Scholar] [CrossRef]
- Niikura, H.; Takada, M.; Yokoyama, S.; Sumi, T.; Masaki, S. Constraints on Earth-mass primordial black holes from OGLE 5-year microlensing events. Phys. Rev. D 2019, 99, 083503. [Google Scholar] [CrossRef]
- Oguri, M.; Diego, J.M.; Kaiser, N.; Kelly, P.L.; Broadhurst, T. Understanding caustic crossings in giant arcs: Characteristic scales, event rates, and constraints on compact dark matter. Phys. Rev. D 2018, 97, 023518. [Google Scholar] [CrossRef]
- Ali-Haïmoud, Y.; Kovetz, E.D.; Kamionkowski, M. Merger rate of primordial black-hole binaries. Phys. Rev. 2017, D96, 123523. [Google Scholar] [CrossRef]
- Bird, S.; Cholis, I.; Muñoz, J.B.; Ali-Haïmoud, Y.; Kamionkowski, M.; Kovetz, E.D.; Raccanelli, A.; Riess, A.G. Did LIGO detect dark matter? Phys. Rev. Lett. 2016, 116, 201301. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, M.; Suyama, T.; Tanaka, T.; Yokoyama, S. Primordial Black Hole Scenario for the Gravitational-Wave Event GW150914. Phys. Rev. Lett. 2016, 117, 061101. [Google Scholar] [CrossRef]
- Cholis, I.; Kovetz, E.D.; Ali-Haïmoud, Y.; Bird, S.; Kamionkowski, M.; Muñoz, J.B.; Raccanelli, A. Orbital eccentricities in primordial black hole binaries. Phys. Rev. D 2016, 94, 084013. [Google Scholar] [CrossRef]
- Clesse, S.; García-Bellido, J. The clustering of massive Primordial Black Holes as Dark Matter: Measuring their mass distribution with Advanced LIGO. Phys. Dark Univ. 2017, 15, 142–147. [Google Scholar] [CrossRef]
- Raccanelli, A.; Kovetz, E.D.; Bird, S.; Cholis, I.; Munoz, J.B. Determining the progenitors of merging black-hole binaries. Phys. Rev. D 2016, 94, 023516. [Google Scholar] [CrossRef]
- Kovetz, E.D. Probing Primordial-Black-Hole Dark Matter with Gravitational Waves. Phys. Rev. Lett. 2017, 119, 131301. [Google Scholar] [CrossRef]
- Abbott, B. et al. [The LIGO Scientific Collaboration]. Search for Subsolar Mass Ultracompact Binaries in Advanced LIGO’s Second Observing Run. Phys. Rev. Lett. 2019, 123, 161102. [Google Scholar] [CrossRef]
- Kavanagh, B.J.; Gaggero, D.; Bertone, G. Merger rate of a subdominant population of primordial black holes. Phys. Rev. D 2018, 98, 023536. [Google Scholar] [CrossRef]
- De Luca, V.; Franciolini, G.; Pani, P.; Riotto, A. Primordial Black Holes Confront LIGO/Virgo data: Current situation. JCAP 2020, 06, 044. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Y.F.; Huang, Q.G.; Li, T.G.F. Constraints on the Primordial Black Hole Abundance from the First Advanced LIGO Observation Run Using the Stochastic Gravitational-Wave Background. Phys. Rev. Lett. 2018, 120, 191102. [Google Scholar] [CrossRef]
- Carr, B. Pregalactic black hole accretion and the thermal history of the universe. Mon. Not. R. Astron. Soc. 1981, 194, 639–668. [Google Scholar] [CrossRef]
- Ricotti, M.; Ostriker, J.P.; Mack, K.J. Effect of Primordial Black Holes on the Cosmic Microwave Background and Cosmological Parameter Estimates. Astrophys. J. 2008, 680, 829. [Google Scholar] [CrossRef]
- Serpico, P.D.; Poulin, V.; Inman, D.; Kohri, K. Cosmic microwave background bounds on primordial black holes including dark matter halo accretion. Phys. Rev. Res. 2020, 2, 023204. [Google Scholar] [CrossRef]
- Kavanagh, B.J. bradkav/PBHbounds: Release Version. 2019. Available online: https://zenodo.org/record/3538999#.Y-yrbOzMLAM (accessed on 26 January 2023). [CrossRef]
- Capela, F.; Pshirkov, M.; Tinyakov, P. Constraints on primordial black holes as dark matter candidates from capture by neutron stars. Phys. Rev. D 2013, 87, 123524. [Google Scholar] [CrossRef]
- Graham, P.W.; Rajendran, S.; Varela, J. Dark Matter Triggers of Supernovae. Phys. Rev. D 2015, 92, 063007. [Google Scholar] [CrossRef]
- Amaro-Seoane, P.; Audley, H.; Babak, S.; Baker, J.; Barausse, E.; Bender, P.; Berti, E.; Binetruy, P.; Born, M.; Bortoluzzi, D.; et al. Laser Interferometer Space Antenna. arXiv 2017, arXiv:1702.00786. [Google Scholar]
- Kaiser, A.R.; McWilliams, S.T. Sensitivity of present and future detectors across the black-hole binary gravitational wave spectrum. Class. Quant. Grav. 2021, 38, 055009. [Google Scholar] [CrossRef]
- Barausse, E.; Berti, E.; Hertog, T.; Hughes, S.A.; Jetzer, P.; Pani, P.; Sotiriou, T.P.; Tamanini, N.; Witek, H.; Yagi, K.; et al. Prospects for Fundamental Physics with LISA. Gen. Rel. Grav. 2020, 52, 81. [Google Scholar] [CrossRef]
- Bartolo, N.; Bertacca, D.; Caldwell, R.; Contaldi, C.R.; Cusin, G.; De Luca, V.; Dimastrogiovanni, E.; Fasiello, M.; Figueroa, D.G.; Franciolini, G. Probing Anisotropies of the Stochastic Gravitational Wave Background with LISA. J. Cosmol. Astropart. Phys. 2022, 2022, 9. [Google Scholar] [CrossRef]
- Seto, N.; Kawamura, S.; Nakamura, T. Possibility of direct measurement of the acceleration of the universe using 0.1-Hz band laser interferometer gravitational wave antenna in space. Phys. Rev. Lett. 2001, 87, 221103. [Google Scholar] [CrossRef] [PubMed]
- Yagi, K.; Seto, N. Detector configuration of DECIGO/BBO and identification of cosmological neutron-star binaries. Phys. Rev. D 2011, 83, 044011. [Google Scholar] [CrossRef]
- Kawamura, S.; Ando, M.; Seto, N.; Sato, S.; Musha, M.; Kawano, I.; Yokoyama, J.; Tanaka, T.; Ioka, K.; Akutsu, T.; et al. Current status of space gravitational wave antenna DECIGO and B-DECIGO. PTEP 2021, 2021, 05A105. [Google Scholar] [CrossRef]
- Lehmann, B.V.; Profumo, S.; Yant, J. The Maximal-Density Mass Function for Primordial Black Hole Dark Matter. JCAP 2018, 4, 7. [Google Scholar] [CrossRef]
- Griest, K.; Cieplak, A.M.; Lehner, M.J. Experimental Limits on Primordial Black Hole Dark Matter from the First 2 yr of Kepler Data. Astrophys. J. 2014, 786, 158. [Google Scholar] [CrossRef]
- Allsman, R.A. et al. [The Macho Collaboration]. MACHO project limits on black hole dark matter in the 1–30 solar mass range. Astrophys. J. Lett. 2001, 550, L169. [Google Scholar] [CrossRef]
- Brandt, T.D. Constraints on MACHO Dark Matter from Compact Stellar Systems in Ultra-Faint Dwarf Galaxies. Astrophys. J. Lett. 2016, 824, L31. [Google Scholar] [CrossRef]
- Ali-Haïmoud, Y.; Kamionkowski, M. Cosmic microwave background limits on accreting primordial black holes. Phys. Rev. D 2017, 95, 043534. [Google Scholar] [CrossRef]
- Carr, B.; Raidal, M.; Tenkanen, T.; Vaskonen, V.; Veermäe, H. Primordial black hole constraints for extended mass functions. Phys. Rev. D 2017, 96, 023514. [Google Scholar] [CrossRef]
- Young, S.; Byrnes, C.T. Primordial black holes in non-Gaussian regimes. J. Cosmol. Astropart. Phys. 2013, 2013, 52. [Google Scholar] [CrossRef]
- Young, S.; Regan, D.; Byrnes, C.T. Influence of large local and non-local bispectra on primordial black hole abundance. J. Cosmol. Astropart. Phys. 2016, 2016, 29. [Google Scholar] [CrossRef]
- Franciolini, G.; Kehagias, A.; Matarrese, S.; Riotto, A. Primordial black holes from inflation and non-Gaussianity. J. Cosmol. Astropart. Phys. 2018, 2018, 16. [Google Scholar] [CrossRef]
- Luca, V.D.; Franciolini, G.; Kehagias, A.; Peloso, M.; Riotto, A.; Ünal, C. The ineludible non-Gaussianity of the primordial black hole abundance. J. Cosmol. Astropart. Phys. 2019, 2019, 48. [Google Scholar] [CrossRef]
- Yoo, C.M.; Gong, J.O.; Yokoyama, S. Abundance of primordial black holes with local non-Gaussianity in peak theory. J. Cosmol. Astropart. Phys. 2019, 2019, 33. [Google Scholar] [CrossRef]
- Kehagias, A.; Musco, I.; Riotto, A. Non-Gaussian formation of primordial black holes: Effects on the threshold. J. Cosmol. Astropart. Phys. 2019, 2019, 29. [Google Scholar] [CrossRef]
- Akrami, Y. et al. [Planck Collaboration]. Planck 2018 results. X. Constraints on inflation. Astron. Astrophys. 2020, 641, A10. [Google Scholar] [CrossRef]
- Aghanim, N. et al. [Planck Collaboration]. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Flauger, R.; McAllister, L.; Pajer, E.; Westphal, A.; Xu, G. Oscillations in the CMB from Axion Monodromy Inflation. JCAP 2010, 6, 9. [Google Scholar] [CrossRef]
- Flauger, R.; McAllister, L.; Silverstein, E.; Westphal, A. Drifting Oscillations in Axion Monodromy. JCAP 2017, 10, 55. [Google Scholar] [CrossRef]
- Gao, X.; Gong, J.O. Towards general patterns of features in multi-field inflation. JHEP 2015, 8, 115. [Google Scholar] [CrossRef]
- Fumagalli, J.; Renaux-Petel, S.; Ronayne, J.W.; Witkowski, L.T. Turning in the landscape: A new mechanism for generating Primordial Black Holes. arXiv 2020, arXiv:2004.08369. [Google Scholar]
- Fumagalli, J.; Renaux-Petel, S.; Witkowski, L.T. Oscillations in the stochastic gravitational wave background from sharp features and particle production during inflation. JCAP 2021, 8, 30. [Google Scholar] [CrossRef]
- Braglia, M.; Chen, X.; Hazra, D.K. Probing Primordial Features with the Stochastic Gravitational Wave Background. arXiv 2020, arXiv:2012.05821. [Google Scholar] [CrossRef]
- Fumagalli, J.; Renaux-Petel, S.E.; Witkowski, L.T. Resonant features in the stochastic gravitational wave background. JCAP 2021, 8, 59. [Google Scholar] [CrossRef]
- Fumagalli, J.; Pieroni, M.; Renaux-Petel, S.; Witkowski, L.T. Detecting primordial features with LISA. JCAP 2022, 7, 20. [Google Scholar] [CrossRef]
- Ananda, K.N.; Clarkson, C.; Wands, D. The Cosmological gravitational wave background from primordial density perturbations. Phys. Rev. D 2007, 75, 123518. [Google Scholar] [CrossRef]
- Baumann, D.; Steinhardt, P.J.; Takahashi, K.; Ichiki, K. Gravitational Wave Spectrum Induced by Primordial Scalar Perturbations. Phys. Rev. D 2007, 76, 084019. [Google Scholar] [CrossRef]
- Kohri, K.; Terada, T. Semianalytic calculation of gravitational wave spectrum nonlinearly induced from primordial curvature perturbations. Phys. Rev. D 2018, 97, 123532. [Google Scholar] [CrossRef]
- Espinosa, J.R.; Racco, D.; Riotto, A. A Cosmological Signature of the SM Higgs Instability: Gravitational Waves. JCAP 2018, 9, 12. [Google Scholar] [CrossRef]
- Domènech, G. Scalar Induced Gravitational Waves Review. Universe 2021, 7, 398. [Google Scholar] [CrossRef]
- Aggarwal, K.; Arzoumanian, Z.; Baker, P.T.; Brazier, A.; Brinson, M.R.; Brook, P.R.; Burke-Spolaor, S.; Chatterjee, S.; Cordes, J.M.; Cornish, N.J.; et al. The NANOGrav 11-Year Data Set: Limits on Gravitational Waves from Individual Supermassive Black Hole Binaries. Astrophys. J. 2019, 880, 2. [Google Scholar] [CrossRef]
- Arzoumanian, Z. et al. [ The NANOGrav Collaboration]. The NANOGrav 12.5 yr Data Set: Search for an Isotropic Stochastic Gravitational-wave Background. Astrophys. J. Lett. 2020, 905, L34. [Google Scholar] [CrossRef]
- Lentati, L.; Taylor, S.R.; Mingarelli, C.M.F.; Sesana, A.; Sanidas, S.A.; Vecchio, A.; Caballero, R.N.; Lee, K.J.; van Haasteren, R.; Babak, S.; et al. European Pulsar Timing Array Limits On An Isotropic Stochastic Gravitational-Wave Background. Mon. Not. Roy. Astron. Soc. 2015, 453, 2576–2598. [Google Scholar] [CrossRef]
- Shannon, R.M.; Ravi, V.; Lentati, L.T.; Lasky, P.D.; Hobbs, G.; Kerr, M.; Manchester, R.N.; Coles, W.A.; Levin, Y.; Bailes, M.; et al. Gravitational waves from binary supermassive black holes missing in pulsar observations. Science 2015, 349, 1522–1525. [Google Scholar] [CrossRef]
- Qin, W.; Boddy, K.K.; Kamionkowski, M.; Dai, L. Pulsar-timing arrays, astrometry, and gravitational waves. Phys. Rev. D 2019, 99, 063002. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [LIGO Scientific Collaboration and Virgo Collaboration]. Search for the isotropic stochastic background using data from Advanced LIGO’s second observing run. Phys. Rev. D 2019, 100, 061101. [Google Scholar] [CrossRef]
- Akutsu, T. Large-scale cryogenic gravitational-wave telescope in Japan: KAGRA. J. Phys. Conf. Ser. 2015, 610, 012016. [Google Scholar] [CrossRef]
- Haino, S.K. Underground Cryogenic Gravitational Wave Telescope. In Proceedings of the 28th International Symposium on Lepton Photon Interactions at High Energies (LP17), Guangzhou, China, 7–12 August 2017; Wang, W., Xing, Z.z., Eds.; WSP: Singapore, 2020; pp. 174–184. [Google Scholar] [CrossRef]
- Maggiore, M.; van den Broeck, C.; Bartolo, N.; Belgacem, E.; Bertacca, D.; Bizouard, M.A.; Branchesi, M.; Clesse, S.; Foffa, S.; García-Bellido, J.; et al. Science Case for the Einstein Telescope. JCAP 2020, 3, 50. [Google Scholar] [CrossRef]
- Badurina, L.; Bentine, E.; Blas, D.; Bongs, K.; Bortoletto, D.; Bowcock, T.; Bridges, K.; Bowden, W.; Buchmueller, O.; Burrage, C.; et al. AION: An Atom Interferometer Observatory and Network. JCAP 2020, 05, 11. [Google Scholar] [CrossRef]
- Ruan, W.H.; Guo, Z.K.; Cai, R.G.; Zhang, Y.Z. Taiji program: Gravitational-wave sources. Int. J. Mod. Phys. A 2020, 35, 2050075. [Google Scholar] [CrossRef]
- Luo, J.; Chen, L.S.; Duan, H.Z.; Gong, Y.G.; Hu, S.; Ji, J.; Liu, Q.; Mei, J.; Milyukov, V.; Sazhin, M.; et al. TianQin: A space-borne gravitational wave detector. Class. Quant. Grav. 2016, 33, 035010. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Mohanty, S.; Parashari, P. Primordial black holes and gravitational waves in nonstandard cosmologies. Phys. Rev. D 2020, 102, 043522. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Mohanty, S.; Parashari, P. Implications of the NANOGrav result on primordial gravitational waves in nonstandard cosmologies. Phys. Rev. D 2021, 103, 063532. [Google Scholar] [CrossRef]
- Dolgov, A.D.; Kirilova, D.P. On particle creation by a time dependent scalar field. Sov. J. Nucl. Phys. 1990, 51, 172–177. [Google Scholar]
- Traschen, J.H.; Brandenberger, R.H. Particle production during out-of-equilibrium phase transitions. Phys. Rev. D 1990, 42, 2491–2504. [Google Scholar] [CrossRef] [PubMed]
- Turner, M.S. Coherent scalar-field oscillations in an expanding universe. Phys. Rev. D 1983, 28, 1243–1247. [Google Scholar] [CrossRef]
- Kofman, L.; Linde, A.D.; Starobinsky, A.A. Reheating after inflation. Phys. Rev. Lett. 1994, 73, 3195–3198. [Google Scholar] [CrossRef] [PubMed]
- Shtanov, Y.; Traschen, J.H.; Brandenberger, R.H. Universe reheating after inflation. Phys. Rev. D 1995, 51, 5438–5455. [Google Scholar] [CrossRef] [PubMed]
- Kofman, L.; Linde, A.D.; Starobinsky, A.A. Towards the theory of reheating after inflation. Phys. Rev. D 1997, 56, 3258–3295. [Google Scholar] [CrossRef]
- Amin, M.A. Inflaton fragmentation: Emergence of pseudo-stable inflaton lumps (oscillons) after inflation. arXiv 2010, arXiv:1006.3075. [Google Scholar]
- Amin, M.A.; Easther, R.; Finkel, H. Inflaton Fragmentation and Oscillon Formation in Three Dimensions. JCAP 2010, 12, 001. [Google Scholar] [CrossRef]
- Amin, M.A.; Easther, R.; Finkel, H.; Flauger, R.; Hertzberg, M.P. Oscillons After Inflation. Phys. Rev. Lett. 2012, 108, 241302. [Google Scholar] [CrossRef] [PubMed]
- Gleiser, M.; Graham, N.; Stamatopoulos, N. Generation of Coherent Structures After Cosmic Inflation. Phys. Rev. D 2011, 83, 096010. [Google Scholar] [CrossRef]
- Lozanov, K.D.; Amin, M.A. Self-resonance after inflation: Oscillons, transients and radiation domination. Phys. Rev. D 2018, 97, 023533. [Google Scholar] [CrossRef]
- Hong, J.P.; Kawasaki, M.; Yamazaki, M. Oscillons from Pure Natural Inflation. Phys. Rev. D 2018, 98, 043531. [Google Scholar] [CrossRef]
- Fukunaga, H.; Kitajima, N.; Urakawa, Y. Efficient self-resonance instability from axions. JCAP 2019, 06, 055. [Google Scholar] [CrossRef]
- Gleiser, M. Pseudostable bubbles. Phys. Rev. D 1994, 49, 2978–2981. [Google Scholar] [CrossRef]
- Copeland, E.J.; Gleiser, M.; Muller, H.R. Oscillons: Resonant configurations during bubble collapse. Phys. Rev. D 1995, 52, 1920–1933. [Google Scholar] [CrossRef]
- Kasuya, S.; Kawasaki, M.; Takahashi, F. I-balls. Phys. Lett. B 2003, 559, 99–106. [Google Scholar] [CrossRef]
- Hindmarsh, M.; Salmi, P. Numerical investigations of oscillons in 2 dimensions. Phys. Rev. D 2006, 74, 105005. [Google Scholar] [CrossRef]
- Amin, M.A.; Shirokoff, D. Flat-top oscillons in an expanding universe. Phys. Rev. D 2010, 81, 085045. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Amin, M.A.; Copeland, E.J.; Saffin, P.M.; Lozanov, K.D. Classical Decay Rates of Oscillons. JCAP 2020, 07, 055. [Google Scholar] [CrossRef]
- Lozanov, K.D.; Amin, M.A. Equation of State and Duration to Radiation Domination after Inflation. Phys. Rev. Lett. 2017, 119, 061301. [Google Scholar] [CrossRef]
- Berera, A. Warm inflation. Phys. Rev. Lett. 1995, 75, 3218–3221. [Google Scholar] [CrossRef]
- Berera, A.; Moss, I.G.; Ramos, R.O. Warm Inflation and its Microphysical Basis. Rept. Prog. Phys. 2009, 72, 026901. [Google Scholar] [CrossRef]
- Vilenkin, A.; Ford, L.H. Gravitational Effects upon Cosmological Phase Transitions. Phys. Rev. D 1982, 26, 1231. [Google Scholar] [CrossRef]
- Coughlan, G.D.; Fischler, W.; Kolb, E.W.; Raby, S.; Ross, G.G. Cosmological Problems for the Polonyi Potential. Phys. Lett. B 1983, 131, 59–64. [Google Scholar] [CrossRef]
- Starobinsky, A.A.; Yokoyama, J. Equilibrium state of a selfinteracting scalar field in the De Sitter background. Phys. Rev. D 1994, 50, 6357–6368. [Google Scholar] [CrossRef]
- Dine, M.; Randall, L.; Thomas, S.D. Supersymmetry breaking in the early universe. Phys. Rev. Lett. 1995, 75, 398–401. [Google Scholar] [CrossRef]
- Chung, D.J.H.; Kolb, E.W.; Riotto, A. Production of massive particles during reheating. Phys. Rev. D 1999, 60, 063504. [Google Scholar] [CrossRef]
- Kane, G.; Sinha, K.; Watson, S. Cosmological Moduli and the Post-Inflationary Universe: A Critical Review. Int. J. Mod. Phys. D 2015, 24, 1530022. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Vilenkin, A. Quintessential inflation. Phys. Rev. D 1999, 59, 063505. [Google Scholar] [CrossRef]
- Ahmad, S.; De Felice, A.; Jaman, N.; Kuroyanagi, S.; Sami, M. Baryogenesis in the paradigm of quintessential inflation. Phys. Rev. D 2019, 100, 103525. [Google Scholar] [CrossRef]
- Choi, K. String or M theory axion as a quintessence. Phys. Rev. D 2000, 62, 043509. [Google Scholar] [CrossRef]
- Gardner, C.L. Quintessence and the transition to an accelerating universe. Nucl. Phys. B 2005, 707, 278–300. [Google Scholar] [CrossRef]
- D’Eramo, F.; Fernandez, N.; Profumo, S. When the Universe Expands Too Fast: Relentless Dark Matter. JCAP 2017, 05, 012. [Google Scholar] [CrossRef]
- Di Marco, A.; Pradisi, G.; Cabella, P. Inflationary scale, reheating scale, and pre-BBN cosmology with scalar fields. Phys. Rev. D 2018, 98, 123511. [Google Scholar] [CrossRef]
- Okada, N.; Seto, O. Relic density of dark matter in brane world cosmology. Phys. Rev. D 2004, 70, 083531. [Google Scholar] [CrossRef]
- Meehan, M.T.; Whittingham, I.B. Dark matter relic density in Gauss-Bonnet braneworld cosmology. JCAP 2014, 12, 034. [Google Scholar] [CrossRef]
- Catena, R.; Fornengo, N.; Masiero, A.; Pietroni, M.; Rosati, F. Dark matter relic abundance and scalar - tensor dark energy. Phys. Rev. D 2004, 70, 063519. [Google Scholar] [CrossRef]
- Dutta, B.; Jimenez, E.; Zavala, I. Dark Matter Relics and the Expansion Rate in Scalar-Tensor Theories. JCAP 2017, 06, 032. [Google Scholar] [CrossRef]
- Ballesteros, G.; Rey, J.; Taoso, M.; Urbano, A. Primordial black holes as dark matter and gravitational waves from single-field polynomial inflation. JCAP 2020, 07, 025. [Google Scholar] [CrossRef]
- Bhaumik, N.; Jain, R.K. Primordial black holes dark matter from inflection point models of inflation and the effects of reheating. JCAP 2020, 1, 37. [Google Scholar] [CrossRef]
- Gangopadhyay, M.R.; Jain, J.C.; Sharma, D.; Yogesh. Production of primordial black holes via single field inflation and observational constraints. Eur. Phys. J. C 2022, 82, 849. [Google Scholar] [CrossRef]
- Mishra, S.S.; Sahni, V. Primordial Black Holes from a tiny bump/dip in the Inflaton potential. JCAP 2020, 04, 007. [Google Scholar] [CrossRef]
- Zhai, R.; Yu, H.; Wu, P. Growth of power spectrum due to decrease of sound speed during inflation. Phys. Rev. D 2022, 106, 023517. [Google Scholar] [CrossRef]
- Kamenshchik, A.Y.; Tronconi, A.; Vardanyan, T.; Venturi, G. Non-Canonical Inflation and Primordial Black Holes Production. Phys. Lett. B 2019, 791, 201–205. [Google Scholar] [CrossRef]
- Kamenshchik, A.Y.; Tronconi, A.; Venturi, G. DBI inflation and warped black holes. JCAP 2022, 1, 51. [Google Scholar] [CrossRef]
- Gorji, M.A.; Motohashi, H.; Mukohyama, S. Inflation with 0 ≤ c s ≤ 1. JCAP 2022, 2, 30. [Google Scholar] [CrossRef]
- Solbi, M.; Karami, K. Primordial black holes and induced gravitational waves in k-inflation. JCAP 2021, 8, 56. [Google Scholar] [CrossRef]
- Solbi, M.; Karami, K. Primordial black holes formation in the inflationary model with field-dependent kinetic term for quartic and natural potentials. Eur. Phys. J. C 2021, 81, 884. [Google Scholar] [CrossRef]
- Yi, Z. Primordial black holes and scalar-induced gravitational waves from scalar-tensor inflation. arXiv 2022, arXiv:2206.01039. [Google Scholar]
- Heydari, S.; Karami, K. Primordial black holes in nonminimal derivative coupling inflation with quartic potential and reheating consideration. Eur. Phys. J. C 2022, 82, 83. [Google Scholar] [CrossRef]
- Ragavendra, H.V.; Sriramkumar, L.; Silk, J. Could PBHs and secondary GWs have originated from squeezed initial states? JCAP 2021, 5, 10. [Google Scholar] [CrossRef]
- Braglia, M.; Hazra, D.K.; Finelli, F.; Smoot, G.F.; Sriramkumar, L.; Starobinsky, A.A. Generating PBHs and small-scale GWs in two-field models of inflation. JCAP 2020, 8, 001. [Google Scholar] [CrossRef]
- Ashoorioon, A.; Rostami, A.; Firouzjaee, J.T. EFT Compatible PBHs: Effective Spawning of the Seeds for Primordial Black Holes during Inflation. arXiv 2019, arXiv:1912.13326. [Google Scholar] [CrossRef]
- Arya, R. Formation of Primordial Black Holes from Warm Inflation. JCAP 2020, 9, 42. [Google Scholar] [CrossRef]
- Correa, M.; Gangopadhyay, M.R.; Jaman, N.; Mathews, G.J. Primordial black-hole dark matter via warm natural inflation. Phys. Lett. B 2022, 835, 137510. [Google Scholar] [CrossRef]
- Vennin, V. Stochastic inflation and primordial black holes. arXiv 2020, arXiv:2009.08715. [Google Scholar]
- Animali, C.; Vennin, V. Primordial black holes from stochastic tunnelling. arXiv 2022, arXiv:2210.03812. [Google Scholar]
- Ando, K.; Vennin, V. Power spectrum in stochastic inflation. JCAP 2021, 4, 57. [Google Scholar] [CrossRef]
- Niemeyer, J.C.; Jedamzik, K. Near-Critical Gravitational Collapse and the Initial Mass Function of Primordial Black Holes. Phys. Rev. Lett. 1998, 80, 5481–5484. [Google Scholar] [CrossRef]
- Niemeyer, J.C.; Jedamzik, K. Dynamics of primordial black hole formation. Phys. Rev. D 1999, 59. [Google Scholar] [CrossRef]
- Musco, I.; Miller, J.C.; Rezzolla, L. Computations of primordial black-hole formation. Class. Quantum Gravity 2005, 22, 1405–1424. [Google Scholar] [CrossRef]
- Musco, I.; Miller, J.C.; Polnarev, A.G. Primordial black hole formation in the radiative era: Investigation of the critical nature of the collapse. Class. Quantum Gravity 2009, 26, 235001. [Google Scholar] [CrossRef]
- Harada, T.; Yoo, C.M.; Kohri, K.; Nakao, K.i.; Jhingan, S. Primordial black hole formation in the matter-dominated phase of the Universe. Astrophys. J. 2016, 833, 61. [Google Scholar] [CrossRef]
- Kuhnel, F. Enhanced Detectability of Spinning Primordial Black Holes. Eur. Phys. J. C 2020, 80, 243. [Google Scholar] [CrossRef]
- De Luca, V.; Franciolini, G.; Kehagias, A.; Pani, P.; Riotto, A. Primordial black holes in matter-dominated eras: The role of accretion. Phys. Lett. B 2022, 832, 137265. [Google Scholar] [CrossRef]
- Matsubara, T.; Terada, T.; Kohri, K.; Yokoyama, S. Clustering of primordial black holes formed in a matter-dominated epoch. Phys. Rev. D 2019, 100, 123544. [Google Scholar] [CrossRef]
- Yoo, C.M.; Harada, T.; Okawa, H. Threshold of Primordial Black Hole Formation in Nonspherical Collapse. Phys. Rev. D 2020, 102, 043526. [Google Scholar] [CrossRef]
- Kokubu, T.; Kyutoku, K.; Kohri, K.; Harada, T. Effect of Inhomogeneity on Primordial Black Hole Formation in the Matter Dominated Era. Phys. Rev. D 2018, 98, 123024. [Google Scholar] [CrossRef]
- Carr, B.; Tenkanen, T.; Vaskonen, V. Primordial black holes from inflaton and spectator field perturbations in a matter-dominated era. Phys. Rev. 2017, D96, 063507. [Google Scholar] [CrossRef]
- Harada, T.; Yoo, C.M.; Kohri, K.; Nakao, K.I. Spins of primordial black holes formed in the matter-dominated phase of the Universe. Phys. Rev. D 2017, 96, 083517. [Google Scholar] [CrossRef]
- Nakama, T.; Wang, Y. Do we need fine-tuning to create primordial black holes? Phys. Rev. D 2019, 99, 023504. [Google Scholar] [CrossRef]
- Khlopov, M.; Polnarev, A. Primordial black holes as a cosmological test of grand unification. Phys. Lett. B 1980, 97, 383–387. [Google Scholar] [CrossRef]
- Polnarev, A.G.; Khlopov, M.Y. Cosmology, primordial black holes, and supermassive particles. Phys. Usp. 1985, 28, 213–232. [Google Scholar] [CrossRef]
- Nadezhin, D.K.; Novikov, I.D.; Polnarev, A.G. The hydrodynamics of primordial black hole formation. Sov. Astron. 1978, 22, 129–138. [Google Scholar]
- Ballesteros, G.; Rey, J.; Rompineve, F. Detuning primordial black hole dark matter with early matter domination and axion monodromy. JCAP 2020, 6, 14. [Google Scholar] [CrossRef]
- Domènech, G.; Pi, S. NANOGrav hints on planet-mass primordial black holes. Sci. China Phys. Mech. Astron. 2022, 65, 230411. [Google Scholar] [CrossRef]
- Das, S.; Maharana, A.; Muia, F. A faster growth of perturbations in an early matter dominated epoch: Primordial black holes and gravitational waves. Mon. Not. Roy. Astron. Soc. 2022, 515, 13–21. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Das, A.; Dutta, K. Solar mass primordial black holes in moduli dominated universe. JCAP 2021, 10, 071. [Google Scholar] [CrossRef]
- Choi, G.; Schiappacasse, E.D. PBH assisted search for QCD axion dark matter. JCAP 2022, 9, 72. [Google Scholar] [CrossRef]
- Bicknell, G.V.; Henriksen, R.N. Formation of primordial black holes. Astrophys. J. 1979, 232, 670–682. [Google Scholar] [CrossRef]
- Novikov, I.D.; Polnarev, A.G. The Hydrodynamics of Primordial Black Hole Formation—Dependence on the Equation of State. Sov. Astron. 1980, 24, 147–151. [Google Scholar]
- Shibata, M.; Sasaki, M. Black hole formation in the Friedmann universe: Formulation and computation in numerical relativity. Phys. Rev. D 1999, 60, 084002. [Google Scholar] [CrossRef]
- Hawke, I.; Stewart, J.M. The dynamics of primordial black hole formation. Class. Quant. Grav. 2002, 19, 3687–3707. [Google Scholar] [CrossRef]
- Green, A.M.; Liddle, A.R.; Malik, K.A.; Sasaki, M. New calculation of the mass fraction of primordial black holes. Phys. Rev. D 2004, 70, 041502. [Google Scholar] [CrossRef]
- Harada, T.; Yoo, C.M.; Kohri, K. Threshold of primordial black hole formation. Phys. Rev. 2013, D88, 084051. [Google Scholar] [CrossRef]
- Musco, I. Threshold for primordial black holes: Dependence on the shape of the cosmological perturbations. Phys. Rev. D 2019, 100, 123524. [Google Scholar] [CrossRef]
- Kalaja, A.; Bellomo, N.; Bartolo, N.; Bertacca, D.; Matarrese, S.; Musco, I.; Raccanelli, A.; Verde, L. From Primordial Black Holes Abundance to Primordial Curvature Power Spectrum (and back). JCAP 2019, 10, 031. [Google Scholar] [CrossRef]
- Germani, C.; Musco, I. Abundance of Primordial Black Holes Depends on the Shape of the Inflationary Power Spectrum. Phys. Rev. Lett. 2019, 122, 141302. [Google Scholar] [CrossRef] [PubMed]
- Kawasaki, M.; Nakatsuka, H. Effect of nonlinearity between density and curvature perturbations on the primordial black hole formation. Phys. Rev. D 2019, 99. [Google Scholar] [CrossRef]
- Germani, C.; Sheth, R.K. Nonlinear statistics of primordial black holes from Gaussian curvature perturbations. Phys. Rev. D 2020, 101, 063520. [Google Scholar] [CrossRef]
- Young, S.; Musso, M. Application of peaks theory to the abundance of primordial black holes. J. Cosmol. Astropart. Phys. 2020, 2020, 22. [Google Scholar] [CrossRef]
- Kuhnel, F.; Schwarz, D.J. Extreme-Value Distributions and Primordial Black-Hole Formation. arXiv 2021, arXiv:2101.10340. [Google Scholar]
- He, M.; Suyama, T. Formation threshold of rotating primordial black holes. Phys. Rev. D 2019, 100, 063520. [Google Scholar] [CrossRef]
- Suyama, T.; Yokoyama, S. A novel formulation of the primordial black hole mass function. PTEP 2020, 2020, 023E03. [Google Scholar] [CrossRef]
- Young, S. Peaks and primordial black holes: The effect of non-Gaussianity. JCAP 2022, 5, 37. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Bond, J.R.; Kaiser, N.; Szalay, A.S. The Statistics of Peaks of Gaussian Random Fields. Astrophys. J. 1986, 304, 15. [Google Scholar] [CrossRef]
- Yoo, C.M.; Harada, T.; Hirano, S.; Kohri, K. Abundance of Primordial Black Holes in Peak Theory for an Arbitrary Power Spectrum. PTEP 2021, 2021, 013E02. [Google Scholar] [CrossRef]
- Ferrante, G.; Franciolini, G.; Iovino, J.A.; Urbano, A. Primordial non-gaussianity up to all orders: Theoretical aspects and implications for primordial black hole models. arXiv 2022, arXiv:2211.01728. [Google Scholar]
- Padilla, L.E.; Hidalgo, J.C.; Malik, K.A. New mechanism for primordial black hole formation during reheating. Phys. Rev. D 2022, 106, 023519. [Google Scholar] [CrossRef]
- Carrion, K.; Hidalgo, J.C.; Montiel, A.; Padilla, L.E. Complex Scalar Field Reheating and Primordial Black Hole production. JCAP 2021, 07, 001. [Google Scholar] [CrossRef]
- Auclair, P.; Vennin, V. Primordial black holes from metric preheating: Mass fraction in the excursion-set approach. JCAP 2021, 2, 38. [Google Scholar] [CrossRef]
- Martin, J.; Papanikolaou, T.; Vennin, V. Primordial black holes from the preheating instability in single-field inflation. JCAP 2020, 1, 24. [Google Scholar] [CrossRef]
- Papanikolaou, T. Toward the primordial black hole formation threshold in a time-dependent equation-of-state background. Phys. Rev. D 2022, 105, 124055. [Google Scholar] [CrossRef]
- Byrnes, C.T.; Hindmarsh, M.; Young, S.; Hawkins, M.R.S. Primordial black holes with an accurate QCD equation of state. JCAP 2018, 8, 41. [Google Scholar] [CrossRef]
- Carr, B.; Clesse, S.; Garcia-Bellido, J.; Kuhnel, F. Cosmic Conundra Explained by Thermal History and Primordial Black Holes. arXiv 2019, arXiv:1906.08217. [Google Scholar] [CrossRef]
- Escrivà, A.; Germani, C.; Sheth, R.K. Analytical thresholds for black hole formation in general cosmological backgrounds. JCAP 2021, 1, 30. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhattacharya, S. Primordial Black Hole Formation in Non-Standard Post-Inflationary Epochs. Galaxies 2023, 11, 35. https://doi.org/10.3390/galaxies11010035
Bhattacharya S. Primordial Black Hole Formation in Non-Standard Post-Inflationary Epochs. Galaxies. 2023; 11(1):35. https://doi.org/10.3390/galaxies11010035
Chicago/Turabian StyleBhattacharya, Sukannya. 2023. "Primordial Black Hole Formation in Non-Standard Post-Inflationary Epochs" Galaxies 11, no. 1: 35. https://doi.org/10.3390/galaxies11010035
APA StyleBhattacharya, S. (2023). Primordial Black Hole Formation in Non-Standard Post-Inflationary Epochs. Galaxies, 11(1), 35. https://doi.org/10.3390/galaxies11010035






