Next Article in Journal
Astro-COLIBRI 2—An Advanced Platform for Real-Time Multi-Messenger Discoveries
Next Article in Special Issue
Young Radio Sources Expanding in Gas-Rich ISM: Using Cold Molecular Gas to Trace Their Impact
Previous Article in Journal
Acknowledgment to the Reviewers of Galaxies in 2022
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Galaxies
Volume 11
Issue 1
10.3390/galaxies11010021
galaxies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Global Inventory of Feedback

by
Timothy M. Heckman
1,* and
Philip N. Best
2
1
The William H. Miller III Department of Physics and Astronomy, The Johns Hopkins University, Baltimore, MD 21218, USA
2
Institute for Astronomy, University of Edinburgh, Royal Observatory, Blackford Hill, Edinburgh EH9 3HJ, UK
*
Author to whom correspondence should be addressed.
Galaxies 2023, 11(1), 21; https://doi.org/10.3390/galaxies11010021
Submission received: 29 December 2022 / Revised: 16 January 2023 / Accepted: 20 January 2023 / Published: 24 January 2023
(This article belongs to the Special Issue The Symbiosis between Radio Source and Galaxy Evolution)
Browse Figures
Review Reports Versions Notes

Abstract

:
Feedback from both supermassive black holes and massive stars plays a fundamental role in the evolution of galaxies and the inter-galactic medium. In this paper, we use available data to estimate the total amount of kinetic energy and momentum created per co-moving volume element over the history of the universe from three sources: massive stars and supernovae, radiation pressure and winds driven by supermassive black holes, and radio jets driven by supermassive black holes. Kinetic energy and momentum injection from jets peaks at z ≈ 1, while the other two sources peak at z ≈ 2. Massive stars are the dominant global source of momentum injection. For supermassive black holes, we find that the amount of kinetic energy from jets is about an order-of-magnitude larger than that from winds. We also find that the amount of kinetic energy created by massive stars is about 2.5 εstar times that carried by jets (where εstar is the fraction of injected energy not lost to radiative cooling). We discuss the implications of these results for the evolution of galaxies and IGM. Because the ratio of the black hole mass to galaxy mass is a steeply increasing function of mass, we show that the relative importance of black hole feedback to stellar feedback likewise increases with mass. We show that there is a trend in the present-day universe which, in the simplest picture, is consistent with galaxies that have been dominated by black hole feedback being generally quenched, while galaxies that have been dominated by stellar feedback are star-forming. We also note that the amount of kinetic energy carried by jets and winds appears to be sufficient to explain the properties of hot gas in massive halos (>1013 Mʘ).

1. Introduction

The basic properties of galaxies, supermassive black holes, and the intra-group/intra-cluster medium cannot be understood without considering the impact of the return of mass, metals, energy, and momentum from both populations of massive stars (stellar winds and supernovae) and supermassive black holes (winds and jets). Examples include the shape of the stellar mass function, the quenching and subsequent suppression of star-formation in massive galaxies, the mass–metallicity and mass–radius relations, the Kennicutt–Schmidt law of star-formation, and the group/cluster X-ray luminosity–temperature relation (see reviews by [1,2,3]).
This input of energy and momentum from massive stars and black holes is generically referred to as feedback. Even the highest resolution numerical simulations cannot fully include all of the relevant physics ab initio and must rely on “sub-grid physics” (essentially, recipes for processes that cannot be spatially resolved). The same is true for semi-analytic models. This underscores the importance of using observations to inform the choices that are made in simulations and models. While there is now a considerable body of data on feedback from both massive stars and supermassive black holes (e.g., [4,5,6]), we still have a very incomplete understanding of the impact of this feedback on the surrounding gas.
In this paper, we take a different approach from previous investigations of feedback, and try to compile a global inventory (that is, integrated over cosmic time) of the amount of kinetic energy and momentum per co-moving volume element injected by massive stars and supermassive black holes. We then compare the respective importance of these feedback sources as a function of time and of galaxy and black hole mass.

2. Methodology

2.1. Massive Stars

To compute the total amount of kinetic energy injected by massive stars (stellar winds and supernovae) per unit volume, we start with the present-day amount of stellar mass per unit volume. We use the compilation in [7], adjusted to a standard Chabrier Initial Mass Function (IMF—[8]). This value is 3.4 × 108 Mʘ Mpc−3. To compute the corresponding amount of kinetic energy, we need to first correct this to account for stars that were formed but are no longer present. This requires multiplication by 1/(1 − R), where R is the so-called returned fraction, which is 0.3 for a Chabrier IMF. Thus, the total mass of stars formed per unit volume is 4.9 × 108 Mʘ Mpc−3. Starburst99 [9] models for a Chabrier IMF yield a total kinetic energy in stellar winds and supernova ejecta of 6.9 × 1015 erg gm−1. This then gives a value for the kinetic energy density due to stars of Ustar = 6.8 × 1057 erg Mpc−3.
How much of this kinetic energy is available to supply feedback? The stellar ejecta initially carrying the energy collide and their kinetic energy is converted to thermal energy. This hot gas can then expand and flow outward with the thermal energy being converted back into kinetic energy (e.g., [10]). Some of the initial thermal energy can be lost through radiative cooling, so that only a fraction εstar remains to provide feedback. Numerical simulations that represent typical conditions in low-z star-forming galaxies yield εstar ≈ 0.1 [11], with a value that increases with the star-formation rate per unit area (SFR/A). At the much higher values of SFR/A seen in starbursts (e.g., [12]), simulations and models predict a far greater efficiency, with εstar ≈ 0.3 to 1.0 [13,14]. This is consistent with X-ray observations of the H-like and He-like Fe Kα emission-lines in starburst galaxies from the very hot (108 K) gas created as the stellar ejecta are thermalized through shocks [6]). These results imply that rather little of the initial kinetic energy is lost through radiative cooling, and this is substantiated by estimates of the rate of PΔV work done by the wind on the ambient gas [6]. While there are no such constraints on galaxies at a high (z > 1) redshift, we do know that these galaxies have values of SFR/A similar to those seen in low-z starbursts (e.g., [15]), and that galactic winds driven by massive stars at this epoch are both ubiquitous and very similar to those seen in low-z starburst galaxies (see [6]). Note that roughly 60% of the total present-day stellar mass was formed at z > 1, during this “windy” epoch [7].
The situation for momentum injection is less uncertain because momentum will be conserved even in the face of significant radiative losses. We can simply use the methodology above, but use Starburst99 to compute the specific injection rate of momentum by massive stars (supernovae, stellar winds, and radiation pressure). The value is 7.4 × 107 cm s−1, and for a total stellar mass density of 4.8 × 108 Mʘ Mpc−3, this yields 7.1 × 1049 gm cm s−1 Mpc−3.

2.2. Black-Hole Driven Winds and Radiation Pressure

Winds driven by supermassive black holes are multi-phase and have been measured in a number of different ways. Molecular outflows have been detected in both emission and absorption (see [4]). Calculating kinetic energy outflow rates is conceptually straightforward. The luminosity of a CO transition can be converted into a total molecular gas mass, albeit with uncertainties [16]. The measured outflow velocity and the radius of the outflow then yields a kinetic energy flux given as ½ Mgas vout3 rout−1. For absorption, the OH column density and outflow velocity yield an outflow rate (for an assumed outflow size and OH/H2 conversion factor). The first compilation of molecular outflows by [17] implied typical kinetic energy fluxes of dEwind/dt ≈ 3% LBol; however, more recent compilations of measurements [18,19] (I. Lamperti, private communication) have yielded much smaller values (median of 0.1%).
Similarly, the outflow rates of warm ionized gas can be measured using the Hα or [OIII]5007 luminosity and measured electron density to derive the total mass of ionized gas and then measuring the outflow velocity and radius of the outflow to determine dEwind/dt. Different recent measurements have produced drastically different results, with median values ranging from as high as 1% of Lbol [20] to 0.3 % [17], to 0.1% [21], to 0.01% [22], to 0.0003% [23].
An independent measurement of the outflow rate in the warm ionized gas comes from observations of BAL QSOs. Here, the absorption lines can provide a column density and outflow velocity. Direct measurements of the electron densities can be made using the ratio of column densities in lines arising from an excited state vs. ground state. Photoionization models using the observed ionizing luminosity (Q) and the inferred value of the ionization parameter (U) then yield a size for the outflow: rout = (Q/4π ne c U)1/2 [24]. With a velocity, radius, and column density, the kinetic energy flux can be estimated. The results span a huge range, from 0.001% to 10% Lbol (median value of 0.3%). Highly ionized outflows are also detected in about 40% of AGN [25] based on X-ray absorption lines. However, because the size scales of these outflows are so uncertain, the kinetic energy outflow rates are also uncertain (by about two orders-of-magnitude, typically ranging between 0.01 and 1% of LBol [26].
It is clear from the above that assigning a value for the ratio of dEwind/dt to Lbol is difficult. If we take median values of 0.1%, 0.3%, and 0.1% LBol for the molecular, warm-ionized, and highly-ionized phases, we obtain a total value of 0.5% LBol. Multiplying this by the total bolometric energy density per co-moving volume element volume produced by supermassive black holes of Urad = 8.6 × 1058 erg Mpc−3 [27], yields Uwind = 4.3 × 1056 ergs Mpc−3. This is 6% as large as the value derived for massive stars. Using the present-day mass per unit volume in supermassive black holes of ρBH = 5 × 105 Mʘ Mpc−3 [27] this wind energy density can also be expressed as Uwind = 5 × 10−4 ρBH c2.
We can also consider the amount of momentum provided by AGN. An initial estimate is implied by the momentum carried by radiation (Urad/c), where Urad is the total amount of radiant energy per unit volume produced over cosmic time by AGN. This yields an amount of momentum per unit volume of 2.9 × 1048 gm cm s−1 Mpc−3 (about 4% of the value for massive stars). As the momentum flux (in the non-relativistic case) is just twice the kinetic energy flux divided by the outflow velocity, we need only consider the momentum carried by the molecular and warm ionized flows (as the BAL QSO and X-ray outflows are over an order-of-magnitude faster, but carry similar kinetic energy fluxes).
For the molecular outflows, the data in [18,19] and I. Lamperti (private communication) yield median values of dpwind/dt = 1.0 and 0.7 LBol/c, respectively. The near equality is consistent with the idea that the molecular outflows are driven by radiation pressure. If so, then combining radiation pressure and the molecular outflows would be double-counting in the inventory of momentum.
As noted above, there is a very wide range in the ratio between the kinetic energy flux in the warm ionized gas and the AGN bolometric luminosity, and this translates directly into uncertainties in the ratio of momentum flux and radiation pressure for this gas phase. The estimated median values of this ratio range from ≈10 [20], to ≈1 [17,21], to ≈0.1 [22], to ≈0.01 [23]. It appears that the momentum flux in the warm ionized outflows is not likely to be significantly larger than those in the molecular gas or to that carried by radiation.
This represents a total injected momentum per unit volume of at most ≈1049 gm cm s−1 Mpc−3, even if we simply add the three sources (radiation, molecular gas, and ionized gas) together. This is still an order of magnitude below the value for massive stars.

2.3. Black-Hole-Driven Jets

The earliest evidence for the outflow of kinetic energy driven by supermassive black holes came from observations of “double lobes” of synchrotron radio emission that straddled massive elliptical galaxies [28]. Subsequent radio observations at a high angular resolution showed narrow collimated features (“jets”) linking the two lobes to the galactic nucleus (see [29]).
It is now possible to quantify the amount of kinetic energy carried by jets as a function of the luminosity of the radio source that they power. This can be done by joint observations of the radio and X-ray emission. The expanding radio sources inflate lobes of relativistic plasma, which in X-rays can be observed as cavities in the surrounding hot gas. Several investigations [30,31,32,33,34] derived the pΔV work (energy) associated with the cavities in a sample of massive galaxies, groups, and clusters, and used the buoyancy timescale (e.g., [35]) to estimate their ages. They combined these cavity powers with the monochromatic 1.4 GHz radio luminosities to show that the two were well-correlated. The largest uncertainty in this method is the determination of the cavity energy from the measured pressure and volume: Ecav = fcavpΔV. For the relativistic plasma of the radio lobes, the enthalpy of the cavity is 4pΔV. Taking fcav = 4, [36] derived the following best-fit relation from the cavity data:
dEjet/dt = 1.3 × 1038 (L1.4 GHz/1026 W Hz−1)0.68 W
This empirical relation is very similar to predictions from theoretical models of radio jets. Willett et al. (1999) used synchrotron properties to derive the following relation:
dEjet/dt = 2.8 × 1036 (fW)3/2 (L1.4 GHz/1026 W Hz−1)0.84 W
Here, fW is a dimensionless factor (in the range 1 to 20) accounting for the uncertainties in the extrapolation from the population of relativistic electrons that produce the observed radio synchrotron emission to the total energy. Agreement with the X-ray cavity data implies fW ≈10 to 20 (see [36]).
We adopt the theoretical relation (Equation (2)), but calibrated by the cavity data (i.e., taking fW = 15), and use this to convert the radio luminosity function of AGN between z = 0.1 and 3 [37] into a measure of the evolution in the rate of kinetic energy injection per unit volume by radio jets.
The results are shown in Figure 1 and show that the peak rate of kinetic energy injection by jets occurs at a significantly lower redshift (z ≈ 1) than the peak rate due to massive stars and black-hole-driven winds (z ≈ 2, as also shown in Figure 1). We then integrate the energy injection rate by interpolating the values at z = 0.1, 0.5, 1.0, 2.0, and 3.0 and extrapolating from z = 0.1 to 0 and from z = 3.0 to infinity (this extrapolation does not add significantly to the total—see Figure 1). This then gives a value for the time-integrated total kinetic energy per unit volume due to jets of Ujet = 2.6 × 1057 erg Mpc−3. These results are broadly in line with similar estimates derived from low-frequency radio luminosity functions (Kondapally et al., private communication).
The time-integrated kinetic energy input from jets is ≈6 times larger than the value estimated for black-hole-driven winds, and 40% (400%) of the total amount of kinetic energy generated by massive stars for εstar = 1 (0.1). Alternatively, using the present-day mass per unit volume in supermassive black holes of ρBH = 5 × 105 Mʘ [27], this jet energy density can also be expressed as Ujet = 2.9 × 10−3 ρBH c2.
The kinetic energy carried by jets is in the form of relativistic bulk motion. In this case, momentum can be taken as p ≈ KE/c. The above value of Ujet then implies a momentum density of 8.7 × 1046 gm cm s−1 Mpc−3. This is much less than the momentum carried by radiation and winds from supermassive black holes and the momentum produced by massive stars. Jets are thus far more important feedback sources in terms of kinetic energy than momentum.

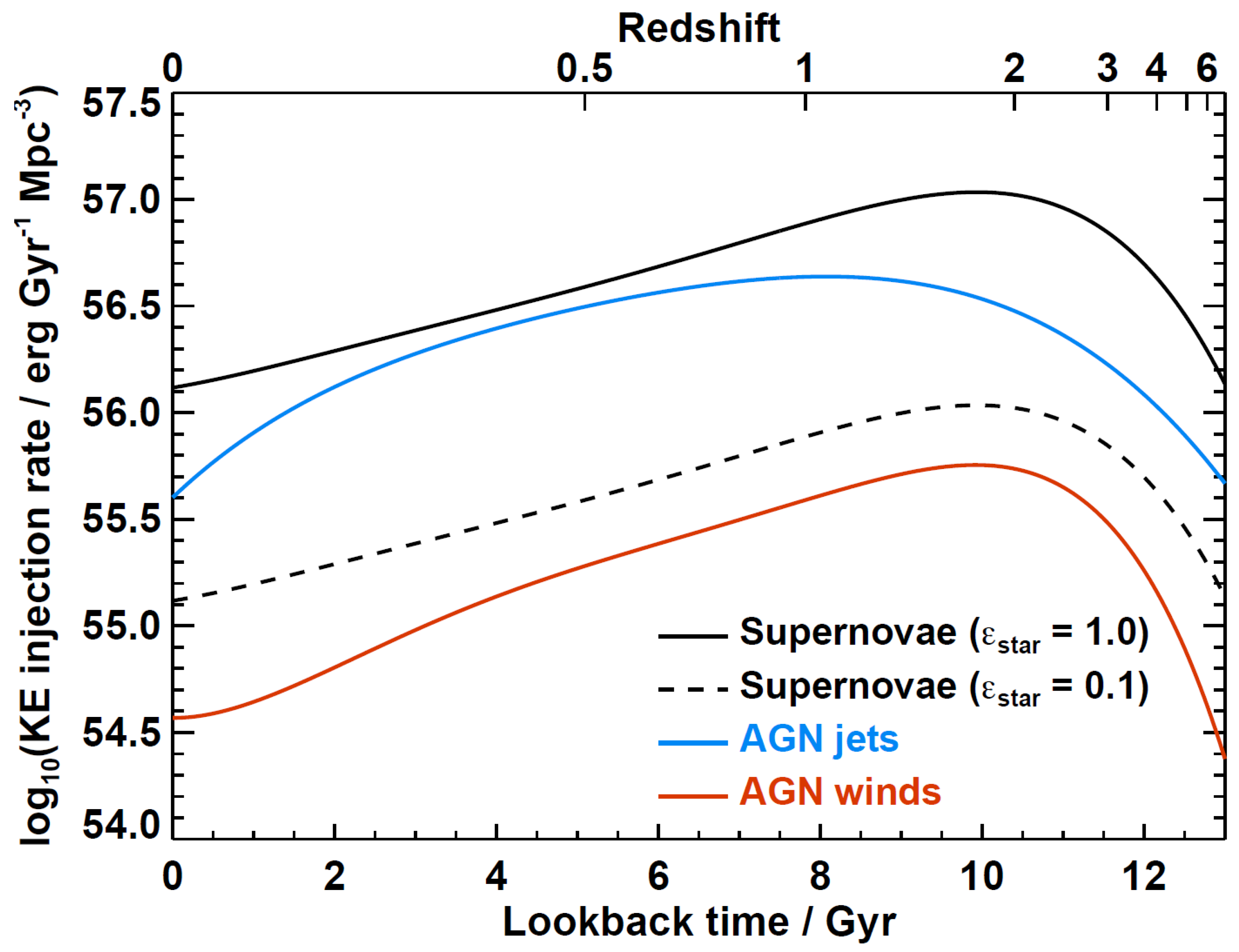
2.4. The Bottom Line

For the total kinetic energy inventory, the largest single source is either massive stars (for εstar > 0.4) or jets (for εstar < 0.4). AGN winds are only important at the <10% level. For the total momentum inventory, massive stars dominate (AGN contribute at the ≈10% level). The peak rate of kinetic energy injection by jets occurs at a substantially lower redshift than that from stars or AGN winds (z ≈ 1 and 2, respectively). These results are summarized in Table 1 and Figure 1.

3. Implications

3.1. For Galaxies

To assess the implications of these results for galaxy evolution, it is essential to consider the dependences of feedback on the masses of both galaxies and supermassive black holes. We can go beyond these simple global values and examine the relative importance of feedback (both kinetic energy and momentum) as a function of the ratio of supermassive black hole mass to galaxy stellar mass. In Figure 2, we show a plot of a black hole vs. galaxy mass that is similar to that in [26] for the z ≈ 0.1 universe (based on SDSS). In this case, these are present day stellar masses, and would need to be increased by a factor of 1/(1 − R) = 1.42 to represent the total mass of stars ever formed. The masses for the black holes were estimated from the M-σ relation from [38]. In Figure 2, we have color-coded the plot by the fraction of galaxies in which star-formation has been quenched, which we define to be SFR/Mstar < 10−11 yr−1. It is clear that the quenched fraction depends strongly on both the stellar and black hole masses.
The mean relation between stellar and black hole mass in Figure 2 can be approximated as log MBH = 2.0 log Mstar −14.0, implying MBH/Mstar α Mstar1.0 α MBH0.50. Thus, the relative importance of feedback integrated over cosmic time from massive stars and black holes should be a strong function of mass. Let us quantify this for kinetic energy and then for momentum. For kinetic energy, in a given galaxy (and assuming that global averages can be applied to individual galaxies; see below), the inventories above imply that the ratio KEBH/KEstar = 315 εstar−1 MBH/Mstar (where Mstar is the present-day stellar mass). For momentum, the corresponding ratio is pBH/pstar = 100 MBH/Mstar. We can then plot these relations in Figure 2 to see the regimes in which the feedback from supermassive black holes exceeds that from stars. For kinetic energy, we show this separately for values of εstar = 0.1 and 1.0.
In terms of momentum input, stars dominate over black holes in almost all cases. However, considering kinetic energy, we find that the transition from galaxies that are mostly quenched to those that are mostly star-forming occurs very near the dividing line between jet-dominated feedback and stellar dominated feedback for a value of εstar ≈ 0.1. This is suggestive evidence that quenching is driven by the feedback of kinetic energy from jets driven by supermassive black holes. However, we caution that the transition from star forming to quiescent galaxies also occurs at the transition from disk dominated to bulge dominated galaxies, so the causal connections between the galaxy structure, star formation, and black hole feedback are not entirely clear.
We emphasize that the relations plotted in Figure 2 explicitly assume that the global relations can be applied to individual galaxies, namely that the amount of feedback from massive stars in a given galaxy is proportional to the stellar mass and that the amount of feedback from jets is proportional to the black hole mass. The former seems to be a safe assumption, but the dependence of the production of radio jets on the black hole mass may be complex. We know that there are essentially two populations of radio galaxies (e.g., [36]). In one case (“radiative mode”) the jets are launched by star-forming galaxies and are accompanied by strong nuclear radiation (QSO-like). In the other class (“jet-mode”), the jets are launched by quenched galaxies, with little accompanying nuclear radiation. The radiative mode becomes more important at higher luminosities and at higher redshifts. For the jet-mode galaxies, [39] found that the probability of producing a jet with a given luminosity depends on both the stellar and black hole mass (and more strongly on the former).
The situation for radiative-mode radio galaxies is less clear, although the indications are that any dependence of the ratio of KE/MBH on MBH or Mstar is weaker (e.g., [39,40]. In the context of Figure 2, it may be that the jet-mode is not the dominant population in terms of actively quenching, since the jet-mode galaxies are already quenched (instead, these may just “maintain” a quenched state). If quenching is due to jets in radiative-mode galaxies, the dividing line between quenched and star-forming galaxies in Figure 2 would imply that time-integrated amount of jet energy contributed by a radiative mode galaxy is proportional to its black hole mass (i.e., the integrated ratio of jet kinetic energy and energy carried by radiation is independent of black hole mass in these galaxies).
Another way to consider this is to ask how the amount of energy supplied by stars and by black holes scales with the binding energy of the galaxy. We take Ebind ≈ Mstar vc2, where vc is the galaxy circular velocity. The Tully-Fischer relation for disk galaxies [41] and the Faber-Jackson relation for ellipticals [42] both imply vc α Mstar1/4. Thus, we have Ebind α Mstar3/2. Given that KEstar α Mstar and KEBH α MBH α Mstar2, this implies that KEstar/Ebind α Mstar−1/2, while KEBH/Ebind α Mstar1/2 α MBH1/4. This again underscores the fundamental difference in the mass-dependence of feedback from massive stars and supermassive black holes: feedback from stars becomes increasingly impactful on the galaxy as the mass decreases, while feedback from black holes has greater impact as the mass increases.

3.2. For the Intra-Group and Intra-Cluster Media

It has long been known that the basic observed properties of the hot gas in groups and clusters of galaxies (Mhalo > 1013 Mʘ) are not consistent with simple models of purely gravitational processes operating during the formation of these systems (see Donahue and Voit 2022 and the references therein). A particularly simple example of this is the observed relationship between the X-ray temperature (a proxy for halo mass) and X-ray luminosity. As the halo masses decrease, the observed X-ray luminosities fall further below the relationship expected simply from gravitational infall and heating. These lower luminosities arise because the hot gas in these less-massive halos is more spatially-extended than the dark matter, with the resulting drop in gas density leading to lower X-ray luminosities.
This could be due to the feedback of energy injected into the hot gas, which “lifts” the gas outward. As described above, there is direct observational evidence in the local universe of radio jets delivering energy to the hot gas in groups and clusters. As discussed in Donahue and Voit (2022), for this to be responsible for lifting the hot gas, an amount of kinetic energy equal to ≈0.5% MBH/c2 must be delivered. This is close to the value for jets and AGN winds that we estimated to be above ≈0.34%. Note that this could be supplemented by the kinetic energy from massive stars (which would be 0.25 to 2.5 the value for jets for εstar = 0.1 and 1.0, respectively).

4. Summary

Based on a global inventory of the amount of kinetic energy and momentum injected by massive stars (stellar winds and supernovae), and by winds and jets driven by supermassive black holes, we draw the following conclusions:
(i)
The major sources of kinetic energy are massive stars and jets. Winds driven by supermassive black holes provide <10% of the total amount. The global ratio of the kinetic energy injected by massive stars to that injected by jets is 2.5 εstar (where εstar is the fraction of injected energy from stars that is not lost to radiative cooling).
(ii)
Massive stars are the dominant source of momentum injection (90% of the total). AGN winds provide 10% and radio jets are negligible.
(iii)
The peak in the feedback from jets occurs at z ≈ 1, considerably later than the contributions of AGN winds and massive stars (peaking at z ≈ 2).
(iv)
As the ratio of the mass of the supermassive black hole to the galaxy stellar mass increases steeply with mass, there will be a mass-dependence in the relative importance of feedback from the two sources.
(v)
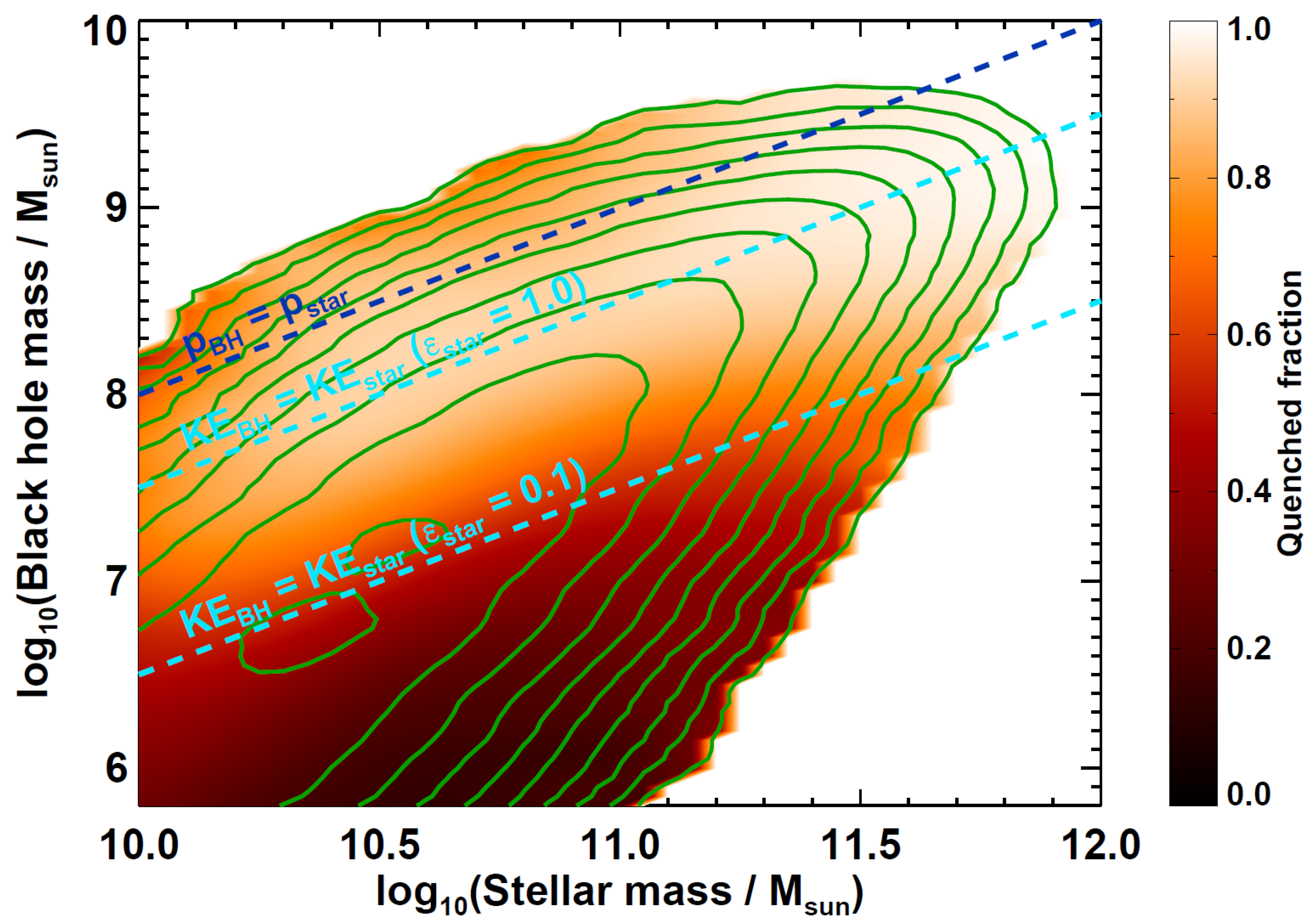
For the assumptions that the total amount of kinetic energy from massive stars is proportional to the galaxy’s stellar mass, and that the total amount of kinetic energy from a supermassive black hole is proportional to its mass, we find that the populations of quenched and star-forming galaxies occur in the regimes where supermassive black hole feedback and massive star feedback dominate, respectively (for a value of εstar ≈ 0.1).
(vi)
By comparing the amount of kinetic energy injected as a function of the binding energy of a galaxy, we show that feedback becomes more impactful as the galaxy mass decreases for massive stars, but more impactful as the galaxy mass increases for black holes.
(vii)
The global amount of kinetic energy injected by radio jets and AGN winds per unit volume, combined with the supermassive black hole mass function, yields an efficiency for producing kinetic energy in jets of 0.34% c2. This is very close to the amount of energy needed to explain the X-ray luminosity–temperature relation in groups and clusters (0.5% c2).

Author Contributions

Conceptualization, T.M.H.; Methodology, T.M.H.; Software, P.N.B.; Formal Analysis, P.N.B.; Writing—original draft, T.M.H.; Writing—review and editing, T.M.H. and P.N.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the endowment of the A. Hermann Pfund Professorship.

Data Availability Statement

Some of the results presented in this paper were based on the MPA-JHU value-added catalog for SDSS data (https://www.sdss.org/dr12/spectro/galaxy_mpajhu/ accessed on 19 January 2023).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Somerville, R.; Davé, R. Physical Models of Galaxy Formation in a Cosmological Framework. Annu. Rev. Astron. Astrophys. 2015, 53, 51–113. [Google Scholar] [CrossRef] [Green Version]
  2. Naab, T.; Ostriker, J.P. Theoretical challenges in galaxy formation. Annu. Rev. Astron. Astrophys. 2017, 55, 59–109. [Google Scholar] [CrossRef] [Green Version]
  3. Donahue, M.; Voit, G.M. Baryon cycles in the biggest galaxies. Phys. Rep. 2022, 973, 1–109. [Google Scholar] [CrossRef]
  4. Veilleux, S.; Maiolino, R.; Bolatto, A.D.; Aalto, S. Cool outflows in galaxies and their implications. Astron. Astrophys. Rev. 2020, 28, 1–173. [Google Scholar] [CrossRef] [Green Version]
  5. McNamara, B.R.; Nulsen, P.E.J. Heating hot atmospheres with active galactic nuclei. Annu. Rev. Astron. Astrophys. 2007, 45, 117–175. [Google Scholar] [CrossRef] [Green Version]
  6. Thompson, T.A.; Heckman, T.M. Theory and Observation of Galactic Winds. Annu. Rev. Astron. Astrophys. 2023; in press. [Google Scholar]
  7. Madau, P.; Dickinson, M. Cosmic star formation history. Annu. Rev. Astron. Astrophys. 2014, 52, 415–486. [Google Scholar] [CrossRef] [Green Version]
  8. Chabrier, G. Galactic Stellar and Sub stellar Initial Mass Function. Publ. Astron. Soc. Pac. 2003, 115, 763. [Google Scholar] [CrossRef] [Green Version]
  9. Leitherer, C.; Schaerer, D.; Goldader, J.D.; Delgado, R.M.G.; Robert, C.; Kune, D.F.; Heckman, T.M. Starburst99: Synthesis models for galaxies with active star formation. Astrophys. J. Suppl. Ser. 1999, 123, 3–40. [Google Scholar] [CrossRef] [Green Version]
  10. Chevalier, R.A.; Clegg, A.W. Wind from a starburst galaxy nucleus. Nature 1985, 317, 44–45. [Google Scholar] [CrossRef]
  11. Kim, C.G.; Ostriker, E.C.; Somerville, R.S.; Bryan, G.L.; Fielding, D.B.; Forbes, J.C.; Pandya, V. First Results from SMAUG: Characterization of Multiphase Galactic Outflows from a Suite of Local Star-forming Galactic Disk Simulations. Astrophys. J. 2020, 900, 61–102. [Google Scholar] [CrossRef]
  12. Kennicutt, R.C., Jr.; Evans, N.J. Star formation in the Milky Way and nearby galaxies. Annu. Rev. Astron. Astrophys. 2012, 50, 531–608. [Google Scholar] [CrossRef] [Green Version]
  13. Schneider, E.E.; Ostriker, E.C.; Robertson, B.E.; Thompson, T.A. The physical nature of starburst-driven Galactic outflows. Astrophys. J. 2020, 895, 43–66. [Google Scholar] [CrossRef]
  14. Fielding, D.; Bryan, G. The Structure of Multiphase Galactic Winds. Astrophys. J. 2022, 984, 82–112. [Google Scholar] [CrossRef]
  15. Forster-Schreiber, N.; Wuyts, S. Star Forming Galaxies at Cosmic Noon. Annu. Rev. Astron. Astrophys 2020, 58, 661–725. [Google Scholar] [CrossRef]
  16. Tacconi, L.J.; Genzel, R.; Sternberg, A. The evolution of the star-forming interstellar medium across cosmic time. Annu. Rev. Astron. Astrophys. 2020, 58, 157–203. [Google Scholar] [CrossRef]
  17. Fiore, F.; Feruglio, C.; Shankar, F.; Bischetti, M.; Bongiorno, A.N.G.E.L.A.; Brusa, M.; Zappacosta, L. AGN wind scaling relations and the co-evolution of black holes and galaxies. Astron. Astrophys. 2017, 601, A143–A163. [Google Scholar] [CrossRef]
  18. Lutz, D.; Sturm, E.; Janssen, A.; Veilleux, S.; Aalto, S.; Cicone, C.; Weiß, A. Molecular outflows in local galaxies: Method comparison and a role of intermittent AGN driving. Astron. Astrophys. 2020, 633, A134–A168. [Google Scholar] [CrossRef]
  19. Lamperti, I.; Pereira-Santaella, M.; Perna, M.; Colina, L.; Arribas, S.; García-Burillo, S.; van der Werf, P. Physics of ULIRGs with MUSE and ALMA: PUMA IV. No tight relation between cold molecular outflow rates and AGN luminosities. arXiv 2022, arXiv:2209.03380. [Google Scholar]
  20. Kakkad, D.; Sani, E.; Rojas, A.F.; Mallmann, N.D.; Veilleux, S.; Bauer, F.E.; Urry, C.M. BASS XXXI: Outflow scaling relations in low redshift X-ray AGN host galaxies with MUSE. Mon. Not. R. Astron. Soc. 2022, 511, 2105–2124. [Google Scholar] [CrossRef]
  21. Revalski, M.; Meena, B.; Martinez, F.; Polack, G.E.; Crenshaw, D.M.; Kraemer, S.B.; Rafelski, M. Quantifying Feedback from Narrow Line Region Outflows in Nearby Active Galaxies. III. Results for the Seyfert 2 Galaxies Markarian 3, Markarian 78, and NGC 1068. Astrophys. J. 2021, 910, 139–172. [Google Scholar] [CrossRef]
  22. de Oliveira, B.D.A.; Storchi-Bergmann, T.; Kraemer, S.B.; Martín, M.V.; Schnorr-Müller, A.; Schmitt, H.R.; Fischer, T.C. Gauging the effect of supermassive black holes feedback on quasar host galaxies. Mon. Not. R. Astron. Soc. 2021, 504, 3890–3908. [Google Scholar] [CrossRef]
  23. Trindade Falcão, A.; Kraemer, S.B.; Fischer, T.C.; Crenshaw, D.M.; Revalski, M.; Schmitt, H.R.; Ward, M.J. Hubble Space Telescope observations of [O III] emission in nearby QSO2s: Physical properties of the ionized outflows. Mon. Not. R. Astron. Soc. 2021, 500, 1491–1504. [Google Scholar] [CrossRef]
  24. Miller, T.R.; Arav, N.; Xu, X.; Kriss, G.A. The contribution of quasar absorption outflows to AGN feedback. Mon. Not. R. Astron. Soc. 2020, 499, 1522–1529. [Google Scholar] [CrossRef]
  25. Tombesi, F.; Cappi, M.; Reeves, J.N.; Palumbo, G.G.C.; Braito, V.; Dadina, M. Evidence for ultra-fast outflows in radio-quiet active galactic nuclei. II. Detailed photoionization modeling of Fe K-shell absorption lines. Astrophys. J. 2011, 742, 44–64. [Google Scholar] [CrossRef] [Green Version]
  26. Tombesi, F.; Cappi, M.; Reeves, J.N.; Braito, V. Evidence for ultrafast outflows in radio-quiet AGNs—III. Location and energetics. Mon. Not. R. Astron. Soc. Lett. 2012, 422, L1–L5. [Google Scholar] [CrossRef]
  27. Hopkins, P.F.; Richards, G.T.; Hernquist, L. An observational determination of the bolometric quasar luminosity function. Astrophys. J. 2007, 654, 731–753. [Google Scholar] [CrossRef]
  28. Baade, W.; Minkowski, R. Identification of the radio sources in Cassiopeia, Cygnus A, and Puppis, A. In Classics in Radio Astronomy; Springer: Dordrecht, The Netherlands, 1954; pp. 251–272. [Google Scholar]
  29. Miley, G. The structure of extended extragalactic radio sources. Annu. Rev. Astron. Astrophys. 1980, 18, 165–218. [Google Scholar] [CrossRef]
  30. Bîrzan, L.; Rafferty, D.A.; McNamara, B.R.; Wise, M.W.; Nulsen, P.E. A systematic study of radio-induced X-ray cavities in clusters, groups, and galaxies. Astrophys. J. 2004, 607, 800. [Google Scholar] [CrossRef] [Green Version]
  31. Bîrzan, L.; McNamara, B.R.; Nulsen, P.E.J.; Carilli, C.L.; Wise, M.W. Radiative efficiency and content of extragalactic radio sources: Toward a universal scaling relation between jet power and radio power. Astrophys. J. 2008, 686, 859–880. [Google Scholar] [CrossRef]
  32. Cavagnolo, K.W.; McNamara, B.R.; Nulsen, P.E.J.; Carilli, C.L.; Jones, C.; Bîrzan, L. A relationship between AGN jet power and radio power. Astrophys. J. 2010, 720, 1066–1072. [Google Scholar] [CrossRef]
  33. Dunn, R.J.; Fabian, A.C.; Taylor, G.B. Radio bubbles in clusters of galaxies. Mon. Not. R. Astron. Soc. 2005, 364, 1343–1353. [Google Scholar] [CrossRef]
  34. Rafferty, D.A.; McNamara, B.R.; Nulsen, P.E.J.; Wise, M.W. The feedback-regulated growth of black holes and bulges through gas accretion and starbursts in cluster central dominant galaxies. Astrophys. J. 2006, 652, 216–231. [Google Scholar] [CrossRef]
  35. Churazov, E.; Böhringer, H.; Brüggen, M.; Forman, W.; Jones, C.; Kaiser, C.; Sunyaev, R. Bobble-Heated Cooling Flows, in Lighthouses of the Universe: The Most Luminous Celestial Objects and Their Use for Cosmology; Springer: Berlin/Heidelberg, Germany, 2002; pp. 37–43. [Google Scholar]
  36. Heckman, T.M.; Best, P.N. The coevolution of galaxies and supermassive black holes: Insights from surveys of the contemporary universe. Annu. Rev. Astron. Astrophys. 2014, 52, 589–660. [Google Scholar] [CrossRef] [Green Version]
  37. Yuan, Z.; Wang, J.; Zhou, M.; Qin, L.; Mao, J. A Mixture Evolution Scenario of the AGN Radio Luminosity Function. II. Do Low-and High-power Radio-loud AGNs Evolve Differently? Astrophys. J. 2017, 846, 78–87. [Google Scholar] [CrossRef] [Green Version]
  38. McConnell, N.J.; Ma, C.P. Revisiting the scaling relations of black hole masses and host galaxy properties. Astrophys. J. 2013, 764, 184–197. [Google Scholar] [CrossRef]
  39. Janssen, R.M.J.; Röttgering, H.J.A.; Best, P.N.; Brinchmann, J. The triggering probability of radio-loud AGN-A comparison of high and low excitation radio galaxies in hosts of different colors. Astron. Astrophys. 2012, 541, A62–A68. [Google Scholar] [CrossRef] [Green Version]
  40. Kondapally, R.; Best, P.N.; Cochrane, R.K.; Sabater, J.; Duncan, K.J.; Hardcastle, M.J.; Wang, L. Cosmic evolution of low-excitation radio galaxies in the LOFAR two-metre sky survey deep fields. Mon. Not. R. Astron. Soc. 2022, 513, 3742–3767. [Google Scholar] [CrossRef]
  41. McGaugh, S.S.; Schombert, J.M.; Bothun, G.D.; De Blok, W.J.G. The baryonic tully-fisher relation. Astrophys. J. 2000, 533, L99–L102. [Google Scholar] [CrossRef] [Green Version]
  42. Bernardi, M.; Sheth, R.K.; Annis, J.; Burles, S.; Eisenstein, D.J.; Finkbeiner, D.P.; York, D.G. Early-type galaxies in the sloan digital sky survey. II. Correlations between observables. Astron. J. 2003, 125, 1849–1865. [Google Scholar] [CrossRef]
Galaxies 11 00021 g001 550
Figure 1. A plot of the amount of kinetic energy injected per Gyr and co-moving cubic Mpc as a function of lookback time for massive stars (supernovae and stellar winds; black) and black-hole-driven jets (blue) and winds (red). For massive stars, we show the cases in which 100% (solid line) and 10% (dashed line) of the kinetic energy created are delivered to the surroundings (i.e., not lost to radiative cooling). Note that for momentum injection, massive stars dominate at all epochs, with the same time dependence as for kinetic energy injection (i.e., as given by the solid black line).
Figure 1. A plot of the amount of kinetic energy injected per Gyr and co-moving cubic Mpc as a function of lookback time for massive stars (supernovae and stellar winds; black) and black-hole-driven jets (blue) and winds (red). For massive stars, we show the cases in which 100% (solid line) and 10% (dashed line) of the kinetic energy created are delivered to the surroundings (i.e., not lost to radiative cooling). Note that for momentum injection, massive stars dominate at all epochs, with the same time dependence as for kinetic energy injection (i.e., as given by the solid black line).
Galaxies 11 00021 g001
Galaxies 11 00021 g002 550
Figure 2. A plot of the distribution of SDSS galaxies in the plane of galaxy stellar mass vs. supermassive black hole mass. The latter were estimated using the MBH vs. σ relation in [38]. The relative numbers of galaxies in each bin are indicated by the green contours (increasing by factors of 2) and the color-coding represents the fraction of galaxies that are quenched (SFR/Mstar < 10−11 yr−1). The dark blue dashed line indicates where the momentum injected by black holes equals that from massive stars. The two light blue dashed lines indicate where the kinetic energy from black holes equals that from massive stars for values of εstar = 0.1 and 1.0 (see text). The transition from predominantly star forming to predominantly quenched galaxies occurs near the relationship for εstar = 0.1.
Figure 2. A plot of the distribution of SDSS galaxies in the plane of galaxy stellar mass vs. supermassive black hole mass. The latter were estimated using the MBH vs. σ relation in [38]. The relative numbers of galaxies in each bin are indicated by the green contours (increasing by factors of 2) and the color-coding represents the fraction of galaxies that are quenched (SFR/Mstar < 10−11 yr−1). The dark blue dashed line indicates where the momentum injected by black holes equals that from massive stars. The two light blue dashed lines indicate where the kinetic energy from black holes equals that from massive stars for values of εstar = 0.1 and 1.0 (see text). The transition from predominantly star forming to predominantly quenched galaxies occurs near the relationship for εstar = 0.1.
Galaxies 11 00021 g002
Table
Table 1. Summary of feedback inventory.
Table 1. Summary of feedback inventory.
123456
SampleLog ρLog sKELog ρKELog spρp
Massive Stars8.69−5.1157.837.8749.85
BH Winds5.70−3.3056.6310.0049.00
BH Jets5.70−2.5457.437.9446.94
Notes: Column 2—The log of the present-day mass density of stars (row 3) and supermassive black holes (rows 4 and 5) formed over cosmic time in units of Mʘ Mpc−3. Column 3—The log of the specific kinetic energy released: energy per unit mass in stars (row 3 and black holes (rows 4 and 5). Given in units of c2 and assuming εstar = 1.0. Column 4—The log of the amount of kinetic energy created per unit volume (in ergs Mpc−3). Column 5—The specific momentum created (momentum per unit mass in stars (row 3) and black holes (rows 4 and 5). In units of cm s−1. Column 6—The log of the amount of momentum created per unit volume (gm cm s−1 Mpc−3).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Heckman, T.M.; Best, P.N. A Global Inventory of Feedback. Galaxies 2023, 11, 21. https://doi.org/10.3390/galaxies11010021

AMA Style

Heckman TM, Best PN. A Global Inventory of Feedback. Galaxies. 2023; 11(1):21. https://doi.org/10.3390/galaxies11010021

Chicago/Turabian Style

Heckman, Timothy M., and Philip N. Best. 2023. "A Global Inventory of Feedback" Galaxies 11, no. 1: 21. https://doi.org/10.3390/galaxies11010021

APA Style

Heckman, T. M., & Best, P. N. (2023). A Global Inventory of Feedback. Galaxies, 11(1), 21. https://doi.org/10.3390/galaxies11010021

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop