Modeling Reconstructed Images of Jets Launched by SANE Super-Eddington Accretion Flows around SMBHs with the ngEHT
Abstract
1. Introduction
2. Numerical Methods
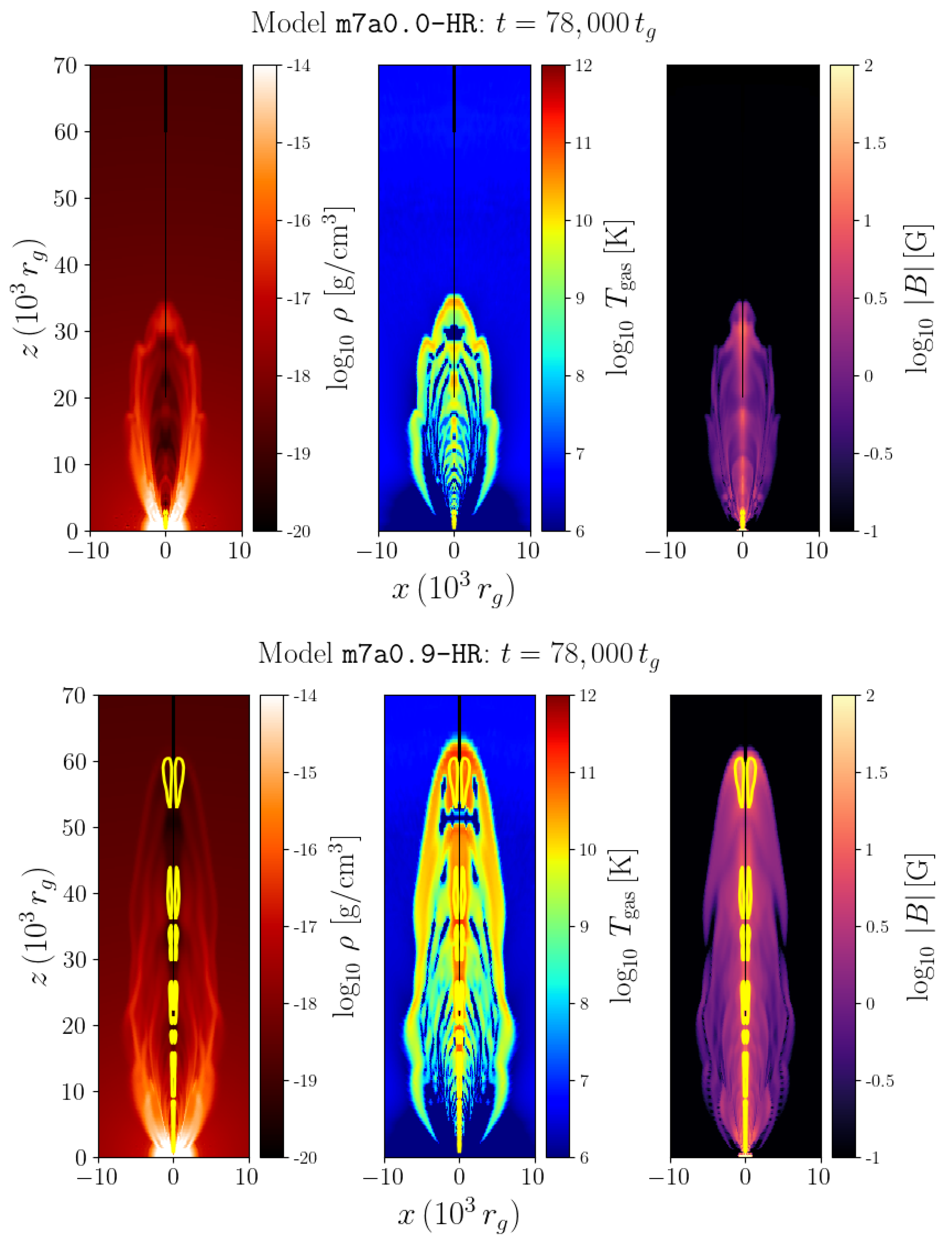
2.1. GRRHMD Simulations
2.2. 230 GHz Emission
2.3. Synthetic ngEHT Observations and Image Reconstruction
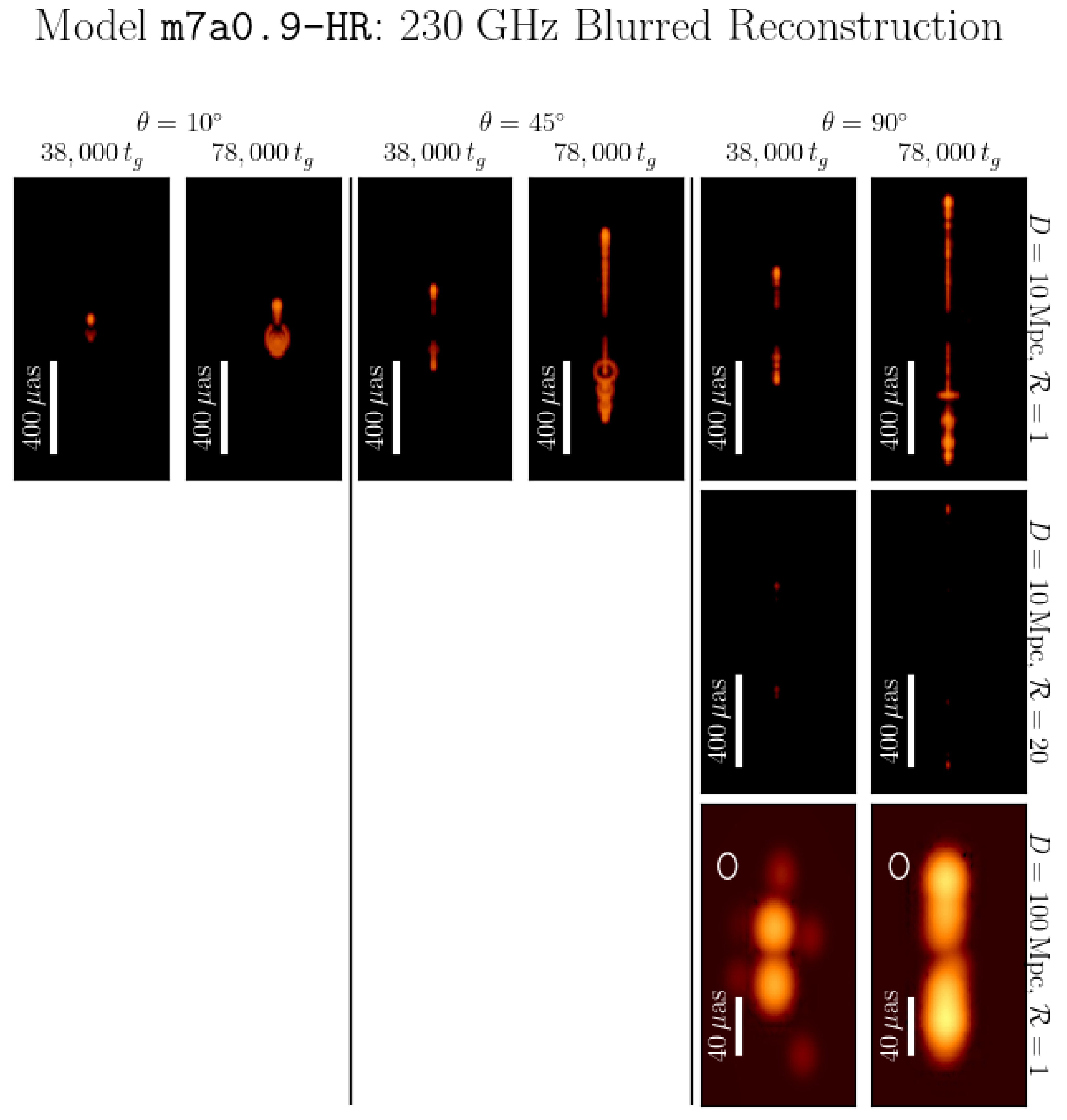
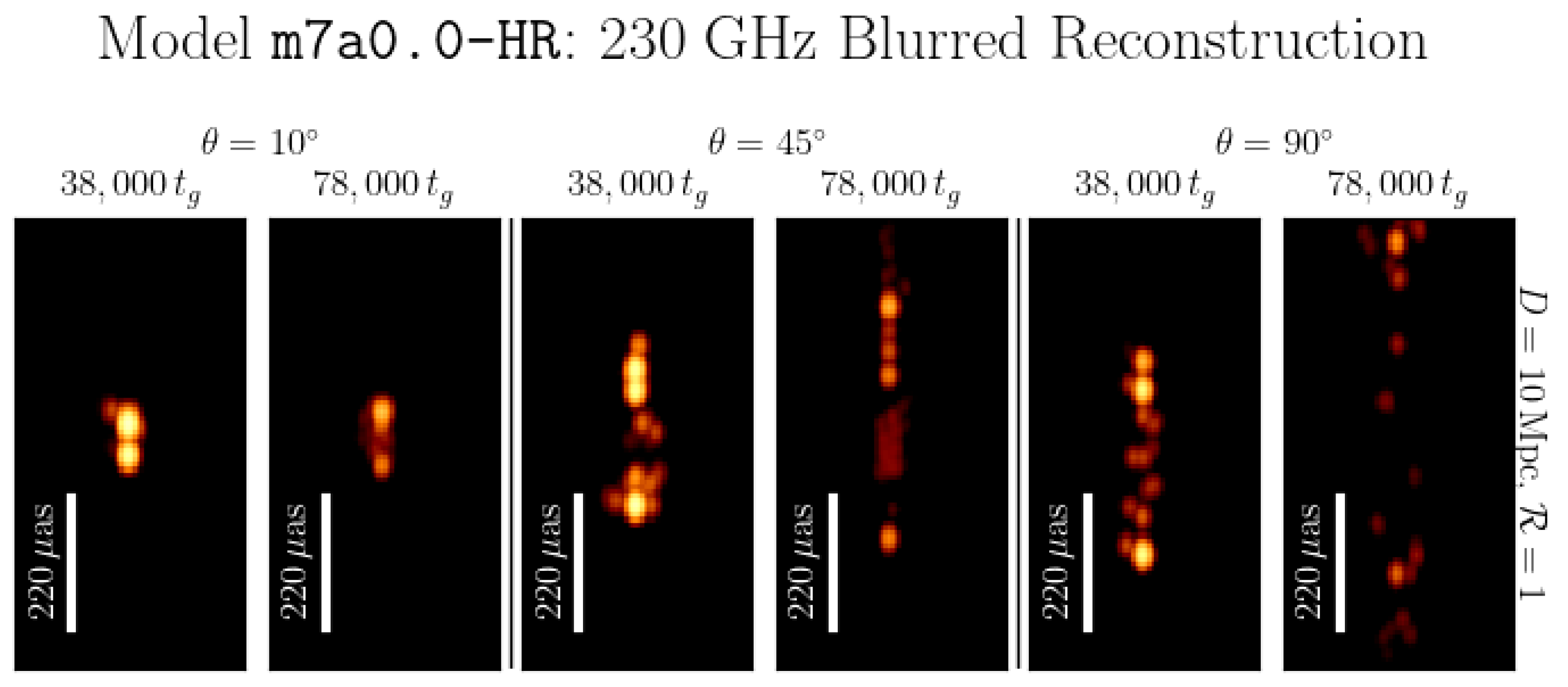
3. Results
3.1. Reconstructed Images
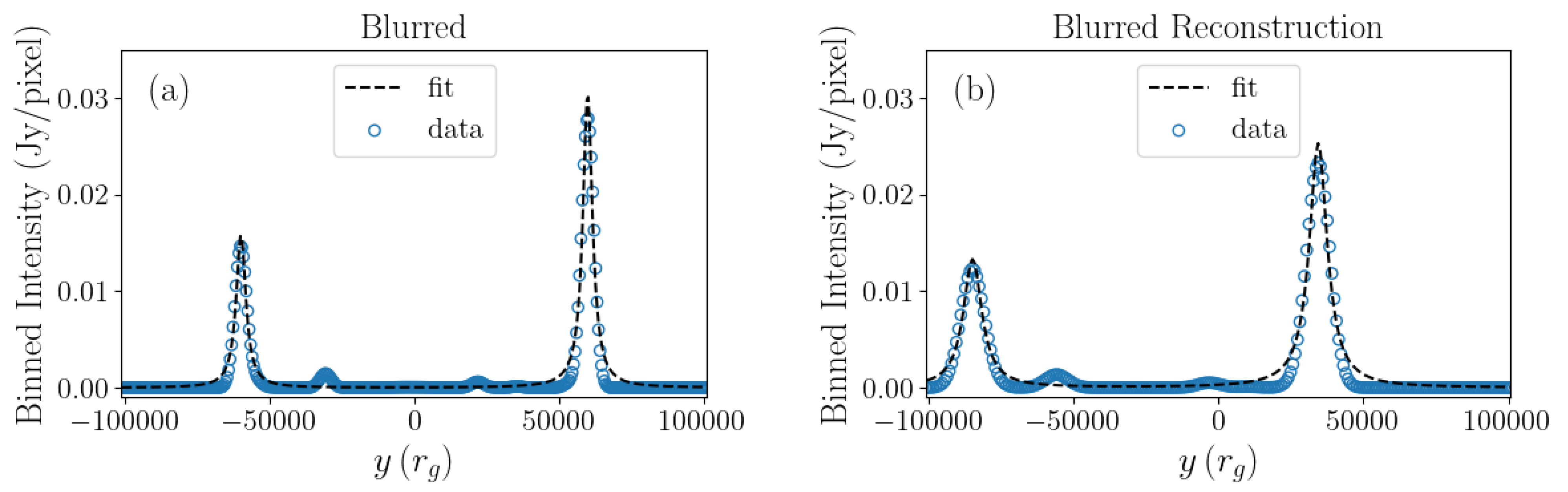
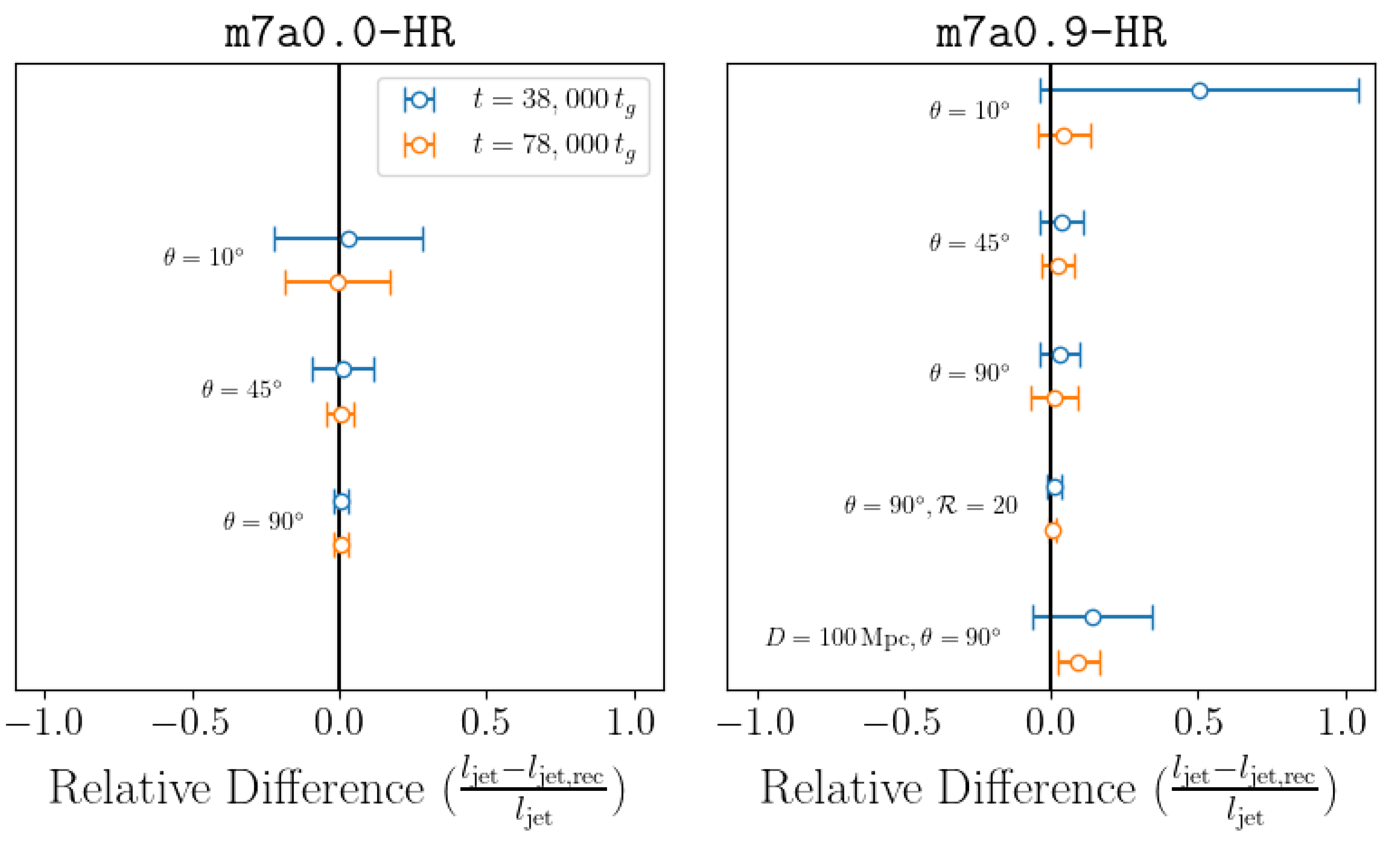
3.2. Tracking Jet Motion
4. Discussion
4.1. Extracting Jet Physics from VLBI Images
4.2. Proposed Observational Methodology
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Full Image Library


Appendix B. Fitting Procedure for Jet Head Position
| 1 | https://github.com/Smithsonian/ngehtsim (accessed on 1 June 2022). |
References
- Hills, J.G. Possible power source of Seyfert galaxies and QSOs. Nature 1975, 254, 295–298. [Google Scholar] [CrossRef]
- Rees, M.J. Tidal disruption of stars by black holes of 106–108 solar masses in nearby galaxies. Nature 1988, 333, 523–528. [Google Scholar] [CrossRef]
- Guillochon, J.; Ramirez-Ruiz, E. Hydrodynamical Simulations to Determine the Feeding Rate of Black Holes by the Tidal Disruption of Stars: The Importance of the Impact Parameter and Stellar Structure. Astrophys. J. 2013, 767, 25. [Google Scholar] [CrossRef]
- Mainetti, D.; Lupi, A.; Campana, S.; Colpi, M.; Coughlin, E.R.; Guillochon, J.; Ramirez-Ruiz, E. The fine line between total and partial tidal disruption events. Astron. Astrophys. 2017, 600, A124. [Google Scholar] [CrossRef]
- Steinberg, E.; Stone, N.C. The Origins of Peak Light in Tidal Disruption Events. arXiv 2022, arXiv:2206.10641. [Google Scholar] [CrossRef]
- Stone, N.; Sari, R.; Loeb, A. Consequences of strong compression in tidal disruption events. MNRAS 2013, 435, 1809–1824. [Google Scholar] [CrossRef]
- Abramowicz, M.A.; Calvani, M.; Nobili, L. Thick accretion disks with super-Eddington luminosities. Astrophys. J. 1980, 242, 772–788. [Google Scholar] [CrossRef]
- Abramowicz, M.A.; Czerny, B.; Lasota, J.P.; Szuszkiewicz, E. Slim Accretion Disks. Astrophys. J. 1988, 332, 646. [Google Scholar] [CrossRef]
- Golightly, E.C.A.; Nixon, C.J.; Coughlin, E.R. On the Diversity of Fallback Rates from Tidal Disruption Events with Accurate Stellar Structure. Astrophys. J. 2019, 882, L26. [Google Scholar] [CrossRef]
- Komossa, S. Tidal disruption of stars by supermassive black holes: Status of observations. J. High Energy Astrophys. 2015, 7, 148–157. [Google Scholar] [CrossRef]
- Gezari, S. Tidal Disruption Events. ARA&A 2021, 59, 21–58. [Google Scholar] [CrossRef]
- Alexander, K.D.; van Velzen, S.; Horesh, A.; Zauderer, B.A. Radio Properties of Tidal Disruption Events. Space Sci. Rev. 2020, 216, 81. [Google Scholar] [CrossRef]
- Dai, L.; McKinney, J.C.; Roth, N.; Ramirez-Ruiz, E.; Miller, M.C. A Unified Model for Tidal Disruption Events. Astrophys. J. 2018, 859, L20. [Google Scholar] [CrossRef]
- Curd, B.; Emami, R.; Anantua, R.; Palumbo, D.; Doeleman, S.; Narayan, R. Jets from SANE Super-Eddington Accretion Disks: Morphology, Spectra, and Their Potential as Targets for ngEHT. arXiv 2022, arXiv:2206.06358. [Google Scholar]
- Gammie, C.F.; McKinney, J.C.; Tóth, G. HARM: A Numerical Scheme for General Relativistic Magnetohydrodynamics. Astrophys. J. 2003, 589, 444–457. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; Metzger, B.D.; Giannios, D.; Kelley, L.Z. Swift J1644+57 gone MAD: The case for dynamically important magnetic flux threading the black hole in a jetted tidal disruption event. MNRAS 2014, 437, 2744–2760. [Google Scholar] [CrossRef]
- Curd, B.; Narayan, R. GRRMHD simulations of tidal disruption event accretion discs around supermassive black holes: Jet formation, spectra, and detectability. MNRAS 2019, 483, 565–592. [Google Scholar] [CrossRef]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. MNRAS 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Abramowicz, M.A.; Ellis, G.F.R.; Lanza, A. Relativistic Effects in Superluminal Jets and Neutron Star Winds. Astrophys. J. 1990, 361, 470. [Google Scholar] [CrossRef]
- Coughlin, E.R.; Begelman, M.C. Structured, relativistic jets driven by radiation. MNRAS 2020, 499, 3158–3177. [Google Scholar] [CrossRef]
- Dadhich, N.; Tursunov, A.; Ahmedov, B.; Stuchlík, Z. The distinguishing signature of magnetic Penrose process. MNRAS 2018, 478, L89–L94. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M.; Kovář, J.; Slaný, P.; Tursunov, A. Influence of Cosmic Repulsion and Magnetic Fields on Accretion Disks Rotating around Kerr Black Holes. Universe 2020, 6, 26. [Google Scholar] [CrossRef]
- Penrose, R. Gravitational Collapse: The Role of General Relativity. Nuovo Cim. Riv. Ser. 1969, 1, 252. [Google Scholar]
- Thomsen, L.L.; Kwan, T.M.; Dai, L.; Wu, S.C.; Roth, N.; Ramirez-Ruiz, E. Dynamical Unification of Tidal Disruption Events. Astrophys. J. 2022, 937, L28. [Google Scholar] [CrossRef]
- Penna, R.F.; Narayan, R.; Sądowski, A. General relativistic magnetohydrodynamic simulations of Blandford-Znajek jets and the membrane paradigm. MNRAS 2013, 436, 3741–3758. [Google Scholar] [CrossRef]
- Doeleman, S.; Blackburn, L.; Dexter, J.; Gomez, J.L.; Johnson, M.D.; Palumbo, D.C.; Weintroub, J.; Farah, J.R.; Fish, V.; Loinard, L.; et al. Studying Black Holes on Horizon Scales with VLBI Ground Arrays. Bull. Am. Astron. Soc. 2019, 51, 256. [Google Scholar]
- Ivezić, Ž.; Kahn, S.M.; Tyson, J.A.; Abel, B.; Acosta, E.; Allsman, R.; Alonso, D.; AlSayyad, Y.; Anderson, S.F.; Andrew, J.; et al. LSST: From Science Drivers to Reference Design and Anticipated Data Products. Astrophys. J. 2019, 873, 111. [Google Scholar] [CrossRef]
- Bricman, K.; Gomboc, A. The Prospects of Observing Tidal Disruption Events with the Large Synoptic Survey Telescope. Astrophys. J. 2020, 890, 73. [Google Scholar] [CrossRef]
- Stone, N.C.; Metzger, B.D. Rates of stellar tidal disruption as probes of the supermassive black hole mass function. MNRAS 2016, 455, 859–883. [Google Scholar] [CrossRef]
- Sadowski, A.; Tejeda, E.; Gafton, E.; Rosswog, S.; Abarca, D. Magnetohydrodynamical simulations of a deep tidal disruption in general relativity. Mon. Not. Roy. Astron. Soc. 2016, 458, 4250–4268. [Google Scholar] [CrossRef]
- Curd, B. Global simulations of tidal disruption event disc formation via stream injection in GRRMHD. Mon. Not. Roy. Astron. Soc. 2021, 507, 3207–3227. [Google Scholar] [CrossRef]
- Novikov, I.D.; Thorne, K.S. Astrophysics of black holes. In Black Holes (Les Astres Occlus); Gordon & Breach: New York, NY, USA, 1973; pp. 343–450. [Google Scholar]
- Sądowski, A.; Narayan, R.; Tchekhovskoy, A.; Abarca, D.; Zhu, Y.; McKinney, J.C. Global simulations of axisymmetric radiative black hole accretion discs in general relativity with a mean-field magnetic dynamo. MNRAS 2015, 447, 49–71. [Google Scholar] [CrossRef]
- Barniol Duran, R.; Tchekhovskoy, A.; Giannios, D. Simulations of AGN jets: Magnetic kink instability versus conical shocks. MNRAS 2017, 469, 4957–4978. [Google Scholar] [CrossRef]
- Mościbrodzka, M.; Gammie, C.F. IPOLE - semi-analytic scheme for relativistic polarized radiative transport. MNRAS 2018, 475, 43–54. [Google Scholar] [CrossRef]
- Yarza, R.; Wong, G.N.; Ryan, B.R.; Gammie, C.F. Bremsstrahlung in GRMHD Models of Accreting Black Holes. Astrophys. J. 2020, 898, 50. [Google Scholar] [CrossRef]
- Wong, G.N.; Prather, B.S.; Dhruv, V.; Ryan, B.R.; Mościbrodzka, M.; Chan, C.k.; Joshi, A.V.; Yarza, R.; Ricarte, A.; Shiokawa, H.; et al. PATOKA: Simulating Electromagnetic Observables of Black Hole Accretion. Astrophys. J. 2022, 259, 64. [Google Scholar] [CrossRef]
- Ohmura, T.; Machida, M.; Nakamura, K.; Kudoh, Y.; Asahina, Y.; Matsumoto, R. Two-Temperature Magnetohydrodynamics Simulations of Propagation of Semi-Relativistic Jets. Galaxies 2019, 7, 14. [Google Scholar] [CrossRef]
- Ohmura, T.; Machida, M.; Nakamura, K.; Kudoh, Y.; Matsumoto, R. Two-temperature magnetohydrodynamic simulations for sub-relativistic active galactic nucleus jets: Dependence on the fraction of the electron heating. MNRAS 2020, 493, 5761–5772. [Google Scholar] [CrossRef]
- Raymond, A.W.; Palumbo, D.; Paine, S.N.; Blackburn, L.; Córdova Rosado, R.; Doeleman, S.S.; Farah, J.R.; Johnson, M.D.; Roelofs, F.; Tilanus, R.P.J.; et al. Evaluation of New Submillimeter VLBI Sites for the Event Horizon Telescope. Astrophys. J. 2021, 253, 5. [Google Scholar] [CrossRef]
- Roelofs, F.; et al. [Black Hole Initiative at Harvard University], 2022; in preparation.
- Chael, A.A.; Johnson, M.D.; Narayan, R.; Doeleman, S.S.; Wardle, J.F.C.; Bouman, K.L. High-resolution Linear Polarimetric Imaging for the Event Horizon Telescope. Astrophys. J. 2016, 829, 11. [Google Scholar] [CrossRef]
- Chael, A.A.; Johnson, M.D.; Bouman, K.L.; Blackburn, L.L.; Akiyama, K.; Narayan, R. Interferometric Imaging Directly with Closure Phases and Closure Amplitudes. Astrophys. J. 2018, 857, 23. [Google Scholar] [CrossRef]
- Doeleman, S.; et al. [Harvard-Smithsonian Center for Astrophysics], 2022; in preparation.
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Paine, S. The Am Atmospheric Model. 2019. Available online: https://zenodo.cern.ch/record/3406496#.Y5fRyH1ByUk (accessed on 1 June 2022).
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. IV. Imaging the Central Supermassive Black Hole. Astrophys. J. 2019, 875, L4. [Google Scholar] [CrossRef]
- Jorstad, S.G.; Marscher, A.P.; Lister, M.L.; Stirling, A.M.; Cawthorne, T.V.; Gear, W.K.; Gómez, J.L.; Stevens, J.A.; Smith, P.S.; Forster, J.R.; et al. Polarimetric Observations of 15 Active Galactic Nuclei at High Frequencies: Jet Kinematics from Bimonthly Monitoring with the Very Long Baseline Array. Astrophys. J. 2005, 130, 1418–1465. [Google Scholar] [CrossRef]
- Lister, M.L.; Aller, M.F.; Aller, H.D.; Homan, D.C.; Kellermann, K.I.; Kovalev, Y.Y.; Pushkarev, A.B.; Richards, J.L.; Ros, E.; Savolainen, T. MOJAVE. X. Parsec-scale Jet Orientation Variations and Superluminal Motion in Active Galactic Nuclei. Astrophys. J. 2013, 146, 120. [Google Scholar] [CrossRef]
- Cohen, M.H.; Meier, D.L.; Arshakian, T.G.; Homan, D.C.; Hovatta, T.; Kovalev, Y.Y.; Lister, M.L.; Pushkarev, A.B.; Richards, J.L.; Savolainen, T. Studies of the Jet in Bl Lacertae. I. Recollimation Shock and Moving Emission Features. Astrophys. J. 2014, 787, 151. [Google Scholar] [CrossRef]
- Kohler, S.; Begelman, M.C.; Beckwith, K. Recollimation boundary layers in relativistic jets. MNRAS 2012, 422, 2282–2290. [Google Scholar] [CrossRef][Green Version]
- Lazzati, D.; Morsony, B.J.; Blackwell, C.H.; Begelman, M.C. Unifying the Zoo of Jet-driven Stellar Explosions. Astrophys. J. 2012, 750, 68. [Google Scholar] [CrossRef]
- Mizuno, Y.; Gómez, J.L.; Nishikawa, K.I.; Meli, A.; Hardee, P.E.; Rezzolla, L. Recollimation Shocks in Magnetized Relativistic Jets. Astrophys. J. 2015, 809, 38. [Google Scholar] [CrossRef]
- Hervet, O.; Meliani, Z.; Zech, A.; Boisson, C.; Cayatte, V.; Sauty, C.; Sol, H. Shocks in relativistic transverse stratified jets. A new paradigm for radio-loud AGN. Astron. Astrophys. 2017, 606, A103. [Google Scholar] [CrossRef]
- Gómez, J.L.; Lobanov, A.P.; Bruni, G.; Kovalev, Y.Y.; Marscher, A.P.; Jorstad, S.G.; Mizuno, Y.; Bach, U.; Sokolovsky, K.V.; Anderson, J.M.; et al. Probing the Innermost Regions of AGN Jets and Their Magnetic Fields with RadioAstron. I. Imaging BL Lacertae at 21 Microarcsecond Resolution. Astrophys. J. 2016, 817, 96. [Google Scholar] [CrossRef]
- Zauderer, B.A.; Berger, E.; Margutti, R.; Pooley, G.G.; Sari, R.; Soderberg, A.M.; Brunthaler, A.; Bietenholz, M.F. Radio Monitoring of the Tidal Disruption Event Swift J164449.3+573451. II. The Relativistic Jet Shuts Off and a Transition to Forward Shock X-Ray/Radio Emission. Astrophys. J. 2013, 767, 152. [Google Scholar] [CrossRef]
- Pasham, D.R.; Cenko, S.B.; Levan, A.J.; Bower, G.C.; Horesh, A.; Brown, G.C.; Dolan, S.; Wiersema, K.; Filippenko, A.V.; Fruchter, A.S.; et al. A Multiwavelength Study of the Relativistic Tidal Disruption Candidate Swift J2058.4+0516 at Late Times. Astrophys. J. 2015, 805, 68. [Google Scholar] [CrossRef]
- Curd, B.; Narayan, R. GRRMHD Simulations of MAD Accretion Disks Declining from Super-Eddington to Sub-Eddington Accretion Rates. arXiv 2022, arXiv:2209.12081. [Google Scholar]
- Liska, M.T.P.; Musoke, G.; Tchekhovskoy, A.; Porth, O.; Beloborodov, A.M. Formation of Magnetically Truncated Accretion Disks in 3D Radiation-transport Two-temperature GRMHD Simulations. Astrophys. J. 2022, 935, L1. [Google Scholar] [CrossRef]
- Cendes, Y.; Berger, E.; Alexander, K.D.; Gomez, S.; Hajela, A.; Chornock, R.; Laskar, T.; Margutti, R.; Metzger, B.; Bietenholz, M.F.; et al. A Mildly Relativistic Outflow Launched Two Years after Disruption in Tidal Disruption Event AT2018hyz. Astrophys. J. 2022, 938, 28. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
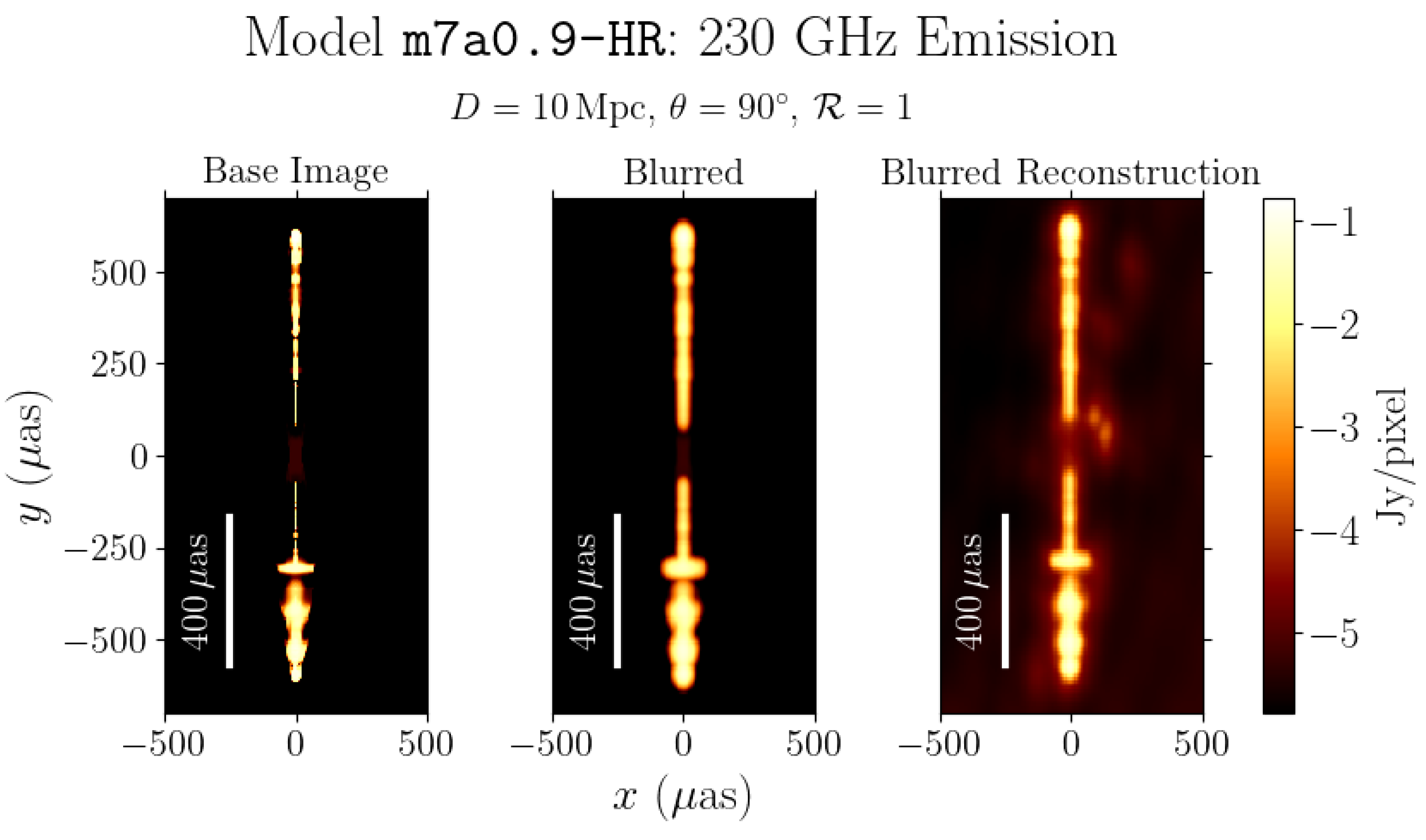
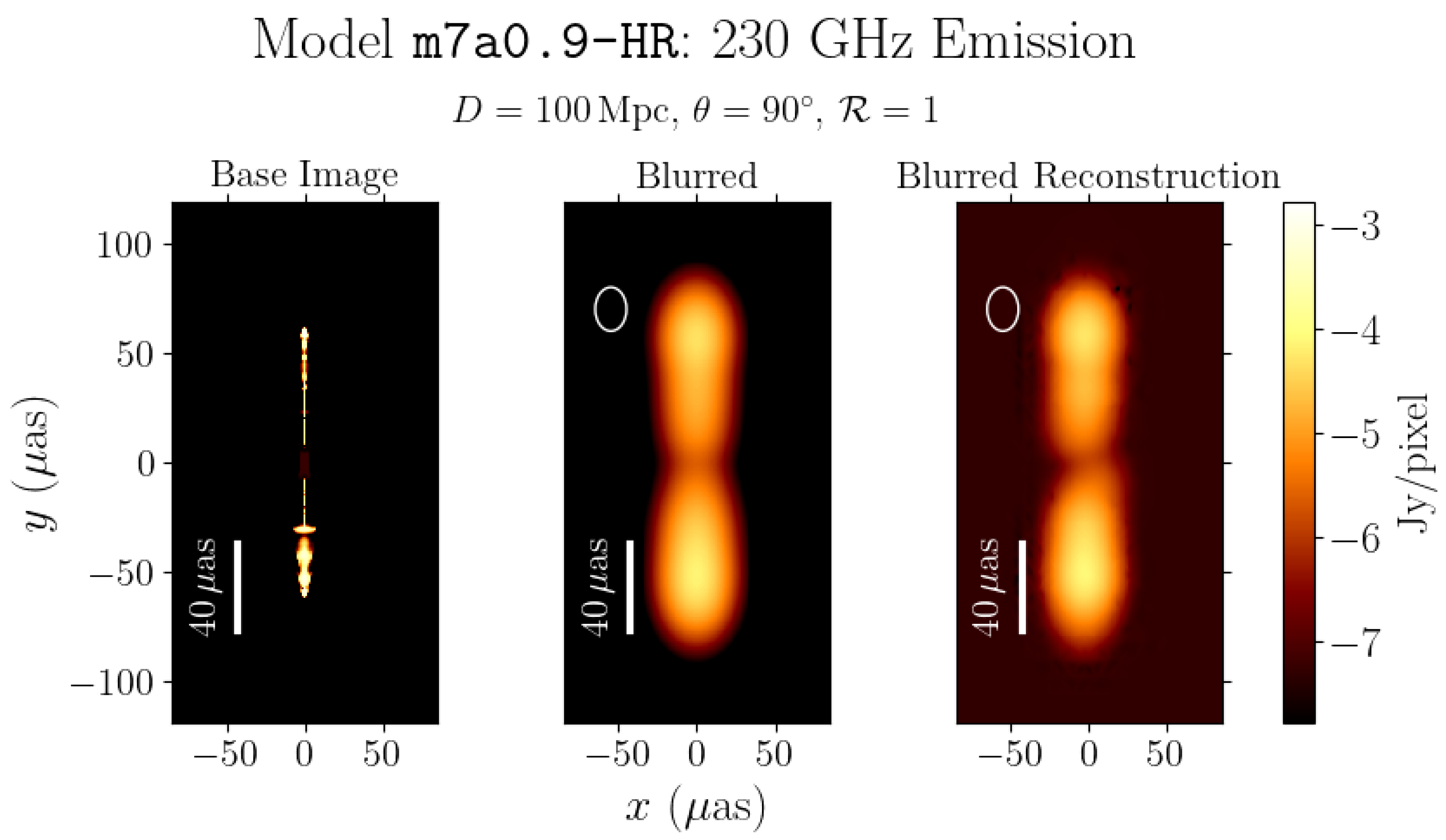
| Model | |||
|---|---|---|---|
| () | |||
| m7a0.0-HR | 12 | 0.24% | 83,000 |
| m7a0.9-HR | 25 | 1.15% | 81,200 |
| Model | Time | Distance | ||||
|---|---|---|---|---|---|---|
| (Mpc) | (Jy) | |||||
| m7a0.0-HR | 38,000 | 10 | 1 | 0.219 | 0.214 | 0.074 |
| 78,000 | 10 | 1 | 0.014 | 0.013 | 0.006 | |
| m7a0.9-HR | 38,000 | 10 | 1 | 2.001 | 4.452 | 6.036 |
| 78,000 | 10 | 1 | 11.968 | 26.780 | 35.092 | |
| 38,000 | 10 | 20 | - | - | 0.190 | |
| 78,000 | 10 | 20 | - | - | 0.485 | |
| 38,000 | 100 | 1 | - | - | 0.060 | |
| 78,000 | 100 | 1 | - | - | 0.351 |
| Model | Time | Distance | ||||
|---|---|---|---|---|---|---|
| (Mpc) | ||||||
| m7a0.0-HR | 38,000 | 10 | 1 | |||
| 78,000 | 10 | 1 | ||||
| 38,000 | 10 | 1 | ||||
| 78,000 | 10 | 1 | ||||
| 38,000 | 10 | 1 | ||||
| 78,000 | 10 | 1 | ||||
| m7a0.9-HR | 38,000 | 10 | 1 | |||
| 78,000 | 10 | 1 | ||||
| 38,000 | 10 | 1 | ||||
| 78,000 | 10 | 1 | ||||
| 38,000 | 10 | 1 | ||||
| 78,000 | 10 | 1 | ||||
| 38,000 | 10 | 20 | ||||
| 78,000 | 10 | 20 | ||||
| 38,000 | 100 | 1 | ||||
| 78,000 | 100 | 1 |
| Model | Distance | v | ||||
|---|---|---|---|---|---|---|
| (Mpc) | ||||||
| m7a0.0-HR | 10 | 1 | ||||
| 10 | 1 | |||||
| 10 | 1 | |||||
| m7a0.9-HR | 10 | 1 | ||||
| 10 | 1 | |||||
| 10 | 1 | |||||
| 10 | 20 | |||||
| 100 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Curd, B.; Emami, R.; Roelofs, F.; Anantua, R. Modeling Reconstructed Images of Jets Launched by SANE Super-Eddington Accretion Flows around SMBHs with the ngEHT. Galaxies 2022, 10, 117. https://doi.org/10.3390/galaxies10060117
Curd B, Emami R, Roelofs F, Anantua R. Modeling Reconstructed Images of Jets Launched by SANE Super-Eddington Accretion Flows around SMBHs with the ngEHT. Galaxies. 2022; 10(6):117. https://doi.org/10.3390/galaxies10060117
Chicago/Turabian StyleCurd, Brandon, Razieh Emami, Freek Roelofs, and Richard Anantua. 2022. "Modeling Reconstructed Images of Jets Launched by SANE Super-Eddington Accretion Flows around SMBHs with the ngEHT" Galaxies 10, no. 6: 117. https://doi.org/10.3390/galaxies10060117
APA StyleCurd, B., Emami, R., Roelofs, F., & Anantua, R. (2022). Modeling Reconstructed Images of Jets Launched by SANE Super-Eddington Accretion Flows around SMBHs with the ngEHT. Galaxies, 10(6), 117. https://doi.org/10.3390/galaxies10060117