Abstract
A three-dimensional numerical model has been developed to study the flow structure in close binary systems with a magnetic field. The model uses a system of equations of modified magnetic hydrodynamics, which allows describing all the main dynamic effects associated with the magnetic field. It takes into account the processes of radiation heating and cooling, heating due to current dissipation, as well as magnetic field diffusion. The model allows calculations in a wide range of magnetic field values. Comparison of the calculation results with observational data confirms the reliability and high efficiency of the model. The paper presents the calculation results of the flow structure in a typical intermediate polar. It is shown that an accretion disk is formed in such a binary system, which has the following characteristic features: “hot line”, tidal shock waves, precession density wave, magnetospheric region, and accretion columns. In this case, the magnetic field in the disk is predominantly toroidal. The paper also presents the results of calculations for typical polars. In such systems, instead of an accretion disk, a collimated stream of matter is formed, moving along the magnetic field lines to the magnetic poles of the white dwarf. It is shown that in synchronous polars, variations of the mass transfer rate lead to a change in the spatial configuration of the flow. In asynchronous polars, changes in the flow structure for different phases of the beat period are observed as well as the processes of switching the flow between the magnetic poles of the accretor. Numerical calculations of the asynchronous system are performed under the assumption of the dipole configuration of the magnetic field for different values of the dipole offset relative to the center of the white dwarf. The paper presents a method for estimating this offset from observational light curves.
Keywords:
close binary star; polar; intermediate polar; accretion disk; MHD; flow structure; donor; accretor; mass transfer; poles switching 1. Introduction
The paper discusses the objects belonging to the subclass of magnetic cataclysmic variable stars, in which the compact component has a magnetic field of a certain magnitude. Magnetic cataclysmic variables (mCV) are close binary systems consisting of a low-mass star of the late spectral class (K or M)–a red dwarf (donor, secondary component) and its companion–a white dwarf (accretor, primary component). When, during evolution, the secondary component fills its Roche lobe, the matter begins to flow into the inner Roche lobe of the white dwarf (see, for example, [1]). This process becomes possible due to the fact that at the inner Lagrange point , the pressure gradient is not balanced by the gravity force. The magnetic field of the white dwarf has no noticeable effect on the outflow of matter from the donor, which depends primarily on the density and velocity of the flow at the inner Lagrange point but significantly determines the geometry of the flow in the magnetosphere of the primary component.
The geometry of the matter flow after it leaves the inner Lagrange point will be determined by two main factors–the mass transfer rate and the strength of the magnetic field of the accretor. The first factor, along with the acting forces in the rotating binary system (Coriolis force and centrifugal force), contributes to the deviation of the flow away from the direction to the white dwarf. In addition, the increase in the mass transfer rate leads to the elongation of the ballistic part of the jet trajectory.
The magnitude of the accretor magnetic field B affects the behavior of the matter flowing from the donor near the accretor. Depending on this value, two characteristic flow configurations are possible, which determine the separation of magnetic cataclysmic variables into polars and intermediate polars.
In the intermediate polars [2], the magnetic field turns out to be weak enough ( MGs) to capture matter immediately after it has left the inner Lagrange point, so in such systems, an accretion disk is formed in the outer part of the accretor Roche lobe to the boundary of its magnetosphere. In the inner part of the magnetosphere, where the disk matter significantly loses its angular momentum, the flow movement already occurs along magnetic field lines to the vicinity of the magnetic poles [3]. Intermediate polars, due to the low magnetic field strength, are characterized by a significant asynchronism of the accretor’s proper rotation with respect to the orbital motion of entire system [4]. This leads to different disk configurations and accretion modes. In particular, with a sufficiently fast rotation of the white dwarf, the complete disappearance of the accretion disk is possible (the so-called <<superpropeller>> mode): the matter flowing from the donor is forced out by the centrifugal force of the accretor into the vicinity of the external Lagrange point , from where it irrevocably leaves the binary system.
With an increase in the magnetic field strength in the polars [1] ( MGs), the Alfven radius of the accretor (the effective radius of its magnetosphere) increases, which becomes comparable to the inter-component distance in these binary systems. This means that the magnetic field is able to control the donor’s outflow matter already in the vicinity of the Lagrange point . Therefore, a collimated jet is formed in the polars instead of a disk. A strong magnetic field also contributes to the synchronization of the rotation of the accretor with the orbital period of the polar [5,6]. Even at the evolutionary phases of flare activity, asynchronism does not exceed [7]. To date, about 100 synchronous and only seven asynchronous polars are known. Synchronism in these binary stars means that the position of the accretor’s magnetic poles relatively to the donor (point ) is constant, so the flow configuration mostly corresponds to unipolar accretion. However, with the specified amount of asynchronism, the process of switching the flow from one magnetic pole to another can occur in the system. In addition, with a significant value of the mass transfer rate, a configuration of bipolar accretion is possible. The fallout of matter in the polars, as well as in the intermediate polars, occurs in the vicinity of the magnetic poles of the white dwarf in the form of accretion columns.
The paper is organized as follows. The second section describes the numerical model we use. The third section represents the results of numerical calculations of the flow structure for polars and intermediate polars. The fourth section is devoted to the description of the methodology for estimating the configuration of the magnetic field from observational light curves. In conclusion, the main inferences of the paper are briefly discussed.
2. Numerical Model
The first numerical simulations of the influence of magnetic field on the flow structure were carried out in the early 1990s. Due to the high complexity of the problem, these investigations had a number of limitations and simplifications. So, for example, in the works [4,8,9,10], the quasi-particle method was used to simulate the flow structure in mCV. It has been shown that the flow structure in intermediate polars, depending on the configuration of the magnetic field, can include both the accretion disk, similar to disks in non-magnetic cataclysmic variables, and accretion flows held by a magnetic field. However, these calculations did not take into account a number of important effects, such as the influence of gas and magnetic pressures, heating–cooling processes, the generation of a magnetic field in the disk, and others.
Accretion processes in the magnetosphere of a white dwarf have been studied more thoroughly. In the works [11,12,13,14], the results of three-dimensional numerical simulation of plasma accretion on a gravitating object with a dipole-type magnetic field, whose axis does not coincide with axis of the orbital rotation, are presented. These works enabled to study in detail the flow structure in the central object region, where the magnetic field plays a dominant role; however, the computational domain of the model included only a small neighborhood of the accretor star.
Another approach to modeling the flow structure in the binary stars under consideration is the smoothed particles hydrodynamics (SPH). Using this approach, in the work [15], a system was investigated, where the axis of the accretor’s proper rotation, the orbital axis and the axis of the magnetic dipole had different directions. Here, the influence of the magnetic field was taken into account by introducing a model external force.
Of particular interest are the investigations of mCV with a fast rotating white dwarf. The study of the interaction of white dwarf magnetic field and a jet of matter flowing in its Roche lobe was carried out until recently under a number of simplifying assumptions [9,16]. In particular, the jet was modeled as a superposition of diamagnetic clumps, which were considered as test particles during the calculations. At the same time, the deformation and heating of the clots were not taken into account. The dispersion of the velocities of outflow matter within the framework of this approach was interpreted in terms of the differences of test particles in masses, radii, and trajectories of their movements in the Roche lobe of the white dwarf. The reasons leading to fragmentation of the initial jet into clots were not considered.
In this paper, we present a recently developed a self-consistent three-dimensional numerical MHD model for calculating the flow structure in close binary stars in the presence of a strong magnetic field [2,17]. This model allows us to eliminate the disadvantages of the above mCV modeling methods and it is based on the approximation of the modified magnetic hydrodynamics [2,17,18,19]. This approximation describes the plasma motion in very strong external magnetic field, and it also takes into account the turbulence of Alfven waves at small magnetic Reynolds numbers () [20].
It is worth noting that in the accretion jets of mCVs, the propagation velocities of Alfven and magnetosonic waves can be many times higher than the velocity of the plasma itself, and in some cases be relativistic, so the use of a non-relativistic ideal MHD does not give a correct result. During the characteristic dynamic time of the evolution of the slow plasma flow, MHD waves can pass through the accretion jet in the longitudinal and transverse directions many times [21]. Therefore, the plasma dynamics in the jet can be considered in the framework of a modified non-relativistic ideal MHD as some averaged flow against the background of wave MHD turbulence [22,23,24].
A complete system of equations of modified MHD describe all the main dynamic effects associated with the magnetic field: the processes of radiation heating and cooling, the diffusion of the magnetic field due to the dissipation of currents in turbulent vortices, magnetic buoyancy and wave MHD turbulence. In the model, the formation and subsequent evolution of the accretion jet occur naturally as a result of the mass transfer process through the internal Lagrange point. In addition, the model is able to take into account some additional effects in the case of a complex magnetic field. For example, such a field configuration, having a significant quadruple component, has the asynchronous polar BY Cam, which is confirmed by numerous observations [25].
Below are the essential points of the model used. In semi-detached binary systems, the donor star fills its internal critical surface, which can be identified as a Roche lobe in the limited three-body problem. In a non-inertial reference frame rotating with a binary star at angular velocity , where is the orbital period of the binary system, around its mass center, the field of forces acting on matter is determined by the Roche potential [2]:
where G is the gravitational constant, A is the distance between the accretor and donor centers, and , are the accretor and donor mass, respectively. The first and second terms in the expression (1) describe the gravitational potentials of the accretor and the donor, and the last term is the centrifugal potential relative to the mass center.
The selected reference frame uses a Cartesian coordinate system (x, y, z). Its beginning is located at the center of the accretor (Figure 1).
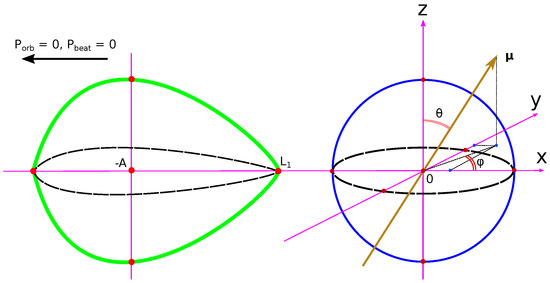
Figure 1.
The Cartesian coordinate system used in the model. The position of the accretor and the donor, the magnetic axis and the reference direction of the orbital phase, as well as the phases of the beat period for the asynchronous system are shown.
The donor’s center is located at a distance A from the origin along the x axis. The z axis is directed along the axis of rotation of the binary system: . For binary systems, the rotation characteristics are the orbital period and the period of proper rotation of the accretor , which coincide in the case of synchronous polars. For asynchronous systems, additionally, we introduced the concept of a beat period numerically equal to the time interval between the same mutual phase positions of the donor and accretor. Its value is calculated by the formula:
In our model, the dipole configuration of the magnetic field is considered. The induction of such a field at an arbitrary point in space is described by the following expression:
where —magnetic moment, —characteristic value of magnetic field induction on the surface of a white dwarf obtained from observations; —accretor radius; R—distance from the center of the magnetic dipole to the observation point of the field; and —unit normal vector to the sphere of radius R, which is raised at the field point observation. The unit vector defines the axis of symmetry of the dipole. Its components in the given Cartesian coordinate system can be written as:
where the angles and determine the axis orientation of the magnetic dipole. The first is counted from the positive direction of the z axis, the second is counted from the positive direction of the x axis counterclockwise (against the orbital rotation of the binary system) (see Figure 1). In the case of a synchronous polar, the angle is constant in time and is equal to the initial value corresponding to the dipole position at the zero phase of the orbital period. For an asynchronous system, this angle already depends on time. Its increase with each orbital period occurs according to the following law:
where , —current time, and N—number of orbital periods from the zero phase of the beat period. The angle in the systems under consideration always remains constant.
It should be noted that the magnetic field , given by the Formula (3), is irrotational:
However, depending on the binary system under consideration, it will be stationary for a synchronous polar
and non-stationary for asynchronous polar
The irrotational nature of the magnetic field allows it to be partially excluded from the corresponding equations describing the structure of the MHD flow [2,26,27,28]. This makes it possible to avoid the errors accumulation by operations with large numbers during the calculation process. This technique consists of representing the total magnetic field as a superposition of the proper field of the accretor and the field , which are induced by electric currents in the accretion flow and the envelope of the binary system:
At the same time, in the difference scheme of numerical calculation, only the magnetic field disturbance is calculated. This splitting of the magnetic field is often used in the simulation of MHD accretion (see, for example, [11,12,13,14]).
In the case of asynchronous rotation of the accretor, the change in the field components over time is described by the following equations [2,17]:
Here, − magnetic lines velocity, vector . The time change of the component occurs according to the induction, as shown in Equation (14).
The following system of equations is used to simulate the flow structure within the modified MHD:
where —density, —velocity, P—pressure, —specific internal gas energy, n—concentration, and —radiation heating and cooling functions. The term in the equation of motion (13) describes the Coriolis force, and the presence of the term –the Roche gradient–is due to the fact that the selected non-inertial reference frame rotates together with a binary system. The last term in Equation (13) describes the effective electromagnetic force acting on the flow velocity component transverse to magnetic force lines (symbol ⊥) [29,30,31,32]. This force is similar to the friction force between the components of a plasma consisting of several types of particles (see, for example, [33,34]).
In the induction Equation (14), the term takes into account the diffusion of the magnetic field, where is the total coefficient of magnetic viscosity.
The energy Equation (14) includes two additional sources: describes the effect of radiative heating and cooling [35,36,37,38], and determines heating due to current dissipation (the work of a friction force with a magnetic field).
The numerical model uses a linear approximation of the functions of heating and cooling from the temperature T in the vicinity of its equilibrium value corresponding to the effective temperature of the white dwarf :
where , and are some constants whose values are set individually for a specific polar. When calculating the difference , the values and are reduced.
Investigating the flow structure in close binary stars under consideration, we used two types of numerical models–stationary and non-stationary. The first one is a sequence of numerical solutions in which the relative position of the donor and accretor at a certain point in time is fixed. In our model, entering of the numerical solution into the stationary mode occurs during at least two orbital periods. The parameters of the stationary model are described by Equations (6) and (7). Additionally, when applying the system of Equations (12)–(15) to the calculation of the flow structure in stationary mode, the magnitude of magnetic lines velocity should be taken equal to zero.
In the non-stationary model, which is usually used for asynchronous and intermediate polars, numerical solutions are obtained with continuous proper rotation of the accretor, which corresponds to the real system as much as possible. This allows us to record changes in its flow structure at very small time intervals. The parameters of the non-stationary model are described by the Equations (5), (6), (8), (10) and (11).
The density, internal energy and pressure are related by the equation of state of an ideal gas:
where is the adiabatic index.
Our model takes into account several mechanisms of magnetic viscosity. The magnetic viscosity coefficient , describing the effect of wave MHD turbulence, is determined by the following expression:
where is a dimensionless coefficient characterizing the efficiency of wave turbulence, and is a characteristic spatial scale of wave pulsations. In this model, the value of is assumed to be 1/3, which corresponds to the isotropic turbulence [39].
For intermediate polars, the total diffusion coefficient of the magnetic field is determined by three factors [5,40]
where —the diffusion coefficient due to the dissipation of currents in turbulent vortices
—the Shakura–Sunyaev dimensionless parameter [41], characterizing the turbulent viscosity in the accretion disk, —the speed of sound, —angular velocity of the Keplerian rotation of the disk; diffusion coefficient due to the buoyancy of the toroidal magnetic field tubes generated in the disk as a result of differential rotation
—the efficiency coefficient of magnetic buoyancy. In the calculations below, the values , were used.
For polars, the diffusion of the magnetic field due to the re-connection of its lines and magnetic buoyancy is negligible. Therefore, the only sufficient source of this diffusion is the wave MHD turbulence, i.e., . Then, the last term in the energy of Equation (15) can be written as follows:
The relaxation time scale for the transverse velocity component is determined by the expression:
The numerical model uses the following initial and boundary conditions. In the envelope of the donor star, the normal velocity component with respect to its surface was set equal to the local speed of sound , corresponding to the effective temperature of the donor . The gas density in the donor envelope is determined from the expression for the mass transfer rate through the internal Lagrange point :
where the cross-sectional area of the jet S from the donor is calculated by the formula [2,42]:
where and are dimensionless parameters depending on the mass ratio components of the binary system and defining, respectively, the major and minor semi-axes of the elliptical cross-section of the jet. The accretor is defined by a sphere with a radius of , at the boundary of which free flow conditions were set. Constant boundary conditions were set at the outer boundaries of the computational domain: density , temperature , magnetic field . Free expiration conditions were set for the velocity : when the velocity is directed outward, symmetric boundary conditions were used, and when the velocity is directed inward, the conditions were used. Initial conditions in the computational domain were density , temperature , velocity and magnetic field .
The result of the numerical solution of Equations (12)–(15) is the spatial distribution of the physical characteristics of a binary star (density, pressure, velocity, magnetic field strength) over the calculated domain. Based on this distribution of values, it is possible to form a visual pattern of the flow structure in the systems under consideration, for example, by density, which is shown in Section 3.
3. Calculation Results
3.1. Intermediate Polar
The system EX Hydrae (EX Hya) [43,44], which is one of the closest (distance about 65 ps) and brightest (magnitude−) cataclysmic variables, was chosen as an object for modeling the flow structure in intermediate polars. The initial parameters of the model are given in Table 1.

Table 1.
The initial parameters for numerical simulation of the intermediate polar EX Hya.
Figure 2 shows the density distribution in the equatorial plane () of the binary system. The resulting solution demonstrates the state of the intermediate polar with a stationary cold (disk temperature is close to the equilibrium temperature 10,460 K) accretion disk formed during the calculation time equal to forty orbital periods.

Figure 2.
Two-dimensional structure of the flow in the area of accretion disk for the intermediate polar EX Hya. The decimal logarithm of the density distribution in units of in the equatorial plane () of the binary system are shown.
Let us note essential features of the flow morphology, which are presented in the figure. In the intermediate polars, as a result of the mass transfer process, in addition to the accretion disk itself, a disk halo and a common inter-component envelope of the binary system [17,45] are formed. The jet flowing from the inner Lagrange point primarily interacts with the halo of the disk in the form of an oblique impact collision. The halo is located outside the disk and has a complex shape. The collision of flows leads to the formation of two shock waves and a tangential gap between them. All this shock structure is located outside the disk and has a complex shape. In this case, the collision of the jet directly with the disk is unstressed. Due to the fact that the distant parts of the halo have a low density, the shock wave caused by their interaction with the jet lies along the edge of the accretion disk. As the gas density in the halo increases, the shock wave bends and eventually occupies a position along the edge of the disk. In Figure 2, a corresponding formation is visible along the edge of the disk at the point where the jet enters it. This area of impact has a sufficiently large extent and can be called a “hotline”. At the point of interaction, the halo gas and the jet gas pass through shock waves corresponding to their flow, mix, and this matter moves along the tangential gap between the two shock waves. In the future, the disk itself, the halo, and the inter-component envelope are formed from this matter.
Another characteristic element of the flow structure under consideration is the two-arm spiral waves [46], which arise due to the tidal action of the donor star. These waves consist of two separate arms located on the outer edges of the accretion disk, and both arms do not fit the accretor but are located in the outer parts of the disk. This element of the flow forms a region of the disk associated with a gas-dynamic disturbance.
Shock waves (“hotline” and two-arm tidal waves) are located in the outer part of the accretion disk. The inner parts of the disk turn out to be gas-dynamically undisturbed. Consequently, in these parts, the gas particles will rotate around the accretor in elliptical orbits. A system of elliptical orbits of these particles with different eccentricities will form in the disk. The influence of the secondary component will lead to the retrograde precession of these elliptical orbits, when the major semi-axis of each orbit rotates in the direction opposite to the orbital motion [1]. Since the current lines cannot intersect in the gas-dynamic solution, the resulting ellipses will nest into each other (i.e., the major semi-axes will lie on the same straight line) and will rotate at the same angular velocity. If we trace the mutual motion of gas particles along these orbits, we obtain a spiral density wave, which is observed in the figure. The precession rate of this structure lies in the range between the precession rates of the outer and inner orbits. The results of calculations show that the precession wave is moving slowly in the reference frame of a remote observer, while in a non-inertial reference frame, the period of its revolution slightly exceeds the orbital one. Since particles with more elongated orbits acquire a higher velocity in the direction of the accretor in the corresponding part of the orbit compared to particles whose orbit has a small eccentricity, the precession density wave is accompanied by an influx of matter in the radial direction to the white dwarf.
In Figure 3, a three-dimensional picture of the flow near the accretor surface is presented. The upper panel of the figure represents a general view of the binary system. All the same flow elements that were described above for the two-dimensional solution are observed here. Additionally, we note that beside the magnetic field of the accretor, the magnetic field of the disk plays an essential role in the system, which by its nature is predominantly toroidal [47]. The magnetic field lines of the accretor shown in black have a distorted character in the outer part of the disk, which is due to the differential rotation of the latter. The superposition of the magnetic fields of the white dwarf and the disk forms a rather complex picture of the general field in the system.
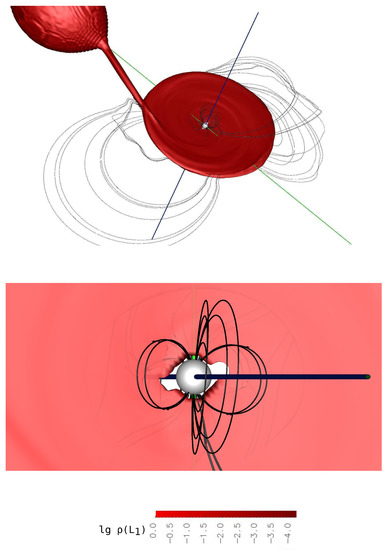
Figure 3.
The result of three-dimensional numerical modeling of the flow structure in the intermediate polar EX Hya. The iso-surfaces of the decimal logarithm of the density in units of are shown. The accretor is represented as a white sphere. The blue vertical line passing through the accretor coincides with its axis of rotation, and the green line coincides with its magnetic one. Black lines with the arrows indicate the magnetic field lines. The upper panel shows a general view of the system, the lower panel represents an accretion area near the surface of white dwarf.
The lower panel Figure 3 illustrates the flow structure in the region of the magnetosphere of white dwarf.
From the inner part of the disk, matter is captured by the magnetic field of the star and moves along its force lines toward the vicinity of the magnetic poles. As shown in works [48,49], the matter accretion to the surface of the primary component occurs in the form of columns. Due to the fact that the axis of the dipole in the polar under consideration lies in the plane of accretion disk (in the orbital plane of the binary system), an axisymmetric matter accretion to the magnetic poles is observed. Vacuum regions have formed in the area of the accretor’s magnetic equator. Their formation is caused by the fact that the magnetic field does not allow matter to penetrate into these regions, since in the area of the magnetic equator, magnetic force lines pass predominately along the surface of the star.
3.2. Synchronous Polar
A typical object V808 Aur was chosen as an illustration of the flow structure in a synchronous polar. It is known from observations that this binary system can be in four states of activity: high, medium, low and very low [50]. To study the flow structure, we performed four numerical calculations for the polar using a stationary model corresponding to the listed states. Their parameters are presented in Table 2.

Table 2.
A numerical calculation variants for the synchronous polar V808 Aur.

Table 3.
The initial data of calculations for synchronous polar V808 Aur.
In Figure 4, numerical solutions for Variants 1 and 2, and in Figure 5–for Variants 3 and 4 are presented.
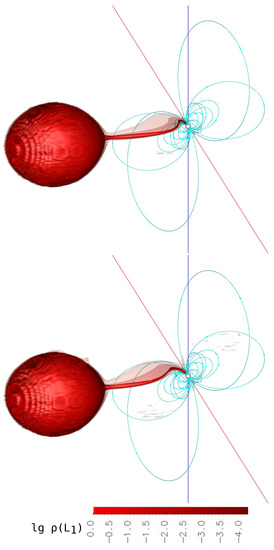
Figure 4.
The result of three-dimensional numerical modeling of the flow structure in the synchronous polar V808 Aur for Variant 1 (upper panel) and Variant 2 (lower panel). The iso-surfaces of the decimal logarithm of the density in units of are shown. The accretor is represented as a white sphere. The blue vertical line passing through the accretor coincides with its axis of rotation, and the inclined green line coincides with its magnetic one. The binary system is shown at the point of view of an Earth observer at the orbital phase 0.15.
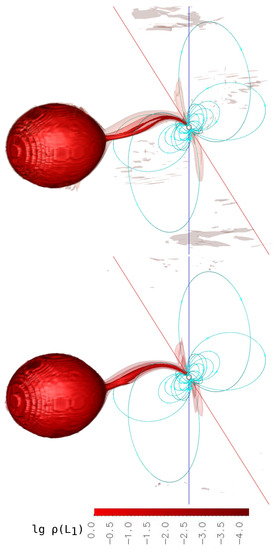
Figure 5.
The same as Figure 4 but for Variant 3 (upper panel) and Variant 4 (lower panel).
Let us note the general features of the resulting flow structure. It can be seen from the presented figures that with a given arrangement of the accretor magnetic poles relative to the orbital plane of the polar, flow geometry has an essentially three-dimensional nature. At the ballistic part of the jet trajectory, the matter moves in the orbital plane of the polar, and reaching the boundary of accretor magnetosphere, it begins to rise above it and is directed along the magnetic force lines to the magnetic pole of the white dwarf. In addition, the unipolar accretion regime prevails in this system. In general, this regime depends on the mass transfer rate and magnetic field strength as well as on the location of the magnetic poles relative to the inner Lagrange point. In the synchronous polar V808 Aur, a given combination of these parameters leads to the fact that the donor matter, leaving the vicinity of the inner Lagrange point , accretes mainly to the north magnetic pole of the white dwarf. From the analysis of the full pattern of the flow, it follows that accretion of matter to the south magnetic pole also takes place in the binary system. We assume that in this case, the source of the matter is the common envelope of the binary system. Its presence is due to the fact that based on the boundary conditions of the numerical model, the density of matter at the edges of the computational domain is not zero. Physically, the formation of a common envelope can occur due to two sources: the scattering a part of flow from the inner Lagrange point and the outflow of matter from the outer Lagrange point under the action of a dissipative process.
The figures also show an increase in the ratio of accretion to the north and south magnetic poles with a decrease in the state of the system (a decrease in the mass transfer rate). However, it should be taken into account that this effect has no physical basis but is associated with the peculiarities of the flow structure synthesis. Since each variant of the calculation has a proper value of the mass transfer rate, and hence, the density at the point , as an initial parameter, then with the same density scale used in the figures, a larger density gradient will be displayed with a decrease in the mass transfer rate, which leads to an apparent increase in the accretion rate to the south pole. In fact, the ratio of accretion rates to both poles for all calculation variants may differ by no more than 10%.
Let us now consider the geometry of the flow for various variants of numerical calculation. Their comparison shows that at a fixed value of the magnetic field strength, with an increase in the mass transfer rate, the jet deviates more strongly from the direction to the magnetic pole as a result of the action of inertia and Coriolis forces. In addition, the heterogeneity of the flow structure is noticeable: the jet consists of several layers, the density of which decreases from the center to the edge. As a result, the denser central layers of the current move along the ballistic part of the trajectory most of the time, while the less dense boundary layers are more quickly captured by the magnetic field of the white dwarf. This leads to a noticeable broadening of the flow at the boundary of the magnetosphere.
At the high polar state (Figure 4, upper panel), the ballistic part of the jet trajectory significantly prevails over the magnetic one, which is observed in the form of a strong bend of the flow line. The differentiation of the flow by density is also significant. This should lead to an increase in the area of the hot spot at the accretion point. The medium state of the polar (Figure 4, lower panel) is characterized by the equality of both parts of the jet trajectory, while the width of the jet at the boundary of the magnetosphere of the white dwarf decreases slightly, which indicates the alignment of the average flux density.
At the low polar state (Figure 5, upper panel), the same structures are presented as were noted in Variants 1 and 2; however, the following flow feature can be observed in the resulting solution. At a specific distance from the Lagrange point , the jet splits into two separate streams, which then merge again into one common stream ending at the magnetic pole region. The observed flow pattern is a confirmation of the hypothesis about the formation of a hierarchical magnetosphere in polars, expressed in [62], and is a consequence of the heterogeneity of the jet matter by density. Less dense layers of the flux are captured by the magnetic field at a greater distance from the accretor star and fill the outer regions of the magnetosphere. At the same time, the denser inner layers of the flux are deflected by the magnetic field at a smaller distance from the star, penetrating into the deep layers of the magnetosphere. Thus, depending on the density, each layer of the flow follows the magnetic pole along the proper magnetic line, which leads to the separation of the initially single current into many discrete flows. It is worth noting that due to insufficient spatial resolution, the calculations performed in [62] did not allow us to detect the described effect. In this study, a difference MHD scheme with a lower numerical viscosity is used, thanks to which a solution with a large number of details is obtained.
The solution in Variant 4 (Figure 5, lower panel) is characterized by the complete absence of the ballistic part of the jet trajectory. Leaving the inner Lagrange point, the matter is almost immediately captured by the accretor’s magnetic field and directed along the force lines to its magnetic pole.
3.3. Asynchronous Polar
As an illustration of the flow structure in this type of binary systems, the results of a study for the typical asynchronous polar CD Ind are presented. A feature of this binary system is the configuration of the magnetic field of a white dwarf with an offset dipole. The magnetic dipole intersects the rotation axis of the accretor, while the center of the dipole is shifted along it below the orbital plane by an amount of . MHD modeling of this polar [63] revealed two characteristic modes of the flow accretion during the beat period of the system due to the asynchronous rotation of the white dwarf. Within this period, the alternation of modes occurs twice. The first mode is performed if the jet matter accretes to the one of magnetic poles of the primary component. Its duration is 0.4. The second accretion mode is realized in the processes of flow switching between the magnetic poles, and its duration does not exceed 0.1. In this case, the actual switching occurs in a time of about one orbital period [64].
Based on these time relations, we performed two types of numerical calculations of the flow structure. In the first, a stationary model was used, as we do it for a synchronous polar. It made it possible to obtain a general pattern of the flow in the polar during the beat period of the system. To study the fleeting processes of switching the flow between the magnetic poles of the accretor, the second type of calculations was applied within the framework of a non-stationary model, which took into account the proper rotation of the primary component. This made it possible to study the dynamics of the flow in these processes in a more detailed manner.
The results of numerical calculations of both types are given below. In all cases, the initial parameters of the CD Ind polar were used, which are summarized in Table 4 [4,8,9,10,16,65,66,67,68,69,70,71,72].

Table 4.
Initial parameters for calculations of the asynchronous polar CD Ind.
To study the general pattern of the flow structure, ten variants of numerical calculation of the first type were performed, corresponding to different phases of the beat period, with a phase step of 0.1. The resulting solutions are shown in Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10. For a visual representation of the flow structure at each phase, the orbital position of the system was distinguished, in which the characteristic details of the flow are clearly visible. So, for phases 0.0–0.4, the orbital phase 0.3 is selected. In this position, it is possible to see the separation of the jet between the poles of the accretor at phase 0.1 and also to follow the change in the trajectory of matter motion during the asynchronous rotation of the accretor. In addition to the flow of matter from the point , in Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, we can see the accumulation of matter in the plane of the accretor’s magnetic equator due to the effect of a magnetic trap, and an additional flow of matter from the common envelope of the binary system, which creates a secondary, much weaker than the main, accretion zone. Therefore, at all phases of the beat period, the accretion of matter can always be observed in the vicinity of both magnetic poles, whereas the main jet, except switching moments, flows only to a single pole.
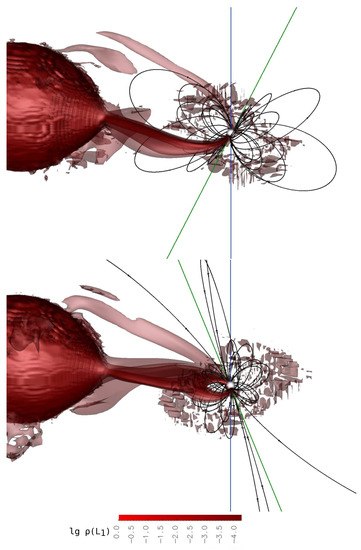
Figure 6.
The result of three-dimensional numerical simulation of the flow structure in the CD In system for phases 0.0 (upper panel) and 0.1 (lower panel) of the beat period. The iso-surfaces of the decimal logarithm of density in units of are shown. The surface of the accretor is represented as a white sphere. The lines with arrows correspond to the magnetic field lines. The vertical blue line passing through the accretor coincides with its axis of rotation, and the inclined green line coincides with its magnetic axis. The system is shown from the point of view of an Earth observer at the orbital phase 0.3.
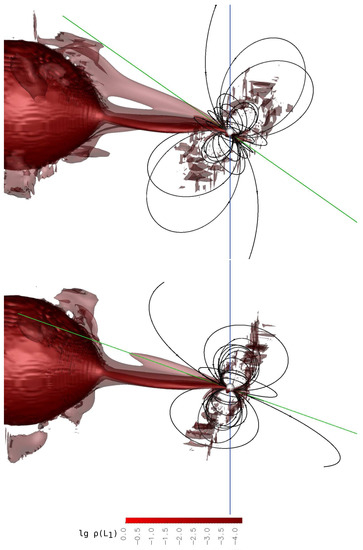
Figure 7.
The same as Figure 6 but for phases 0.2 (upper panel) and 0.3 (lower panel).
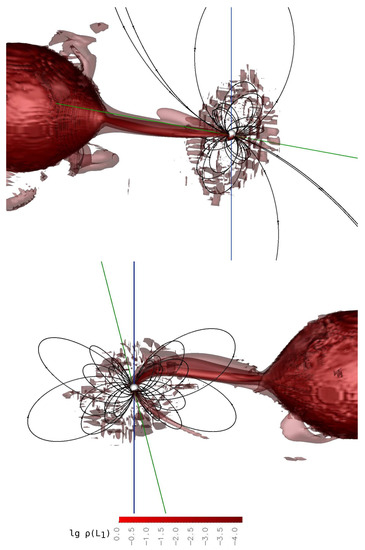
Figure 8.
The same as Figure 6 but for phases 0.4 (upper panel) and 0.5 (lower panel). The system is shown from the point of view of an Earth observer at the orbital phase 0.3 for upper panel and phase 0.7 for lower panel.
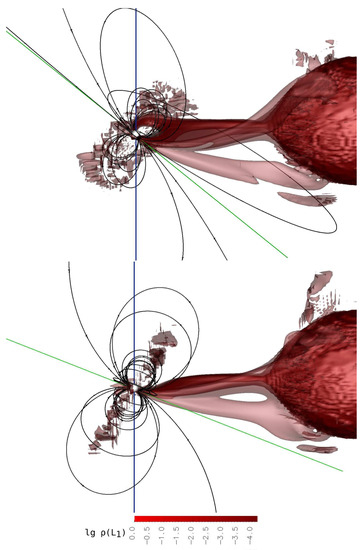
Figure 9.
The same as Figure 6 but for phases 0.6 (upper panel) and 0.7 (lower panel). The system is shown from the point of view of an Earth observer at the orbital phase 0.7.
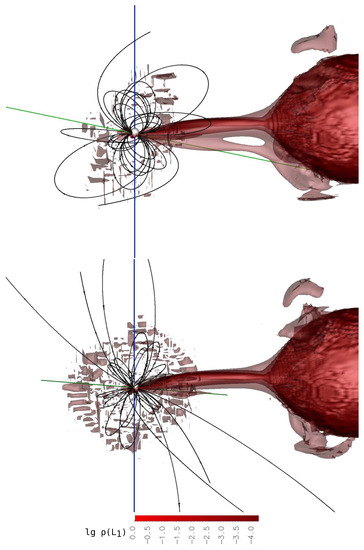
Figure 10.
The same as Figure 6 but for phases 0.8 (upper panel) and 0.9 (lower panel). The system is shown from the point of view of an Earth observer at the orbital phase 0.7.
The density of the jet matter near the inner Lagrange point for the mass transfer rate /year is g/cm. In the vicinity of the beat period phases 0.0 and 0.5, i.e., when the accretion zone is located at a significant angle to the donor, the Coriolis force increases the length of the ballistic part of the jet trajectory relative to its magnetic part. On the contrary, in the case of the maximum convergence of the magnetic poles with the point at phases 0.3 and 0.7, the jet matter is almost immediately captured by the magnetic field of the primary component and rushes to its surface. Therefore, the ballistic part of the trajectory turns out to be the shortest.
It can be seen from the figures that the asynchronous system has the same characteristic flow element that was described for the synchronous polar: the inhomogeneity of the jet cross-section by density. Due to the sufficiently high value of the mass transfer rate, the splitting of the flow into several separate flows does not occur here. Instead, there is a slight broadening of the jet at the boundary of the magnetosphere. Taking into account such a flow pattern is important, since it can affect the results of analysis and interpretation of observational data.
The analysis of calculation results of the first type shows that the flow switching between the magnetic poles is observed at phases (switching from the south pole to the north one ) and (switching from the north pole to the south one) of the beat period. For a detailed study of the flow structure in these processes, numerical calculations of the second type were performed in these phase intervals. At given values of and for CD Ind, each process calculation covers approximately 10 orbital periods of the system.
In Figure 11 and Figure 12, the results of calculations for the process of switching the flow from the south magnetic pole to the north and in Figure 13 and Figure 14 for the process of switching the flow from the north magnetic pole to the south are presented. Calculations have shown that qualitatively, the flow structure in both switching processes has similar elements. However, due to a change in the orientation of the axis of the magnetic dipole, when the switching direction is reversed, a corresponding change in the plane of the flow of matter in the region of the magnetosphere of the accretor should be expected, which is observed in the presented figures. At the same time, on the ballistic part, the jet moves along a constant trajectory. On the other side, our quantitative estimates of the flow dynamics revealed significant differences in the parameters of the motion of matter in both processes (individual accretion rates for each magnetic poles, local switching times etc.), but their consideration is beyond the scope of this study. They are given in more detail in our recent work [64].
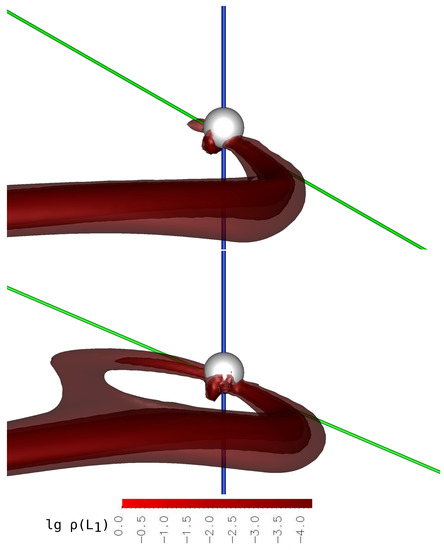
Figure 11.
The three-dimensional numerical modeling results of the flow structure in the asynchronous polar CD Ind with an offset dipole for the moment of switching from the south magnetic pole to the north one. The iso-surfaces of the decimal logarithm of the density are shown in units of . The flow structure is represented near the accretor. The accretor is indicated as a white sphere. The vertical blue line passing through the accretor coincides with its axis of rotation, and the inclined green line coincides with its magnetic axis. The binary system is at the orbital phase 0.15. The upper panel coincides with Phase 1, and the lower panel coincides with Phase 2 of the switching process.
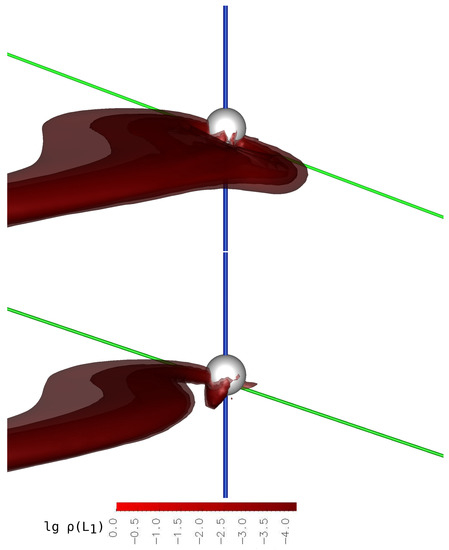
Figure 12.
The same as in Figure 11 but for Phase 3 (upper panel)) and Phase 4 (lower panel).
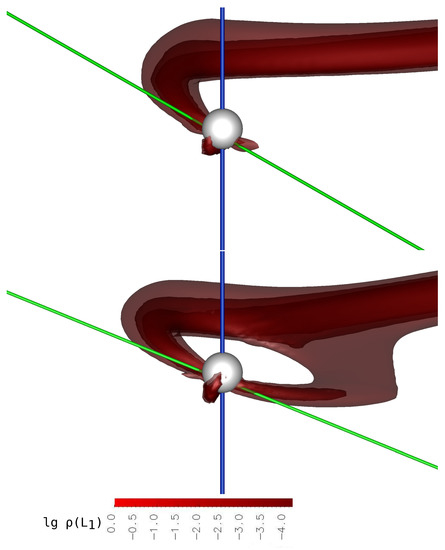
Figure 13.
The three-dimensional numerical modeling results of the flow structure in the asynchronous polar with an offset dipole for the moment of switching from the north magnetic pole to the south one. The iso-surfaces of the decimal logarithm of the density are presented in units of . The flow structure represented near the accretor. The accretor is indicated as a white sphere. The binary system is at the orbital phase 0.65. The upper panel coincides with Phase 1, and the lower panel coincides with Phase 2 of the switching process.
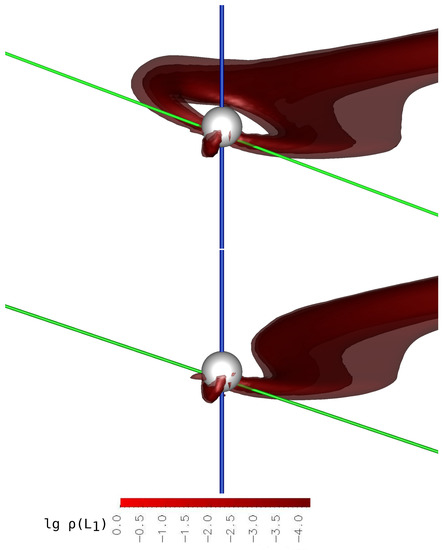
Figure 14.
The same as in Figure 13 but for Phase 3 (upper panel)) and Phase 4 (lower panel).
The figures demonstrates four characteristic phases of the switching process: Phase 1–the beginning of switching (Figure 11, upper panel, Figure 13, upper panel), Phase 2–the moment of formation of the arch of matter in the magnetosphere of the accretor (Figure 11, lower panel, Figure 13, lower panel), Phase 3–the moment of accumulation of matter in the arch and an increase in its volume (Figure 12, upper panel, Figure 14, upper panel), and Phase 4–completion of switching (Figure 12, lower panel, Figure 14, lower panel). The characteristic features of the flow structure for both switching processes are described below, since they have a qualitative similarity; however, the designation of the magnetic poles is given for the first switching process (from south to north pole).
Phase 1 corresponds to the 1st orbital period from the zero phase and is characterized by the mode of unipolar accretion of the jet to the south magnetic pole. Due to the position of the dipole axis indicated in the figure, the ballistic part of the jet trajectory at a given mass transfer velocity has a much longer length than the magnetic one.
At the Phase 2 coinciding with the 5th orbital period, two characteristic features in the flow structure can be observed. Firstly, it is worth noting that the re-locking of the jet to the other pole does not happen instantly: for a while, the system sets the mode of bipolar accretion. Depending on the current position of the poles relative to the inner Lagrange point, the flow is divided into two streams of different densities at the boundary of the magnetosphere of the star, which looks like an arch of matter. Compared to unipolar accretion (Figure 11, upper panel), at the moment of arch formation, the trajectory of the jet changes. The length of its ballistic part decreases to the upper boundary of the magnetosphere, and the magnetic part is formed by two flows: less dense layers form accretion near the north magnetic pole, and denser layers near the south pole.
At Phase 3, the arch of matter formed at the previous stage undergoes changes. At the 9th orbital period, its outer radius still coincides with the upper boundary of the magnetosphere, and the inner one decreases, which together lead to growth of the volume of the arch. This circumstance indicates the moment there is an accumulation of matter in the flow structure. It can also be seen from the figure that part of the flow in the arch to the north magnetic pole has a significant broadening and a pronounced heterogeneity in density. The flow of matter in this region is determined by the same factors that were considered above for the synchronous polar.
At the final stage of switching (Phase 4), corresponding to the 13th orbital period, the destruction of the arch of matter in the magnetosphere of the accretor occurs as does the formation of accretion to the north magnetic pole. At the same time, the geometry of the flow to this pole, noted at the previous phase, is preserved. The broadening of the jet in the region of the magnetosphere of the white dwarf is still determined by the inhomogeneity of the flow in density as well as the deflection of the jet as a result of the Coriolis force. From the comparison of the figures (Figure 12, lower panel, and Figure 11, upper panel), it can be concluded that at Phase 1, the broadening of the jet had a smaller value relative to the width of the flow at this Phase 4. This may be due to the greater distance of the south magnetic pole from the inner Lagrange point in relation to the north one; as a result, it has a weaker effect on the movement of matter in the magnetosphere.
Note another feature of the flow observed in the numerical solutions obtained (Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14). The figures show the formation of a matter belt on the surface of a white dwarf along the line of the magnetic equator. Unlike a similar structure, which is formed above the surface of the primary component and is caused by the effect of a magnetic trap, the material for the creating of this belt is the matter, which is already accreted on the star. Due to the offset of the dipole axis, part of the closed magnetic field lines in the lower part of the equatorial plane lock the matter above the surface of the white dwarf. The same part of the field line in the upper part of the equator closes inside the star, so the retention of matter on the surface does not occur. In the case of the central position of the dipole, as it was shown for the synchronous polar, the field lines in the vicinity of the equator are always hidden inside the accretor; as a result, the accumulation of matter on its surface is not observed.
4. A Method for Estimating the Configuration of the Magnetic Field of a White Dwarf from the Light Curves
Based on the results of numerical calculations of the asynchronous polar CD Ind, bolometric light curves were constructed, which are shown in Figure 15. The technique we use for the synthesis of light curves is described in detail in [73]. In the figure, the red dotted line highlights the 9th orbital period, which accounts for the actual moment of switching the flow between the poles. In addition, the curve points corresponding to hot spots are marked for this period.
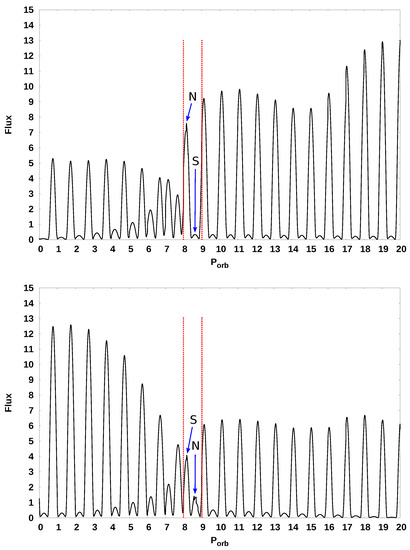
Figure 15.
Bolometric light curves of the CD Ind polar for the magnitude of the dipole displacement −0.5. The upper panel corresponds to switching from the south pole to the north, the lower panel does from the north pole to the south. The value of the flux is indicated in units erg/s. The red dotted lines highlight the orbital period corresponding directly to the moment of switching. On the light curves, arrows mark the positions of the northern (N) and southern (S) hot spots.
The analysis of these curves showed that in the binary system with an offset dipole (by offset value of ), the luminosities differ significantly, by a factor of about 2, during periods of unipolar accretion. At the moments of accretion switching, rapid fluctuations in luminosity can differ by a factor of 3.5 depending on the direction of the process. The revealed dependence suggests that from a comparison of observational and synthetic light curves, it is possible to develop a method for estimating the magnitude of the dipole displacement by the difference in luminosities of the northern and southern hot spots at the moments of accretion switching. The feature of this method is that the displacement of the dipole axis obtained from the light curves will correspond exactly only to the binary system for which the estimation was performed. The application of the method to other asynchronous polars is possible only at a qualitative level, since the specific quantitative ratios of the luminosities of the spots at the switching time will be determined by the parameters of the system under study.
In order to demonstrate the application of the described method to the CD Ind polar, 11 numerical calculations were performed for various values of the dipole displacement. The dipole center was shifted only along the axis of rotation of the white dwarf (along the z axis). Since at the extreme points (at the geographical poles of the star), the magnetic field of the dipole will tend to infinity, in order to avoid uncertainty in the calculations, the maximum offset values were limited to 0.9 and −0.9, respectively.
Figure 16 and Figure 17 show a family of synthetic bolometric light curves of the CD Ind polar at the moment of pole switching for different values of the dipole displacement. Note that when constructing these curves, the angles at which the Earth observer sees hot spots were taken into account. Therefore, the ratio of the radiation fluxes from the spots both in the mode of unipolar accretion and at the moment of switching will differ from the ratio of the maximum fluxes corresponding to the radiation along the normal vector to the plane of the spot. However, this does not have a noticeable effect on the qualitative estimating of the dipole displacement.
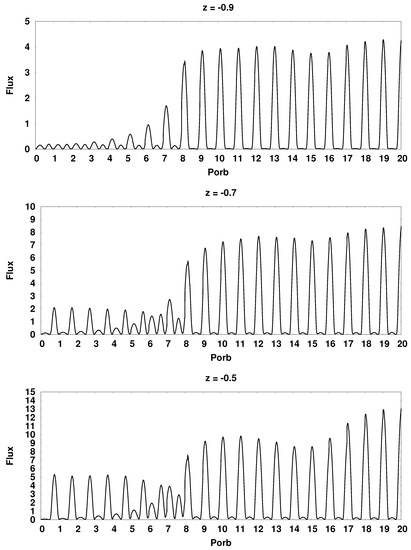
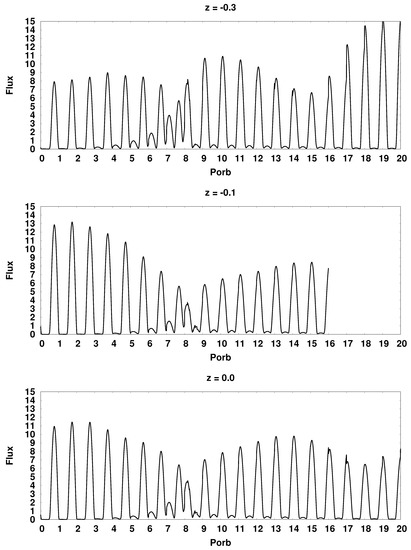
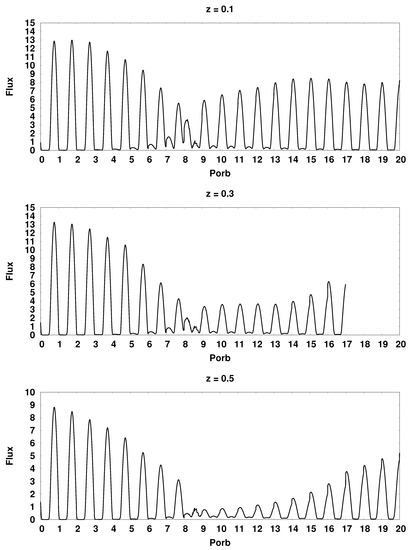
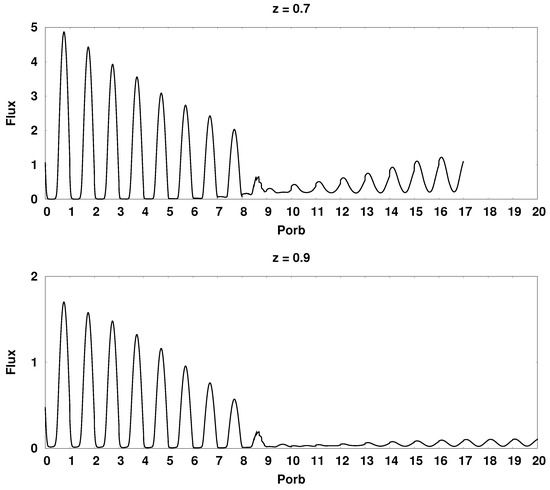
Figure 16.
Synthetic bolometric light curves of the CD Ind polar for various values of the dipole displacement at the moment of switching the flow from the south magnetic pole to the north. The flux values are in units erg/s. At the top of each panel, the value of the displacement of the dipole center is indicated.
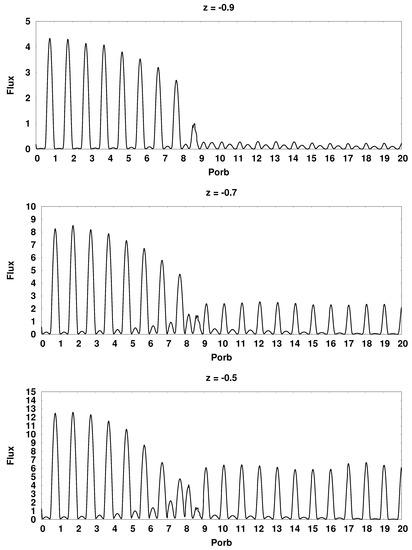
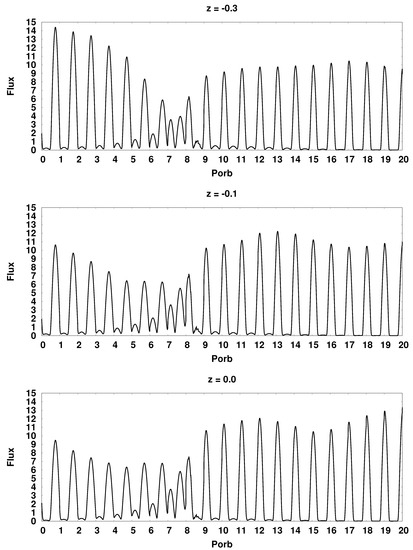

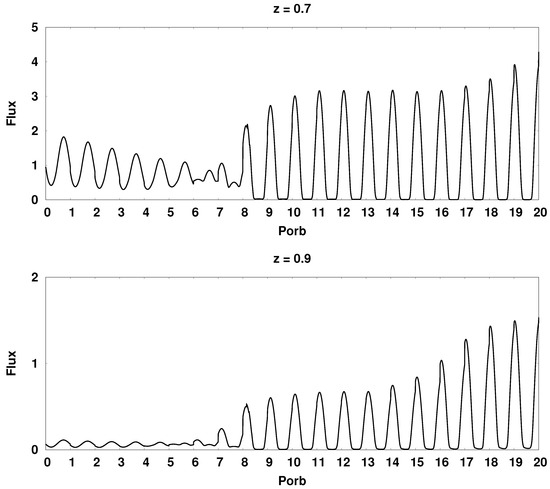
Figure 17.
Synthetic bolometric light curves of the CD Ind polar for various values of the dipole displacement at the moment of switching the flow from the north magnetic pole to the south. The flux values are in units erg/s. At the top of each panel, the value of the displacement of the dipole center is indicated.
The analysis of the presented light curves revealed the following features.
At the given orientation angles of the magnetic dipole and , the position of the hot spot on the equator of the white dwarf corresponds to a displacement of +0.34 for the southern spot and −0.34 for the northern one. In this position, the spot passes as close as possible to the inner Lagrange point, which provides the highest value of the accretion rate and radiation flux. Indeed, in the above figures, the maximum of the radiation flux in the vicinity of the switching moment is achieved on panels showing the light curves for the displacement values of −0.3 and +0.3. When switching from the south magnetic pole to the north, the displacement of the dipole −0.3 corresponds to the greatest flux from the north spot, and the displacement +0.3 corresponds to the greatest flux from the southern spot. For reverse switching, the pattern changes to the opposite.
At the boundaries of the calculation range, i.e., for the displacement values −0.9 and +0.9, there is a significant difference in the luminosities of the spots, which is associated with a sharp increase in the magnetic field strength in the spots, both its absolute value and the ratio of values for both spots. In addition, the angle of hot spots position relative to the observer in the case under consideration is rapidly approaching , which also contributes to a strong difference in radiation fluxes. Numerical simulation of the flow structure for these displacement values showed that the duration of the magnetic pole switching processes increases by about one orbital period compared to the central positions of the dipole. A strong magnetic field keeps the matter in the arch longer, and the subsequent accretion of the accumulated matter proceeds more smoothly.
Of particular interest is the appearance of the light curve at the central location of the dipole (). In this position of the magnetic axis, both magnetic poles have the same field strength and therefore presumably should cause symmetrical accretion. However, on the corresponding light curves (see Figure 16 and Figure 17), there is a slight difference in flows in the area of unipolar accretion, and the south magnetic pole looks more <<strong>>. First of all, the difference in the luminosities of the spots for this dipole displacement is due to the presence of the Coriolis force. Due to the deviation of the jet away from the accretor at the moment of switching the flow from the south pole to the north, most of the matter is directed to the first. When switching back from the north pole to the south, a similar appearance of the light curve is observed at a displacement value of −0.1. The zero offset here is somewhat different from the previous case. It can be seen from the light curve that immediately before switching, a small accumulation of matter occurs in the vicinity of the north pole (in the previous switching, the accumulation of matter takes place only at the moment of the pole change, and does not precede it), which then quickly falls out to the south pole and enables greater brightness of the southern hot spot compared to the northern one.
From the obtained light curves, it is possible to estimate the ratio of radiation fluxes of hot spots at the moment of switching, which coincides with the 9th orbital period. The position of the hot spots on the light curve for each switching is shown in Figure 15. In order to obtain comparable values of the desired ratio, a larger value of the flow was chosen as the divisible one. Thus, to switch from the south pole to the north one, the ratio of the flows of the northern spot to the southern is calculated, and when switching back−the southern spot to the northern .
The revealed dependence is clearly shown in Figure 18.
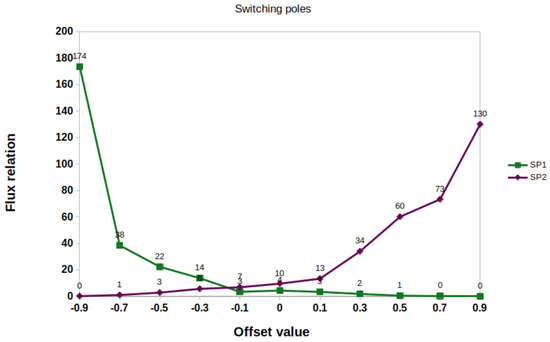
Figure 18.
Dependence of the ratio of the hot spots luminosities on the magnitude of the dipole displacement for the asynchronous polar CD Ind. The curve SP1 corresponds to the flow switching from the south magnetic pole to the north, the curve SP2–from the north to the south.
The plots show the symmetry of the ratios for hot spots luminosities at both switching processes in the range of dipole displacements from −0.1 to +0.1. Further displacement of the dipole downwards for switching from the south pole to the north (curve SP1) and up for switching from the north pole to the south (curve SP2) demonstrates an increase in the ratio of flows by a factor of about 2. This indicates that an increase in the magnetic induction of the south pole leads faster to an increase in the luminosity of the corresponding hot spot. However, at the maximum displacements of +0.9 and −0.9, the ratio of the radiation fluxes of hot spots becomes comparable. This is due to an exponential increase in the magnetic field strength as the magnetic poles approach the center of the dipole and a rapid increase in the angle of inclination of the spots. Large values of the dipole displacement in real polars have not yet been detected, but the modeling of such situations is undoubtedly of interest for understanding the physics of matter accretion to a white dwarf in critical cases. At the same time, these displacements are easily detected by the observational light curves based on the proposed method.
5. Conclusions
The paper presents the results of numerical calculations of the flow structure in magnetic cataclysmic variables−synchronous and asynchronous polars and intermediate polar. To study the flow structure in these objects, a three-dimensional numerical model is used. It is based on the approximation of modified magnetic hydrodynamics, which describes the dynamics of plasma in a very strong external magnetic field. Such a model, unlike previously used approaches, makes it possible to fully take into account a number of dynamic effects associated with the presence of a magnetic field. Since the calculation domain completely includes the Roche lobes of the accretor and the donor, the model makes it possible to form a natural outflow of matter from the donor envelope in the vicinity of the inner Lagrange point as well as to provide all the necessary material to determine the synthetic characteristics of the polars. For the numerical solution of the equations of magnetic hydrodynamics, the Roe–Osher–Einfeldt difference scheme is used in this work, which has a much lower numerical viscosity. This makes it possible to obtain solutions with a higher spatial resolution. In addition, the calculation domain contains an adaptive grid with a step exponentially decreasing toward the center of the accretor, which also contributes to an increase in the resolution of the scheme. Thanks to these properties of the model, it was possible to study in detail the accretion of matter on the surface of the primary component as well as to identify the characteristic features of the geometry of the matter flow in binary systems.
The results of the MHD simulation of the flow in the intermediate polar EX Hya show the formation of a flow structure with well-known features. In this binary system, a stationary cold accretion disk is formed, with which the jet interacts in an unstressed manner. In addition to the disk, there is a disk halo and a common interstellar envelope in the system. With these elements of the structure, the interaction of the jet has an oblique shock character; as a result, an extended shock wave is formed on the outer boundary of the disk−<<hotline>>. There is a pronounced spiral density wave in the disk itself, which contributes to a noticeable movement of matter along the radius of the disk. In the region of the magnetosphere of a white dwarf, matter from the inner parts of the disk moves along the magnetic field lines of the star, while accretion of matter on the surface of the star occurs in the vicinity of the magnetic poles in the form of columns. In the area of the magnetic equator, a vacuum region appears near the surface of the accretor, where the disk matter does not penetrate, since it cannot move across magnetic lines.
The study of the flow structure in the synchronous polar V808 Aur confirmed an unambiguous correspondence between the state of polar activity and the value of the mass transfer rate. In addition, the simulation showed that variations in the rate lead to noticeable changes in the geometry of the flow: an increase in the mass transfer rate causes the elongation of the ballistic part of the jet trajectory; as a result, it deviates more strongly from the direction to the accretor.. In the high and medium polar states, this leads to a noticeable broadening of the jet at the boundary of the magnetosphere, and the flow itself has a density gradient in the radial direction. In a very low state, the matter flowing from the point almost immediately begins to be controlled by a magnetic field. As a result, its flow occurs along the nearest magnetic lines. Therefore, the accretion zone on the surface of the white dwarf is located closest to the north magnetic pole.
For an asynchronous CD Ind polar having a magnetic field configuration with a displaced dipole, two types of numerical calculations were performed at a fixed value of the mass transfer rate—using stationary and non-stationary models. In the first case, it was possible to obtain a general pattern of the flow structure depending on the phase of the beat period. Taking into account the similarity of the modeling conditions with the synchronous polar, the revealed variations in the flow geometry are only caused by the asynchronous rotation of the accretor and not the mass transfer rate.
In addition, during the calculations, it was found that in the CD Ind system, the flow between the magnetic poles switches twice in the beat period, within the configuration of the accretion jet changes dramatically. At the beginning of this process, one magnetic pole is active, to which accretion goes, and at its end, another magnetic pole becomes active. At the same time, due to the displaced center of the dipole relative to the center of the star, as well as due to the inclination of the dipole relative to the axis of rotation, this process occurs in an asymmetric manner in time. To identify the dynamics of the flow in these processes, a non-stationary model was used, which takes into account the proper rotation of the accretor.
Qualitative changes in the flow structure were revealed in the processes of switching the flow from one magnetic pole to another. One of the characteristic elements of the flow in the magnetosphere region is an increase in the cross-section of the jet at the beginning of the magnetic part of the trajectory. This change in structure is due to the density gradient of the matter flowing from the donor. Another characteristic feature of the structure is the formation of an arch of dense matter in the inner region of the white dwarf magnetosphere facing the donor. The formation of this element occurs for about five orbital periods, after which its inner radius begins to decrease. Together, this leads to an increase in the volume of the arch, which can be interpreted as a process of short-term accumulation of jet matter in the magnetosphere. At the 9th orbital period, a rapid destruction of the arch of matter occurs due to the separation of the jet from the previous magnetic pole and the formation of a new unipolar accretion. It is worth noting that the actual switching processes have different durations: the jet opening away from the south pole occurs in half of the orbital period and away from the stronger north pole—approximately within one orbital period.
Synthetic bolometric light curves have shown that luminosities in a system with a displaced dipole differ significantly (by factor of about 2) during periods of unipolar accretion. At the moments of accretion switching, rapid fluctuations in luminosity can differ by a factor of 3.5 depending on the direction of the process. This made it possible for such binary systems to implement a method for determining the configuration of the magnetic field from observational light curves. For example, by the ratio of luminosities of the northern and southern hot spots at the moments of accretion switching, it is possible to estimate the magnitude of the magnetic dipole displacement relative to the center of the white dwarf. Since at the moments of switching, the brightness of the binary system experiences sharper fluctuations compared to the state of unipolar accretion, the accuracy of the estimation of the dipole displacement increases at these moments. Note that the synthesized dependence has a qualitative character, since it is determined by the parameters of a specific binary system.
Author Contributions
Conceptualization, supervision, project administration, D.B.; writing—original draft preparation, writing—review and editing, investigation, numerical calculation, A.S.; software, validation, A.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the Russian Foundation for Basic Research (project 19-52-60001).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The work was performed using the equipment of the center for collective use “Complex of modeling and data processing of mega-class research facilities” SIC “Kurchatov Institute”, http://ckp.nrcki.ru/ (accessed from 14 May 2019 to 30 November 2020). The work was performed using the computing cluster of the Interdepartmental Supercomputer Center of the Russian Academy of Sciences (accessed from 15 May 2020 to 5 October 2022).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Warner, B. Cataclysmic Variable Stars; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Bisikalo, D.V.; Zhilkin, A.G.; Boyarchuk, A.A. Gas Dynamics of Close Binary Stars; Fizmatlit: Moscow, Russia, 2013. [Google Scholar]
- Schwope, A.; Thomas, H.; Beuermann, K.; Burwitz, V.; Jordan, S.; Haefner, R. Two-pole accretion in the high-field polar RXJ 1938.6-4612. Astron. Astrophys. 1995, 293, 764. [Google Scholar]
- Norton, A.; Wynn, J.; Somerscales, R. The spin periods and magnetic moments of white dwarfs in magnetic cataclysmic variables. Astrophys. J. 2004, 614, 349. [Google Scholar] [CrossRef]
- Campbell, C. Magnetohydrodynamics in Binary Stars; Kluwer Acad. Publishers: Dordrecht, The Netherlands, 1997. [Google Scholar]
- Campbell, C.; Schwope, A. Asynchronous rotation in the polars. Astron. Astrophys. 1999, 343, 132–136. [Google Scholar]
- Patterson, J. The DQ Herculis Stars. Publ. Astron. Soc. Pac. 1994, 106, 209. [Google Scholar] [CrossRef]
- King, A. The accretion of diamagnetic blobs by a rotating magnetosphere. Mon. Not. R. Astron. Soc. 1993, 261, 144. [Google Scholar] [CrossRef]
- Ikhsanov, N.; Neustroev, V.; Beskrovnaya, N. On the mass transfer in AE Aquarii. Astron. Astrophys. 2004, 421, 1131. [Google Scholar] [CrossRef]
- Norton, A.; Butters, O.; Parker, T.; Wynn, G. The accretion flows and evolution of magnetic cataclysmic variables. Astrophys. J. 2008, 672, 524. [Google Scholar] [CrossRef]
- Koldoba, A.V.; Romanova, M.M.; Ustyugova, G.V.; Lovelace, R.V.E. Three-dimensional magnetohydrodynamic simulations of accretion to an inclined rotator: The “cubed sphere” method. Astrophys. J. 2002, 576, L53. [Google Scholar] [CrossRef]
- Romanova, M.M.; Ustyugova, G.V.; Koldoba, A.V.; Wick, J.V.; Lovelace, R.V.E. Three-dimensional simulations of disk accretion to an inclined dipole. I. Magnetospheric flows at different Θ. Astrophys. J. 2003, 595, 1009. [Google Scholar] [CrossRef]
- Romanova, M.M.; Ustyugova, G.V.; Koldoba, A.V.; Wick, J.V.; Lovelace, R.V.E. Three-dimensional simulations of disk accretion to an inclined dipole. II. Hot spots and variability. Astrophys. J. 2004, 610, 920. [Google Scholar] [CrossRef]
- Romanova, M.M.; Ustyugova, G.V.; Koldoba, A.V.; Wick, J.V.; Lovelace, R.V.E. The propeller regime of disk accretion to a rapidly rotating magnetized star. Astrophys. J. 2004, 616, L151. [Google Scholar] [CrossRef]
- Thomas, D.; Wood, M. The emergence of negative superhumps in cataclysmic variables: Smoothed particle hydrodynamics simulations. Astrophys. J. 2015, 803, 55. [Google Scholar] [CrossRef]
- Wynn, G.; King, A.; Horne, K. A magnetic propeller in the cataclysmic variable AE Aquarii. Mon. Not. R. Astron. Soc. 1997, 286, 436. [Google Scholar] [CrossRef]
- Zhilkin, A.; Bisikalo, D.; Boyarchuk, A. Flow structure in magnetic close binary stars. Adv. Phys. Sci. 2012, 182, 121. [Google Scholar]
- Zhilkin, A.; Bisikalo, D. Formation of an accretion disc in close binary systems with magnetic field. Astron. J. 2010, 87, 1155. [Google Scholar]
- Kurbatov, E.; Zhilkin, A.; Bisikalo, D. Modified magnetohydrodynamics model including wave turbulence: Astrophysical applications. Adv. Phys. 2017, 187, 857. [Google Scholar] [CrossRef]
- Braginsky, S.I. Magnetohydrodynamics of Weakly Conducting Liquids. J. Exp. Theor. Phys. 1960, 37, 1417. [Google Scholar]
- Galtier, S.; Nazarenko, S.V.; Newell, A.C.; Pouquet, A. A weak turbulence theory for incompressible magnetohydrodynamics. J. Plasma Phys. 2000, 63, 447. [Google Scholar] [CrossRef]
- Zakharov, V.E. Solving model of a poor turbulence. Appl. Mech. Tech. Phys. 1965, 1, 14–20. [Google Scholar]
- Iroshnikov, P.S. Turbulence in conductive liquid in a strong magnetic field. Astron. J. 1963, 40, 742–750. [Google Scholar]
- Kraichnan, R.H. Lagrangian-history closure approximation for turbulence. Phys. Fluids 1965, 8, 575–598. [Google Scholar] [CrossRef]
- Mason, P.; Ramsay, G.; Andronov, I.; Kolesnikov, S.; Shakhovskoy, N.; Pavlenko, E. Evidence for pole switching in the magnetic cataclysmic variable BY Cam. Mon. Not. R. Astron. Soc. 1998, 295, 511–518. [Google Scholar] [CrossRef]
- Tanaka, T. Finite volume tvd scheme on an unstructured grid system for three-dimensional mhd simulation of inhomogeneous systems including strong background potential fields. J. Comput. Phys. 1994, 111, 381. [Google Scholar] [CrossRef]
- Powell, K.; Roe, P.; Linde, T.; Gombosi, T.; Zeeuw, D. A solution-adaptive upwind scheme for ideal magnetohydrodynamics. J. Comput. Phys. 1999, 154, 284. [Google Scholar] [CrossRef]
- Kulikovsky, A.; Pogorelov, H.; Semenov, A. Mathematical Questions of Numerical Solving of Hyperbolic Eqations Systems; Fizmatlit: Moscow, Russia, 2001. [Google Scholar]
- Drell, S.D.; Foley, H.M.; Ruderman, M.A. Drag and propulsion of large satellites in the ionosphere: An Alfvén propulsion engine in space. J. Geophys. Res. 1965, 70, 3131–3145. [Google Scholar] [CrossRef]
- Gurevich, A.V.; Krylov, A.L.; Fyodorov, E.N. Induction interaction of conducting bodies with magnetized plasma. J. Theor. Exp. Phys. 1978, 75, 2132–2140. [Google Scholar]
- Rafikov, R.R.; Gurevich, A.V.; Zybin, K.P. Induction interaction of conducting fast-moving rotating bodies with magnetized plasma. J. Theor. Exp. Phys. 1999, 115, 542–563. [Google Scholar]
- Isakova, P.; Iskhanov, N.; Zhilkin, A.; Bisikalo, D.; Bescrovnaya, N. Matter flow features in the pecular explosive (cataclysmic) variable AE Aqr. Astron. J. 2016, 93, 474. [Google Scholar]
- Frank-Kamenetsky, D.A. Lectures on Plasma Physics; Atomizdat: Moscow, Russia, 1968. [Google Scholar]
- Chen, F. Introduction Introduction to Plasma Physics; Mir: Moscow, Russia, 1987. [Google Scholar]
- Cox, D.; Daltabuit, E. Radiative cooling of a low-density plasma. Astrophys. J. 1971, 167, 113. [Google Scholar] [CrossRef]
- Dalgarno, A.; McCray, R. Heating and ionization of HI regions. Annu. Rev. Astron. Astrophys. 1972, 10, 375. [Google Scholar] [CrossRef]
- Raymond, J.; Cox, D.; Smith, B. Radiative cooling of a low-density plasma. Astrophys. J. 1976, 204, 290. [Google Scholar] [CrossRef]
- Spizer, L. Physical Processes in the Interstellar Media; Mir: Moscow, Russia, 1981. [Google Scholar]
- Zhilkin, A.; Bisikalo, D.; Ustyugov, V. New magnetohydrodynamic model for close binary stars: Applicability for moderate magnetic fields. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2013; Volume 1551, p. 22. [Google Scholar]
- Bisnovatyi-Kogan, G.S.; Ruzmaikin, A.A. The accretion of matter by a collapsing star in the presence of a magnetic field. II: Self-consistent stationary picture. Astrophys. Space Sci. 1976, 42, 401–424. [Google Scholar] [CrossRef]
- Shakura, N.I.; Sunyaev, R.A. Black holes in binary systems. Observational appearance. Astron. Astrophys. 1973, 24, 337–355. [Google Scholar]
- Lubov, S.H.; Shu, F.H. Gas dynamics of semidetached binaries. Astrophys. J. 1975, 198, 383–405. [Google Scholar]
- Semena, A.N.; Revnivtsev, M.G. Aperiodical variability of Periodic variability of the brightness of EX Ua in the X-ray range and the area of the base of the accretion column on the surface of the white dwarf. Lett. Astron. J. 2014, 40, 529–538. [Google Scholar]
- Hellier, C.; Mason, K.O.; Rosen, S.R.; Cordova, F.A. Time resolved optical spectroscopy of the eclipsing intermediate polar EX Hydrae. Mon. Not. R. Astron. Soc. 1987, 228, 463–481. [Google Scholar] [CrossRef][Green Version]
- Zhilkin, A.; Bisikalo, D. Impact of the magnetic field on the structure of accretion disks in semi-detached binaries. Astron. J. 2009, 86, 475. [Google Scholar] [CrossRef]
- Sawada, K.; Matsuda, T.; Hachisu, I. Accretion shocks in a close binary system. Mon. Not. R. Astron. Soc. 1986, 221, 679–686. [Google Scholar] [CrossRef][Green Version]
- Zhilkin, A.; Bisikalo, D. Magnetic field structure in accretion discs of semi-detached binaries. Astron. J. 2010, 87, 913. [Google Scholar]
- Isakova, P.; Zhilkin, A.; Bisikalo, D. Numerical model of accretion process in the intermediate polars with dipole magnetic field. Astron. J. 2015, 92, 720. [Google Scholar]
- Isakova, P.; Zhilkin, A.; Bisikalo, D.; Semena, A.N.; Revnivtsev, M.G. Features of accretion in the intermediate polar EX Hydrae: Results of numerical simulation. Astron. J. 2017, 94, 566–579. [Google Scholar]
- Zhilkin, A.; Sobolev, A.; Bisikalo, D.; Gabdeev, M. Flow structure in the eclipsing polar V808 Aur. Results of 3D numerical simulations. Astron. J. 2019, 96, 748. [Google Scholar] [CrossRef]
- Templeton, M.; Oksanen, A.; Boyd, D.; Pickard, R.; Maehara, H. Variable Star in Auriga. Cent. Bur. Electron. Telegrams 2009, 1652, 1. [Google Scholar]
- Drake, A.; Djorgovski, S.; Mahabal, A.; Beshore, E. First results from the Catalina real-time transient survey. Astrophys. J. 2009, 696, 870. [Google Scholar] [CrossRef]
- Drake, A.; Gansicke, B.; Djorgovski, S. Cataclysmic variables from the catalina real-time transient survey. Mon. Not. R. Astron. Soc. 2014, 441, 1186. [Google Scholar] [CrossRef]
- Kazarovets, E.; Samus, N.; Durlevich, O.; Kireeva, N.; Pastukhova, E. The 81st name-list of variable stars. Inform. Bull. Var. Stars 2015, 6151, 1–22. [Google Scholar]
- Samus, N.; Kazarovets, E.; Durlevich, O.; Kireeva, N.; Pastukhova, E. General catalogue of variable stars: Version GCVS 5.1. Astron. Rep. 2017, 61, 80. [Google Scholar] [CrossRef]
- Brown, A.; Vallenari, A.; Prusti, T.; Bruijne, J. Gaia Data Release 2. Summary of the contents and survey properties. Astron. Astrophys. 2018, 616, A1. [Google Scholar]
- Schwope, A.; Mackebrandt, F.; Thinius, B.; Littlefield, C.; Garnavich, P.; Oksanen, A.; Granzer, T. Multi-epoch time-resolved photometry of the eclipsing polar CSS081231:071126+440405. Astron. Nachr. 2015, 336, 115. [Google Scholar] [CrossRef]
- Worpel, H.; Schwope, A. XMM-Newton and optical observations of the eclipsing polar CSS081231:071126+440405. Astron. Astrophys. 2015, 583, 130. [Google Scholar] [CrossRef]
- Borisov, N.; Gabdeev, M.; Afanasiev, V. Photopolarimetric Observations of the Sample of Polar Candidates. Astrophys. Bull. 2016, 71, 95. [Google Scholar] [CrossRef]
- Borisov, N.; Gabdeev, M.; Shimansky, V.; Katysheva, N.; Kolbin, I.; Shugarov, S.; Goranskij, V. hotometric and Spectral Studies of the Eclipsing Polar CRTS CSS 081231 J071126+440405. Astrophys. Bull. 2016, 71, 101. [Google Scholar] [CrossRef]
- Kolbin, A.; Serebryakova, N.; Gabdeev, M.; Borisov, N. Analysis of the Optical Cyclotron Emission of Polar CRTS CSS081231 J071126+440405. Astrophys. Bull. 2019, 74, 80. [Google Scholar] [CrossRef]
- Isakova, P.; Zhilkin, A.; Bisikalo, D. Flow structure features in vicinity of the inner Lagrange point in polars. Astron. J. 2018, 95, 7519. [Google Scholar]
- Sobolev, A.; Zhilkin, A.; Bisikalo, D.; Buckley, D. Three-dimensional numerical simulation of a flow structure in the asynchronous polar CD Ind in the approximation of an offset dipole magnetic field of a white dwarf. Astron. Rep. 2020, 64, 467–498. [Google Scholar] [CrossRef]
- Sobolev, A.; Zhilkin, A.; Bisikalo, D.; Buckley, D. Three-dimensional model of the flow structure in the asynchronous polar CD Ind during magnetic pole switching. Astron. Rep. 2021, 65, 392–411. [Google Scholar] [CrossRef]
- Vennes, S.; Wickramasinghe, D.; Thorstensen, J.; Christian, D.; Bessell, M. On the Orbital Period of the New Cataclysmic Variable EUVE J2115-586. Astron. J. 1996, 112, 2254. [Google Scholar] [CrossRef][Green Version]
- Schwope, A.; Buckley, D.; O’Donoghue, D.; Hasinger, G.; Trümper, J.; Voges, W. RX J2115.7-5840: A short-period, asynchronous polar. Astron. Astrophys. 1997, 326, 195. [Google Scholar]
- Ramsay, G.; Buckley, D.; Cropper, M.; Harrop- Allin, M. RX J2115-5840: Confirmation of a new near-synchronous polar. Mon. Not. R. Astron. Soc. 1999, 303, 96. [Google Scholar]
- Ramsay, G.; Buckley, D.; Cropper, M.; Harrop-Allin, M.; Potter, S. Simultaneous optical polarimetry and X-ray data of the near-synchronous polar RX J2115-5840. Mon. Not. R. Astron. Soc. 2000, 316, 225. [Google Scholar] [CrossRef]
- Hakala, P.; Ramsay, G.; Potter, S.; Beardmore, A.; Buckley, D.; Wynn, G. TESS observations of the asynchronous polar CD Ind: Mapping the changing accretion geometry. Mon. Not. R. Astron. Soc. 2019, 486, 2549. [Google Scholar] [CrossRef]
- Myers, G.; Patterson, J.; Miguel, E.; Hambsch, F. Resynchronization of the Asynchronous Polar CD Ind. Publ. Astron. Soc. Pac. 2017, 129, 4204. [Google Scholar] [CrossRef]
- Wynn, G.; King, A. Diamagnetic accretion in intermediate polars-I. Blob orbits and spin evolution. Mon. Not. R. Astron. Soc. 1995, 275, 9. [Google Scholar] [CrossRef]
- King, A.; Wynn, G. The spin period of EX Hydrae. Mon. Not. R. Astron. Soc. 1999, 310, 203. [Google Scholar] [CrossRef]
- Sobolev, A.V.; Zhilkin, A.G.; Bisikalo, D.V. Method of constructing a synthetic light curve for eclipsed polars. INASAN Sci. Rep. 2019, 3, 231–236. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).