Cosmological Model Tests with JWST

Abstract

The James Webb Space Telescope (JWST), which has recently become operational, is capable of detecting objects at record-breaking redshifts, $z\gtrsim 15$. This is a crucial advance for observational cosmology, as at these redshifts the differences between alternative cosmological models manifest themselves in the most obvious way. In recent years, some observational hints have emerged indicating that the Standard Cosmological Model could require correcting. One of these hints is related to the discovery of remote galaxies whose redshifts correspond to the very young Universe (less than one billion years after the Big Bang) but which are similar to nearby galaxies. The issue is that such galaxies in the early Universe do not have enough time to evolve into something similar to the late-Universe galaxies. JWST observations of high-redshift objects are expected to shed light on the origin of this issue. Here we provide results on performing the “angular diameter—redshift” cosmological test for the first JWST observation data. We compare this result with predictions of the standard $\mathsf{\Lambda }$CDM cosmological model and some static cosmological models, including Zwicky’s “tired-light” model. The latter is currently assumed to be ruled out by observations. We challenge this assumption and show that a static model can provide a natural and straightforward way of solving the puzzle of the well-evolved galaxies and better agreements with the results of the JWST “angular diameter—redshift” test at high redshifts than the correcting evolution model within the $\mathsf{\Lambda }$CDM framework. We discuss several cosmological tests that will be important for further research on the possibility of revising the expanding Universe paradigm.

1. Introduction

One of the main scientific goals of the James Webb Space Telescope (JWST) is to explore the Universe’s history following the end of the period of the so-called “dark ages”. JWST has been designed to detect the appearance of the first sources of light in the Universe and uncover the history of the assembly of first galaxies [1]. An analysis of observations made by large telescopes prior to JWST indicated that the first stars and galaxies might have appeared between 250 and 350 million years ($z>15$) after the Big Bang [2,3]. Indeed, based on the first JWST observations, Donnan et al. [4] report a newly discovered galaxy with a redshift $z\sim 16.7$. This redshift corresponds to approximately 250 million years after the beginning of the Universe. In principle, JWST was designed to detect objects in the early Universe, only several tens of million of years old (should such objects exist). This is achievable because the red wavelength cut-off of the NIRCam instrument onboard JWST extends to 5 $\mathsf{\mu }$m.

Another group of researches, Atel et al. [5], has reported the discovery of two galaxy candidates at $z\sim 16$, two candidates at $z=12$ and eleven candidates at $10<z<11$ (these redshifs have been estimated photometrically for the galaxies gravitationally lensed by the massive galaxy cluster SMACS J0723-73). The morphologies of these high-redshift galaxies turn out to be consistent with disks, while their sizes are smaller compared to similar galaxies at lower redshifts. The unexpected excess of bulges and disk-shaped galaxies at high redshifts has also been confirmed by the morphological study [6] of 217 sources at redshifts $1<z<5$.

A flanking field around the same cluster SMACS J0723-73 (not magnified by gravitational lensing) has been studied by Yan et al. [7], who searched for galaxies at a redshift larger than 11 and which found 88 candidates, some of them might be at redshifts as high as $z=20$. The large number of such objects at high redshifts was not previously predicted by standard cosmology.

By contrast, Castellano et al. [8] found a smaller number of high-redshift galaxies on a flanking field around the Frontier Fields cluster A2744: nine objects at $9<z<12.3$, two of the brightest of them at $z>10$, being unexpected given the survey volume.

Spectroscopic studies of three remote gravitationally lensed galaxies at $z=7.7$ and $z=8.7$ within the field of the cluster SMACS J0723-73 [9] reveal a strong resemblance of emission line properties to the spectra of their local-Universe counterparts. Similarly, the measurements of the rest-frame ultraviolet continuum slopes of galaxies at $8<z<15$ show that these galaxies are no bluer than the bluest galaxies in the local Universe [10]. These slopes are indicators of ultra-young stellar populations, which are expected to be prevalent in the high-redshift Universe—but they are not.

Measurements of remote galaxy masses and sizes (half-mass radii) suggest an inverse relationship between these quantities; that is, the most massive high-redshift galaxies are more compact and dense  [11]. This study has been made for galaxies at redshifts $z=7$ to 11 prior the first JWST data release. A similar study based on the JWST data [12] also reveals that the high-redshift galaxies are very compact and massive, showing the same trend (i.e., smaller galaxies having larger masses). These authors conclude that their result impacts our understanding of the size growth and evolution of galaxies in the early Universe.

It is noticeable that most of these studies of the first JWST data release have something in common. Namely,

• There is an excessively large number of galaxies at very high redshifts, which is not foreseen by the Standard Cosmological Model;
• Galaxies at these redshifts have disks and bulges, which indicates that they have passed through a long period of evolution;
• Spectroscopically, these galaxies resemble their counterparts in the local Universe;
• Smaller galaxies are more massive than larger ones, which is quite the opposite of the common view.

These issues indicate that the galaxies at redshifts $z>15$ discovered by JWST do not have enough time within the framework of the standard cosmological model to evolve into what is observed.

Even before the operational period of JWST, other large telescopes, such as HST (the Hubble Space Telescope) or VLT (the Very Large Telescope), were finding an ever-increasing number of high-redshift objects, whose age from the beginning of the Universe was below a billion years, and whose formation within the $\mathsf{\Lambda }$CDM cosmological model is difficult to explain [13,14,15]. These objects are fully evolved, very large and very bright galaxies, ultra-luminous optical and X-ray quasars with the masses of their central blackholes reaching a few billion solar masses.

The existence of such objects would require new models of their formation. Alternatively, some brightness-amplification effects, such as gravitational lensing of high-redshift quasars [16], might reduce the estimated masses of supermassive blackhole populating the early Universe. However, this effect cannot help explain complicated morphologies of high-redshift galaxies. Another alternative for the explanation of supermassive blackholes in the early Universe is to postulate the appearance of primordial blackholes (PBH) at the very beginning of the Universe’s existence, before the time of recombination or even before the beginning of baryonic acoustic oscillations (BAO), which are currently regarded as the main cause of structure formation in the early-Universe. The main objective of the PBH model promoted by A.D. Dolgov [17] is to explain the existence of well-evolved objects whose formation is believed to be impossible within the $\mathsf{\Lambda }$CDM framework due to the very short period of available time 1.

This lack of evolution time is also a problem for known quasars containing supermassive blackholes with masses exceeding ${10}^{10}$ M${}_{\odot }$ at redshifts $z>6$ [18,19,20], whose existence is inconsistent with their age of shorter than a billion years after the Big Bang. This is also a challenge to the standard cosmological model itself [17,21]. In principle, the issues of very small, but very massive and well-developed galaxies seen at very high redshifts, could be solved by ad hoc adjustments to galaxy formation and growth models. However, a much simpler, although quite radical solution, might be found by shifting the paradigm from an expanding to static Universe, as was proposed by LaViolette [22] and some other researches [23,24,25,26], including one of the authors of the present article [27].

The JWST is expected to detect light emitted by the first stars in the Universe, when the first galaxies or protogalaxies were coming into existence. This prediction is based on the standard $\mathsf{\Lambda }$CDM cosmology. However, the existence of well-developed galaxies, should they be detected by JWST, is not foreseen within the framework of $\mathsf{\Lambda }$CDM.

Here we shall analyse the possibilities provided by the JWST for testing cosmological models using ultra-high redshift objects and comparing the observed photometric, spectrophotometric and geometric parameters of these objects with the predictions of the standard Lambda–Cold–Dark Matter model ($\mathsf{\Lambda }$CDM) and some alternative cosmological models. Throughout this paper, we use a standard cosmology with the parameters $H_0=70$ km s${}^{-1}$ Mpc${}^{-1}$ (the Hubble constant), ${\mathsf{\Omega }}_{\mathsf{\Lambda }}=0.7$ (the dimensionless density of dark energy) and ${\mathsf{\Omega }}_{\mathrm{M}}=1-{\mathsf{\Omega }}_{\mathsf{\Lambda }}=0.3$ (the density of matter, including both baryonic and dark matter), assuming a flat Universe with the curvature energy density ${\mathsf{\Omega }}_k=0$.

2. Materials and Methods

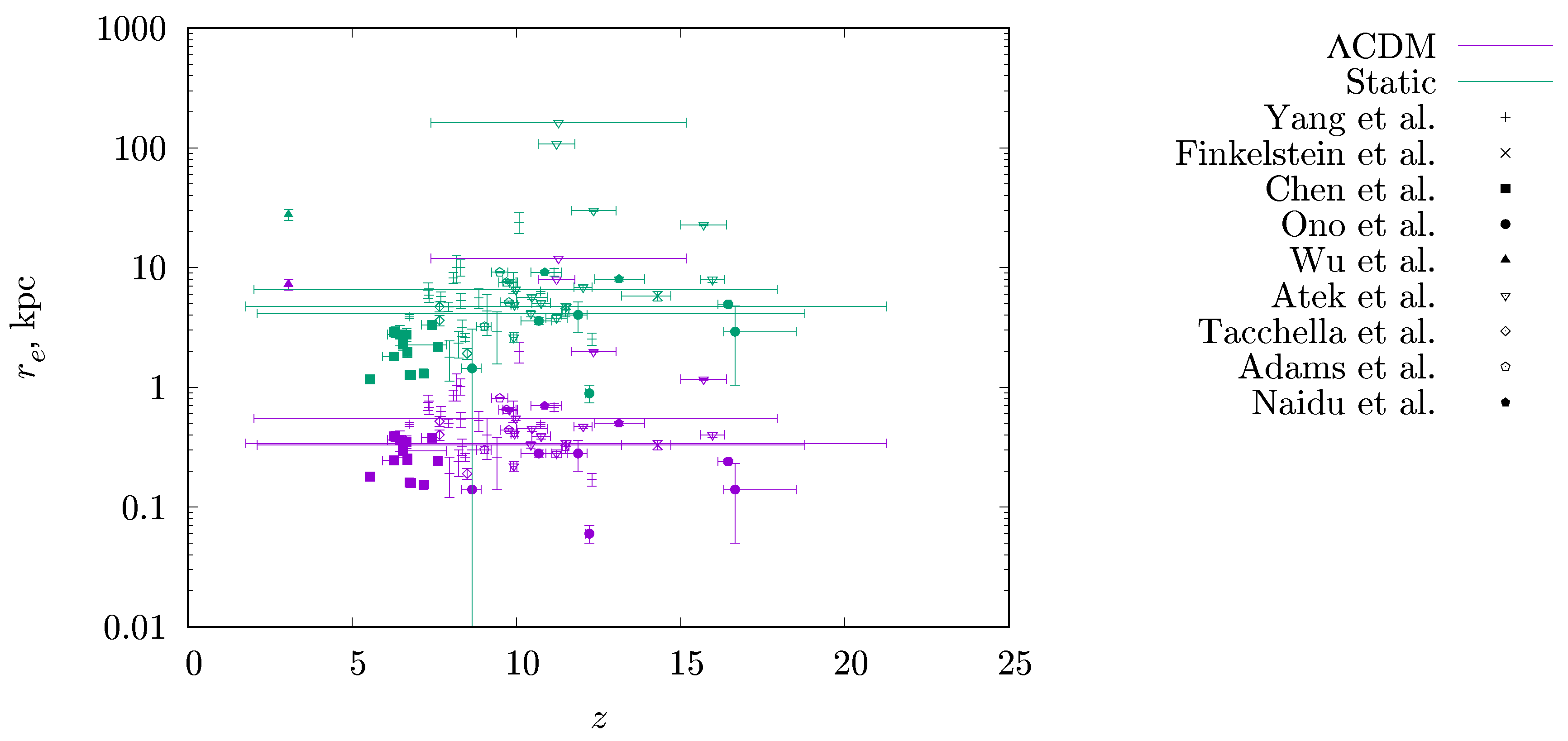
2.1. Observational Data for the Early-Universe Objects

The observations used for our analysis are publicly available JWST datasets, which include NIRCam images in F090W, F150W, F200W, F277W, F356W and F444W filters; MIRI images in F770W, F1000W, F1500W and F1800W filters; NIRSpec spectra in F170LP and F190LP, as well as NIRISS spectra obtained with F115W and F200W filters. These data were released on 12 July 2022 at https://webbtelescope.org/contents/news-releases/2022/news-2022-035 (accessed on 30 July 2022), as well as at the Mikulski Archive for Space Telescopes (MAST) 2 under program ID 2736. The associated programmatic interface 3 provides scripts for the data access and reduction. Some results of the JWST data reduction are also made publicly available. For example, the calibrated and distortion-corrected NIRCam and NIRISS images processed by G. Brammer are accessible https://s3.amazonaws.com/grizli-v2/SMACS0723/Test/image_index.html (accessed on 1 October 2022). The catalogues of ultra-high-redshift objects detected by the JWST instruments in the SMACS-0723 deep field are also publicly available at https://zenodo.org/record/6874301#.YubQUfHMJes (accessed on 1 October 2022).

We make use of the preliminary results from these data analyses published by various research groups, mainly in the form of arXiv e-print manuscripts at https://arXiv.org (accessed on 1 October 2022). Most of these authors report an unexpectedly large number of well-evolved galaxies at redshifts corresponding to their age from the beginning of the Universe of ∼200–250 Myrs. JWST images and spectra provide information about photometric and geometric parameters of remote galaxies, such as their brightnesses, sizes and redshifts, which have already been estimated and published by other authors. The accuracy of available photometric redshifts is not very high. Most of the redshift error bars on photometric redshifts in the recent publications on JWST data are within the range $0.1<{\sigma }_z<2.0$, while spectroscopic redshifts estimated by using spectral lines identified from the JWST/NIRSpec data have ${\sigma }_z<0.01$, see, e.g., [28]. However, some of the redshifts are unreliable, with ${\sigma }_z>6$ (see Section 3). For example, one of the JPWS high-redshift galaxies can be fit with the redshift either $z\approx 17$ or $z\approx 5$ [29]. In our analysis here, we use approximate redshifts from the published JWST galaxy data with ${\sigma }_z<3$.

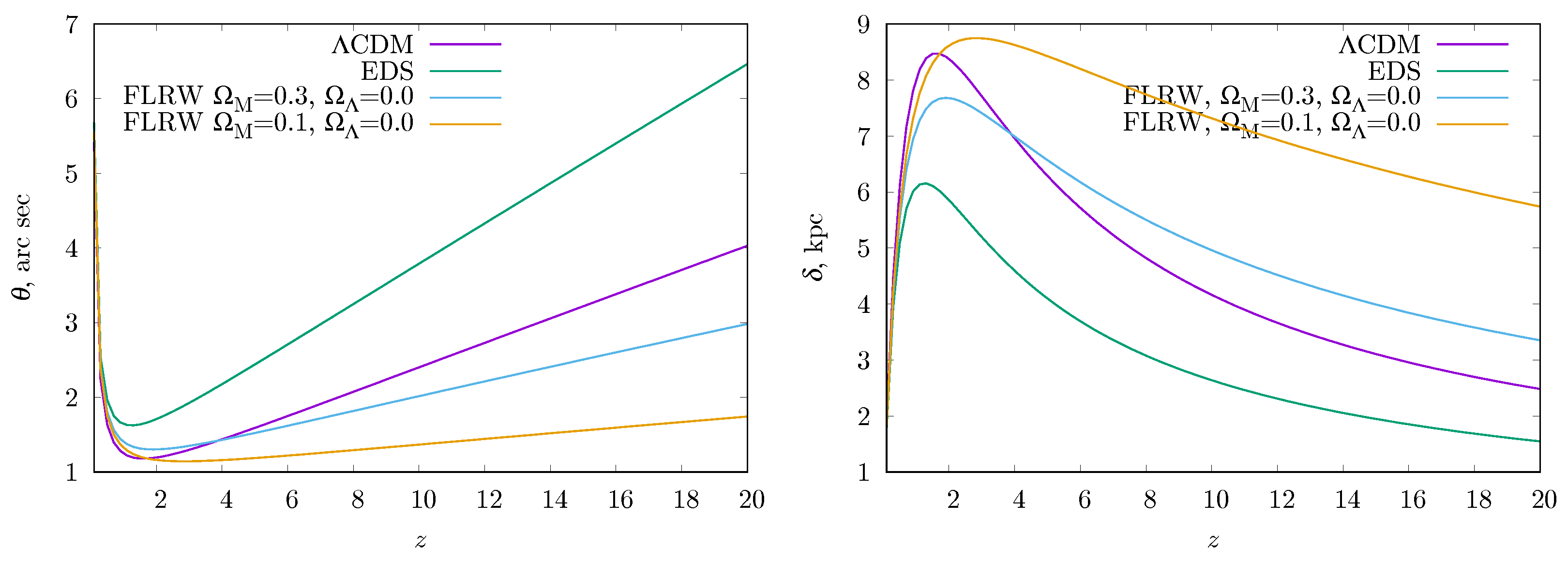
2.2. Cosmographic Tests

The methodology underlying our analysis is based on cosmographic theories described in classical [30,31,32,33,34,35] and modern [36,37,38,39] textbooks, as well as in some dedicated reviews [40] and papers cited below. Here we shall focus primarily on the angular size–redshift relationship, $\theta \left(z\right)$.

This relationship has been widely used for comparing different cosmological models. For example, N. Nabokov and Yu. Baryshev [41] measured angular sizes of galaxies in the Hubble ultra deep field for $0.5<z<6.5$ with the purpose to find inhomogeneitis in their radial distribution and concluded that the the current model of the evolution of galaxy sizes is not yet reliable enough for using $\theta \left(z\right)$ as a cosmological test at the studied redshifts. However, they noted that at $z\approx 6.5$ the measured galaxy angular sizes do not match well with the predictions of the standard cosmological model. M. Lopez-Corredoira [42] also noted that there is degeneracy between expansion combined with galaxy size evolution and non-expansion. Furthermore, he showed that a simple static model with no evolution in size and no dark matter ratio variation fits the observed $\theta \left(z\right)$ relationship better than the standard model.

Other tests, such as the Tolman surface-brightness test, the cosmological time dilation; number density–redshift relationship, galaxy-number-count–magnitude; photon-flight-time–redshift relationship and some others are of equal importance. We shall postpone their discussion to future works, as the angular-size test alone already provides insight into the problem.

The main purpose of these tests is to shed light on the origin of the cosmological redshift. This could be due to the growth with time of the global scale factor of the Universe, which can be viewed in the form of radial velocities of all galaxies with respect to each other. Alternatively, the cosmological redshift might be caused by some physical effects, such as possible photon energy dissipation along the photon’s path or photon energy change in gravitational potential wells.

Accordingly, cosmological models can be divided in two groups:

• Expanding universes based on the Friedmann–Lemaitre–Robertson–Walker (FLRW) metric with a time-dependent scale factor;
• static universes based, e.g., on the metric including a scale factor in metric’s time component [43] or Zwicky’s model based on the photon-energy dissipation along the photon’s travelling path [44].

A mixture of these two model types is also possible [45,46] when a physical effect enhances the redshift due to the growing scale factor. In which case, the expansion rate of the Universe would be smaller than predicted by the observed cosmological redshift within the expanding-Universe model. Correspondingly, the age of the objects in the Universe in a mixed-type model could be larger than the age deduced from pure FLRW models, which would mitigate the problem of the well-evolved galaxies discovered by the JWST at ultra-high redshifts, not having enough time for their formation and evolution.

The commonly accepted model of the first type is the standard $\mathsf{\Lambda }$CDM cosmological model, which best fits observational data among other expanding-Universe models 4. Those other models played an important role in the past for the development of the methods of observational cosmology. Therefore, perhaps it is worthwhile mentioning one of them—the steady-state cosmological model, first proposed by A. Einstein [47] in 1931 5 and then independently by H. Bondi, T.Gold [49] and F. Hoyle [50] in 1948. In this model, the Universe is stationary (although expanding) at the expense of the proposed continuous creation of matter. It was well-elaborated in detail, but was failing to pass through cosmological tests. Thuss, it required introducing numerous additional features [51,52,53,54,55] and eventually was abandoned.

The most discussed model of the second type is Zwicky’s model based on the idea of a photon’s energy dissipation, which is not commonly accepted, but which was found to be the best fit of all cosmological tests together [22] when compared with the same tests applied to the $\mathsf{\Lambda }$CDM model.

Here we shall discuss the two possibilities—expanding or static Universe—because the predictions of cosmological model tests for them are known to be very distinct at the high redshifts achievable by the JWST. The most obvious distinction consists of the predicted observed angular size of a galaxy as a function of its redshift [56,57,58,59,60], both angular size and redshift being directly observable quantities.

This difference in the predicted angular sizes of galaxies obviously affects their surface brightnesses. Therefore, the Tolman surface brightness test [61,62] would be among other important tests for distinguishing the origin of the cosmological redshift.

Another significant distinction between the expanding- and static-Universe models consists of the relationship between the increase in the line-of-sight distances corresponding to redshift increments $\mathsf{\Delta }z$. In the FLRW models, the physical-to-comoving volume ratio is strongly reduced at high redshifts. Since, by definition, the number of objects locked in a comoving volume is constant, the number-density of these objects in the corresponding physical volume would be dramatically increasing in expanding-Universe models. Thus, the number-count of high-redshift galaxies observed by the JWST can serve as yet another cosmological test for distinguishing between the two redshift types. Although this kind of test is complicated by the fact that the galaxy number densities at high redshifts are related to the galaxy formation through the number of galaxy systems formed during their evolution, the ultra-high redshifts accessible by the JWST can help disentangle the evolutionary- and cosmological-model-related issues.

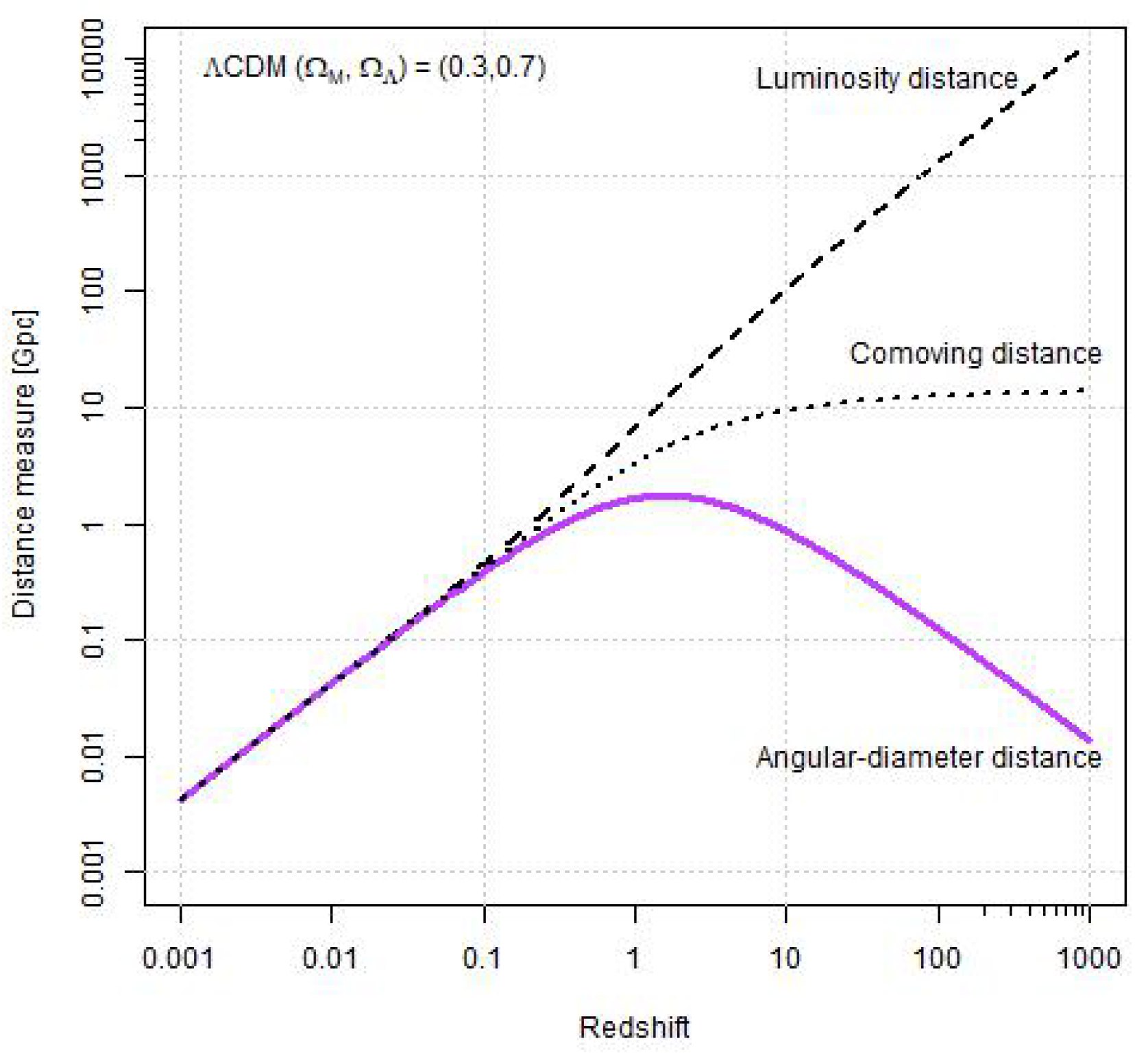
2.2.1. Angular Diameter—Redshift Relationship in the ΛCDM Model

The observable cosmological-distance measure is the cosmological redshift z defined as the difference between the wavelength ${\lambda }_{\mathtt{obs}}$ measured in the coordinate frame of the observer and the wavelength ${\lambda }_{\mathtt{src}}$ emitted by a remote source:

$$z=\frac{{\lambda }_{\mathtt{obs}}-{\lambda }_{\mathtt{src}}}{{\lambda }_{\mathtt{src}}}.$$

(1)

The source is assumed to be at rest with respect to the Hubble flow—the coordinate frame moving away from the observer with the recession speed [63]

$$v=\frac{c}{a_0}\frac{da\left(t\right)}{dt}\underset{0}{\overset{z}{\int }}\frac{d{z}^{\prime }}{H\left(z^{\prime }\right)},$$

(2)

which is $\approx H_{0}D$ for small z, where D is distance (in Mpc) in the expanding Universe; $a\left(t\right)/a_0$ is the normalised scale factor; and $H\left(z^{\prime }\right)={(1+{\mathsf{\Omega }}_M[{(1+z^{\prime })}^3-1])}^{-1/2}$.

The angular diameter distance $D_A$ of an astronomical object (from an observer) is the ratio of the (perpendicular to the line-of-sight) physical linear size $\delta$ of the object (e.g., its diameter) to its angular size $\theta \left(z\right)$ as measured by the observer:

$$D_A\left(z\right)=\frac{\delta }{\theta \left(z\right)},$$

(3)

z being the redshift of photons emitted from the object. $D_A$ is a model-dependent quantity determined in the simplest approximation of the standard cosmology for a flat universe as

$$D_A{\left(z\right)}^{\mathsf{\Lambda }\mathrm{CDM}}=\frac{c}{H_0}\frac{1}{1+z}\underset{0}{\overset{z}{\int }}\frac{\mathrm{d}{z}^{\prime }}{\sqrt{1+{\mathsf{\Omega }}_{\mathrm{M}}[{(1+z^{\prime })}^3-1]}}.$$

(4)

The angular diameter distance, as calculated for the standard $\mathsf{\Lambda }$CDM model, is plotted in Figure 1 (the purple curve). At redshifts higher than $z\approx 1.61$, the angular diameter distance diminishes because the scale factor (“size” of the Universe) is smaller at the moment of time when light from a remote source is emitted than at the moment of time when this light is detected by the observer.

Figure 1 also shows two other cosmological distance measures:

• the comoving distance

$$D_C\left(z\right)=(1+z)D_A\left(z\right)$$

(5)

• and the luminosity distance

$$D_L\left(z\right)={(1+z)}^2{D}_A\left(z\right),$$

(6)

• the latter being defined as the relationship between the bolometric flux F and the bolometric luminosity L:

$$D_L\left(z\right)=\sqrt{\frac{L}{4\pi F\left(z\right)}}.$$

(7)

The expression (6) is sometimes called the Etherington’s distance-duality relationship because it is based on the reciprocity theorem for null geodesics proven by Etherington in 1933 [64]. It was explicitly identified by G.C. McVittie 1956 [31] but was implicit in R.C. Tolman’s 1930s works [30,61].

The angular-diameter distance (3) and angular size $\theta$ are inversely related to each other. Therefore, the theoretical angular diameter

$$\theta \left(z\right)=\frac{\delta }{D_A{\left(z\right)}^{\mathsf{\Lambda }\mathrm{CDM}}}$$

(8)

in the framework of the $\mathsf{\Lambda }$CDM model is expected to be increasing at $z>1.61$ for an astronomical object of a fixed linear diameter $\delta$. This is illustrated by the plot of $\theta \left(z\right)$—the purple curve on the left panel of Figure 2 for an object having a fixed size $\delta =10$ kpc (slightly smaller than the Milky Way size).

Since it is the angular size $\theta$ that is the typical observable for remote galaxies, we can determine the linear size of an object with redshift z by using the formula

$$\delta \left(z\right)=\theta D_A^{\mathsf{\Lambda }\mathrm{CDM}}\left(z\right).$$

(9)

The corresponding plot is presented in the right panel of Figure 2. It shows the linear measure (in kpc) for each arcsec of the apparent angular size of an object whose cosmological redshift is z. We can see that since the angular resolution of JWST is ∼${0.1}^{″}$ 6, this telescope can easily resolve the sizes of high-redshift galaxies for any FLRW model.

The $\mathsf{\Lambda }$CDM framework suggests that the JWST must find large images of remote galaxies whose surface brightness is low. However, what is currently observed is something opposite to what is expected: there are small (by their angular size) galaxies with bright surfaces at ultra-high redshifts. Perhaps this can be explained by modifying galaxy formation and evolution theories. However, for the sake of impartiality and simplicity, one also has to check the congruency of JWST data to the static- or slowly-expanding universe models with alternative physical mechanisms of the cosmological redshift.

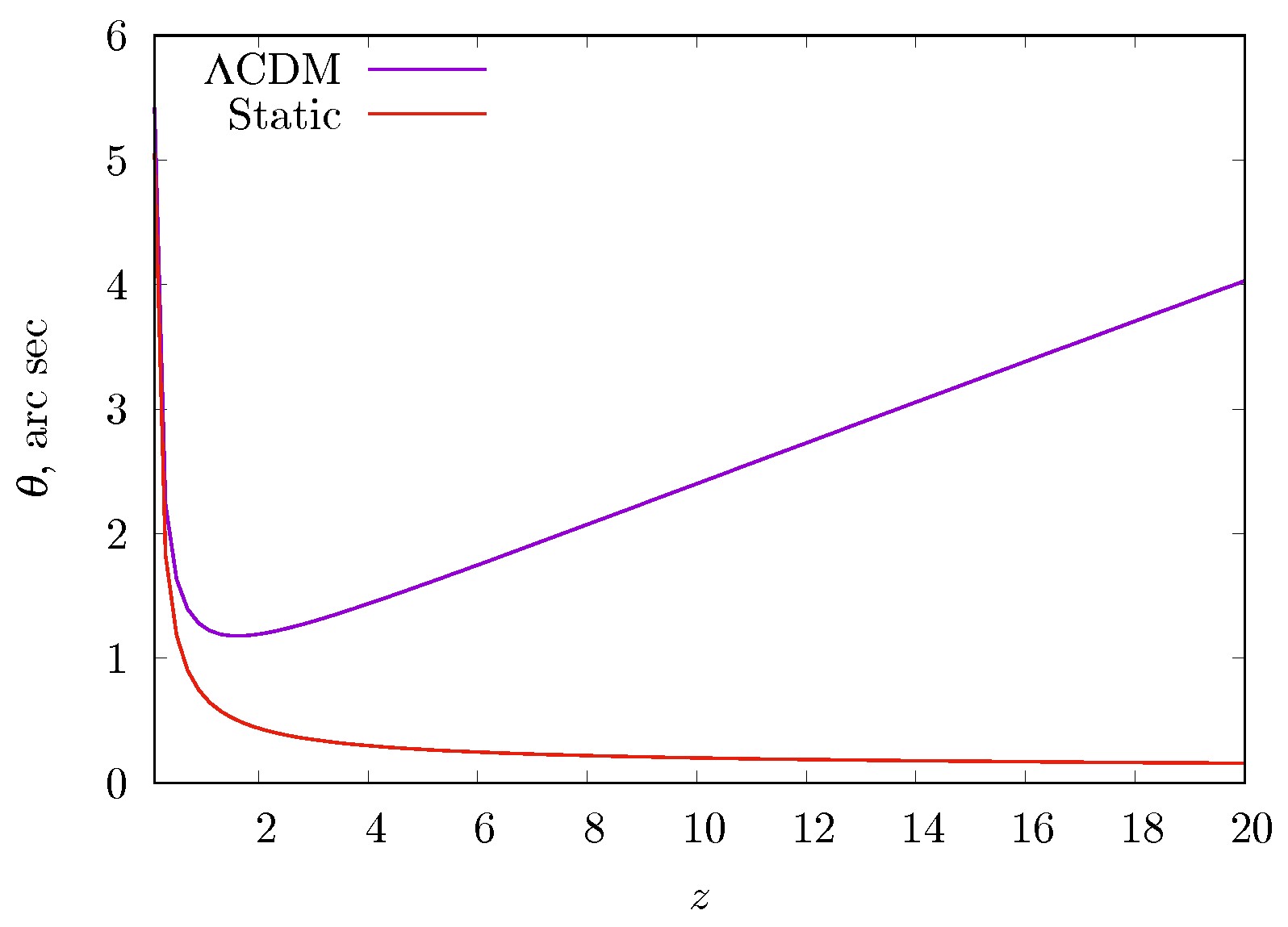
2.2.2. Static-Universe Models

In order to compare the $\mathsf{\Lambda }$CDM-interpretation of JWST observations with interpretations based on alternative cosmologies, we shall examine the most widely discussed alternative cosmology based on F. Zwicky’s proposal in which he attributes the cosmological redshift to one of the possible physical mechanisms of photon-energy loss [44].

In his work, Zwicky analysed three possible physical mechanisms that could provide the necessary energy loss of photons on their path through spacetime:

• Compton scattering on free electrons;
• Gravitational redshift due to gravitational potential wells of galaxies or galaxy clusters along the photon’s path;
• General-relativistic transfer of photon energy/mass to the masses distributed along the photon’s path.

When checking the viability of these three mechanisms, F. Zwicky demonstrated that the first two of them were not helpful in the explanation of the cosmological redshift and must be rejected. Whereas the third possibility could still be regarded as a viable alternative to the FLRW-mechanism of the photons stretching in the expanding space. Later R. Tolman coined Zwicky’s proposal as the “tired-light” (TL) theory. Nowadays, the prevailing modern interpretation of this theory is based on the photon-scattering mechanism. Following this tradition, here we shall use the notation TL referring to this particular mechanism of the cosmological redshft. It is commonly believed that the photon-scattering mechanism is likely to be wrong. It was rejected straightaway by Zwicky himself in his original paper. One of the main observational evidence against this mechanism is the absence of blurring of remote galaxy images. Indeed, photon scattering, e.g., on electrons, results in a significant photon-scattering angle. However, in principle, it is possible to explain the photon-electron interaction with the corresponding photon-energy loss without any scattering angle. For example, in Ashmore’s theory [65], photons are absorbed and re-emitted by electrons in the intergalactic medium. The electron recoils and the photon loses energy. There is no angular spread in this mechanism, as it is equivalent to photon transmission in a transparent medium. According to [65], an electron density ${\rho }_0=0.8h_{100}$ [m${}^{-3}$] produces the required cosmological redshift magnitude. Therefore, we assume here that the TL-model cannot be completely disregarded on the basis that it disagrees with observations. This model is still under discussion, and its theoretical aspects are rigorously formulated [66]. This theoretical consideration leads to the following expression for the redshift-distance relationship:

$$z\left(r\right)=\frac{\mathsf{\Delta }\lambda }{{\lambda }_0}=exp\left(\beta r\right)-1,$$

(10)

where z is the redshift of the photon’s initial wavelength ${\lambda }_0$ after the photon has travelled a distance r; and $\beta =H_0/c$ is the energy attenuation coefficient. The form of (10) is exponential because photon-scattering is cumulative along the photon’s path.

Unlike the $\mathsf{\Lambda }$CDM model, in which the metric of spacetime is Riemannian, the metric in the TL model is Euclidean, where the angular size of an object is inversely proportional to its distance from the observer. Thus, the predictions of this model are essentially different from those based on the expanding-Universe concept.

Consequently, the relationship between the angular $\theta$ and linear $\delta$ sizes in TL is

$$\theta {(\delta ,z)}^{\mathrm{TL}}=\frac{H_0}{c}\frac{\delta }{ln(1+z)},$$

(11)

with the corresponding angular-diameter distance being

$$D_A^{\mathrm{TL}}\left(z\right)=\frac{c}{H_0}ln(1+z).$$

(12)

Even before Zwicky’s works, static cosmological models were proposed, in which the cosmological redshift was explained by general-relativistic (i.e., geometrical or gravitational) change of photon energy with distance. The first static general-relativistic cosmological model was introduced by Einstein in 1917 [67]. At that time, he was not concerned with the cosmological redshift problem because there was not then available observational evidence for such a phenomenon, and the Universe was commonly believed to be static. However, based on Einstein’s theory alone, it was already possible to foresee the existence of the cosmological redshift.

This was done by W. de Sitter in his prophetic 1917-paper [68], where he considered positively curved 3-manifolds of spherical, ${\mathbb{S}}^3$, and elliptical shapes, the latter being also called projective space, ${\mathbb{P}}^3$. The elliptic space in de Sitter’s considerations models the physical world by projecting it onto the Euclidean space ${\mathbb{E}}^3$. The projection corresponds to the coordinate transformation

$$r=Rtan\chi ,$$

(13)

where $R^{-2}$ is the constant positive curvature of ${\mathbb{S}}^3$ or ${\mathbb{P}}^3$. Thus, it uses other coordinates instead of (r, $\psi$, $\theta$). Locally, ${\mathbb{S}}^3$ and ${\mathbb{P}}^3$ are identical to ${\mathbb{E}}^3$. However, such quantities as velocity and energy are related to different coordinate systems. Hence, they may change when observed in one or another reference frame. De Sitter argues that since the time-component of the metric $g_{44}={cos}^2\chi$ diminishes in the elliptical space with the increase of the distance parameter $\chi$, then “the frequency of light vibrations diminishes with increasing distance from the origin of coordinates. The lines in the spectra of very distant stars or nebulae must therefore be systematically displaced towards the red.”

This 1917-prediction (sometimes called the de Sitter effect) that the spectra of remote objects are redshifted in a static universe endowed with Einstein’s curvature was made by de Sitter in the same year when Slipher discovered that the spectra of the majority of galaxies (84%), which he was observing were redshifted [69]. This prediction was made well before Lundmark’s discovery that Slipher’s redshifts of galaxies were proportional to their distances [70]. Furthermore, the Hubble–Lemaître law [71,72] was discovered much later in 1927–1929. It is interesting to note that a few years before the Lemaître–Hubble’s discovery, Eddington warned against the possible wrong interpretation of galaxy redshifts as due to their recession. In 1923 he wrote: “in de Sitter’s theory, there is the general displacement of spectral lines to the red in distant objects due to the slowing down of atomic vibrations which would be erroneously interpreted as a motion of recession” [73]. That is why Hubble, in his discovery paper [72], recites the de Sitter effect as one of the possible mechanisms responsible for the distance-redshift relationship. This redshift mechanism in the Einstein–de Sitter’s model of the Universe was later discussed in more detail by F. Hoyle [74].

Based on his prediction, de Sitter estimated the angular size $\theta$ of a remote object at a distance $r=R\chi$ from the observer, which was one of the first attempts to link the size of the Universe and cosmological redshift.

De Sitter’s ideas were further developed in 1974 by I.E. Segal in his Chronometric Cosmology theory [75]. Segal pointed out [76] that “time and its conjugate variable, energy, in the Universe with the Einstein curvature are fundamentally different from the conventional time and energy in the local flat Minkowski space that approximates the Einstein Universe at the point of observation”. Despite being very closely related to the Einstein–de Sitter model of the Universe, Segal’s cosmology is rejected by the astronomical community because it fails to match observational data. Although he used the correct approach by making a distinction between space and time approximations in the curved and flat spacetimes, Segal arrived at incorrect expressions for the redshift-to-distance law and other quantities needed for testing cosmological models.

More recently, de Sitter’s idea of using the Einstein Universe curvature has been revived by J.H. Marr [77] who literally follows the logic of the de Sitter’s 1917 work, but strangely does not mention it. Nevertheless, by using his visualisation tool for representing photon paths in the form of logarithmic spirals, $1+z=e^{\psi }$, Marr derived the following expression for the angular-diameter distance

$$D_A^{\mathrm{Marr}}\left(z\right)=\frac{c}{H_0}ln(1+z),$$

(14)

which coincides exactly with the expression (12) of the TL model due to the use of the exponential form of the logarithmic curves representing photon paths. The Hubble diagram built by Marr with the use of the luminosity distance based on Equation (14) agrees satisfactorily with the distance moduli of the type-Ia supernova, having the same level of accuracy as the $\mathsf{\Lambda }$CDM-based Hubble diagram or even better.

Despite the obvious possibility of Einstein’s curvature being the basis of one of the possible explanations of the observed cosmological redshift, Einstein himself abandoned his static-Universe solution as being unstable. Instead, in 1931, he proposed a cyclic-Universe model [48]; thus, siding with the Lemaître’s dynamical interpretation of the cosmological redshift. Unfortunately, Einstein did not know that 39 years later his static solution would be proven stable by his collaborator N. Rosen [78]. Nevertheless, Einstein still had his reservations with respect to the expanding-Universe model, expressing some doubts in his 1931 paper. Commenting on the estimated time from the beginning of the expanding Universe he wrote: “The greatest difficulty of this whole approach is that the elapsed time since P = 0 comes out at only about ${10}^{10}$ years”. He chose the word “difficulty” because he was well aware of the fact that this estimated timespan was smaller than the ages of some stars, which were found to be of about ${10}^{13}$ years [79]. A more recent example of a star with an age $14.46\pm 0.31 \mathrm{Gyr}$, which exceeds the presumed time from the beginning of the Universe, is HD 140283 [80].

At low redshifts ($z<0.1$), the distance-to-redshift relationship is approximately linear:

$$z=\frac{H_0}{c}r,$$

(15)

with the corresponding angular-diameter function

$$\theta {(\delta ,z)}^{H_0}=\frac{H_0}{c}\frac{\delta }{z}.$$

(16)

At higher redshifts, different cosmological models deviate from this linear relatioship in diverse ways, which allows the use of the angular size measurements to differentiate between cosmological models. Here, for comparison purposes, we shall use this simplest linear relationship in our plot of galaxy angular sizes (see Section 3) to highlight that neither $\mathsf{\Lambda }$CDM, nor the linear function, match the JWST data.

If we compare the angular diameter functions for the expanding- and static-Universe models (see Figure 3), we note that the static (TL) model predicts much smaller angular sizes of high-redshift galaxies than $\mathsf{\Lambda }$CDM. Therefore, according to this prediction, JWST should observe small (by their angular size) galaxies with large surface brightnesses. Within the framework of the expanding-Universe model, a typical 10-kpc-galaxy, as seen from the distance corresponding to $z=14-16$, would appear as a 3″-angular-size object. Whereas, according to the static-Universe model, JWST should observe it to be very small—a fraction of an arcsecond. With its large aperture, JWST has a high angular resolution (better that 0.1″). Thus, it will definitely observe very small galaxies as extended sources (see the next section).

3. Results

Figure 4 summarises graphically the findings of various research groups that are processing the JWST first deep-field images. We are interested here in the correspondence between the galaxy sizes (effective radii, $r_e$) and galaxy redshifts. The purple points in Figure 4 indicate galaxy physical sizes (in kpc) as determined by different authors from the observed angular sizes within the standard $\mathsf{\Lambda }$CDM model. Most of the galaxies found within the JWST field of view are extremely small, their effective radii varying from 0.1 kpc to 3 kpc at redshifts $z=6-10$. Assuming their masses are comparable to the masses of the local-Universe galaxies (${10}^8$ to ${10}^{11}$ M${}_{\odot }$), these galaxies look extremely odd. They have well-developed disks and bulges and contain dust. Furthermore, their chemical composition is similar to that of local galaxies. Some of them are likely to contain the same number of stars as the Milky Way, but they look like a Milky Way squeezed to 1/10th of its size.

By contrast, if we look at them from the point of view of an observer in a non-expanding universe (the green points in Figure 4) we would find that their sizes are comparable to the sizes of local galaxies ($r_e=2$ to 30 kpc), and the peculiarity of a “squeezed Milky Way” disappears.

The observed galaxy sizes shown in Figure 4 are also presented (in the form of angular diameters, $2r_e$) in Figure 5 as red points. They are compared with the plotted theoretical angular-diameter curves for a ∼10 kpc-object. This is the size of a typical galaxy in the local Universe as it would be seen from distances corresponding to the redshifts $0.1<z<20$. The scatter of the points in this plot is quite large, and most of the redshift estimations here are photometric, with large error-bars (as we have already mentioned in Section 2.1, the photometric redshifts are within the redshift error-bars in Figure 5 to avoid confusion.

The theoretical angular sizes of such objects are plotted for three cases:

• An expanding Universe (dashed curve) with the expansion parameters corresponding to the standard $\mathsf{\Lambda }$CDM cosmological model, Equation (8);
• A static Universe with the photon-energy loss and the angular size parametrised according to Equations (12) or (14), dotted curve;
• A static Universe with the linear form of the $\theta -z$ relationship, Equation (16), solid curve.

The JWST observations are supplemented in this Figure with some pre-JWST observations (black points) made with the use of the Hubble Space Telescope and some large ground-based telescopes [88,89,90,91,92,93,94,95,96,97]. In order to get a more definitive result we have added to this plot the angular sizes of galaxies from two large galaxy surveys (small black points), one containing 7003 objects [98] with redshifts from $z=1$ to ∼$2.5$ and another containing 670,722 objects [99] with redshifts $0<z<0.3$. Only 2% of this latter sample is shown on the plot, otherwise its statistical properties would be visually obscured.

4. Discussion

The angular sizes of galaxies seen in Figure 5 exhibit a clear evolutionary trend, with galaxy angular sizes diminishing to $\theta \approx {0.2}^{″}$ as the redshifts increase to $z\approx 15$. This is currently understood in terms of their time-evolution, from some protogalaxies at very high redshifts to large size galaxies appearing via merging of smaller galaxies. There is a problem here: those small size galaxies detected by the JWST at high redshifts are too massive to be protogalaxy candidates. This suggests that what is occurring is a pseudo-evolution.

This (pseudo-)evolution has been noticed by many researches. For example, Ono et al. [84] demonstrate that the effective radii $r_e$ of galaxies tend to diminish from 50 kpc to 0.1 kpc as their redshifts increase from $z=0$ to $z=17$. These authors point out that a few galaxy candidates, such as GL-z12-1 ($z\approx 12$), whose sizes are exceptionally small ($r_e^{\mathrm{GL}-\mathrm{z}12-1}=61\pm 11$ pc), have masses too high (∼$3\times {10}^8$ M${}_{\odot }$) for them to be protogalaxies.

Other researches [29] have found a similar compact galaxy at $z\approx 17$, and its mass is also very big: $M_{*}\approx 5\times {10}^9$ M${}_{\odot }$. According to the $\mathsf{\Lambda }$CDM-approach, this galaxy was formed a mere ∼220 Myr after the Big Bang. Numerical simulations predict galaxy masses to be below ${10}^8$ M${}_{\odot }$ at this cosmic time [100]. So, the authors of [29] came to the conclusion that such a galaxy “challenges virtually every early galaxy evolution model that assumes $\mathsf{\Lambda }$CDM cosmology”. They also point out that, given the relatively small area currently explored by JWST (less than 60 square arcminutes), the number of very bright objects found within this area is surprisingly large. For example, Naidu et al. [86] have found two very bright galaxy candidates at $z=11$ and $z=13$ and calculated the corresponding number densities (UV-luminosity functions) ${\varphi }_{UV}\approx 6.3\times {10}^{-7}$ [mag${}^{-1}$ Mpc${}^{-3}$] for $M_{UV}\approx -22.1$ and ${\varphi }_{UV}\approx 1\times {10}^{-5}$ [mag${}^{-1}$ Mpc${}^{-3}$] for $M_{UV}\approx -20.8$. If we compare these values with similar estimations made by Bowler et al. [101] for lower redshifts ($z=9$), ${\varphi }_{UV}\approx 8\times {10}^{-7}$ [mag${}^{-1}$ Mpc${}^{-3}$] for $M_{UV}\approx -22.1$ and ${\varphi }_{UV}\approx 9\times {10}^{-5}$ [mag${}^{-1}$ Mpc${}^{-3}$] for $M_{UV}\approx -20.8$, then we see that number densities of bright galaxies are practically the same for $9<z<13$, although theoretically they should substantially diminish at higher redshifts.

This discrepancy also follows from the results of hydrodynamic simulations of the Millennium-TNG project [102]. It turns out that beyond $z\ge 12$, this simulation underpredicts the abundance of luminous galaxies and their star-formation rates by almost an order of magnitude. The authors of this simulation comment that the same discrepancy is typical for most other similar works. They suggest an explanation that there might be some missing physical processes that are not included in simulations. However, as we shall see in Figure 6 below, this discrepancy might be simply due to the underestimation of cosmic time.

Standard UV-luminosity functions predict a much smaller number of bright objects within 60 square arcminutes. That is why the authors of [29] hypothesise that JWST is discovering new, hitherto unknown galaxy populations, which was previously suggested for explaining HST observations [13] (alas, Occam’s razor 7 is yet again abandoned or forgotten here).

As for the galaxy mergers, as far as we know, the early JWST observations have revealed only one candidate of a merging galaxy pair MACS0647–JD (possibly a triplet) at $z\approx 11$ [103]. The theoretical merger rate for $z>6$ is estimated to be ∼$0.1$ [Gyr${}^{-1}$] per galaxy [104]. Since JWST has detected about a dozen galaxy candidates at $z\sim 11$, the theoretically expected number of detected galaxy mergers approximately matches the observed number, given the cosmic time ∼$0.43$ Gyr corresponding to $z\sim 11$. However, this theoretical merger rate is likely to be underestimated because it does not differ from the merger rate estimated for low-redshift galaxies, whereas the current galaxy formation theory expects small galaxies at high redshifts to form large galaxies at low redshift by multiple mergers. That is why other simulations of galaxy formation give much higher expectation values for the theoretical merger rate, ∼$4-5$ [Gyr${}^{-1}$] per galaxy for $z=10$ [105].

The masses of the high-redshift galaxies estimated by using JWST observations [5,7,12,28,29,82,83,84,85,86,87] are shown in Figure 6 (red points). The black points indicate masses deduced from some pre-JWST observations [97,98,106,107,108,109] made by using large ground-based telescopes and the Hubble Space Telescope.

We note the evolutionary (pseudo-evolutionary) decline in galaxy masses toward the high-redshifts (which is highlighted by the dashed curve on the left panel of Figure 6). If real, this evolution feeds into the $\mathsf{\Lambda }$CDM narrative. Although, there are still some problems related to the lack of time for the possible build-up of protogalaxies. It is difficult to ignore the fact that these alleged protogalaxies are fully developed, smooth (i.e., they are not disturbed by merging with other galaxies), with their disks, bulges and a chemical composition similar to the chemical composition of local galaxies 8. It is clearly pointing out that these galaxies are practically the same as our nearby galaxies in the late Universe.

Concerning this evolutionary trend, we have plotted it in the left-hand side panel of Figure 6 in the form of the function ${(1+z)}^{-2}$ (the dashed curve). We know that galaxy masses are estimated from their luminosities (see, e.g., [112,113]), and the luminosity–distance function in the expanding-Universe models is reduced by the same factor of ${(1+z)}^{-2}$. If we correct the galaxy masses estimated within the $\mathsf{\Lambda }$CDM framework by this factor, we see that not only morphologies and chemical composition of the remote galaxies are similar to the local-Universe’s galaxies but their masses as well (see the right panel of Figure 6).

Still there is some noticeable evolutionary trend remaining in the high-redshift galaxy masses (indicated by the dotted light-blue curve in the right-hand side panel of Figure 6). This means that remote galaxies, indeed, grow and evolve, but this happens at a much slower pace than is assumed by the standard cosmological model.

It must also be noted that the cosmological test based on the redshift-dependent angular-sizes of galaxies alone do not provide sufficiently strong evidence against the $\mathsf{\Lambda }$CDM model since the observed evolution of galaxy sizes might be real. Therefore, it would be important to perform other cosmological tests, by studying, for example, the relationship between the redshift and the number-density of high-redshift galaxies and other objects, such as galaxy clusters or quasars. In static- and expanding-Universe models, this relationship is different, the distinction is of the factor ${(1+z)}^3$, which is quite large.

Within the $\mathsf{\Lambda }$CDM model, the number-density of remote objects within the spherical layers of thickness $\mathsf{\Delta }z$ is fixed (by definition). However, the volumes of these spherical layers strongly decrease with the increase of z. This should lead to dramatic increases of the proper (metrical) number-density of objects in the high-redshift volumes. Eventually, this number-density would become an impossible quantity from the point of view of any physical model. The same would be (and is) seen in the number-density of stars within the volumes of high-redshift galaxies, as their physical sizes are strongly decreased when estimated within the expanding-Universe formalism, while the stellar masses of these galaxies remain approximately the same as the local-Universe galaxies.

Another important distinctive parameter is the cosmological time dilation. It can be used for determining the nature of the cosmological redshift. For example, the static cosmological model with photon-energy dissipation predicts no time dilation. Whereas the FRLW models and the static models with the cosmological redshift of the general-relativistic (gravitational) nature predict the time-dilation factor scaling with the factor of $(1+z)$.

The time-dilation effect is actually observed in the light-curves of the type-Ia supernovae [114,115,116], which strongly supports the expanding-Universe models or the static-Universe models of the Einstein-de-Sitter type. Nevertheless, additional studies of this effect are still needed because there exist some evidence against the cosmological time-dilation. In particular, gamma-ray bursts, nova-like stars, quasars and fast radio-bursts are poorly explored in terms of their light-curve duration. Available publications with the results of temporal behaviour of their light-curves in relation to their redshifts are contradictory [117,118]. New research in this direction would reduce systematic errors and check more rigorously the functional dependence of the time-dilation factor on z. It would be important for revealing possible combined types of cosmologies (e.g., the TL-redshift mixed with the the redshift due to the Universe expansion).

Further study of galaxy angular-sizes and number-densities at high reshifts is also very important for determining more accurately the cosmological-model parameters. Additionally, finding transient objects at high-redshifts, such as supernovae, gamma-ray bursts or fast radio-bursts, and measuring parameters of their light-curves would help specify more accurately the nature of the cosmological time-dilation effect. New goal-settings would likely emerge on the course of these studies, as there might be some unexpected findings on this way.

Consequently, it would be very important to continue gathering and analysing JWST observations of the high-redshift Universe, compiling large catalogues of photometric and spectrophotometric redshifts of remote objects.

Although our analysis of JWST observations favours a static (TL) model of the Universe rather than the standard (expanding-Universe) cosmology, the latter is strongly supported by other observational evidence. The main challenges which any static cosmological model must face are the cosmic microwave background (CMB), the abundance of chemical elements in the Universe and the formation of cosmic structure.

In the standard model, the CMB, with its black-body spectral energy distribution with $T=7$ K was predicted by G. Gamow [119] to exist before it was actually discovered. It would be fair to acknowledge that for the static Universe, a similar thermalised radiation with $T=3$ K was predicted even earlier, in 1926, by A.S. Eddington [120] and with $T=2.8$ K by W. Nernst in 1937 [121]. For more comprehensive reviews as to the possibility of explaining the CMB radiation within the framework of static-Universe models see, for example, [122,123].

There are also static-Universe alternatives to the standard model predictions with respect to the light element abundances and baryon fraction. For example, G.R. Burbidge and F. Hoyle discussed the possibility of helium creation in massive objects [124,125]. R. Salvaterra and A. Ferrara [126] proposed that the primordial He abundance could be created by population III stars. On the other hand, the standard Big Bang nucleosynthesis theory is not without serious problems [127,128,129].

The only open issue for static-Universe models that remains is the origin of the overdensities, which leads to cosmic structure formation and which is elegantly solved in the standard cosmology by the mechanism of initial quantum fluctuations and baryonic acoustic oscillations. However, although we have used here the tired-light model as a static-Universe model example, from the right-hand side panel of Figure 6 we see that the Universe is evolving with respect to this model. That means the real picture is more complicated than a pure static cosmological solution. Therefore, the physical mechanism for the original overdensities and cosmic structure formation could well be the same as in the $\mathsf{\Lambda }$CDM cosmology, including quantum fluctuations and the baryonic acoustic oscillations. Although with respect to the latter, various authors mention that there might be some problems with their statistical analysis and accuracy [38,39,130,131].

5. Conclusions

We conclude that the first JWST observations of high-redshift objects cannot be explained by the expanding-Universe model. Everything points to the possibility that the actual age of the objects in the Universe is far larger than predicted by $\mathsf{\Lambda }$CDM cosmology. Of course, we should be cautious about such a conclusion. Thus, before dismissing the expanding-Universe paradigm, it is important to robustly confirm the new findings.

No doubt, much longer exposures and much deeper fields will be acquired in the forthcoming years by the JWST. These longer exposures would likely result in new galaxies discovered at $z\approx 20$ or more. Based on our conclusion, we predict that the JWST should discover even smaller galaxies (in terms of their angular-sizes) and that those smaller galaxies would be observed as very luminous, with well-developed morphology. They would be approximately the same (perhaps, slightly less-evolved) as the galaxies of the late Universe. In such a case, the expanding-Universe paradigm would require correction and modification, in line with the discussion presented here.