Modeling Nearby Low-Luminosity Active-Galactic-Nucleus Jet Images at All VLBI Scales
Abstract
1. Introduction
2. GRMHD Paradigm of Jet Formation for LLAGN
3. Constructing Jet Model
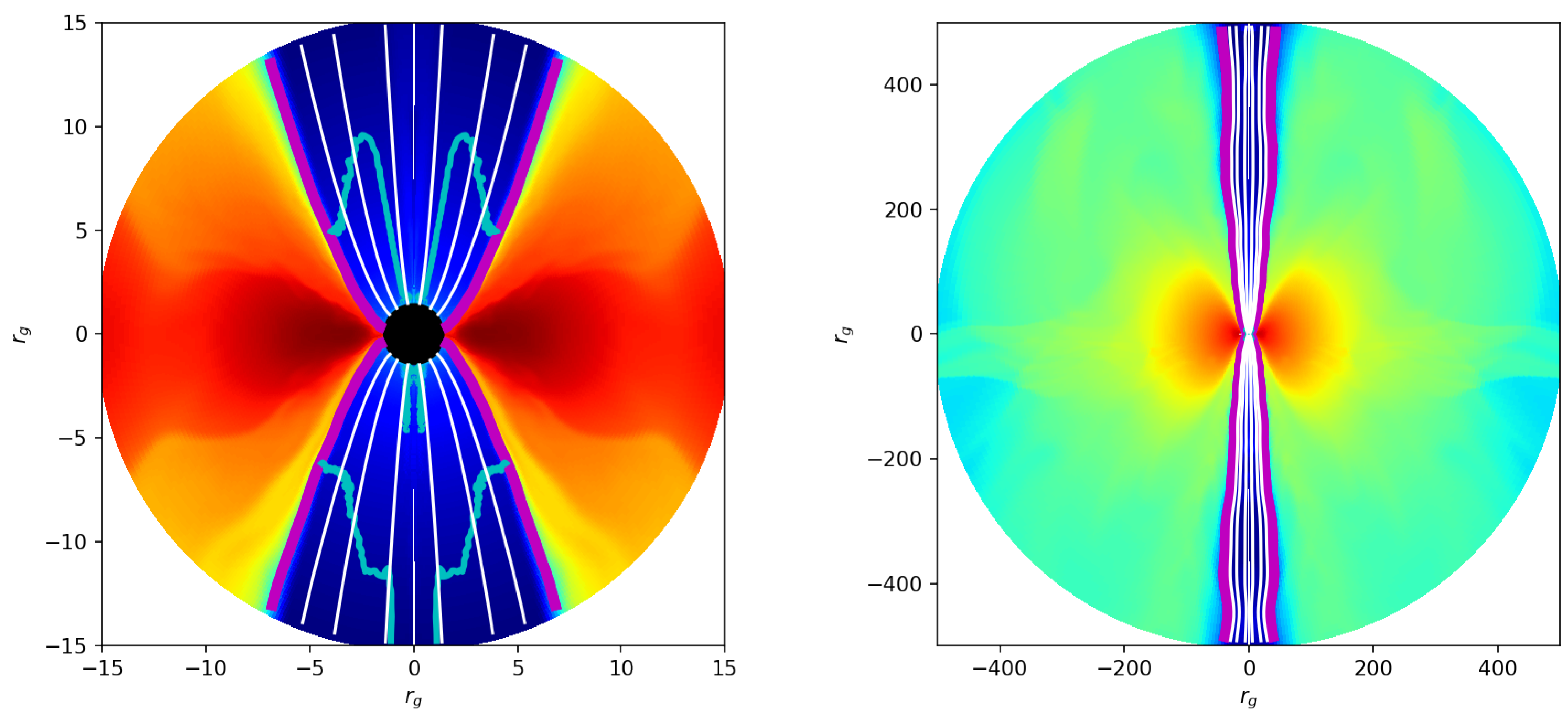
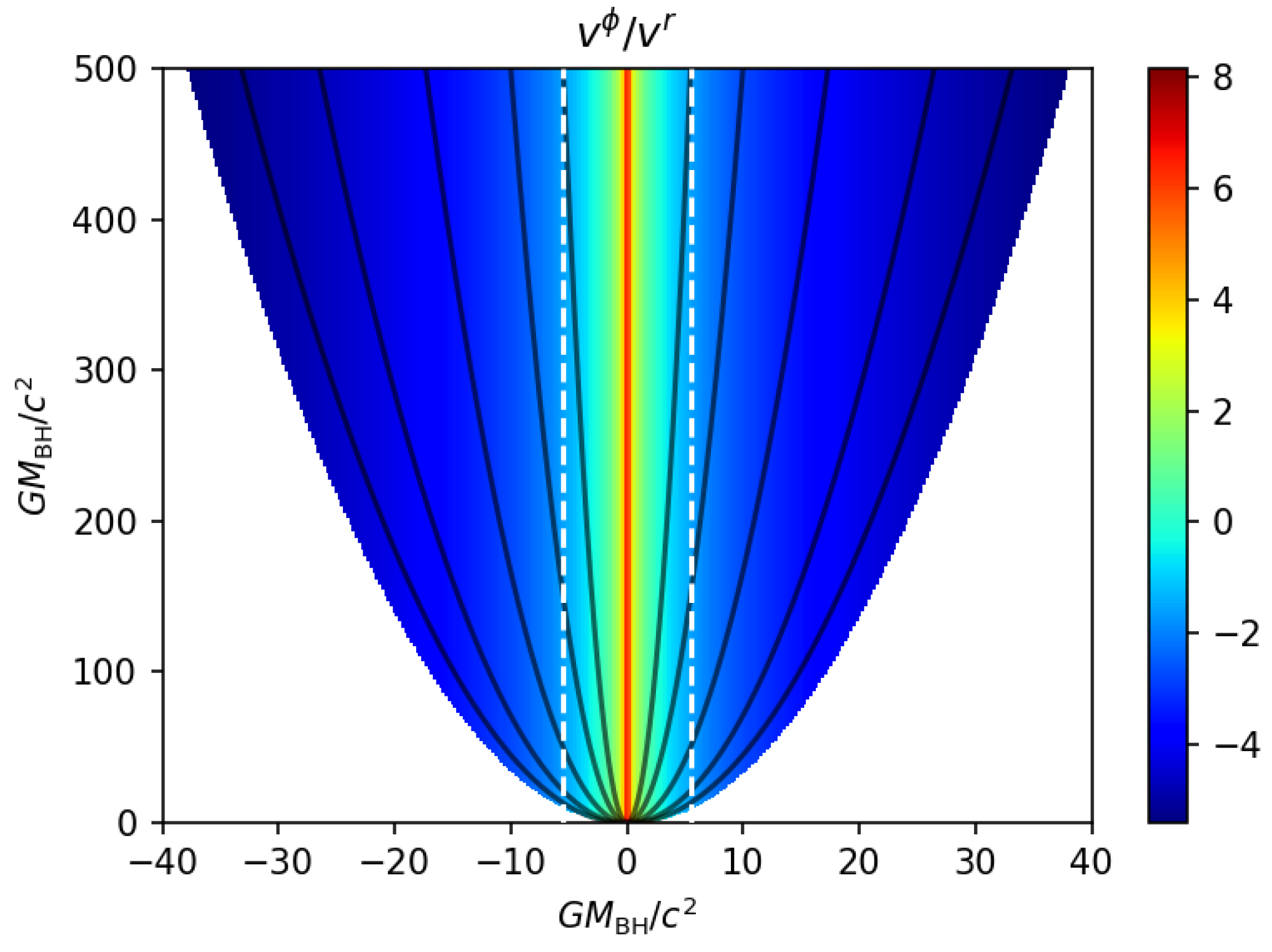
3.1. Semi-Analytical Jet Models
3.2. GRMHD Simulation Models
3.3. General Features
4. Modeling Jet Emission
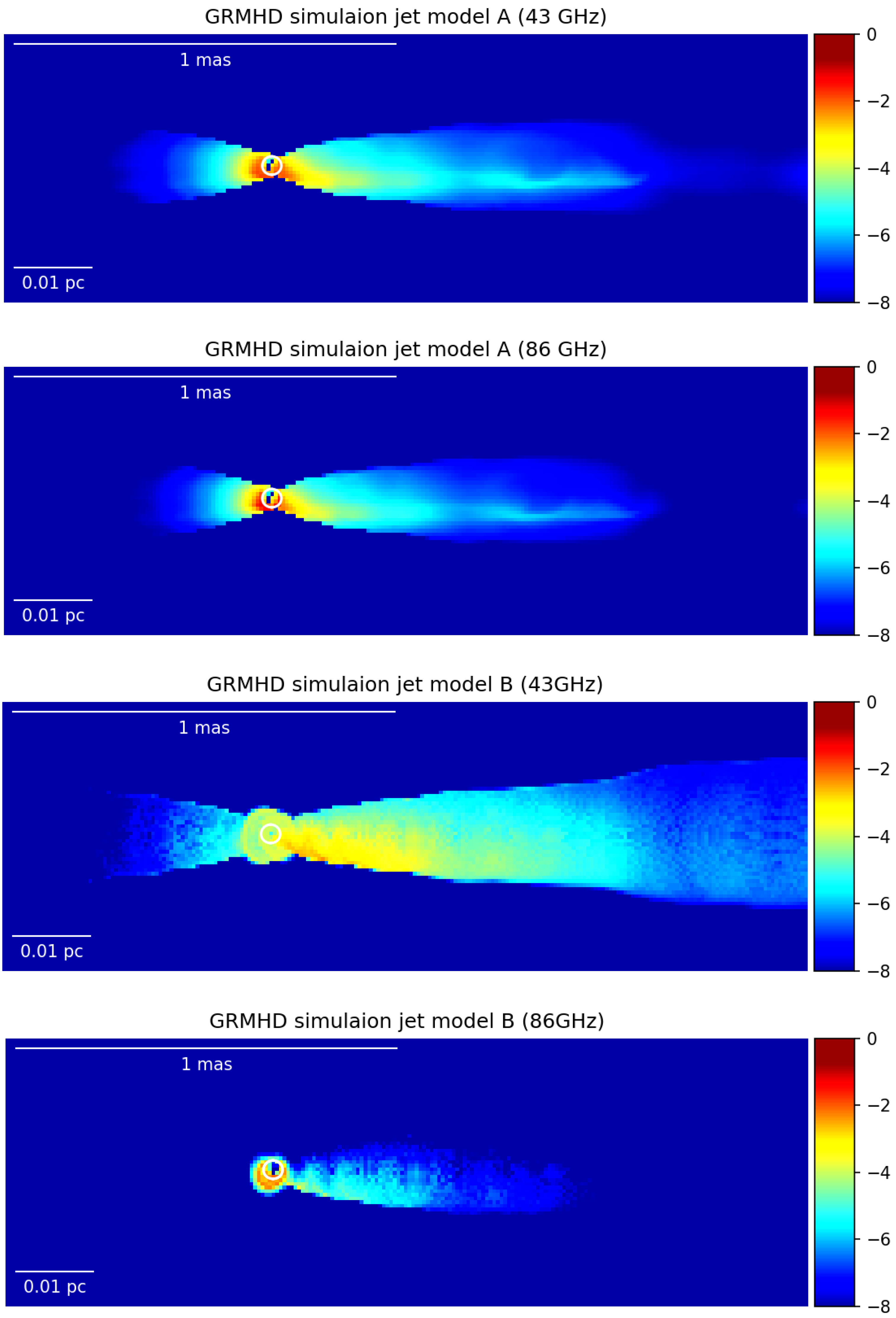
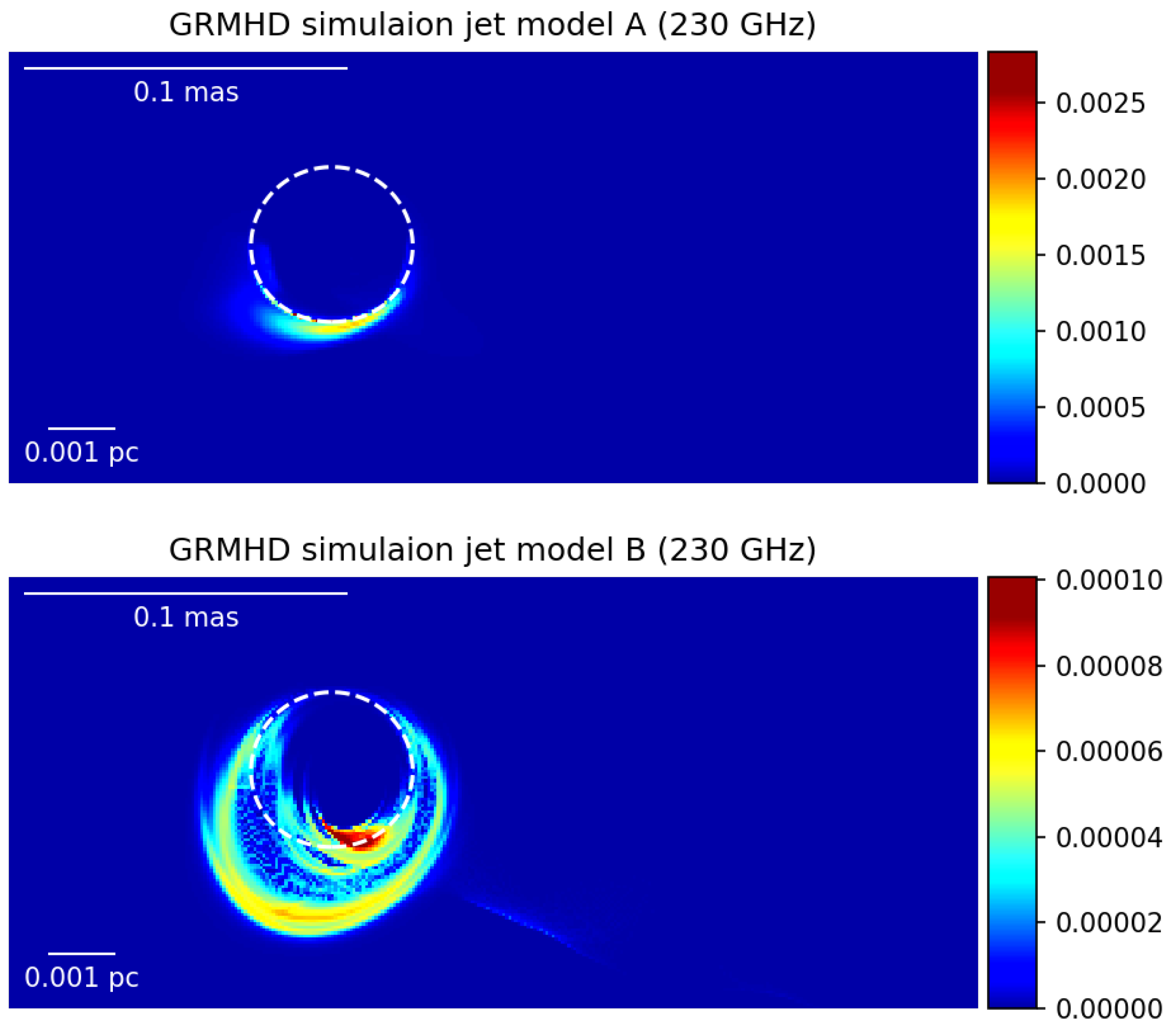
4.1. Modeling Black Hole Jets at Sub-Parsec Scales
4.2. Modeling Black Hole Jets Close to the Jet Base
5. Discussion and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| VLBI | Very-Long Baseline Interferometry |
| MHD | Magnetohydrodynamics |
| GRMHD | General Relativistic Magnetohydrodynamics |
| GRRT | General Relativistic Radiative Transfer |
| MAD | Magnetically Arrested Disk |
| SANE | Standard And Normal Evolution |
| EHT | Event Horizon Telescope |
| GSE | Grad–Shafranov Equation |
References
- Nagar, N.M.; Falcke, H.; Wilson, A.S.; Ulvestad, J.S. Radio sources in low-luminosity active galactic nuclei. III. “AGNs“ in a distance-limited sample of “LLAGNs”. Astron. Astrophys. 2002, 392, 53–82. [Google Scholar] [CrossRef]
- Nagar, N.M.; Falcke, H.; Wilson, A.S. Radio sources in low-luminosity active galactic nuclei. IV. Radio luminosity function, importance of jet power, and radio properties of the complete Palomar sample. Astron. Astrophys. 2005, 435, 521–543. [Google Scholar] [CrossRef]
- Doeleman, S.S.; Weintroub, J.; Rogers, A.E.E.; Plambeck, R.; Freund, R.; Tilanus, R.P.J.; Friberg, P.; Ziurys, L.M.; Moran, J.M.; Corey, B.; et al. Event-horizon-scale structure in the supermassive black hole candidate at the Galactic Centre. Nature 2008, 455, 78–80. [Google Scholar] [CrossRef]
- Hada, K.; Doi, A.; Nagai, H.; Inoue, M.; Honma, M.; Giroletti, M.; Giovannini, G. Evidence for a Nuclear Radio Jet and its Structure down to lsim100 Schwarzschild Radii in the Center of the Sombrero Galaxy (M 104, NGC 4594). Astrophys. J. 2013, 779, 6. [Google Scholar] [CrossRef]
- Hada, K.; Kino, M.; Doi, A.; Nagai, H.; Honma, M.; Hagiwara, Y.; Giroletti, M.; Giovannini, G.; Kawaguchi, N. The Innermost Collimation Structure of the M87 Jet Down to ~10 Schwarzschild Radii. Astrophys. J. 2013, 775, 70. [Google Scholar] [CrossRef]
- Mezcua, M.; Prieto, M.A. Evidence of Parsec-scale Jets in Low-luminosity Active Galactic Nuclei. Astrophys. J. 2014, 787, 62. [Google Scholar] [CrossRef]
- Hada, K.; Kino, M.; Doi, A.; Nagai, H.; Honma, M.; Akiyama, K.; Tazaki, F.; Lico, R.; Giroletti, M.; Giovannini, G.; et al. High-sensitivity 86 GHz (3.5 mm) VLBI Observations of M87: Deep Imaging of the Jet Base at a Resolution of 10 Schwarzschild Radii. Astrophys. J. 2016, 817, 131. [Google Scholar] [CrossRef]
- Boccardi, B.; Krichbaum, T.P.; Ros, E.; Zensus, J.A. Radio observations of active galactic nuclei with mm-VLBI. Astron. Astrophys. Rev. 2017, 25, 4. [Google Scholar] [CrossRef]
- Kim, J.Y.; Krichbaum, T.P.; Lu, R.S.; Ros, E.; Bach, U.; Bremer, M.; de Vicente, P.; Lindqvist, M.; Zensus, J.A. The limb-brightened jet of M87 down to the 7 Schwarzschild radii scale. Astron. Astrophys. 2018, 616, A188. [Google Scholar] [CrossRef]
- Park, J.; Hada, K.; Kino, M.; Nakamura, M.; Hodgson, J.; Ro, H.; Cui, Y.; Asada, K.; Algaba, J.C.; Sawada-Satoh, S.; et al. Kinematics of the M87 Jet in the Collimation Zone: Gradual Acceleration and Velocity Stratification. Astrophys. J. 2019, 887, 147. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. VI. The Shadow and Mass of the Central Black Hole. Astrophys. J. Lett. 2019, 875, L6. [Google Scholar] [CrossRef]
- Laing, R.A.; Bridle, A.H. Systematic properties of decelerating relativistic jets in low-luminosity radio galaxies. Mon. Not. R. Astron. Soc. 2014, 437, 3405–3441. [Google Scholar] [CrossRef]
- Potter, W.J.; Cotter, G. Synchrotron and inverse-Compton emission from blazar jets - II. An accelerating jet model with a geometry set by observations of M87. Mon. Not. R. Astron. Soc. 2013, 429, 1189–1205. [Google Scholar] [CrossRef]
- Ho, L.C. Nuclear activity in nearby galaxies. Annu. Rev. Astron. Astrophys. 2008, 46, 475–539. [Google Scholar] [CrossRef]
- Fernández-Ontiveros, J.A.; Prieto, M.A.; Acosta-Pulido, J.A.; Montes, M. The SED of Low-Luminosity AGNs at high-spatial resolution. J. Phys. Conf. Ser. 2012, 372, 012006. [Google Scholar] [CrossRef]
- Prieto, M.A.; Fernández-Ontiveros, J.A.; Markoff, S.; Espada, D.; González-Martín, O. The central parsecs of M87: Jet emission and an elusive accretion disc. Mon. Not. R. Astron. Soc. 2016, 457, 3801–3816. [Google Scholar] [CrossRef]
- Mahadevan, R. Scaling Laws for Advection-dominated Flows: Applications to Low-Luminosity Galactic Nuclei. Astrophys. J. 1997, 477, 585–601. [Google Scholar] [CrossRef]
- Ichimaru, S. Bimodal behavior of accretion disks: Theory and application to Cygnus X-1 transitions. Astrophys. J. 1977, 214, 840–855. [Google Scholar] [CrossRef]
- Narayan, R.; Yi, I.; Mahadevan, R. Advection-dominated accretion model of Sagittarius A* and other accreting black holes. J. Astron. Astrophys. Suppl. Ser. 1996, 120, 287–290. [Google Scholar]
- Kato, S.; Fukue, J.; Mineshige, S. Black-Hole Accretion Disks: Towards a New Paradigm. 2008. Available online: https://ui.adsabs.harvard.edu/abs/2008bhad.book.....K/abstract (accessed on 1 October 2022).
- Hada, K.; Doi, A.; Kino, M.; Nagai, H.; Hagiwara, Y.; Kawaguchi, N. An origin of the radio jet in M87 at the location of the central black hole. Nature 2011, 477, 185–187. [Google Scholar] [CrossRef] [PubMed]
- Sokolovsky, K.V.; Kovalev, Y.Y.; Pushkarev, A.B.; Lobanov, A.P. A VLBA survey of the core shift effect in AGN jets. I. Evidence of dominating synchrotron opacity. Astron. Astrophys. 2011, 532, A38. [Google Scholar] [CrossRef]
- Blandford, R.D.; Königl, A. Relativistic jets as compact radio sources. Astrophys. J. 1979, 232, 34–48. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. II. Array and Instrumentation. Astrophys. J. Lett. 2019, 875, L2. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. III. Data Processing and Calibration. Astrophys. J. Lett. 2019, 875, L3. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. IV. Imaging the Central Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L4. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. V. Physical Origin of the Asymmetric Ring. Astrophys. J. Lett. 2019, 875, L5. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Algaba, J.C.; Alberdi, A.; Alef, W.; Anantua, R.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; et al. First M87 Event Horizon Telescope Results. VII. Polarization of the Ring. Astrophys. J. Lett. 2021, 910, L12. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Algaba, J.C.; Alberdi, A.; Alef, W.; Anantua, R.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; et al. First M87 Event Horizon Telescope Results. VIII. Magnetic Field Structure near The Event Horizon. Astrophys. J. Lett. 2021, 910, L13. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; et al. First Sagittarius A* Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole in the Center of the Milky Way. Astrophys. J. Lett. 2022, 930, L12. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; et al. First Sagittarius A* Event Horizon Telescope Results. II. EHT and Multiwavelength Observations, Data Processing, and Calibration. Astrophys. J. Lett. 2022, 930, L13. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; et al. First Sagittarius A* Event Horizon Telescope Results. III. Imaging of the Galactic Center Supermassive Black Hole. Astrophys. J. Lett. 2022, 930, L14. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; et al. First Sagittarius A* Event Horizon Telescope Results. IV. Variability, Morphology, and Black Hole Mass. Astrophys. J. Lett. 2022, 930, L15. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; et al. First Sagittarius A* Event Horizon Telescope Results. V. Testing Astrophysical Models of the Galactic Center Black Hole. Astrophys. J. Lett. 2022, 930, L16. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; et al. First Sagittarius A* Event Horizon Telescope Results. VI. Testing the Black Hole Metric. Astrophys. J. Lett. 2022, 930, L17. [Google Scholar] [CrossRef]
- Kim, J.Y.; Krichbaum, T.P.; Broderick, A.E.; Wielgus, M.; Blackburn, L.; Gómez, J.L.; Johnson, M.D.; Bouman, K.L.; Chael, A.; Akiyama, K.; et al. Event Horizon Telescope imaging of the archetypal blazar 3C 279 at an extreme 20 microarcsecond resolution. Astron. Astrophys. 2020, 640, A69. [Google Scholar] [CrossRef]
- Issaoun, S.; Wielgus, M.; Jorstad, S.; Krichbaum, T.P.; Blackburn, L.; Janssen, M.; Chan, C.k.; Pesce, D.W.; Gómez, J.L.; Akiyama, K.; et al. Resolving the Inner Parsec of the Blazar J1924-2914 with the Event Horizon Telescope. Astrophys. J. 2022, 934, 145. [Google Scholar] [CrossRef]
- Doeleman, S.; Blackburn, L.; Dexter, J.; Gomez, J.L.; Johnson, M.D.; Palumbo, D.C.; Weintroub, J.; Farah, J.R.; Fish, V.; Loinard, L.; et al. Studying Black Holes on Horizon Scales with VLBI Ground Arrays. Bull. Am. Astron. Soc. 2019, 51, 256. [Google Scholar]
- Pesce, D.W.; Palumbo, D.C.M.; Narayan, R.; Blackburn, L.; Doeleman, S.S.; Johnson, M.D.; Ma, C.P.; Nagar, N.M.; Natarajan, P.; Ricarte, A. Toward Determining the Number of Observable Supermassive Black Hole Shadows. Astrophys. J. 2021, 923, 260. [Google Scholar] [CrossRef]
- Cappellari, M.; Verolme, E.K.; van der Marel, R.P.; Verdoes Kleijn, G.A.; Illingworth, G.D.; Franx, M.; Carollo, C.M.; de Zeeuw, P.T. The Counterrotating Core and the Black Hole Mass of IC 1459. Astrophys. J. 2002, 578, 787–805. [Google Scholar] [CrossRef]
- Graham, A.W. Populating the Galaxy Velocity Dispersion - Supermassive Black Hole Mass Diagram: A Catalogue of (Mbh, σ) Values. Publ. Astron. Soc. Aust. 2008, 25, 167–175. [Google Scholar] [CrossRef][Green Version]
- Lo, W.P.; Physics, National Taiwan University; Institute of Astronomy & Astrophysics, Taipei Taiwan; Academia Sinica, Taipei, Taiwan. Flux Density Survey of Low-Luminosity Active Galactic Nuclei at mm/submm wavelengths. 2023; manuscript in preparation. [Google Scholar]
- Janssen, M.; Falcke, H.; Kadler, M.; Ros, E.; Wielgus, M.; Akiyama, K.; Baloković, M.; Blackburn, L.; Bouman, K.L.; Chael, A.; et al. Event Horizon Telescope observations of the jet launching and collimation in Centaurus A. Nature Astron. 2021, 5, 1017–1028. [Google Scholar] [CrossRef]
- Harris, G.L.H.; Rejkuba, M.; Harris, W.E. The Distance to NGC 5128 (Centaurus A). Publ. Astron. Soc. Aust. 2010, 27, 457–462. [Google Scholar] [CrossRef]
- Paraschos, G.F.; Kim, J.Y.; Krichbaum, T.P.; Zensus, J.A. Pinpointing the jet apex of 3C 84. Astron. Astrophys. 2021, 650, L18. [Google Scholar] [CrossRef]
- Giovannini, G.; Savolainen, T.; Orienti, M.; Nakamura, M.; Nagai, H.; Kino, M.; Giroletti, M.; Hada, K.; Bruni, G.; Kovalev, Y.Y.; et al. A wide and collimated radio jet in 3C84 on the scale of a few hundred gravitational radii. Nature Astron. 2018, 2, 472–477. [Google Scholar] [CrossRef]
- Brenneman, L.W.; Weaver, K.A.; Kadler, M.; Tueller, J.; Marscher, A.; Ros, E.; Zensus, A.; Kovalev, Y.Y.; Aller, M.; Aller, H.; et al. Spectral Analysis of the Accretion Flow in NGC 1052 with Suzaku. Astrophys. J. 2009, 698, 528–540. [Google Scholar] [CrossRef]
- Falcke, H.; Melia, F.; Agol, E. Viewing the Shadow of the Black Hole at the Galactic Center. Astrophys. J. Lett. 2000, 528, L13–L16. [Google Scholar] [CrossRef] [PubMed]
- Manmoto, T. Advection-dominated Accretion Flow around a Kerr Black Hole. Astrophys. J. 2000, 534, 734–746. [Google Scholar] [CrossRef]
- Yuan, F.; Quataert, E.; Narayan, R. Nonthermal Electrons in Radiatively Inefficient Accretion Flow Models of Sagittarius A*. Astrophys. J. 2003, 598, 301–312. [Google Scholar] [CrossRef]
- De Villiers, J.P.; Hawley, J.F.; Krolik, J.H. Magnetically Driven Accretion Flows in the Kerr Metric. I. Models and Overall Structure. Astrophys. J. 2003, 599, 1238–1253. [Google Scholar] [CrossRef]
- Hirose, S.; Krolik, J.H.; De Villiers, J.P.; Hawley, J.F. Magnetically Driven Accretion Flows in the Kerr Metric. II. Structure of the Magnetic Field. Astrophys. J. 2004, 606, 1083–1097. [Google Scholar] [CrossRef]
- De Villiers, J.P.; Hawley, J.F.; Krolik, J.H.; Hirose, S. Magnetically Driven Accretion in the Kerr Metric. III. Unbound Outflows. Astrophys. J. 2005, 620, 878–888. [Google Scholar] [CrossRef]
- Krolik, J.H.; Hawley, J.F.; Hirose, S. Magnetically Driven Accretion Flows in the Kerr Metric. IV. Dynamical Properties of the Inner Disk. Astrophys. J. 2005, 622, 1008–1023. [Google Scholar] [CrossRef]
- Igumenshchev, I.V.; Narayan, R.; Abramowicz, M.A. Three-dimensional Magnetohydrodynamic Simulations of Radiatively Inefficient Accretion Flows. Astrophys. J. 2003, 592, 1042–1059. [Google Scholar] [CrossRef]
- McKinney, J.C.; Gammie, C.F. A Measurement of the Electromagnetic Luminosity of a Kerr Black Hole. Astrophys. J. 2004, 611, 977–995. [Google Scholar] [CrossRef]
- McKinney, J.C. General relativistic magnetohydrodynamic simulations of the jet formation and large-scale propagation from black hole accretion systems. Mon. Not. R. Astron. Soc. 2006, 368, 1561–1582. [Google Scholar] [CrossRef]
- Hawley, J.F.; Krolik, J.H. Magnetically Driven Jets in the Kerr Metric. Astrophys. J. 2006, 641, 103–116. [Google Scholar] [CrossRef]
- Noble, S.C.; Leung, P.K.; Gammie, C.F.; Book, L.G. Simulating the emission and outflows from accretion discs. Class. Quantum Gravity 2007, 24, S259–S274. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; McKinney, J.C.; Narayan, R. Simulations of ultrarelativistic magnetodynamic jets from gamma-ray burst engines. Mon. Not. R. Astron. Soc. 2008, 388, 551–572. [Google Scholar] [CrossRef]
- Mościbrodzka, M.; Gammie, C.F.; Dolence, J.C.; Shiokawa, H.; Leung, P.K. Radiative Models of SGR A* from GRMHD Simulations. Astrophys. J. 2009, 706, 497–507. [Google Scholar] [CrossRef]
- Punsly, B.; Igumenshchev, I.V.; Hirose, S. Three-Dimensional Simulations of Vertical Magnetic Flux in the Immediate Vicinity of Black Holes. Astrophys. J. 2009, 704, 1065–1085. [Google Scholar] [CrossRef]
- Noble, S.C.; Krolik, J.H.; Hawley, J.F. Direct Calculation of the Radiative Efficiency of an Accretion Disk Around a Black Hole. Astrophys. J. 2009, 692, 411–421. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; Narayan, R.; McKinney, J.C. Black Hole Spin and The Radio Loud/Quiet Dichotomy of Active Galactic Nuclei. Astrophys. J. 2010, 711, 50–63. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; Narayan, R.; McKinney, J.C. Efficient generation of jets from magnetically arrested accretion on a rapidly spinning black hole. Mon. Not. R. Astron. Soc. 2011, 418, L79–L83. [Google Scholar] [CrossRef]
- Shiokawa, H.; Dolence, J.C.; Gammie, C.F.; Noble, S.C. Global General Relativistic Magnetohydrodynamic Simulations of Black Hole Accretion Flows: A Convergence Study. Astrophys. J. 2012, 744, 187. [Google Scholar] [CrossRef][Green Version]
- Porth, O.; Chatterjee, K.; Narayan, R.; Gammie, C.F.; Mizuno, Y.; Anninos, P.; Baker, J.G.; Bugli, M.; Chan, C.k.; Davelaar, J.; et al. The Event Horizon General Relativistic Magnetohydrodynamic Code Comparison Project. Astrophys. J. Suppl. Ser. 2019, 243, 26. [Google Scholar] [CrossRef]
- Martí, J.M. Numerical Simulations of Jets from Active Galactic Nuclei. Galaxies 2019, 7, 24. [Google Scholar] [CrossRef]
- Takahashi, M.; Nitta, S.; Tatematsu, Y.; Tomimatsu, A. Magnetohydrodynamic Flows in Kerr Geometry: Energy Extraction from Black Holes. Astrophys. J. 1990, 363, 206. [Google Scholar] [CrossRef]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Pu, H.Y.; Nakamura, M.; Hirotani, K.; Mizuno, Y.; Wu, K.; Asada, K. Steady General Relativistic Magnetohydrodynamic Inflow/Outflow Solution Along Large-Scale Magnetic Fields that Thread a Rotating Black Hole. Astrophys. J. 2015, 801, 56. [Google Scholar] [CrossRef]
- Lyubarsky, Y.E. Transformation of the Poynting flux into kinetic energy in relativistic jets. Mon. Not. R. Astron. Soc. 2010, 402, 353–361. [Google Scholar] [CrossRef]
- Takahashi, M.; Tomimatsu, A. Constraints on the evolution of black hole spin due to magnetohydrodynamic accretion. Phys. Rev. D 2008, 78, 023012. [Google Scholar] [CrossRef]
- Pu, H.Y.; Takahashi, M. Properties of Trans-fast Magnetosonic Jets in Black Hole Magnetospheres. Astrophys. J. 2020, 892, 37. [Google Scholar] [CrossRef]
- Chatterjee, K.; Liska, M.; Tchekhovskoy, A.; Markoff, S.B. Accelerating AGN jets to parsec scales using general relativistic MHD simulations. Mon. Not. R. Astron. Soc. 2019, 490, 2200–2218. [Google Scholar] [CrossRef]
- Narayan, R.; Igumenshchev, I.V.; Abramowicz, M.A. Magnetically Arrested Disk: An Energetically Efficient Accretion Flow. Publ. Astron. Soc. Jpn. 2003, 55, L69–L72. [Google Scholar] [CrossRef]
- Igumenshchev, I.V. Magnetically Arrested Disks and the Origin of Poynting Jets: A Numerical Study. Astrophys. J. 2008, 677, 317–326. [Google Scholar] [CrossRef]
- McKinney, J.C.; Tchekhovskoy, A.; Blandford, R.D. General relativistic magnetohydrodynamic simulations of magnetically choked accretion flows around black holes. Mon. Not. R. Astron. Soc. 2012, 423, 3083–3117. [Google Scholar] [CrossRef]
- Narayan, R.; Chael, A.; Chatterjee, K.; Ricarte, A.; Curd, B. Jets in magnetically arrested hot accretion flows: Geometry, power, and black hole spin-down. Mon. Not. R. Astron. Soc. 2022, 511, 3795–3813. [Google Scholar] [CrossRef]
- Narayan, R.; SÄ dowski, A.; Penna, R.F.; Kulkarni, A.K. GRMHD simulations of magnetized advection-dominated accretion on a non-spinning black hole: Role of outflows. Mon. Not. R. Astron. Soc. 2012, 426, 3241–3259. [Google Scholar] [CrossRef]
- Sądowski, A.; Narayan, R.; Penna, R.; Zhu, Y. Energy, momentum and mass outflows and feedback from thick accretion discs around rotating black holes. Mon. Not. R. Astron. Soc. 2013, 436, 3856–3874. [Google Scholar] [CrossRef]
- Mościbrodzka, M.; Falcke, H. Coupled jet-disk model for Sagittarius A*: Explaining the flat-spectrum radio core with GRMHD simulations of jets. Astron. Astrophys. 2013, 559, L3. [Google Scholar] [CrossRef]
- Chan, C.K.; Psaltis, D.; Özel, F.; Narayan, R.; Sadowski, A. The Power of Imaging: Constraining the Plasma Properties of GRMHD Simulations using EHT Observations of Sgr A*. Astrophys. J. 2015, 799, 1. [Google Scholar] [CrossRef]
- Dexter, J.; Agol, E.; Fragile, P.C.; McKinney, J.C. The Submillimeter Bump in Sgr A* from Relativistic MHD Simulations. Astrophys. J. 2010, 717, 1092–1104. [Google Scholar] [CrossRef]
- Chael, A.; Rowan, M.; Narayan, R.; Johnson, M.; Sironi, L. The role of electron heating physics in images and variability of the Galactic Centre black hole Sagittarius A*. Mon. Not. R. Astron. Soc. 2018, 478, 5209–5229. [Google Scholar] [CrossRef]
- Chael, A.; Narayan, R.; Johnson, M.D. Two-temperature, Magnetically Arrested Disc simulations of the jet from the supermassive black hole in M87. Mon. Not. R. Astron. Soc. 2019, 486, 2873–2895. [Google Scholar] [CrossRef]
- Davelaar, J.; Mościbrodzka, M.; Bronzwaer, T.; Falcke, H. General relativistic magnetohydrodynamical κ-jet models for Sagittarius A*. Astron. Astrophys. 2018, 612, A34. [Google Scholar] [CrossRef]
- Davelaar, J.; Olivares, H.; Porth, O.; Bronzwaer, T.; Janssen, M.; Roelofs, F.; Mizuno, Y.; Fromm, C.M.; Falcke, H.; Rezzolla, L. Modeling non-thermal emission from the jet-launching region of M 87 with adaptive mesh refinement. Astron. Astrophys. 2019, 632, A2. [Google Scholar] [CrossRef]
- Cruz-Osorio, A.; Fromm, C.M.; Mizuno, Y.; Nathanail, A.; Younsi, Z.; Porth, O.; Davelaar, J.; Falcke, H.; Kramer, M.; Rezzolla, L. State-of-the-art energetic and morphological modelling of the launching site of the M87 jet. Nature Astronomy 2022, 6, 103–108. [Google Scholar] [CrossRef]
- Chael, A.A.; Narayan, R.; Sadowski, A. Evolving non-thermal electrons in simulations of black hole accretion. Mon. Not. R. Astron. Soc. 2017, 470, 2367–2386. [Google Scholar] [CrossRef]
- Beskin, V.S. MHD Flows in Compact Astrophysical Objects: Accretion, Winds and Jets; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Fendt, C.; Camenzind, M.; Appl, S. On the collimation of stellar magnetospheres to jets. I. Relativistic force-free 2D equilibrium. Astron. Astrophys. 1995, 300, 791. [Google Scholar]
- Pan, Z.; Yu, C.; Huang, L. Analytic Properties of Force-free Jets in the Kerr Spacetime. III. Uniform Field Solution. Astrophys. J. 2017, 836, 193. [Google Scholar] [CrossRef]
- Huang, L.; Pan, Z.; Yu, C. Toward a Full MHD Jet Model of Spinning Black Holes. I. Framework and a Split Monopole Example. Astrophys. J. 2019, 880, 93. [Google Scholar] [CrossRef]
- Asada, K.; Nakamura, M. The Structure of the M87 Jet: A Transition from Parabolic to Conical Streamlines. Astrophys. J. Lett. 2012, 745, L28. [Google Scholar] [CrossRef]
- Nakamura, M.; Asada, K. The Parabolic Jet Structure in M87 as a Magnetohydrodynamic Nozzle. Astrophys. J. 2013, 775, 118. [Google Scholar] [CrossRef]
- Nakamura, M.; Asada, K.; Hada, K.; Pu, H.Y.; Noble, S.; Tseng, C.; Toma, K.; Kino, M.; Nagai, H.; Takahashi, K.; et al. Parabolic Jets from the Spinning Black Hole in M87. Astrophys. J. 2018, 868, 146. [Google Scholar] [CrossRef]
- Broderick, A.E.; Loeb, A. Imaging the Black Hole Silhouette of M87: Implications for Jet Formation and Black Hole Spin. Astrophys. J. 2009, 697, 1164–1179. [Google Scholar] [CrossRef]
- Narayan, R.; McKinney, J.C.; Farmer, A.J. Self-similar force-free wind from an accretion disc. Mon. Not. R. Astron. Soc. 2007, 375, 548–566. [Google Scholar] [CrossRef]
- Lu, R.S.; Broderick, A.E.; Baron, F.; Monnier, J.D.; Fish, V.L.; Doeleman, S.S.; Pankratius, V. Imaging the Supermassive Black Hole Shadow and Jet Base of M87 with the Event Horizon Telescope. Astrophys. J. 2014, 788, 120. [Google Scholar] [CrossRef]
- Mościbrodzka, M.; Dexter, J.; Davelaar, J.; Falcke, H. Faraday rotation in GRMHD simulations of the jet launching zone of M87. Mon. Not. R. Astron. Soc. 2017, 468, 2214–2221. [Google Scholar] [CrossRef]
- Jeter, B.; Broderick, A.E.; Gold, R. Differentiating disc and black hole-driven jets with EHT images of variability in M87. Mon. Not. R. Astron. Soc. 2020, 493, 5606–5616. [Google Scholar] [CrossRef]
- Takahashi, K.; Toma, K.; Kino, M.; Nakamura, M.; Hada, K. Fast-spinning Black Holes Inferred from Symmetrically Limb-brightened Radio Jets. Astrophys. J. 2018, 868, 82. [Google Scholar] [CrossRef]
- Ogihara, T.; Takahashi, K.; Toma, K. A Mechanism for the Triple-ridge Emission Structure of AGN Jets. Astrophys. J. 2019, 877, 19. [Google Scholar] [CrossRef]
- Camenzind, M. Centrifugally driven MHD-winds in active galactic nuclei. Astron. Astrophys. 1986, 156, 137–151. [Google Scholar]
- Camenzind, M. Hydromagnetic flows from rapidly rotating compact objects. I—Cold relativistic flows from rapid rotators. Astron. Astrophys. 1986, 162, 32–44. [Google Scholar]
- Camenzind, M. Hydromagnetic flows from rapidly rotating compact objects. II—The relativistic axisymmetric jet equilibrium. Astron. Astrophys. 1987, 184, 341–360. [Google Scholar]
- Fendt, C.; Camenzind, M. On collimated stellar jet magnetospheres. II. Dynamical structure of collimating wind flows. Astron. Astrophys. 1996, 313, 591–604. [Google Scholar]
- Fendt, C.; Greiner, J. Magnetically driven superluminal motion from rotating black holes. Solution of the magnetic wind equation in Kerr metric. Astron. Astrophys. 2001, 369, 308–322. [Google Scholar] [CrossRef]
- Fendt, C.; Ouyed, R. Ultrarelativistic Magnetohydrodynamic Jets in the Context of Gamma-Ray Bursts. Astrophys. J. 2004, 608, 378–390. [Google Scholar] [CrossRef]
- Pu, H.Y.; Hirotani, K.; Chang, H.K. Launching and Quenching of Black Hole Relativistic Jets at Low Accretion Rate. Astrophys. J. 2012, 758, 113. [Google Scholar] [CrossRef][Green Version]
- Beskin, V.S.; Kuznetsova, I.V.; Rafikov, R.R. On the MHD effects on the force-free monopole outflow. Mon. Not. R. Astron. Soc. 1998, 299, 341–348. [Google Scholar] [CrossRef]
- Beskin, V.S.; Nokhrina, E.E. The effective acceleration of plasma outflow in the paraboloidal magnetic field. Mon. Not. R. Astron. Soc. 2006, 367, 375–386. [Google Scholar] [CrossRef]
- Tomimatsu, A.; Takahashi, M. Relativistic Acceleration of Magnetically Driven Jets. Astrophys. J. 2003, 592, 321–331. [Google Scholar] [CrossRef]
- Ogihara, T.; Ogawa, T.; Toma, K. Matter Density Distribution of General Relativistic Highly Magnetized Jets Driven by Black Holes. Astrophys. J. 2021, 911, 34. [Google Scholar] [CrossRef]
- Dexter, J.; McKinney, J.C.; Agol, E. The size of the jet launching region in M87. Mon. Not. R. Astron. Soc. 2012, 421, 1517–1528. [Google Scholar] [CrossRef]
- Balbus, S.A.; Hawley, J.F. A Powerful Local Shear Instability in Weakly Magnetized Disks. I. Linear Analysis. Astrophys. J. 1991, 376, 214. [Google Scholar] [CrossRef]
- O’ Riordan, M.; Pe’er, A.; McKinney, J.C. Observational Signatures of Mass-loading in Jets Launched by Rotating Black Holes. Astrophys. J. 2018, 853, 44. [Google Scholar] [CrossRef]
- Leung, P.K.; Gammie, C.F.; Noble, S.C. Numerical Calculation of Magnetobremsstrahlung Emission and Absorption Coefficients. Astrophys. J. 2011, 737, 21. [Google Scholar] [CrossRef]
- Pandya, A.; Zhang, Z.; Chandra, M.; Gammie, C.F. Polarized Synchrotron Emissivities and Absorptivities for Relativistic Thermal, Power-law, and Kappa Distribution Functions. Astrophys. J. 2016, 822, 34. [Google Scholar] [CrossRef]
- Dexter, J. A public code for general relativistic, polarised radiative transfer around spinning black holes. Mon. Not. R. Astron. Soc. 2016, 462, 115–136. [Google Scholar] [CrossRef]
- Özel, F.; Psaltis, D.; Narayan, R. Hybrid Thermal-Nonthermal Synchrotron Emission from Hot Accretion Flows. Astrophys. J. 2000, 541, 234–249. [Google Scholar] [CrossRef]
- Fromm, C.M.; Cruz-Osorio, A.; Mizuno, Y.; Nathanail, A.; Younsi, Z.; Porth, O.; Olivares, H.; Davelaar, J.; Falcke, H.; Kramer, M.; et al. Impact of non-thermal particles on the spectral and structural properties of M87. Astron. Astrophys. 2022, 660, A107. [Google Scholar] [CrossRef]
- Fuerst, S.V.; Wu, K. Radiation transfer of emission lines in curved space-time. Astron. Astrophys. 2004, 424, 733–746. [Google Scholar] [CrossRef]
- Younsi, Z.; Wu, K.; Fuerst, S.V. General relativistic radiative transfer: Formulation and emission from structured tori around black holes. Astron. Astrophys. 2012, 545, A13. [Google Scholar] [CrossRef]
- Gold, R.; Broderick, A.E.; Younsi, Z.; Fromm, C.M.; Gammie, C.F.; Mościbrodzka, M.; Pu, H.Y.; Bronzwaer, T.; Davelaar, J.; Dexter, J.; et al. Verification of Radiative Transfer Schemes for the EHT. Astrophys. J. 2020, 897, 148. [Google Scholar] [CrossRef]
- Broderick, A.E.; McKinney, J.C. Parsec-scale Faraday Rotation Measures from General Relativistic Magnetohydrodynamic Simulations of Active Galactic Nucleus Jets. Astrophys. J. 2010, 725, 750–773. [Google Scholar] [CrossRef]
- Chatterjee, K.; Markoff, S.; Neilsen, J.; Younsi, Z.; Witzel, G.; Tchekhovskoy, A.; Yoon, D.; Ingram, A.; van der Klis, M.; Boyce, H.; et al. General relativistic MHD simulations of non-thermal flaring in Sagittarius A*. Mon. Not. R. Astron. Soc. 2021, 507, 5281–5302. [Google Scholar] [CrossRef]
- Gammie, C.F.; McKinney, J.C.; Tóth, G. HARM: A Numerical Scheme for General Relativistic Magnetohydrodynamics. Astrophys. J. 2003, 589, 444–457. [Google Scholar] [CrossRef]
- Noble, S.C.; Gammie, C.F.; McKinney, J.C.; Del Zanna, L. Primitive Variable Solvers for Conservative General Relativistic Magnetohydrodynamics. Astrophys. J. 2006, 641, 626–637. [Google Scholar] [CrossRef]
- Pu, H.Y.; Yun, K.; Younsi, Z.; Yoon, S.J. Odyssey: A Public GPU-based Code for General Relativistic Radiative Transfer in Kerr Spacetime. Astrophys. J. 2016, 820, 105. [Google Scholar] [CrossRef]
- Mościbrodzka, M.; Falcke, H.; Shiokawa, H. General relativistic magnetohydrodynamical simulations of the jet in M 87. Astron. Astrophys. 2016, 586, A38. [Google Scholar] [CrossRef]
- Ball, D.; Sironi, L.; Özel, F. Electron and Proton Acceleration in Trans-relativistic Magnetic Reconnection: Dependence on Plasma Beta and Magnetization. Astrophys. J. 2018, 862, 80. [Google Scholar] [CrossRef]
- Ball, D.; Özel, F.; Psaltis, D.; Chan, C.k. Particle Acceleration and the Origin of X-Ray Flares in GRMHD Simulations of SGR A. Astrophys. J. 2016, 826, 77. [Google Scholar] [CrossRef]
- Broderick, A.E.; Tchekhovskoy, A. Horizon-scale Lepton Acceleration in Jets: Explaining the Compact Radio Emission in M87. Astrophys. J. 2015, 809, 97. [Google Scholar] [CrossRef]
- Pu, H.Y.; Wu, K.; Younsi, Z.; Asada, K.; Mizuno, Y.; Nakamura, M. Observable Emission Features of Black Hole GRMHD Jets on Event Horizon Scales. Astrophys. J. 2017, 845, 160. [Google Scholar] [CrossRef]
- Kawashima, T.; Toma, K.; Kino, M.; Akiyama, K.; Nakamura, M.; Moriyama, K. A Jet-bases Emission Model of the EHT2017 Image of M87*. Astrophys. J. 2021, 909, 168. [Google Scholar] [CrossRef]
- Ressler, S.M.; Tchekhovskoy, A.; Quataert, E.; Chandra, M.; Gammie, C.F. Electron thermodynamics in GRMHD simulations of low-luminosity black hole accretion. Mon. Not. R. Astron. Soc. 2015, 454, 1848–1870. [Google Scholar] [CrossRef]
- Ryan, B.R.; Dolence, J.C.; Gammie, C.F. bhlight: General Relativistic Radiation Magnetohydrodynamics with Monte Carlo Transport. Astrophys. J. 2015, 807, 31. [Google Scholar] [CrossRef]
- Sądowski, A.; Wielgus, M.; Narayan, R.; Abarca, D.; McKinney, J.C.; Chael, A. Radiative, two-temperature simulations of low-luminosity black hole accretion flows in general relativity. Mon. Not. R. Astron. Soc. 2017, 466, 705–725. [Google Scholar] [CrossRef]
- Ressler, S.M.; Tchekhovskoy, A.; Quataert, E.; Gammie, C.F. The disc-jet symbiosis emerges: Modelling the emission of Sagittarius A* with electron thermodynamics. Mon. Not. R. Astron. Soc. 2017, 467, 3604–3619. [Google Scholar] [CrossRef]
- Ryan, B.R.; Ressler, S.M.; Dolence, J.C.; Gammie, C.; Quataert, E. Two-temperature GRRMHD Simulations of M87. Astrophys. J. 2018, 864, 126. [Google Scholar] [CrossRef]
- Liska, M.; Hesp, C.; Tchekhovskoy, A.; Ingram, A.; van der Klis, M.; Markoff, S. Formation of precessing jets by tilted black hole discs in 3D general relativistic MHD simulations. Mon. Not. R. Astron. Soc. 2018, 474, L81–L85. [Google Scholar] [CrossRef]
- White, C.J.; Quataert, E.; Blaes, O. Tilted Disks around Black Holes: A Numerical Parameter Survey for Spin and Inclination Angle. Astrophys. J. 2019, 878, 51. [Google Scholar] [CrossRef]
- Liska, M.; Hesp, C.; Tchekhovskoy, A.; Ingram, A.; van der Klis, M.; Markoff, S.B. A Phase Lag between Disk and Corona in GRMHD Simulations of Precessing Tilted Accretion Disks. arXiv 2019, arXiv:1901.05970. [Google Scholar]
- Chatterjee, K.; Younsi, Z.; Liska, M.; Tchekhovskoy, A.; Markoff, S.B.; Yoon, D.; van Eijnatten, D.; Hesp, C.; Ingram, A.; van der Klis, M.B.M. Observational signatures of disc and jet misalignment in images of accreting black holes. Mon. Not. R. Astron. Soc. 2020, 499, 362–378. [Google Scholar] [CrossRef]
- Liska, M.; Hesp, C.; Tchekhovskoy, A.; Ingram, A.; van der Klis, M.; Markoff, S.B.; Van Moer, M. Disc tearing and Bardeen-Petterson alignment in GRMHD simulations of highly tilted thin accretion discs. Mon. Not. R. Astron. Soc. 2021, 507, 983–990. [Google Scholar] [CrossRef]
- Mościbrodzka, M.; Gammie, C.F.; Dolence, J.C.; Shiokawa, H. Pair Production in Low-luminosity Galactic Nuclei. Astrophys. J. 2011, 735, 9. [Google Scholar] [CrossRef]
- Emami, R.; Anantua, R.; Chael, A.A.; Loeb, A. Positron Effects on Polarized Images and Spectra from Jet and Accretion Flow Models of M87* and Sgr A*. Astrophys. J. 2021, 923, 272. [Google Scholar] [CrossRef]
- Wong, G.N.; Ryan, B.R.; Gammie, C.F. Pair Drizzle around Sub-Eddington Supermassive Black Holes. Astrophys. J. 2021, 907, 73. [Google Scholar] [CrossRef]
- Mizuno, Y. GRMHD Simulations and Modeling for Jet Formation and Acceleration Region in AGNs. Universe 2022, 8, 85. [Google Scholar] [CrossRef]
- Ricarte, A.; Qiu, R.; Narayan, R. Black hole magnetic fields and their imprint on circular polarization images. Mon. Not. R. Astron. Soc. 2021, 505, 523–539. [Google Scholar] [CrossRef]




| D | BH Shadow Size * | Accretion Rate | ||
|---|---|---|---|---|
| () | () | () | () | |
| M87 | 65 [11,12] | 16.8 [11,12] | 38.2 | ∼ [28] |
| IC 1459 | 11 [41] | 29.2 [42] | 3.72 | ∼ [43] |
| Centaurus A | 0.55 [44] | 3.8 [45] | 1.43 | ∼ [44] |
| 3C 84 | 9 [46] | 76.9 [46] | 1.15 | ∼ [47] |
| Cygnus A | 25 [42] | 232 [42] | 1.06 | ∼ [43] |
| NGC 1052 | 1.54 [48] | 20.7 [48] | 0.73 | ∼ [43] |
| NGC 6251 | 5.9 [42] | 104.6 [42] | 0.56 | ∼ [43] |
| >0 | <0 | |
| <0 | <0 | |
| <0 | >0 | |
| >0 | >0 | |
| <0 | >0 | |
| >0 | >0 |
| Inflow | Outflow | Inflow | Outflow | |
|---|---|---|---|---|
| <0 | >0 | <0 | >0 | |
| >0 | <0 | <0 | >0 | |
| >0 | >0 | >0 | >0 | |
| >0 | >0 | >0 | >0 | |
| <0 | >0 | <0 | >0 | |
| >0 | >0 | >0 | >0 | |
| <0 | >0 | <0 | >0 | |
| <0 | >0 | <0 | >0 | |
| >0 | >0 | >0 | >0 | |
| <0 | >0 | <0 | >0 | |
| >0 | >0 | >0 | >0 | |
| <0 | >0 | <0 | >0 | |
| >0 | >0 | >0 | >0 | |
| Jet Model | Emission | ||
|---|---|---|---|
| Thermal Synchrotron | Non-Thermal Synchrotron | Applying Floor | |
| semi-analytical force-free jet model (with floor) | ✔ | ✔ | |
| GRMHD simulation jet model A | ✔ | ||
| GRMHD simulation jet model A (with floor) | ✔ | ✔ | |
| GRMHD simulation jet model B | ✔ | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pu, H.-Y.; Asada, K.; Nakamura, M. Modeling Nearby Low-Luminosity Active-Galactic-Nucleus Jet Images at All VLBI Scales. Galaxies 2022, 10, 104. https://doi.org/10.3390/galaxies10060104
Pu H-Y, Asada K, Nakamura M. Modeling Nearby Low-Luminosity Active-Galactic-Nucleus Jet Images at All VLBI Scales. Galaxies. 2022; 10(6):104. https://doi.org/10.3390/galaxies10060104
Chicago/Turabian StylePu, Hung-Yi, Keiichi Asada, and Masanori Nakamura. 2022. "Modeling Nearby Low-Luminosity Active-Galactic-Nucleus Jet Images at All VLBI Scales" Galaxies 10, no. 6: 104. https://doi.org/10.3390/galaxies10060104
APA StylePu, H.-Y., Asada, K., & Nakamura, M. (2022). Modeling Nearby Low-Luminosity Active-Galactic-Nucleus Jet Images at All VLBI Scales. Galaxies, 10(6), 104. https://doi.org/10.3390/galaxies10060104







