Biomarker-Guided Non-Adaptive Trial Designs in Phase II and Phase III: A Methodological Review
Abstract
:1. Introduction
2. Methods and Findings
2.1. Single Arm Designs
2.2. Enrichment Designs
2.3. Randomize-All Designs
2.3.1. Marker Stratified Designs
2.3.2. Hybrid Designs
2.4. Biomarker-Strategy Designs
2.4.1. Biomarker-Strategy Design with Biomarker Assessment in the Control Arm
2.4.2. Biomarker-Strategy Design without Biomarker Assessment in the Control Arm
2.4.3. Biomarker-Strategy Design with Treatment Randomization in the Control Arm
2.4.4. Reverse Marker-Based Strategy Design
2.5. Other Designs
A Randomized Phase II Trial Design with Biomarker Proposed by Freidlin et al., 2012
3. Discussion
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- George, S.L. Statistical issues in translational cancer research. Clin. Cancer Res. 2008, 14, 5954–5958. [Google Scholar] [CrossRef] [PubMed]
- Chabner, B. Advances and challenges in the use of biomarkers in clinical trials. Clin. Adv. Hematol. Oncol. 2008, 6, 42–43. [Google Scholar] [PubMed]
- Group, B.D.W. Biomarkers and surrogate endpoints: Preferred definitions and conceptual framework. Clin. Pharmacol. Ther. 2001, 69, 89–95. [Google Scholar]
- Shi, Q.; Mandrekar, S.J.; Sargent, D.J. Predictive biomarkers in colorectal cancer: Usage, validation, and design in clinical trials. Scand. J. Gastroenterol. 2012, 47, 356–362. [Google Scholar] [CrossRef] [PubMed]
- Pihlstrom, B.L.; Barnett, M.L. Design, operation, and interpretation of clinical trials. J. Dent. Res. 2010, 89, 759–772. [Google Scholar] [CrossRef] [PubMed]
- Rigatto, C.; Barrett, B.J. Biomarkers and surrogates in clinical studies. Methods Mol. Biol. 2009, 473, 137–154. [Google Scholar] [PubMed]
- Mandrekar, S.J.; An, M.-W.; Sargent, D.J. A review of phase II trial designs for initial marker validation. Contemp. Clin. Trials 2013, 36, 597–604. [Google Scholar] [CrossRef] [PubMed]
- Karuri, S.W.; Simon, R. A two-stage bayesian design for co-development of new drugs and companion diagnostics. Stat. Med. 2012, 31, 901–914. [Google Scholar] [CrossRef] [PubMed]
- Matsui, S. Genomic biomarkers for personalized medicine: Development and validation in clinical studies. Comput. Math. Methods Med. 2013, 2013, 865980. [Google Scholar] [CrossRef] [PubMed]
- Buyse, M.; Michiels, S. Omics-based clinical trial designs. Curr. Opin. Oncol. 2013, 25, 289–295. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Shi, Q.; Sargent, D.J. Statistical considerations for the next generation of clinical trials. Semin. Oncol. 2011, 38, 598–604. [Google Scholar] [CrossRef] [PubMed]
- Sargent, D.J.; Conley, B.A.; Allegra, C.; Collette, L. Clinical trial designs for predictive marker validation in cancer treatment trials. J. Clin. Oncol. 2005, 23, 2020–2027. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.J.; Lu, T.-P.; Chen, D.-T.; Wang, S.-J. Biomarker adaptive designs in clinical trials. Transl. Cancer Res. 2014, 3, 279–292. [Google Scholar]
- Freidlin, B.; Sun, Z.; Gray, R.; Korn, E.L. Phase III clinical trials that integrate treatment and biomarker evaluation. J. Clin. Oncol. 2013, 31, 3158–3161. [Google Scholar] [CrossRef] [PubMed]
- Gosho, M.; Nagashima, K.; Sato, Y. Study designs and statistical analyses for biomarker research. Sensors 2012, 12, 8966–8986. [Google Scholar] [CrossRef] [PubMed]
- Ming-Wen An, S.J.M.; Daniel, J.S. Biomarkers-guided targeted drugs: New clinical trials design and practice necessity. Adv. Personal. Cancer Manag. 2011, 30–41. [Google Scholar]
- Buyse, M. Towards validation of statistically reliable biomarkers. Eur. J. Cancer Suppl. 2007, 5, 89–95. [Google Scholar] [CrossRef]
- Lee, C.K.; Lord, S.J.; Coates, A.S.; Simes, R.J. Molecular biomarkers to individualise treatment: Assessing the evidence. Med. J. Aust. 2009, 190, 631–636. [Google Scholar] [PubMed]
- Simon, R. Clinical trial designs for evaluating the medical utility of prognostic and predictive biomarkers in oncology. Personal. Med. 2010, 7, 33–47. [Google Scholar] [CrossRef] [PubMed]
- Fraser, G.A.M.; Meyer, R.M. Biomarkers and the design of clinical trials in cancer. Biomark. Med. 2007, 1, 387–397. [Google Scholar] [CrossRef] [PubMed]
- Mandrekar, S.J.; Sargent, D.J. Design of clinical trials for biomarker research in oncology. Clin. Investig. 2011, 1, 1629–1636. [Google Scholar] [CrossRef] [PubMed]
- Simon, R. Advances in clinical trial designs for predictive biomarker discovery and validation. Curr. Breast Cancer Rep. 2009, 1, 216–221. [Google Scholar] [CrossRef]
- Polley, M.-Y.C.; Freidlin, B.; Korn, E.L.; Conley, B.A.; Abrams, J.S.; McShane, L.M. Statistical and practical considerations for clinical evaluation of predictive biomarkers. J. Natl. Cancer Inst. 2013, 105, 1677–1683. [Google Scholar] [CrossRef] [PubMed]
- Bradley, E. Incorporating biomarkers into clinical trial designs: Points to consider. Nat. Biotechnol. 2012, 30, 596–599. [Google Scholar] [CrossRef] [PubMed]
- Beckman, R.A.; Clark, J.; Chen, C. Integrating predictive biomarkers and classifiers into oncology clinical development programmes. Nat. Rev. Drug Discov. 2011, 10, 735–748. [Google Scholar] [CrossRef] [PubMed]
- Young, K.Y.; Laird, A.; Zhou, X.H. The efficiency of clinical trial designs for predictive biomarker validation. Clin. Trials 2010, 7, 557–566. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.J.; Xuemin, G.; Suyu, L. Bayesian adaptive randomization designs for targeted agent development. Clin. Trials 2010, 7, 584–596. [Google Scholar] [CrossRef] [PubMed]
- Simon, R. Clinical trials for predictive medicine: New challenges and paradigms. Clin. Trials 2010, 7, 516–524. [Google Scholar] [CrossRef] [PubMed]
- Buyse, M.; Sargent, D.J.; Grothey, A.; Matheson, A.; de Gramont, A. Biomarkers and surrogate end points—The challenge of statistical validation. Nat. Rev. Clin. Oncol. 2010, 7, 309–317. [Google Scholar] [CrossRef] [PubMed]
- Mandrekar, S.J.; Sargent, D.J. Clinical trial designs for predictive biomarker validation: Theoretical considerations and practical challenges. J. Clin. Oncol. 2009, 27, 4027–4034. [Google Scholar] [CrossRef] [PubMed]
- Mandrekar, S.J.; Sargent, D.J. Clinical trial designs for predictive biomarker validation: One size does not fit all. J. Biopharm. Stat. 2009, 19, 530–542. [Google Scholar] [CrossRef] [PubMed]
- Hoering, A.; Leblanc, M.; Crowley, J.J. Randomized phase III clinical trial designs for targeted agents. Clin. Cancer Res. 2008, 14, 4358–4367. [Google Scholar] [CrossRef] [PubMed]
- Kelloff, G.J.; Sigman, C.C. Cancer biomarkers: Selecting the right drug for the right patient. Nat. Rev. Drug Discov. 2012, 11, 201–214. [Google Scholar] [CrossRef] [PubMed]
- Chow, S.-C. Adaptive clinical trial design. Annu. Rev. Med. 2014, 65, 405–415. [Google Scholar] [CrossRef] [PubMed]
- Antoniou, M.; Jorgensen, A.L.; Kolamunnage-Dona, R. Biomarker-guided adaptive trial designs in phase II and phase III: A methodological review. PLoS ONE 2016, 11, e0149803. [Google Scholar] [CrossRef] [PubMed]
- Tajik, P.; Zwinderman, A.H.; Mol, B.W.; Bossuyt, P.M. Trial designs for personalizing cancer care: A systematic review and classification. Clin. Cancer Res. 2013, 19, 4578–4588. [Google Scholar] [CrossRef] [PubMed]
- Lader, E.W.; Cannon, C.P.; Ohman, E.M.; Newby, L.K.; Sulmasy, D.P.; Barst, R.J.; Fair, J.M.; Flather, M.; Freedman, J.E.; Frye, R.L.; et al. The clinician as investigator: Participating in clinical trials in the practice setting: Appendix 1: Fundamentals of study design. Circulation 2004, 109, e302–e304. [Google Scholar] [CrossRef] [PubMed]
- Stingl Kirchheiner, J.C.; Brockmöller, J. Why, when, and how should pharmacogenetics be applied in clinical studies? Current and future approaches to study designs. Clin. Pharm. Ther. 2011, 89, 198–209. [Google Scholar] [CrossRef] [PubMed]
- Sambucini, V. A bayesian predictive two-stage design for phase II clinical trials. Stat. Med. 2008, 27, 1199–1224. [Google Scholar] [CrossRef] [PubMed]
- Ang, M.-K.; Tan, S.-B.; Lim, W.-T. Phase II clinical trials in oncology: Are we hitting the target? Expert Rev. Anticancer Ther. 2010, 10, 427–438. [Google Scholar] [CrossRef] [PubMed]
- Farley, J.; Rose, P.G.; Farley, J.; Rose, P.G. Trial design for evaluation of novel targeted therapies. Gynecol. Oncol. 2010, 116, 173. [Google Scholar] [CrossRef] [PubMed]
- Kaplan, R.; Maughan, T.; Crook, A.; Fisher, D.; Wilson, R.; Brown, L.; Parmar, M. Evaluating many treatments and biomarkers in oncology: A new design. J. Clin. Oncol. 2013, 31, 4562–4568. [Google Scholar] [CrossRef] [PubMed]
- Hodgson, D.R.; Wellings, R.; Harbron, C. Practical perspectives of personalized healthcare in oncology. New Biotechnol. 2012, 29, 656–664. [Google Scholar] [CrossRef] [PubMed]
- Mandrekar, S.J.; Sargent, D.J. Predictive biomarker validation in practice: Lessons from real trials. Clin. Trials 2010, 7, 567–573. [Google Scholar] [CrossRef] [PubMed]
- Galanis, E.; Wu, W.; Sarkaria, J.; Chang, S.M.; Colman, H.; Sargent, D.; Reardon, D.A. Incorporation of biomarker assessment in novel clinical trial designs: Personalizing brain tumor treatments. Curr. Oncol. Rep. 2011, 13, 42–49. [Google Scholar] [CrossRef] [PubMed]
- Van Schaeybroeck, S.; Allen, W.L.; Turkington, R.C.; Johnston, P.G. Implementing prognostic and predictive biomarkers in CRC clinical trials. Nat. Rev. Clin. Oncol. 2011, 8, 222–232. [Google Scholar] [CrossRef] [PubMed]
- Buyse, M.; Michiels, S.; Sargent, D.J.; Grothey, A.; Matheson, A.; de Gramont, A. Integrating biomarkers in clinical trials. Expert rev. Mol. Diagn. 2011, 11, 171–182. [Google Scholar] [CrossRef] [PubMed]
- Sparano, J.A.; Paik, S. Development of the 21-gene assay and its application in clinical practice and clinical trials. J. Clin. Oncol. 2008, 26, 721–728. [Google Scholar] [CrossRef] [PubMed]
- Freidlin, B.; Korn, E.L. Biomarker enrichment strategies: Matching trial design to biomarker credentials. Nat. Rev. Clin. Oncol. 2014, 11, 81–90. [Google Scholar] [CrossRef] [PubMed]
- Simon, R.; Polley, E. Clinical trials for precision oncology using next-generation sequencing. Personal. Med. 2013, 10, 485–495. [Google Scholar] [CrossRef]
- Baker, S.G.; Kramer, B.S.; Sargent, D.J.; Bonetti, M. Biomarkers, subgroup evaluation, and clinical trial design. Discov. Med. 2012, 13, 187–192. [Google Scholar] [PubMed]
- Buch, M.H.; Pavitt, S.; Parmar, M.; Emery, P. Creative trial design in RA: Optimizing patient outcomes. Nat. Rev. Rheumatol. 2013, 9, 183–194. [Google Scholar] [CrossRef] [PubMed]
- Simon, R. Clinical trials for predictive medicine. Stat. Med. 2012, 31, 3031–3040. [Google Scholar] [CrossRef] [PubMed]
- Scher, H.I.; Nasso, S.F.; Rubin, E.H.; Simon, R. Adaptive clinical trial designs for simultaneous testing of matched diagnostics and therapeutics. Clin. Cancer Res. 2011, 17, 6634–6640. [Google Scholar] [CrossRef] [PubMed]
- Sato, Y.; Laird, N.M.; Yoshida, T. Biostatistic tools in pharmacogenomics—Advances, challenges, potential. Curr. Pharm. Des. 2010, 16, 2232–2240. [Google Scholar] [CrossRef] [PubMed]
- Mandrekar, S.J.; Sargent, D.J.; Mandrekar, S.; Sargent, D. Genomic advances and their impact on clinical trial design. Genome Med. 2009, 1, 69. [Google Scholar] [CrossRef] [PubMed]
- Simon, R. Designs and adaptive analysis plans for pivotal clinical trials of therapeutics and companion diagnostics. Expert opin. Med. Diagn. 2008, 2, 721–729. [Google Scholar] [CrossRef] [PubMed]
- Dobbin, K.K. Statistical design and evaluation of biomarker studies. Methods Mol. Biol. 2014, 1102, 667–677. [Google Scholar] [PubMed]
- Ananthakrishnan, R.; Menon, S. Design of oncology clinical trials: A review. Crit. Rev. Oncol./Hematol. 2013, 88, 144–153. [Google Scholar] [CrossRef] [PubMed]
- Simon, R. The use of genomics in clinical trial design. Clin. Cancer Res. 2008, 14, 5984–5993. [Google Scholar] [CrossRef] [PubMed]
- Freidlin, B.; McShane, L.M.; Korn, E.L. Randomized clinical trials with biomarkers: Design issues. J. Natl. Cancer Inst. 2010, 102, 152–160. [Google Scholar] [CrossRef] [PubMed]
- Johnson, D.R.; Galanis, E. Incorporation of prognostic and predictive factors into glioma clinical trials. Curr. Oncol. Rep. 2013, 15, 56–63. [Google Scholar] [CrossRef] [PubMed]
- Sparano, J. TAILORx: Trial assigning individualized options for treatment (Rx). Clin. Breast Cancer 2006, 7, 347–350. [Google Scholar] [CrossRef] [PubMed]
- Di Maio, M.; Gallo, C.; De Maio, E.; Morabito, A.; Piccirillo, M.C.; Gridelli, C.; Perrone, F. Methodological aspects of lung cancer clinical trials in the era of targeted agents. Lung Cancer 2010, 67, 127–135. [Google Scholar] [CrossRef] [PubMed]
- Maitournam, A.; Simon, R. On the efficiency of targeted clinical trials. Stat. Med. 2005, 24, 329–339. [Google Scholar] [CrossRef] [PubMed]
- Collette, L.; Bogaerts, J.; Suciu, S.; Fortpied, C.; Gorlia, T.; Coens, C.; Mauer, M.; Hasan, B.; Collette, S.; Ouali, M.; et al. Statistical methodology for personalized medicine: New developments at EORTC headquarters since the turn of the 21st century. Eur. J. Cancer Suppl. 2012, 10, 13. [Google Scholar] [CrossRef]
- Mandrekar, S.J.; Sargent, D.J. All-comers versus enrichment design strategy in phase II trials. J. Thorac. Oncol. 2011, 6, 658–660. [Google Scholar] [CrossRef] [PubMed]
- Simon, R. Development and validation of biomarker classifiers for treatment selection. J. Stat. Plan. Inference 2008, 138, 308–320. [Google Scholar] [CrossRef] [PubMed]
- Freidlin, B.; Korn, E.L.; Gray, R. Marker sequential test (MaST) design. Clin. Trials 2014, 11, 19–27. [Google Scholar] [CrossRef] [PubMed]
- Wason, J.; Marshall, A.; Dunn, J.; Stein, R.C.; Stallard, N. Adaptive designs for clinical trials assessing biomarker-guided treatment strategies. Br. J. Cancer 2014, 110, 1950–1957. [Google Scholar] [CrossRef] [PubMed]
- Freidlin, B.; McShane, L.M.; Polley, M.-Y.C.; Korn, E.L. Randomized phase II trial designs with biomarkers. J. Clin. Oncol. 2012, 30, 3304–3309. [Google Scholar] [CrossRef] [PubMed]
- Ziegler, A.; Koch, A.; Krockenberger, K.; Grosshennig, A. Personalized medicine using DNA biomarkers: A review. Hum. Genet. 2012, 131, 1627–1638. [Google Scholar] [CrossRef] [PubMed]
- Freidlin, B.; Korn, E.L. Biomarker-adaptive clinical trial designs. Pharmacogenomics 2010, 11, 1679–1682. [Google Scholar] [CrossRef] [PubMed]
- Eickhoff, J.C.; Kim, K.; Beach, J.; Kolesar, J.M.; Gee, J.R. A bayesian adaptive design with biomarkers for targeted therapies. Clin. Trials 2010, 7, 546–556. [Google Scholar] [CrossRef] [PubMed]
- Ferraldeschi, R.; Attard, G.; de Bono, J.S. Novel strategies to test biological hypotheses in early drug development for advanced prostate cancer. Clin. Chem. 2013, 59, 75–84. [Google Scholar] [CrossRef] [PubMed]
- Coyle, V.M.; Johnston, P.G. Genomic markers for decision making: What is preventing us from using markers? Nat. Rev. Clin. Oncol. 2010, 7, 90–97. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.F.; Lin, J.R.; Liu, J.P. Statistical inference on censored data for targeted clinical trials under enrichment design. Pharm. Stat. 2013, 12, 165–173. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.P.; Lin, J.R. Statistical methods for targeted clinical trials under enrichment design. J. Formos. Med. Assoc. 2008, 107, 35–42. [Google Scholar] [CrossRef]
- Scheibler, F.; Zumbé, P.; Janssen, I.; Viebahn, M.; Schröer-Günther, M.; Grosselfinger, R.; Hausner, E.; Sauerland, S.; Lange, S. Randomized controlled trials on pet: A systematic review of topics, design, and quality. J. Nucl. Med. 2012, 53, 1016–1025. [Google Scholar] [CrossRef] [PubMed]
- An, M.-W.; Mandrekar, S.J.; Sargent, D.J. A 2-stage phase II design with direct assignment option in stage II for initial marker validation. Clin. Cancer Res. 2012, 18, 4225–4233. [Google Scholar] [CrossRef] [PubMed]
- Zheng, G.; Wu, C.O.; Yang, S.; Waclawiw, M.A.; DeMets, D.L.; Geller, N.L. NHLBI clinical trials workshop: An executive summary. Stat. Med. 2012, 31, 2938. [Google Scholar] [CrossRef] [PubMed]
- Bria, E.; Di Maio, M.; Carlini, P.; Cuppone, F.; Giannarelli, D.; Cognetti, F.; Milella, M. Targeting targeted agents: Open issues for clinical trial design. J. Exp. Clin. Cancer Res. 2009, 28, 66. [Google Scholar] [CrossRef] [PubMed]
- French, B.; Joo, J.; Geller, N.L.; Kimmel, S.E.; Rosenberg, Y.; Anderson, J.L.; Gage, B.F.; Johnson, J.A.; Ellenberg, J.H. Statistical design of personalized medicine interventions: The Clarification of Optimal Anticoagulation through Genetics (Coag) trial. Trials 2010, 11, 108. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.-A.; He, P. Reinventing clinical trials: A review of innovative biomarker trial designs in cancer therapies. Br. Med. Bull. 2015, 114, 17–27. [Google Scholar] [CrossRef] [PubMed]
- Renfro, L.A.; Mallick, H.; An, M.-W.; Sargent, D.J.; Mandrekar, S.J. Clinical trial designs incorporating predictive biomarkers. Cancer Treat. Rev. 2016, 43, 74–82. [Google Scholar] [CrossRef] [PubMed]
- Ondra, T.; Dmitrienko, A.; Friede, T.; Graf, A.; Miller, F.; Stallard, N.; Posch, M. Methods for identification and confirmation of targeted subgroups in clinical trials: A systematic review. J. Biopharm. Stat. 2016, 26, 99–119. [Google Scholar] [CrossRef] [PubMed]
- Simon, R.; Wang, S.J. Use of genomic signatures in therapeutics development in oncology and other diseases. Pharmacogenom. J. 2006, 6, 166–173. [Google Scholar] [CrossRef] [PubMed]
- European Medicines Agency. Reflection Paper on Methodological Issues Associated with Pharmacogenomic Biomarkers in Relation to Clinical Development and Patient Selection. Available online: http://www.ema.europa.eu/docs/en_GB/document_library/Scientific_guideline/2011/07/WC500108672.pdf (accessed on 10 October 2015).
- Lai, T.L.; Liao, O.Y.-W.; Kim, D.W. Group sequential designs for developing and testing biomarker-guided personalized therapies in comparative effectiveness research. Contemp. Clin. Trials 2013, 36, 651–663. [Google Scholar] [CrossRef] [PubMed]
- Foley, R.N. Analysis of randomized controlled clinical trials. Methods Mol. Biol. 2009, 473, 113–126. [Google Scholar] [PubMed]
- Tajik, P.; Bossuyt, P.M. Genomic markers to tailor treatments: Waiting or initiating? Hum. Genet. 2011, 130, 15–18. [Google Scholar] [CrossRef] [PubMed]
- Eng, K.H. Randomized reverse marker strategy design for prospective biomarker validation. Stat. Med. 2014, 33, 3089–3099. [Google Scholar] [CrossRef] [PubMed]
- Baker, S.G. Biomarker evaluation in randomized trials: Addressing different research questions. Stat. Med. 2014, 33, 4139–4140. [Google Scholar] [CrossRef] [PubMed]
- Matsui, S.; Choai, Y.; Nonaka, T. Comparison of statistical analysis plans in randomize-all phase III trials with a predictive biomarker. Clin. Cancer Res. 2014, 20, 2820–2830. [Google Scholar] [CrossRef] [PubMed]
- Cappuzzo, F.; Ciuleanu, T.; Stelmakh, L.; Cicenas, S.; Szczésna, A.; Juhász, E.; Esteban, E.; Molinier, O.; Brugger, W.; Melezínek, I.; et al. Erlotinib as maintenance treatment in advanced non-small-cell lung cancer: A multicentre, randomised, placebo-controlled phase 3 study. Lancet Oncol. 2010, 11, 521. [Google Scholar] [CrossRef]
- Hoffmann-La Roche. A Randomized, Double-Blind Study to Evaluate the Effect of Tarceva or Placebo Following Platinum-Based CT on Overall Survival and Disease Progression in Patients with Advanced, Recurrent or Metastatic NSCLS Who Have Not Experienced Disease Progression or Unacceptable Toxicity during Chemotherapy. Available online: https://clinicaltrials.gov/ct2/show/NCT00556712?term=NCT00556712&rank=1 (accessed on 10 October 2015).
- Choai, Y.; Matsui, S. Estimation of treatment effects in all-comers randomized clinical trials with a predictive marker: Estimating treatment effects in marker-based randomized trials. Biometrics 2015, 71, 25. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.-J.; O’Neill, R.T.; Hung, H.M.J. Approaches to evaluation of treatment effect in randomized clinical trials with genomic subset. Pharm. Stat. 2007, 6, 227–244. [Google Scholar] [CrossRef] [PubMed]
- Cree, I.A.; Kurbacher, C.M.; Lamont, A.; Hindley, A.C.; Love, S. A prospective randomized controlled trial of tumour chemosensitivity assay directed chemotherapy versus physician’s choice in patients with recurrent platinum-resistant ovarian cancer. Anti-Cancer Drugs 2007, 18, 1093. [Google Scholar] [CrossRef] [PubMed]
- Cobo, M.; Isla, D.; Massuti, B.; Montes, A.; Sanchez, J.M.; Provencio, M.; Viñolas, N.; Paz-Ares, L.; Lopez-Vivanco, G.; Muñoz, M.A.; et al. Customizing cisplatin based on quantitative excision repair cross-complementing 1 mRNA expression: A phase III trial in non-small-cell lung cancer. J. Clin. Oncol. 2007, 25, 2747. [Google Scholar] [CrossRef] [PubMed]
- Lijmer, J.G.; Bossuyt, P.M.M. Various randomized designs can be used to evaluate medical tests. J. Clin. Epidemiol. 2009, 62, 364. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.-J. Biomarker as a classifier in pharmacogenomics clinical trials: A tribute to 30th anniversary of PSI. Pharm. Stat. 2007, 6, 283–296. [Google Scholar] [CrossRef] [PubMed]
- Cho, D.; McDermott, D.; Atkins, M. Designing clinical trials for kidney cancer based on newly developed prognostic and predictive tools. Curr. Urol. Rep. 2006, 7, 8–15. [Google Scholar] [CrossRef] [PubMed]
- Af Geijerstam, J.L.; Oredsson, S.; Britton, M. Medical outcome after immediate computed tomography or admission for observation in patients with mild head injury: Randomised controlled trial. Br. Med. J. 2006, 333, 465. [Google Scholar] [CrossRef] [PubMed]
- Ferrante di Ruffano, L.; Davenport, C.; Eisinga, A.; Hyde, C.; Deeks, J.J. A capture-recapture analysis demonstrated that randomized controlled trials evaluating the impact of diagnostic tests on patient outcomes are rare. J. Clin. Epidemiol. 2012, 65, 282. [Google Scholar] [CrossRef] [PubMed]
- Mandrekar, S.J.; Grothey, A.; Goetz, M.P.; Sargent, D.J. Clinical trial designs for prospective validation of biomarkers. Am. J. Pharmacogenom. 2005, 5, 317–325. [Google Scholar] [CrossRef]
- Therasse, P.; Carbonnelle, S.; Bogaerts, J. Clinical trials design and treatment tailoring: General principles applied to breast cancer research. Crit. Rev. Oncol. Hematol. 2006, 59, 98–105. [Google Scholar] [CrossRef] [PubMed]
- Sargent, D.; Allegra, C. Issues in clinical trial design for tumor marker studies. Semin. Oncol. 2002, 29, 222–230. [Google Scholar] [CrossRef] [PubMed]
- Tanniou, J.; van der Tweel, I.; Teerenstra, S.; Roes, K.C.B. Subgroup analyses in confirmatory clinical trials: Time to be specific about their purposes. BMC Med. Res. Methodol. 2016, 16, 20. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, L.V.; Gail, M.H.; Santner, T.J. Planning the duration of a comparative clinical trial with loss to follow-up and a period of continued observation. J. Chronic Dis. 1981, 34, 469–479. [Google Scholar] [CrossRef]
- Simon, R.; Maitournam, A. Evaluating the efficiency of targeted designs for randomized clinical trials: Supplement and correction. Clin. Cancer Res. 2006, 12, 3229. [Google Scholar] [CrossRef] [PubMed]
- Simon, R.; Maitournam, A. Evaluating the efficiency of targeted designs for randomized clinical trials. Clin. Cancer Res. 2004, 10, 6759. [Google Scholar] [CrossRef] [PubMed]
- Biomarker targeted randomized design. Available online: http://brb.nci.nih.gov/brb/samplesize/td.html (accessed on 15 September 2016).
- Harrington, R.A. Applied Bioinformatics and Biostatistics in Cancer Research. In Designs for Clinical Trials: Perspectives on Current Issues; Springer Science+Business Media, LLC: New York, NY, USA, 2012. [Google Scholar]
- Biomarker stratified randomized design. Available online: https://brb.nci.nih.gov/brb/samplesize/sdpap.html (accessed on 15 September 2016).
- Freidlin, B. Randomized phase ii trial designs with biomarkers. Available online: http://brb.nci.nih.gov/Data/FreidlinB/RP2BM (accessed on 15 September 2016).
- Tajik, P.; Zwinderman, A.H.; Mol, B.W.; Bossuyt, P.M. Evaluating putative predictive biomarkers in randomized clinical trials. Available online: http://www.zonmw.nl/fileadmin/documenten/DO_Farmacotherapie_Dure_Weesgeneesmiddelen/HTA_pharmacotherapy_predictive_markers_guidance_document.pdf (accessed on 15 September 2016).
- Zaslavsky, B.G.; Scott, J. Sample size estimation in single-arm clinical trials with multiple testing under frequentist and bayesian approaches. J. Biopharm. Stat. 2012, 22, 819–835. [Google Scholar] [CrossRef] [PubMed]
- Wittes, J. Sample size calculations for randomized controlled trials. Epidemiol. Rev. 2002, 24, 39–53. [Google Scholar] [CrossRef] [PubMed]
- Collette, L. Chapman & Hall/CRC Texts in Statistical Science Series. In Modelling Survival Data in Medical Research, 2nd ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Kleinbaum, D.G.; Klein, M. Statistics for Biology and Health. Survival Analysis: A Self-Learning Text, 3rd ed.; Springer: New York, NY, USA, 2012. [Google Scholar]
- Freedman, L.S. Tables of the number of patients required in clinical trials using the logrank test. Stat. Med. 1982, 1, 121–129. [Google Scholar] [CrossRef] [PubMed]
- Schoenfeld, D.A. Sample-size formula for the proportional-hazards regression model. Biometrics 1983, 39, 499–503. [Google Scholar] [CrossRef] [PubMed]
- Bland, J.M.; Altman, D.G. Multiple significance tests: The bonferroni method. Br. Med. J. 1995, 310, 170. [Google Scholar] [CrossRef]
- Jiang, W.; Freidlin, B.; Simon, R. Biomarker-adaptive threshold design: A procedure for evaluating treatment with possible biomarker-defined subset effect. J. Natl. Cancer Inst. 2007, 99, 1036–1043. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.-J.; Hung, H.M.J.; O’Neill, R.T. Adaptive patient enrichment designs in therapeutic trials. Biom. J. 2009, 51, 358–374. [Google Scholar] [CrossRef] [PubMed]
- Alosh, M.; Huque, M.F.; Alosh, M.; Huque, M.F. A flexible strategy for testing subgroups and overall population. Stat. Med. 2009, 28, 3. [Google Scholar] [CrossRef] [PubMed]
- Spiessens, B.; Debois, M. Adjusted significance levels for subgroup analyses in clinical trials. Contemp. Clin. Trials 2010, 31, 647. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Chi, G.Y.H.; Song, Y.; Chi, G.Y.H. A method for testing a prespecified subgroup in clinical trials. Stat. Med. 2007, 26, 3535. [Google Scholar] [CrossRef] [PubMed]
- Chang, M. Chapman & Hall/CRC Biostatistics Series. In Adaptive Design Theory and Implementation Using SAS and R, 2nd ed.; CRC Press: London, UK, 2014. [Google Scholar]
- Dimairo, M.; Boote, J.; Julious, S.A.; Nicholl, J.P.; Todd, S. Missing steps in a staircase: A qualitative study of the perspectives of key stakeholders on the use of adaptive designs in confirmatory trials. Trials 2015, 16, 430. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Spira, A.; Edmiston, K.H. Clinical trial design in the age of molecular profiling. Methods Mol. Biol. 2012, 823, 19–34. [Google Scholar] [PubMed]
- Medline Plus basic course manual 2012. Available online: http://www.google.co.uk/url?sa=t&rct=j&q=&esrc=s&frm=1&source=web&cd=1&ved=0ahUKEwjS7_OmodvJAhWGVhQKHZr0AZMQFggdMAA&url=http%3A%2F%2Fbma.org.uk%2F-%2Fmedia%2Ffiles%2Fpdfs%2Fabout%2520the%2520bma%2Flibrary%2Fmedline%2520plus%2520basic%2520course%2520manual%25202012.pdf&usg=AFQjCNGFxcWiS11CJsroeeIETAWjW0neUA (accessed on 15 September 2016).
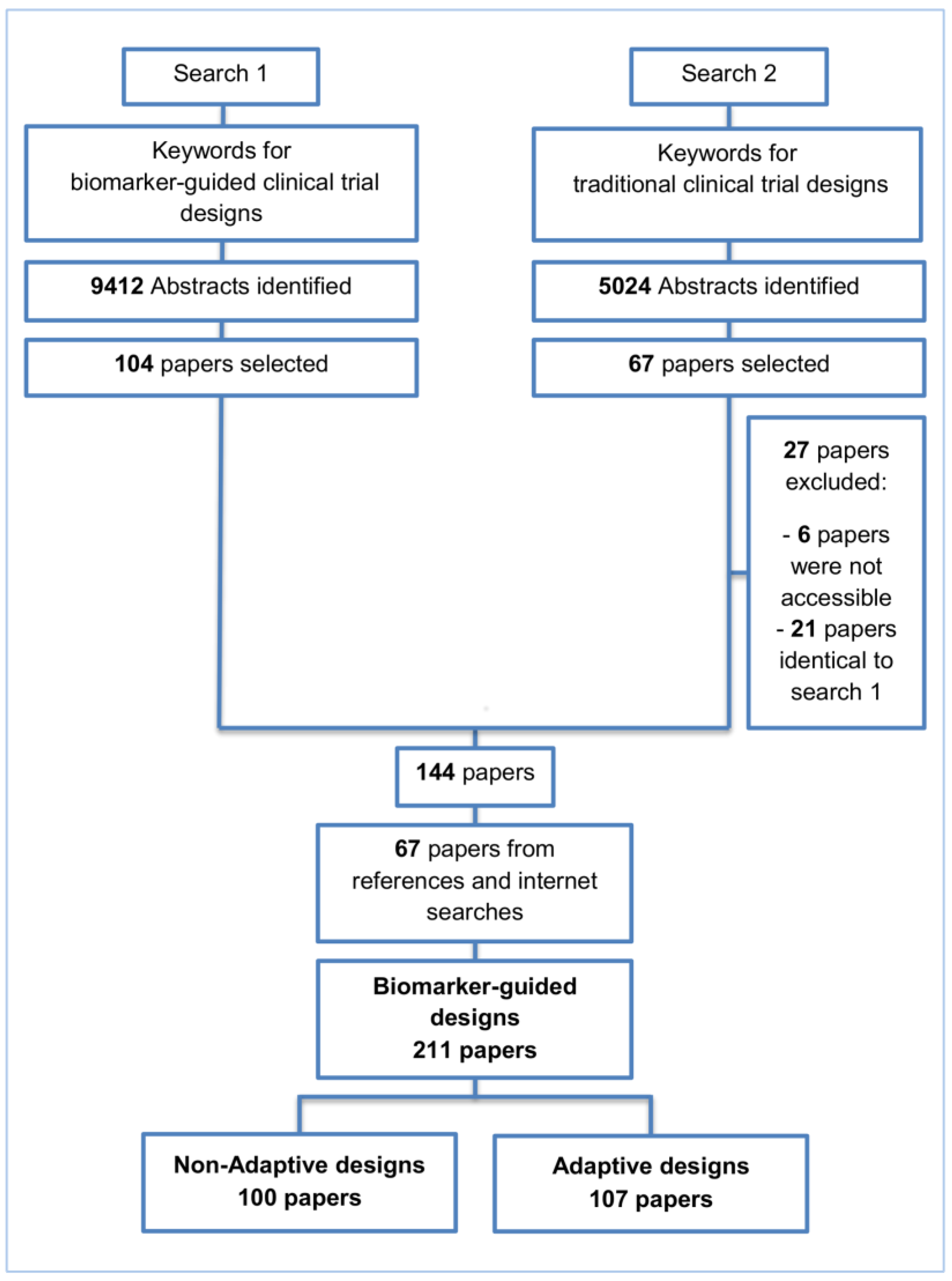
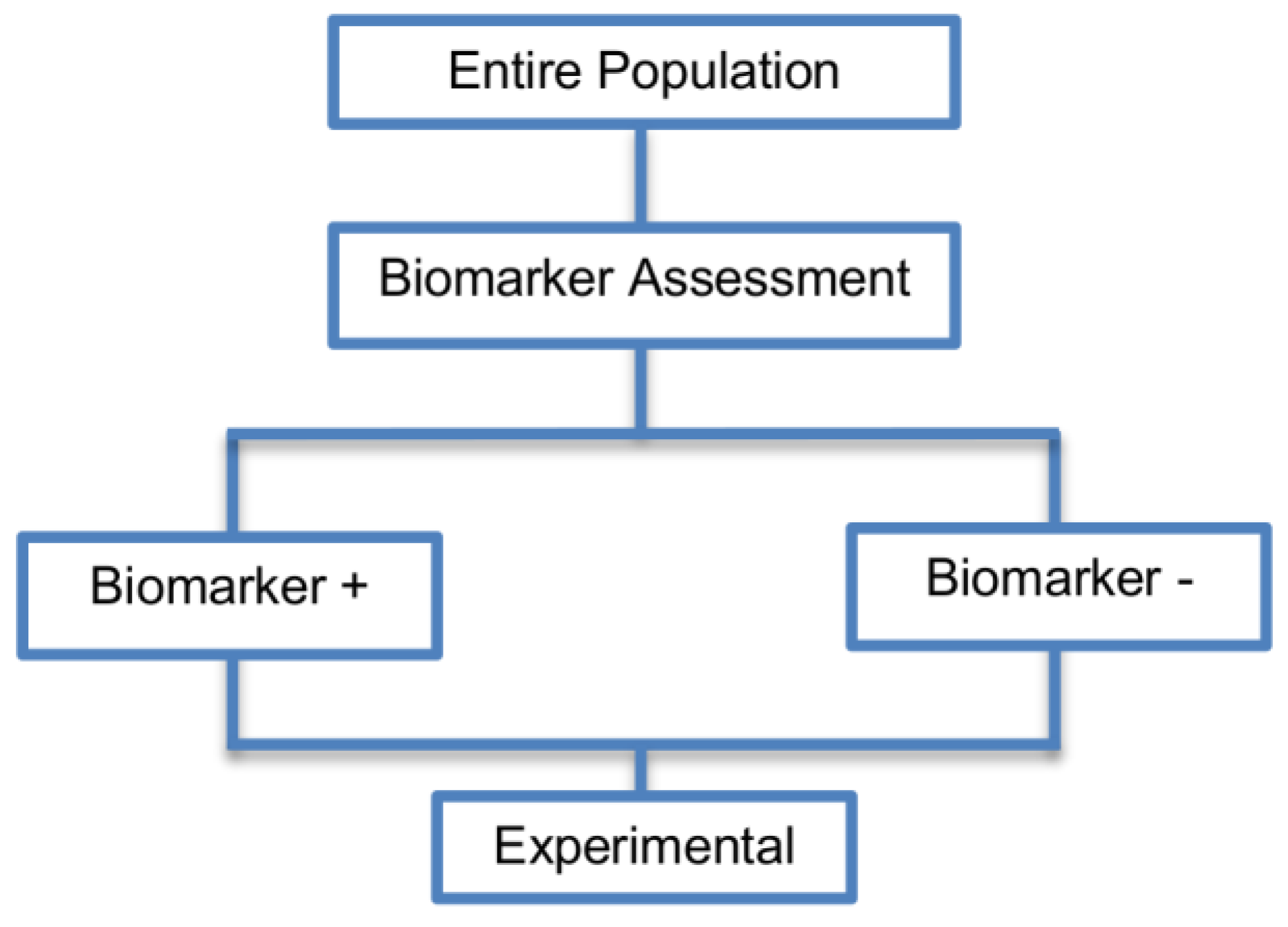
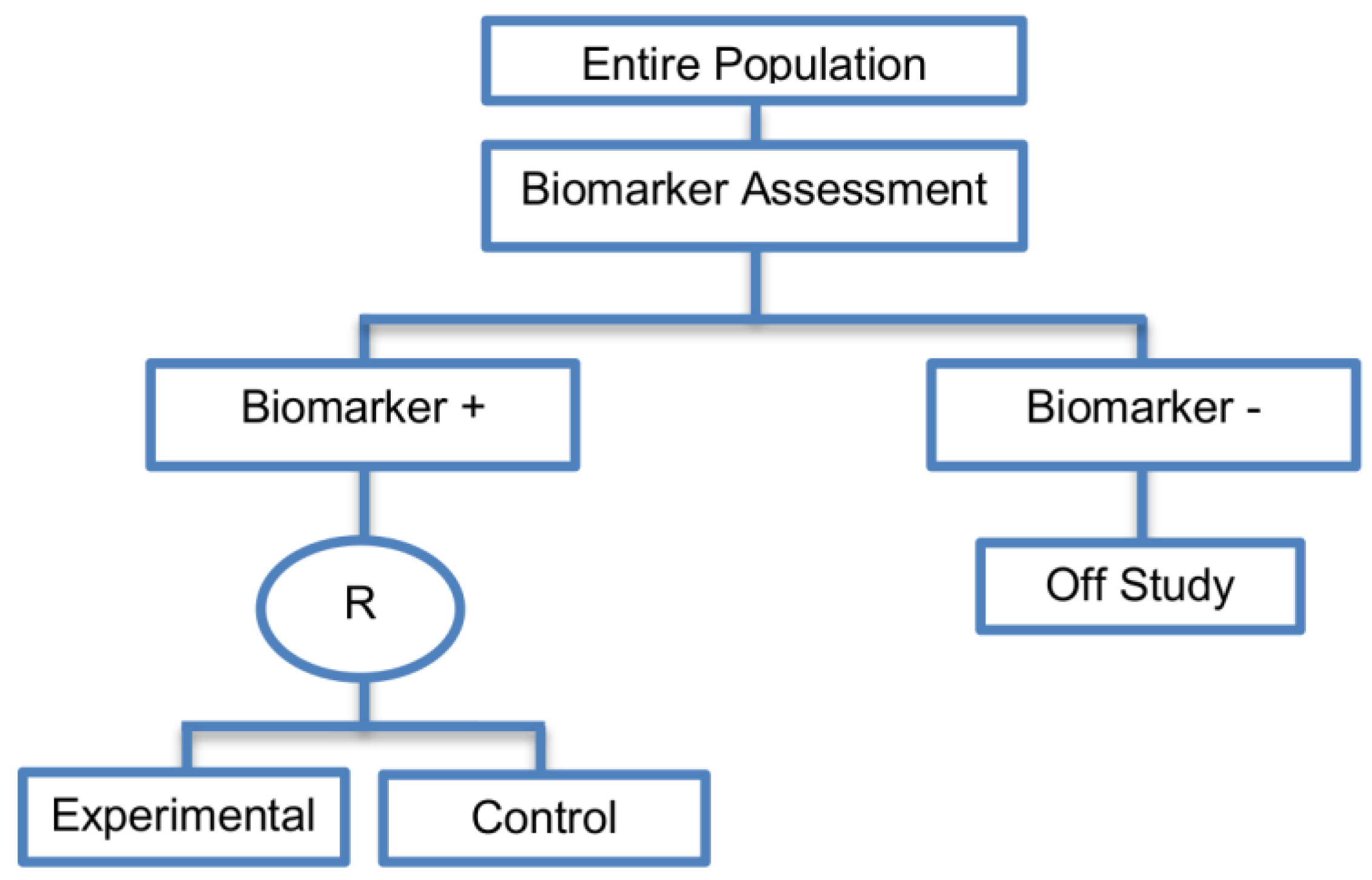
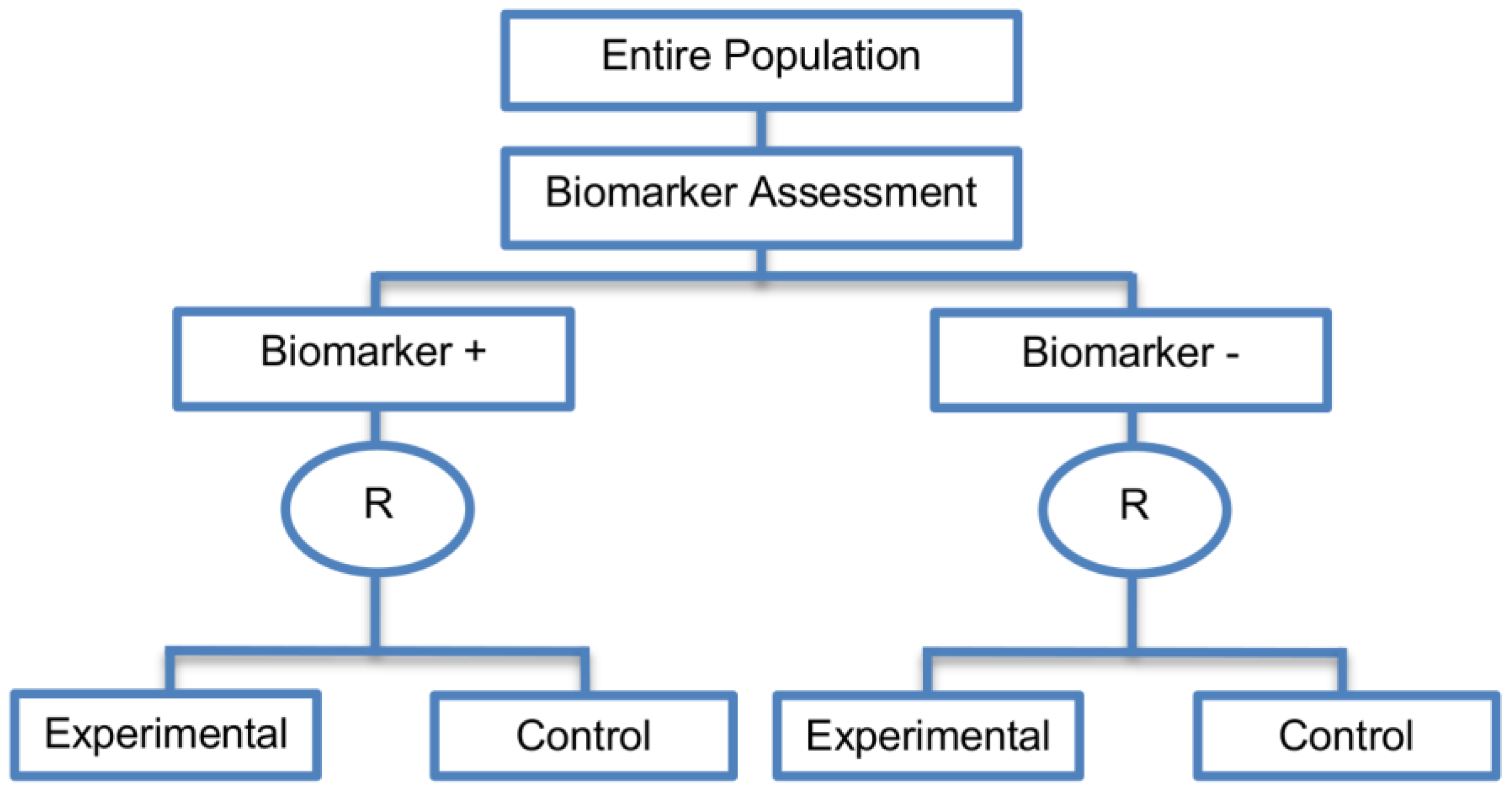
| Types of Biomarker-Guided Non-Adaptive Trial Designs | Utility | Advantages | Limitations |
|---|---|---|---|
| Single arm designs (7 papers) [30,36,37,38,39,40,41] (see Figure 2) | Useful for initial identification and/or validation of a biomarker. | (A1) Considered as a simple statistical design as there is no need for randomization of patients. | (L1) There is no distinction between prognostic and predictive biomarker as patients are not randomized to experimental and control treatment arms. |
| Also called: Nonrandomized clinical trial design, Uncontrolled Cohort Pharmacogenetic Study design | (A2) Simple logistics. | ||
| Examples of actual trials: None identified a | (A3) Not complex statistical design | ||
| (A4) In some cases, these designs may be viewed as ethical as all patients are given the opportunity to experience the experimental treatment. However, they may be viewed as unethical if the novel treatment does not benefit a subgroup of patients or causes adverse events. | |||
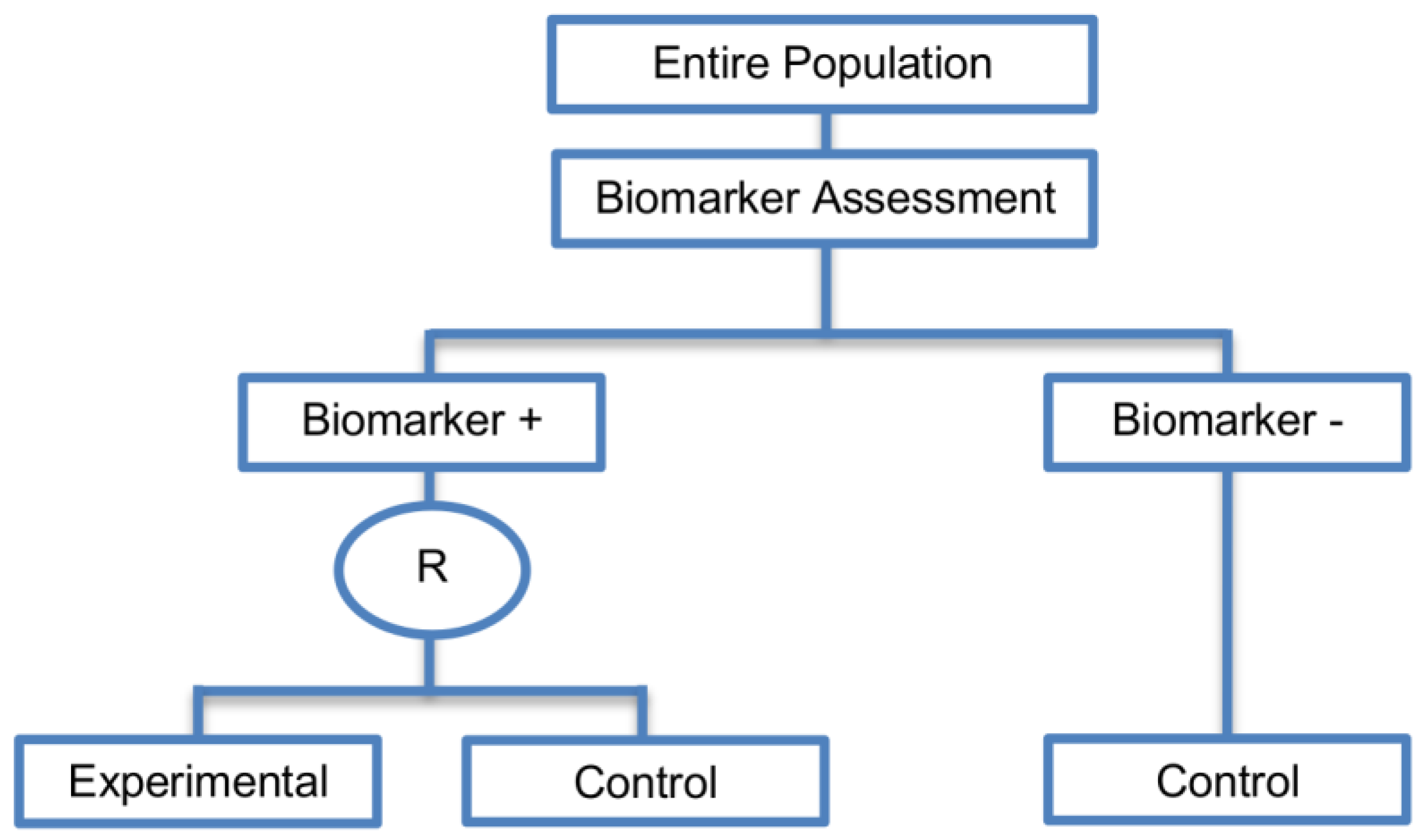
| Enrichment designs (71 papers) [1,4,7,8,9,11,13,15,16,18,19,21,23,25,26,27,28,29,30,31,32,33,36,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86] (see Figure 3) | Useful when we aim to test the treatment effect only in biomarker-positive subset for which there is prior evidence that the novel treatment is beneficial, but the candidate biomarker requires prospective validation. | (A5) Evaluates the effect of the experimental treatment in the biomarker-positive subgroup in a simple and efficient way. | (L2) Do not assess whether the experimental treatment benefits the biomarker-negative patients, thus we cannot obtain information about this subgroup. Also unable to demonstrate whether the targeted treatment is beneficial in the entire study population. |
| Also called: Targeted design, Selection design, Efficient Targeted design, Biomarker-Enrichment design, Marker-enrichment design, Gene enrichment design, Enriched design, Clinically enriched Phase III study design, Clinically Enriched Trial design, Biomarker-Enriched design, Biomarker Enriched design, Biomarker Selected trial design, Screening enrichment design, Randomized Controlled Trial (RCT) of test positive design, Population enrichment design | Useful when it is not ethical to assign biomarker-negative patients to the novel treatment for which there is prior evidence that it will not be beneficial for this subpopulation, or that it will harm them. | (A6) Provides clear information about whether the novel treatment is effective for the biomarker-positive subgroup, thus these designs can identify the best treatment for these patients and confirm the usefulness of the biomarker. | (L3) Do not inform us directly about whether the biomarker is itself predictive because the relative treatment efficacy may be the same in the unevaluated biomarker-negative patients. Since these designs only enrol a subgroup of patients, they do not allow for full validation of the marker’s predictive ability. For full validation, a trial would need to randomize all patients in order to test for a treatment–biomarker interaction. |
| Examples of actual trials: CRYSTAL [49], BRIM 3 [49,50,51], EURTAC [49], CLEOPATRA [49], PROFILE 1007 [49,50], LUX-Lung [49], NSABP B-31 and NCCTG N9831 [4,15,16,18,19,28,29,30,31,36,44,46,52,53,54,55,56,57,58,59,60], CALGB-10603 [61], CATNON [62], CODEL [62], Evaluation of epidermal growth factor receptor variant III (EGFRvIII) peptide vaccination [62], N0923 [7,21] , Flex study [64], TOGA trial [47], IPASS [33,43], N0147 [29], PetaCC-8 [29,47], C80405 [29], ECOG E5202 [29] | Recommended when both the cut-off point for determination of biomarker-status of patients and the analytical validity of a biomarker are well established. | (A7) Reduced sample size as the assessment of treatment effect is restricted only to biomarker-positive subgroup. Therefore, if the selected biomarker is “biologically correct” and reliably measured, the used enrichment strategy could result in a large saving of randomized patients. | (L4) Researchers should carefully decide whether or not to follow this strategy as it may be of limited value due to the exclusion of biomarker-negative patients. It may be that the entire population could benefit from the experimental treatment equally irrespective of biomarker status, in which case enrolling only the biomarker-positive patients will result in slow trial accrual, increase of expenses and unnecessary limitation of the size of the indicated patient population. |
| (A8) Enables rapid accumulation of efficacy data. | (L5) Concern over an ethical problem as we cannot include individuals in a clinical trial if it is believed that the treatment is not effective for them, as raised by the US Food and Drug Administration (FDA) [50]. It was based on the facts that the experimental treatment can only be approved for a particular biomarker-defined subpopulation (i.e., biomarker-positive patients) if a companion diagnostic test is also approved, and how the test can be approved if the Phase III trial does not show that the novel treatment does not benefit the biomarker-negative patients. | ||
| (A9) Allow us to avoid potential dilution of the results due to the absence of biomarker-negative patients. For example, if the design had included the biomarker-negative population and the biomarker positivity rate was low as compared to the biomarker negative rate, then the estimation of the overall treatment effectiveness could be diluted as it would be driven by the biomarker-negative subset. | (L6) The accuracy of diagnostic devices used to identify the biomarkers, e.g., biomarker assays, is not always correct [45]. This can result in incorrect selection of biomarker-positive patients and therefore these patients will erroneously be enrolled in a trial yielding biased treatment effect estimates. For example, even when the experimental treatment works well for a specific subgroup, if the biomarker assay is not able to identify this subgroup robustly then a promising treatment may be abandoned. | ||
| (A10) Can be attractive in terms of speed and cost, meaning that patients are provided with tailored treatment sooner. | |||
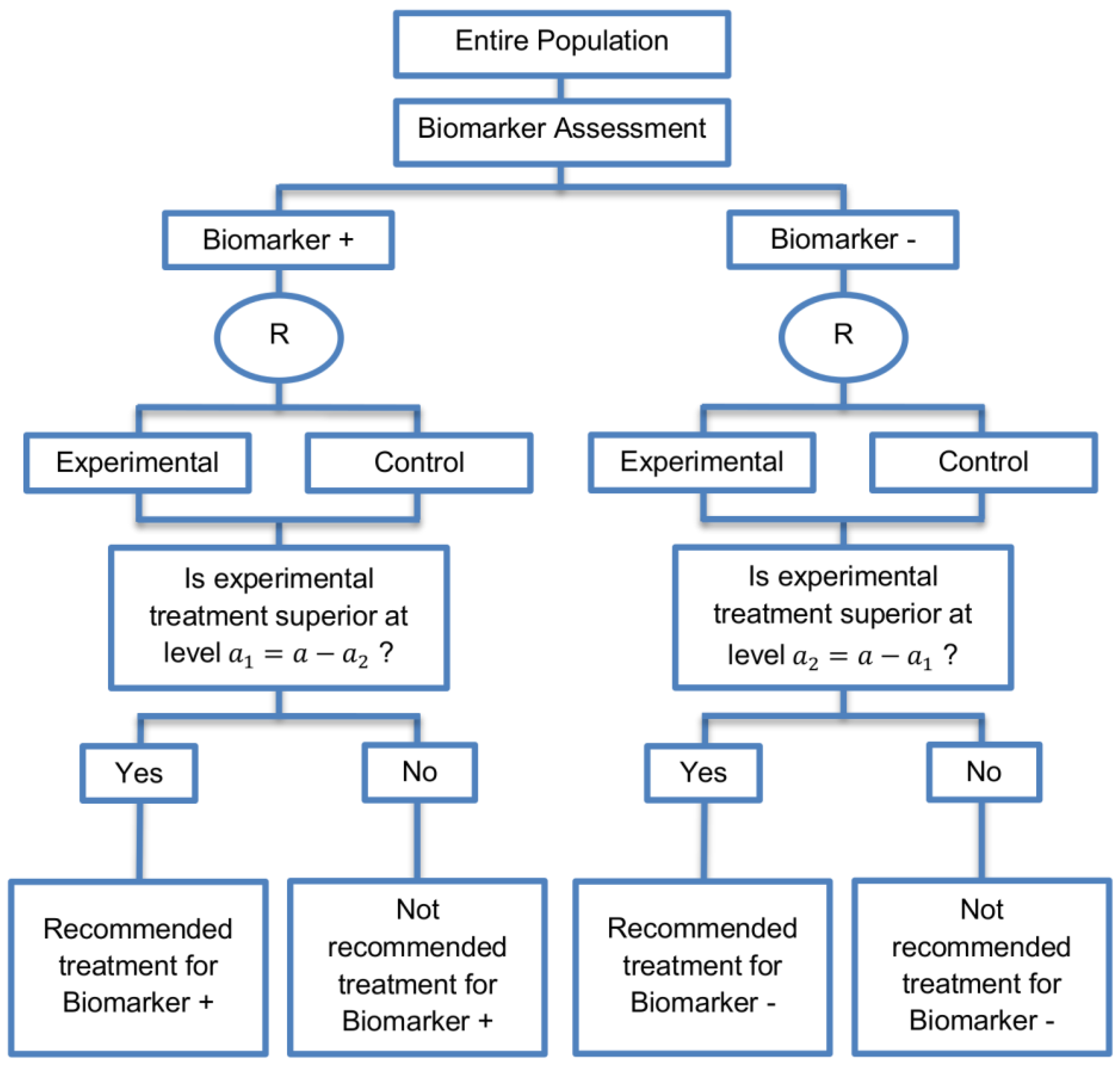
| Marker Stratified designs (45 papers) [4,10,12,13,15,16,17,18,19,21,25,26,27,30,31,33,44,45,46,49,50,51,53,58,61,62,66,68,71,72,73,74,79,80,81,84,85,86,87,88,89,90,91,92,93] (see Figure 4) | Useful when there is evidence that the novel treatment is more effective in the positive biomarker-defined subgroup than in the negative biomarker-defined subgroup but there is insufficient compelling data indicating that the experimental treatment does not benefit the biomarker-negative patients. | (A11) Ability to assess the treatment effect not only in the entire population but also in each biomarker-defined subgroup. Thus, this design can find the optimal treatment in the entire population and in each biomarker-defined subgroup. | (L7) In situations where there are several biomarkers and treatments this design may not be feasible as it involves randomization of patients between all possible treatment options and may require a large sample size. |
| Also called: Marker-stratified design, Biomarker-stratified design, Stratified-Randomized design, Stratification design, Stratified design, Stratified Analysis design, Marker by treatment – interaction design, Marker-by-treatment interaction design, Treatment by marker interaction design, Treatment-by-marker interaction design, Marker × treatment interaction design, Treatment-marker interaction design, Biomarker-by-treatment interaction design, Non-targeted RCT (stratified by marker) design, Genomic Signature stratified designs, Signature-Stratified design, Randomization or analysis stratified by biomarker status design, marker-interaction design. | (A12) An ethical design even in situations where the biomarker is not useful as no treatment decisions are made based on biomarker status; all decisions are made randomly. Consequently, if the biomarker’s value is in doubt, this design may be preferred. | (L8) May not be feasible when the prevalence of the biomarker is low. | |
| Examples of actual trials: MARVEL (N023) [4,16,30,31,33,44,61,89], GALGB-30506 [15,61], RTOG0825 [45], EORTC 10994 p53 [12,66], IBCSG trial IX [18], MINDACT [18] | (L9) Might be expensive to test the entire population for its biomarker status. | ||
| (L10) Measuring the biomarker up front may be logistically difficult. | |||
| (L11) There is no guarantee of balanced groups for analysis. | |||
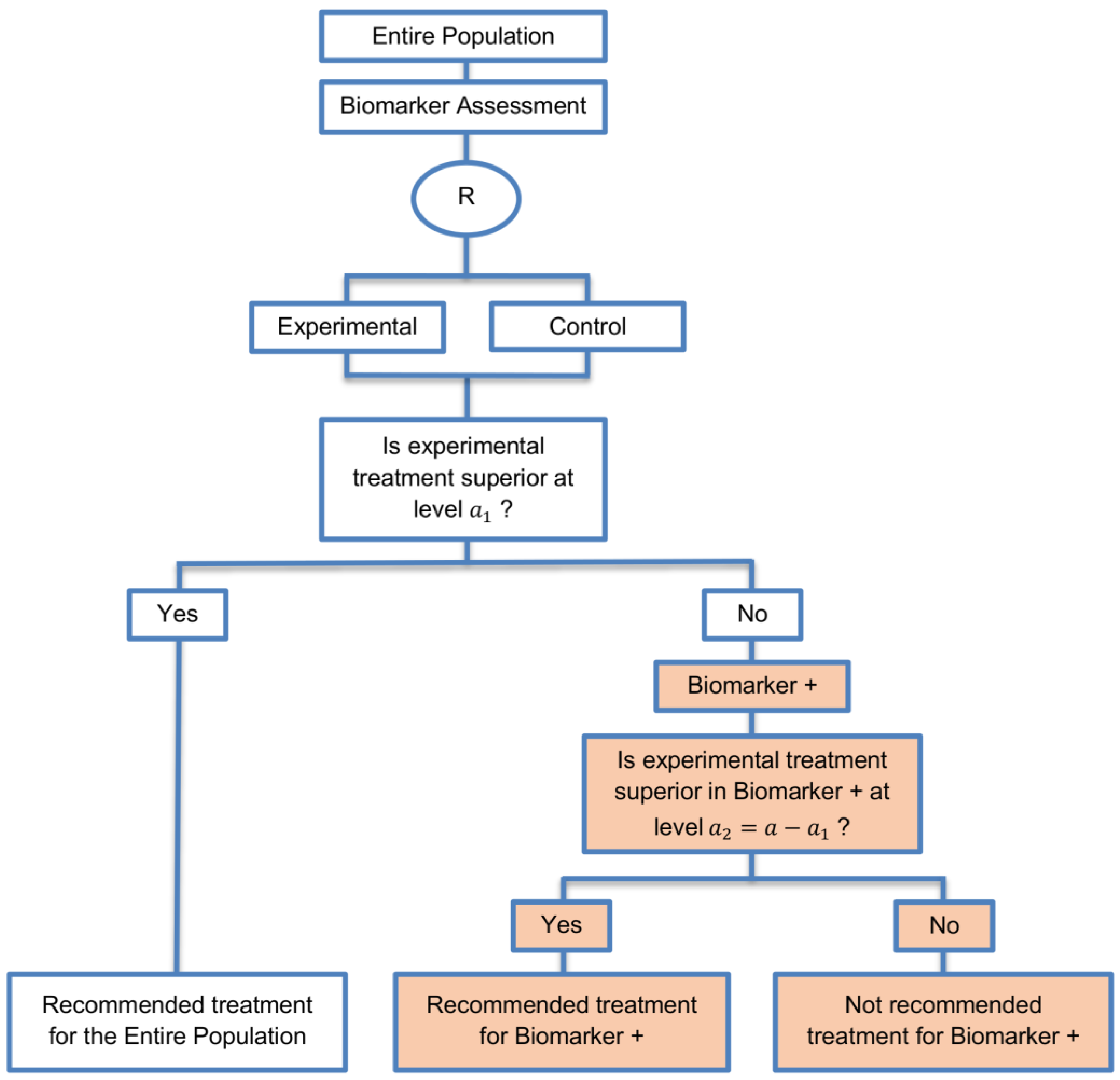
| Sequential Subgroup-Specific design (11 papers) [13,14,19,22,53,57,58,60,69,91,94] (see Figure 5) | Recommended when prior evidence indicates that the biomarker-positive subpopulation benefits more from the novel treatment as compared to the biomarker-negative subpopulation. | (A13) Allows for the estimation of treatment effect in biomarker-positive and biomarker-negative subgroups. | (L12) Has less power when there is homogeneity of treatment across the different biomarker defined subgroups as compared to the overall/biomarker-positive designs. |
| Also called: sequential design, Fixed-sequence 2 design, hierarchical fixed sequence testing procedure | (A14) Preserves the overall type I error rates and allows for a smaller sample size than the parallel version mentioned below. | (L13) Need a much larger sample size than the overall/biomarker positive designs if we assume that the treatment effect is relatively homogeneous across the biomarker-defined subsets. | |
| Examples of actual trials: PRIME [49], MARVEL [49] | (A15) Considered as the best direct evidence for clinical decision making as it tests the treatment effectiveness in both the biomarker-positive and biomarker-negative subset in a sequential way. | ||
| (A16) Do not require larger sample size than the overall/biomarker-positive designs when the prevalence of the biomarker-positive patients is small. | |||
| Parallel Subgroup-Specific design (3 papers) [14,49,69] (see Figure 6) | Appropriate when the aim of the study is to give treatment recommendations for each biomarker-defined subgroup separately at the same time. | (A17) Same as (A13), (A16) | (L14) Same as (L12) |
| Also called: Phase III Biomarker-Stratified design | (L15) Allocates the overall level between the two biomarker-defined subgroup tests which means that it will be more difficult to achieve statistical significance in the biomarker-positive subgroup. | ||
| Examples of actual trials: None identified a | |||
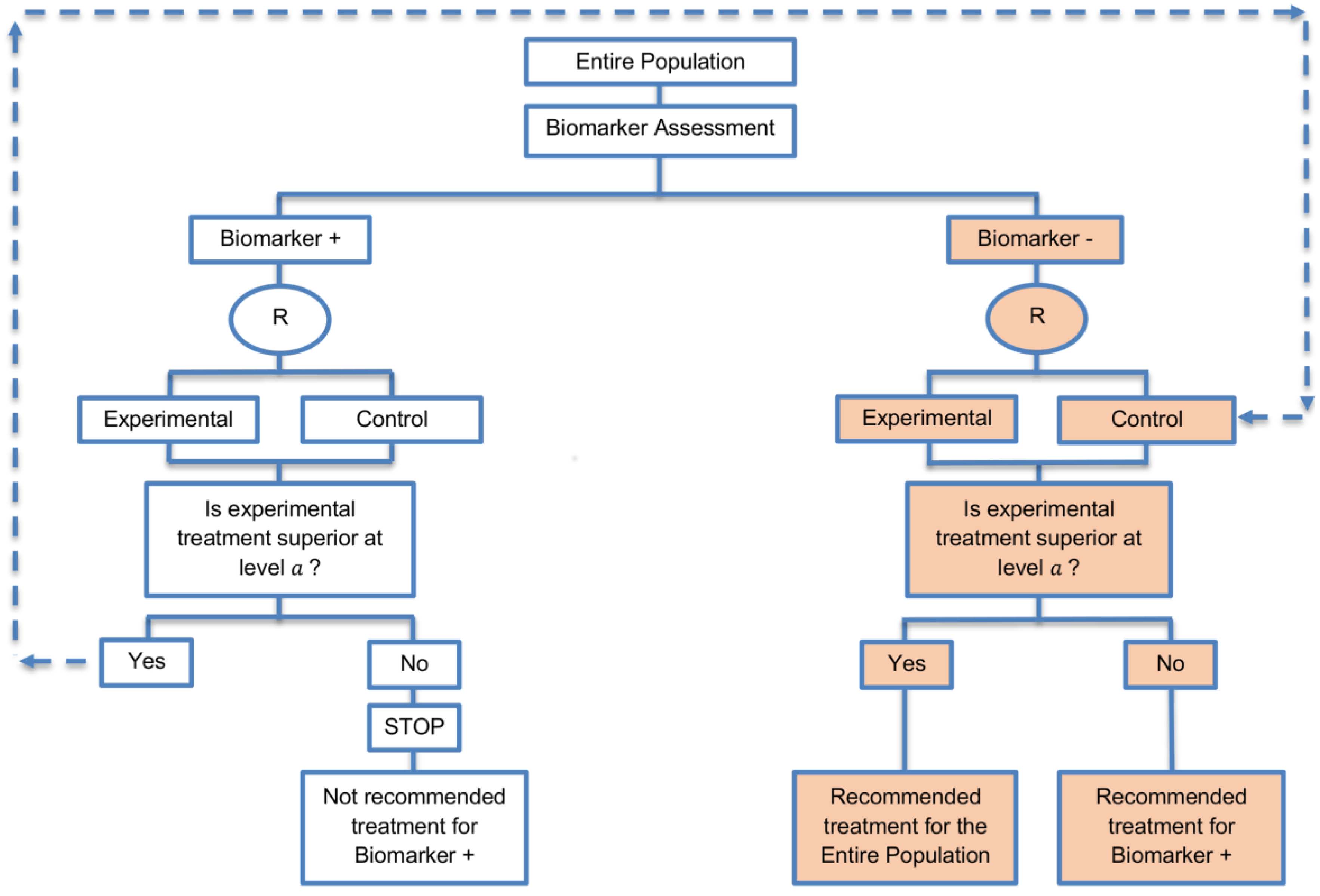
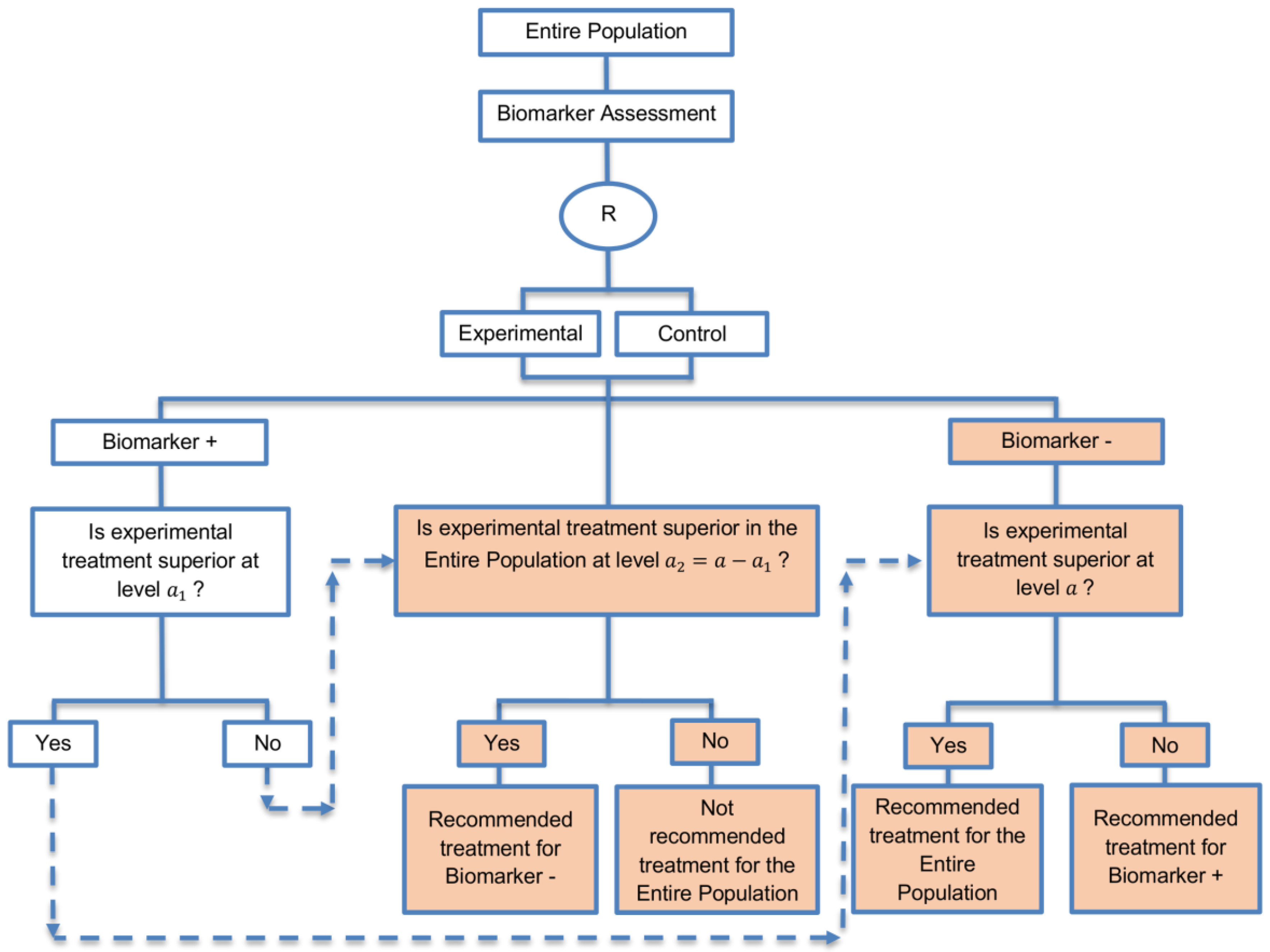
| Biomarker-positive and overall strategies with parallel assessment (8 papers) [1,14,36,47,49,69,95,96] (see Figure 7) | Recommended when the aim of the study is to assess the treatment effect in both the entire population and in the biomarker-positive subset but not in the biomarker-negative population. | (A18) Can control the overall type I error . | (L16) Can be overly conservative as in the SATURN trial because of the correlation between the test of treatment effect in the overall study population and in the biomarker subgroups. |
| Also called: Overall/biomarker-positive design with parallel assessment, prospective subset design, hybrid design | (A19) Can require smaller sample size as compared to the subgroup-specific designs, especially when we assume that the novel treatment equally benefits both biomarker-defined subgroups. | (L17) Cannot control the probability of rejecting the null hypothesis of no treatment effect in the biomarker-negative subset when the treatment benefit is restricted to biomarker-positive patients. Consequently, there is a high risk of inappropriately recommending the novel treatment for biomarker-negative patients due to the large treatment effect in biomarker-positive subset. | |
| Examples of actual trials: S0819 [14,49], SATURN [14,36,47,49,95,96], MONET1 [14,49], ARCHER [14,49], ZODIAC [49], MERiDiAN [49] | |||
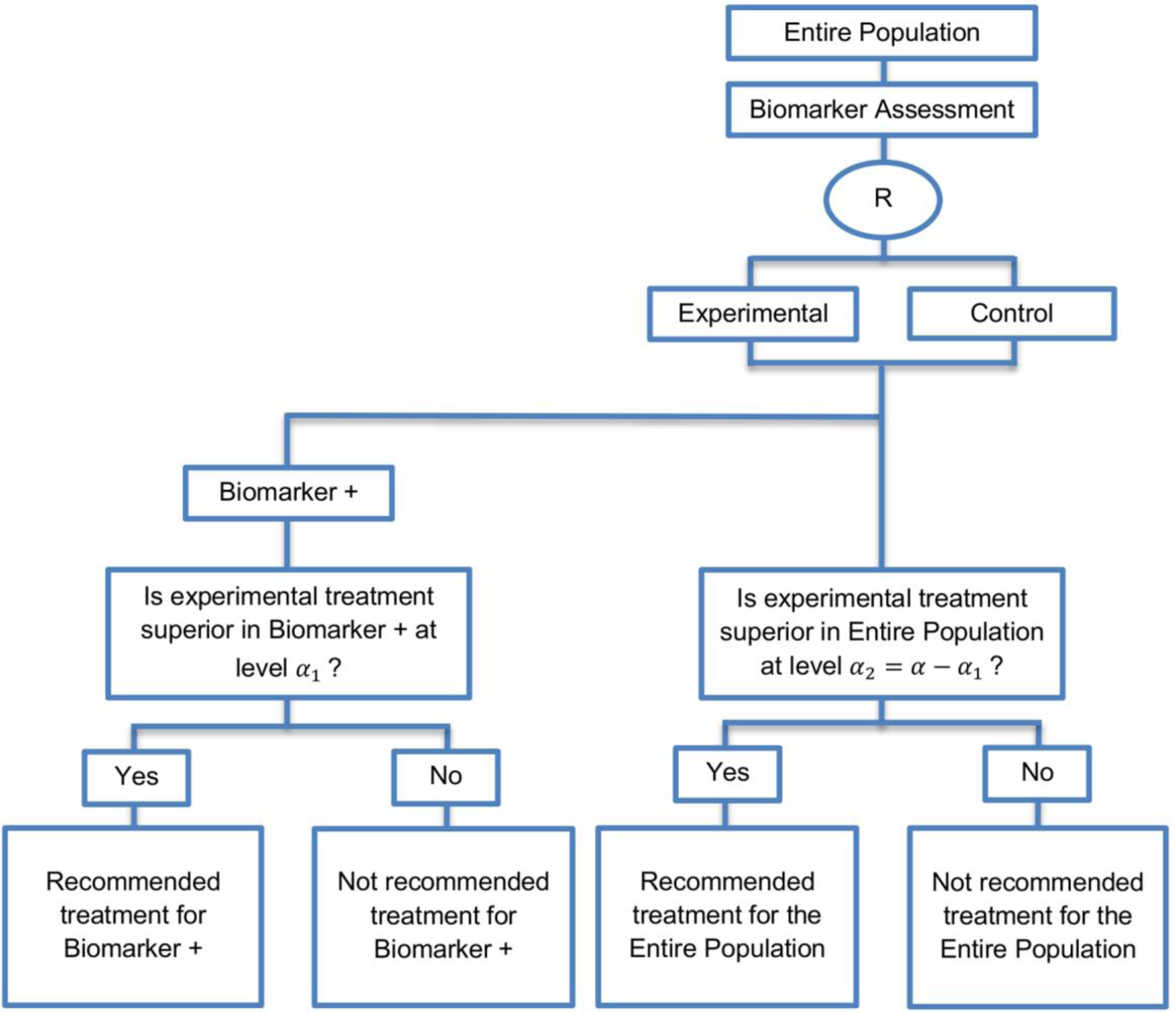
| Biomarker-positive and overall strategies with sequential assessment (11 papers) [13,14,30,44,49,69,80,84,85,88,94] (see Figure 8) | Might be useful in cases where the experimental treatment is expected to be effective in the overall population. | (A20) Same as (A18), (A19) | (L18) Can be problematic for determining whether the treatment is beneficial in the biomarker-negative subgroup. |
| Also called: Overall/biomarker-positive design with sequential assessment, sequential design, Fixed-sequence 2 design, hierarchical fixed sequence testing procedure | (L19) Same as (L17) | ||
| Examples of actual trials: Trial of letrozole plus lapatinib versus letrozole plus placebo in breast cancer, with the biomarker defined by human epidermal growth factor receptor 2 (HER2) [14], N0147 [30,49] | |||
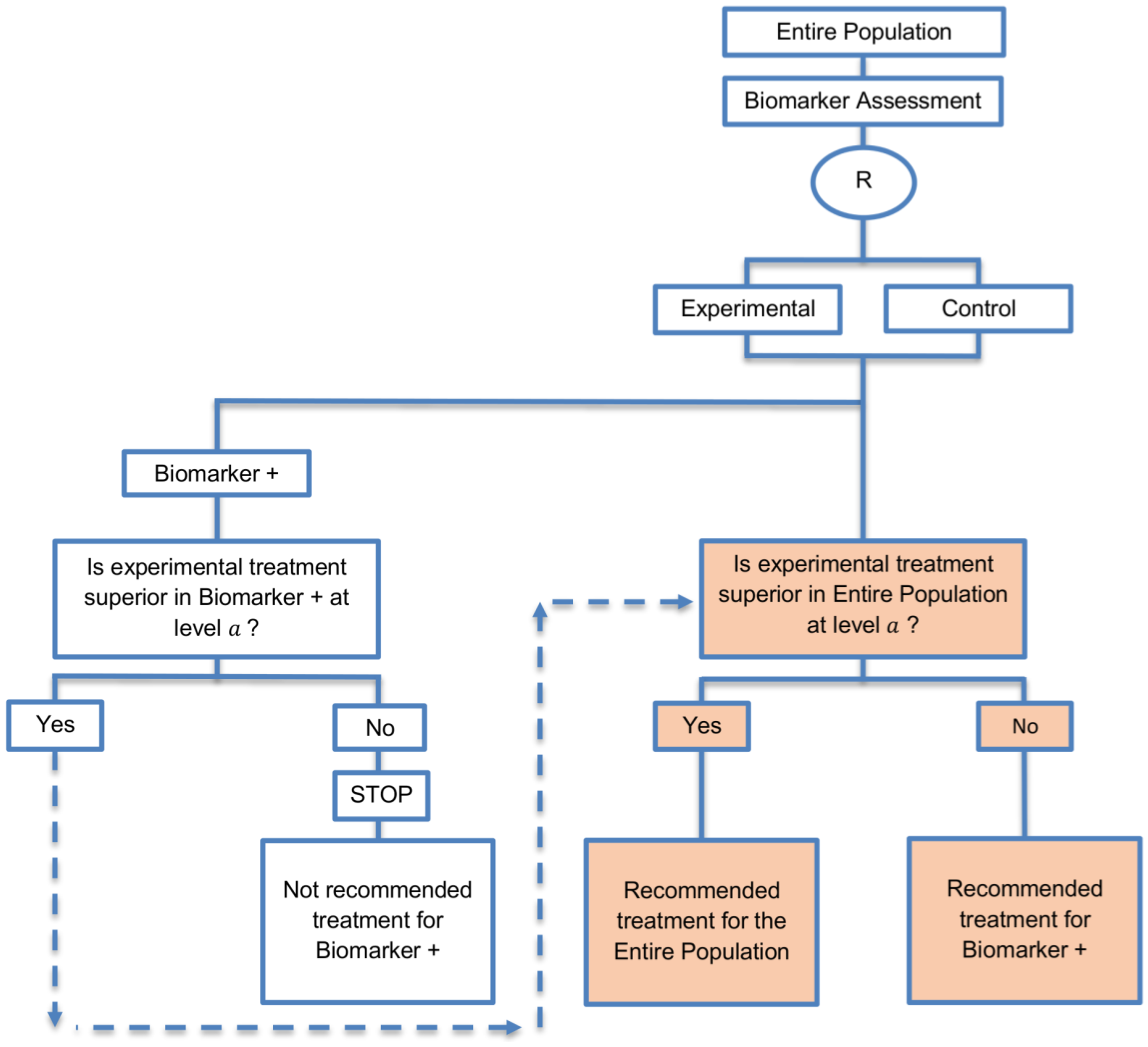
| Biomarker-positive and overall strategies with fall-back analysis (15 papers) [10,30,36,44,47,49,53,57,60,69,84,88,94,96,97] (see Figure 9) | Recommended when there is insufficient confidence in the predictive value of the biomarker and the novel treatment is assumed to probably benefit all patients. | (A21) Can assess the treatment effect in the biomarker-positive patients, if no benefit is detected in the overall population. | (L20) Same as (L17), (L18) |
| Also called: Biomarker-stratified design with fall-back analysis, fall-back design, prospective subset design, sequential design, other analysis plan design, Fallback design | (A22) Same as (A18), (A19) | ||
| Examples of actual trials: None identified a | |||
| Marker Sequential test design (4 papers) [14,49,69,94] (see Figure 10) | Recommended when biomarkers with strong credentials are available and we have convincing evidence that the novel treatment is more effective in biomarker-positive than in biomarker-negative patients. | (A23) Can provide clear evidence of treatment benefit in the biomarker-positive subgroup and in the biomarker-negative subgroup. | (L21) In situations where biomarker status is not available for some of the patients included in the study, this design can either exclude these patients or include them in the global test, however, further statistical adjustments might be required in that case. |
| Also called: MaST design, hybrid design | Appropriate when we can assume that the treatment will not be beneficial in the biomarker-negative subpopulation unless it is effective for the biomarker-positive subpopulation. | (A24) Enables sequential testing of the treatment effect in the entire study population and in the biomarker-defined subgroups to restrict testing of the treatment effect in the entire population when there is no significant result in the biomarker-positive subset, while controlling the appropriate type I error rates. | (L22) Does not decrease the sample size of the study as it was developed in order to increase the power compared to the sequential subgroup-specific design in situations where the novel treatment benefits equally both biomarker-negative and biomarker-positive patients. |
| Examples of actual trials: ECOG E1910 [14,49] | (A25) Results in higher power as compared to the sequential subgroup-specific design in cases where the treatment effect is homogeneous across the biomarker-defined subgroups. | ||
| (A26) Preserves the power in situations where the treatment effect is restricted only to the biomarker-positive patients and at the same time it controls the relevant type I error rates. | |||
| (A27) Control the type I error rate for the biomarker-negative subgroup over all possible prevalence values. | |||
| (A28) The probability of erroneously concluding that the novel treatment is beneficial for the entire population when the global effect is driven by the biomarker-positive patients is minimized since the design only tests the treatment effect in the entire population when no significant effect is detected in the biomarker-positive subgroup. | |||
| Hybrid designs (14 papers) [1,13,15,29,30,31,36,46,48,55,66,84,88,98] (see Figure 11) | Can be used when there is prior evidence indicating that only a particular treatment is beneficial to a biomarker-defined subgroup which makes it unethical to randomize patients with that specific biomarker status to other treatment options. | (A29) The feasibility of a prognostic biomarker can be tested. | None found. |
| Also called: Mixture design, Combination of trial designs, hybrid biomarker design | (A30) Allows for better risk assessment and improved individualized treatment since it assigns patients to treatments based on risk assessment scores instead of their biomarker status (biomarker-positive and biomarker-negative patients). | ||
| Examples of actual trials: TAILORx [15,48,55,58,63,66], EORTC MINDACT [15,48,55,66], ECOG 5202 study [30,46] | |||
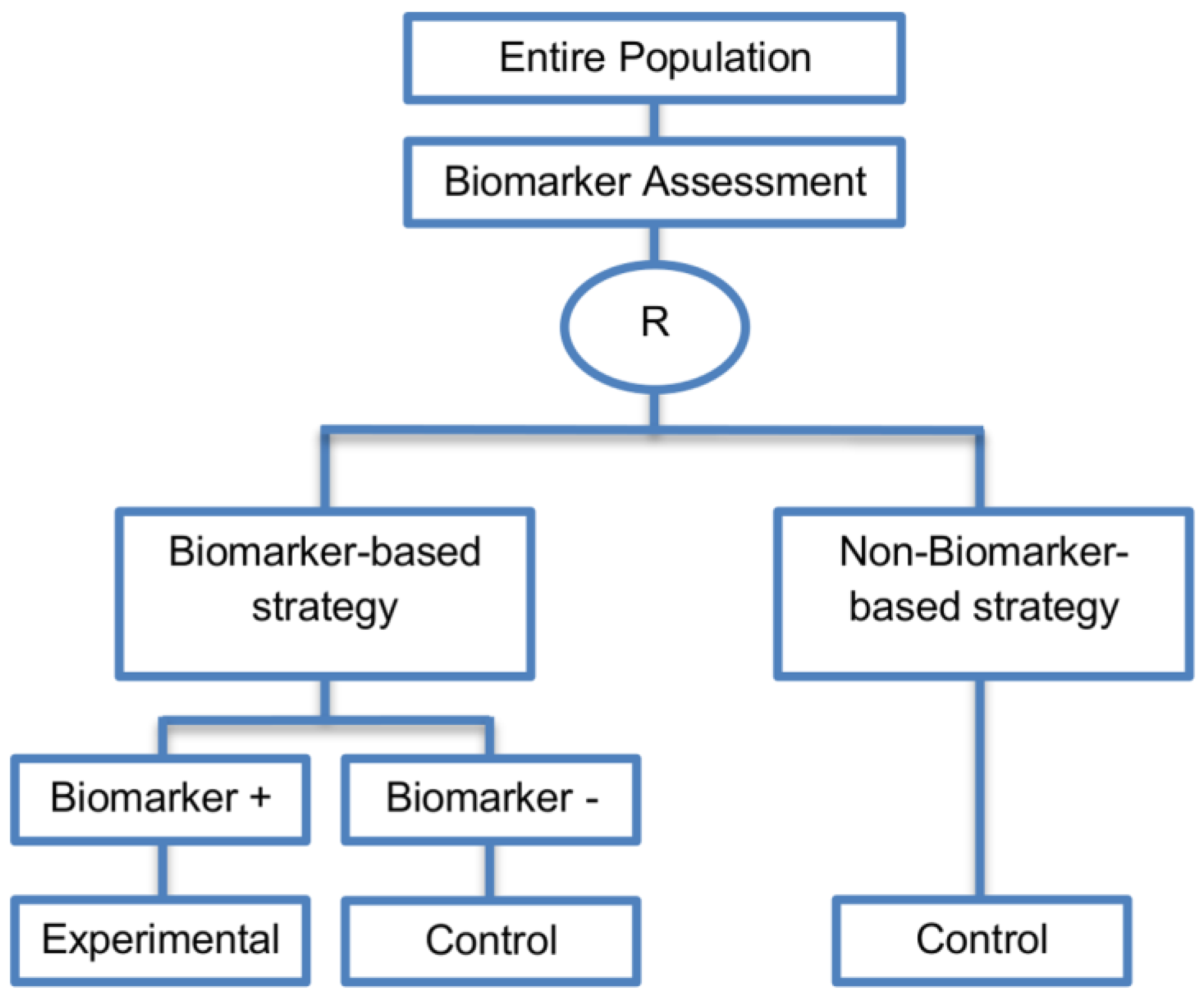
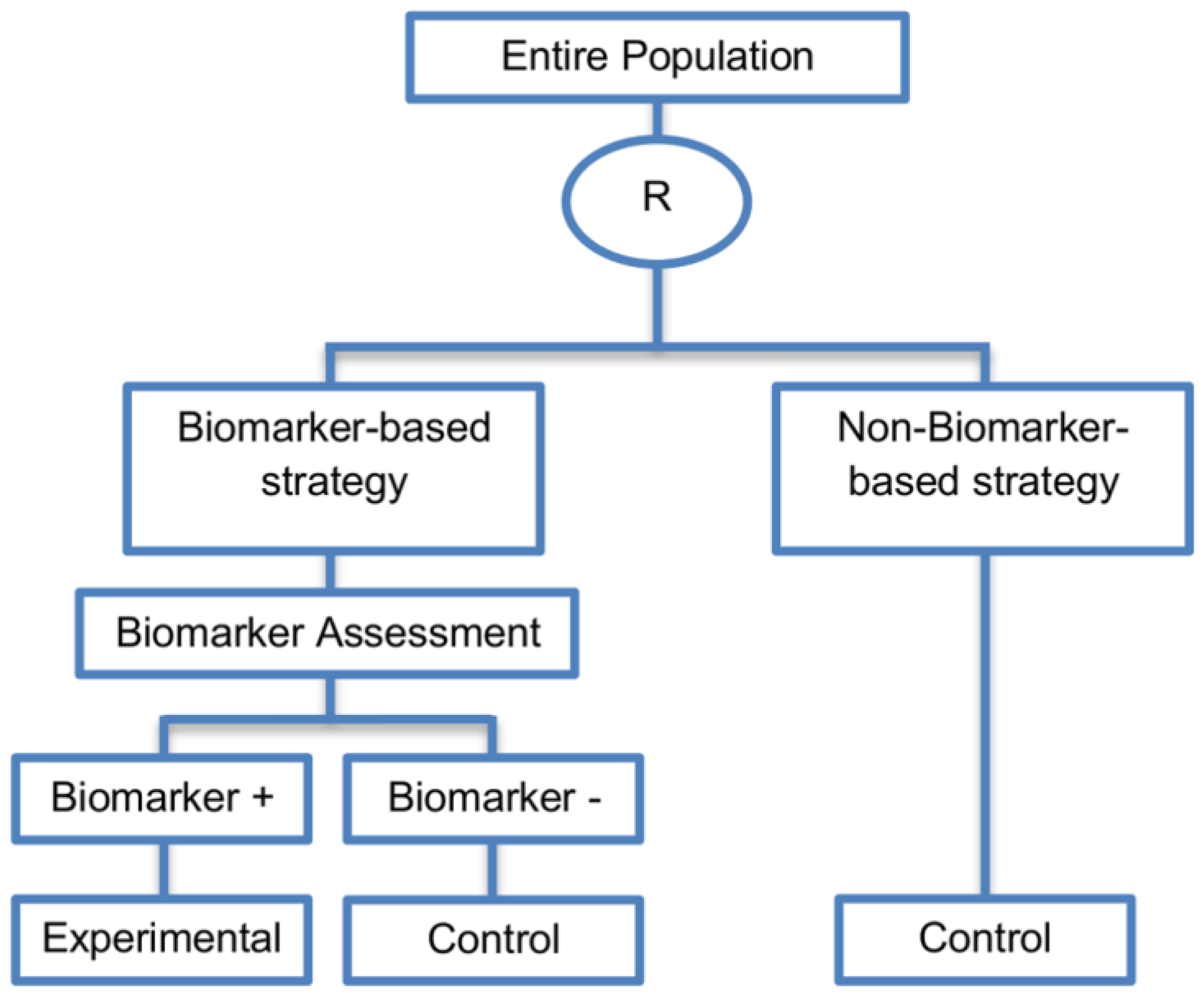
| Biomarker-strategy designs with biomarker assessment in the control arm (21 papers) [15,25,26,32,33,36,45,61,62,64,79,82,85,86,92,93,99,100,101,102,103] (see Figure 12) | Useful when we want to test the hypothesis that the treatment effect based on the personalized approach is superior to that of the standard of care. | (A31) Biomarker can be validated without including all possible biomarker–treatment combinations [26] as in the non-biomarker-based arm all patients receive only the control treatment. | (L23) Unable to inform us whether the biomarker is predictive as these designs are able to answer the question about whether the biomarker-based strategy is more effective than standard treatment, irrespective of the biomarker status of the study population. |
| Also called: Marker strategy design, Biomarker-strategy design, Strategy design, Marker-based strategy design, Marker-based design, Random disclosure design, Customized strategy design, Parallel controlled pharmacogenetic study design, Marker-based strategy design I, Biomarker-guided design, Biomarker-based assignment of specific drug therapy design, Marker-based strategy I design, Biomarker-strategy design with a standard control, Marker strategy design for prognostic biomarkers | (A32) Have the option of testing the biomarker status of patients in the non-biomarker-strategy arm which can aid secondary analyses [26]. | (L24) The evaluation of the true biomarker by treatment effect is not possible as the biomarker-positive patients receive only the experimental treatment and not the alternative treatment (control treatment). Consequently, this design cannot detect the case in which the control treatment might be more beneficial for the entire population. | |
| Examples of actual trials: GILT docetaxel [15], Randomized phase III trial conducted in Spain, dedicated to patients with advanced Non-Small Cell Lung Cancer (NSCLC) candidates for first-line chemotherapy [32,64,100], Study the effect of Magnetic Resonance Imaging (MRI) in patients with low back pain on patient outcome and to evaluate Doppler US of the umbilical artery in the management of women with intrauterine growth retardation (IUGR), Randomized controlled trial in recurrent platinum-resistant ovarian carcinoma [101] | (A33) Able to inform us whether the biomarker is prognostic. | (L25) In case that the number of biomarker-positive patients is very small, then the treatment received will be similar in biomarker-strategy arm and non-biomarker strategy arm. Consequently, the trial might give little information regarding the efficacy of the experimental treatment or it might not be able to detect it. As a result, this type of design should be used when there is an adequate number of biomarker-positive and biomarker-negative patients. | |
| (A34) Can be expanded to investigate several biomarkers and treatments [103]. Additionally, these designs can be attractive when evaluating multiple biomarkers or the predictive value of molecular profiling between several treatment options is to be assessed [45]. | (L26) Unable to compare directly experimental treatment to control treatment as the aim is to compare not the treatments but the biomarker-strategies. | ||
| (A35) Might be used more frequently in the future due to the wide variety of molecular biomarkers, complexity of gene expression arrays, and several treatments directed at similar targets [103]. | (L27) Less efficient designs than biomarker-stratified designs [4,73] and a poor substitute for clinical trials which aim to compare the experimental treatment to control treatment, since it is possible for some patients in both the biomarker-based strategy arm and non-biomarker-based strategy arm to be assigned to the same treatment (due to the existence of biomarker-negative patients in both strategy arms the treatment effect can be diluted) [51]. Consequently, as a large overlap of patients receiving the same treatment might have occurred, the comparison of the two biomarker-strategy arms results in a hazard ratio which is forced towards unity, i.e., no treatment effect exists as the effect of experimental versus control treatment is diluted by the biomarker-based treatment selection. For this reason, a large sample size is needed to detect at least a small overall difference in outcomes between the two biomarker-strategy arms. | ||
| (L28) Should be used only if you want to evaluate a complex biomarker-guided strategy with a variety of treatment options or biomarker categories [73]. | |||
| Biomarker-strategy design without biomarker assessment in the control arm (14 papers) [9,13,17,18,20,25,36,38,61,74,101,104,105,106] (see Figure 13) | In situations where it is not feasible or unethical to test the biomarker in the entire population. | (A36) Galanis et al., 2011 [45] stated that these designs can be attractive when evaluating multiple biomarkers or the predictive value of molecular profiling between several treatment options is to be assessed. Also, Freidlin and Korn, 2010 [73] claimed that these biomarker-strategy designs should be used only if researchers want to evaluate a complex biomarker-guided strategy with a variety of treatment options or biomarker categories. | (L29) Criticized for their potential cost increase due to the fact that patients without predicted responsive biomarker are double enrolled in the trial (biomarker-negative patients receive control treatment in both strategy arms). |
| Also called: Biomarker-strategy design with standard control, Direct-predictive biomarker-based, RCT of testing, Test-treatment, Parallel controlled pharmacogenetic diagnostic study, Marker strategy, Marker-based with no randomization in the non-marker-based arm, Classical, Marker-based strategy, Marker strategy design for prognostic biomarkers | (A37) Same as (A31), (A32), (A33) | (L30) Biomarker-positive and biomarker-negative subpopulations might be more imbalanced as compared with the first type of biomarker-strategy design due to the fact that the randomization to different treatment strategies is performed before the evaluation of the biomarker status (balancing the randomization is useful to ensure that all randomized patients have tissue available). This can happen especially when the number of patients is very small. | |
| Examples of actual trials: A study, which evaluated the use of immediate computed tomography in patients with acute mild head injury [101,104]. | (L31) Same as (L23), (L24), (L25), (L26), (L27) | ||
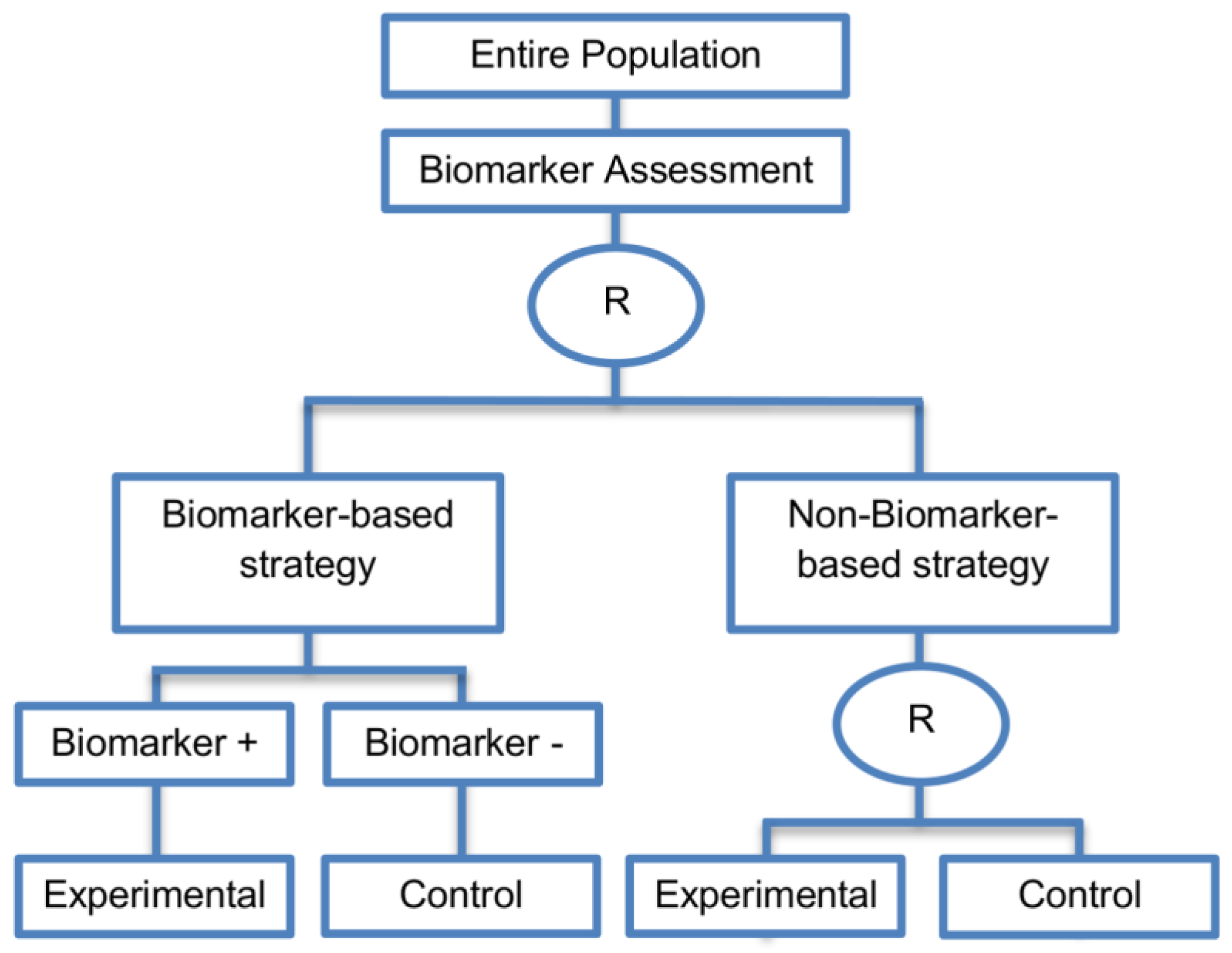
| Biomarker-strategy design with treatment randomization in the control arm (17 papers) [15,17,26,27,32,36,45,62,64,66,74,86,92,93,106,107,108] (see Figure 14) | In cases where we want to know whether the biomarker is not only prognostic but also predictive, these designs are preferable as compared to the two previously mentioned biomarker-strategy designs. | (A38) These designs have the ability to inform researchers about the potential superiority of the control treatment in the whole population or among a particular biomarker-defined subpopulation. | (L32) Generally require a larger sample size as compared to the marker-stratified designs. |
| Also called: Biomarker-strategy design with a randomized control, Modified marker-based strategy design (for predictive biomarkers), Biomarker-strategy design with randomized control, Marker-based design with randomization in the non-marker-based arm, Marker-based strategy design II, Marker-strategy design, Augmented strategy design, Trial design allowing the evaluation of both the treatment and the marker effect | (A39) Able to inform us whether the biomarker is prognostic or predictive. | (L33) Same as (L27) | |
| Examples of actual trials: None identified a | (A40) Allow clarification of whether the results which indicate efficacy of the biomarker-directed approach to treatment are caused due to a true effect of the biomarker status or to an improved treatment irrespective of the biomarker status. | ||
| (A41) Same as (A36) | |||
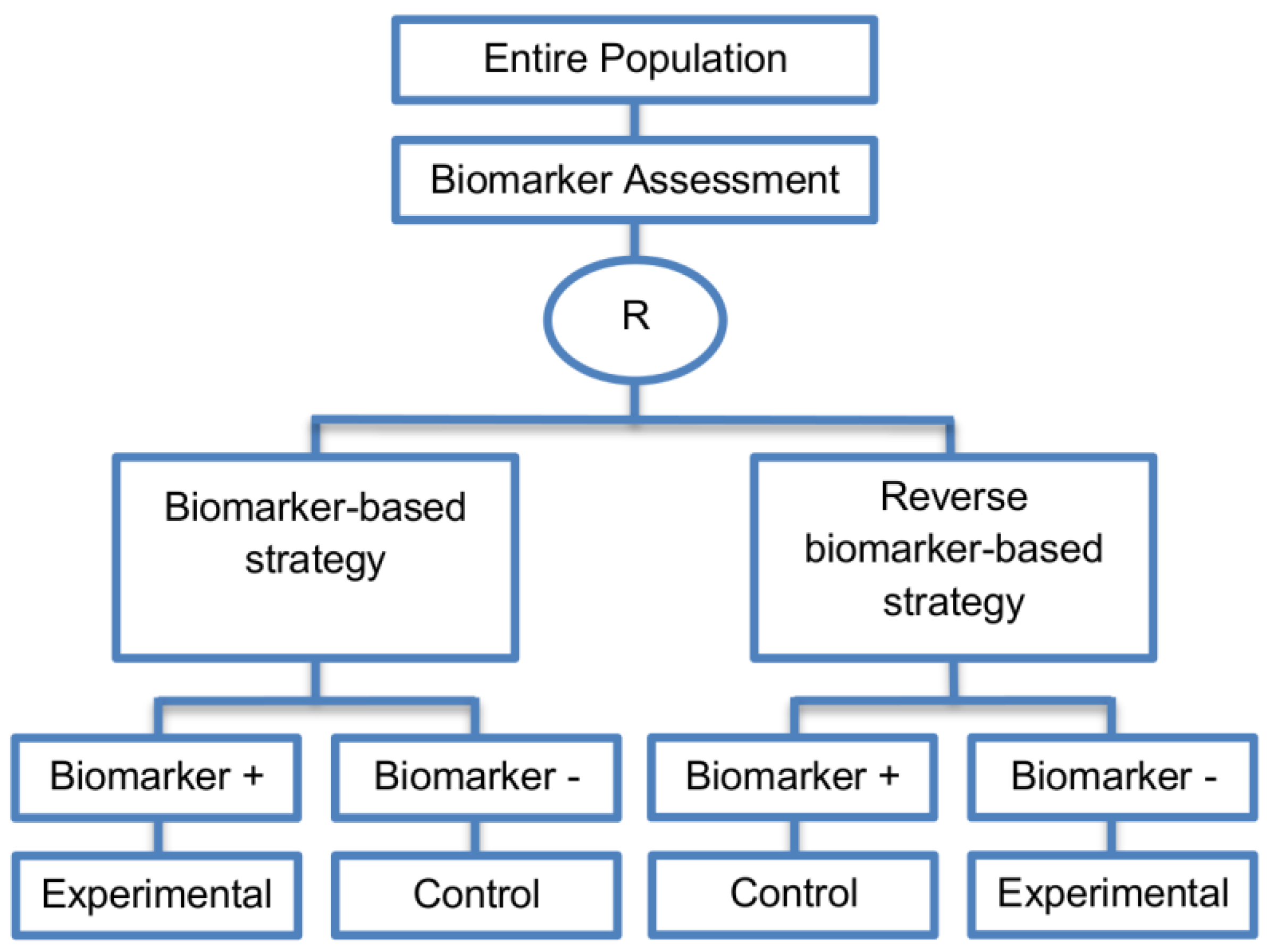
| Reverse marker-based strategy (4 papers) [86,92,93,109] (see Figure 15) | Enables testing the interaction hypothesis of treatment and biomarker in a more efficient way as compared to the first (i.e., Biomarker-strategy design with biomarker assessment in the control arm) and third biomarker-strategy subtype design (i.e., Biomarker-strategy design with randomization in the control arm and the marker stratified design) | (A42) Can estimate directly the marker-strategy response rate. | (L34) It has been claimed by Baker, 2014 [93] that other designs than the reverse marker-based strategy are more appropriate in order to investigate questions which include both treatment effect of biomarker-defined subgroups and the biomarker strategy treatment effect. These designs should allow the estimation of treatment effects within biomarker-defined subgroups as well as the estimation of the global treatment effect. |
| Also called: None found | (A43) Allows the estimation of the effect size of the experimental treatment compared to the control treatment for each biomarker-defined subset separately. | ||
| Examples of actual trials: None identified a | (A44) There is no chance that the same treatment will be tailored to biomarker-positive patients who are randomized either to the biomarker-based strategy arm or the reverse marker strategy. Also, there is no possibility of the same treatment assignment to biomarker-negative patients who are randomly assigned to the two biomarker-based strategy arms. | ||
| (A45) It has been demonstrated by Eng, 2014 [92] that this new type of design is more than four times more efficient for testing the interaction between treatment and biomarker compared to Biomarker-strategy design with biomarker assessment in the control arm, Biomarker-strategy design with randomization in the control arm and the marker stratified design. | |||
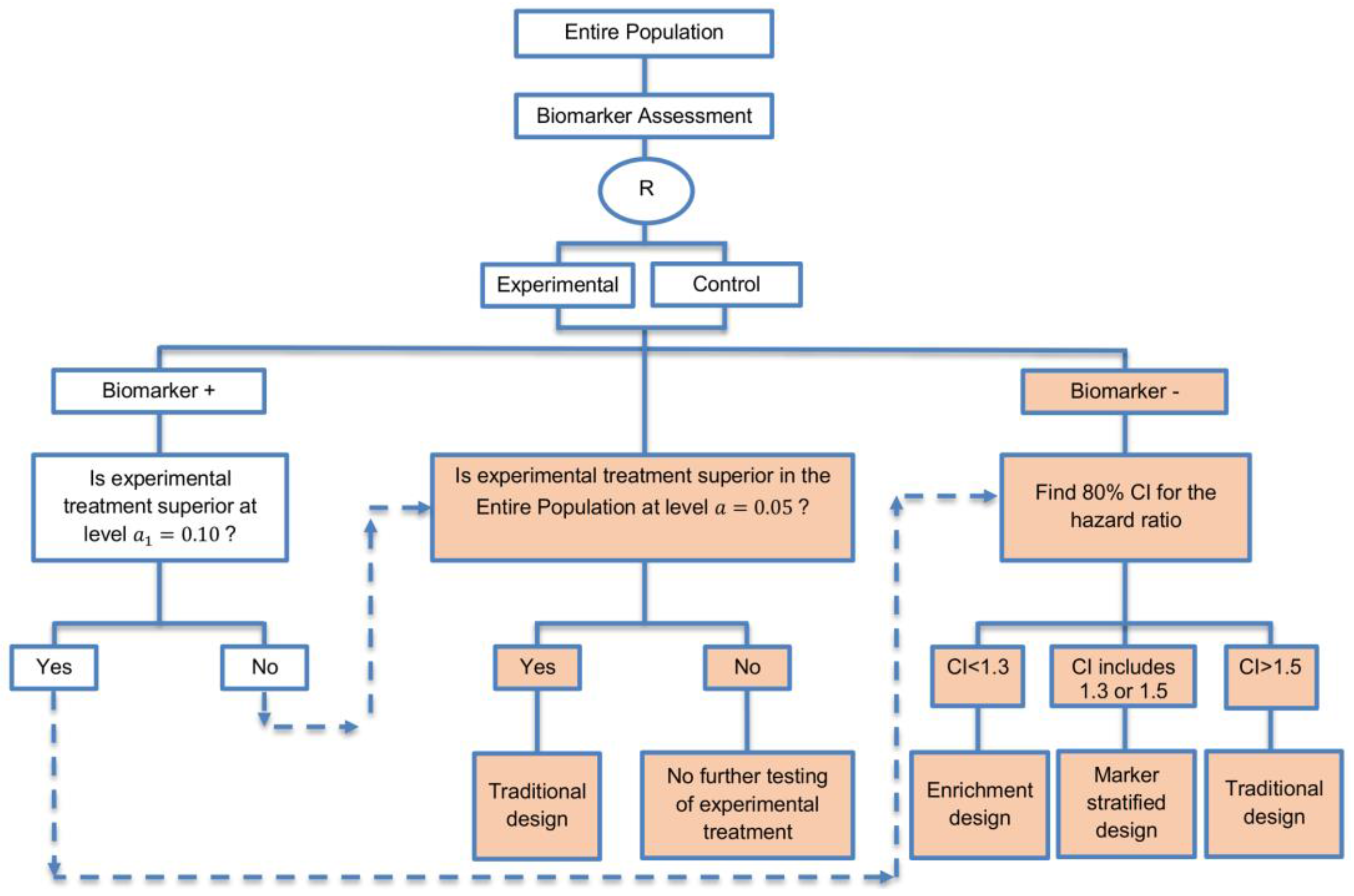
| A specific randomized phase II trial design that can be used to guide decision making for further development of an experimental therapy. (1 paper) [71] (see Figure 16) | Recommended when we want to conduct a Phase II randomized trial which allows decisions to be made about which type of Phase III biomarker-guided trial should be used. | (A46) Works well in providing recommendations for phase III trial design. | None found |
| Types of Biomarker-Guided Non-Adaptive Trial Designs | Sample Size Formula | Definition |
|---|---|---|
| Single arm designs | Standard sample size formula can be used, more information can be found in the ‘methodology’ part of the ‘Single arm designs’ section in the main text. | |
| Enrichment designs [55,61,65,110,111,112] | Online tool for sample size calculation when using either binary or time-to-event endpoints is available on the following website: http://brb.nci.nih.gov/brb/samplesize/td.html [113]. | |
| is referred to the expected number of events per treatment arm (time-to-event outcome), corresponds to either the experimental or the control treatment group, ratio between the two treatment arms (experimental:control) is assumed, corresponds to the event hazard rate, is the loss to follow-up rate, denotes the accrual time, patients enter the trial according to a Poisson process with rate per year over the accrual period of years, τ corresponds to the follow-up period. | ||
| is referred to the required total number of events (time-to-event outcome), ratio between the two treatment arms (experimental:control) is assumed, denote the upper - and upper -points respectively of a standard normal distribution, and denote the assumed type I error and type II error respectively, denotes the assumed hazard ratio between the two treatment groups (control vs experimental) in the biomarker-positive subset. | ||
| is referred to the required number of patients per treatment arm (binary outcome), ratio between the two treatment arms (experimental:control) is assumed, and are the response probabilities in the experimental and control groups respectively, . | ||
| is referred to the required total number of patients per treatment arm (continuous response endpoints), ratio between the two treatment arms (experimental:control) is assumed, denotes the anticipated common variance, and the mean responses for biomarker-positive patients in the experimental and control treatment arm respectively. | ||
| is referred to the required total number of patients per treatment arm (continuous response endpoints when accounting for error in the assaying of the study population), ratio between the two treatment arms (experimental:control) is assumed, measures the accuracy of the assay and corresponds to the PPV (positive predictive value of the assay, i.e., the proportion of patients who are assigned biomarker positive status according to the assay who are truly biomarker positive), is the treatment effect in the biomarker-positive patients and (where is the treatment effect in the biomarker-negative patients). | ||
| Marker Stratified designs [31,53,60,92,111,112,114] | Online tool for sample size calculation when using either binary or time-to-event endpoints is available on the following website: http://brb.nci.nih.gov/brb/samplesize/sdpap.html [115]. | |
| is referred to the required total number of events for the achievement of sufficient power in each biomarker-defined subgroup separately (time-to-event endpoint), ratio between the two treatment arms (experimental:control) is assumed, corresponds to the hazard ratio of biomarker-negative subgroup, . | ||
| is referred to the required total number of events for the achievement of sufficient power in the overall population (time-to-event endpoint), is the proportion biomarker-positive patients, ratio between the two treatment arms (experimental:control) is assumed. | ||
| is referred to the required total number of patients for the achievement of sufficient power in the overall population (time-to-event endpoint), ratio between the two treatment arms (experimental:control) is assumed, , are the probabilities of an event in biomarker-positive subset and biomarker-negative subset respectively. | ||
| is referred to the ratio of the required number of events between marker stratified and enrichment design (time-to-event endpoint). | ||
| is referred to the ratio of the required number of patients between marker stratified and enrichment design (binary outcome), , , correspond to the treatment effectiveness in biomarker-negative and biomarker-positive subgroup respectively. | ||
| is referred to the required total number of patients (binary outcome), denotes a baseline effect, denotes the added effect of the experimental treatment, denotes the biomarker-positive effect and denotes the nonadditive effect, corresponds to the target level, corresponds to the power, are the assumed response rates of biomarker-positive patients receiving the experimental and the control treatment respectively, are the assumed response rates of biomarker-negative patients receiving the experimental and the control treatment respectively. | ||
| Sequential Subgroup-Specific design [57] | is referred to the required number of biomarker-positive patients (binary outcome), is the required number of biomarker-positive patients (binary outcome) in the enrichment design. | |
| is referred to the required total number of patients (binary outcome), is the required number of biomarker-positive patients (binary outcome) in the enrichment design. | ||
| is referred to the required number of biomarker-negative patients (binary outcome), is the required number of biomarker-positive patients (binary outcome) in the enrichment design. | ||
| is referred to the required number of events for biomarker-positive patients (time-to-event outcome), is the required number of events for biomarker-positive patients (time-to-event outcome). | ||
| is referred to the required number of events for biomarker-negative patients (time-to-event outcome), is the required number of events for biomarker-positive patients (time-to-event outcome), , , are the event rates in biomarker-negative and biomarker-positive control subgroups. | ||
| Parallel Subgroup-Specific design | Same formula proposed for marker stratified designs could be considered to achieve sufficient power in each biomarker-defined subgroup simultaneously. However, in order to control the overall type I error rate of the design at the overall level of significance it is required to allocate this overall between the test for the biomarker-positive subgroup and the test for the biomarker-negative. Consequently, for biomarker-positive subgroup the reduced significance level can be used whereas the reduced significance level can be used for biomarker-negative subgroup. | |
| Biomarker-positive and overall strategies with parallel assessment | If there is significant confidence that the biomarker is predictive, the sample size estimation is aimed at having a sufficient number of biomarker-positive individuals to enable the treatment effect in the biomarker positive subgroup to be detected. Standard formula for sample size calculation of biomarker-positive subgroup proposed for the enrichment designs could be considered by using the reduced significance level . On the other hand, if there is no confidence in the predictive value of the biomarker, the sample size estimation is aimed at having a sufficient number of patients to detect a treatment effect in the overall study population; consequently, for the sample size calculation, the same formula proposed for marker stratified designs aiming to achieve sufficient power in the overall population could be applied by using the reduced significance level . | |
| Biomarker-positive and overall strategies with sequential assessment | At the first stage, the standard formula for a traditional randomized trial which is the same with the formula proposed for enrichment designs can be applied for the biomarker-positive subgroup. At the second stage, the sample size formula proposed for marker stratified designs aiming to yield appropriate power for the entire population could be considered. | |
| Biomarker-positive and overall strategies with fall-back analysis | At the first stage, the sample size formula proposed for marker stratified designs aiming to yield appropriate power for the entire population could be considered by using the reduced significance level . At the second stage, the formula proposed for enrichment designs could be applied for the biomarker-positive subgroup by using the reduced significance level . | |
| Marker Sequential test design (MaST) | A standard sample size calculation (i.e., the same sample size calculation as for the enrichment designs) can be applied for the biomarker-positive subpopulation. However, in order to have sufficient number of biomarker-positive patients to detect treatment effectiveness in that particular biomarker-defined subset and consequently to reach the desired power, the sample size should be calculated by using the reduced significance level instead of the global significance level which is used in the sample size formulae of the enrichment designs. The same formula could be considered for the sample size calculation of the biomarker-negative subgroup; however, the corresponding hazard ratio of that subgroup and the global significance level should be used. For the sample size calculation of the entire population, the same formula proposed for marker stratified designs aiming to achieve sufficient power in the overall population could be considered by using the reduced significance level . | |
| Biomarker-strategy, design with biomarker assessment in the control arm [26,61,92] | is referred to the required total number of events (time-to-event outcome), ratio between the two treatment arms (experimental:control) is assumed. | |
| is referred to the required total sample size (continuous clinical endpoints), ratio between the two treatment arms (experimental:control) is assumed, , denote the lower - and lower -points respectively of a standard normal distribution, and denote the mean response from the biomarker-based strategy arm and the non-biomarker-based strategy arm respectively, and denote the variance of response for the biomarker-based strategy arm and non-biomarker-based strategy arm respectively. | ||
| is referred to the required total number of patients per arm (binary outcome), is the expected response rate in the biomarker-based strategy arm, is the expected response rate in the non biomarker-based strategy arm, , can be found by calculating the formulae and respectively, denotes the marginal effect of treatment B (control treatment). | ||
| Biomarker-strategy design without biomarker assessment in the control arm | Same formulae as for the ‘Biomarker-strategy design with biomarker assessment in the control arm’ can be considered. | |
| Biomarker-strategy design with treatment randomization in the control arm [26,31,92] | is referred to the required total number of events (time-to-event outcome), ratio between the two treatment arms (experimental:control) is assumed, , denote the median survival for biomarker-positive and biomarker-negative patients receiving control and experimental treatments respectively. | |
| is referred to the required total sample size (continuous clinical endpoints), ratio between the two treatment arms (experimental:control) is assumed, denotes the mean response from the non-biomarker-based strategy arm, denotes the variance of response for the non-biomarker-based strategy arm respectively. | ||
| is referred to the required total number of patients per arm (binary outcome), is the expected response rate in the non biomarker-based strategy arm and , the expected response rate can be found by calculating the formula , denotes the marginal effect of treatment A (experimental treatment). | ||
| Reverse marker-based strategy [92] | is referred to the required total number of patients per arm (binary outcome), is the expected response rate in the reverse biomarker-based strategy arm and , the expected response rate can be found by calculating the formula , are the assumed response rates of biomarker-positive patients receiving the control treatment and biomarker-negative patients receiving the experimental treatment. | |
| Randomized Phase II trial design with biomarkers [71] | Online tool for sample size calculation is available on the following website: http://brb.nci.nih.gov/Data/FreidlinB/RP2BM [116]. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antoniou, M.; Kolamunnage-Dona, R.; Jorgensen, A.L. Biomarker-Guided Non-Adaptive Trial Designs in Phase II and Phase III: A Methodological Review. J. Pers. Med. 2017, 7, 1. https://doi.org/10.3390/jpm7010001
Antoniou M, Kolamunnage-Dona R, Jorgensen AL. Biomarker-Guided Non-Adaptive Trial Designs in Phase II and Phase III: A Methodological Review. Journal of Personalized Medicine. 2017; 7(1):1. https://doi.org/10.3390/jpm7010001
Chicago/Turabian StyleAntoniou, Miranta, Ruwanthi Kolamunnage-Dona, and Andrea L. Jorgensen. 2017. "Biomarker-Guided Non-Adaptive Trial Designs in Phase II and Phase III: A Methodological Review" Journal of Personalized Medicine 7, no. 1: 1. https://doi.org/10.3390/jpm7010001
APA StyleAntoniou, M., Kolamunnage-Dona, R., & Jorgensen, A. L. (2017). Biomarker-Guided Non-Adaptive Trial Designs in Phase II and Phase III: A Methodological Review. Journal of Personalized Medicine, 7(1), 1. https://doi.org/10.3390/jpm7010001






