Ordinal Regression Research Based on Dual Loss Function—An Example on Lumbar Vertebra Classification in CT Images
Abstract
1. Introduction
2. Related Work
2.1. Ordinal Regression Based on Binary Classification
2.2. Addressing Inconsistencies in Predicted Probabilities Across Ordinal Levels
2.3. Other Neural Network-Based Methods for Ordinal Regression
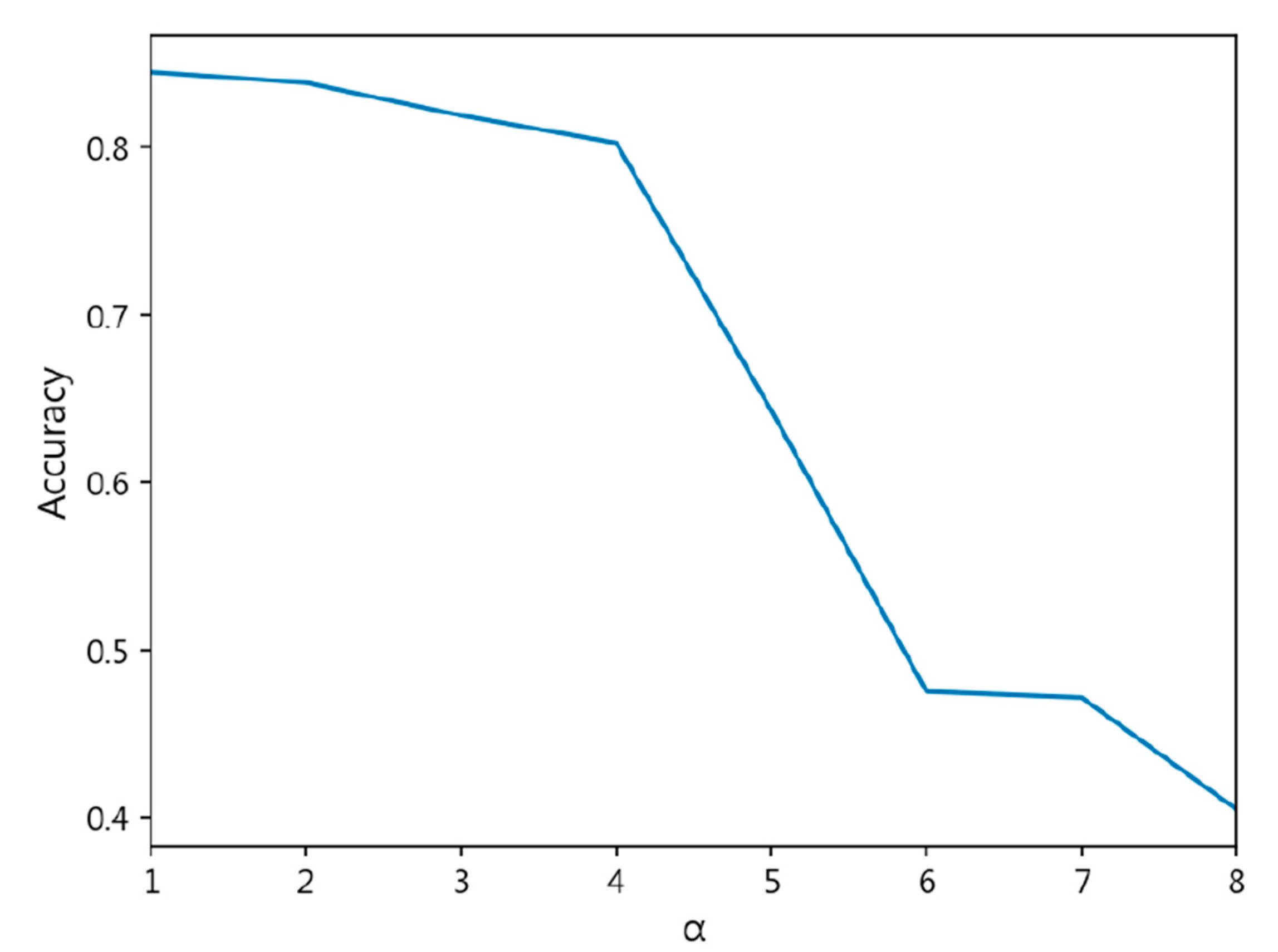
- The exponent a in the CDW-CE formula requires manual tuning of different values, making the process more time-consuming. Additionally, as a increases, the penalty intensity also increases, leading to higher loss values and longer training times.
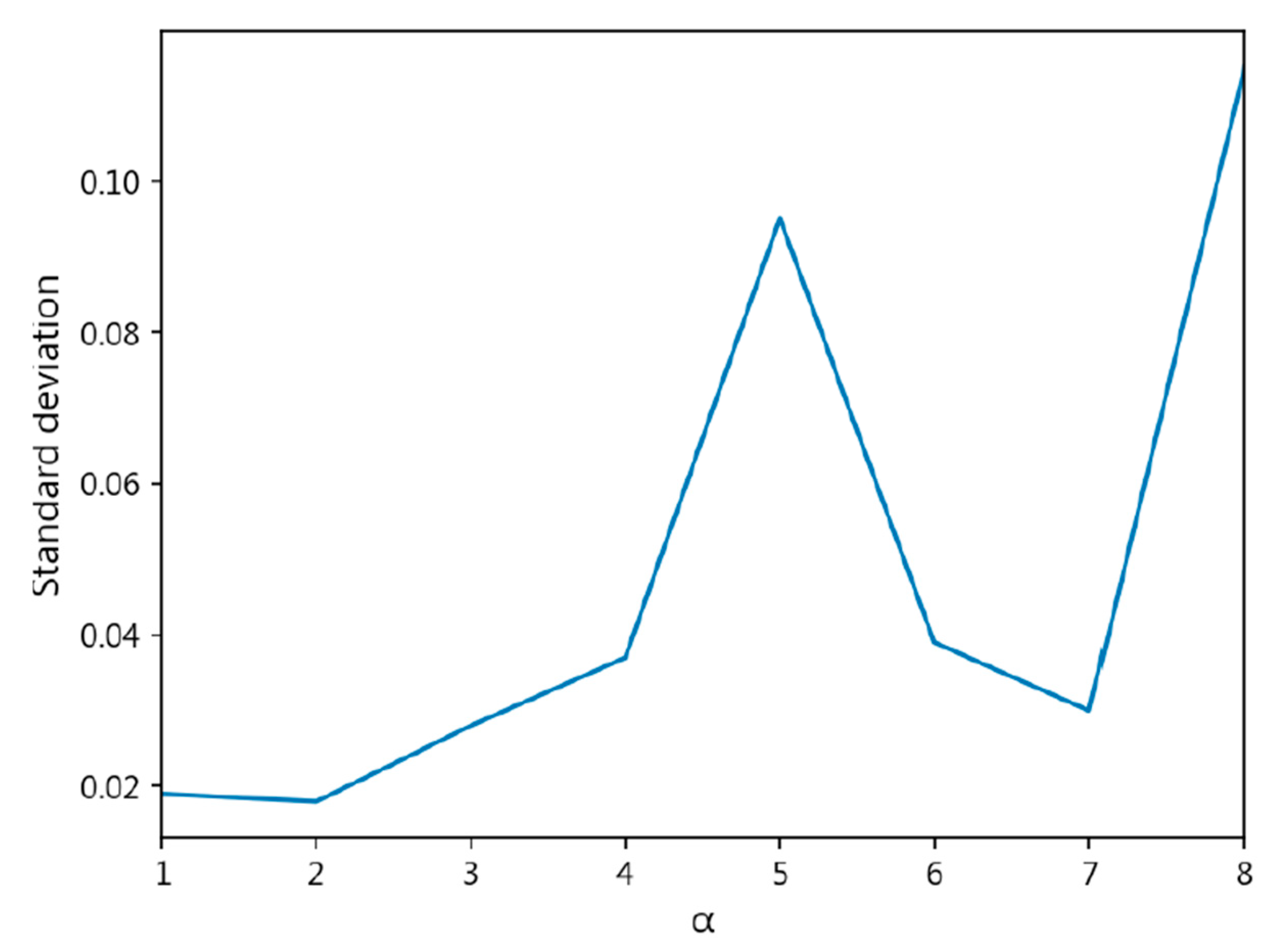
- Through cross-validation training, larger a values result in less stable training, with a significant increase in standard deviation.
3. Materials and Methods
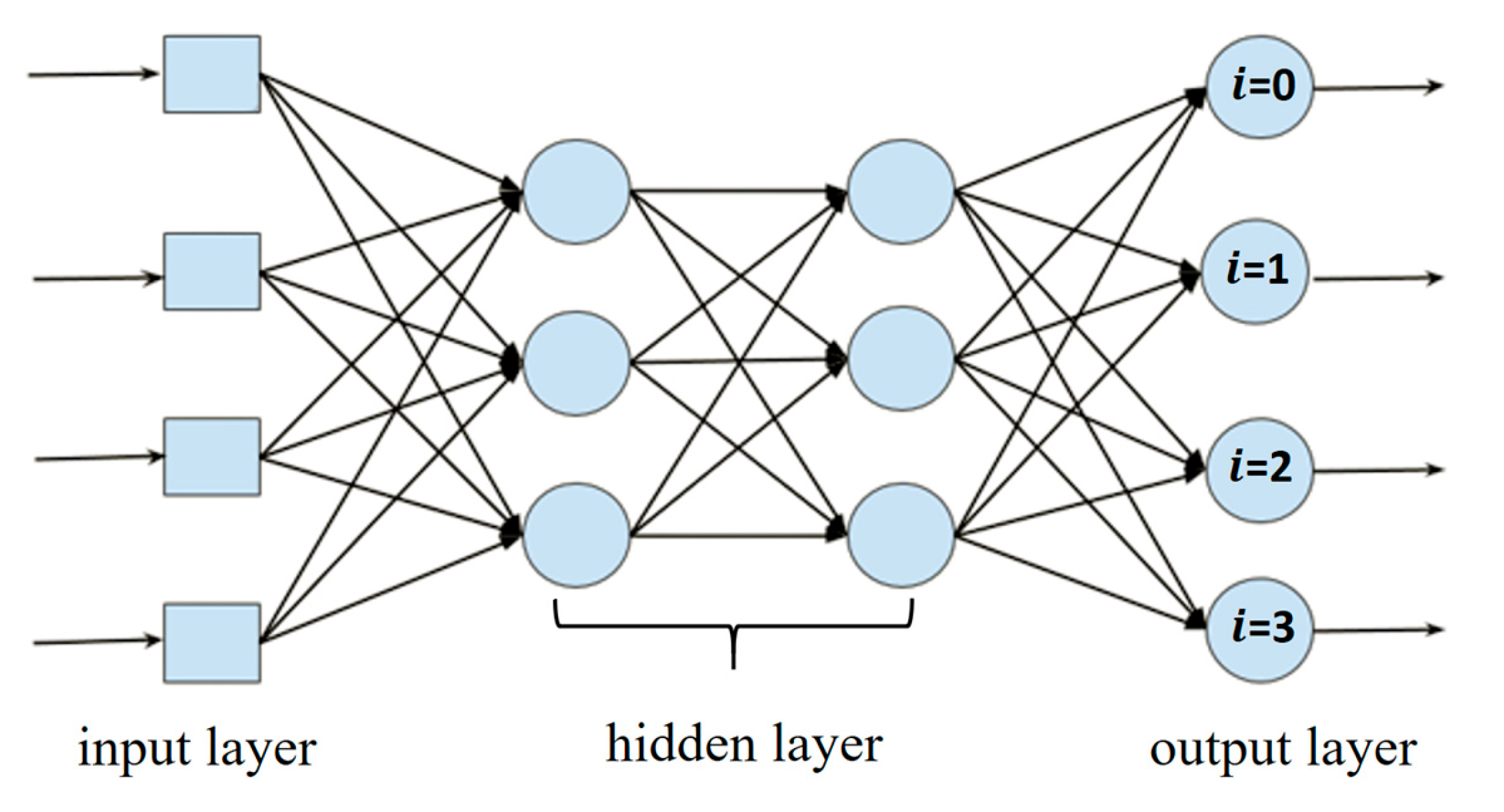
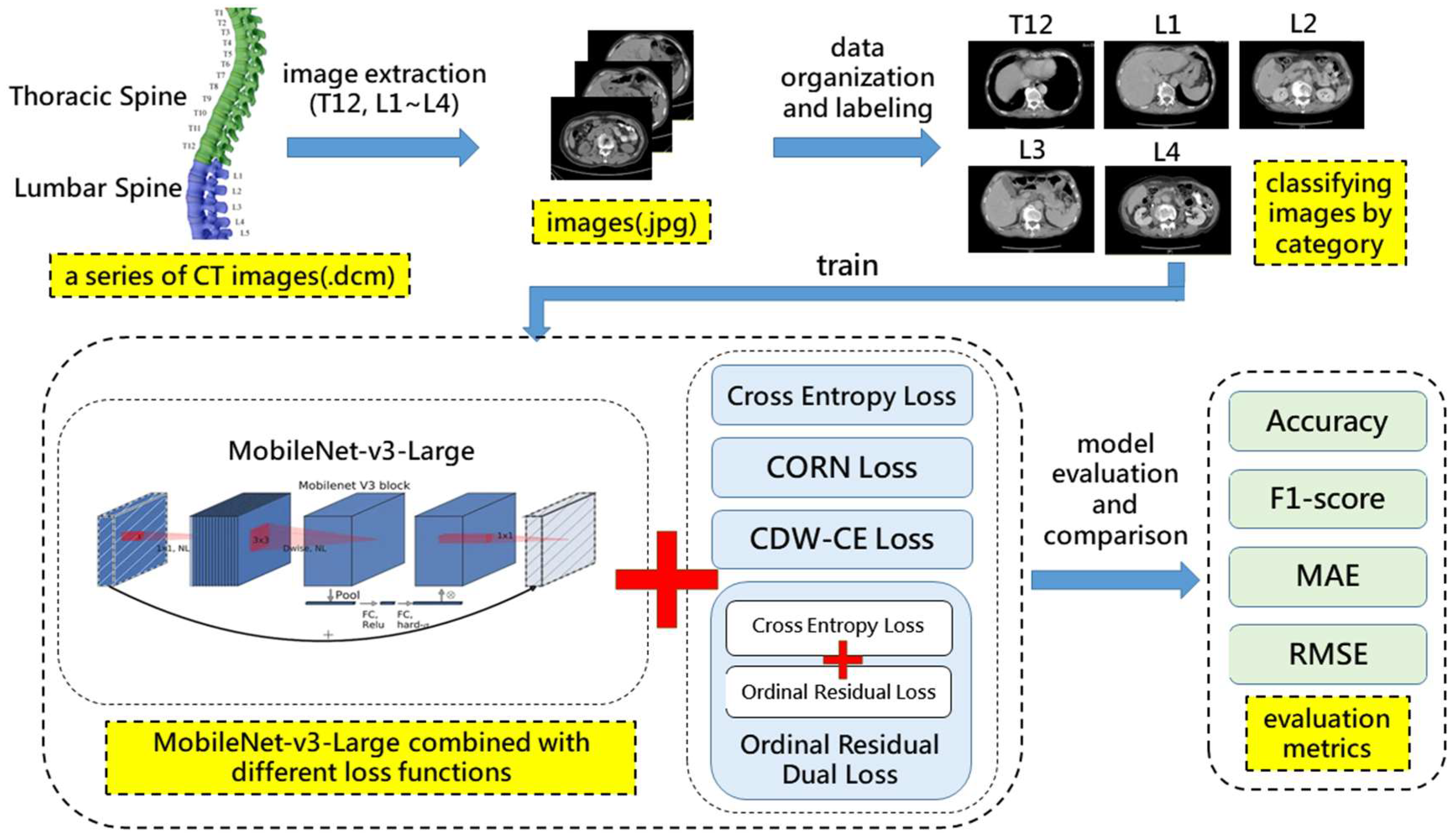
3.1. Research Framework
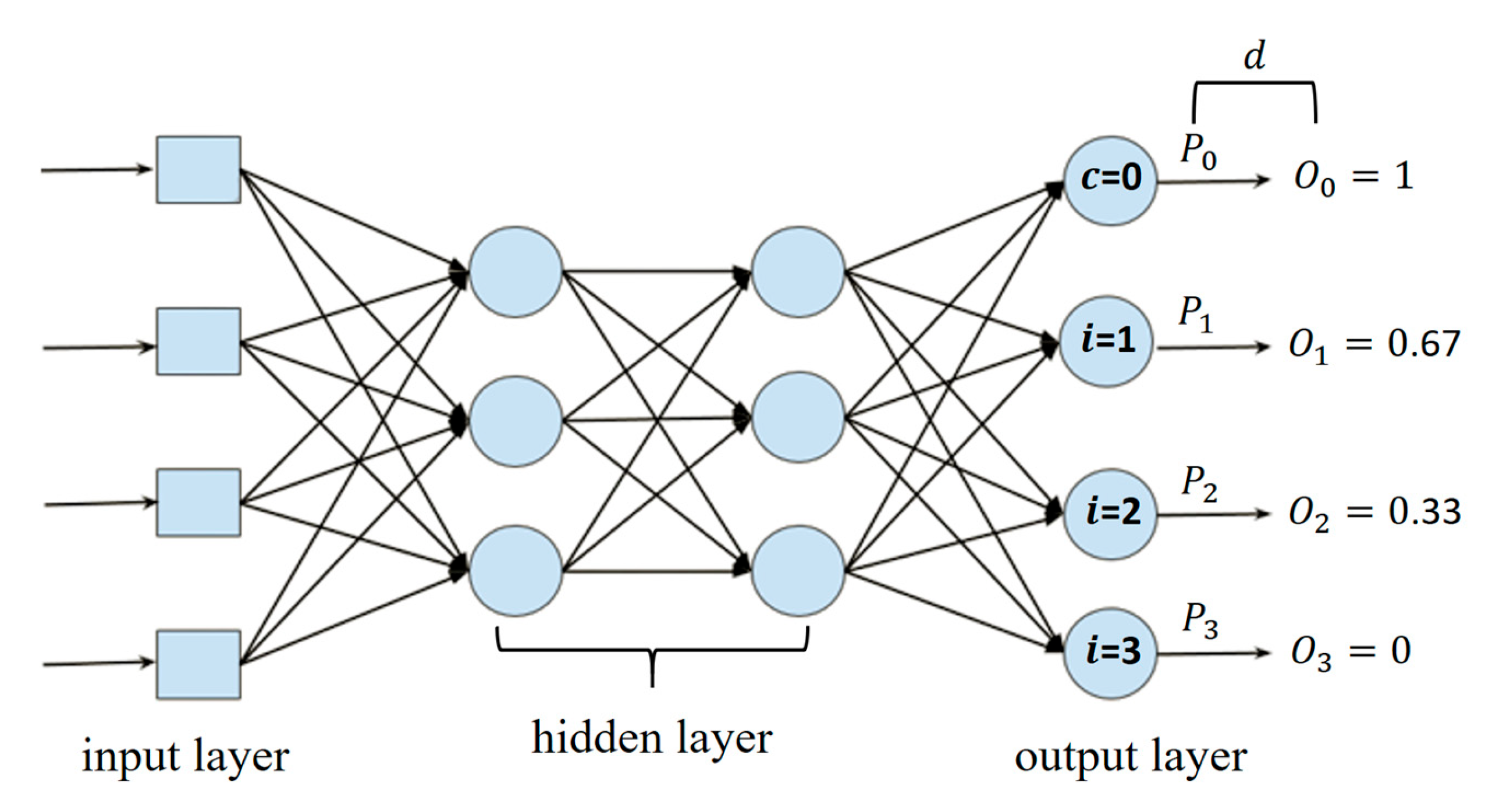
3.2. Ordinal Residual Dual Loss
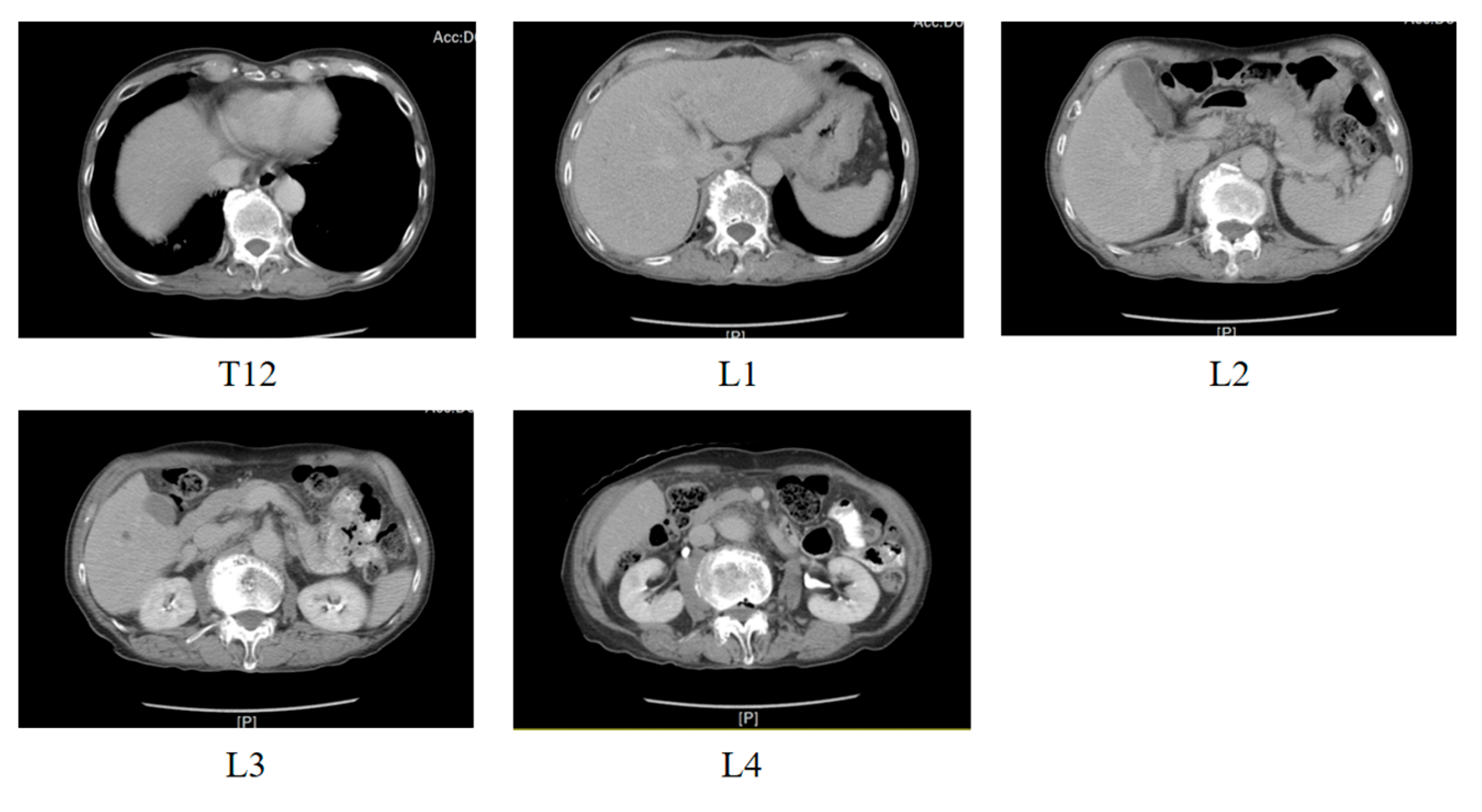
3.3. CT Image Dataset
3.3.1. Dataset Description
3.3.2. Dataset Partitioning and Data Preprocessing
4. Results
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Amini, B.; Boyle, S.P.; Boutin, R.D.; Lenchik, L. Approaches to assessment of muscle mass and myosteatosis on computed tomography: A systematic review. J. Gerontol. Ser. A 2019, 74, 1671–1678. [Google Scholar] [CrossRef] [PubMed]
- Pickhardt, P.J.; Graffy, P.M.; Zea, R.; Lee, S.J.; Liu, J.; Sandfort, V.; Summers, R.M. Automated abdominal CT imaging biomarkers for opportunistic prediction of future major osteoporotic fractures in asymptomatic adults. Radiology 2020, 297, 64–72. [Google Scholar] [CrossRef] [PubMed]
- Pickhardt, P.J.; Graffy, P.M.; Zea, R.; Lee, S.J.; Liu, J.; Sandfort, V.; Summers, R.M. Automated CT biomarkers for opportunistic prediction of future cardiovascular events and mortality in an asymptomatic screening population: A retrospective cohort study. Lancet Digit. Health 2020, 2, e192–e200. [Google Scholar] [CrossRef] [PubMed]
- Amarasinghe, K.C.; Lopes, J.; Beraldo, J.; Kiss, N.; Bucknell, N.; Everitt, S.; Jackson, P.; Litchfield, C.; Denehy, L.; Blyth, B.J. A deep learning model to automate skeletal muscle area measurement on computed tomography images. Front. Oncol. 2021, 11, 580806. [Google Scholar] [CrossRef] [PubMed]
- Pickhardt, P.J.; Perez, A.A.; Garrett, J.W.; Graffy, P.M.; Zea, R.; Summers, R.M. Fully Automated Deep Learning Tool for Sarcopenia Assessment on CT: L1 Versus L3 Vertebral Level Muscle Measurements for Opportunistic Prediction of Adverse Clinical Outcomes. AJR Am. J. Roentgenol. 2022, 218, 124–131. [Google Scholar] [CrossRef] [PubMed]
- Vangelov, B.; Bauer, J.; Kotevski, D.; Smee, R.I. The use of alternate vertebral levels to L3 in computed tomography scans for skeletal muscle mass evaluation and sarcopenia assessment in patients with cancer: A systematic review. Br. J. Nutr. 2022, 127, 722–735. [Google Scholar] [CrossRef] [PubMed]
- Derstine, B.A.; Holcombe, S.A.; Ross, B.E.; Wang, N.C.; Su, G.L.; Wang, S.C. Optimal body size adjustment of L3 CT skeletal muscle area for sarcopenia assessment. Sci. Rep. 2021, 11, 279. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Liu, M.; Yu, K.; Fang, Y.; Zhao, J.; Shi, Y. A Deep Learning-Based Fully Automated Vertebra Segmentation and Labeling Workflow. Br. J. Hosp. Med. 2025, 86, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Garrett, J.W.; Lee, M.H.; Zea, R.; Summers, R.M.; Pickhardt, P.J. Fully automated CT-based adiposity assessment: Comparison of the L1 and L3 vertebral levels for opportunistic prediction. Abdom. Radiol. 2023, 48, 787–795. [Google Scholar] [CrossRef] [PubMed]
- Chan, A.; Coutts, B.; Parent, E.; Lou, E. Development and Evaluation of CT-to-3D Ultrasound Image Registration Algorithm in Vertebral Phantoms for Spine Surgery. Ann. Biomed. Eng. 2021, 49, 310–321. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; Cao, W.; Raschka, S. Deep neural networks for rank-consistent ordinal regression based on conditional probabilities. Pattern Anal. Appl. 2023, 26, 941–955. [Google Scholar] [CrossRef]
- Li, L.; Lin, H.-T. Ordinal regression by extended binary classification. Adv. Neural Inf. Process. Syst. 2006, 19. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Niu, Z.; Zhou, M.; Wang, L.; Gao, X.; Hua, G. Ordinal regression with multiple output cnn for age estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4920–4928. [Google Scholar]
- Cao, W.; Mirjalili, V.; Raschka, S. Rank consistent ordinal regression for neural networks with application to age estimation. Pattern Recognit. Lett. 2020, 140, 325–331. [Google Scholar] [CrossRef]
- Diaz, R.; Marathe, A. Soft labels for ordinal regression. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4738–4747. [Google Scholar]
- Polat, G.; Ergenc, I.; Kani, H.T.; Alahdab, Y.O.; Atug, O.; Temizel, A. Class distance weighted cross-entropy loss for ulcerative colitis severity estimation. In Proceedings of the Medical Image Understanding and Analysis: 26th Annual Conference, MIUA 2022, Cambridge, UK, 27–29 July 2022; pp. 157–171. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Howard, A.; Sandler, M.; Chu, G.; Chen, L.-C.; Chen, B.; Tan, M.; Wang, W.; Zhu, Y.; Pang, R.; Vasudevan, V. Searching for mobilenetv3. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1314–1324. [Google Scholar]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning deep features for discriminative localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2921–2929. [Google Scholar]
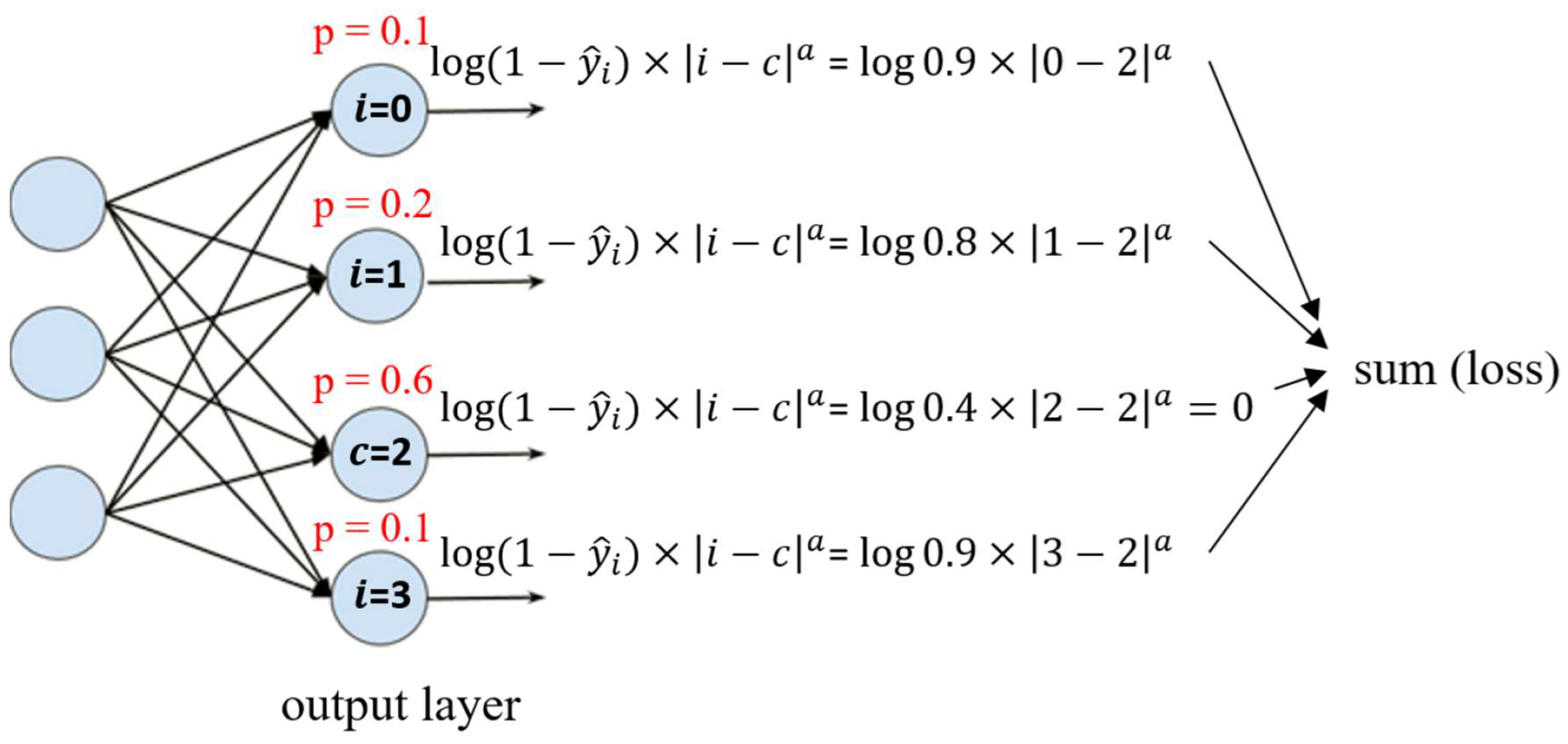
| Class | Predicted Probabilities | |
|---|---|---|
| Case 1 (Correct) | Case 2 (Incorrect) | |
| 1 | 0.2 | 0.1 |
| 2 | 0.7 | 0.6 |
| 3 | 0.1 | 0.1 |
| 4 | 0 | 0.2 |
| All | T12 | L1 | L2 | L3 | L4 | |
|---|---|---|---|---|---|---|
| Number of Datasets | 2512 | 474 | 482 | 510 | 548 | 498 |
| Number of Patients | Number of Datasets | T12 | L1 | L2 | L3 | L4 | |
|---|---|---|---|---|---|---|---|
| Training dataset | 67 | 2003 | 383 | 380 | 408 | 441 | 391 |
| Testing dataset | 17 | 509 | 91 | 102 | 102 | 107 | 107 |
| MobileNet-v3-Large | Accuracy | F1-Score | MAE | RMSE | |
|---|---|---|---|---|---|
| Cross Entropy Loss | 0.8467 ± 0.016 | 0.8464 ± 0.017 | 0.1652 ± 0.025 | 0.4435 ± 0.072 | |
| CORN | 0.7958 ± 0.051 | 0.7950 ± 0.050 | 0.2125 ± 0.057 | 0.4747 ± 0.074 | |
| CDW-CE | = 1 | 0.8447 ± 0.019 | 0.8441 ± 0.021 | 0.1652 ± 0.024 | 0.4309 ± 0.043 |
| = 2 | 0.8384 ± 0.018 | 0.8402 ± 0.017 | 0.1716 ± 0.016 | 0.4390 ± 0.018 | |
| = 3 | 0.8189 ± 0.028 | 0.8192 ± 0.027 | 0.1939 ± 0.026 | 0.4700 ± 0.029 | |
| = 4 | 0.8025 ± 0.037 | 0.8013 ± 0.037 | 0.2054 ± 0.036 | 0.4690 ± 0.037 | |
| = 5 | 0.6429 ± 0.095 | 0.5906 ± 0.142 | 0.3674 ± 0.096 | 0.6192 ± 0.080 | |
| = 6 | 0.4753 ± 0.039 | 0.3532 ± 0.029 | 0.5338 ± 0.038 | 0.7426 ± 0.026 | |
| = 7 | 0.4717 ± 0.030 | 0.3481 ± 0.022 | 0.5386 ± 0.032 | 0.7479 ± 0.026 | |
| = 8 | 0.4049 ± 0.115 | 0.2839 ± 0.112 | 0.8575 ± 0.614 | 1.1068 ± 0.700 | |
| = 9 | NaN | ||||
| = 10 | NaN | ||||
| Ordinal Residual Dual Loss | 0.8726 ± 0.020 | 0.8726 ± 0.019 | 0.1373 ± 0.022 | 0.4015 ± 0.040 | |
| Ordinal Residual Dual Loss | Accuracy | F1-Score | MAE | RMSE |
|---|---|---|---|---|
| MobileNet-v3-Large | 0.8726 ± 0.020 | 0.8726 ± 0.019 | 0.1373 ± 0.022 | 0.4015 ± 0.040 |
| ResNet-34 | 0.8702 ± 0.026 | 0.8706 ± 0.026 | 0.1377 ± 0.030 | 0.3918 ± 0.050 |
| EfficientNetV2-s | 0.8718 ± 0.022 | 0.8699 ± 0.021 | 0.1429 ± 0.024 | 0.4189 ± 0.041 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, C.-P.; Chang, H.-Y.; Hsu, Y.-M.; Lin, T.-L. Ordinal Regression Research Based on Dual Loss Function—An Example on Lumbar Vertebra Classification in CT Images. Diagnostics 2025, 15, 2949. https://doi.org/10.3390/diagnostics15232949
Tang C-P, Chang H-Y, Hsu Y-M, Lin T-L. Ordinal Regression Research Based on Dual Loss Function—An Example on Lumbar Vertebra Classification in CT Images. Diagnostics. 2025; 15(23):2949. https://doi.org/10.3390/diagnostics15232949
Chicago/Turabian StyleTang, Chia-Pei, Hong-Yi Chang, Yu-Ming Hsu, and Tu-Liang Lin. 2025. "Ordinal Regression Research Based on Dual Loss Function—An Example on Lumbar Vertebra Classification in CT Images" Diagnostics 15, no. 23: 2949. https://doi.org/10.3390/diagnostics15232949
APA StyleTang, C.-P., Chang, H.-Y., Hsu, Y.-M., & Lin, T.-L. (2025). Ordinal Regression Research Based on Dual Loss Function—An Example on Lumbar Vertebra Classification in CT Images. Diagnostics, 15(23), 2949. https://doi.org/10.3390/diagnostics15232949






