Performance of Dual-Layer Flat-Panel Detectors
Abstract
1. Introduction
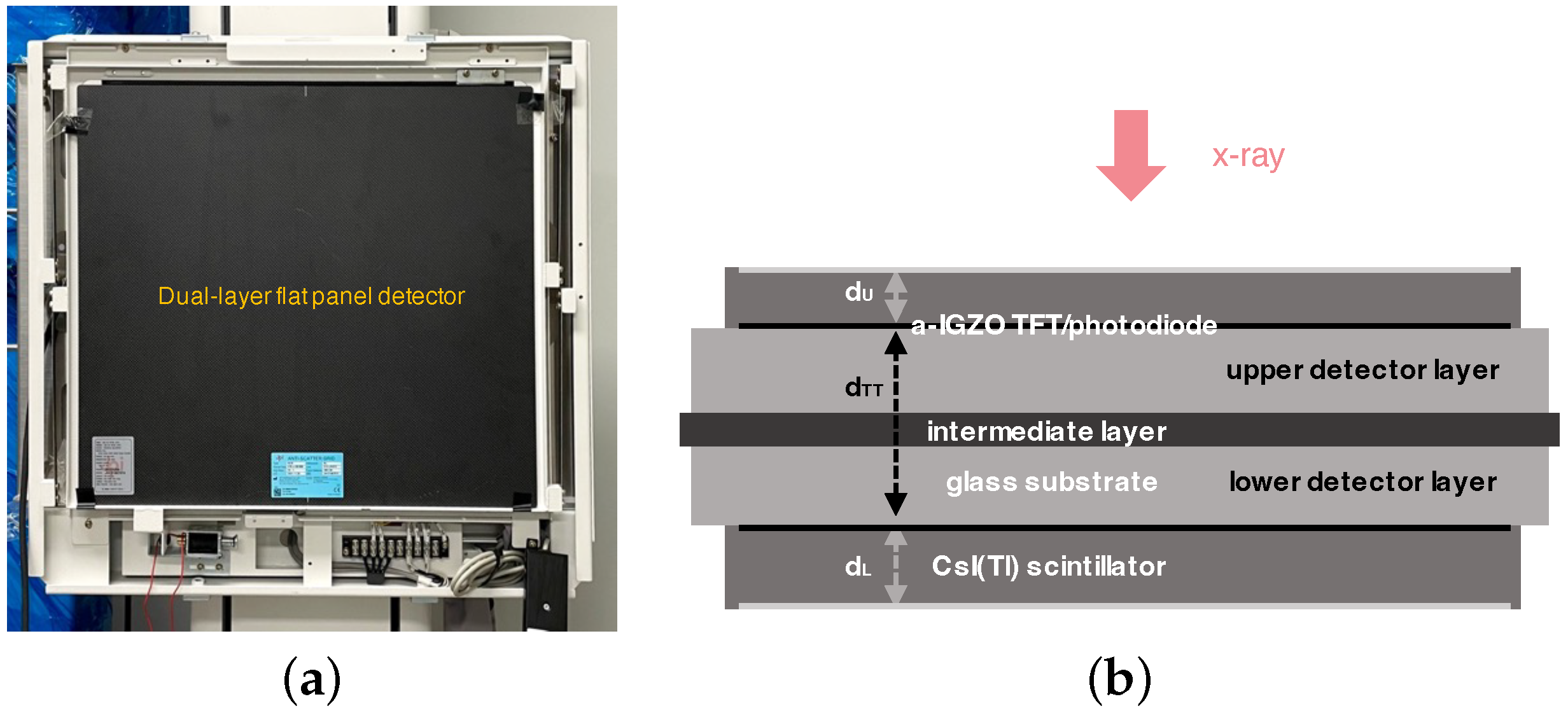
2. Materials and Methods
2.1. Modulation Transfer Function
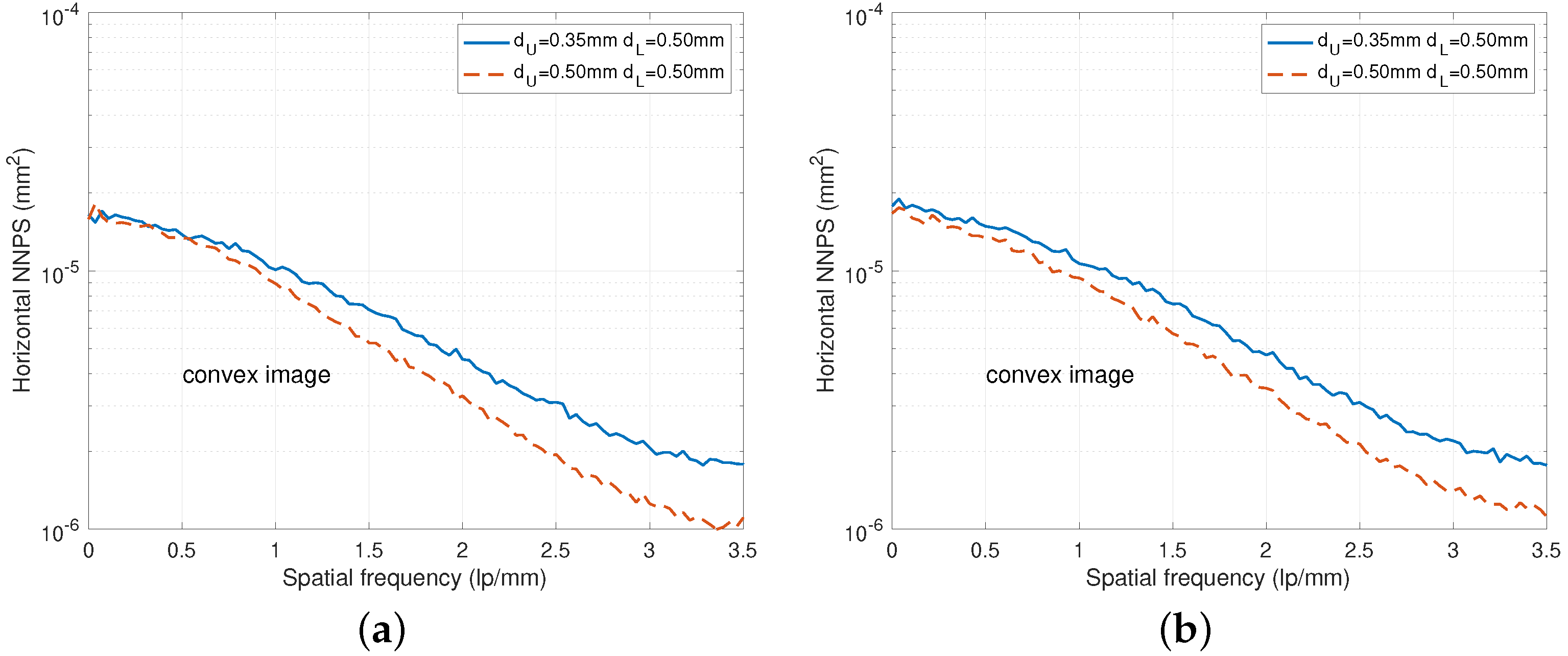
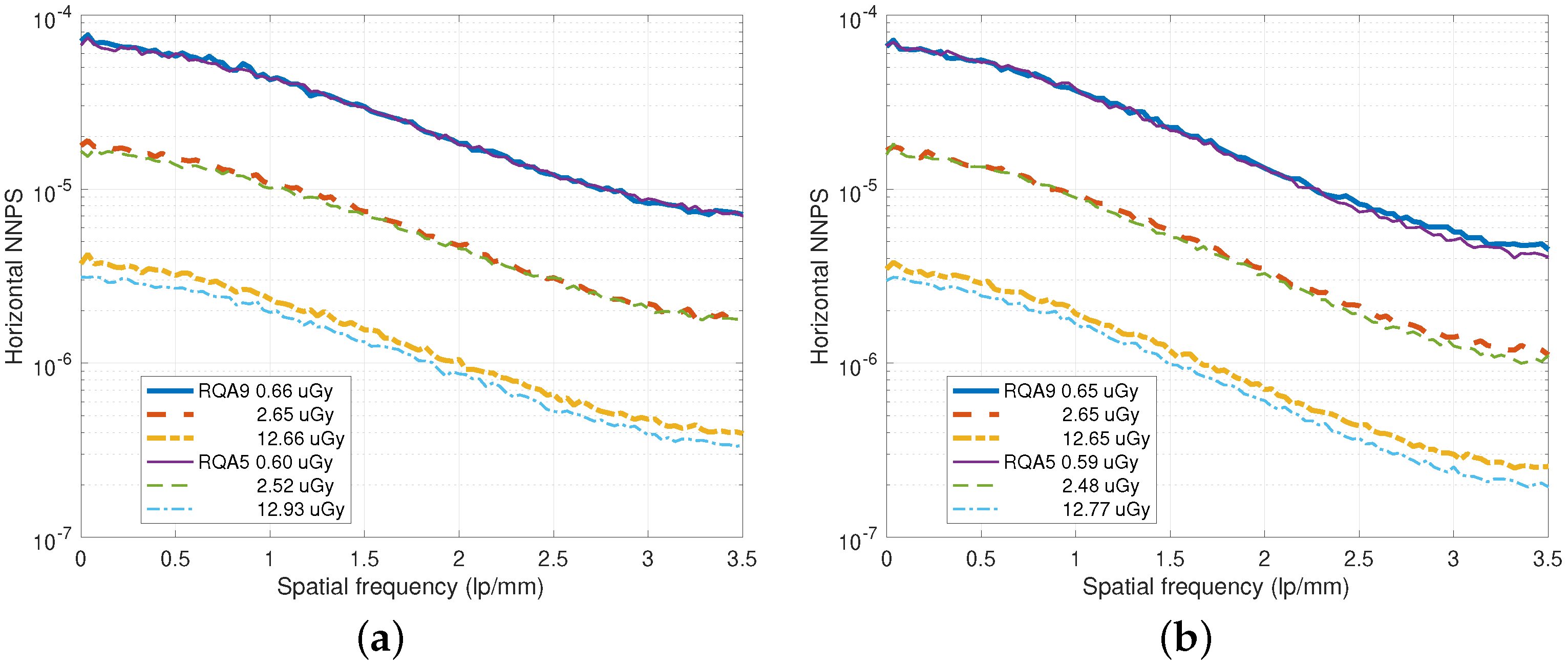
2.2. Noise Power Spectrum
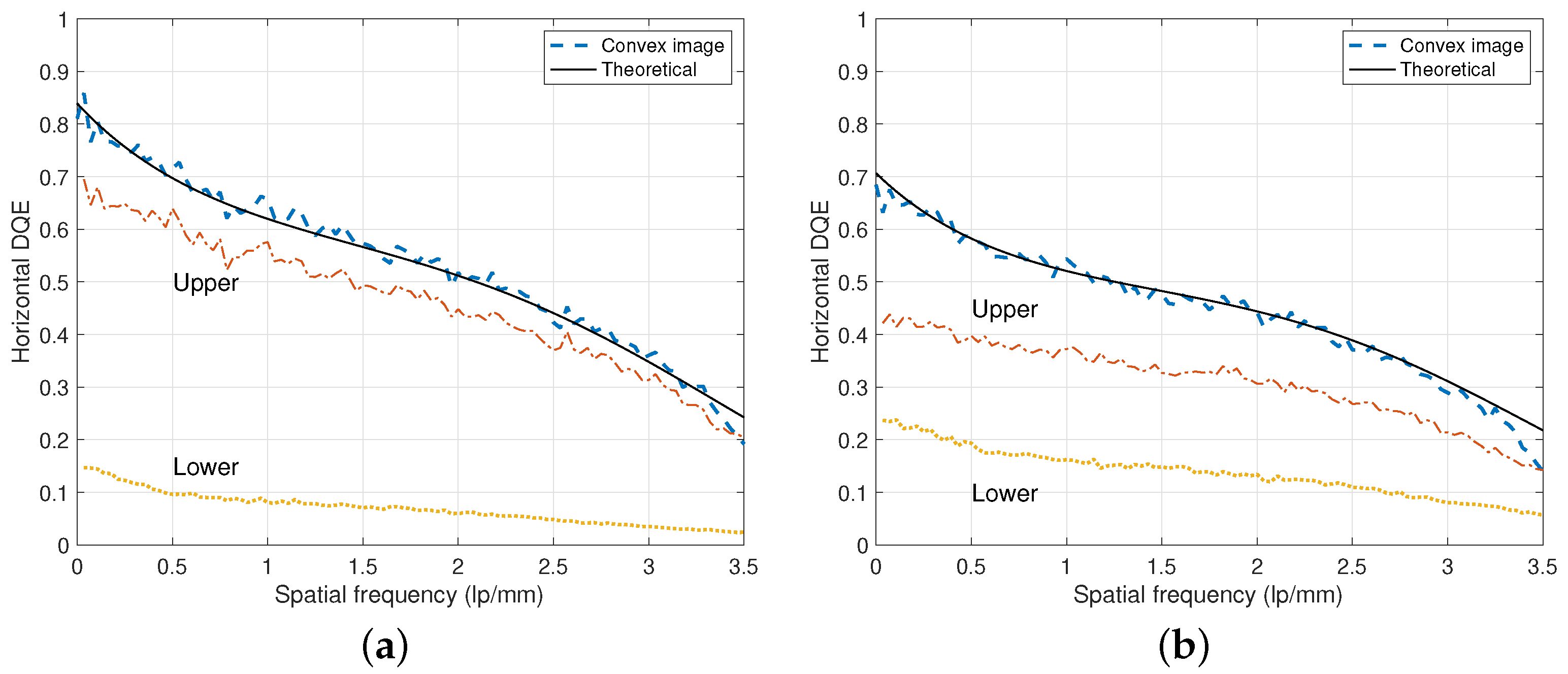
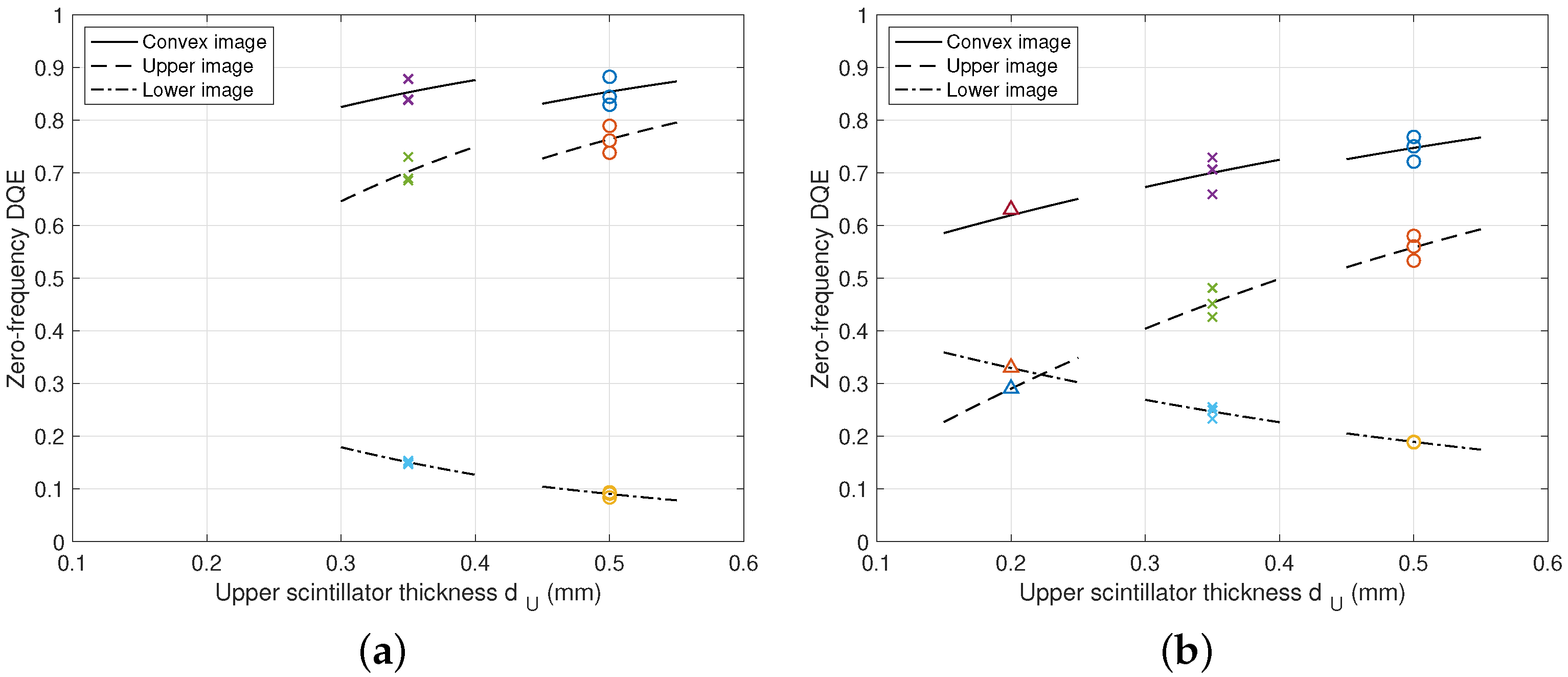
2.3. Detective Quantum Efficiency
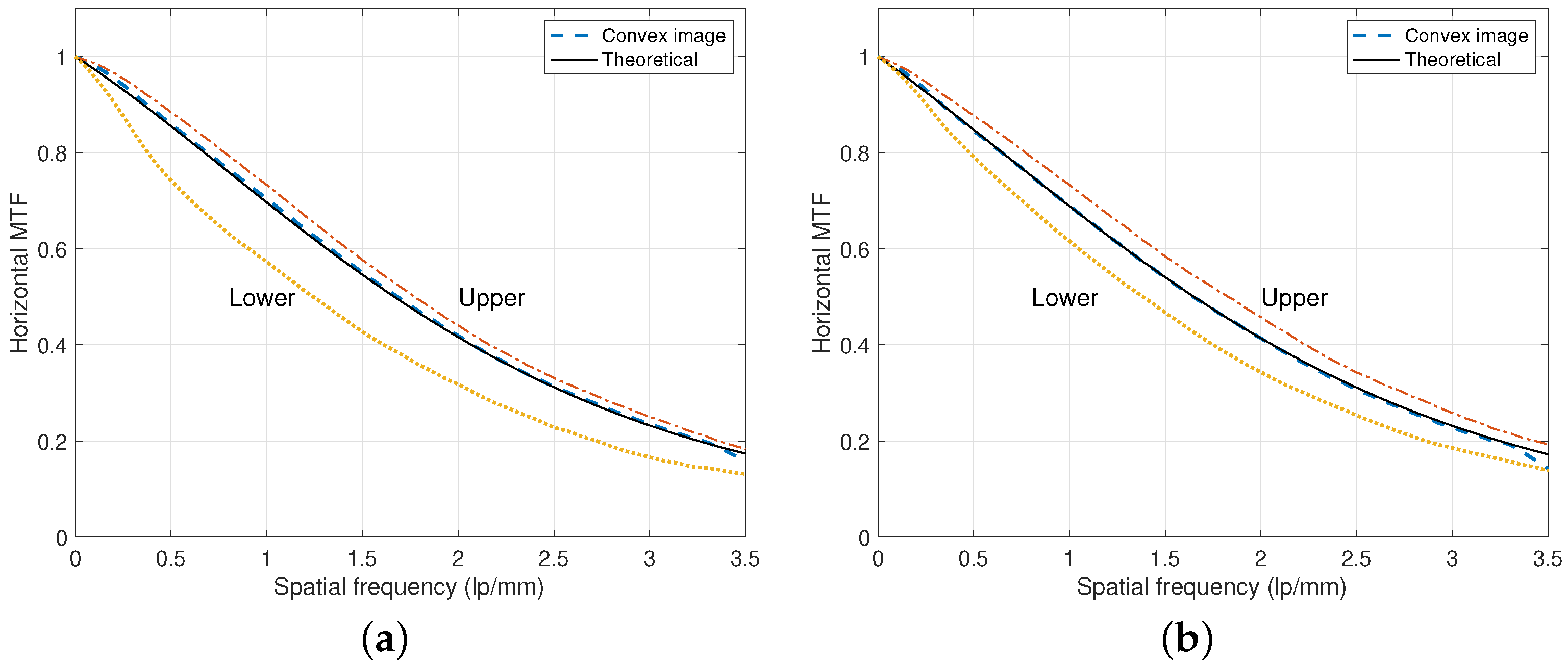
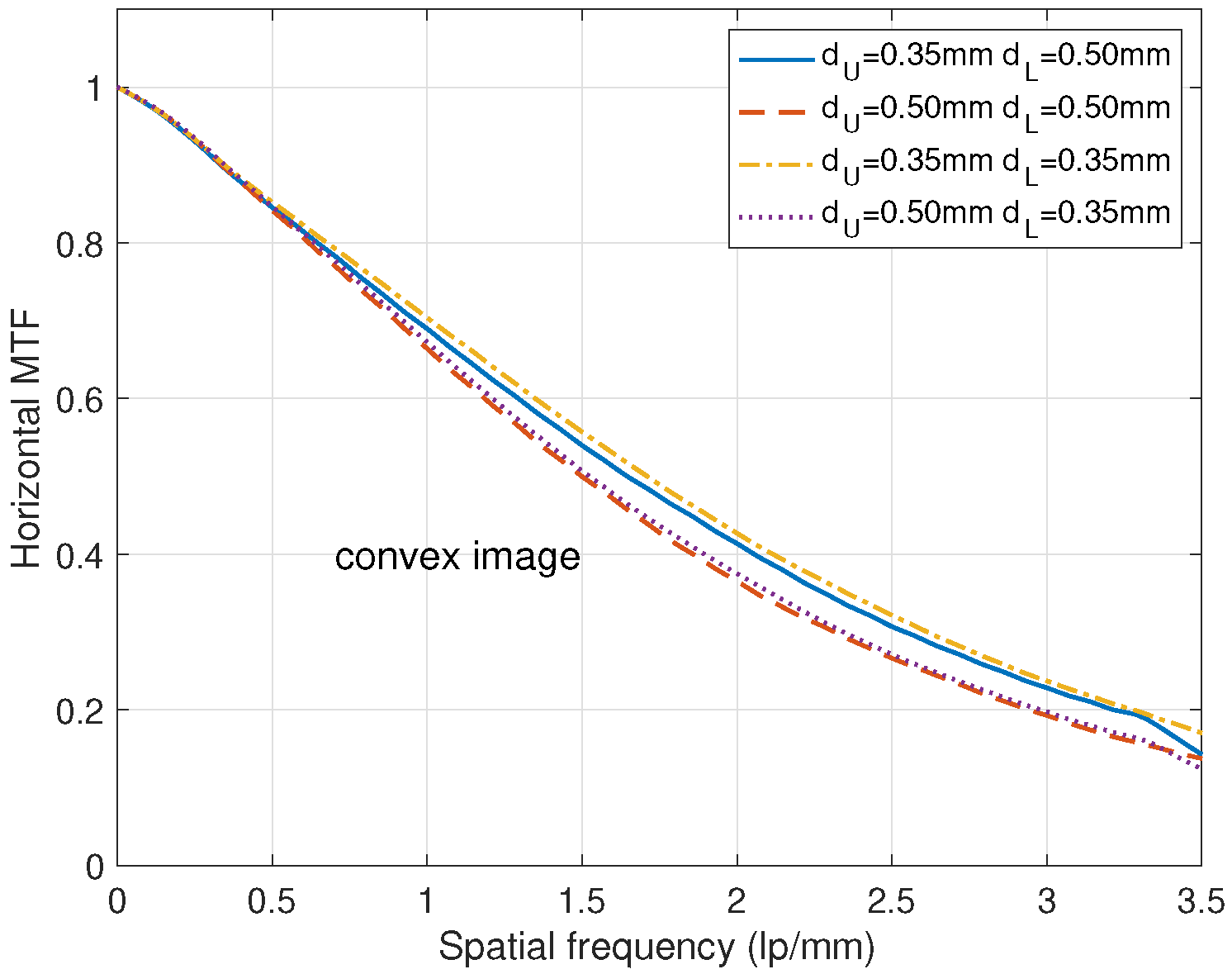
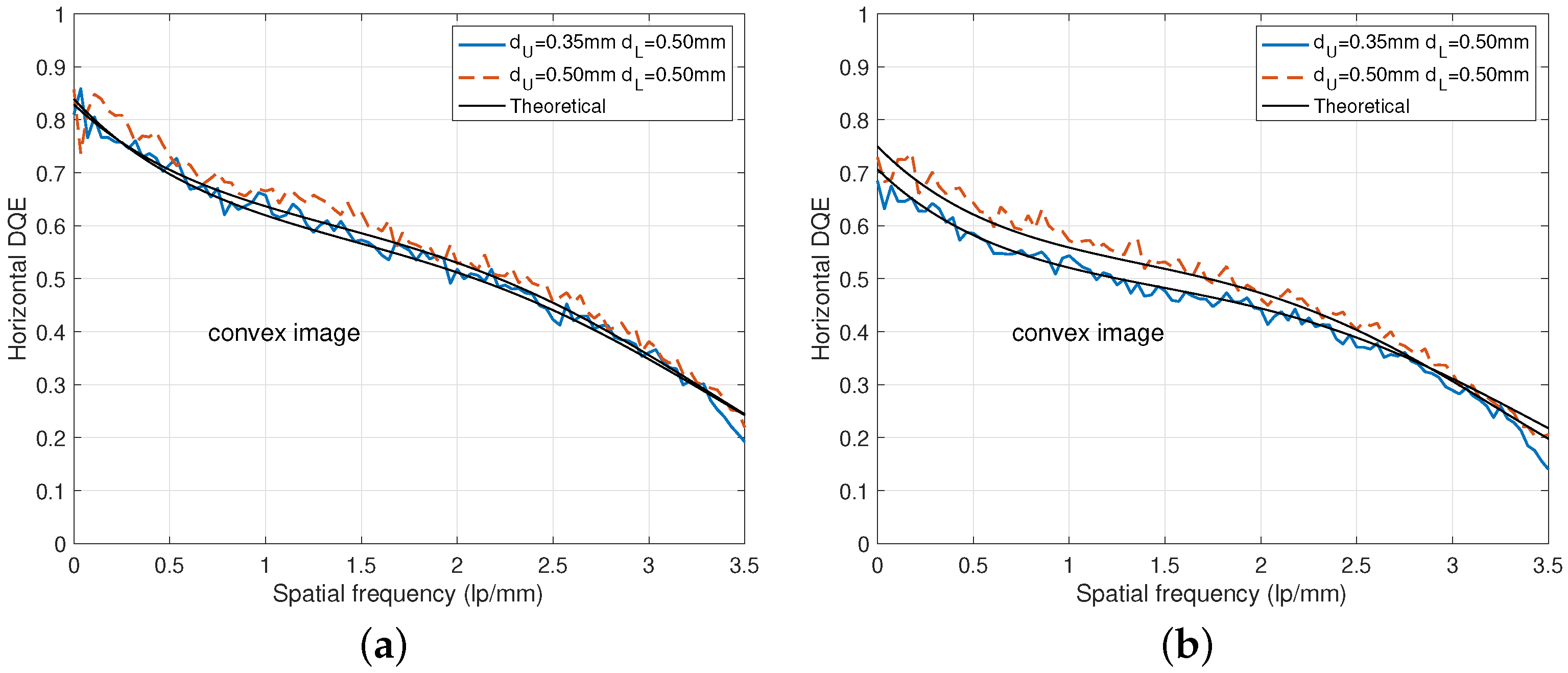
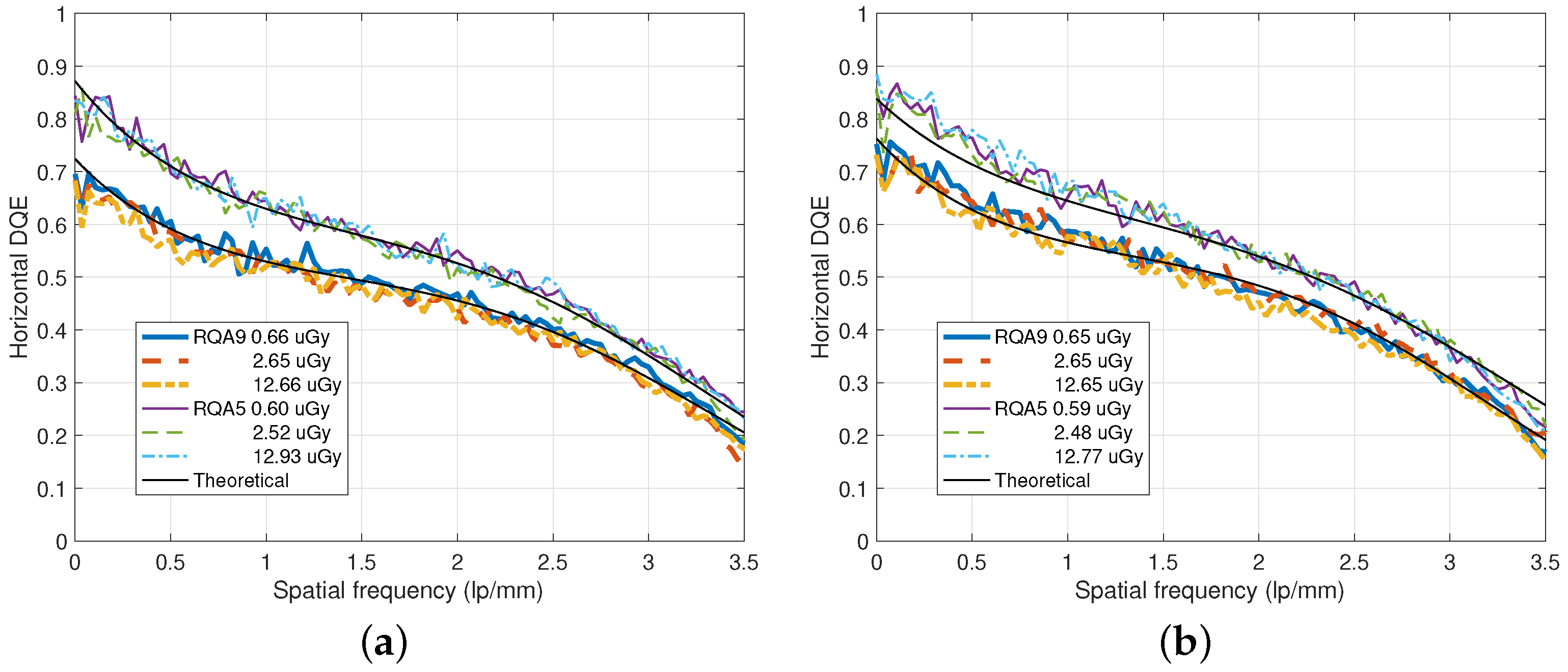
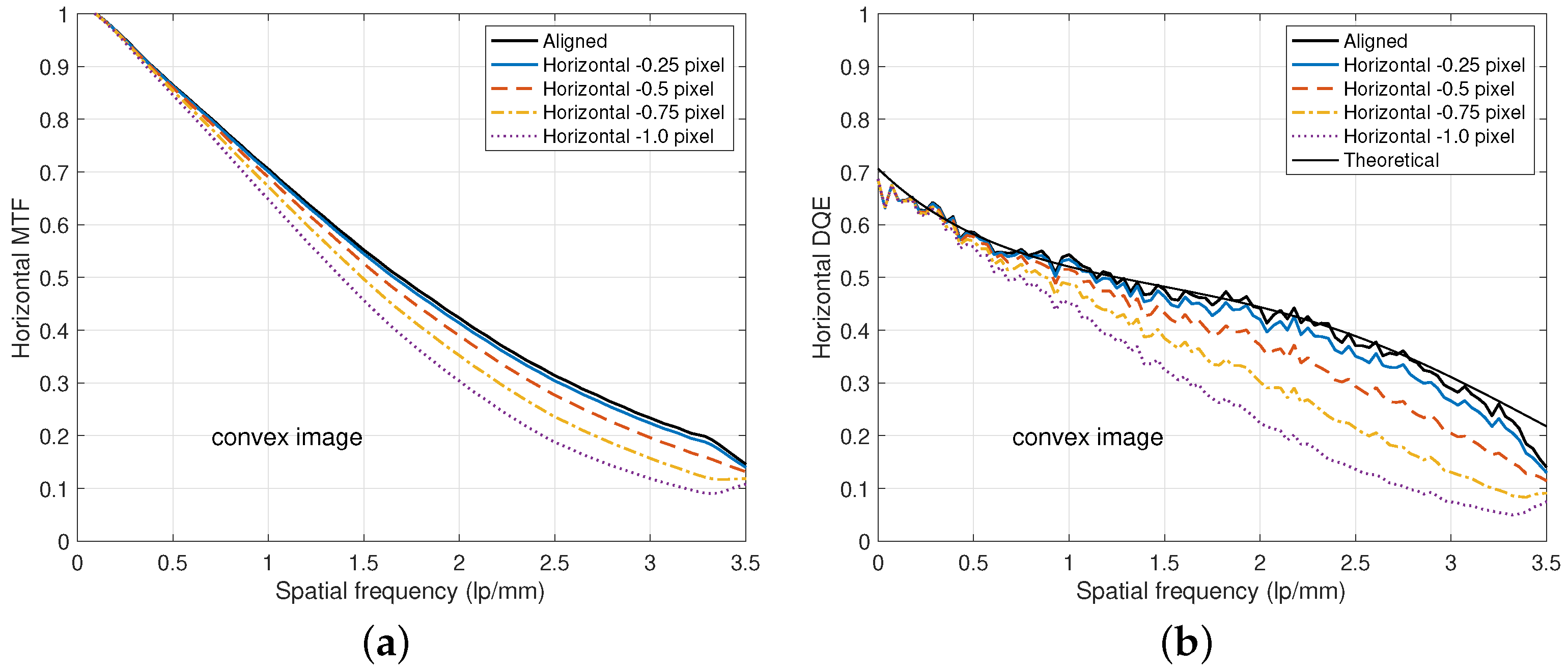
3. Results
4. Discussion
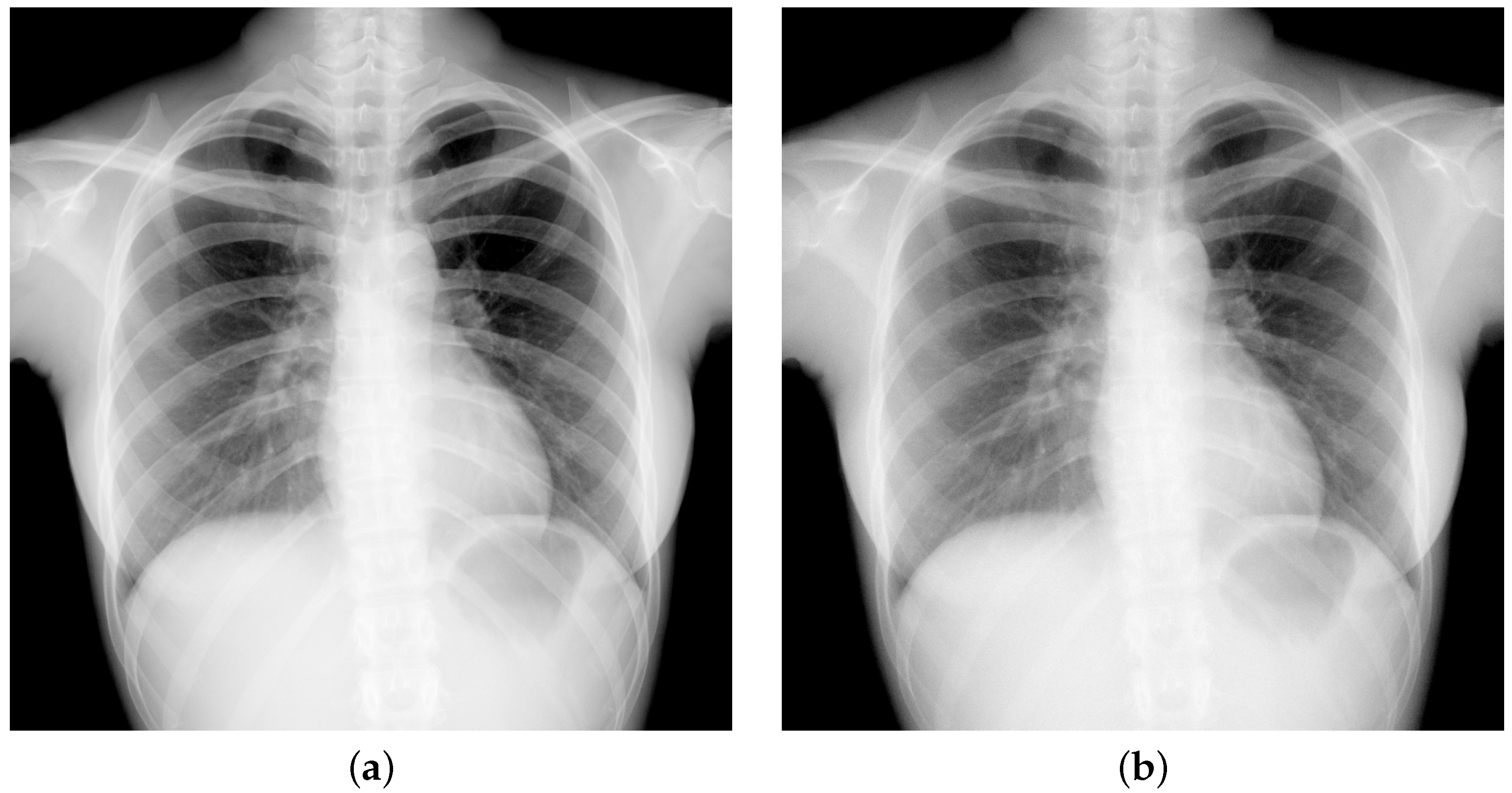
4.1. Alignment of Lower Images
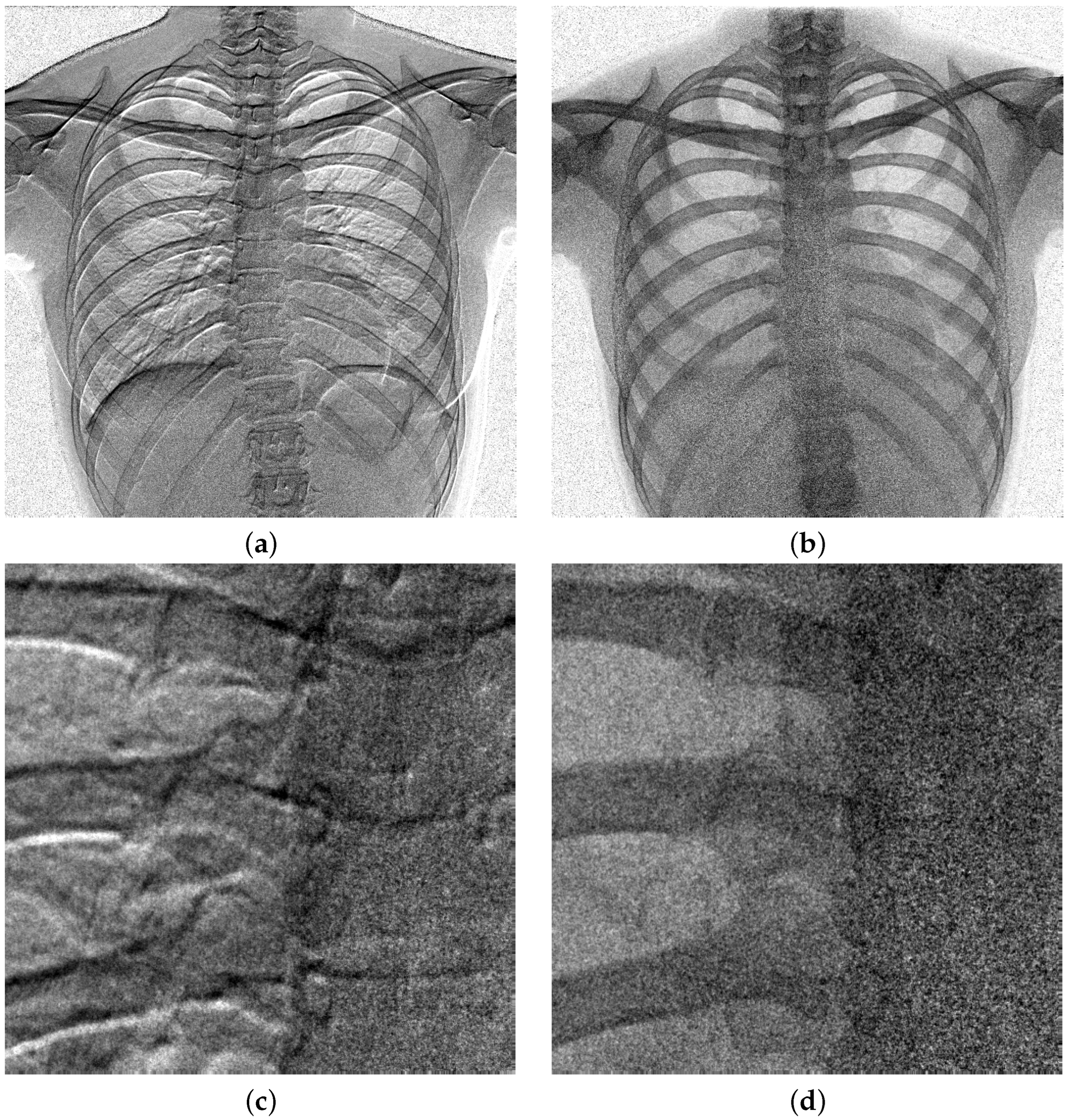
4.2. Low-Dose Radiography Imaging
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DFD | Dual-layer flat-panel detector |
| DQE | Detective quantum efficiency |
| MTF | Modulation transfer function |
| NNPS | Normalized noise power spectrum |
| NPS | Noise power spectrum |
| TFT | Thin-film-transistor |
| SNR | Singal-to-noise ratio |
| SID | Source-to-image distance |
References
- Barnes, G.T.; Sones, R.A.; Tesic, M.M.; Morgan, D.R.; Sanders, J.N. Detector for dual-energy digital radiography. Radiology 1985, 156, 537–540. [Google Scholar] [CrossRef] [PubMed]
- Ishigaki, T.; Sakuma, S.; Horikawa, Y.; Ikeda, M.; Yamaguchi, H. One-shot dual-energy subtraction imaging. Radiology 1986, 161, 271–273. [Google Scholar] [CrossRef]
- Stewart, B.K.; Huang, H.K. Single-exposure dual-energy computed radiography. Med. Phys. 1990, 17, 866–875. [Google Scholar] [CrossRef]
- Ergun, D.L.; Mistretta, C.A.; Brown, D.E.; Bystrianyk, R.T.; Sze, W.K.; Kelcz, F.; Naidich, D.P. Single-exposure dual-energy computed radiography: Improved detection and processing. Radiology 1990, 174, 243–249. [Google Scholar] [CrossRef]
- Alvarez, R.E.; Seibert, J.A.; Thompson, S.K. Comparison of dual energy detector system performance. Med. Phys. 2004, 31, 556–565. [Google Scholar] [CrossRef]
- Yun, S.; Han, J.C.; Kim, D.W.; Youn, H.; Kim, H.K.; Tanguay, J.; Cunningham, I.A. Feasibility of active sandwich detectors for single-shot dual-energy imaging. Med. Imaging Phys. Med. Imaging 2014, 9033, 90335T. [Google Scholar] [CrossRef]
- McCollough, C.H.; Leng, S.; Yu, L.; Fletcher, J.G. Dual- and Multi-Energy CT: Principles, Technical Approaches, and Clinical Applications. Radiology 2015, 276, 637–653. [Google Scholar] [CrossRef]
- Shi, L.; Bennett, N.R.; Star-Lack, J.; Lu, M.; Wang, A.S. Projection-domain metal artifact correction using a dual layer detector. Med. Imaging Phys. Med. Imaging 2020, 11312, 516–521. [Google Scholar]
- Lueck, F.; Beister, M.; Garcia-Allende, P.B.; Ritschl, L.; Syben, C.; Kappler, S. Towards quantitative spectral mammography using triple-energy K-edge imaging and a two-pass reconstruction approach. Med. Imaging Phys. Med. Imaging 2025, 13405, 134050M. [Google Scholar]
- Engel, K.J.; Menser, B.; Rohr, P.; Ruetten, W.; Simon, M.; Thran, A. Dual layer x-ray detector simulation. Med. Imaging Phys. Med. Imaging 2020, 11312, 398–409. [Google Scholar] [CrossRef]
- Kim, D.S. Convex Combination of Images From Dual-Layer Detectors for High Detective Quantum Efficiencies. IEEE Trans. Biomed. Eng. 2023, 70, 1804–1814. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.S.; Kim, H.; Jeon, Y.; Kim, Y.; Lee, D.; Choi, I.; Shin, C.W. On the performance of a stacked dual-layer flat-panel detector. Med. Imaging Phys. Med. Imaging 2025, 13405, 134050C. [Google Scholar] [CrossRef]
- Kim, D.S.; Lee, E. On the performance of the noise power spectrum from the gain-corrected radiography images. SPIE J. Med. Imaging 2018, 5, 013508. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhou, H.; Gu, S.; Xia, Y.; Liao, H.; Deng, Y.; Gao, H. Dual-energy head cone-beam CT using a dual-layer flat-panel detector: Hybrid material decomposition and a feasibility study. Med. Phys. 2023, 50, 6762–6778. [Google Scholar] [CrossRef]
- Kim, D.S. Measurements of the noise power spectrum for digital x-ray imaging devices. Phys. Med. Biol. 2024, 69, 03TR01. [Google Scholar] [CrossRef]
- Maurino, S.L.; Badano, A.; Cunningham, I.A.; Karim, K.S. Theoretical and Monte Carlo optimization of a stacked three-layer flat-panel x-ray imager for applications in multi-spectral diagnostic medical imaging. Med. Imaging Phys. Med. Imaging 2016, 9783, 97833Z. [Google Scholar] [CrossRef]
- Jiang, X.; Stayman, J.W.; Gang, G.J. Approaches for three material decomposition using a triple-layer flat-panel detector. Med. Imaging Phys. Med. Imaging 2023, 12463, 124630X. [Google Scholar]
- Jiang, X.; Tivnan, M.; Zhang, X.; Stayman, J.W.; Gang, G.J. Design optimization of a triple-layer flat-panel detector for three-material decomposition. Med. Imaging Phys. Med. Imaging 2024, 12925, 129250U. [Google Scholar]
- Su, T.; Zhu, J.; Zhang, X.; Tan, Y.; Cui, H.; Zeng, D.; Guo, J.; Zheng, H.; Ma, J.; Liang, D.; et al. Super Resolution Dual-Energy Cone-Beam CT Imaging With Dual-Layer Flat-Panel Detector. IEEE Trans. Med. Imaging 2024, 43, 734–744. [Google Scholar] [CrossRef]
- Lu, M.; Wang, A.; Shapiro, E.; Shiroma, A.; Zhang, J.; Steiger, J.; Star-Lack, J. Dual energy imaging with a dual-layer flat panel detector. Med. Imaging Phys. Med. Imaging 2019, 10948, 269–278. [Google Scholar]
- Shi, L.; Bennett, N.R.; Shapiro, E.; Colbeth, R.E.; Star-Lack, J.; Lu, M.; Wang, A.S. Comparative study of dual energy cone-beam CT using a dual-layer detector and kVp switching for material decomposition. Med. Imaging Phys. Med. Imaging 2020, 11312, 481–486. [Google Scholar]
- Cai, E.Y.; De Caro, C.; Treb, K.; Li, K. Benefits of using removable filters in dual-layer flat panel detectors. Phys. Med. Biol. 2023, 68, 085013. [Google Scholar] [CrossRef]
- Kim, D.S.; Lee, D. Two-step image registration for dual-layer flat-panel detectors. Diagnostics 2024, 14, 2742. [Google Scholar] [CrossRef]
- Lubinsky, A.R.; Howansky, A.F.; Zheng, H.; Zhao, W. Back-irradiated and dual-screen sandwich detector configurations for radiography. SPIE J. Med. Imaging 2019, 6, 033501. [Google Scholar]
- Howansky, A.; Mishchenko, A.; Lubinsky, A.R.; Zhao, W. Comparison of CsI:Tl and Gd2O2S:Tb indirect flat panel detector x-ray imaging performance in front- and back-irradiation geometries. Med. Phys. 2019, 46, 4857–4868. [Google Scholar] [CrossRef] [PubMed]
- Mogami, H.; Onoike, Y.; Miyano, H.; Arakawa, K.; Inoue, H.; Sakae, K.; Kawakami, T. Lung cancer screening by single-shot dual-energy subtraction using flat-panel detector. Jpn. J. Radiol. 2021, 39, 1168–1173. [Google Scholar] [CrossRef] [PubMed]
- Takarabe, S.; Kuramoto, T.; Shibayama, Y.; Yamasaki, Y.; Kitamura, Y.; Yoshikawa, H.; Kato, T. Is the image quality of conventional chest radiography obtained from a two-layer flat panel detector affected by the internal structure of the detector? Phys. Medica 2022, 95, 176–181. [Google Scholar] [CrossRef]
- Tian, Q.; Huhns, M.N. Algorithms for subpixel registration. Comput. Vis. Graph Image Process. 1986, 35, 220–233. [Google Scholar] [CrossRef]
- Proakis, J.G.; Manolakis, D. Digital Signal Processing, 4th ed.; Prentice Hall: Albany, NY, USA, 2007. [Google Scholar]
- Lee, D.; Kim, D.S. Subpixel registration for dual-layer detectors based on the amplitude response. IEEE Access 2024, 12, 153019–153029. [Google Scholar] [CrossRef]
- Bazaraa, M.S.; Sherali, H.D.; Shetty, C.M. Nonlinear Programming, Theory and Algorithms, 2nd ed.; John Wiely & Sons, Inc.: New York, NY, USA, 1993. [Google Scholar]
- IEC 62220-1-1; Medical Electrical Equipment Characteristics of Digital X-Ray Imaging Devices-Part1-1: Determination of the Detective Quantum Efficiency Detectors used in Radiographic Imaging. International Electrotechnical Commission: Geneva, Switzerland, 2015.
- Fujita, H.; Tsai, D.Y.; Itoh, T.; Doi, K.; Morishita, J.; Ueda, K.; Ohtsuka, A. A simple method for determining the modulation transfer function in digital radiography. IEEE Trans. Med. Imaging 1992, 11, 34–39. [Google Scholar] [CrossRef]
- Buhr, E.; Guenther-Kohfahl, S.; Neitzel, U. Simple method for modulation transfer function determination of digital imaging detectors from edge images. Med. Imaging Phys. Med. Imaging 2003, 5030, 877–884. [Google Scholar] [CrossRef]
- Kim, D.S. Noise power spectrum measurements in digital imaging with gain nonuniformity correction. IEEE Trans. Image Process. 2016, 25, 3712–3722. [Google Scholar] [CrossRef] [PubMed]
- Maintz, J.; Viergever, M.A. A survey of medical image registration. Med. Image Anal. 1998, 2, 1–36. [Google Scholar] [CrossRef]
- Zitová, B.; Flusser, J. Image registration methods: A survey. Image Vis. Comput. 2003, 21, 977–1000. [Google Scholar] [CrossRef]
- Shi, L.; Lu, M.; Bennett, N.R.; Shapiro, E.; Zhang, J.; Colbeth, R.; Star-Lack, J.; Wang, A.S. Characterization and potential applications of a dual-layer flat-panel detector. Med. Phys. 2020, 47, 3332–3343. [Google Scholar] [CrossRef]
- Du, W.; Gao, S.; Jiang, W.; Kudchadker, R.J. Independent evaluation of the effectiveness of IsoCal in improving image center accuracy on Varian TrueBeam and Clinac machines. J. Appl. Clin. Med. Phys. 2018, 19, 483–490. [Google Scholar] [CrossRef]


| Intermediate | CsI Scintillator | Distance | |||
|---|---|---|---|---|---|
| Filter | Applications | ||||
| Lu et al. [20], 2019 | 1 Cu | 0.2 | 0.55 | 2.5 | D |
| Shi et al. [21], 2020 | 1 Cu | 0.2 | 0.55 | 2.5 | D |
| Mogami et al. [26], 2021 | - | CsI | GOS | - | D |
| Takarabe et al. [27], 2022 | - | CsI | GOS | - | P (upper) |
| Kim [11], 2023 | None, 0.5 Cu | 0.5 | 0.5 | 1.3–2.2 | P (convex) |
| Wang et al. [14], 2023 | None | 0.55 | 0.55 | - | D, P (convex) |
| Cai et al. [22], 2023 | Liquid 0.76 I | 0.2 | 0.55 | - | D, P |
| Su et al. [19], 2024 | 1 Cu | 0.26 | 0.55 | 6.6 | S |
| Kim et al. [12,23], 2025 | None | 0.35–0.5 | 0.5 | 1.1 | P (convex) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, D.S.; Lee, D. Performance of Dual-Layer Flat-Panel Detectors. Diagnostics 2025, 15, 1889. https://doi.org/10.3390/diagnostics15151889
Kim DS, Lee D. Performance of Dual-Layer Flat-Panel Detectors. Diagnostics. 2025; 15(15):1889. https://doi.org/10.3390/diagnostics15151889
Chicago/Turabian StyleKim, Dong Sik, and Dayeon Lee. 2025. "Performance of Dual-Layer Flat-Panel Detectors" Diagnostics 15, no. 15: 1889. https://doi.org/10.3390/diagnostics15151889
APA StyleKim, D. S., & Lee, D. (2025). Performance of Dual-Layer Flat-Panel Detectors. Diagnostics, 15(15), 1889. https://doi.org/10.3390/diagnostics15151889






