Automated Analysis of Vertebral Body Surface Roughness for Adult Age Estimation: Ellipse Fitting and Machine-Learning Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Size and Demographics
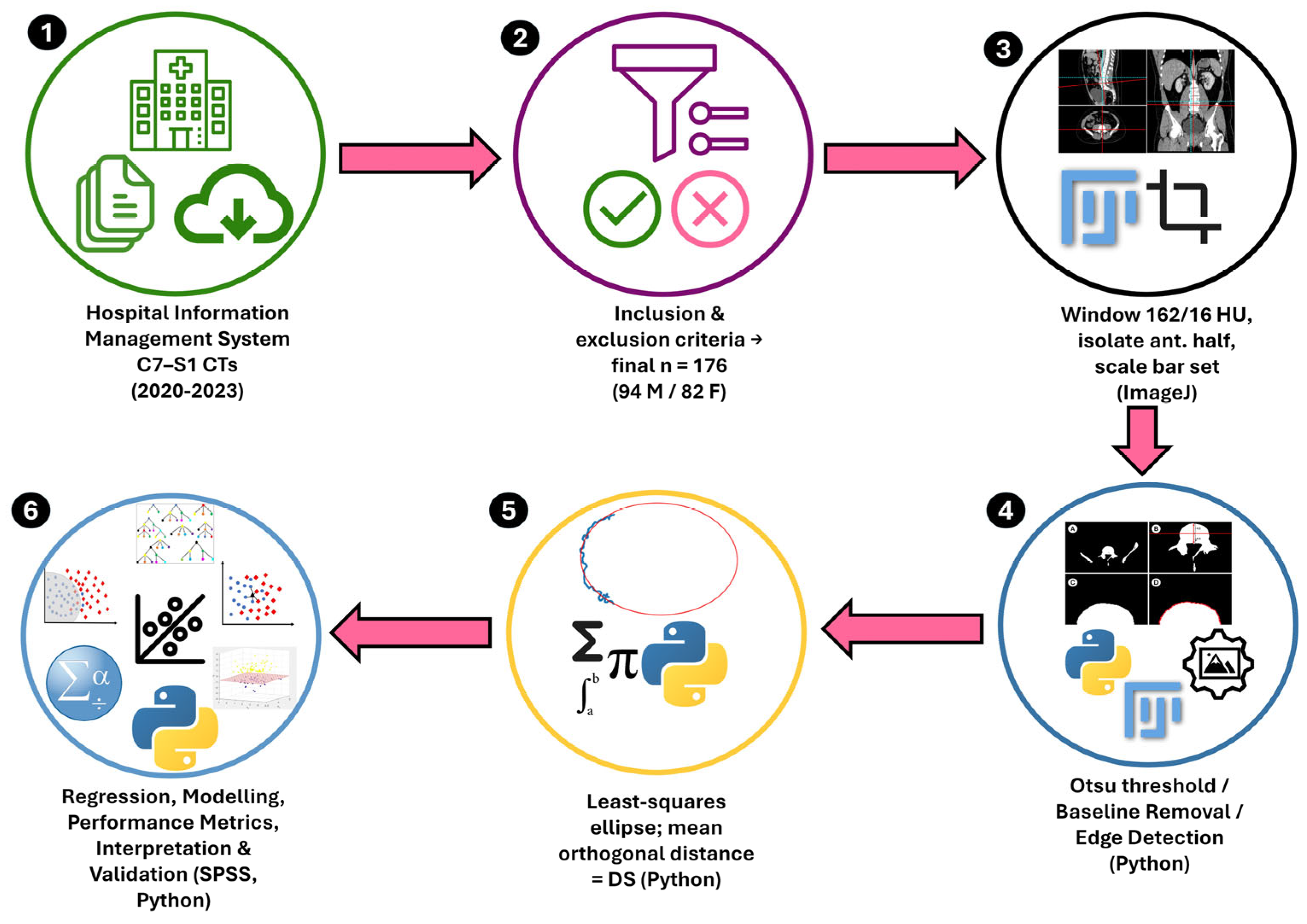
2.2. Case Selection
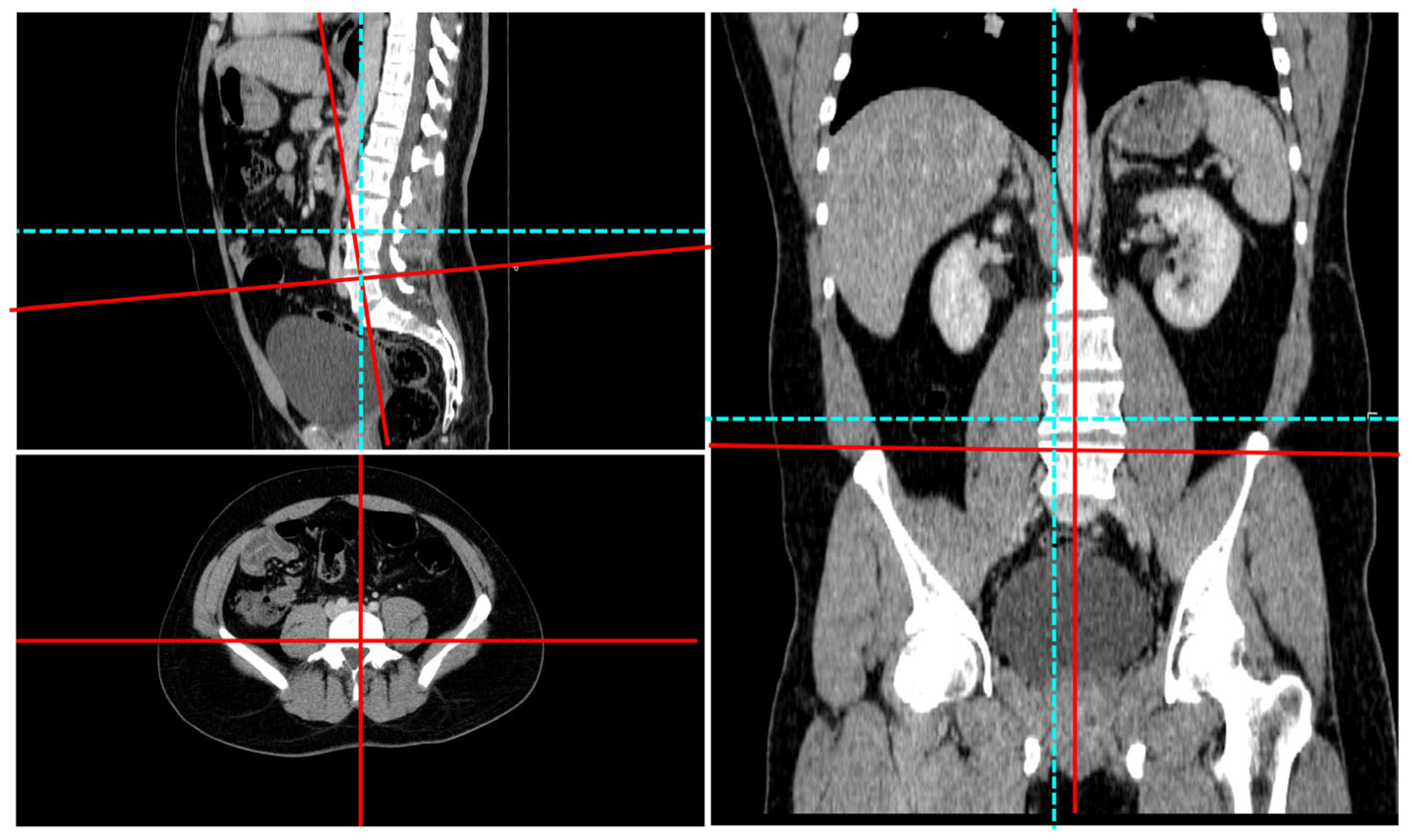
2.3. Radiologic Imaging
- (i)
- This surface bears the highest compressive and shear loads during standing and flexion;
- (ii)
- (iii)
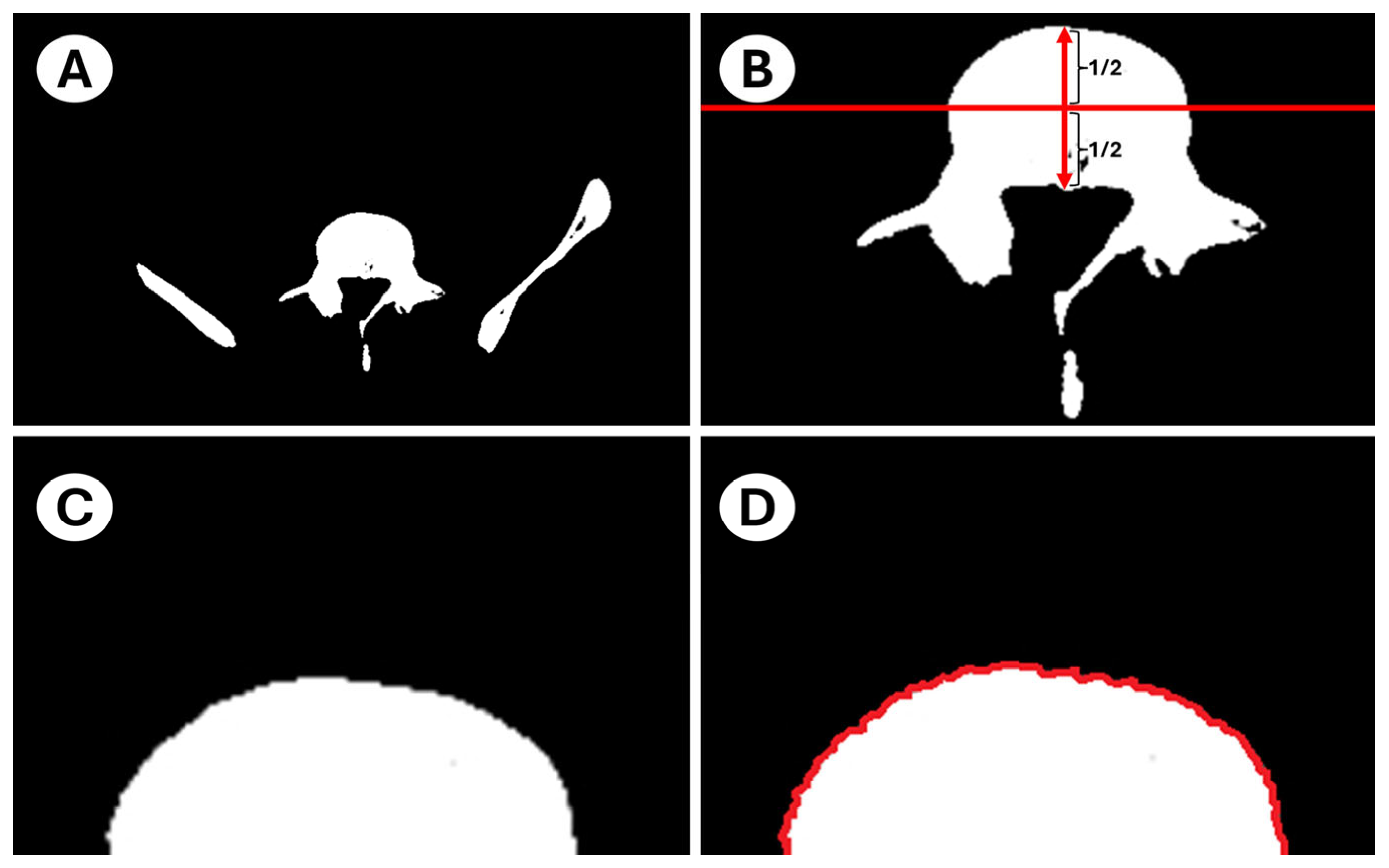
- The outline of the intact anterior half approximates an ellipse in young adults, providing a mathematically convenient reference shape. The posterior half was purposefully excluded to avoid pedicle interference and because its load path is dominated by trabecular rather than cortical bone. By fitting a least-squares ellipse to the intact anterior rim and computing the mean orthogonal distance of every boundary node to that ellipse, we obtain a single, observer-independent roughness index that quantifies cumulative cortical remodeling.
2.4. Image Preparation
2.5. Image Processing
2.6. Statistical Analysis
3. Results
3.1. Descriptive Statistics
3.2. Correlation Between Age and Vertebral Surface Roughness (Table 2; Figure 6 and Figure 7)
| Males | Females | |||
|---|---|---|---|---|
| Variable | r | p | r | p |
| C7 DS | 0.089 | 0.395 | 0.194 | 0.081 |
| T1 DS | −0.108 | 0.301 | 0.096 | 0.392 |
| T2 DS | −0.039 | 0.711 | 0.355 | <0.01 (*) |
| T3 DS | 0.078 | 0.453 | 0.334 | <0.01 (*) |
| T4 DS | 0.014 | 0.893 | 0.362 | <0.001 (**) |
| T5 DS | 0.059 | 0.575 | 0.314 | <0.01 (*) |
| T6 DS | 0.129 | 0.214 | 0.287 | <0.01 (*) |
| T7 DS | 0.279 | <0.01 (*) | 0.352 | <0.01 (*) |
| T8 DS | 0.324 | <0.01 (*) | 0.522 | <0.001 (**) |
| T9 DS | 0.322 | <0.01 (*) | 0.459 | <0.001 (**) |
| T10 DS | 0.352 | <0.001 (**) | 0.471 | <0.001 (**) |
| T11 DS | 0.284 | <0.01 (*) | 0.367 | <0.001 (**) |
| T12 DS | 0.175 | 0.092 | 0.324 | <0.01 (*) |
| L1 DS | 0.280 | <0.01 (*) | 0.495 | <0.001 (**) |
| L2 DS | 0.424 | <0.001 (**) | 0.553 | <0.001 (**) |
| L3 DS | 0.600 | <0.001 (**) | 0.509 | <0.001 (**) |
| L4 DS | 0.448 | <0.001 (**) | 0.538 | <0.001 (**) |
| L5 DS | 0.395 | <0.001 (**) | 0.588 | <0.001 (**) |
| S1 DS | 0.403 | <0.001 (**) | 0.074 | 0.508 |
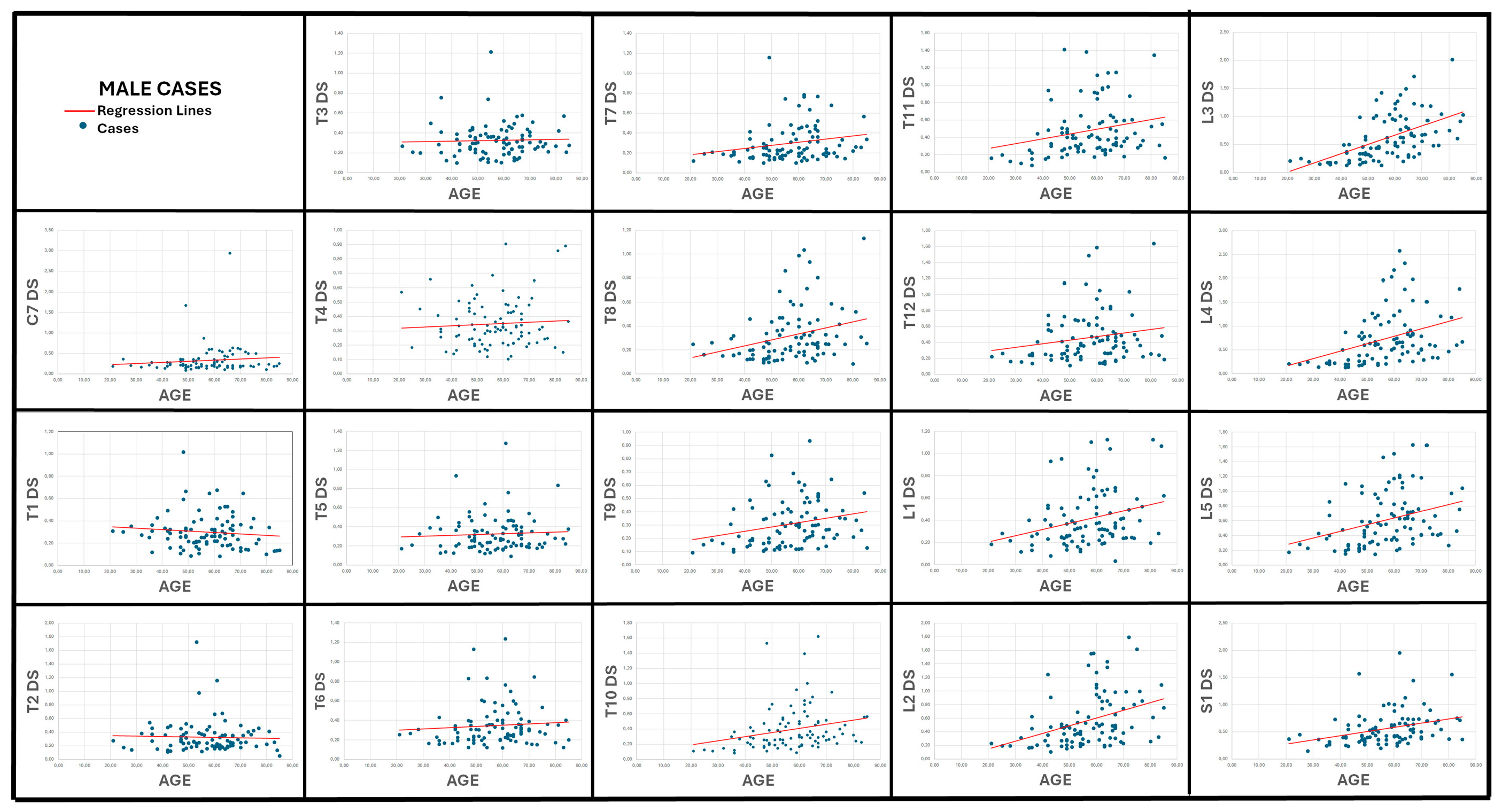

3.3. Multiple Linear Regression (Table 3)
| Statistic | Females (n = 81) | Males (n = 94) |
|---|---|---|
| R | 0.685 | 0.631 |
| R2 | 0.469 | 0.399 |
| Adjusted R2 | 0.304 | 0.244 |
| SEE (years) | 12.29 | 11.44 |
| F (df) | 2.84 (19, 61) | 2.58 (19, 74) |
| Model p | 0.001 | 0.002 |
| Max VIF (variable) | 3.22 (L2 DS) | 2.36 (T8 DS) |
| Min tolerance (variable) | 0.311 (L2 DS) | 0.424 (T8 DS) |
| Max condition index | 17.3 | 17.6 |
| Collinearity flag | none | none |
3.4. LASSO Regression
3.5. Machine Learning Models (Table 4)
| Sex | Model | Holdout R2 | 95% CI (R2) | SEE (y) | 95% CI (SEE) | MAE (y) | RMSE (y) | CV R2 | OOB R2 † |
|---|---|---|---|---|---|---|---|---|---|
| Male | RF | 0.468 | −0.01–0.67 | 8.49 | 5.8–10.9 | 6.69 | 8.49 | 0.432 | 0.446 |
| Male | SVR-rbf | −0.184 | −1.37–0.32 | 12.65 | 9.0–15.8 | 10.39 | 12.65 | 0.442 | — |
| Male | SVR-lin | 0.118 | −0.70–0.41 | 10.92 | 7.6–14.0 | 8.77 | 10.92 | 0.098 | — |
| Male | KNN | 0.257 | −0.79–0.66 | 10.03 | 6.3–13.5 | 7.12 | 10.03 | 0.367 | — |
| Male | GNB-Reg | −1.147 | −4.30–−0.13 | 17.04 | 13.0–21.0 | 14.46 | 17.04 | −0.120 | — |
| Female | RF | 0.221 | −0.74–0.73 | 12.83 | 5.9–18.4 | 9.06 | 12.83 | 0.374 | 0.418 |
| Female | SVR-rbf | 0.097 | −0.69–0.42 | 13.81 | 9.6–17.5 | 10.85 | 13.81 | 0.311 | — |
| Female | SVR-lin | −0.271 | −2.10–0.41 | 16.39 | 9.9–22.5 | 12.11 | 16.39 | 0.153 | — |
| Female | KNN | 0.448 | −0.26–0.77 | 10.80 | 6.3–14.8 | 7.98 | 10.80 | 0.304 | — |
| Female | GNB-Reg | −0.202 | −1.77–0.33 | 15.94 | 11.9–19.5 | 14.04 | 15.94 | −0.080 | — |
3.6. Post Hoc Power Analysis
4. Discussion
4.1. Synopsis of the Main Findings
4.2. How DS Compares with Conventional Vertebral Scores
4.3. DS Versus Deep Learning Pipelines
4.4. Population-, Sex-, and Age-Specific Patterns
4.5. Model Diagnostics and Practical Performance
4.6. Practical Significance of the Results
4.7. Population and Sex Variation and Taphonomic Considerations
4.8. Ethical and Legal Implications of Bone Surface Roughness-Based Age Estimation
4.9. Pathophysiological Basis of the DS Metric
5. Limitations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Age Distribution of Cases

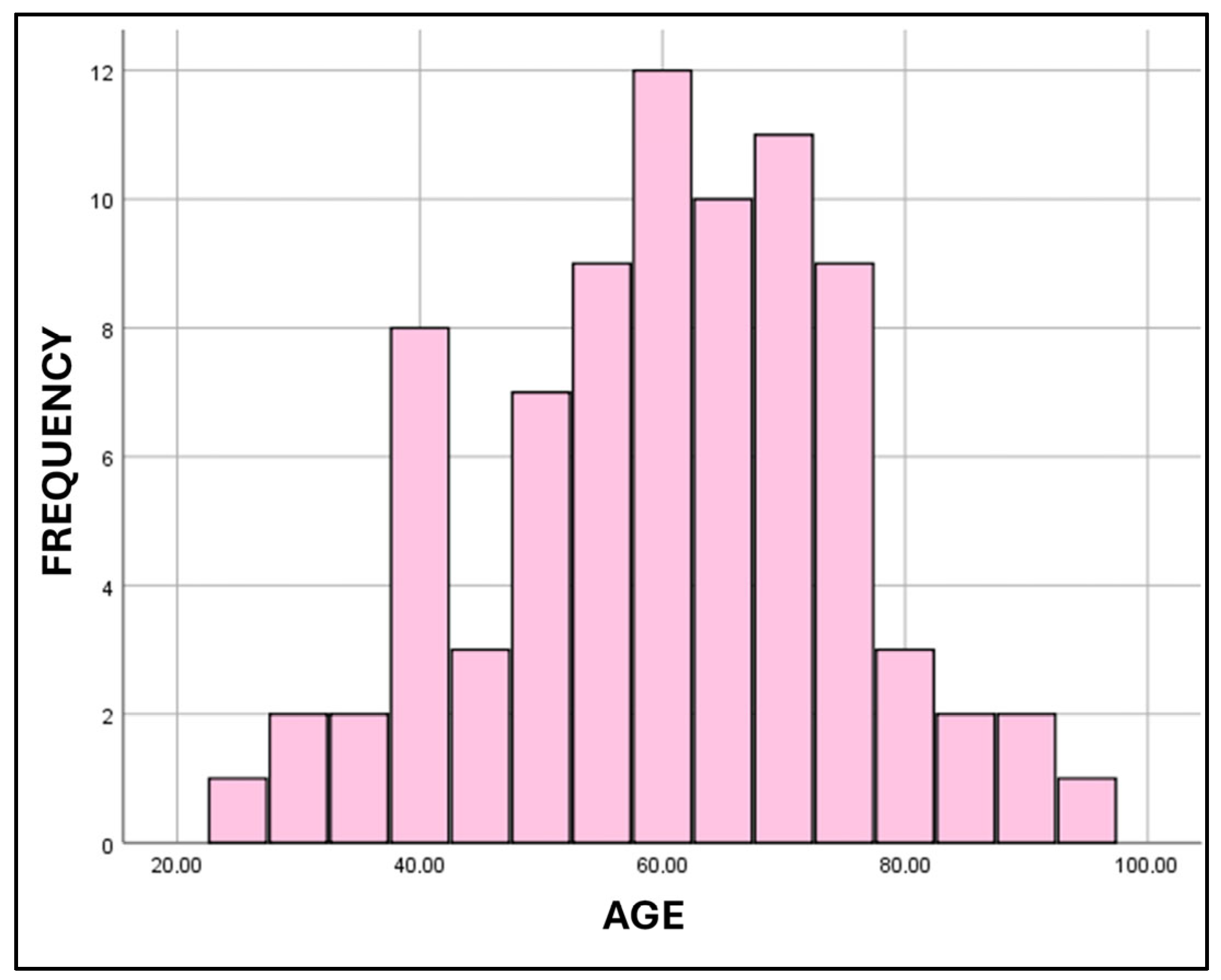

| Measures of Central Tendency for Age | ||||
| Total Sample | Males | Females | ||
| N | 176 | 94 | 82 | |
| Mean ± SD | 58.5 ± 14.0 | 57.0 ± 13.2 | 60.2 ± 14.7 | |
| Median (IQR) | 60.0 (18.8) | 58.5 (17.3) | 60.0 (20.3) | |
| Range | 21–95 | 21–85 | 25–95 | |
| Distribution of Cases According to Age Groups | ||||
| Age Group | Males | Females | ||
| 21–29 | 3 | 1 | ||
| 30–39 | 6 | 6 | ||
| 40–49 | 19 | 10 | ||
| 50–59 | 21 | 20 | ||
| 60–69 | 30 | 22 | ||
| 70–79 | 10 | 17 | ||
| 80–89 | 5 | 4 | ||
| 90–99 | 0 | 2 | ||
Appendix A.2. Detailed Multiple Linear Regression Analysis Results
| Unstandardized Coefficients | Standardized Coefficients | t | Sig. | Collinearity Statistics | |||
|---|---|---|---|---|---|---|---|
| B | Std. Error | Beta | Tolerance | VIF | |||
| Constant | 46.452 | 4.789 | 9.701 | 0.000 | |||
| C7 | 1.777 | 3.665 | 0.046 | 0.485 | 0.629 | 0.895 | 1.118 |
| T1 | −16.004 | 8.915 | −0.188 | −1.795 | 0.077 | 0.743 | 1.347 |
| T2 | −7.800 | 6.335 | −0.133 | −1.231 | 0.222 | 0.700 | 1.429 |
| T3 | 4.118 | 8.767 | 0.051 | 0.47 | 0.640 | 0.698 | 1.432 |
| T4 | −5.765 | 8.731 | −0.072 | −0.66 | 0.511 | 0.685 | 1.46 |
| T5 | −0.129 | 8.727 | −0.002 | −0.015 | 0.988 | 0.553 | 1.809 |
| T6 | −0.829 | 7.127 | −0.013 | −0.116 | 0.908 | 0.661 | 1.512 |
| T7 | 2.550 | 7.768 | 0.037 | 0.328 | 0.744 | 0.655 | 1.528 |
| T8 | −0.481 | 8.205 | −0.008 | −0.059 | 0.953 | 0.424 | 2.359 |
| T9 | 9.864 | 9.526 | 0.131 | 1.035 | 0.304 | 0.507 | 1.971 |
| T10 | 0.645 | 5.355 | 0.014 | 0.12 | 0.904 | 0.589 | 1.697 |
| T11 | −1.740 | 5.065 | −0.040 | −0.344 | 0.732 | 0.594 | 1.682 |
| T12 | 0.821 | 4.903 | 0.020 | 0.167 | 0.868 | 0.597 | 1.676 |
| L1 | −1.368 | 6.173 | −0.026 | −0.222 | 0.825 | 0.577 | 1.732 |
| L2 | 5.756 | 4.323 | 0.171 | 1.332 | 0.187 | 0.492 | 2.033 |
| L3 | 13.878 | 4.292 | 0.426 | 3.234 | 0.002 | 0.468 | 2.137 |
| L4 | 0.005 | 3.232 | 0.000 | 0.002 | 0.999 | 0.449 | 2.225 |
| L5 | 1.429 | 4.940 | 0.039 | 0.289 | 0.773 | 0.450 | 2.223 |
| S1 | 4.726 | 4.367 | 0.112 | 1.082 | 0.283 | 0.756 | 1.323 |
| Unstandardized Coefficients | Standardized Coefficients | t | Sig. | Collinearity Statistics | |||
|---|---|---|---|---|---|---|---|
| B | Std. Error | Beta | Tolerance | VIF | |||
| Constant | 42.974 | 5.011 | 8.576 | 0.000 | |||
| C7 DS | −3.223 | 6.484 | −0.071 | −0.497 | 0.621 | 0.422 | 2.372 |
| T1 DS | −8.138 | 7.034 | −0.141 | −1.157 | 0.252 | 0.582 | 1.719 |
| T2 DS | 13.016 | 9.327 | 0.178 | 1.396 | 0.168 | 0.532 | 1.879 |
| T3 DS | −1.765 | 14.115 | −0.018 | −0.125 | 0.901 | 0.442 | 2.261 |
| T4 DS | 14.262 | 10.591 | 0.173 | 1.347 | 0.183 | 0.526 | 1.901 |
| T5 DS | 0.051 | 2.987 | 0.002 | 0.017 | 0.986 | 0.935 | 1.07 |
| T6 DS | 1.799 | 9.097 | 0.028 | 0.198 | 0.844 | 0.444 | 2.251 |
| T7 DS | −9.794 | 9.464 | −0.111 | −1.035 | 0.305 | 0.753 | 1.328 |
| T8 DS | 15.991 | 10.782 | 0.228 | 1.483 | 0.143 | 0.367 | 2.721 |
| T9 DS | 10.704 | 7.059 | 0.185 | 1.516 | 0.135 | 0.582 | 1.718 |
| T10 DS | 0.348 | 9.074 | 0.005 | 0.038 | 0.969 | 0.476 | 2.101 |
| T11 DS | −7.186 | 7.710 | −0.145 | −0.932 | 0.355 | 0.362 | 2.763 |
| T12 DS | −3.296 | 3.881 | −0.104 | −0.849 | 0.399 | 0.576 | 1.735 |
| L1 DS | 5.593 | 14.074 | 0.059 | 0.397 | 0.692 | 0.401 | 2.496 |
| L2 DS | 11.203 | 6.644 | 0.282 | 1.686 | 0.097 | 0.311 | 3.216 |
| L3 DS | 1.008 | 1.65 | 0.078 | 0.611 | 0.543 | 0.532 | 1.880 |
| L4 DS | 4.870 | 4.314 | 0.153 | 1.129 | 0.263 | 0.475 | 2.107 |
| L5 DS | 3.338 | 4.522 | 0.103 | 0.738 | 0.463 | 0.447 | 2.236 |
| S1 DS | −2.306 | 3.682 | −0.064 | −0.626 | 0.533 | 0.827 | 1.209 |
Appendix A.3. Learning Curve Panels—Male Cases (Figure A4, Figure A5, Figure A6, Figure A7 and Figure A8)



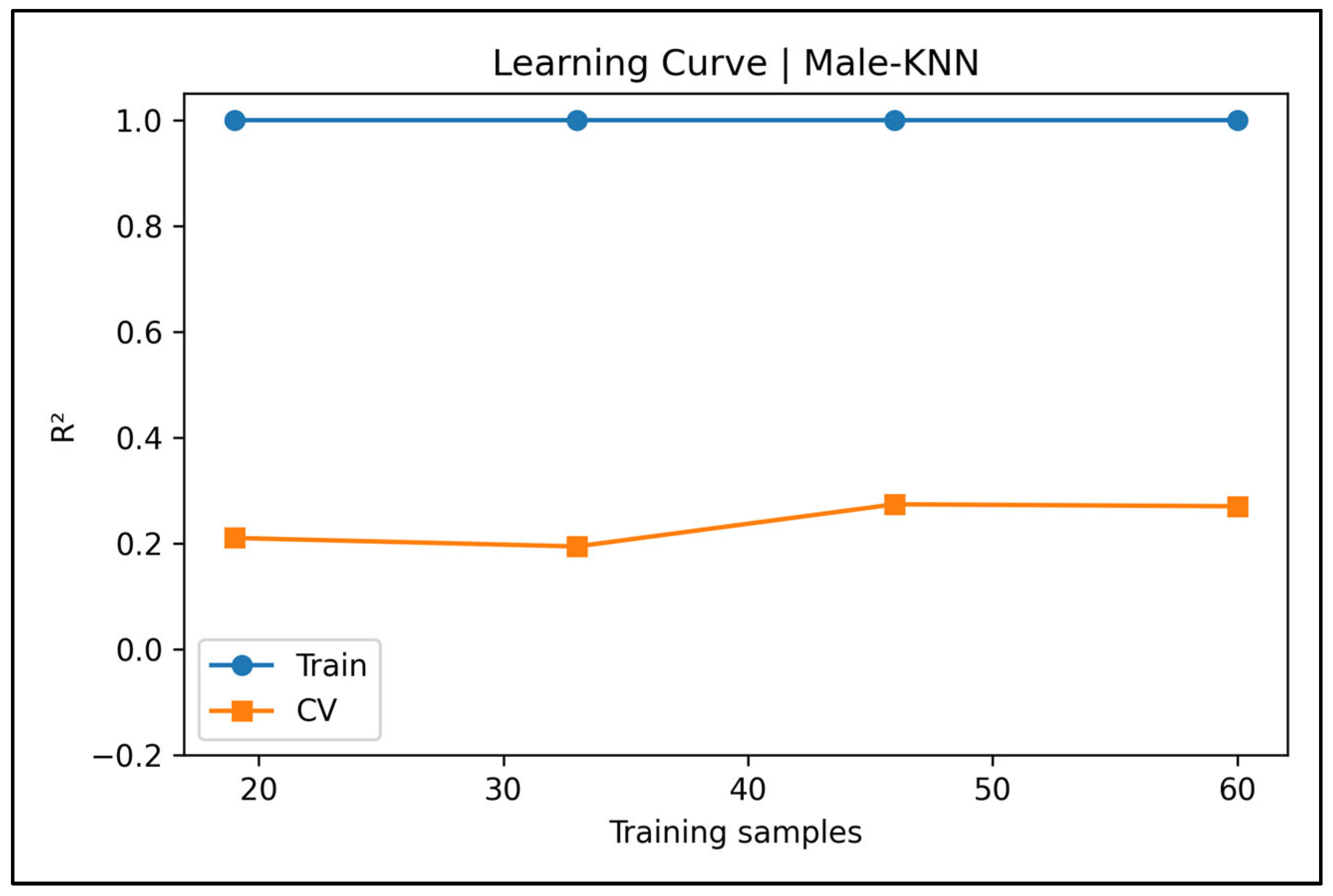
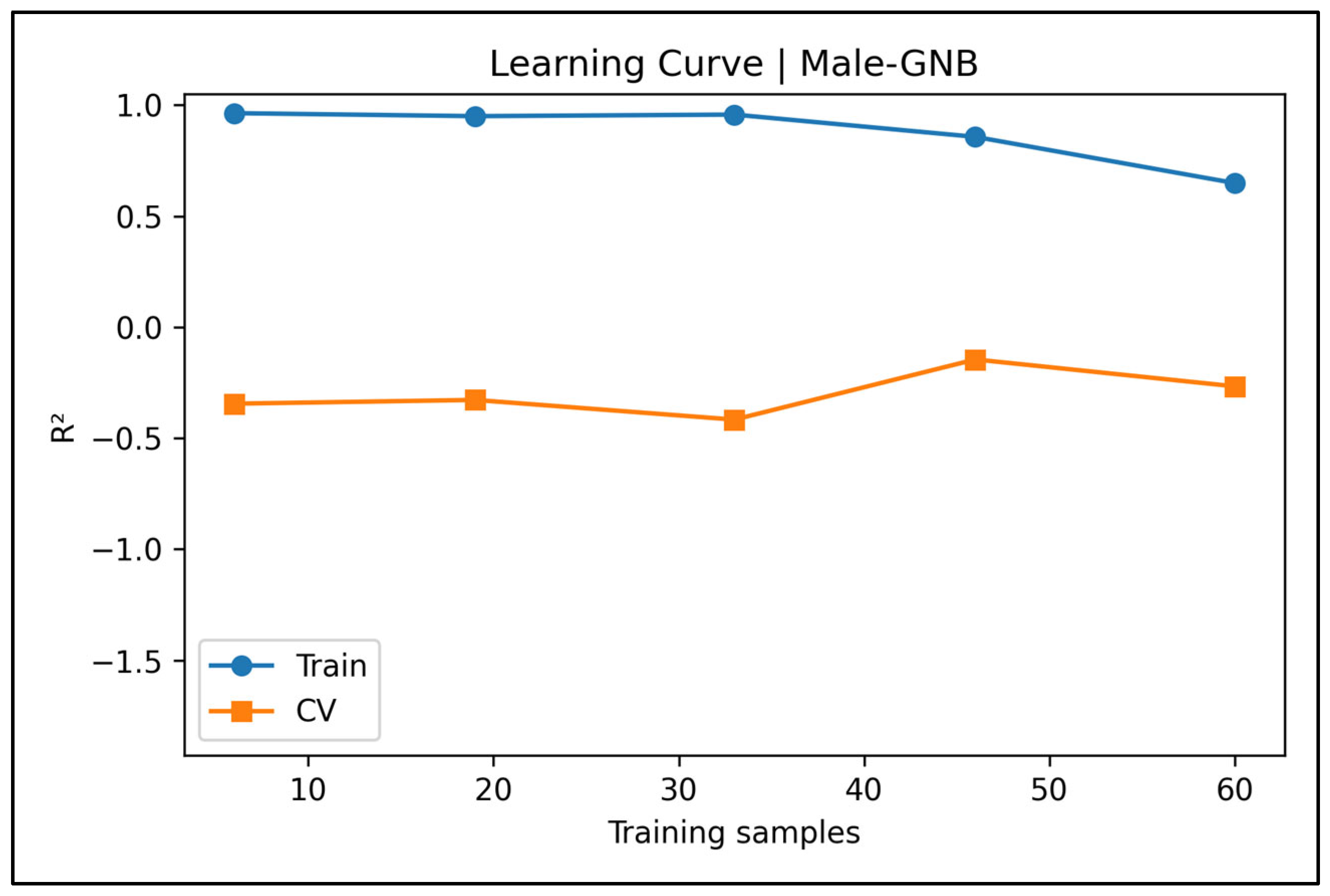
Appendix A.4. Bland–Altman Plots—Male Cases (Figure A9, Figure A10, Figure A11, Figure A12 and Figure A13)



Appendix A.5. Permutation Importance Plots—Male Cases (Figure A14, Figure A15, Figure A16, Figure A17 and Figure A18)



Appendix A.6. Predicted vs. True Scatter Plots—Male Cases (Figure A19, Figure A20, Figure A21, Figure A22 and Figure A23)

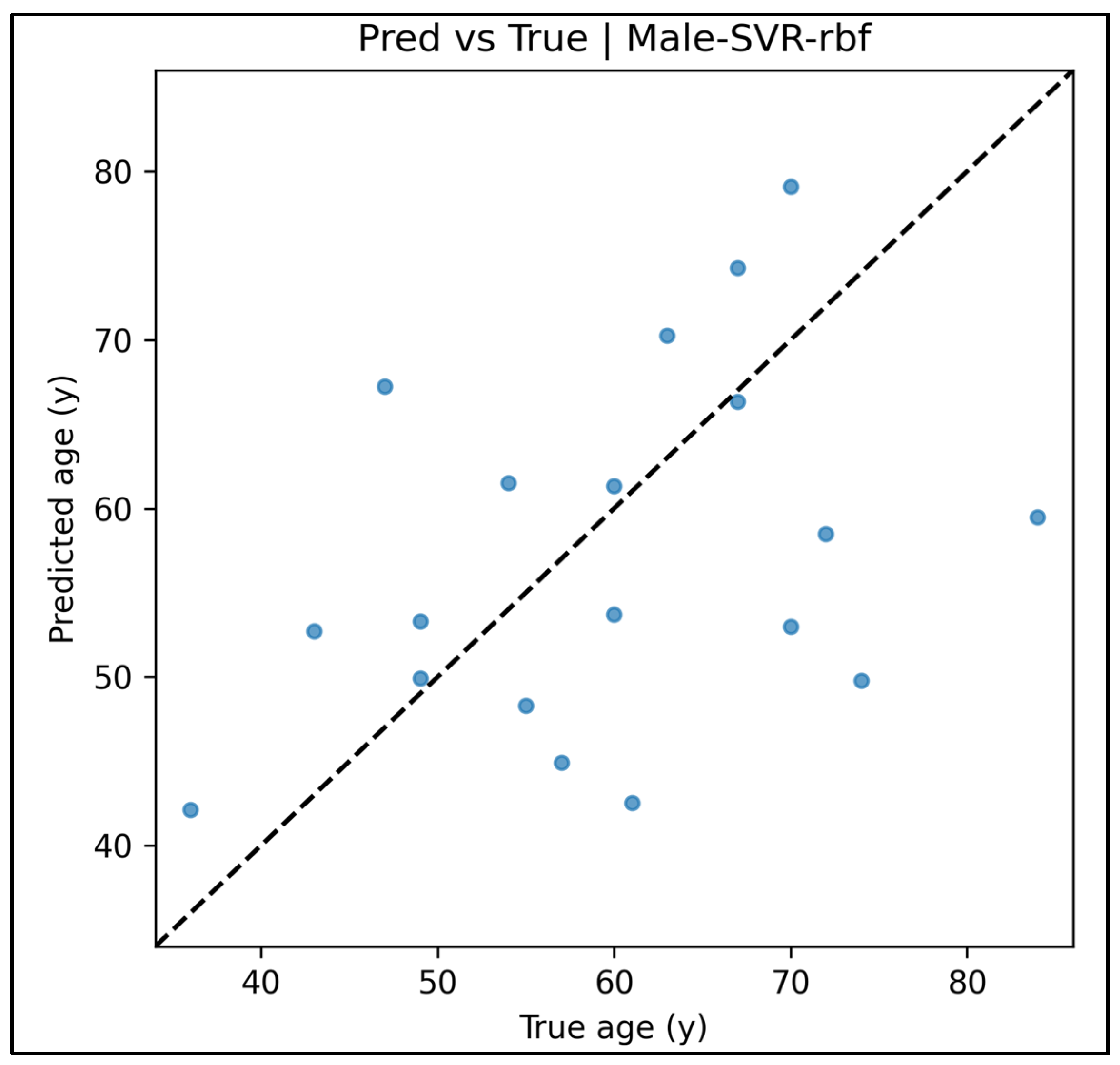
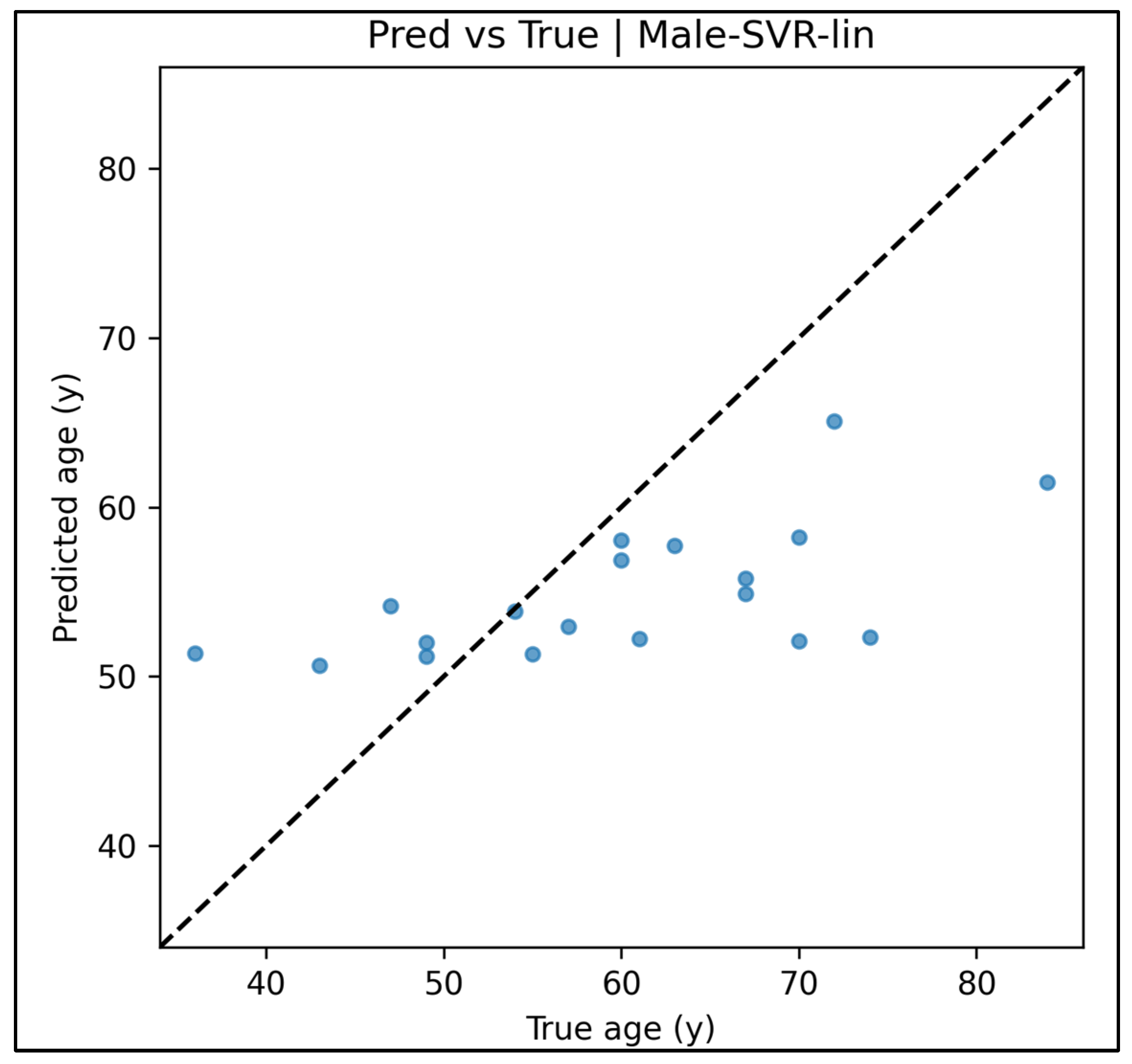


Appendix A.7. Residual vs. Fitted Plots—Male Cases (Figure A24, Figure A25, Figure A26, Figure A27 and Figure A28)





Appendix A.8. Residual Histograms—Male Cases (Figure A29, Figure A30, Figure A31, Figure A32 and Figure A33)

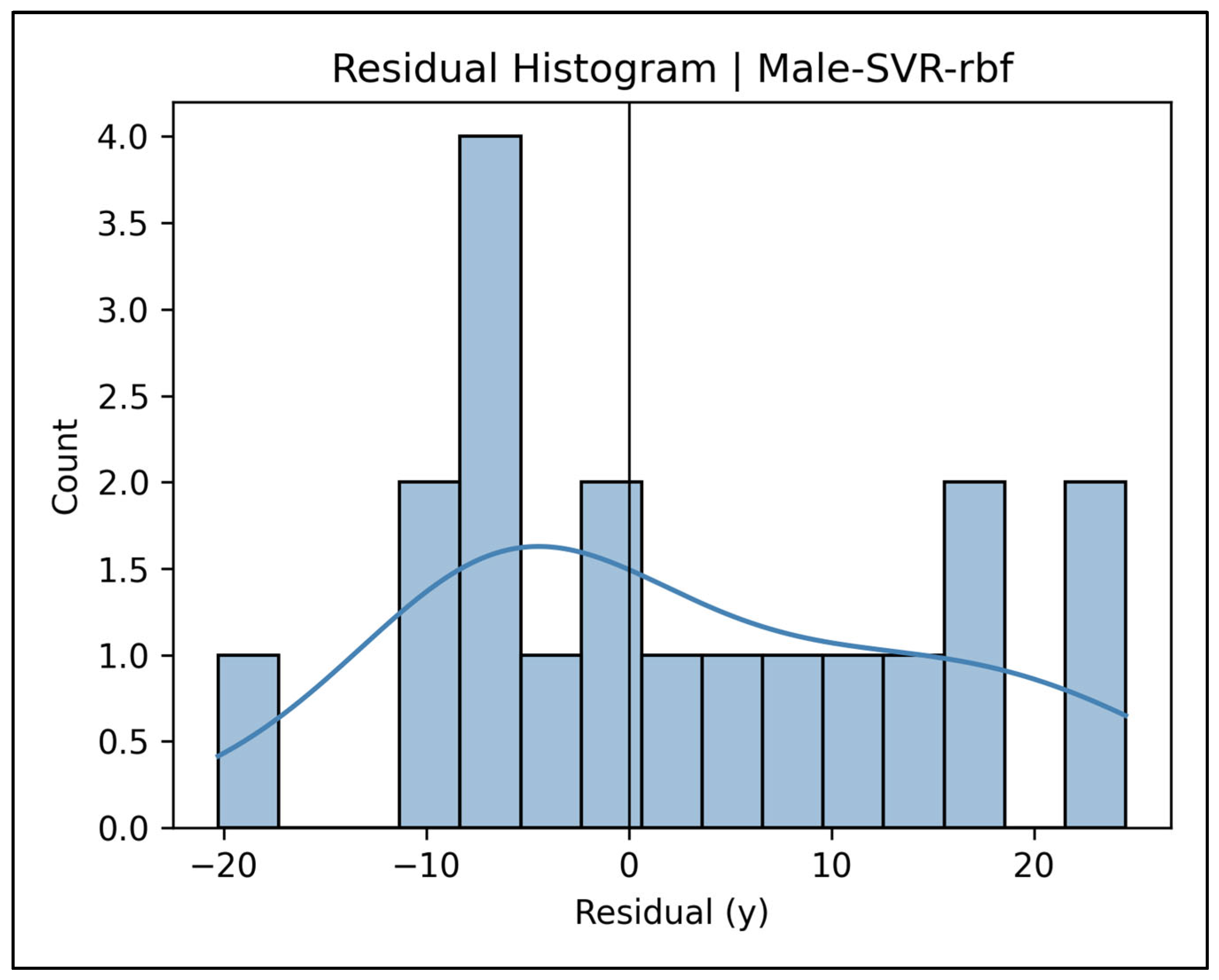
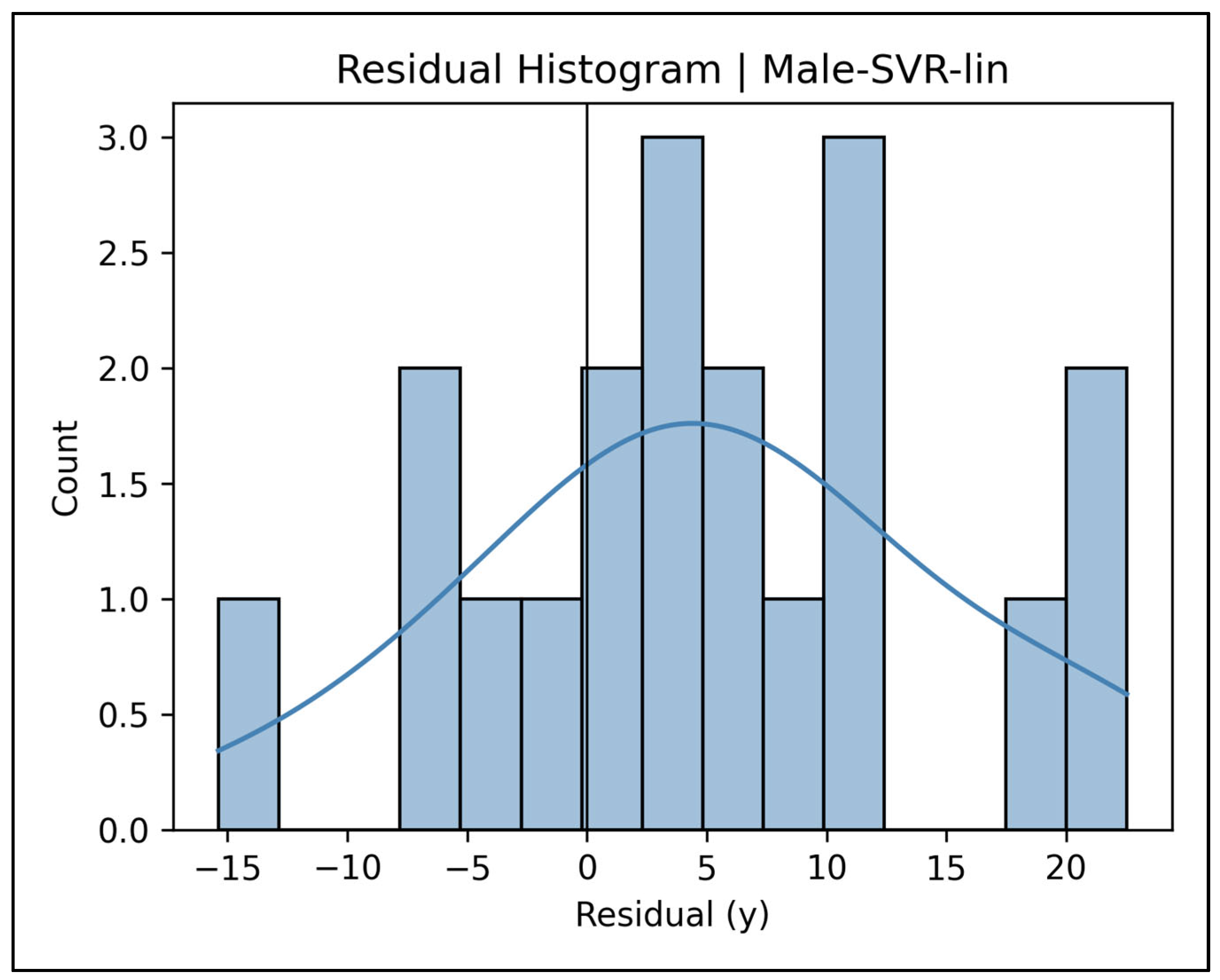
Appendix A.9. Learning Curve Panels—Female Cases (Figure A34, Figure A35, Figure A36, Figure A37 and Figure A38)




Appendix A.10. Bland–Altman Plots—Female Cases (Figure A39, Figure A40, Figure A41, Figure A42 and Figure A43)



Appendix A.11. Permutation-Importance Plots—Female Cases (Figure A44, Figure A45, Figure A46, Figure A47 and Figure A48)



Appendix A.12. Predicted vs. True Scatter Plots—Female Cases (Figure A49, Figure A50, Figure A51, Figure A52 and Figure A53)
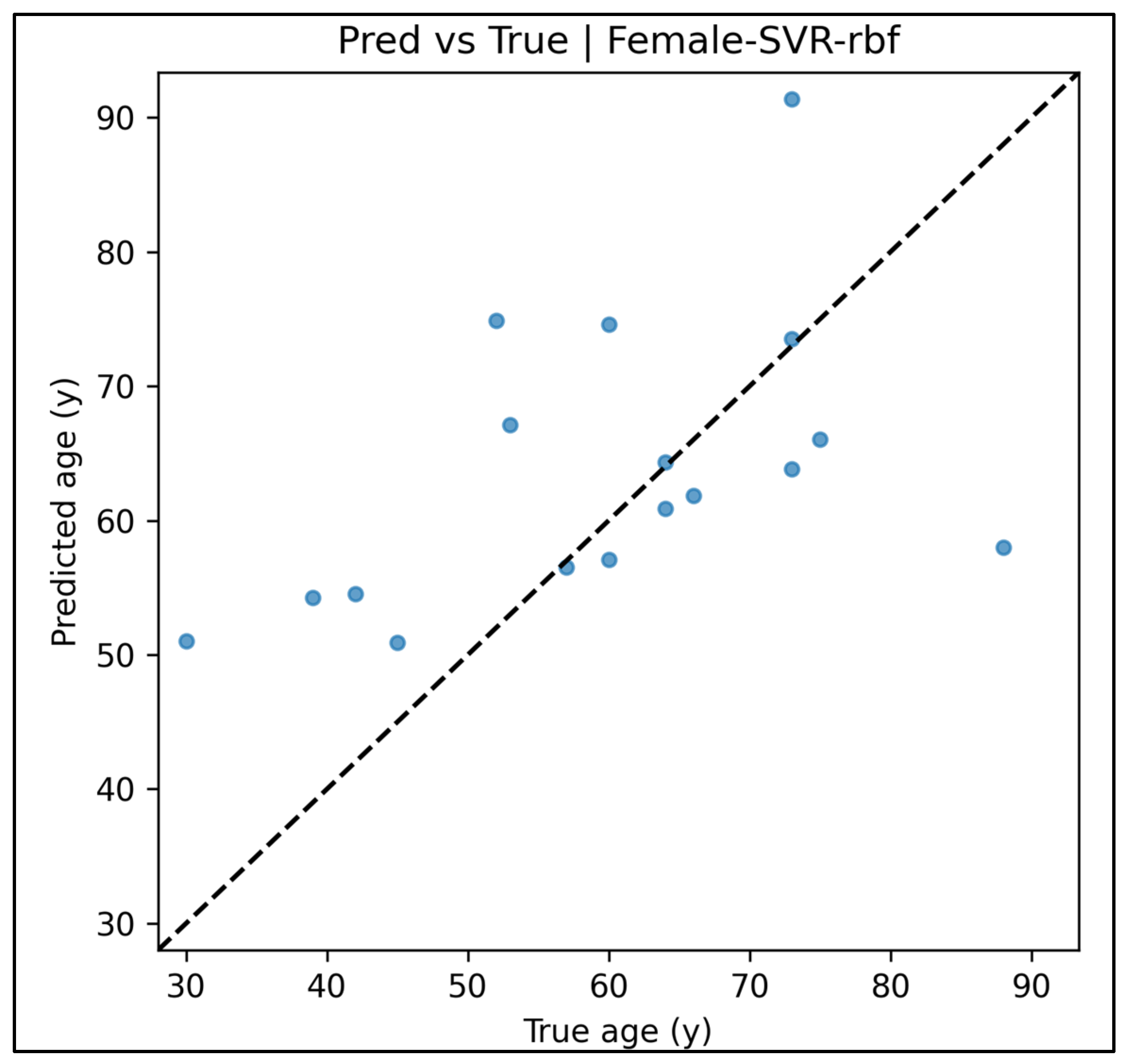
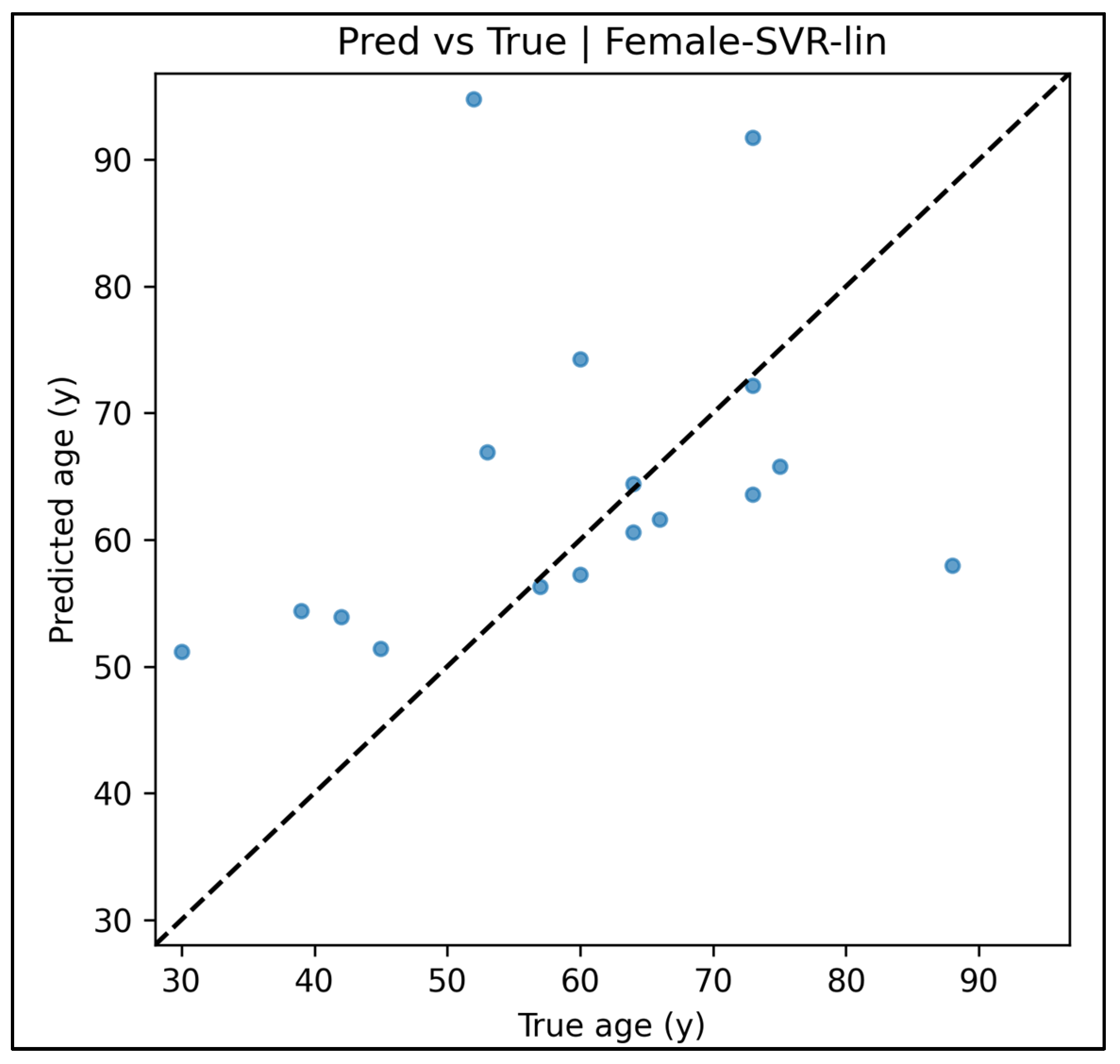
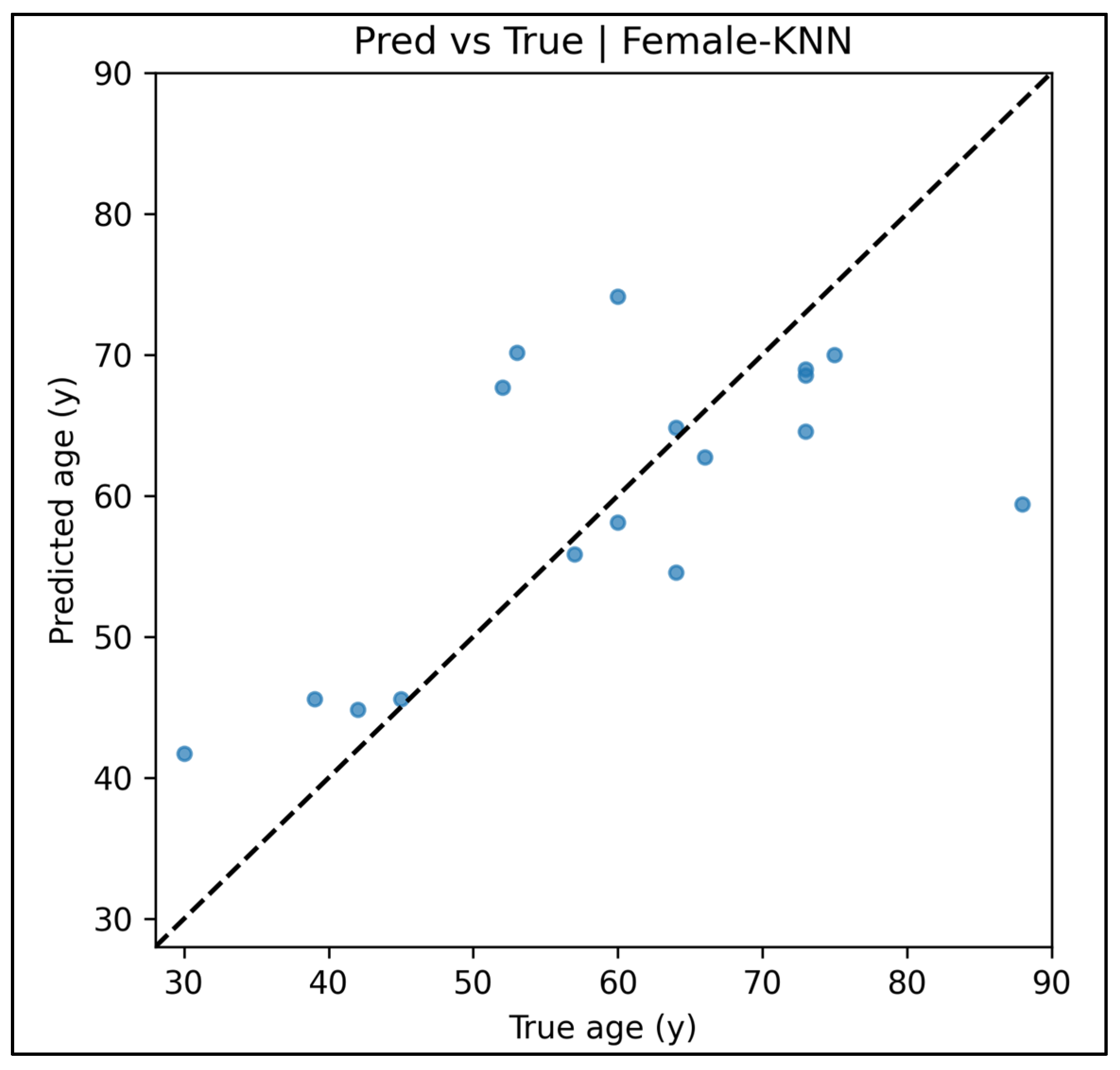
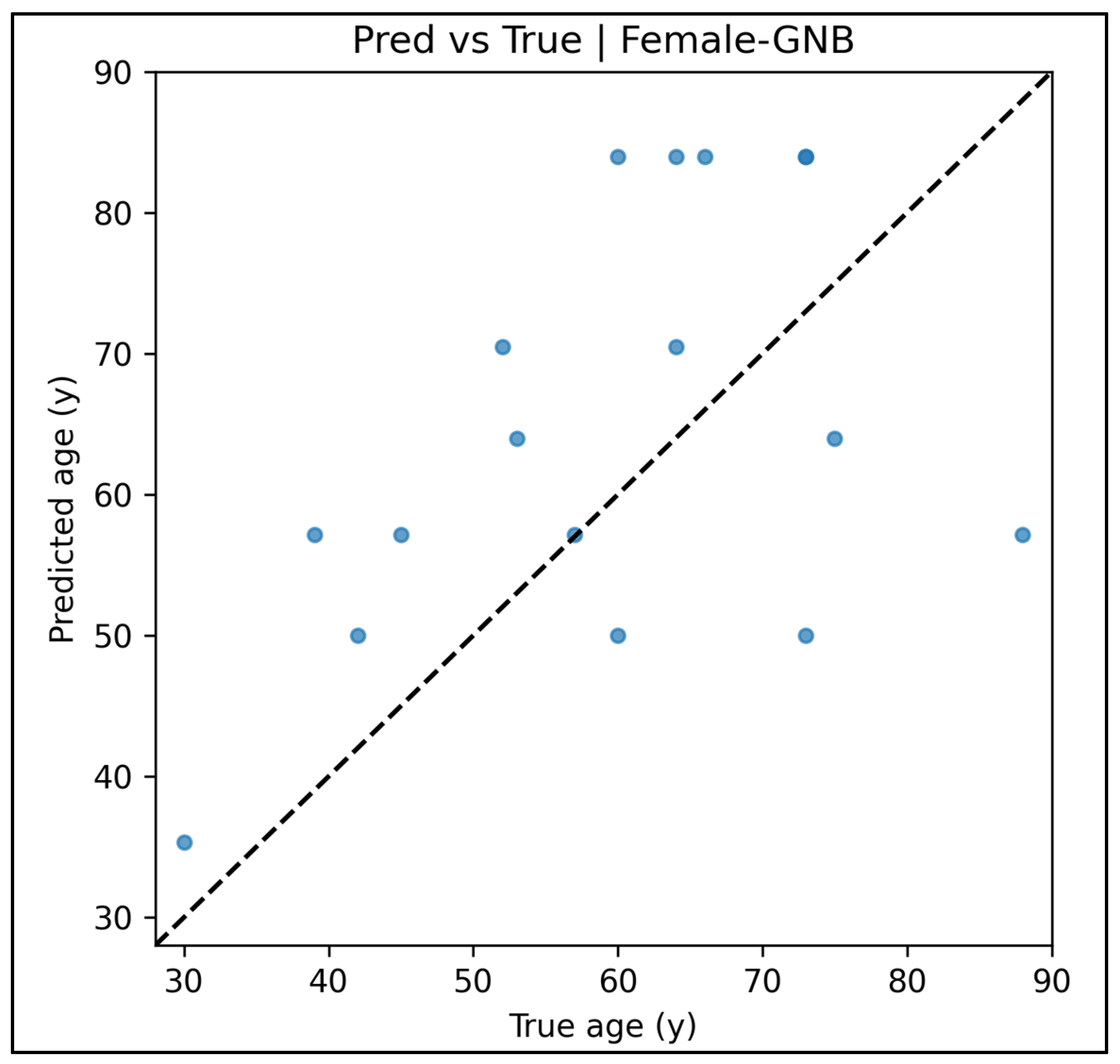
Appendix A.13. Residual vs. Fitted Plots—Female Cases (Figure A54, Figure A55, Figure A56, Figure A57 and Figure A58)


Appendix A.14. Residual Histograms—Female Cases (Figure A59, Figure A60, Figure A61, Figure A62 and Figure A63)

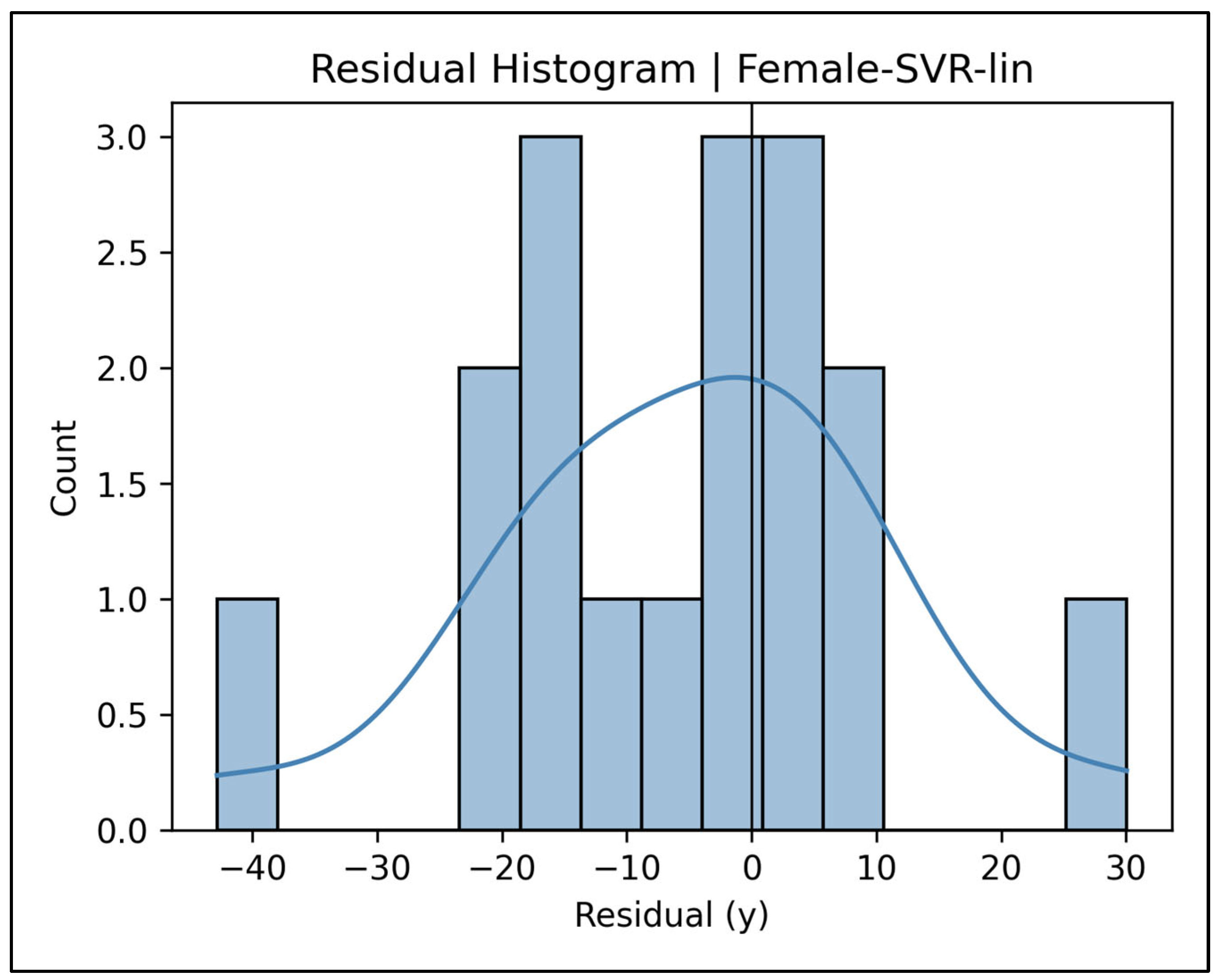

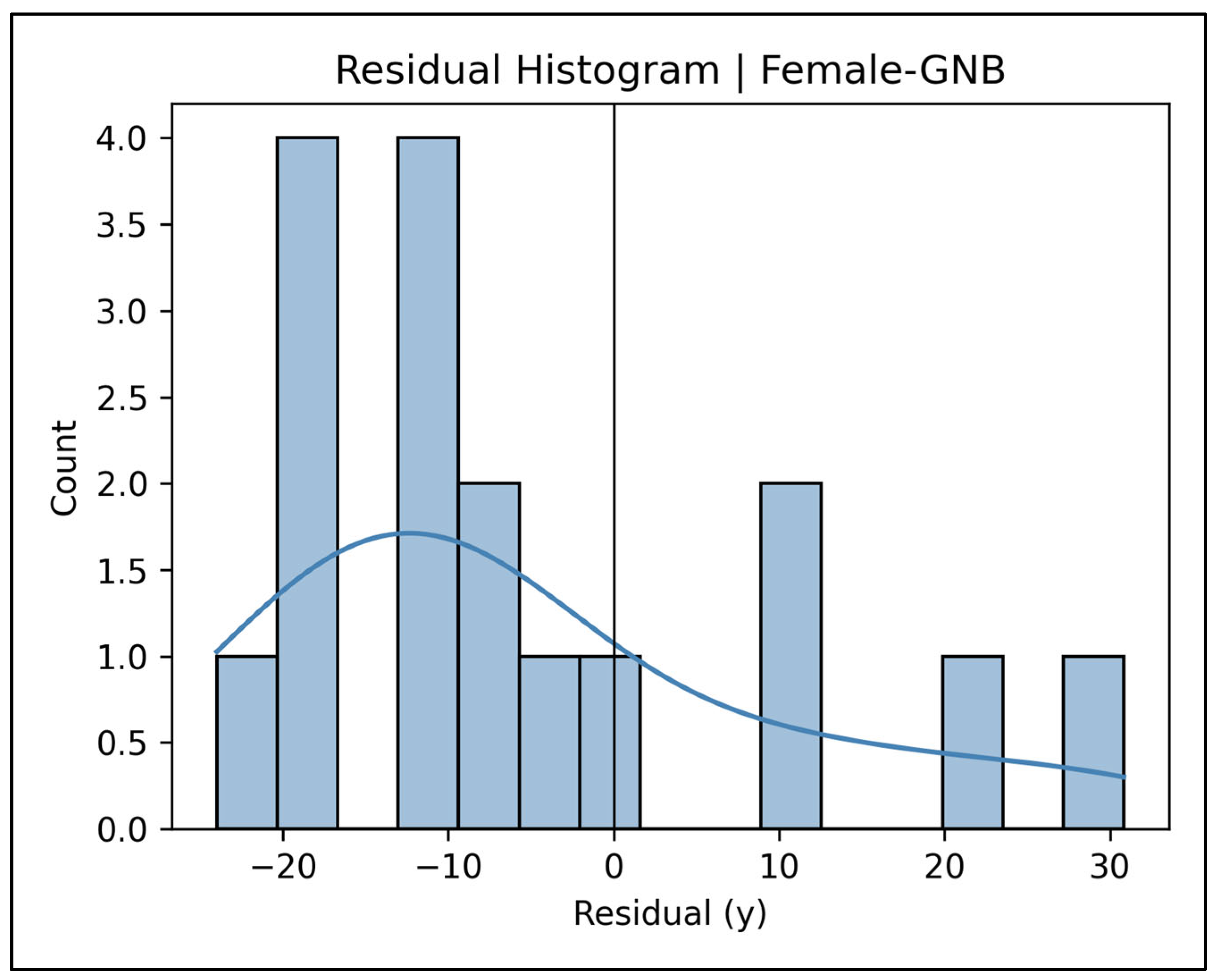
Appendix A.15. Pooled Total Sample Results
| Statistic | Pooled Total Sample (n = 176) |
|---|---|
| R | 0.566 |
| R2 | 0.321 |
| Adjusted R2 | 0.238 |
| SEE (years) | 12.18 |
| F (df) | 3.88 |
| Model p | 0.000 |
| Max VIF (variable) | 2.075 (L2 DS) |
| Min tolerance (variable) | 0.482 (L2 DS) |
| Max condition index | 15.3 |
| Collinearity flag | none |
| Unstandardized Coefficients | Standardized Coefficients | t | Sig. | Collinearity Statistics | |||
|---|---|---|---|---|---|---|---|
| B | Std. Error | Beta | Tolerance | VIF | |||
| Constant | 43.363 | 3.290 | 13.18 | 0.000 | |||
| C7 | 3.605 | 3.083 | 0.088 | 1.169 | 0.244 | 0.768 | 1.302 |
| T1 | −12.051 | 4.864 | −0.190 | −2.477 | 0.014 | 0.741 | 1.350 |
| T2 | 1.112 | 4.928 | 0.017 | 0.226 | 0.822 | 0.767 | 1.305 |
| T3 | 4.441 | 6.912 | 0.050 | 0.643 | 0.521 | 0.724 | 1.382 |
| T4 | 0.917 | 6.331 | 0.011 | 0.145 | 0.885 | 0.692 | 1.444 |
| T5 | 0.365 | 2.747 | 0.009 | 0.133 | 0.894 | 0.927 | 1.079 |
| T6 | 0.024 | 5.287 | 0.000 | 0.005 | 0.996 | 0.649 | 1.542 |
| T7 | −2.829 | 5.871 | −0.036 | −0.482 | 0.631 | 0.772 | 1.295 |
| T8 | 6.925 | 5.899 | 0.107 | 1.174 | 0.242 | 0.519 | 1.925 |
| T9 | 13.773 | 5.348 | 0.213 | 2.575 | 0.011 | 0.638 | 1.567 |
| T10 | 0.396 | 4.285 | 0.007 | 0.092 | 0.927 | 0.685 | 1.460 |
| T11 | −0.569 | 3.833 | −0.012 | −0.148 | 0.882 | 0.620 | 1.613 |
| T12 | −2.887 | 2.872 | −0.081 | −1.005 | 0.316 | 0.675 | 1.481 |
| L1 | 0.040 | 5.467 | 0.001 | 0.007 | 0.994 | 0.594 | 1.685 |
| L2 | 6.241 | 3.417 | 0.174 | 1.826 | 0.070 | 0.482 | 2.075 |
| L3 | 1.903 | 1.345 | 0.113 | 1.414 | 0.159 | 0.686 | 1.457 |
| L4 | 2.712 | 2.518 | 0.100 | 1.077 | 0.283 | 0.509 | 1.965 |
| L5 | 5.463 | 2.658 | 0.180 | 2.056 | 0.041 | 0.566 | 1.768 |
| S1 | 2.387 | 2.587 | 0.064 | 0.923 | 0.358 | 0.894 | 1.119 |
| Group | Model | Holdout R2 | 95% CI (R2) | SEE (y) | 95% CI (SEE) | MAE (y) | RMSE (y) | CV R2 | OOB R2 † |
|---|---|---|---|---|---|---|---|---|---|
| Pooled Total | LASSO | 0.061 | −0.32–0.25 | 19.61 | 15.9–23.2 | 10.72 | 13.07 | −0.037 | - |
| Pooled Total | RF | 0.191 | −0.29–0.44 | 18.20 | 14.6–21.4 | 10.14 | 12.13 | 0.454 | 0.443 |
| Pooled Total | SVR-rbf | 0.073 | −0.58–0.42 | 19.49 | 14.8–23.5 | 10.34 | 12.99 | 0.258 | - |
| Pooled Total | SVR-lin | 0.080 | −0.22–0.22 | 19.41 | 15.4–22.9 | 10.77 | 12.94 | 0.014 | - |
| Pooled Total | KNN | 0.153 | −0.33–0.41 | 18.62 | 15.0–21.8 | 10.41 | 12.41 | 0.211 | - |
| Pooled Total | GNB-Reg | −0.989 | −2.61–0.20 | 28.54 | 23.6–33.5 | 16.30 | 19.02 | 0.068 | - |
References
- Kotěrová, A.; Navega, D.; Štepanovský, M.; Buk, Z.; Brůžek, J.; Cunha, E. Age estimation of adult human remains from hip bones using advanced methods. Forensic Sci. Int. 2018, 287, 163–175. [Google Scholar] [CrossRef] [PubMed]
- Mansour, H.; Fuhrmann, A.; Paradowski, I.; van Well, E.J.; Püschel, K. The role of forensic medicine and forensic dentistry in estimating the chronological age of living individuals in Hamburg, Germany. Int. J. Leg. Med. 2017, 131, 593–601. [Google Scholar] [CrossRef]
- Yi, P.H.; Wei, J.; Kim, T.K.; Shin, J.; Sair, H.I.; Hui, F.K.; Hager, G.D.; Lin, C.T. Radiology “forensics”: Determination of age and sex from chest radiographs using deep learning. Emerg. Radiol. 2021, 28, 949–954. [Google Scholar] [CrossRef]
- Balan, H.; Alrasheedi, A.F.; Askar, S.S.; Abouhawwash, M. An Intelligent Human Age and Gender Forecasting Framework Using Deep Learning Algorithms. Appl. Artif. Intell. 2022, 36, 2073724. [Google Scholar] [CrossRef]
- İşcan, M.; Steyn, M. (Eds.) Skeletal Age. In The Human Skeleton in Forensic Medicine, 3rd ed.; Charles C Thomas: Springfield, IL, USA, 2013; pp. 59–142. [Google Scholar]
- Boldsen, J.L.; Milner, G.R.; Konigsberg, L.W.; Wood, J.W.; Hoppa, R.D.; Vaupel, J.W. Transition analysis: A new method for estimating age from skeletons. In Paleodemography; Academic Press: New York, NY, USA, 2002; pp. 73–106. [Google Scholar]
- Lye, R.; Obertová, Z.; Bachtiar, N.A.; Franklin, D. Skeletal age-at-death estimation: Validating the Suchey-Brooks method using 3D reconstructed models in a contemporary Indonesian population. Int. J. Leg. Med. 2025, 139, 1–13. [Google Scholar] [CrossRef]
- Marcante, B.; Marino, L.; Cattaneo, N.E.; Delicati, A.; Tozzo, P.; Caenazzo, L. Advancing forensic human chronological age estimation: Biochemical, genetic, and epigenetic approaches from the last 15 years: A systematic review. Int. J. Mol. Sci. 2025, 26, 3158. [Google Scholar] [CrossRef] [PubMed]
- Appel, N.S.; Edgar, H.J.H. A pilot study of age estimation and cause of death: Insights into skeletal aging. Forensic Sci. 2024, 4, 508–522. [Google Scholar] [CrossRef]
- Baccino, E.; Schmitt, A. Determination of adult age at death in the forensic context. In Forensic Anthropology and Medicine: Complementary Sciences from Recovery to Cause of Death; DiGangi, E.A., Bethard, J.D., Eds.; Springer: New York, NY, USA, 2006; pp. 259–280. [Google Scholar]
- Bertsatos, A.; Chovalopoulou, M.E.; Boskovits, N.M.; Garoufi, N.; Nikita, E. The impact of activity on pelvic age-at-death estimation. Int. J. Osteoarchaeol. 2021, 31, 218–231. [Google Scholar] [CrossRef]
- Milner, G.R.; Getz, S.M.; Weise, S.; Boldsen, J.L. Ongoing Work with Adult Skeletal Age Estimation: What Works and What Doesn’t. Forensic Anthropol. 2024, 7, 187–196. [Google Scholar] [CrossRef]
- Sluis, I.F.; Bartholdy, B.P.; Hoogland, M.L.P.; Schrader, S.A. Age estimation using vertebral bone spurs; Testing the efficacy of three methods on a European population. Forensic Sci. Int. Rep. 2022, 6, 100301. [Google Scholar] [CrossRef]
- Algee-Hewitt, B.F.B.; Kim, J. Remodeling Forensic Skeletal Age: Modern Applications and New Research Directions, 1st ed.; Academic Press: Cambridge, MA, USA, 2021; pp. 1–260. [Google Scholar]
- Snodgrass, J. Sex Differences and Aging of the Vertebral Column. J. Forensic Sci. 2004, 49, JFS2003198-6. [Google Scholar] [CrossRef]
- Thomsen, J.S.; Jensen, M.V.; Niklassen, A.S.; Ebbesen, E.N.; Brüel, A. Age-related changes in vertebral and iliac crest 3D bone microstructure—Differences and similarities. Osteoporos. Int. 2015, 26, 219–228. [Google Scholar] [CrossRef]
- Watanabe, S.; Terazawa, K. Age estimation from the degree of osteophyte formation of vertebral columns in Japanese. Leg. Med. 2006, 8, 156–160. [Google Scholar] [CrossRef]
- Cardoso, H.F.V.; Ríos, L. Age estimation from stages of epiphyseal union in the presacral vertebrae. Am. J. Phys. Anthropol. 2011, 144, 238–247. [Google Scholar] [CrossRef]
- Praneatpolgrang, S.; Prasitwattanaseree, S.; Mahakkanukrauh, P. Age estimation equations using vertebral osteophyte formation in a Thai population: Comparison and modified osteophyte scoring method. Anat. Cell Biol. 2019, 52, 149–160. [Google Scholar] [CrossRef]
- Uys, A.; Bernitz, H.; Pretorius, S.; Steyn, M. Age estimation from anterior cervical vertebral ring apophysis ossification in South Africans. Int. J. Leg. Med. 2019, 133, 1935–1948. [Google Scholar] [CrossRef]
- Chiba, F.; Inokuchi, G.; Hoshioka, Y.; Sakuma, A.; Makino, Y.; Torimitsu, S.; Yamaguchi, R.; Saitoh, H.; Kono, M.; Iwase, H. Age estimation by evaluation of osteophytes in thoracic and lumbar vertebrae using postmortem CT images in a modern Japanese population. Int. J. Leg. Med. 2022, 136, 261–267. [Google Scholar] [CrossRef]
- Adams, B.J.; Butler, E.; Fuehr, S.M.; Olivares-Pérez, F.; Tamayo, A.S. Radiographic age estimation based on degenerative changes of vertebrae. J. Forensic Sci. 2024, 69, 391–399. [Google Scholar] [CrossRef]
- Nurzynska, K.; Piórkowski, A.; Strzelecki, M.; Kociołek, M.; Banyś, R.P.; Obuchowicz, R. Differentiating age and sex in vertebral body CT scans—Texture analysis versus deep learning approach. Biocybern. Biomed. Eng. 2024, 44, 20–30. [Google Scholar] [CrossRef]
- Kawashita, I.; Fukumoto, W.; Mitani, H.; Narita, K.; Chosa, K.; Nakamura, Y.; Nagao, M.; Awai, K. Development of a deep-learning algorithm for age estimation on CT images of the vertebral column. Leg. Med. 2024, 69, 102444. [Google Scholar] [CrossRef] [PubMed]
- Kaçar, E.; Unlu, E.; Beker-Acay, M.; Balcik, C.; Gultekin, M.A.; Kocak, U.; Eroglu, S.; Yucel, A. Age estimation by assessing the vertebral osteophytes with the aid of 3D CT imaging. Aust. J. Forensic Sci. 2017, 49, 449–458. [Google Scholar] [CrossRef]
- Zangpo, D.; Uehara, K.; Kondo, K.; Yoshimiya, M.; Nakatome, M.; Iino, M. A novel method to estimate adult age from the lumbar vertebral body using 3D PMCT images in Japanese. Leg. Med. 2023, 61, 102215. [Google Scholar] [CrossRef]
- Malatong, Y.; Palee, P.; Sinthubua, A.; Na Lampang, S.; Mahakkanukrauh, P. Estimating age from digital radiographic images of lumbar vertebrae in a Thai population using an image analysis technique. Med. Sci. Law 2022, 62, 180–187. [Google Scholar] [CrossRef]
- Garoufi, N.; Bertsatos, A.; Jørkov, M.L.S.; Villa, C.; Chovalopoulou, M.E. The impact of age on the morphology of the 12th thoracic vertebral endplates. Anat. Cell Biol. 2022, 55, 441–451. [Google Scholar] [CrossRef]
- Ramadan, N.; Abd El-Salam, M.H.A.E.; Hanon, A.F.; El-Sayed, N.F.; Al-Amir, A.Y. Age and Sex Identification Using Multi-slice Computed Tomography of the Last Thoracic Vertebrae of an Egyptian Sample. J. Forensic Res. 2017, 8, 386. [Google Scholar] [CrossRef]
- Rizos, L.; Garoufi, N.; Valakos, E.; Nikita, E.; Chovalopoulou, M.E. Testing the accuracy of the DRNNAGE software for age estimation in a modern Greek sample. Int. J. Leg. Med. 2024, 138, 917–926. [Google Scholar] [CrossRef]
- Schanandore, J.V.; Ford, J.M.; Decker, S.J. Predicting chronological age based on age-related osteophyte development in the superior and inferior vertebral centrum margins of T12-L5. J. Forensic Sci. 2024, 69, 18–27. [Google Scholar] [CrossRef]
- Zangpo, D.; Uehara, K.; Kondo, K.; Kato, M.; Yoshimiya, M.; Nakatome, M.; Iino, M. Estimating age at death by Hausdorff distance analyses of the fourth lumbar vertebral bodies using 3D postmortem CT images. Forensic Sci. Med. Pathol. 2024, 20, 472–479. [Google Scholar] [CrossRef]
- Suwanlikhid, N.; Prasitwattanaseree, S.; Palee, P.; Mahakkanukrauh, P. Age Estimation of Lumbar Vertebrae by Visual Assessment in a Thai Population. Clin. Ter. 2018, 169, e204–e212. [Google Scholar] [CrossRef]
- Etli, Y. Adult Bone Age Estimation by Sacral Base Surface Roughness: A Pilot Study Using Image Processing. In Proceedings of the 4th International TURAZ Academy International Congress in Clinical Medicolegal Perspective & Forensic Sciences, Forensic Medicine and Pathology, Antalya, Türkiye, 5–8 October 2023. [Google Scholar] [CrossRef]
- Kontopoulos, I.; Nystrom, P.; White, L. Experimental taphonomy: Post-mortem microstructural modifications in Sus scrofa domesticus bone. Forensic Sci. Int. 2016, 266, 320–328. [Google Scholar] [CrossRef] [PubMed]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed]
- Vishwanatha, J.S.; Srinivasa Pai, P.; D’Mello, G.; Sampath Kumar, L.; Bairy, R.; Nagaral, M.; Channa Keshava Naik, N.; Lamani, V.T.; Chandrashekar, A.; Yunus Khan, T.M.; et al. Image-processing-based model for surface roughness evaluation in titanium based alloys using dual tree complex wavelet transform and radial basis function neural networks. Sci. Rep. 2024, 14, 28261. [Google Scholar] [CrossRef]
- Askaruly, S.; Ahn, Y.; Kim, H.; Vavilin, A.; Ban, S.; Kim, P.U.; Jung, W. Quantitative evaluation of skin surface roughness using optical coherence tomography in vivo. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 6800908. [Google Scholar] [CrossRef]
- Hossain, U.; Ghouse, S.; Nai, K.; Jeffers, J.R.T. Mechanical and morphological properties of additively manufactured SS316L and Ti6Al4V micro-struts as a function of build angle. Addit. Manuf. 2021, 46, 102050. [Google Scholar] [CrossRef]
- Grabherr, S.; Grimm, J.; Dominguez, A.; Vanhaebost, J.; Mangin, P. Advances in post-mortem CT-angiography. Br. J. Radiol. 2014, 87, 20130488. [Google Scholar] [CrossRef] [PubMed]
- Timme, M.; Steinacker, J.M.; Schmeling, A. Age estimation in competitive sports. Int. J. Leg. Med. 2017, 131, 225–233. [Google Scholar] [CrossRef] [PubMed]
- Thicot, F.; Egger, C.; Castiglioni, C.; Magnin, V.; Boudabbous, S.; Angelakopoulos, N.; Grabherr, S.; Genet, P. Forensic age estimation at the University Center of Legal Medicine Lausanne-Geneva: A retrospective study over 12 years. Int. J. Leg. Med. 2024, 138, 1881–1889. [Google Scholar] [CrossRef]
- Conder, R.; Zamani, R.; Akrami, M. The Biomechanics of Pregnancy: A Systematic Review. J. Funct. Morphol. Kinesiol. 2019, 4, 72. [Google Scholar] [CrossRef]
- Schini, M.; Vilaca, T.; Gossiel, F.; Salam, S.; Eastell, R. Bone Turnover Markers: Basic Biology to Clinical Applications. Endocr. Rev. 2023, 44, 417–473. [Google Scholar] [CrossRef]
- White, L.; Booth, T.J. The origin of bacteria responsible for bioerosion to the internal bone microstructure: Results from experimentally-deposited pig carcasses. Forensic Sci. Int. 2014, 239, 92–102. [Google Scholar] [CrossRef]
- Landsman, C.; Myburgh, J.; Meyer, A. The taphonomic effects of long-term burial in the South African Highveld. Int. J. Leg. Med. 2024, 138, 2093–2105. [Google Scholar] [CrossRef] [PubMed]
- Shanley, C.; Obertová, Z.; Franklin, D. Dimensional Accuracy of Structured Light Scans and 3D Prints of Various Human Skeletal Elements. Forensic Sci. Int. 2024, 361, 112138. [Google Scholar] [CrossRef]
- Morrison, M.; Bell, J.; George, C.; Harmon, S.; Munsie, M.; Kaye, J. The European General Data Protection Regulation: Challenges and Considerations for iPSC Researchers and Biobanks. Regen. Med. 2017, 12, 693–703. [Google Scholar] [CrossRef]
- Deliversky, J.; Deliverska, M. Ethical and Legal Considerations in Biometric Data Usage—Bulgarian Perspective. Front. Public Health 2018, 6, 25. [Google Scholar] [CrossRef] [PubMed]
- Heldring, N.; Rezaie, A.R.; Larsson, A.; Gahn, R.; Zilg, B.; Camilleri, S.; Saade, A.; Wesp, P.; Palm, E.; Kvist, O. A probability model for estimating age in young individuals relative to key legal thresholds: 15, 18 or 21-year. Int. J. Leg. Med. 2025, 139, 197–217. [Google Scholar] [CrossRef] [PubMed]
- Schmeling, A.; Dettmeyer, R.; Rudolf, E.; Vieth, V.; Geserick, G. Forensic Age Estimation. Dtsch. Arztebl. Int. 2016, 113, 44–50. [Google Scholar] [CrossRef]
- Raftery, K.A.; Kargarzadeh, A.; Tavana, S.; Newell, N. Disc degeneration influences the strain magnitude and stress distribution within the adjacent trabecular bone. Front. Bioeng. Biotechnol. 2024, 12, 1511685. [Google Scholar] [CrossRef]
- Arlot, M.E.; Burt-Pichat, B.; Roux, J.P.; Vashishth, D.; Bouxsein, M.L.; Delmas, P.D. Microarchitecture influences microdamage accumulation in human vertebral trabecular bone. J. Bone Miner. Res. 2008, 23, 1613–1618. [Google Scholar] [CrossRef]
- Piemontese, M.; Almeida, M.; Robling, A.G.; Kim, H.N.; Xiong, J.; Thostenson, J.D.; Weinstein, R.S.; Manolagas, S.C.; O’Brien, C.A.; Jilka, R.L. Old age causes de novo intracortical bone remodeling and porosity in mice. JCI Insight 2017, 2, e93771. [Google Scholar] [CrossRef]
- Cooper, D.M.; Thomas, C.D.; Clement, J.G.; Turinsky, A.L.; Sensen, C.W.; Hallgrímsson, B. Age-dependent change in the 3D structure of cortical porosity at the human femoral midshaft. Bone 2007, 40, 957–965. [Google Scholar] [CrossRef]
- Maggiano, I.S.; Maggiano, C.M.; Clement, J.G.; Thomas, C.D.; Carter, Y.; Cooper, D.M. Three-dimensional reconstruction of Haversian systems in human cortical bone using synchrotron radiation-based micro-CT: Morphology and quantification of branching and transverse connections across age. J. Anat. 2016, 228, 719–732. [Google Scholar] [CrossRef] [PubMed]
- Tabassum, A.; Singh, M.K.C.; Ibrahim, N.; Sanjeevan, V.; Yusof, M.Y.P.M. Trabecular bone microstructure parameters as predictors for chronological age: A systematic review. Forensic Sci. Med. Pathol. 2024; advance online publication. [Google Scholar] [CrossRef]
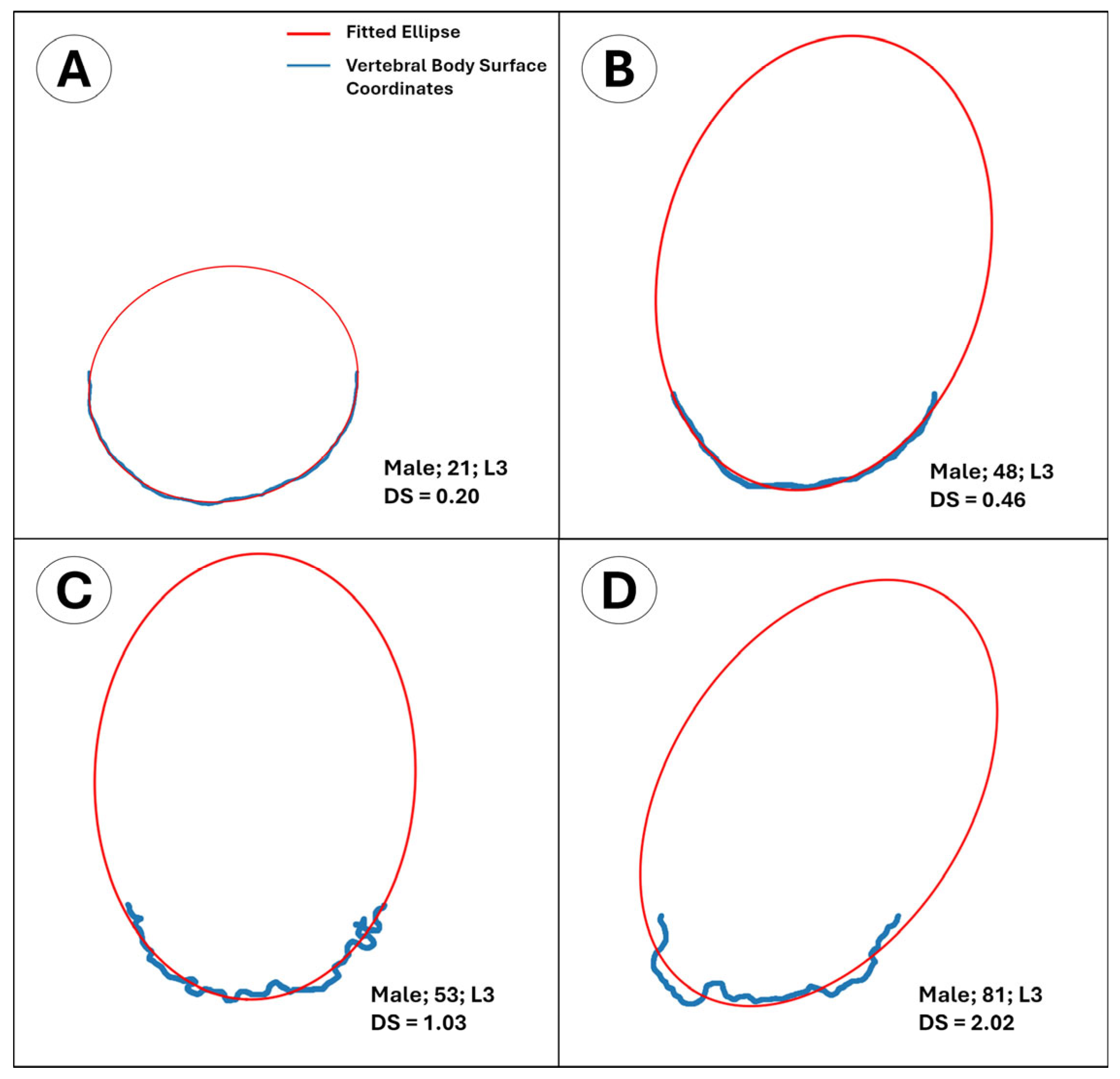
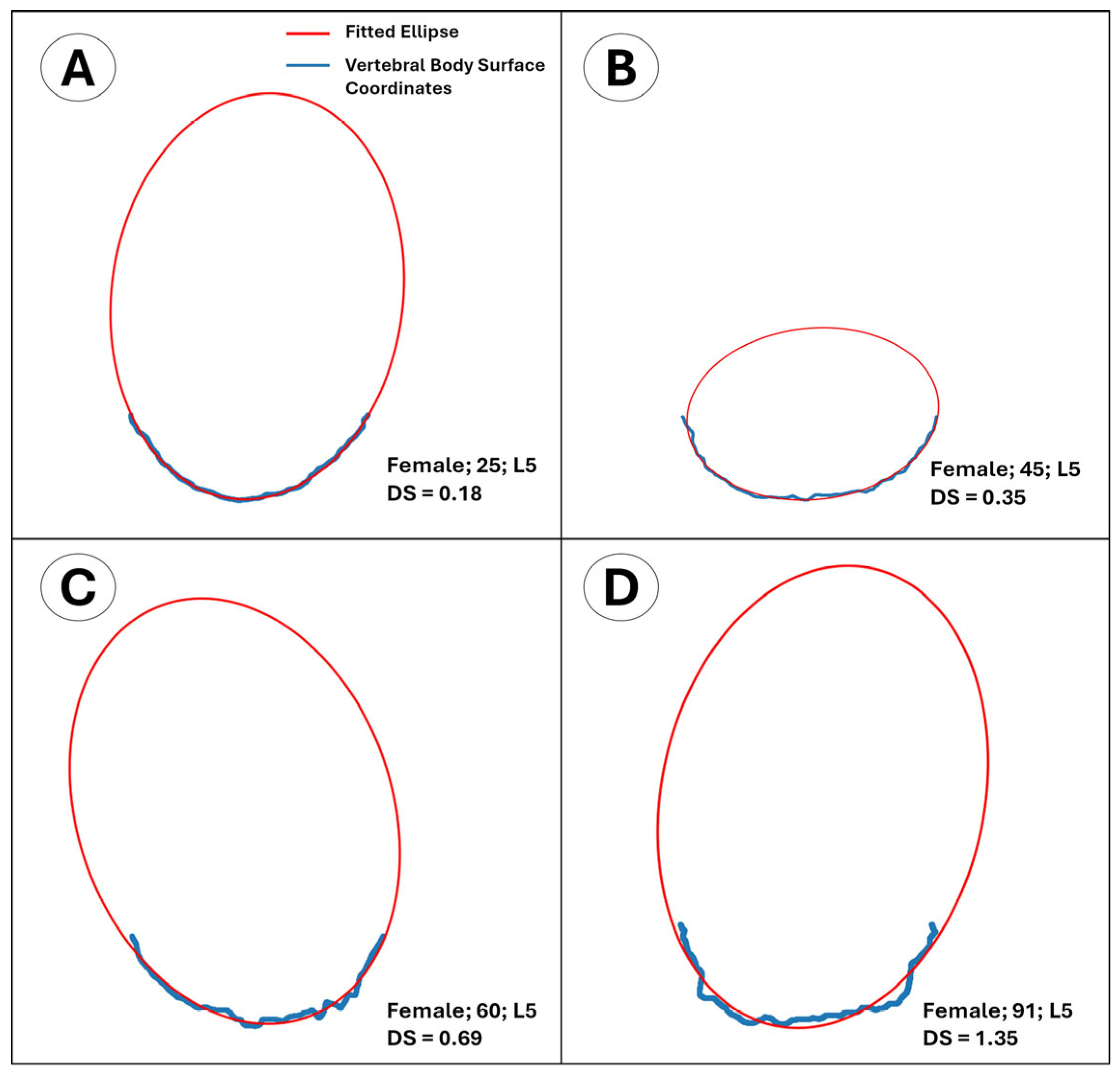
| Variable | Male (N = 94) | Female (N = 82) | p | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean ± SD | Median | Min–Max | 95% CI | Mean ± SD | Median | Min–Max | 95% CI | ||
| C7 DS | 0.33 ± 0.34 | 0.24 | 0.09–2.93 | 0.26–0.40 | 0.35 ± 0.34 | 0.26 | 0.09–2.23 | 0.28–0.43 | 0.917 |
| T1 DS | 0.30 ± 0.15 | 0.27 | 0.08–1.02 | 0.27–0.33 | 0.34 ± 0.28 | 0.27 | 0.08–1.68 | 0.28–0.40 | 0.991 |
| T2 DS | 0.33 ± 0.22 | 0.26 | 0.06–1.73 | 0.28–0.37 | 0.30 ± 0.20 | 0.24 | 0.06–1.17 | 0.25–0.34 | 0.136 |
| T3 DS | 0.33 ± 0.16 | 0.30 | 0.10–1.22 | 0.29–0.36 | 0.27 ± 0.15 | 0.25 | 0.08–1.03 | 0.24–0.30 | 0.005 * |
| T4 DS | 0.35 ± 0.16 | 0.31 | 0.10–0.90 | 0.32–0.38 | 0.27 ± 0.18 | 0.22 | 0.08–1.19 | 0.23–0.31 | 0.000 * |
| T5 DS | 0.33 ± 0.18 | 0.28 | 0.09–1.28 | 0.29–0.36 | 0.32 ± 0.47 | 0.24 | 0.09–4.30 | 0.22–0.42 | 0.022 * |
| T6 DS | 0.35 ± 0.20 | 0.31 | 0.12–1.24 | 0.30–0.39 | 0.29 ± 0.23 | 0.24 | 0.02–1.54 | 0.24–0.34 | 0.003 * |
| T7 DS | 0.30 ± 0.19 | 0.23 | 0.10–1.16 | 0.26–0.34 | 0.27 ± 0.17 | 0.23 | 0.06–0.96 | 0.24–0.31 | 0.374 |
| T8 DS | 0.32 ± 0.22 | 0.25 | 0.08–1.13 | 0.27–0.36 | 0.28 ± 0.21 | 0.22 | 0.06–1.34 | 0.23–0.32 | 0.135 |
| T9 DS | 0.31 ± 0.17 | 0.27 | 0.09–0.94 | 0.27–0.34 | 0.33 ± 0.25 | 0.23 | 0.07–1.43 | 0.28–0.39 | 0.801 |
| T10 DS | 0.39 ± 0.29 | 0.30 | 0.08–1.62 | 0.33–0.45 | 0.33 ± 0.22 | 0.25 | 0.09–1.01 | 0.28–0.38 | 0.073 |
| T11 DS | 0.48 ± 0.30 | 0.40 | 0.08–1.41 | 0.41–0.54 | 0.36 ± 0.30 | 0.27 | 0.07–1.68 | 0.29–0.42 | 0.000 * |
| T12 DS | 0.46 ± 0.31 | 0.39 | 0.11–1.64 | 0.40–0.52 | 0.41 ± 0.46 | 0.28 | 0.08–3.18 | 0.31–0.51 | 0.021 * |
| L1 DS | 0.41 ± 0.25 | 0.33 | 0.03–1.13 | 0.36–0.46 | 0.31 ± 0.16 | 0.25 | 0.07–0.88 | 0.28–0.35 | 0.009 * |
| L2 DS | 0.57 ± 0.39 | 0.46 | 0.10–1.79 | 0.49–0.65 | 0.49 ± 0.38 | 0.35 | 0.10–1.97 | 0.41–0.58 | 0.112 |
| L3 DS | 0.62 ± 0.40 | 0.50 | 0.13–2.02 | 0.54–0.70 | 0.62 ± 1.13 | 0.41 | 0.12–10.25 | 0.38–0.87 | 0.094 |
| L4 DS | 0.74 ± 0.55 | 0.61 | 0.13–2.58 | 0.63–0.85 | 0.68 ± 0.47 | 0.53 | 0.12–1.93 | 0.58–0.78 | 0.633 |
| L5 DS | 0.61 ± 0.36 | 0.52 | 0.15–1.63 | 0.54–0.68 | 0.65 ± 0.56 | 0.47 | 0.13–3.57 | 0.53–0.78 | 0.622 |
| S1 DS | 0.56 ± 0.31 | 0.47 | 0.15–1.96 | 0.50–0.63 | 0.66 ± 0.43 | 0.53 | 0.20–2.61 | 0.57–0.76 | 0.079 |
| Reference | Population and Sample Size | Vertebral Region and Imaging/Data | Age Indicators and Modelling Approach | Reported Performance † | Key Contribution/Remarks |
| Adams et al., 2024 [22] | 240 medico-legal cases (120 males and 120 females; 18–101 y) | Lower T-spine and upper L-spine; digital radiographs | 3-phase degenerative score of T11–L3 → Bayesian transition analysis | Bin-1 → <36 y, Bin-3 → >47 y (90% CI); no sex effect | Practical radiographic protocol for fleshed remains; usable when skeletal sampling impossible. |
| Cardoso & Ríos 2011 [18] | 104 documented skeletons (47 males and 57 females; 9–30 y) | Cervical, thoracal, and lumbar vertebrae; dry bone | 3-stage scoring of epiphyseal-ring union | Stage 0 always < 18 y; stage 3 appears ≥ 15 y | Detailed fusion timetable for adolescent vertebrae; fills gap for 10–25 y age window. |
| Chiba et al., 2022 [21] | 250 PMCT cadavers (125 females and 125 males; 20–95 y) | T- and L-spine; post-mortem CT | Osteophyte score O (0–5) + bridge score B (0–2); regression | Best SEE ≈ 10 y using “number of vertebrae with O ≥ 2” | Demonstrates CT-based scoring viable even with partial columns. |
| Reference | Population and sample size | Vertebral region and imaging/data | Age indicators and modelling approach | Reported performance † | Key contribution/remarks |
| Etli 2023 [34] | 140 Turkish CT cases (70 males and 70 females; 21–90 y) | Sacral base; abdominal–pelvic CT | Distance-to-fitted-ellipse surface roughness score (DS); sex-specific linear regression | MAE 12.5–14.8 y, RMSE 14.7–18.1 y; DS ≥ 50 y class accuracy >80% | Pilots the DS concept, showing moderate precision with sacral DS. |
| Garoufi et al., 2022 [28] | 275 Europeans (168 Greek modern; 93 males and 75 females; 107 Danish archaeological; 56 males and 51 females; 21–82 y) | T12 superior and inferior end-plates; digital photographs | 9 geometric variables → generalized additive regression | Max. R2 0.46; correct-decade hit-rate 33% (archaeol. set) | Introduces continuous 2-D shape metrics; moderate age signal, highlighted size-related sex effects. |
| Kaçar et al., 2017 [25] | 564 living Turkish adults (279 males and 285 females; 20–84 y) | (T1–L5); 0.5 mm MDCT scans reconstructed to 3-D volume-rendered images | Vertebral osteophyte severity (0–4 scale); Linear regression for age estimation (upper/lower limits). | Significant age correlation (40–70 yrs, both sexes). Sex-specific thoracic/lumbar age formulas (p < 0.05). Inter/intra-rater reliability: 0.85/0.88. | First large CT study on living adults; shows osteophyte severity peaks in mid-thoracic region and plateaus after 70 years; detects male-biased osteophyte frequency at T9–T12; provides practical formulas for forensic age estimation. |
| Kawashita et al., 2024 [24] | Training: 1120 clinical CTs; 560 males and 560 females; 20–99 y; Test: 219 PMCT cadavers; 137 males and 82 females; 21–94 y | Whole spine; axial CT slices → VGG-16 regression ensemble | Deep learning regression (bagged VGG-16) | MAE = 4.36 y; SEE = 5.48 y; ICC = 0.96 | First end-to-end DL model on spine; accuracy surpasses classic scores, robust to 20–90 years. |
| Malatong Y et al., 2022 [27] | Thai skeletal radiograph bank; 220 lumbar DR images (110 males, 110 females; 20–86 y) | L1–L5; posterior–anterior digital radiographs | Image-analysis of trabecular “black-pixel” content: total % (TP), mean % (MP), black/white ratio (BW); stepwise linear regression by sex | Best equations: male (L4) SEE 15.4 y, female (L1) SEE 13.8 y; r = 0.21–0.46 | Introduces automated pixel-density metric as surrogate for bone porosity on plain films. |
| Nurzynska et al., 2024 [23] | 166 routine axial CTs (95 males and 71 females; 20–80 y) | L-vertebral bodies; axial CT ROIs | (a) qMaZda texture features + ML regression; (b) custom CNN | Texture-ML: MAE 3.14 y, R2 0.79; CNN slightly worse | Shows grey-level texture alone can predict age within ±3 y on moderate dataset. |
| Praneatpolgrang et al., 2019 [19] | 400 Thai skeletons (262 males and 138 females, 22–97 y) | C2–L5; dry bone | Length-based osteophyte score (modified Snodgrass/Watanabe) | Lumbar female: r = 0.80; SEE ≈ 10–11 y (author-reported) | Provides full sex-/region-specific equations for tropical Southeast-Asian population. |
| Ramadan et al., 2017 [29] | 123 clinical CTs (61 males and 62 females, 10–64 y) | Last thoracic (T12); MDCT axial slices | 15 linear dimensions; stepwise multiple regression | Sex-classification 88.6%; age r ≤ 0.40, SEE not reported | Shows T12 size grows with age but correlation too weak for precise aging; useful primarily for sexing. |
| Rizos et al., 2024 [30] | 219 documented Greeks (121 males and 98 females; 19–99 y) | 64 skeletal traits incl. vertebral osteophytes; macroscopic scoring | Deep randomized neural network ensembles | MAE ≈ 6 y in >50 y group; poor (<10%) correct-decade in <50 y | Independent test questions “universal” accuracy. claims; stresses population-specific training. |
| Reference | Population and sample size | Vertebral region and imaging/data | Age indicators and modelling approach | Reported performance † | Key contribution/remarks |
| Schanandore et al., 2024 [31] | North-American medical CT archive; 319 scans (149 males and 170 females; 10–89 y) | T12–L5; clinical CT (0.6–1.3 mm slices); 3-D surface models in Mimics® | Six-point semi-quantitative osteophyte score on superior and inferior margins of each level (0–2); single and multiple linear regressions, 6-fold CV ×100 | Best models (L1–L5 mean or multi-level totals): RMSE ≈ 8.4 y, R2 0.85; 73–77% of cases ± 10 y; ICC 0.80–0.95 | First to subdivide each margin; demonstrates lumbar (esp. L4) dominance; high accuracy with simple scores. |
| Sluis et al., 2022 [13] | 88 19th-c. Dutch skeletons (40 males and 48 females; 19–90 y) | Full spine; dry bone | Mean osteophyte stage by three published methods | Correct age bin assignment 73–76% | External validation of three scoring schemes; supplies Dutch-specific regressions. |
| Snodgrass 2004 [15] | 384 Terry Collection cases (192 males and 192 females; 20–80 y) | T- and L-spine; dry bone | 5-stage osteophyte scale; sex comparison | Greater variability in female; recommends wider CI | Found broadly parallel aging curves; underscores need for sex-specific intervals. |
| Suwanlikhid et al., 2018 [33] | 250 Thai dry vertebral columns (125 males and 125 females; 22–89 y) | L1–L5 macroporosity, cortical roughness, osteophytes; naked-eye scoring | Multiple linear regressions per surface | Best: L1-inferior surface R2 0.41, SEE 11.7 y | Simple portable method; advocates combining three degenerative traits for tropical skeletal sets. |
| Thomsen et al., 2015 [16] | 80 cadaver pairs (39 males and 41 females; 19–96 y) | L2 and iliac crest; μCT 3-D | Trabecular BV/TV, Tb.Th, SMI etc. vs. age | No explicit SEE; shows linear BV/TV decline (r ≈ −0.8) | Highlights microstructural trajectories; useful explanatory context for imaging biomarkers. |
| Watanabe & Terazawa 2006 [17] | 225 Japanese autopsy cases (138 males and 87 females; 20–88 y) | Whole column; direct inspection and palpation | 0–3 height-based scores averaged to “osteophyte index”; sex-specific regression | SEE 12.6 y (M)/11.9 y (F); r ≈ 0.70 | Classic benchmark for simple inspection-based ageing in East Asian population. |
| Zangpo et al., 2023 [26] | 200 Japanese PMCT cases (126 males/74 females, 25–99 y) | L4 body; 3-D PMCT surface mesh vs. convex-hull volumes | VR = mesh/hull; VD = (hull–mesh)/mesh; simple regressions | SEE 11.9 y (M)/12.5 y (F); ρ = ±0.76 | First to quantify age from global 3-D surface bulging/concavity rather than marginal osteophytes. |
| Zangpo et al., 2024 [32] | 200 Japanese PMCT cases (same cohort as 2023 study) | L4 body; max Hausdorff-distance (maxHD) between mesh and smoothed template | maxHD vs. age; sex-specific linear regression | SEE 12.5 y (M)/13.1 y (F); ρ ≈ 0.74 | Confirms 3-D surface-deformation signal with an intuitive shape-difference metric (HD). |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kartal, E.; Etli, Y. Automated Analysis of Vertebral Body Surface Roughness for Adult Age Estimation: Ellipse Fitting and Machine-Learning Approach. Diagnostics 2025, 15, 1794. https://doi.org/10.3390/diagnostics15141794
Kartal E, Etli Y. Automated Analysis of Vertebral Body Surface Roughness for Adult Age Estimation: Ellipse Fitting and Machine-Learning Approach. Diagnostics. 2025; 15(14):1794. https://doi.org/10.3390/diagnostics15141794
Chicago/Turabian StyleKartal, Erhan, and Yasin Etli. 2025. "Automated Analysis of Vertebral Body Surface Roughness for Adult Age Estimation: Ellipse Fitting and Machine-Learning Approach" Diagnostics 15, no. 14: 1794. https://doi.org/10.3390/diagnostics15141794
APA StyleKartal, E., & Etli, Y. (2025). Automated Analysis of Vertebral Body Surface Roughness for Adult Age Estimation: Ellipse Fitting and Machine-Learning Approach. Diagnostics, 15(14), 1794. https://doi.org/10.3390/diagnostics15141794





