Six-Degree-of-Freedom Freehand 3D Ultrasound: A Low-Cost Computer Vision-Based Approach for Orthopedic Applications
Abstract
:1. Introduction
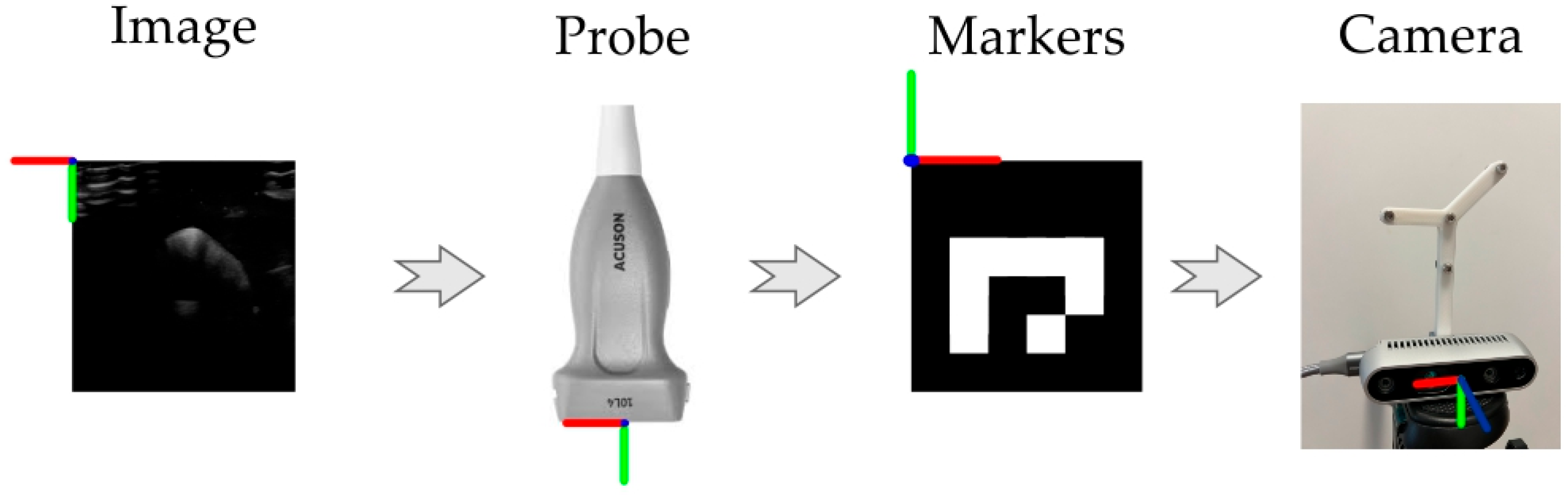
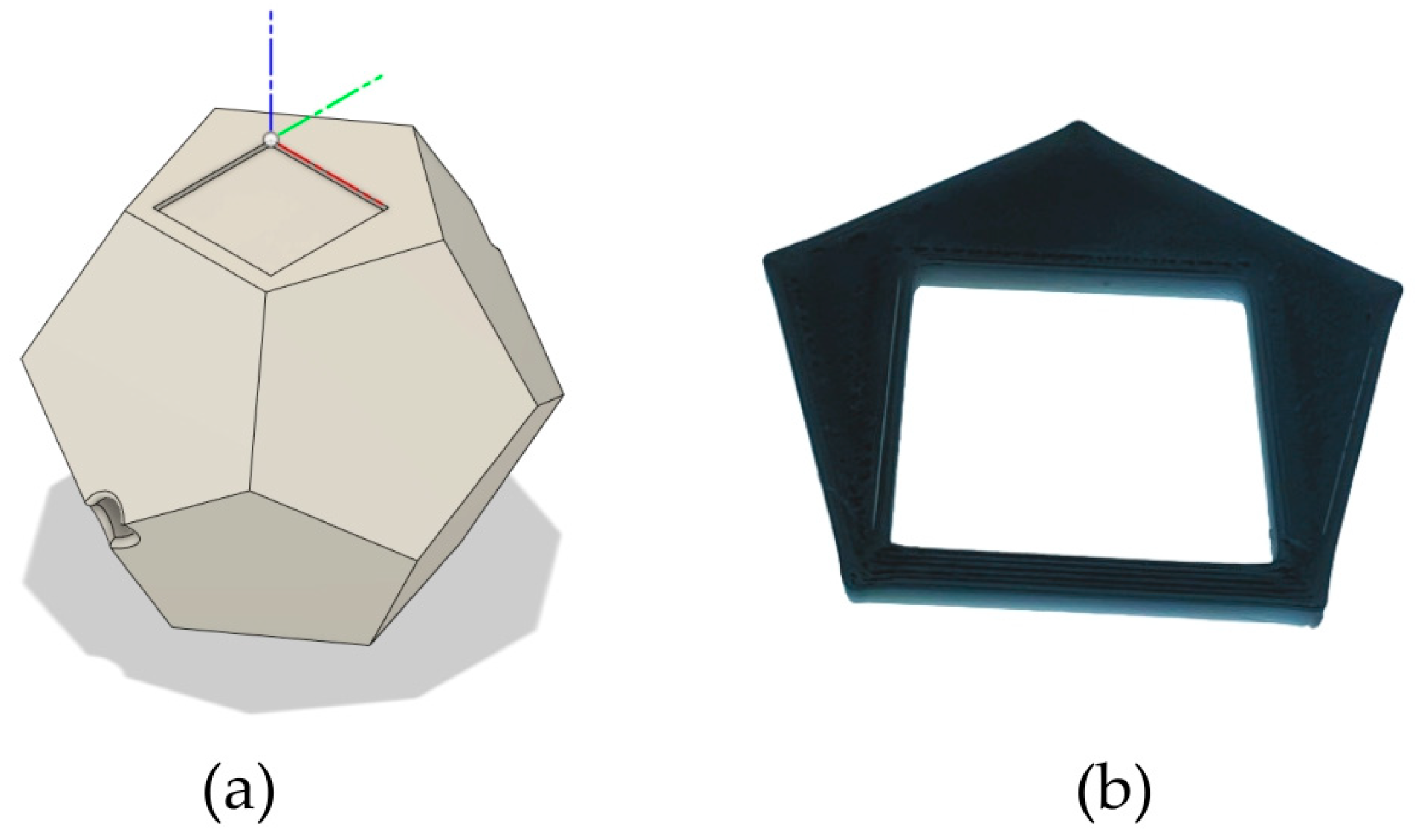
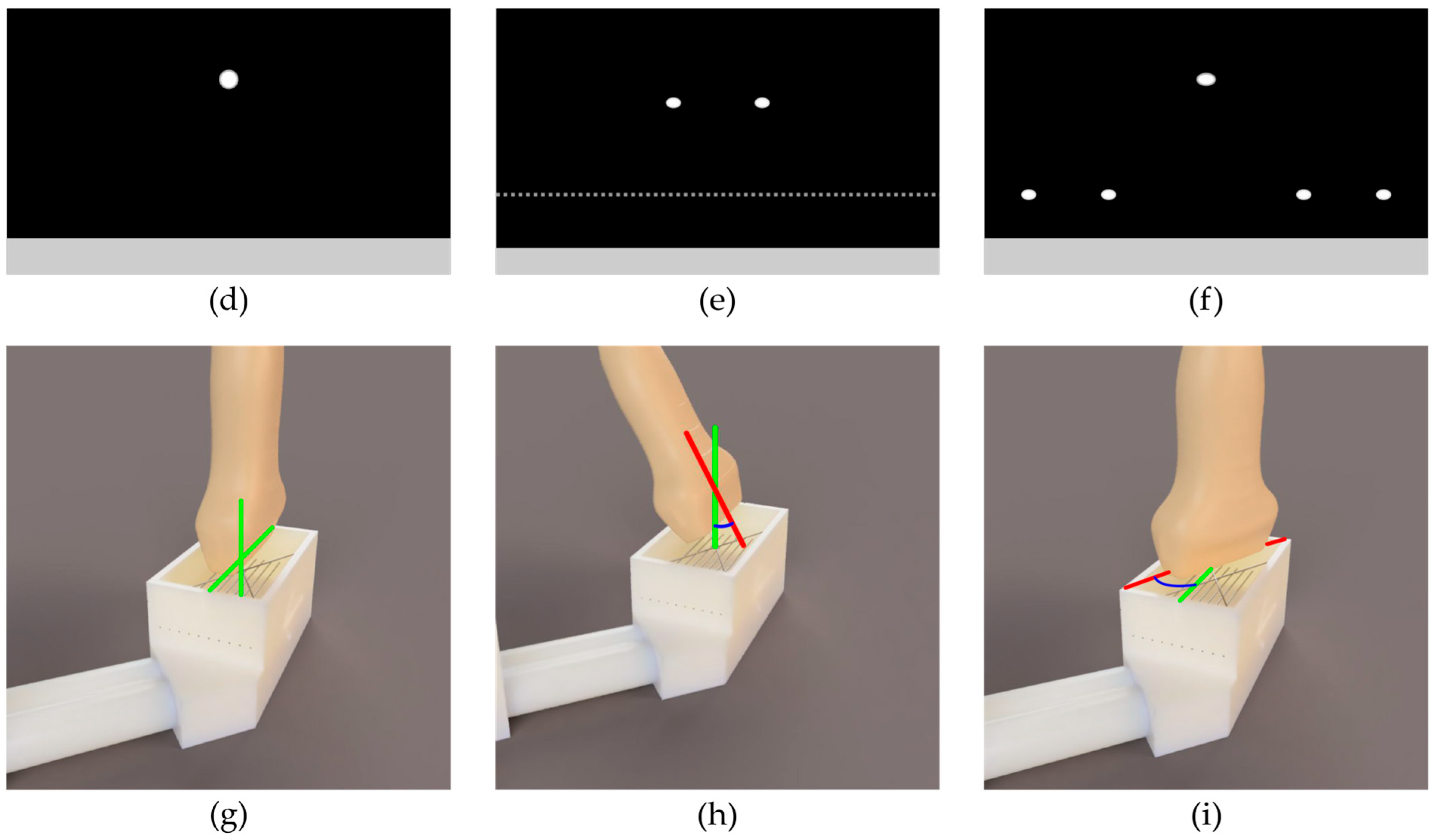
2. Materials and Methods
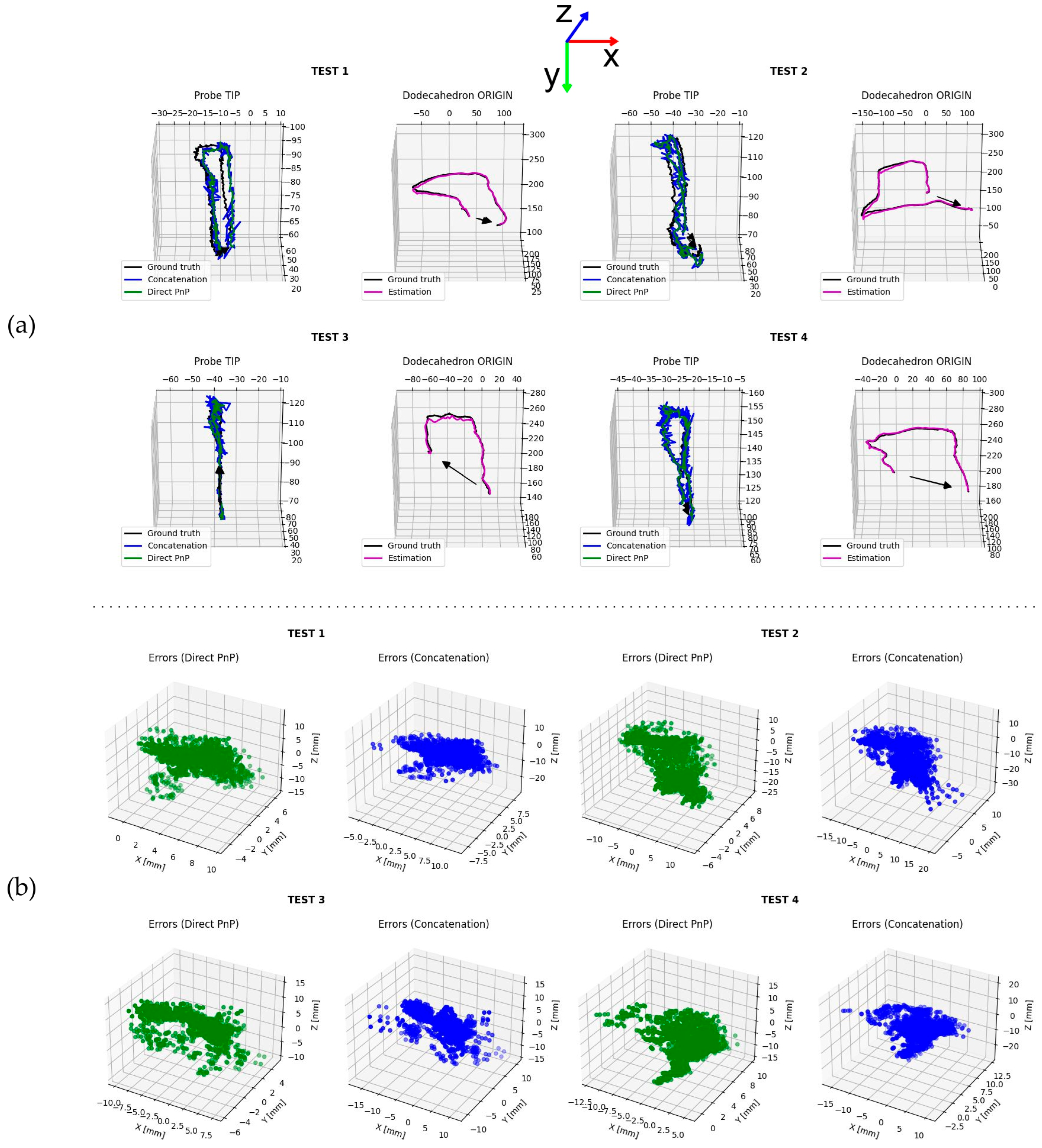
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Combes, D.; Lancigu, R.; de Cepoy, P.; Caporilli-Razza, F.; Hubert, L.; Rony, L.; Aubé, C. Imaging of Shoulder Arthroplasties and Their Complications: A Pictorial Review. Insights Imaging 2019, 10, 90. [Google Scholar] [CrossRef] [PubMed]
- Maffulli, N.; Longo, U.G.; Berton, A.; Loppini, M.; Denaro, V. Biological Factors in the Pathogenesis of Rotator Cuff Tears. Sports Med. Arthrosc. Rev. 2011, 19, 194–201. [Google Scholar] [CrossRef] [PubMed]
- Kolk, A.; Henseler, J.F.; de Witte, P.B.; van Zwet, E.W.; van der Zwaal, P.; Visser, C.P.J.; Nagels, J.; Nelissen, R.G.H.H.; de Groot, J.H. The Effect of a Rotator Cuff Tear and Its Size on Three-Dimensional Shoulder Motion. Clin. Biomech. 2017, 45, 43–51. [Google Scholar] [CrossRef] [PubMed]
- Neer, C.S.; Craig, E.V.; Fukuda, H. Cuff-Tear Arthropathy. J. Bone Jt. Surg. Am. 1983, 65, 1232–1244. [Google Scholar] [CrossRef] [PubMed]
- Longo, U.G.; Facchinetti, G.; Marchetti, A.; Candela, V.; Risi Ambrogioni, L.; Faldetta, A.; De Marinis, M.G.; Denaro, V. Sleep Disturbance and Rotator Cuff Tears: A Systematic Review. Medicina 2019, 55, 453. [Google Scholar] [CrossRef] [PubMed]
- Pope, T.; Bloem, J.L.; Morrison, W.B.; Wilson, D.J.; White, L. Musculoskeletal Imaging; Elsevier Health Sciences: Amsterdam, The Netherlands, 2020; ISBN 978-3-030-57376-8. [Google Scholar]
- Greenspan, A.; Beltran, J. Orthopaedic Imaging: A Practical Approach; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2020; ISBN 1975136497. [Google Scholar]
- Valentin, J. 2. How High Are the Doses? Ann. ICRP 2000, 30, 19–24. [Google Scholar] [CrossRef]
- Martin, C.J. Radiation Shielding for Diagnostic Radiology. Radiat. Prot. Dosim. 2015, 165, 376–381. [Google Scholar] [CrossRef]
- Sammet, S. Magnetic Resonance Safety. Abdom. Radiol. 2016, 41, 444–451. [Google Scholar] [CrossRef]
- Aldrich, J.E. Basic Physics of Ultrasound Imaging. Crit. Care Med. 2007, 35, S131–S137. [Google Scholar] [CrossRef]
- ter Haar, G. Ultrasound Bioeffects and Safety. Proc. Inst. Mech. Eng. Part H 2009, 224, 363–373. [Google Scholar] [CrossRef]
- Martin, K. Introduction to B-Mode Imaging. In Diagnostic Ultrasound, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2019; pp. 1–5. ISBN 9781138893603. [Google Scholar]
- Gee, A.; Prager, R.; Treece, G.; Berman, L. Engineering a Freehand 3D Ultrasound System. Pattern Recognit. Lett. 2003, 24, 757–777. [Google Scholar] [CrossRef]
- Mills, P.H.; Fuchs, H. 3D Ultrasound Display Using Optical Tracking. In Proceedings of the First Conference on Visualization in Biomedical Computing, Atlanta, GA, USA, 22–25 May 1990; pp. 490–497. [Google Scholar]
- Wu, H.; Lin, Q.; Yang, R.; Zhou, Y.; Zheng, L.; Huang, Y.; Wang, Z.; Lao, Y.; Huang, J. An Accurate Recognition of Infrared Retro-Reflective Markers in Surgical Navigation. J. Med. Syst. 2019, 43, 153. [Google Scholar] [CrossRef]
- Longo, U.G.; De Salvatore, S.; Carnevale, A.; Tecce, S.M.; Bandini, B.; Lalli, A.; Schena, E.; Denaro, V. Optical Motion Capture Systems for 3D Kinematic Analysis in Patients with Shoulder Disorders. Int. J. Environ. Res. Public Health 2022, 19, 12033. [Google Scholar] [CrossRef]
- Mozaffari, M.H.; Lee, W.-S. Freehand 3-D Ultrasound Imaging: A Systematic Review. Ultrasound Med. Biol. 2017, 43, 2099–2124. [Google Scholar] [CrossRef]
- Huang, Q.; Zeng, Z. A Review on Real-Time 3D Ultrasound Imaging Technology. Biomed. Res. Int. 2017, 2017, 6027029. [Google Scholar] [CrossRef]
- Huang, Q.; Xie, B.; Ye, P.; Chen, Z. Correspondence-3-D Ultrasonic Strain Imaging Based on a Linear Scanning System. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2015, 62, 392–400. [Google Scholar] [CrossRef]
- Huang, Q.-H.; Yang, Z.; Hu, W.; Jin, L.-W.; Wei, G.; Li, X. Linear Tracking for 3-D Medical Ultrasound Imaging. IEEE Trans. Cybern. 2013, 43, 1747–1754. [Google Scholar] [CrossRef]
- Peng, C.; Cai, Q.; Chen, M.; Jiang, X. Recent Advances in Tracking Devices for Biomedical Ultrasound Imaging Applications. Micromachines 2022, 13, 1855. [Google Scholar] [CrossRef]
- Léger, É.; Gueziri, H.E.; Collins, D.L.; Popa, T.; Kersten-Oertel, M. Evaluation of Low-Cost Hardware Alternatives for 3D Freehand Ultrasound Reconstruction in Image-Guided Neurosurgery. In Proceedings of the Simplifying Medical Ultrasound, Strasbourg, France, 27 September 2021; Noble, J.A., Aylward, S., Grimwood, A., Min, Z., Lee, S.-L., Hu, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 106–115. [Google Scholar]
- Kalaitzakis, M.; Cain, B.; Carroll, S.; Ambrosi, A.; Whitehead, C.; Vitzilaios, N. Fiducial Markers for Pose Estimation. J. Intell. Robot. Syst. 2021, 101, 71. [Google Scholar] [CrossRef]
- Wu, P.-C.; Wang, R.; Kin, K.; Twigg, C.; Han, S.; Yang, M.-H.; Chien, S.-Y. DodecaPen: Accurate 6DoF Tracking of a Passive Stylus. In Proceedings of the 30th Annual ACM Symposium on User Interface Software and Technology, Quebec, QC, Canada, 22–25 October 2017; Association for Computing Machinery: New York, NY, USA, 2017; pp. 365–374. [Google Scholar]
- Eade, E. Lie Groups for 2d and 3d Transformations. 2013; Volume 117. Available online: http://ethaneade.com/lie.pdf (accessed on 18 May 2024).
- Siciliano, B.; Khatib, O.; Kröger, T. Springer Handbook of Robotics; Springe: Berlin/Heidelberg, Germany, 2008; Volume 200. [Google Scholar]
- Prager, R.W.; Rohling, R.N.; Gee, A.H.; Berman, L. Rapid Calibration for 3-D Freehand Ultrasound. Ultrasound Med. Biol. 1998, 24, 855–869. [Google Scholar] [CrossRef]
- Manickam, K.; Machireddy, R.R.; Seshadri, S. Characterization of Biomechanical Properties of Agar Based Tissue Mimicking Phantoms for Ultrasound Stiffness Imaging Techniques. J. Mech. Behav. Biomed. Mater. 2014, 35, 132–143. [Google Scholar] [CrossRef]
- Merchel Piovesan Pereira, B.; Tagkopoulos, I. Benzalkonium Chlorides: Uses, Regulatory Status, and Microbial Resistance. Appl. Environ. Microbiol. 2019, 85, e00377-19. [Google Scholar] [CrossRef]
- Souza, R.M.; Santos, T.Q.; Oliveira, D.P.; Alvarenga, A.V.; Costa-Felix, R.P.B. Standard Operating Procedure to Prepare Agar Phantoms. Proc. J. Phys. Conf. Ser. 2016, 733, 12044. [Google Scholar]
- de Assis, M.K.M.; Souza, R.M.; Costa-Félix, R.P.B.; Alvarenga, A.V. Assessment of Ultrasonic Properties of an Agarose Phantom at the Frequency Range 2.25 MHz to 10 MHz. J. Phys. Conf. Ser. 2021, 1826, 012005. [Google Scholar] [CrossRef]
- Madsen, E.L.; Sathoff, H.J.; Zagzebski, J.A. Ultrasonic Shear Wave Properties of Soft Tissues and Tissuelike Materials. J. Acoust. Soc. Am. 1983, 74, 1346–1355. [Google Scholar] [CrossRef]
- IEEE Std 1588–2008 (Revision of IEEE Std 1588–2002); IEEE Standard for a Precision Clock Synchronization Protocol for Networked Measurement and Control Systems. IEEE: Piscataway, NJ, USA, 2008; pp. 1–269.
- Scheiterer, R.L.; Na, C.; Obradovic, D.; Steindl, G. Synchronization Performance of the Precision Time Protocol in Industrial Automation Networks. IEEE Trans. Instrum. Meas. 2009, 58, 1849–1857. [Google Scholar] [CrossRef]
- Marchand, E.; Uchiyama, H.; Spindler, F. Pose Estimation for Augmented Reality: A Hands-On Survey. IEEE Trans. Vis. Comput. Graph. 2016, 22, 2633–2651. [Google Scholar] [CrossRef]
- Terzakis George and Lourakis, M. A Consistently Fast and Globally Optimal Solution to the Perspective-n-Point Problem. In Proceedings of the Computer Vision—ECCV 2020, Online, 23–28 August 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.M., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 478–494. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Eade, E. Gauss-Newton/Levenberg-Marquardt Optimization. Tech. Rep. 2013. Available online: https://www.ethaneade.org/optimization.pdf (accessed on 18 May 2024).
- Madsen, K.; Nielsen, H.B.; Tingleff, O. Methods for Non-Linear Least Squares Problems; Technical University of Denmark: Copenhagen, Denmark, 2004. [Google Scholar]
- Gorry, P.A. General Least-Squares Smoothing and Differentiation by the Convolution (Savitzky-Golay) Method. Anal. Chem. 1990, 62, 570–573. [Google Scholar] [CrossRef]
- Kabsch, W. A Solution for the Best Rotation to Relate Two Sets of Vectors. Acta Crystallogr. Sect. A 1976, 32, 922–923. [Google Scholar] [CrossRef]
- Umeyama, S. Least-Squares Estimation of Transformation Parameters between Two Point Patterns. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 376–380. [Google Scholar] [CrossRef]
- Shoemake, K. Animating Rotation with Quaternion Curves. SIGGRAPH Comput. Graph. 1985, 19, 245–254. [Google Scholar] [CrossRef]
- Scholten, H.J.; Weijers, G.; de Wild, M.; Korsten, H.H.M.; de Korte, C.L.; Bouwman, R.A. Differences in Ultrasound Elevational Beam Width (Slice Thickness) between Popular Handheld Devices. WFUMB Ultrasound Open 2023, 1, 100009. [Google Scholar] [CrossRef]
- Goldstein, A. Slice Thickness Measurements. J. Ultrasound Med. 1988, 7, 487–498. [Google Scholar] [CrossRef] [PubMed]
- Del Grosso, V.A.; Mader, C.W. Speed of Sound in Pure Water. J. Acoust. Soc. Am. 1972, 52, 1442–1446. [Google Scholar] [CrossRef]
- Zell, K.; Sperl, J.I.; Vogel, M.W.; Niessner, R.; Haisch, C. Acoustical Properties of Selected Tissue Phantom Materials for Ultrasound Imaging. Phys. Med. Biol. 2007, 52, N475–N484. [Google Scholar] [CrossRef] [PubMed]
- Lane, J.M.; Russell, L.; Khan, S.N. Osteoporosis. Clin. Orthop. Relat. Res. 2000, 372, 139–150. [Google Scholar] [CrossRef]
- Huang, Q.; Lu, M.; Zheng, Y.; Chi, Z. Speckle Suppression and Contrast Enhancement in Reconstruction of Freehand 3D Ultrasound Images Using an Adaptive Distance-Weighted Method. Appl. Acoust. 2009, 70, 21–30. [Google Scholar] [CrossRef]
- Huang, Q.; Gao, B.; Wang, M. Robot-Assisted Autonomous Ultrasound Imaging for Carotid Artery. IEEE Trans. Instrum. Meas. 2024, 73, 1–9. [Google Scholar] [CrossRef]
- Prevost, R.; Salehi, M.; Jagoda, S.; Kumar, N.; Sprung, J.; Ladikos, A.; Bauer, R.; Zettinig, O.; Wein, W. 3D Freehand Ultrasound without External Tracking Using Deep Learning. Med. Image Anal. 2018, 48, 187–202. [Google Scholar] [CrossRef]





| Method | Test # | [mm] | [mm] | [mm] | [mm] | ||||
|---|---|---|---|---|---|---|---|---|---|
| x | y | z | x | y | z | ||||
| Origin 1 | 1 | 0.197 | 0.663 | −0.045 | 0.693 | 2.655 | 2.686 | 3.312 | 5.024 |
| 2 | −0.135 | 1.734 | −3.149 | 3.597 | 4.352 | 2.184 | 7.550 | 8.241 | |
| 3 | −0.181 | 1.765 | 1.464 | 2.301 | 1.110 | 1.219 | 4.206 | 4.518 | |
| 4 | −1.712 | 0.611 | 4.020 | 4.414 | 2.992 | 2.216 | 3.427 | 5.061 | |
| Direct | 1 | 3.947 | 0.895 | 0.792 | 4.124 | 1.899 | 2.020 | 5.005 | 5.722 |
| 2 | 0.928 | 0.599 | −2.934 | 3.135 | 4.352 | 2.184 | 7.550 | 8.984 | |
| 3 | −0.857 | 0.453 | 2.689 | 2.858 | 2.908 | 1.920 | 4.299 | 5.534 | |
| 4 | 0.675 | 3.860 | 0.373 | 3.937 | 2.206 | 1.773 | 5.817 | 6.469 | |
| Concatenation | 1 | 3.893 | 0.928 | 0.629 | 4.051 | 2.578 | 2.478 | 5.965 | 6.954 |
| 2 | 0.964 | 0.589 | −2.797 | 3.017 | 4.860 | 2.678 | 7.643 | 9.445 | |
| 3 | −0.846 | 0.505 | 2.596 | 2.777 | 3.539 | 2.496 | 4.561 | 6.290 | |
| 4 | 0.884 | 3.581 | 1.348 | 3.927 | 3.296 | 2.342 | 6.792 | 7.905 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Sanctis, L.; Carnevale, A.; Antonacci, C.; Faiella, E.; Schena, E.; Longo, U.G. Six-Degree-of-Freedom Freehand 3D Ultrasound: A Low-Cost Computer Vision-Based Approach for Orthopedic Applications. Diagnostics 2024, 14, 1501. https://doi.org/10.3390/diagnostics14141501
De Sanctis L, Carnevale A, Antonacci C, Faiella E, Schena E, Longo UG. Six-Degree-of-Freedom Freehand 3D Ultrasound: A Low-Cost Computer Vision-Based Approach for Orthopedic Applications. Diagnostics. 2024; 14(14):1501. https://doi.org/10.3390/diagnostics14141501
Chicago/Turabian StyleDe Sanctis, Lorenzo, Arianna Carnevale, Carla Antonacci, Eliodoro Faiella, Emiliano Schena, and Umile Giuseppe Longo. 2024. "Six-Degree-of-Freedom Freehand 3D Ultrasound: A Low-Cost Computer Vision-Based Approach for Orthopedic Applications" Diagnostics 14, no. 14: 1501. https://doi.org/10.3390/diagnostics14141501
APA StyleDe Sanctis, L., Carnevale, A., Antonacci, C., Faiella, E., Schena, E., & Longo, U. G. (2024). Six-Degree-of-Freedom Freehand 3D Ultrasound: A Low-Cost Computer Vision-Based Approach for Orthopedic Applications. Diagnostics, 14(14), 1501. https://doi.org/10.3390/diagnostics14141501








