Novel Prediction Method Applied to Wound Age Estimation: Developing a Stacking Ensemble Model to Improve Predictive Performance Based on Multi-mRNA
Abstract
1. Introduction
2. Materials and Methods
2.1. Ethics
2.2. Animals
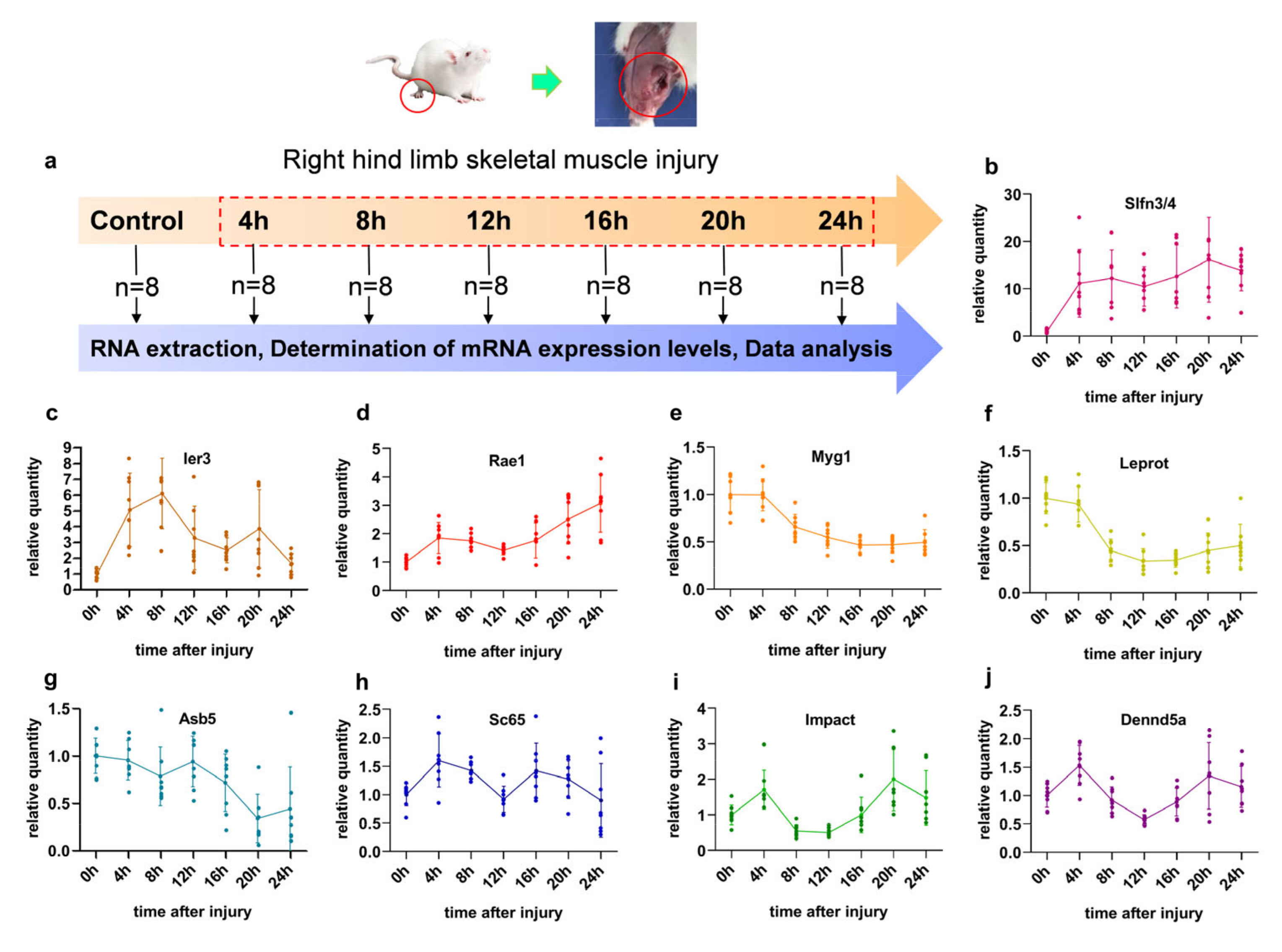
2.3. Skeletal Muscle Contusion and Sample Collection
2.4. Relative Quantitative Protocol of Nine mRNAs’ Expression
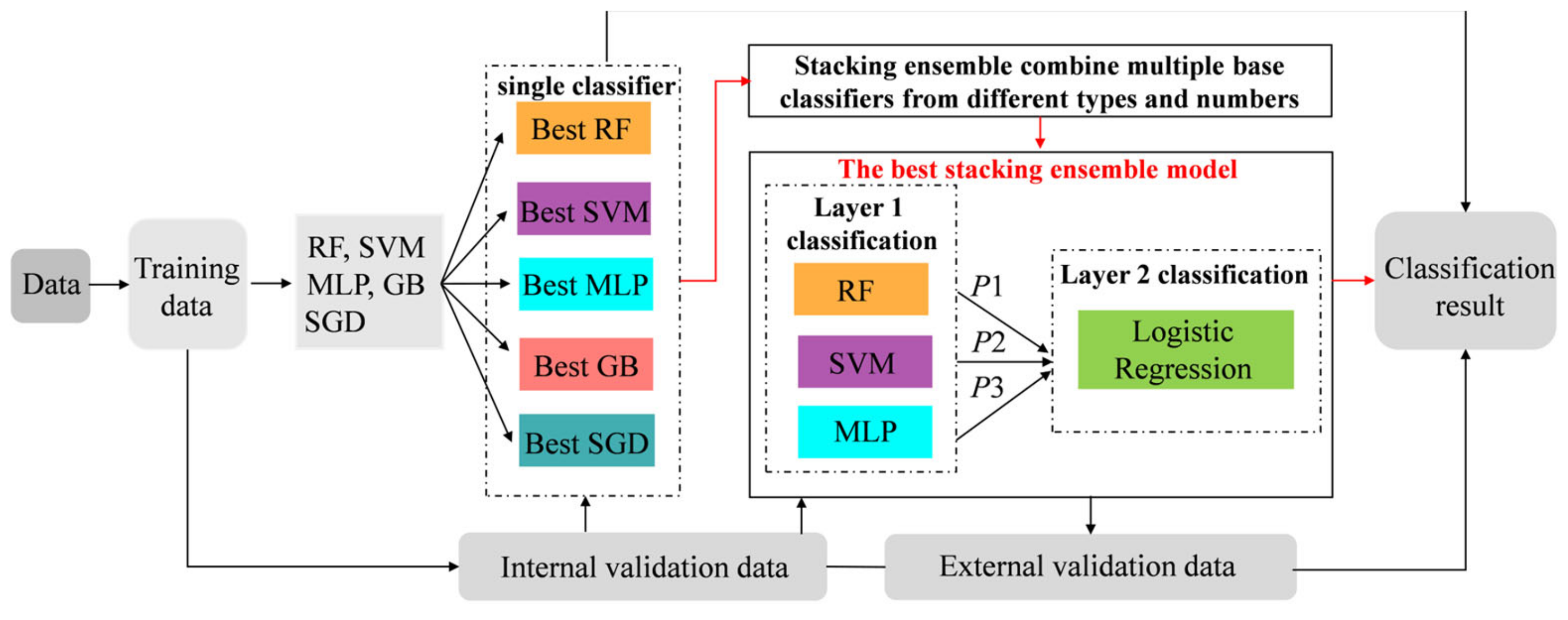
2.5. Model Development and Validation
2.6. Evaluation of the Predictive Performance
3. Results
3.1. The Characteristics of Different Genes in Contused Skeletal Muscle
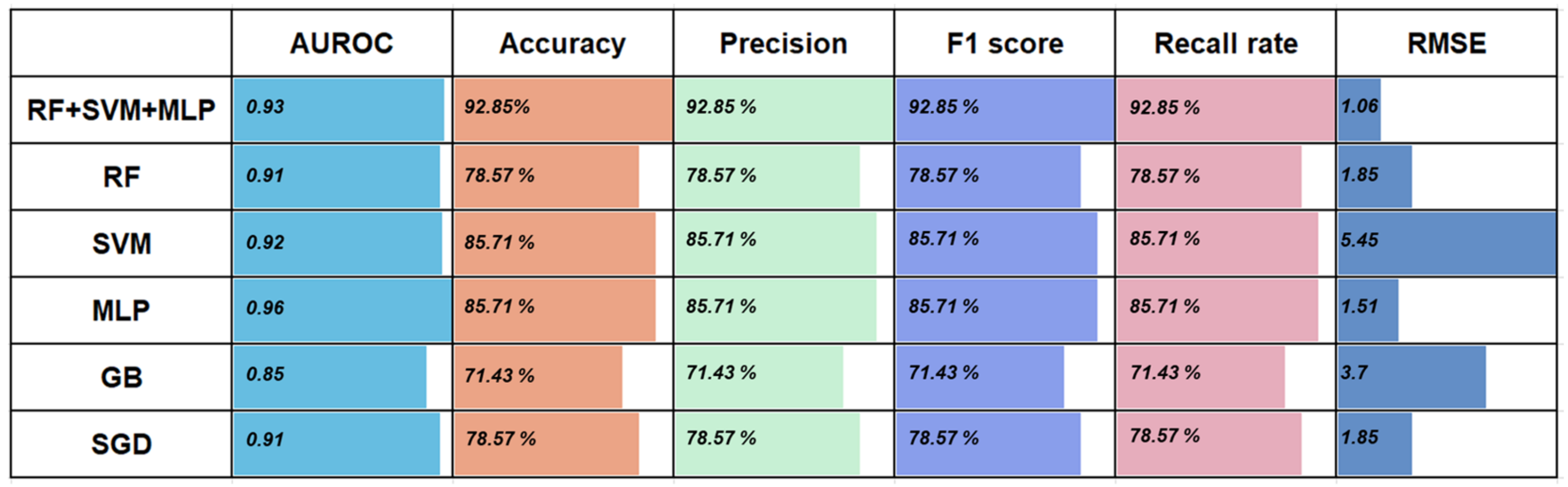
3.2. Performance of the Five Basic Classifiers for Wound Age Estimation
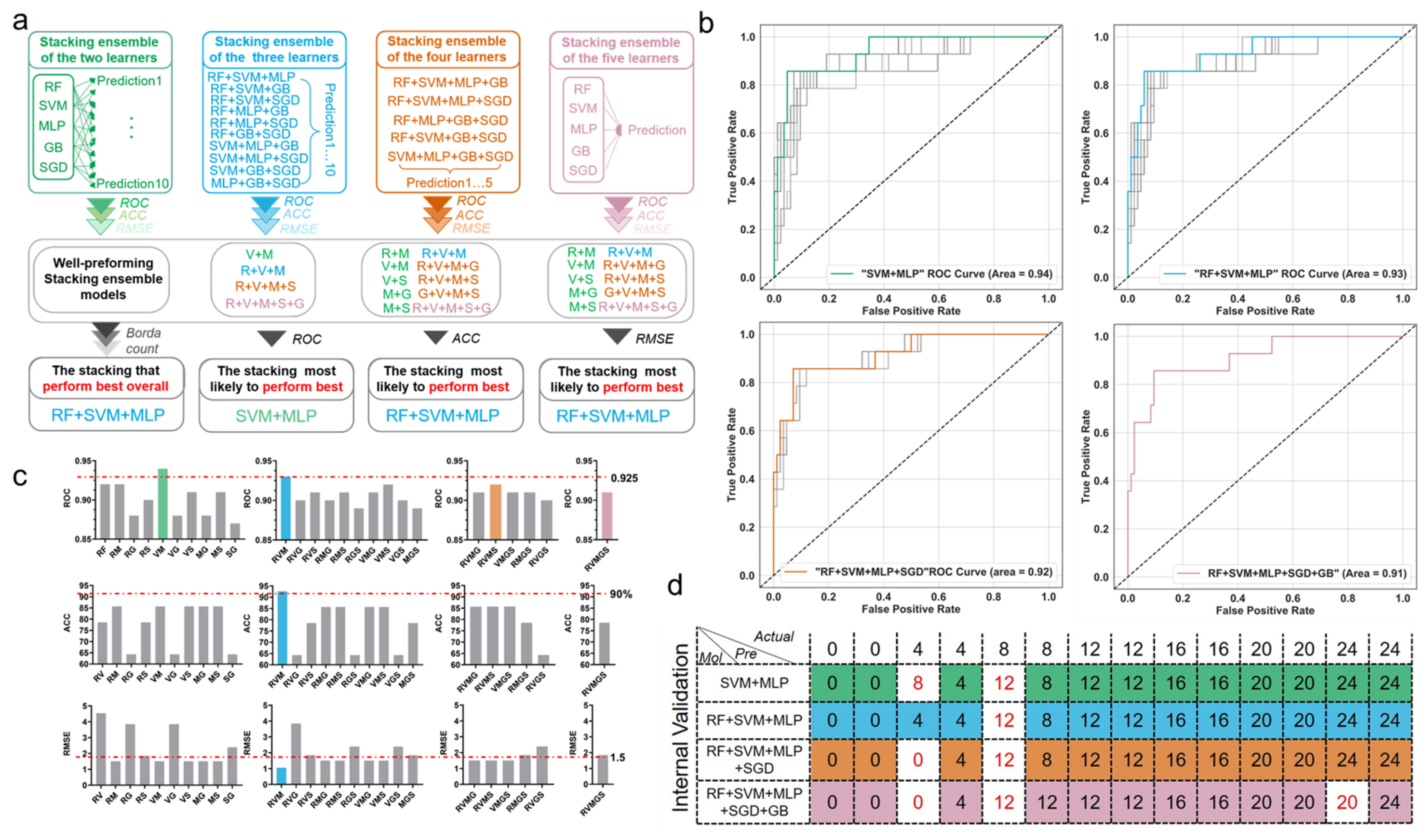
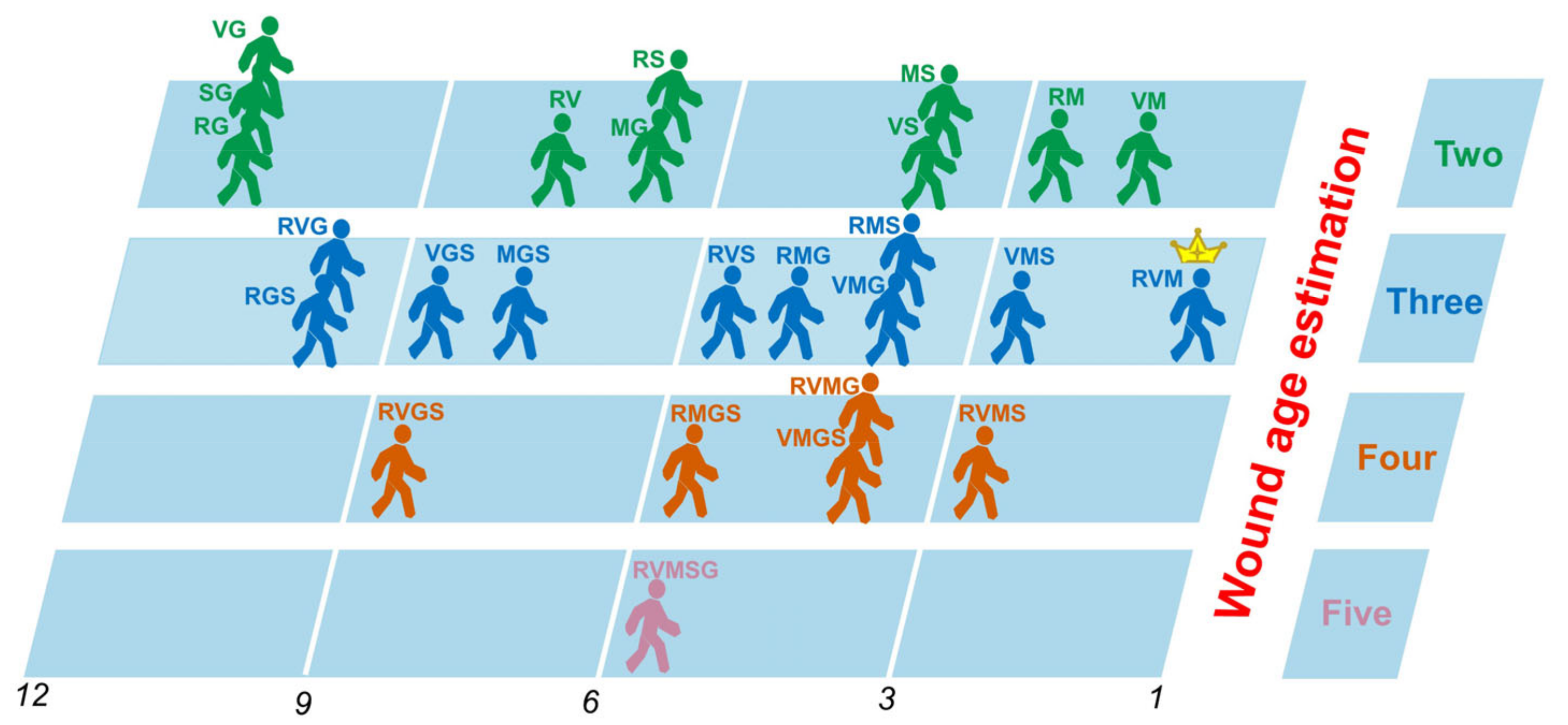
3.3. Comparison of Prediction Power of Multiple Stacking Ensembles
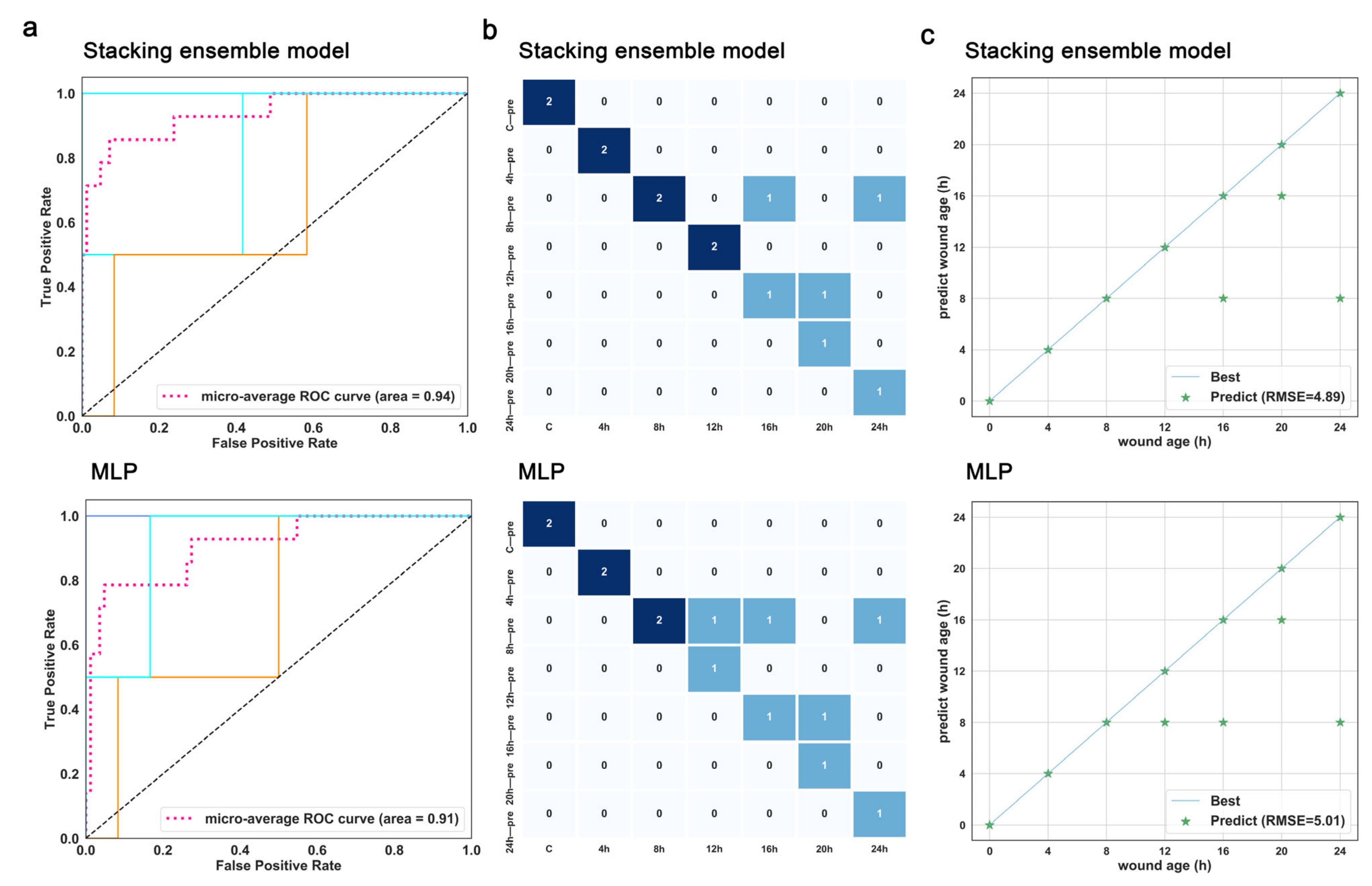
3.4. Further Comparison of the Performance of the Best-Performing Stacking Model and the Basic Classifiers
3.5. Validation for the Best-Performing Stacking Ensemble and the Optimal Base Classifier
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Niedecker, A.; Huhn, R.; Ritz-Timme, S.; Mayer, F. Complex challenges of estimating the age and vitality of muscle wounds: A study with matrix metalloproteinases and their inhibitors on animal and human tissue samples. Int. J. Leg. Med. 2021, 135, 1843–1853. [Google Scholar] [CrossRef] [PubMed]
- Bertozzi, G.; Ferrara, M.; La Russa, R.; Pollice, G.; Gurgoglione, G.; Frisoni, P.; Alfieri, L.; De Simone, S.; Neri, M.; Cipolloni, L. Wound Vitality in Decomposed Bodies: New Frontiers through Immunohistochemistry. Front. Med. 2021, 8, 802841. [Google Scholar] [CrossRef] [PubMed]
- Ros, A.C.; Bacci, S.; Luna, A.; Legaz, I. Forensic Impact of the Omics Science Involved in the Wound: A Systematic Review. Front. Med. 2021, 8, 786798. [Google Scholar] [CrossRef] [PubMed]
- Du, Q.X.; Wang, L.; Li, D.; Niu, J.J.; Zhang, X.D.; Sun, J.H. Estimating the time of skeletal muscle contusion based on the spatial distribution of neutrophils: A practical approach to forensic problems. Int. J. Leg. Med. 2021, 136, 149–158. [Google Scholar] [CrossRef]
- Li, N.; Li, C.; Li, D.; Dang, L.H.; Ren, K.; Du, Q.X.; Cao, J.; Jin, Q.Q.; Wang, Y.Y.; Bai, R.F.; et al. Identifying biomarkers for evaluating wound extent and age in the contused muscle of rats using microarray analysis: A pilot study. PeerJ 2021, 9, e12709. [Google Scholar] [CrossRef]
- Li, N.; Bai, R.F.; Li, C.; Dang, L.H.; Du, Q.X.; Jin, Q.Q.; Cao, J.; Wang, Y.Y.; Sun, J.H. Insight into molecular profile changes after skeletal muscle contusion using microarray and bioinformatics analyses. Biosci. Rep. 2021, 41, BSR20203699. [Google Scholar] [CrossRef]
- Ren, K.; Wang, L.; Wang, L.; Du, Q.; Cao, J.; Jin, Q.; An, G.; Li, N.; Dang, L.; Tian, Y.; et al. Investigating Transcriptional Dynamics Changes and Time-Dependent Marker Gene Expression in the Early Period after Skeletal Muscle Injury in Rats. Front. Genet. 2021, 12, 650874. [Google Scholar] [CrossRef]
- Zhu, W.; Zhai, X.; Jia, Z.; Wang, Y.; Mo, Y. Bioinformatics analysis of sequential gene expression profiling after skin and skeletal muscle wound in mice. Leg. Med. (Tokyo Jpn.) 2021, 54, 101982. [Google Scholar] [CrossRef]
- Li, N.; Du, Q.; Bai, R.; Sun, J. Vitality and wound-age estimation in forensic pathology: Review and future prospects. Forensic Sci. Res. 2020, 5, 15–24. [Google Scholar] [CrossRef]
- Ishida, Y.; Nosaka, M.; Kondo, T. Bone Marrow-Derived Cells and Wound Age Estimation. Front. Med. 2022, 9, 822572. [Google Scholar] [CrossRef]
- Abd-Elhakim, Y.M.; Omran, B.H.F.; Ezzeldein, S.A.; Ahmed, A.I.; El-Sharkawy, N.I.; Mohamed, A.A. Time-dependent expression of high-mobility group box-1 and toll-like receptors proteins as potential determinants of skin wound age in rats: Forensic implication. Int. J. Leg. Med. 2022, 136, 1781–1789. [Google Scholar] [CrossRef]
- Du, Q.X.; Li, N.; Dang, L.H.; Dong, T.N.; Lu, H.L.; Shi, F.X.; Jin, Q.Q.; Jie, C.; Sun, J.H. Temporal expression of wound healing-related genes inform wound age estimation in rats after a skeletal muscle contusion: A multivariate statistical model analysis. Int. J. Leg. Med. 2020, 134, 273–282. [Google Scholar] [CrossRef]
- Khalaf, A.A.; Hassanen, E.I.; Zaki, A.R.; Tohamy, A.F.; Ibrahim, M.A. Histopathological, immunohistochemical, and molecular studies for determination of wound age and vitality in rats. Int. Wound J. 2019, 16, 1416–1425. [Google Scholar] [CrossRef]
- Li, Q.; Luo, Z. Transcriptional Regulatory Network Analysis to Reveal the Key Genes Involved in Skeletal Muscle Injury. J. Comput. Biol. A J. Comput. Mol. Cell Biol. 2019, 26, 1090–1099. [Google Scholar] [CrossRef]
- Karlsson, H.; Guthenberg, C.; von Döbeln, U.; Kristenssson, K. Extraction of RNA from dried blood on filter papers after long-term storage. Clin. Chem. 2003, 49 Pt 1, 979–981. [Google Scholar] [CrossRef]
- Zubakov, D.; Hanekamp, E.; Kokshoorn, M.; van Ijcken, W.; Kayser, M. Stable RNA markers for identification of blood and saliva stains revealed from whole genome expression analysis of time-wise degraded samples. Int. J. Leg. Med. 2008, 122, 135–142. [Google Scholar] [CrossRef]
- Zhang, F.Y.; Wang, L.L.; Dong, W.W.; Zhang, M.; Tash, D.; Li, X.J.; Du, S.K.; Yuan, H.M.; Zhao, R.; Guan, D.W. A preliminary study on early postmortem submersion interval (PMSI) estimation and cause-of-death discrimination based on nontargeted metabolomics and machine learning algorithms. Int. J. Leg. Med. 2022, 136, 941–954. [Google Scholar] [CrossRef]
- Liu, R.; Gu, Y.; Shen, M.; Li, H.; Zhang, K.; Wang, Q.; Wei, X.; Zhang, H.; Wu, D.; Yu, K.; et al. Predicting postmortem interval based on microbial community sequences and machine learning algorithms. Environ. Microbiol. 2020, 22, 2273–2291. [Google Scholar] [CrossRef]
- Peña-Solórzano, C.A.; Albrecht, D.W.; Bassed, R.B.; Gillam, J.; Harris, P.C.; Dimmock, M.R. Semi-supervised labelling of the femur in a whole-body post-mortem CT database using deep learning. Comput. Biol. Med. 2020, 122, 103797. [Google Scholar] [CrossRef]
- Kim, C.; You, S.C.; Reps, J.M.; Cheong, J.Y.; Park, R.W. Machine-learning model to predict the cause of death using a stacking ensemble method for observational data. J. Am. Med. Inform. Assoc. 2021, 28, 1098–1107. [Google Scholar] [CrossRef]
- Yang, J.J.; Li, J.; Shen, R.; Zeng, Y.; He, J.; Bi, J.; Li, Y.; Zhang, Q.; Peng, L.; Wang, Q. Exploiting ensemble learning for automatic cataract detection and grading. Comput. Methods Programs Biomed. 2016, 124, 45–57. [Google Scholar] [CrossRef] [PubMed]
- Layeghian Javan, S.; Sepehri, M.M.; Layeghian Javan, M.; Khatibi, T. An intelligent warning model for early prediction of cardiac arrest in sepsis patients. Comput. Methods Programs Biomed. 2019, 178, 47–58. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Du, L.; Zhang, P.; Zhao, R.; Chen, X.; Fang, Z. Early Sepsis Prediction Using Ensemble Learning with Deep Features and Artificial Features Extracted from Clinical Electronic Health Records. Crit. Care Med. 2020, 48, e1337–e1342. [Google Scholar] [CrossRef]
- Chang, S.C.; Chu, C.L.; Chen, C.K.; Chang, H.N.; Wong, A.M.K.; Chen, Y.P.; Pei, Y.C. The Comparison and Interpretation of Machine-Learning Models in Post-Stroke Functional Outcome Prediction. Diagnostics 2021, 11, 1784. [Google Scholar] [CrossRef] [PubMed]
- Liang, M.; Chang, T.; An, B.; Duan, X.; Du, L.; Wang, X.; Miao, J.; Xu, L.; Gao, X.; Zhang, L.; et al. A Stacking Ensemble Learning Framework for Genomic Prediction. Front. Genet. 2021, 12, 600040. [Google Scholar] [CrossRef]
- Kalagotla, S.K.; Gangashetty, S.V.; Giridhar, K. A novel stacking technique for prediction of diabetes. Comput. Biol. Med. 2021, 135, 104554. [Google Scholar] [CrossRef]
- Yang, Y.; Wei, L.; Hu, Y.; Wu, Y.; Hu, L.; Nie, S. Classification of Parkinson’s disease based on multi-modal features and stacking ensemble learning. J. Neurosci. Methods 2021, 350, 109019. [Google Scholar] [CrossRef]
- Zhu, X.Y.; Du, Q.X.; Li, S.Q.; Sun, J.H. Comparison of the homogeneity of mRNAs encoding SFRP5, FZD4, and Fosl1 in post-injury intervals: Subcellular localization of markers may influence wound age estimation. J. Forensic Leg. Med. 2016, 43, 90–96. [Google Scholar] [CrossRef]
- Dang, L.H.; Feng, N.; An, G.S.; Cao, J.; Du, Q.X.; Jin, Q.Q.; Huang, P.; Sun, J.H. Novel insights into wound age estimation: Combined with “up, no change, or down” system and cosine similarity in python environment. Int. J. Leg. Med. 2020, 134, 2177–2186. [Google Scholar] [CrossRef]
- Sun, J.H.; Nan, L.H.; Gao, C.R.; Wang, Y.Y. Validation of reference genes for estimating wound age in contused rat skeletal muscle by quantitative real-time PCR. Int. J. Leg. Med. 2012, 126, 113–120. [Google Scholar] [CrossRef]
- Pettit, R.W.; Fullem, R.; Cheng, C.; Amos, C.I. Artificial intelligence, machine learning, and deep learning for clinical outcome prediction. Emerg. Top. Life Sci. 2021, 5, 729–745. [Google Scholar] [CrossRef]
- Ahmed, A.; Saeed, F.; Salim, N.; Abdo, A. Condorcet and borda count fusion method for ligand-based virtual screening. J. Cheminform. 2014, 6, 19. [Google Scholar] [CrossRef]
- Gaballah, M.H.; Horita, T.; Takamiya, M.; Yokoji, K.; Fukuta, M.; Kato, H.; Aoki, Y. Time-Dependent Changes in Local and Serum Levels of Inflammatory Cytokines as Markers for Incised Wound Aging of Skeletal Muscles. Tohoku J. Exp. Med. 2018, 245, 29–35. [Google Scholar] [CrossRef]
- Horita, T.; Gaballah, M.H.; Fukuta, M.; Kanno, S.; Kato, H.; Takamiya, M.; Aoki, Y. Time course analysis of large-scale gene expression in incised muscle using correspondence analysis. PLoS ONE 2020, 15, e0230737. [Google Scholar] [CrossRef]
- Peyron, P.A.; Colomb, S.; Becas, D.; Adriansen, A.; Gauchotte, G.; Tiers, L.; Marin, G.; Lehmann, S.; Baccino, E.; Delaby, C.; et al. Cytokines as new biomarkers of skin wound vitality. Int. J. Leg. Med. 2021, 135, 2537–2545. [Google Scholar] [CrossRef]
- Barington, K.; Jensen, H.E.; Skovgaard, K. Forensic aspects of gene expression signatures for age determination in bruises as evaluated in an experimental porcine model. Forensic Sci. Med. Pathol. 2017, 13, 151–160. [Google Scholar] [CrossRef]
- Philips, M.A.; Vikeså, J.; Luuk, H.; Jønson, L.; Lilleväli, K.; Rehfeld, J.F.; Vasar, E.; Kõks, S.; Nielsen, F.C. Characterization of MYG1 gene and protein: Subcellular distribution and function. Biol. Cell 2009, 101, 361–377. [Google Scholar] [CrossRef]
- Gruenwald, K.; Castagnola, P.; Besio, R.; Dimori, M.; Chen, Y.; Akel, N.S.; Swain, F.L.; Skinner, R.A.; Eyre, D.R.; Gaddy, D.; et al. Sc65 is a novel endoplasmic reticulum protein that regulates bone mass homeostasis. J. Bone Miner. Res. Off. J. Am. Soc. Bone Miner. Res. 2014, 29, 666–675. [Google Scholar] [CrossRef]
- Wong, R.W.; Blobel, G.; Coutavas, E. Rae1 interaction with NuMA is required for bipolar spindle formation. Proc. Natl. Acad. Sci. USA 2006, 103, 19783–19787. [Google Scholar] [CrossRef]
- Arlt, A.; Schäfer, H. Role of the immediate early response 3 (IER3) gene in cellular stress response, inflammation and tumorigenesis. Eur. J. Cell Biol. 2011, 90, 545–552. [Google Scholar] [CrossRef]
- Nierobisz, L.S.; Sporer, K.R.; Strasburg, G.M.; Reed, K.M.; Velleman, S.G.; Ashwell, C.M.; Felts, J.V.; Mozdziak, P.E. Differential expression of genes characterizing myofibre phenotype. Anim. Genet. 2012, 43, 298–308. [Google Scholar] [CrossRef] [PubMed]
- Cambiaghi, T.D.; Pereira, C.M.; Shanmugam, R.; Bolech, M.; Wek, R.C.; Sattlegger, E.; Castilho, B.A. Evolutionarily conserved IMPACT impairs various stress responses that require GCN1 for activating the eIF2 kinase GCN2. Biochem. Biophys. Res. Commun. 2014, 443, 592–597. [Google Scholar] [CrossRef]
- Van Zuylen, W.J.; Garceau, V.; Idris, A.; Schroder, K.; Irvine, K.M.; Lattin, J.E.; Ovchinnikov, D.A.; Perkins, A.C.; Cook, A.D.; Hamilton, J.A.; et al. Macrophage activation and differentiation signals regulate schlafen-4 gene expression: Evidence for Schlafen-4 as a modulator of myelopoiesis. PLoS ONE 2011, 6, e15723. [Google Scholar] [CrossRef] [PubMed]
- Yoshimura, S.; Gerondopoulos, A.; Linford, A.; Rigden, D.J.; Barr, F.A. Family-wide characterization of the DENN domain Rab GDP-GTP exchange factors. J. Cell Biol. 2010, 191, 367–381. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Stein, J.; Nallasamy, N. Evaluation of the Nallasamy formula: A stacking ensemble machine learning method for refraction prediction in cataract surgery. Br. J. Ophthalmol. 2022, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Charoenkwan, P.; Chiangjong, W.; Nantasenamat, C.; Hasan, M.M.; Manavalan, B.; Shoombuatong, W. StackIL6: A stacking ensemble model for improving the prediction of IL-6 inducing peptides. Brief. Bioinform. 2021, 22, bbab172. [Google Scholar] [CrossRef]
- Ye, S.; Zhang, H.; Shi, F.; Guo, J.; Wang, S.; Zhang, B. Ensemble Learning to Improve the Prediction of Fetal Macrosomia and Large-for-Gestational Age. J. Clin. Med. 2020, 9, 380. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Peppes, N.; Daskalakis, E.; Alexakis, T.; Adamopoulou, E.; Demestichas, K. Performance of Machine Learning-Based Multi-Model Voting Ensemble Methods for Network Threat Detection in Agriculture 4.0. Sensors 2021, 21, 7475. [Google Scholar] [CrossRef]
- Wu, Z.; Zhu, M.; Kang, Y.; Leung, E.L.; Lei, T.; Shen, C.; Jiang, D.; Wang, Z.; Cao, D.; Hou, T. Do we need different machine learning algorithms for QSAR modeling? A comprehensive assessment of 16 machine learning algorithms on 14 QSAR data sets. Brief. Bioinform. 2021, 22, bbaa321. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dang, L.; Li, J.; Bai, X.; Liu, M.; Li, N.; Ren, K.; Cao, J.; Du, Q.; Sun, J. Novel Prediction Method Applied to Wound Age Estimation: Developing a Stacking Ensemble Model to Improve Predictive Performance Based on Multi-mRNA. Diagnostics 2023, 13, 395. https://doi.org/10.3390/diagnostics13030395
Dang L, Li J, Bai X, Liu M, Li N, Ren K, Cao J, Du Q, Sun J. Novel Prediction Method Applied to Wound Age Estimation: Developing a Stacking Ensemble Model to Improve Predictive Performance Based on Multi-mRNA. Diagnostics. 2023; 13(3):395. https://doi.org/10.3390/diagnostics13030395
Chicago/Turabian StyleDang, Lihong, Jian Li, Xue Bai, Mingfeng Liu, Na Li, Kang Ren, Jie Cao, Qiuxiang Du, and Junhong Sun. 2023. "Novel Prediction Method Applied to Wound Age Estimation: Developing a Stacking Ensemble Model to Improve Predictive Performance Based on Multi-mRNA" Diagnostics 13, no. 3: 395. https://doi.org/10.3390/diagnostics13030395
APA StyleDang, L., Li, J., Bai, X., Liu, M., Li, N., Ren, K., Cao, J., Du, Q., & Sun, J. (2023). Novel Prediction Method Applied to Wound Age Estimation: Developing a Stacking Ensemble Model to Improve Predictive Performance Based on Multi-mRNA. Diagnostics, 13(3), 395. https://doi.org/10.3390/diagnostics13030395




