Acquisition of Lower-Limb Motion Characteristics with a Single Inertial Measurement Unit—Validation for Use in Physiotherapy
Abstract
1. Introduction
2. Materials and Methods
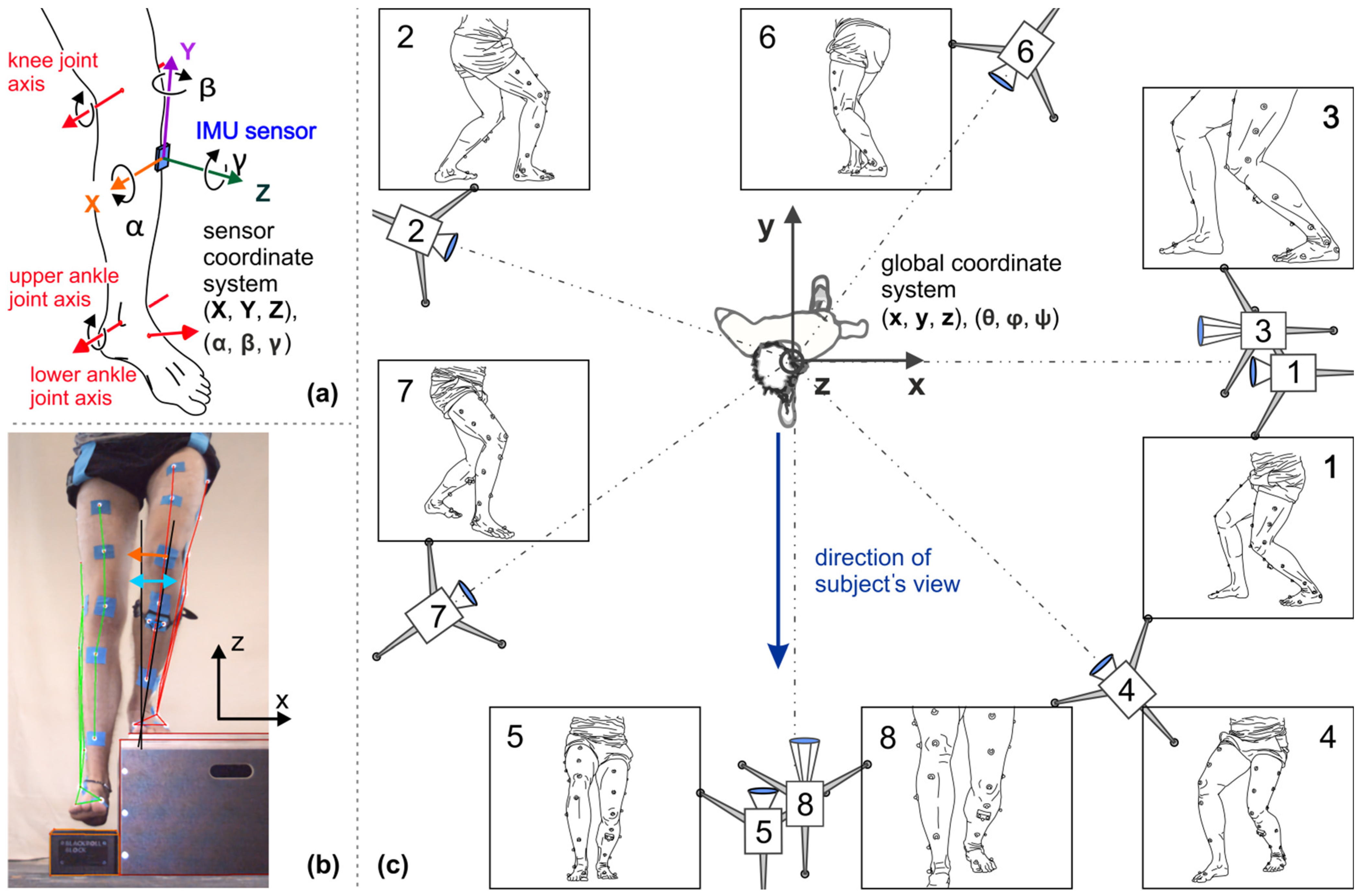
2.1. The IMU System
2.2. Video Motion Analysis
2.3. Volunteers
2.4. The Motion Tests
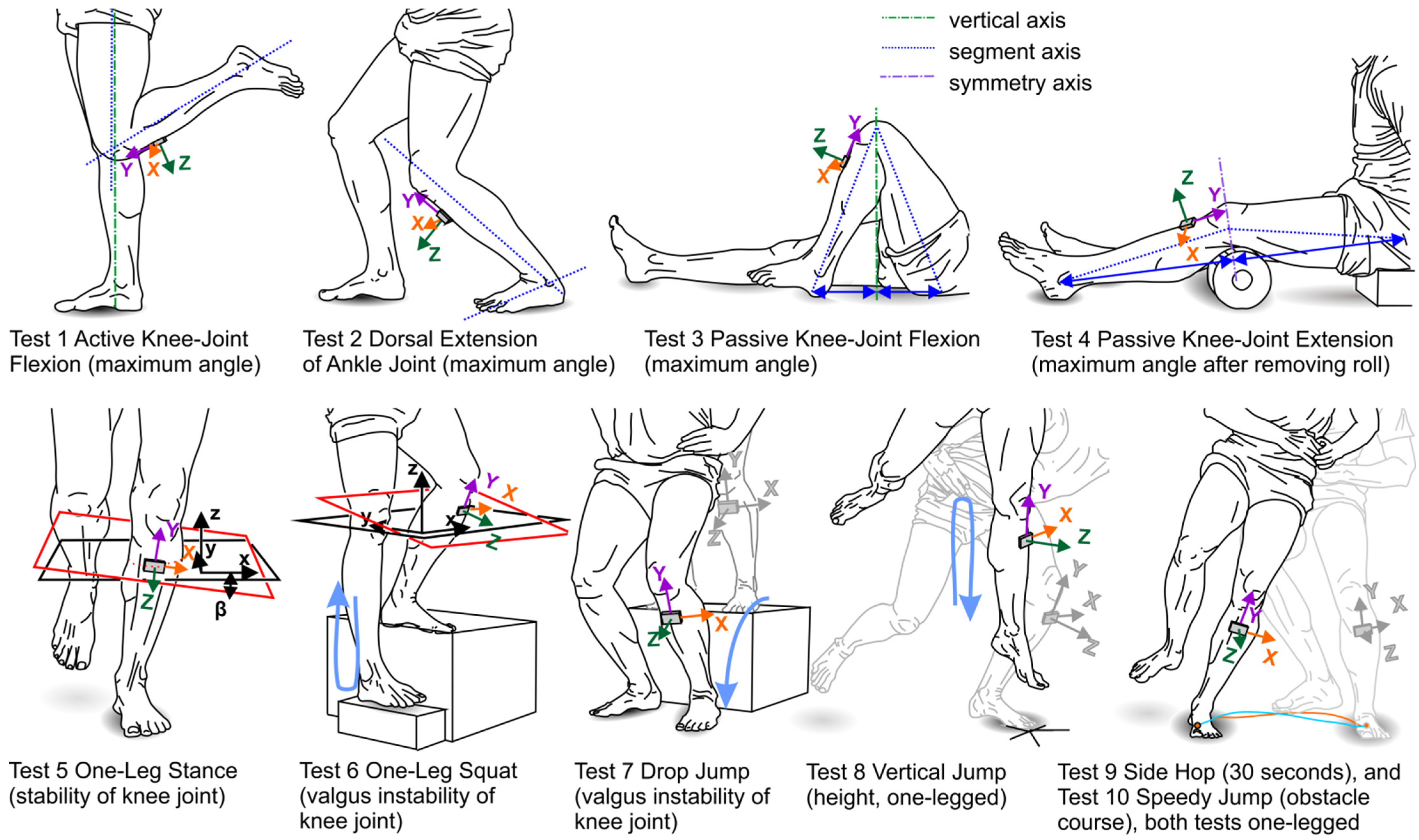
2.4.1. Set A, Tests 1–4—Measurement of Angular ROM
2.4.2. Set B, Tests 5–7—Stability and Knee Valgus
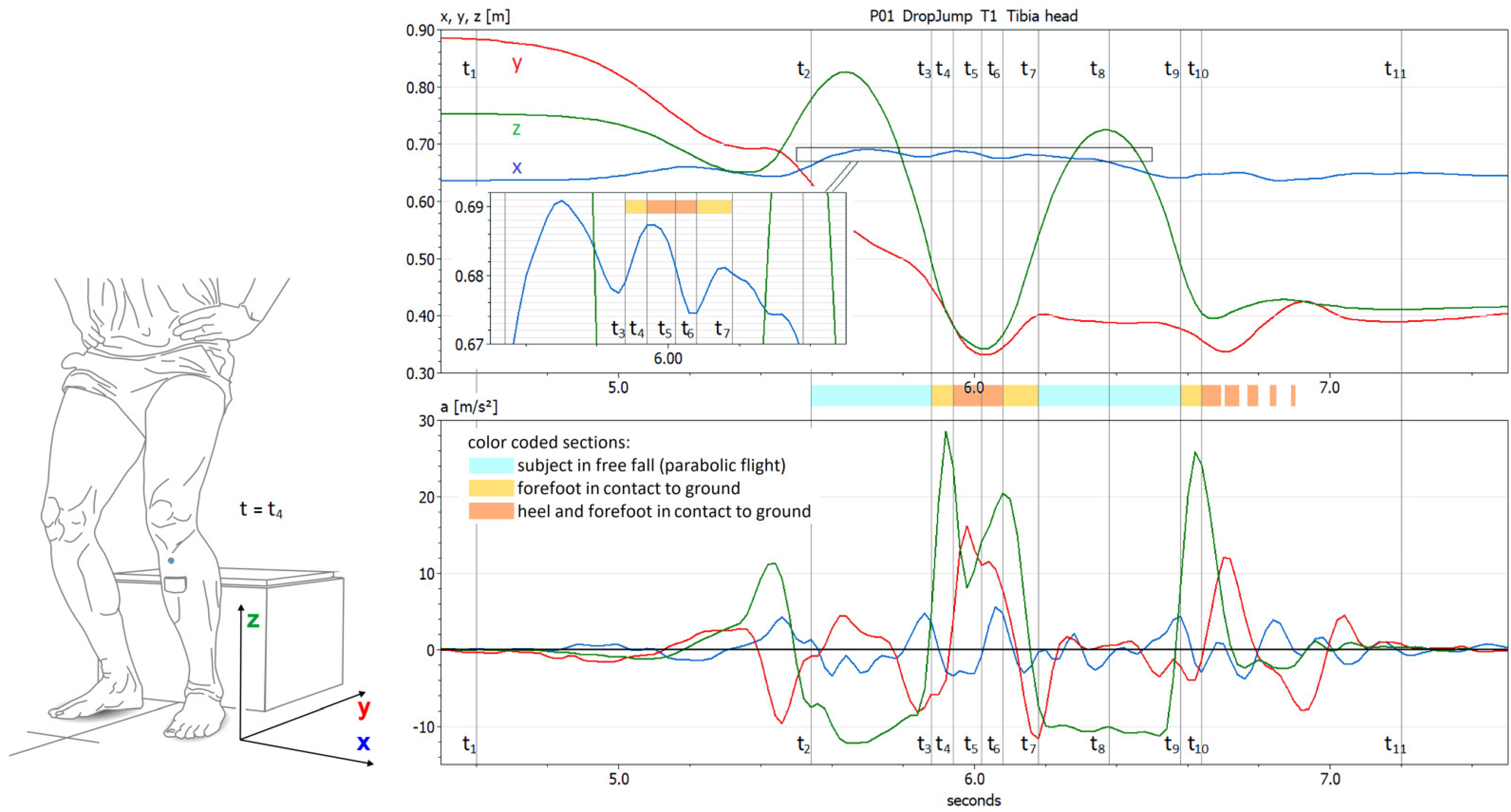
2.4.3. Set C, Tests 8–10—Jump Tests
3. Results
3.1. Overview
3.2. Set A Tests—Measurement of Angular ROM
3.3. Set B Tests—Knee Valgus Instability
3.4. Set C Tests—Jump Tests
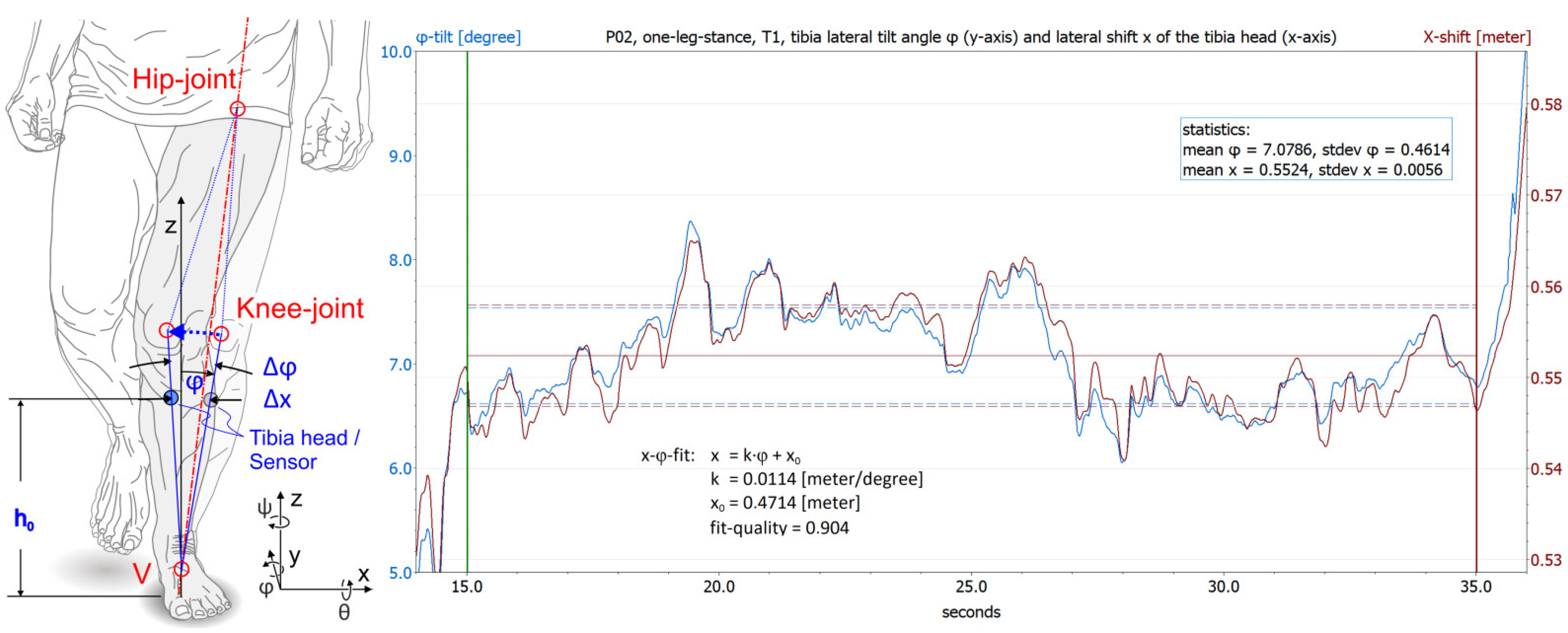
3.5. Decoupling (Mechanical Isolation) of Tibia Tilt and Tibia Shift
4. Discussion
5. Conclusions
6. Limitations
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zwipp, H. Biomechanik der Sprunggelenke [Biomechanics of the ankle joint]. Unfallchirurg 1989, 92, 98–102. (In German) [Google Scholar]
- Bell, K.M.; Onyeukwu, C.; McClincy, M.P.; Allen, M.; Bechard, L.; Mukherjee, A.; Hartman, R.A.; Smith, C.; Lynch, A.D.; Irrgang, J.J. Verification of a Portable Motion Tracking System for Remote Management of Physical Rehabilitation of the Knee. Sensors 2019, 19, 1021. [Google Scholar] [CrossRef]
- Beravs, T.; Reberšek, P.; Novak, D.; Podobnik, J.; Munih, M. Development and validation of a wearable inertial measurement system for use with lower limb exoskeletons. In Proceedings of the 11th IEEE-RAS International Conference on Humanoid Robots, Bled, Slovenia, 26–28 October 2011; pp. 212–217. [Google Scholar] [CrossRef]
- Roetenberg, D.; Luinge, H.; Slycke, P. XSens MVN: Full 6DOF Human Motion Tracking Using Miniature Inertial Sensors; Technical Report; Xsens Motion Technologies B.V.: Enschede, The Netherlands, 2009; Volume 1. [Google Scholar]
- Gujarathi, T.; Bhole, K. Gait Analysis Using IMU Sensor. In Proceedings of the 10th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Kanpur, India, 6–8 July 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Chow, D.H.K.; Tremblay, L.; Lam, C.Y.; Yeung, A.W.Y.; Cheng, W.H.W.; Tse, P.T.W. Comparison between Accelerometer and Gyroscope in Predicting Level Ground Running Kinematics by Treadmill Running Kinematics Using a Single Wearable Sensor. Sensors 2021, 21, 4633. [Google Scholar] [CrossRef] [PubMed]
- Hsu, W.C.; Sugiarto, T.; Lin, Y.J.; Yang, F.C.; Lin, Z.Y.; Sun, C.T.; Hsu, C.L.; Chou, K.N. Multiple-Wearable-Sensor-Based Gait Classification and Analysis in Patients with Neurological Disorders. Sensors 2018, 18, 3397. [Google Scholar] [CrossRef] [PubMed]
- Teufl, W.; Taetz, B.; Miezal, M.; Lorenz, M.; Pietschmann, J.; Jöllenbeck, T.; Fröhlich, M.; Bleser, G. Towards an Inertial Sensor-Based Wearable Feedback System for Patients after Total Hip Arthroplasty: Validity and Applicability for Gait Classification with Gait Kinematics-Based Features. Sensors 2019, 19, 5006. [Google Scholar] [CrossRef] [PubMed]
- Versteyhe, M.; De Vroey, H.; Debrouwere, F.; Hallez, H.; Claeys, K. A Novel Method to Estimate the Full Knee Joint Kinematics Using Low Cost IMU Sensors for Easy to Implement Low Cost Diagnostics. Sensors 2020, 20, 1683. [Google Scholar] [CrossRef] [PubMed]
- Cooper, G.; Sheret, I.; Mcmillan, L.; Siliverdis, K.; Sha, N.; Hodgins, D. Inertial sensor-based knee flexion/extension angle estimation. J. Biomech. 2009, 42, 2678–2685. [Google Scholar] [CrossRef]
- Giggins, O.; Kelly, D.; Caulfield, B. Evaluating rehabilitation exercise performance using a single inertial measurement unit. In Proceedings of the 7th International Conference on Pervasive Computing Technologies for Healthcare (PervasiveHealth ’13), Venice, Italy, 5–8 May 2013; pp. 49–56. [Google Scholar] [CrossRef]
- Bonnet, V.; Joukov, V.; Kulić, D.; Fraisse, P.; Ramdani, N.; Venture, G. Monitoring of Hip and Knee Joint Angles Using a Single Inertial Measurement Unit During Lower Limb Rehabilitation. IEEE Sens. J. 2016, 16, 1557–1564. [Google Scholar] [CrossRef]
- Weygers, I.; Kok, M.; Konings, M.; Hallez, H.; Vroey, H.D.; Claeys, K. Inertial Sensor-Based Lower Limb Joint Kinematics: A Methodological Systematic Review. Sensors 2020, 20, 673. [Google Scholar] [CrossRef]
- Côté-Allard, U.; Gagnon-Turcotte, G.; Laviolette, F.; Gosselin, B. A Low-Cost, Wireless, 3-D-Printed Custom Armband for sEMG Hand Gesture Recognition. Sensors 2019, 19, 2811. [Google Scholar] [CrossRef]
- Wyndow, N.; Collins, N.J.; Vicenzino, B.; Tucker, K.; Crossley, K.M. Foot and ankle characteristics and dynamic knee valgus in individuals with patellofemoral osteoarthritis. J. Foot Ankle Res. 2018, 11, 65. [Google Scholar] [CrossRef] [PubMed]
- Munro, A.; Herrington, L.; Carolan, M. Reliability of 2-dimensional video assessment of frontal-plane dynamic knee valgus during common athletic screening tasks. J. Sport Rehabil. 2012, 21, 7–11. [Google Scholar] [CrossRef] [PubMed]
- Scinicarelli, G.; Trofenik, M.; Froböse, I.; Wilke, C. The Reliability of Common Functional Performance Tests within an Experimental Test Battery for the Lower Extremities. Sports 2021, 9, 100. [Google Scholar] [CrossRef] [PubMed]
- Hora, M.; Soumar, L.; Pontzer, H.; Sládek, V. Body size and lower limb posture during walking in humans. PLoS ONE 2017, 12, e0172112. [Google Scholar] [CrossRef]
- Contini, R.; Drillis, R.J.; Bluestein, M. Determination of Body Segment Parameters. Hum. Factors 1963, 5, 493–504. [Google Scholar] [CrossRef] [PubMed]
- Wilczyński, B.; Zorena, K.; Ślęzak, D. Dynamic Knee Valgus in Single-Leg Movement Tasks. Potentially Modifiable Factors and Exercise Training Options. A Literature Review. Int. J. Environ. Res. Public Health 2020, 17, 8208. [Google Scholar] [CrossRef]
- Udompanich, N.; Thanasootr, K.O.; Chanavirut, R.; Chatchawan, U.; Hunsawong, T. The Cut-Off Score of Four Clinical Tests to Quantify Balance Impairment in Individuals with Chronic Ankle Instability. Malays. J. Med. Sci. (MJMS) 2021, 28, 87–96. [Google Scholar] [CrossRef]
- Trojian, T.H.; McKeag, D.B. Single leg balance test to identify risk of ankle sprains. Br. J. Sports Med. 2006, 40, 610–613. [Google Scholar] [CrossRef]
- Nielsen, E.T.; Jørgensen, P.B.; Mechlenburg, I.; Sørensen, H. Validation of an inertial measurement unit to determine countermovement jump height. Asia-Pac. J. Sports Med. Arthrosc. Rehabil. Technol. 2019, 16, 8–13. [Google Scholar] [CrossRef]
- Marković, S.; Dopsaj, M.; Tomažič, S.; Kos, A.; Nedeljković, A.; Umek, A. Can IMU Provide an Accurate Vertical Jump Height Estimate? Appl. Sci. 2021, 11, 12025. [Google Scholar] [CrossRef]
- Linens, S.W.; Ross, S.E.; Arnold, B.L.; Gayle, R.; Pidcoe, P. Postural-stability tests that identify individuals with chronic ankle instability. J. Athl. Train. 2014, 49, 15–23. [Google Scholar] [CrossRef] [PubMed]
- Greisberg, J.; Gould, P.; Vosseller, J.T.; Greisberg, M.; Bandasak, N.; Dolar, R.; Ahmad, C. Performance Function Tests in Assessing Ankle Fitness. Journal of the American Academy of Orthopaedic Surgeons. Glob. Res. Rev. 2019, 3, e096. [Google Scholar] [CrossRef]
- Kapteyn, T.S.; Bles, W.; Njiokiktjien, C.J.; Kodde, L.; Massen, C.H.; Mol, J.M. Standardization in platform stabilometry being a part of posturography. Agressologie 1983, 24, 321–326. [Google Scholar] [PubMed]
- Winter, D.A.; Eng, P. Human balance and posture control during standing and walking. Gait Posture 1995, 3, 193–214. [Google Scholar] [CrossRef]
- Inman, V.T.; Ralston, H.J.; Todd, F. Human Walking; Williams & Wilkins: Baltimore, MD, USA; London, UK, 1981. [Google Scholar]
- Hintermann, B.; Nigg, B.M. Pronation aus der Sicht der Bewegungsübertragung zwischen Kalkaneus und Tibia [Pronation from the viewpoint of the transfer of movement between the calcaneus and the tibia]. Schweiz. Z. Sportmed. 1993, 41, 151–156. (In German) [Google Scholar] [PubMed]
- Hintermann, B.; Nigg, B.M. Pronation in Runners—Implications for Injuries. Sports Med. 1998, 26, 169–176. [Google Scholar] [CrossRef] [PubMed]
- Hewett, T.E.; Ford, K.R.; Hoogenboom, B.J.; Myer, G.D. Understanding and preventing acl injuries: Current biomechanical and epidemiologic considerations—Update 2010. N. Am. J. Sports Phys. Ther. 2010, 5, 234–251. [Google Scholar]
- Paterno, M.V.; Schmitt, L.C.; Ford, K.R.; Rauh, M.J.; Myer, G.D.; Huang, B. Biomechanical measures during landing and postural stability predict second anterior cruciate ligament injury after anterior cruciate ligament reconstruction and return to sport. Am. J. Sports Med. 2010, 38, 1968–1978. [Google Scholar] [CrossRef]
- Bates, N.A.; Myer, G.D.; Hale, R.F.; Schilaty, N.D.; Hewett, T.E. Prospective Frontal Plane Angles Used to Predict ACL Strain and Identify Those at High Risk for Sports-Related ACL Injury. Orthop. J. Sports Med. 2020, 8, 2325967120957646. [Google Scholar] [CrossRef]
- Mehl, J.; Diermeier, T.; Herbst, E.; Imhoff, A.B.; Stoffels, T.; Zantop, T. Evidence-based concepts for prevention of knee and ACL injuries. 2017 guidelines of the ligament committee of the German Knee Society (DKG). Arch. Orthop. Trauma Surg. 2018, 138, 51–61. [Google Scholar] [CrossRef]
- Nilstad, A.; Andersen, T.E.; Kristianslund, E.; Bahr, R.; Myklebust, G.; Krosshaug, T. Physiotherapists Can Identify-Female Football Players with High Knee Valgus Angles During Vertical Drop Jumps Using Real-Time Observational Screening. J. Orthop. Sports Phys. Ther. 2010, 44, 358–365. [Google Scholar] [CrossRef] [PubMed]
- Munro, A.; Herrington, L.; Comfort, P. The Relationship Between 2-Dimensional Knee-Valgus Angles During Single-Leg Squat, Single-Leg-Land, and Drop-Jump Screening Tests. J. Sport Rehabil. 2017, 26, 72–77. [Google Scholar] [CrossRef] [PubMed]
- Mcdonald, S.W.; Tavener, G. Pronation and supination of the foot: Confused terminology. Foot 1999, 9, 6–11. [Google Scholar] [CrossRef]
- International Society of Biomechanics. Standards—Standardization Proposals by the ISB Standardization Committee. [Online]. Available online: https://isbweb.org/activities/standards (accessed on 4 July 2020).
- Mainzer, K. Vorwort. In Die Berechnung der Welt: Von der Weltformel zu Big Data, 1st ed.; The Calculation of the World: From the World Formula towards Big Data; Verlag C.H.Beck: München, Germany, 2014; pp. 13–16. Available online: http://www.jstor.org/stable/j.ctv1169450.3 (accessed on 14 May 2022). (In German)
- Zhou, L.; Fischer, E.; Tunca, C.; Brahms, C.M.; Ersoy, C.; Granacher, U.; Arnrich, B. How We Found Our IMU: Guidelines to IMU Selection and a Comparison of Seven IMUs for Pervasive Healthcare Applications. Sensors 2020, 20, 4090. [Google Scholar] [CrossRef] [PubMed]

| Tests | Measured Score Values | Comparison of IMU and VMA Results | |||||||
|---|---|---|---|---|---|---|---|---|---|
| No. | Set | Motion Pattern | Unit | IMU Score | VMA Score | SD | RMS | SD (%) | RMS (%) |
| 1 | A | Knee flexion (active) | (degrees) | 97.5 | 96.5 | 6.03 | 6.12 | 6.2 | 7.4 |
| 2 | A | Ankle extension | (degrees) | 37.3 | 36.0 | 1.62 | 2.05 | 4.5 | 5.8 |
| 3 | A | Knee flexion (passive) | (degrees) | 127.6 | 124.6 | 3.36 | 4.51 | 2.7 | 3.4 |
| 4 | A | Knee extension (passive) | (degrees) | 25.5 | 24.9 | 1.2 | 1.34 | 4.8 | 5.7 |
| 5 | B | One-leg stance (stability) | (mm) | 2.5 | 2.7 | 0.4 | 0.41 | 14.8 | 19.3 |
| 6 | B | One-leg squat (knee valgus) | (degrees) | 3.78 | 3.77 | 1.23 | 1.35 | 32.6 | 53.9 |
| 7 | B | Drop jump (knee valgus) | (degrees) | 1.29 | 2.57 | 1.77 | 2.19 | 68.9 | 99 |
| 8 | C | Vertical jump height | (cm) | 20.5 | 20.5 | 0.77 | 0.77 | 3.8 | 3.8 |
| 9 | C | Side hop | (counts) | 52.2 | 52.2 | - | - | - | - |
| 10 | C | Speedy jump | (s) | 7.84 | 7.71 | 0.12 | 0.18 | 1.6 | 2.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mitternacht, J.; Hermann, A.; Carqueville, P. Acquisition of Lower-Limb Motion Characteristics with a Single Inertial Measurement Unit—Validation for Use in Physiotherapy. Diagnostics 2022, 12, 1640. https://doi.org/10.3390/diagnostics12071640
Mitternacht J, Hermann A, Carqueville P. Acquisition of Lower-Limb Motion Characteristics with a Single Inertial Measurement Unit—Validation for Use in Physiotherapy. Diagnostics. 2022; 12(7):1640. https://doi.org/10.3390/diagnostics12071640
Chicago/Turabian StyleMitternacht, Jürgen, Aljoscha Hermann, and Patrick Carqueville. 2022. "Acquisition of Lower-Limb Motion Characteristics with a Single Inertial Measurement Unit—Validation for Use in Physiotherapy" Diagnostics 12, no. 7: 1640. https://doi.org/10.3390/diagnostics12071640
APA StyleMitternacht, J., Hermann, A., & Carqueville, P. (2022). Acquisition of Lower-Limb Motion Characteristics with a Single Inertial Measurement Unit—Validation for Use in Physiotherapy. Diagnostics, 12(7), 1640. https://doi.org/10.3390/diagnostics12071640






