Physics Informed Neural Networks (PINN) for Low Snr Magnetic Resonance Electrical Properties Tomography (MREPT)
Abstract
1. Introduction
2. Materials and Methods
2.1. MREPT Formulations
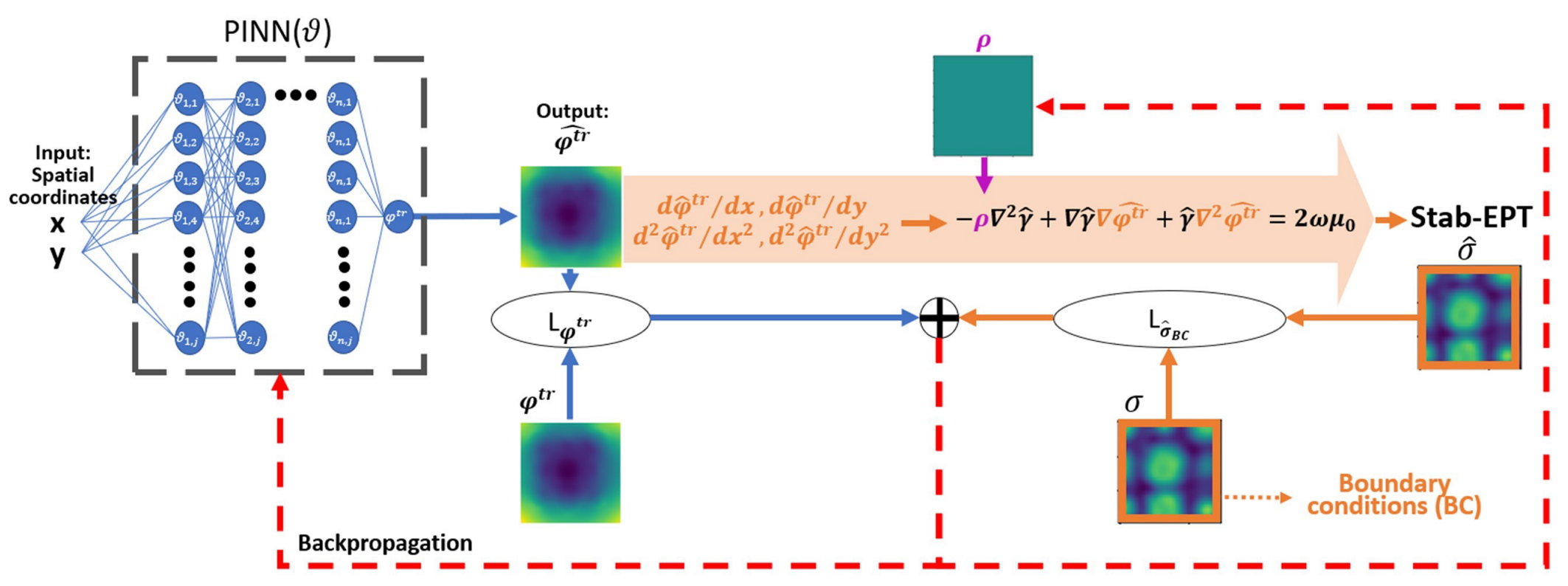
2.2. PINN-MREPT
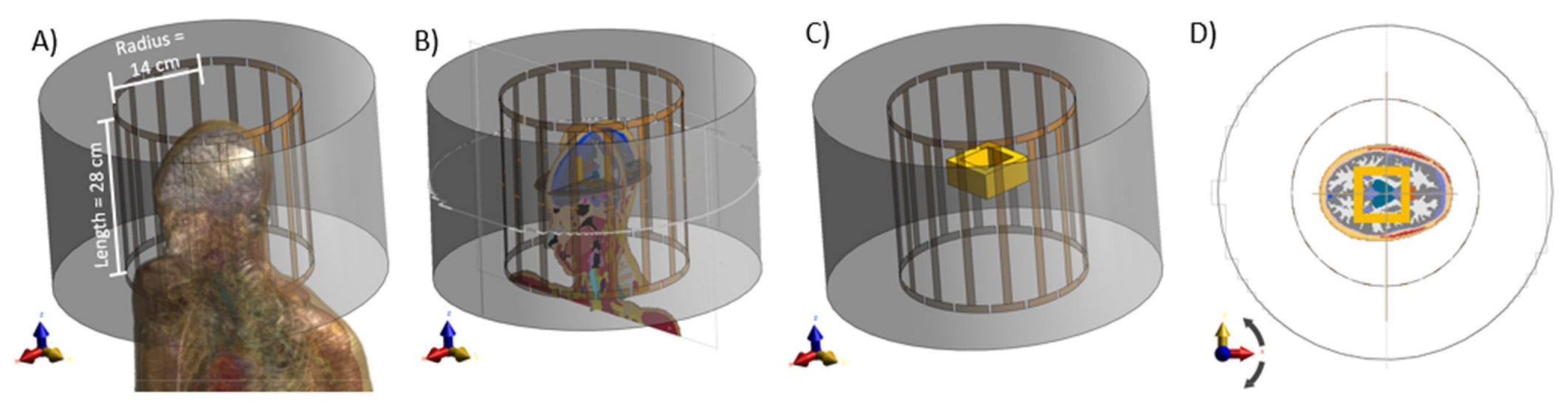
2.3. Numerical Simulations for Sample Preparations
2.4. Noise
2.5. Phantom Preparation and Scanning
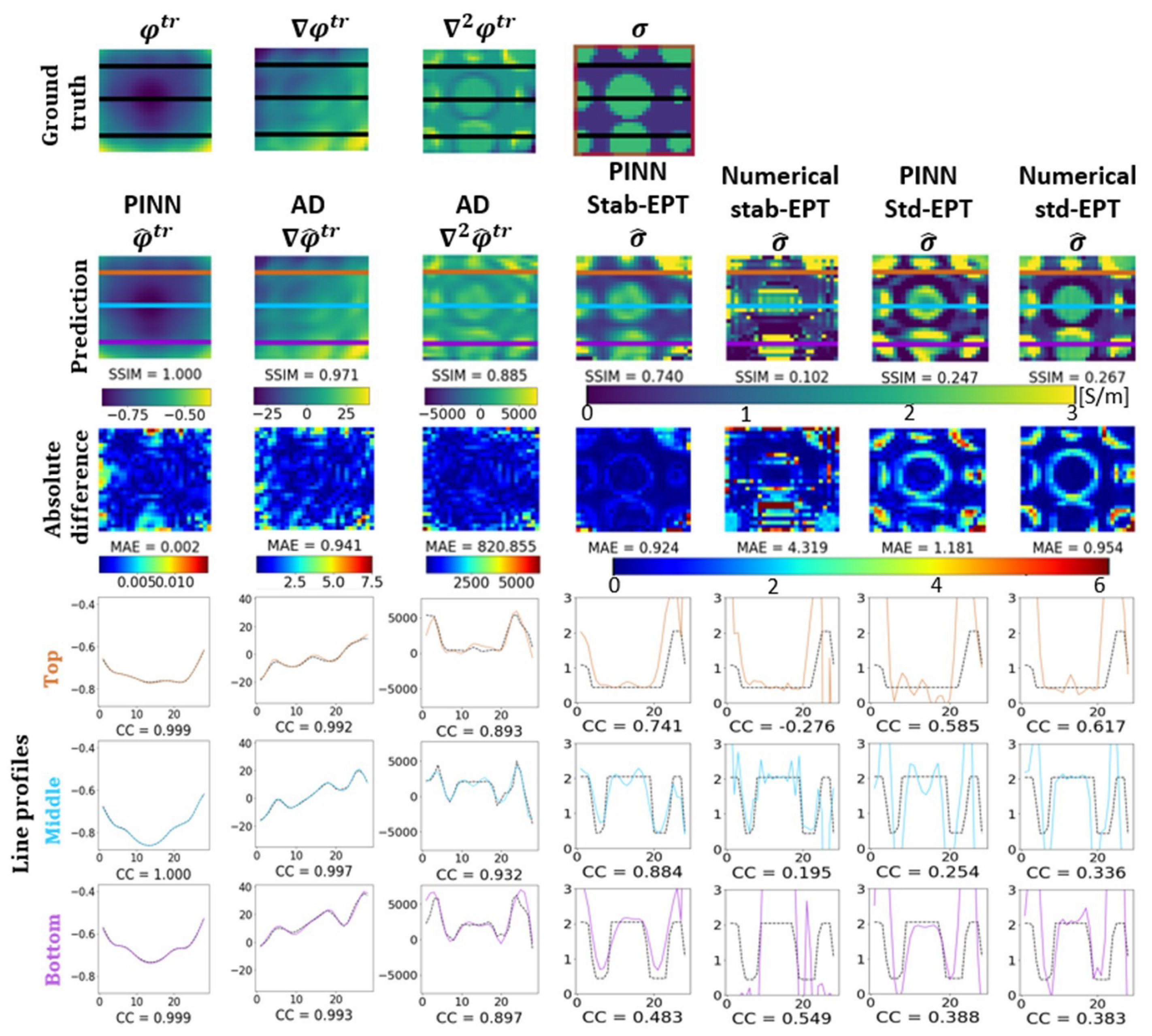
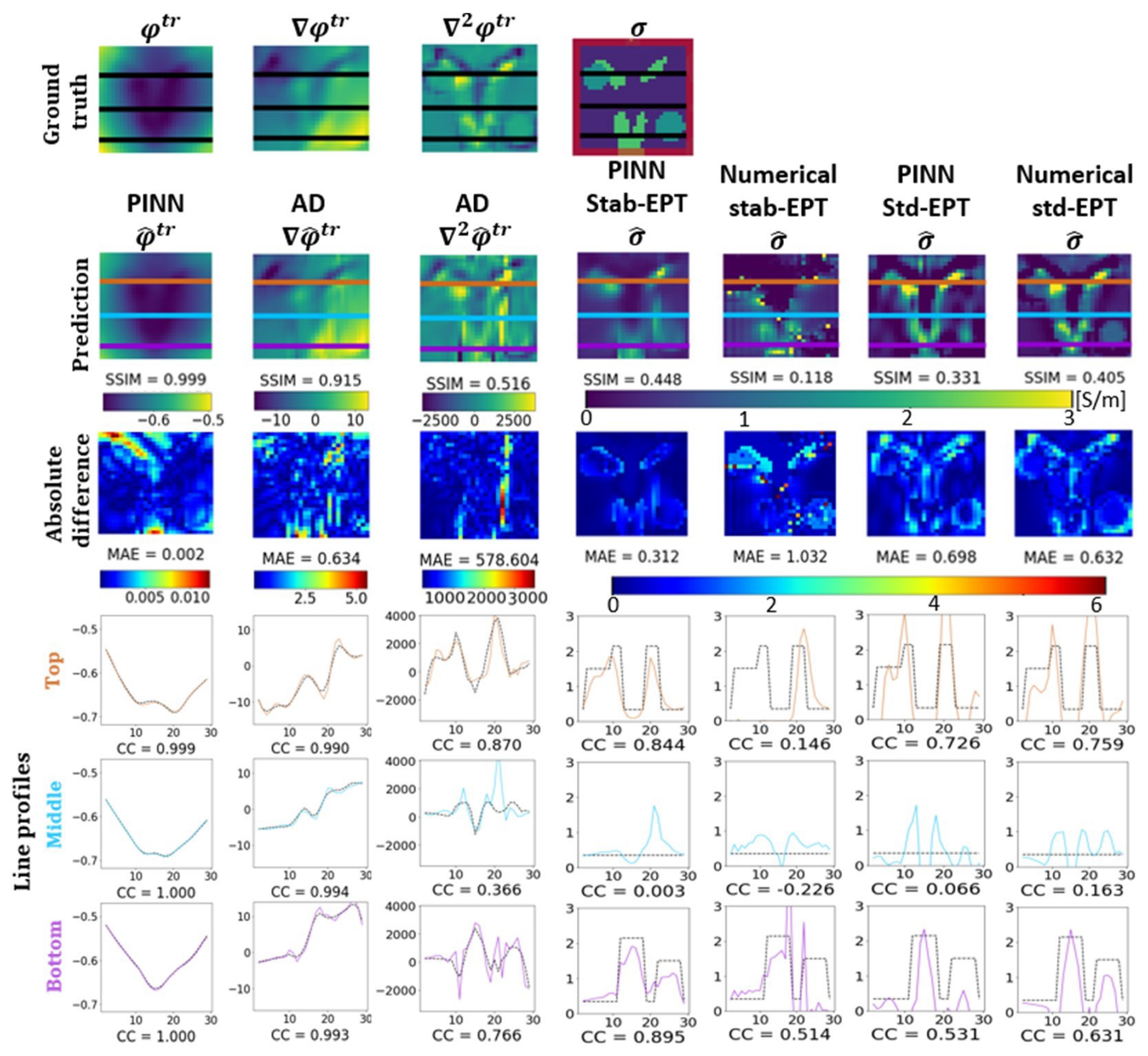
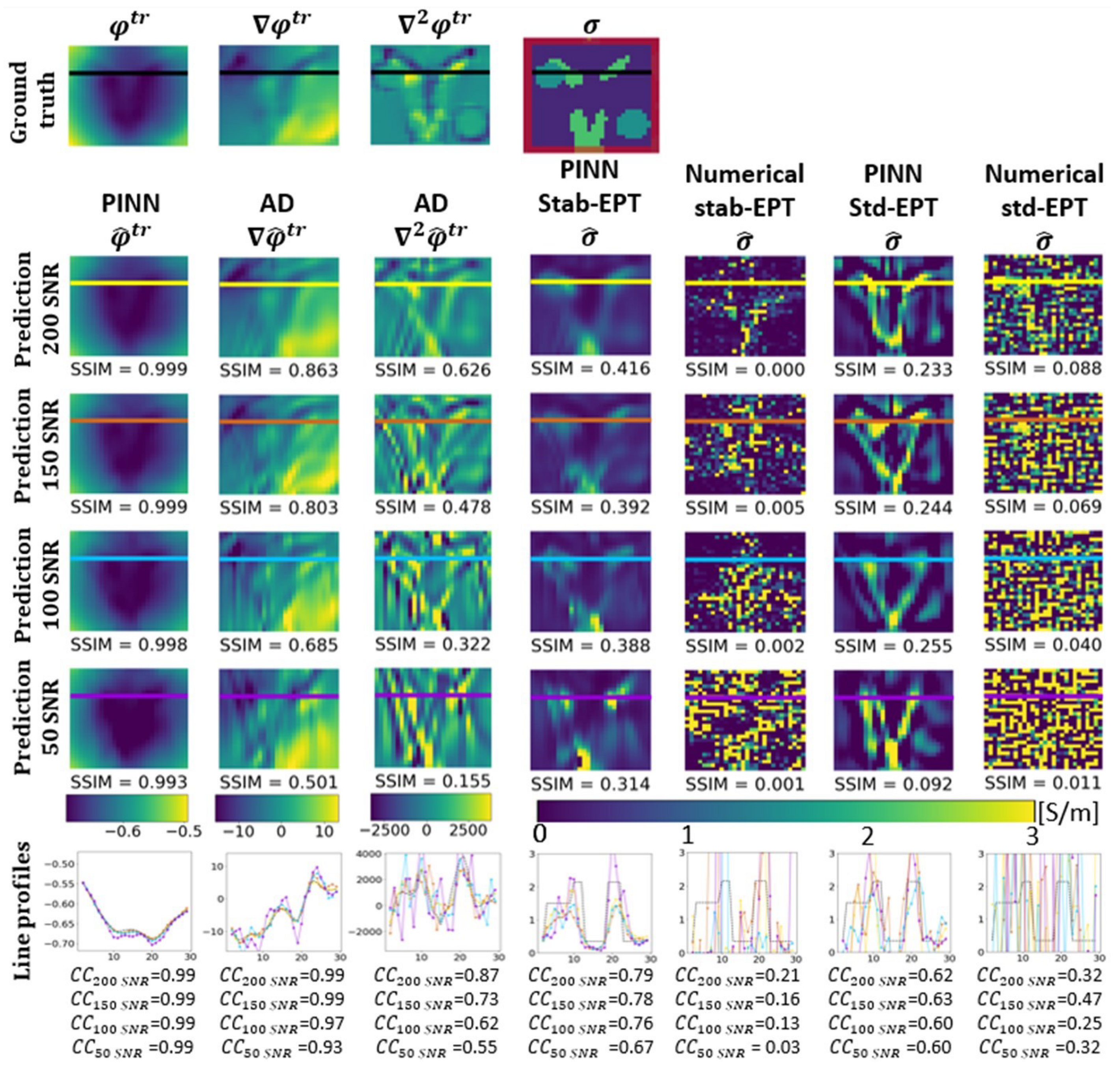
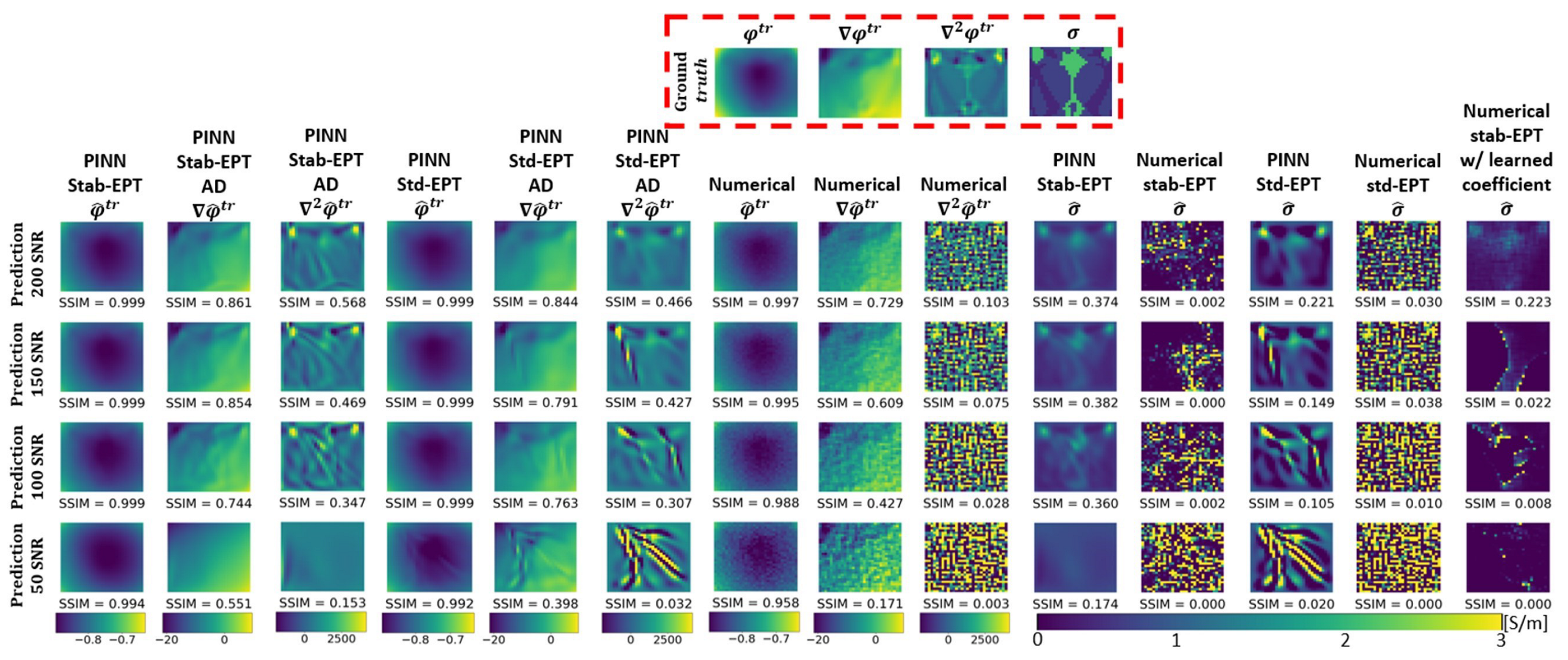
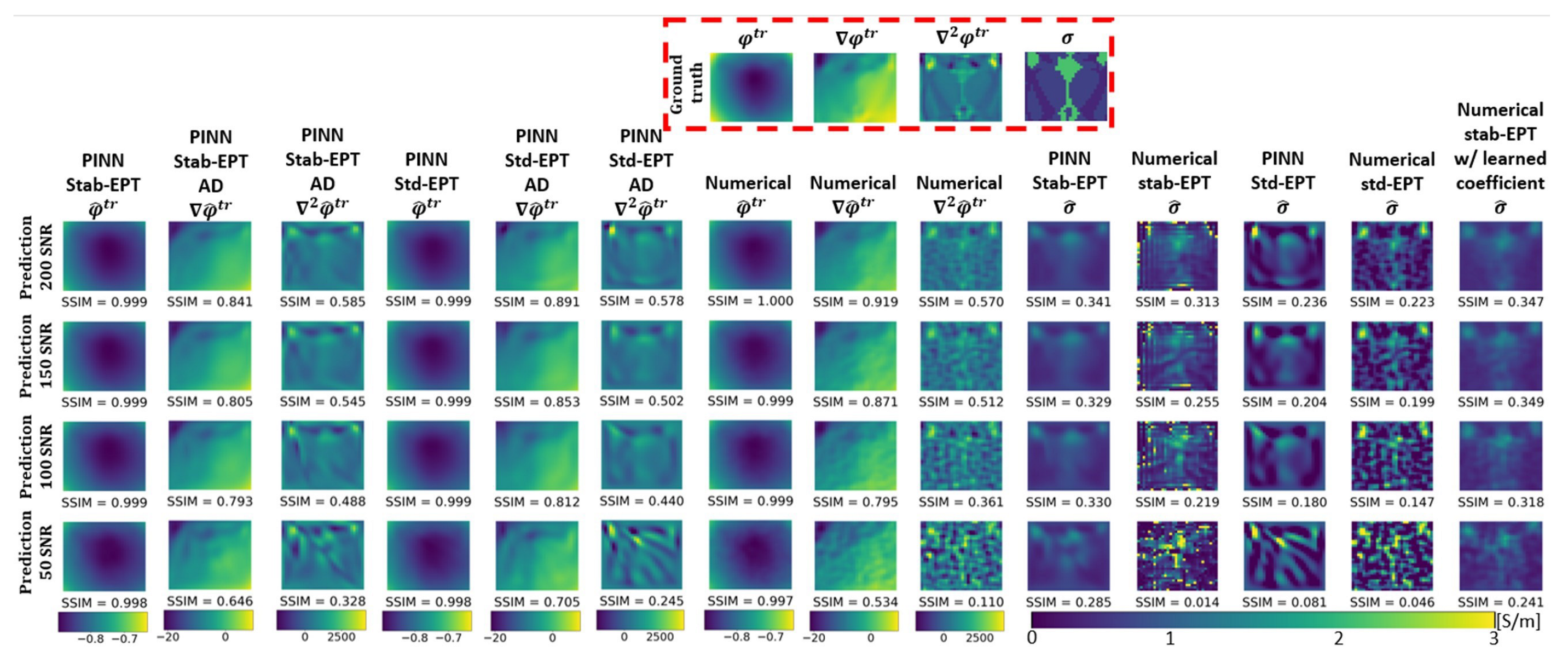
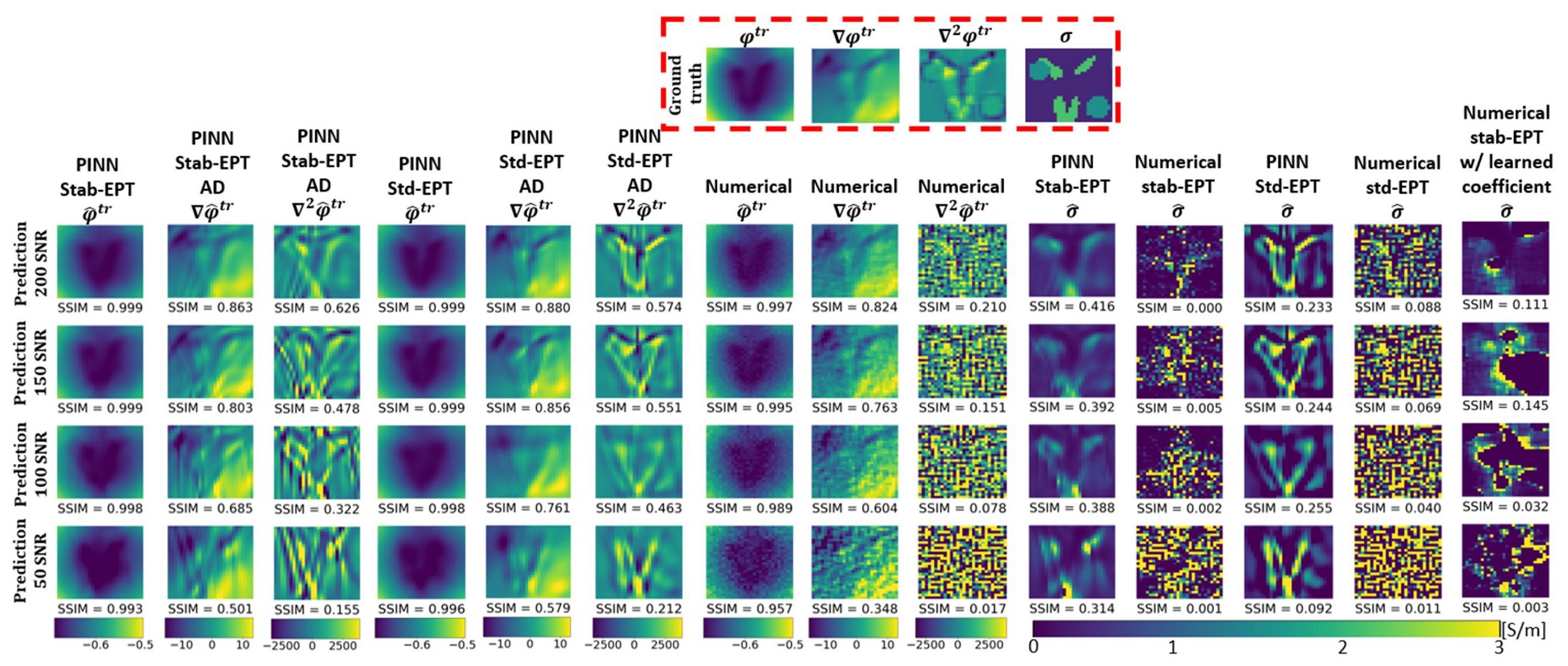
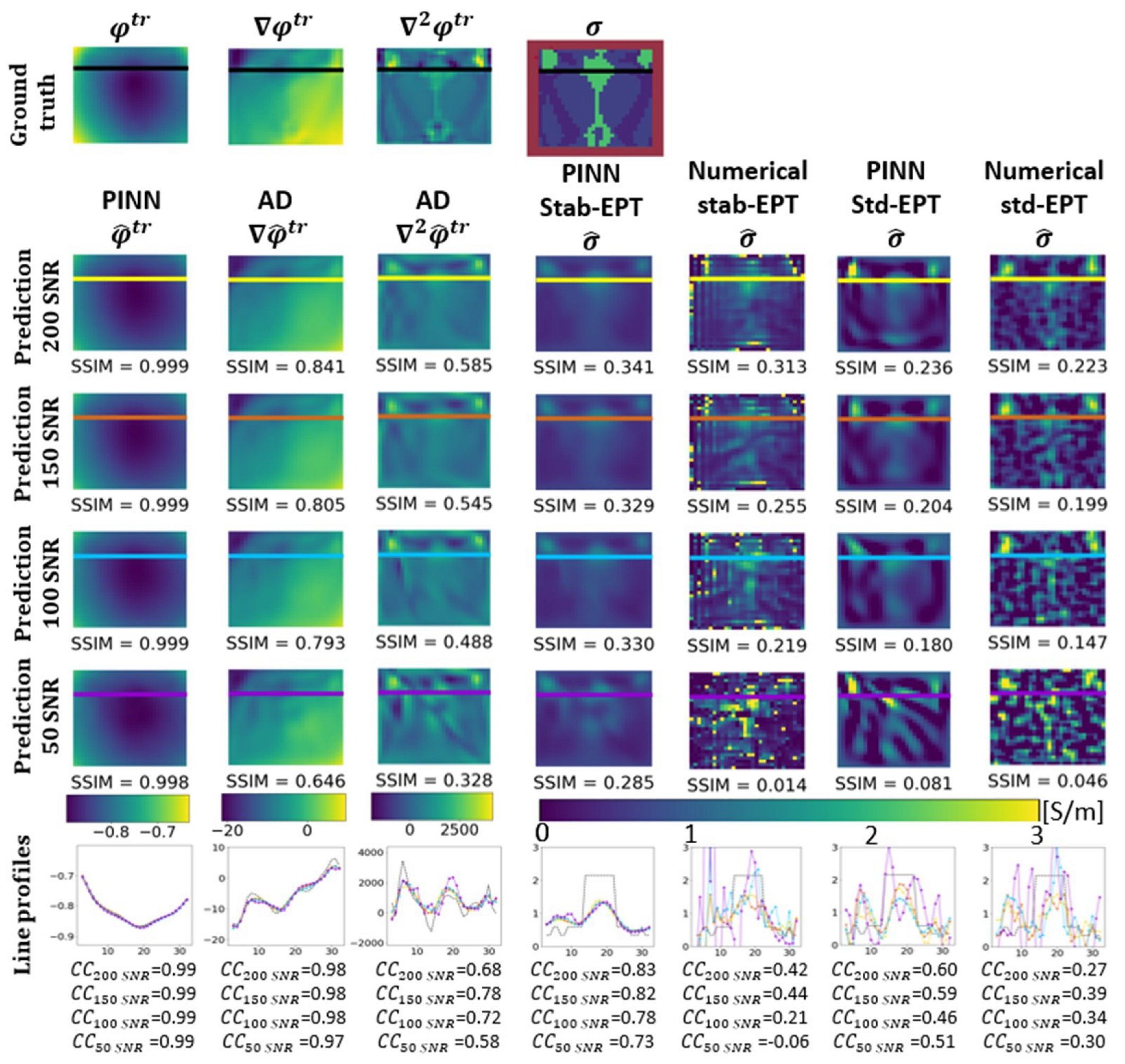
3. Results
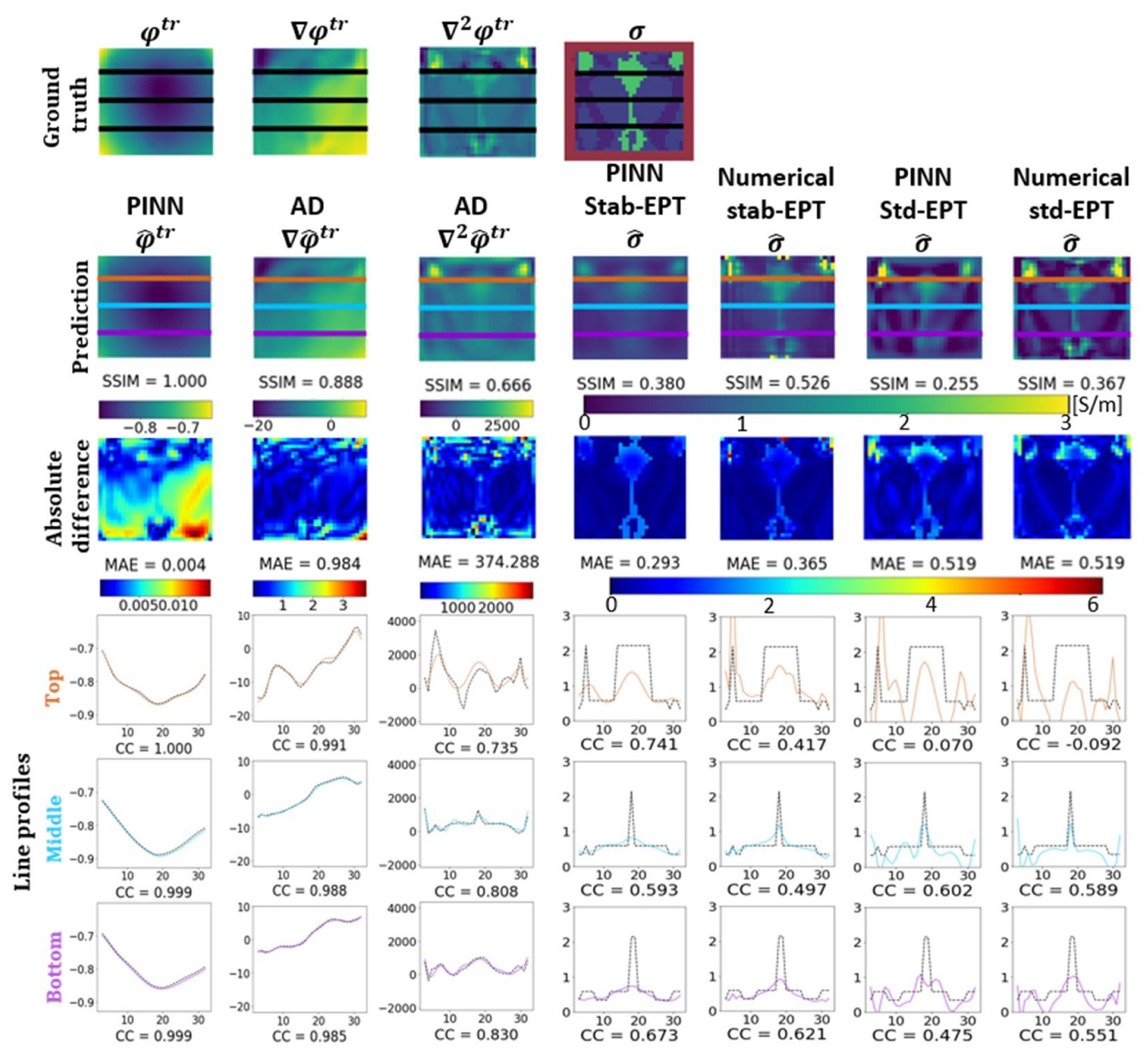
3.1. Conductivity Reconstruction
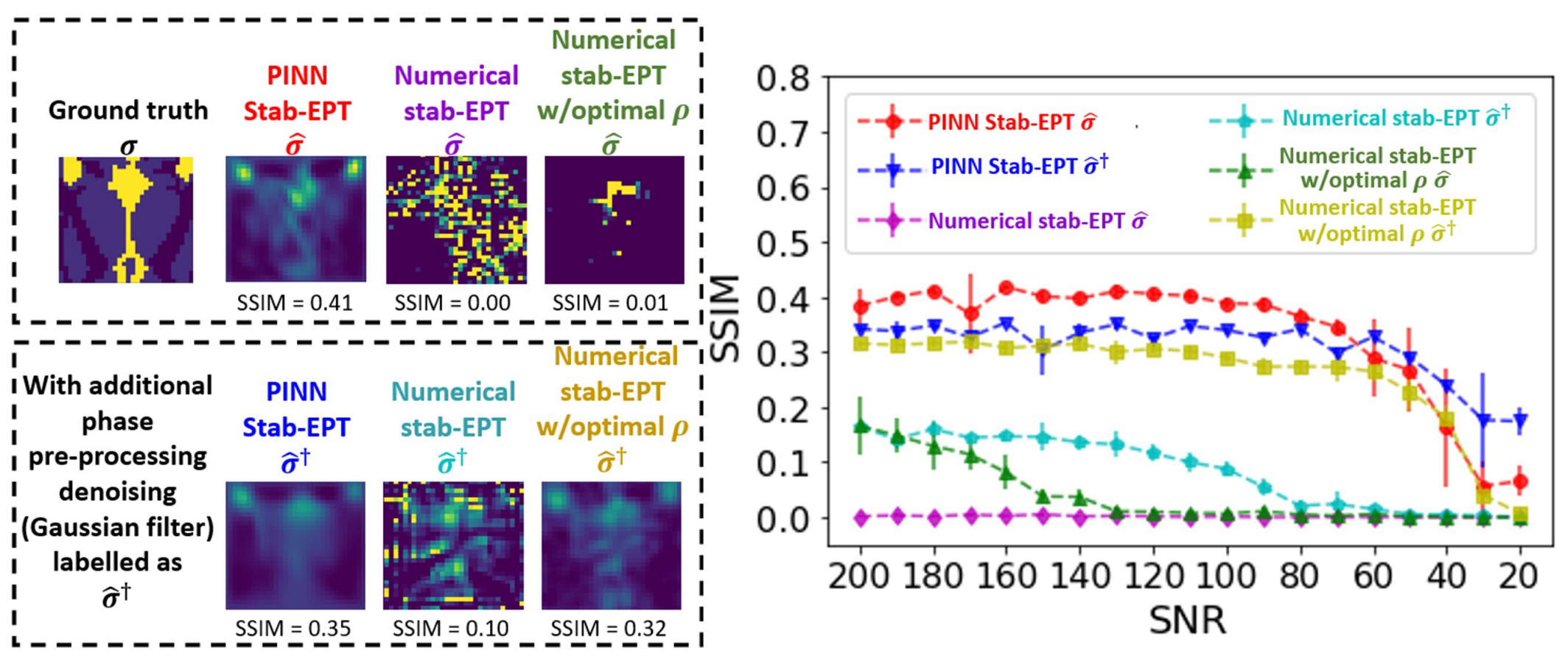
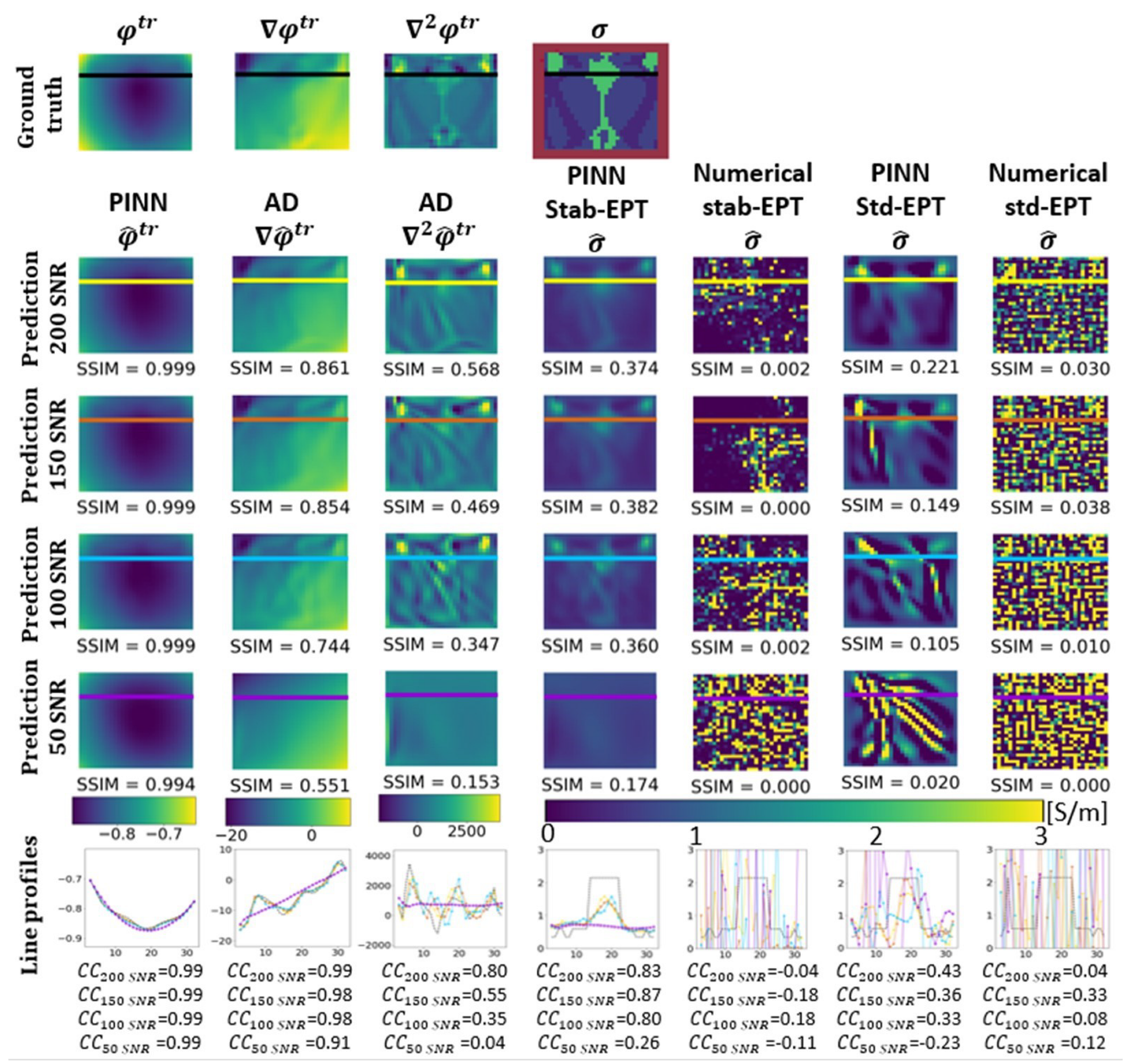
3.2. Noise Robustness
3.3. Tissue Sensitivity
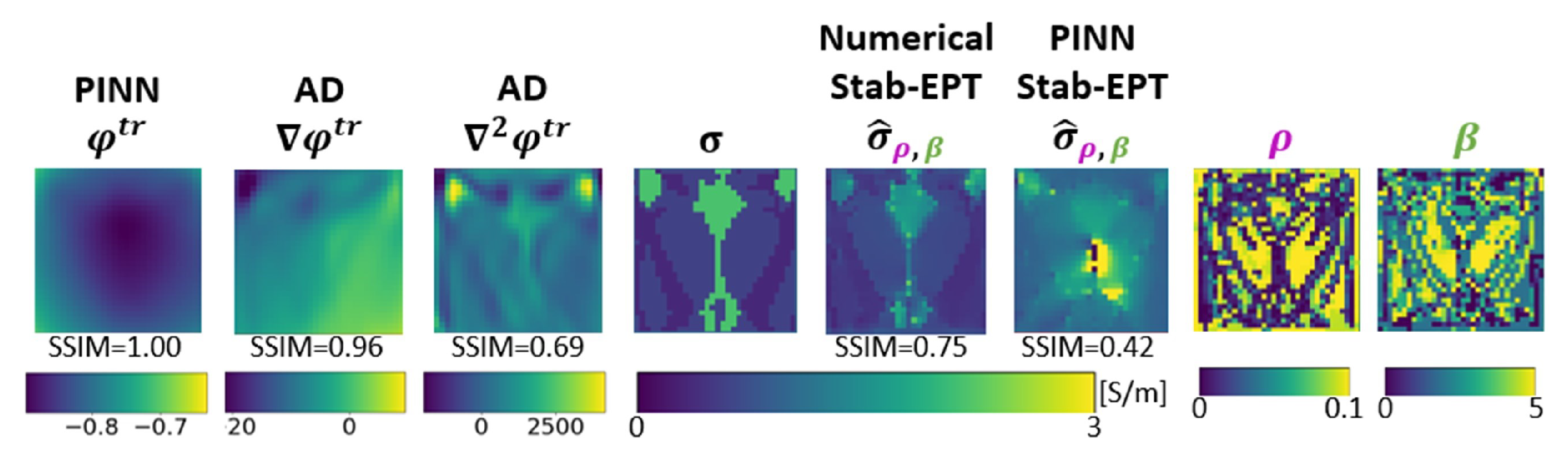
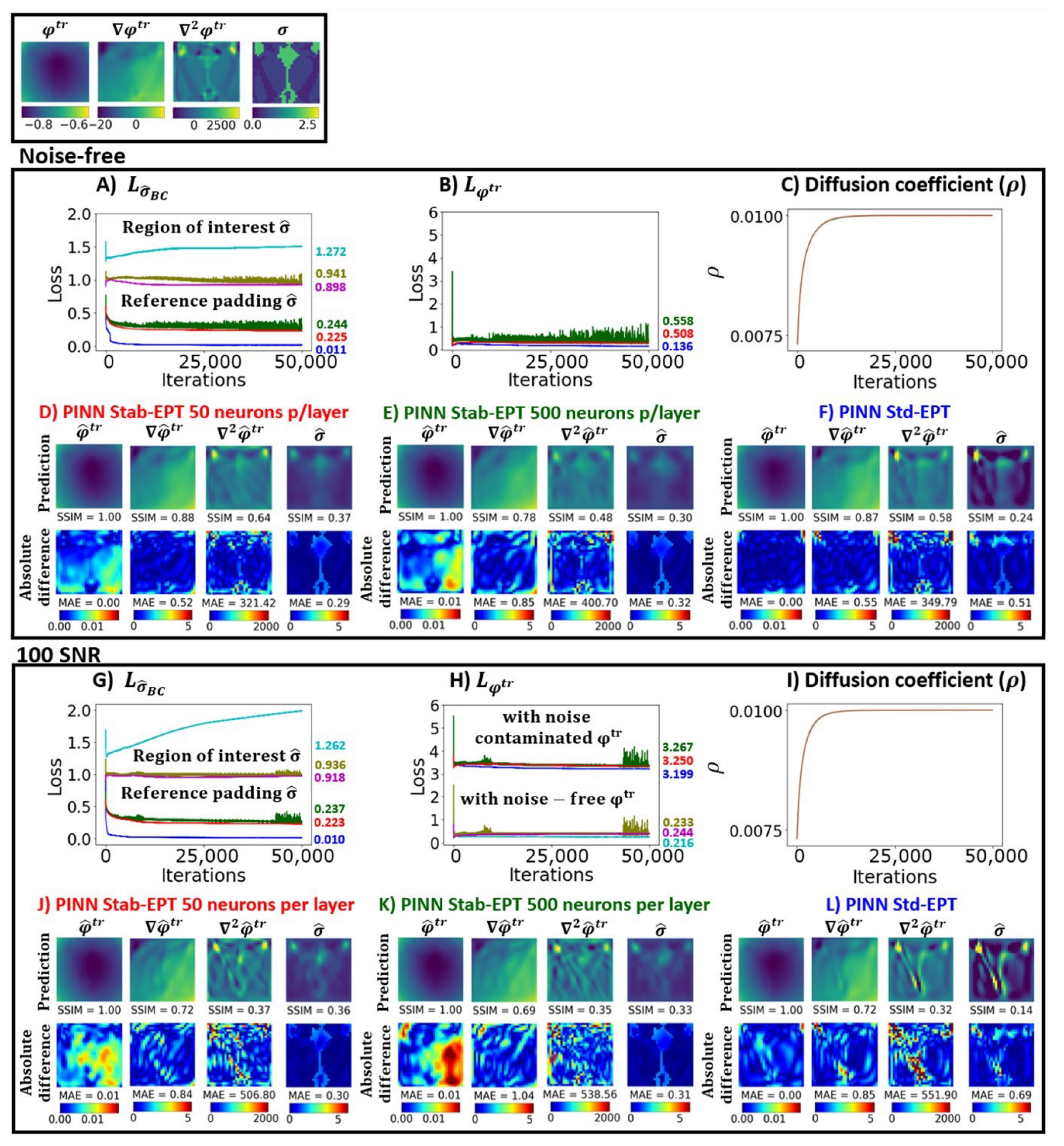
3.4. Optimization Details
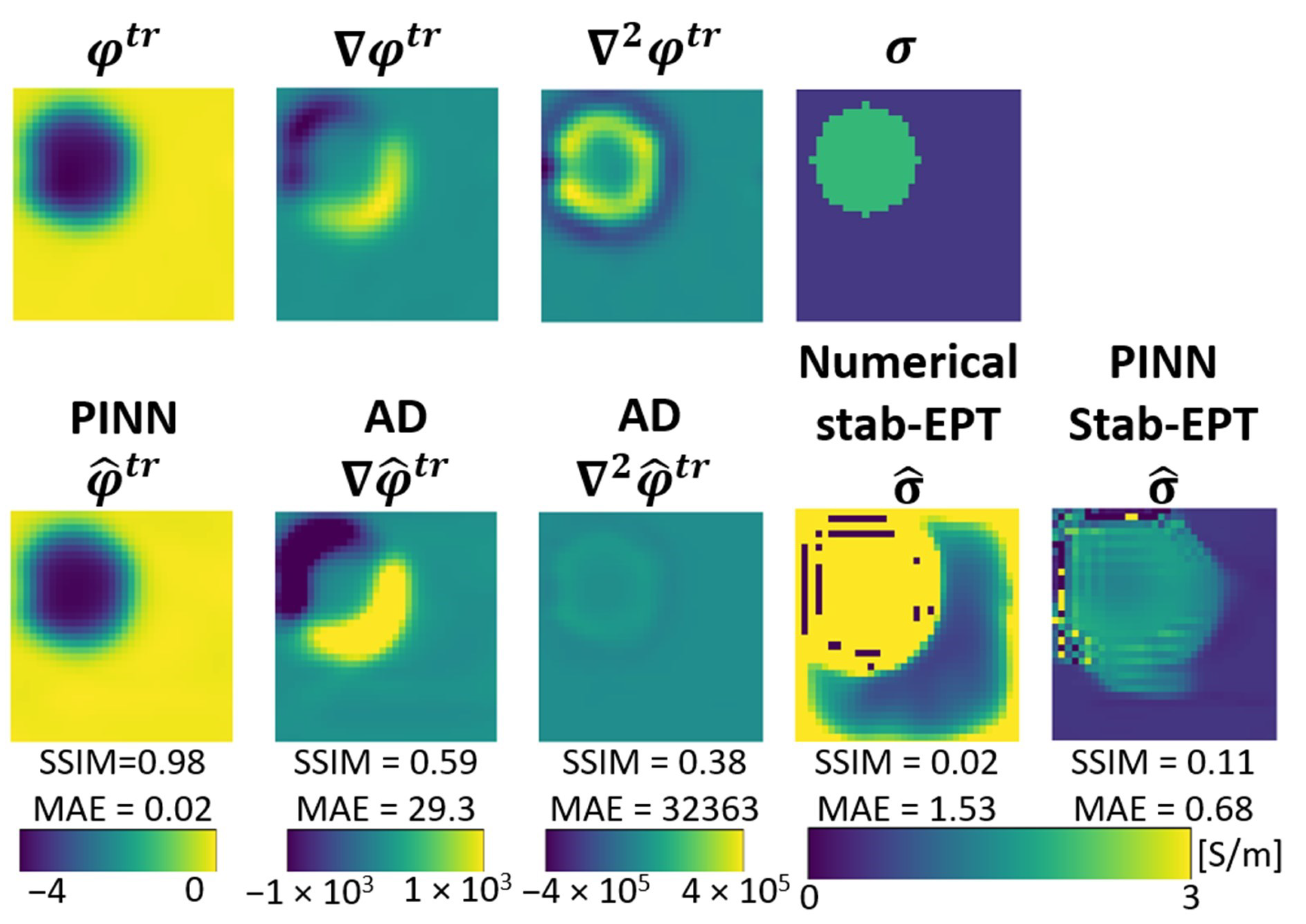
3.5. Phantom Reconstruction
4. Discussion
4.1. Noise Robust Reconstructions
4.1.1. AD & Noise-Filtering of NN
4.1.2. The Role and Optimization of the Diffusion Coefficient
4.1.3. Tissue Sensitivity
4.2. Providing Collocation Points for Single Sample MREPT
4.3. Computational Cost
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A


References
- Bodenstein, M.; David, M.; Markstaller, K. Principles of electrical impedance tomography and its clinical application. Crit. Care Med. 2009, 37, 713–724. [Google Scholar] [CrossRef] [PubMed]
- Mori, N.; Tsuchiya, K.; Sheth, D.; Mugikura, S.; Takase, K.; Katscher, U.; Abe, H. Diagnostic value of electric properties tomography (EPT) for differentiating benign from malignant breast lesions: Comparison with standard dynamic contrast-enhanced MRI. Eur. Radiol. 2019, 29, 1778–1786. [Google Scholar] [CrossRef] [PubMed]
- Suh, J.; Kim, J.H.; Kim, S.Y.; Cho, N.; Kim, D.H.; Kim, R.; Kim, E.S.; Jang, J.M.; Ha, S.M.; Lee, S.H.; et al. Noncontrast-Enhanced MR-Based Conductivity Imaging for Breast Cancer Detection and Lesion Differentiation. J. Magn. Reson. Imaging 2021, 54, 631–645. [Google Scholar] [CrossRef]
- Kim, S.Y.; Shin, J.; Kim, D.H.; Kim, E.K.; Moon, H.J.; Yoon, J.H.; You, J.K.; Kim, M.J. Correlation between electrical conductivity and apparent diffusion coefficient in breast cancer: Effect of necrosis on magnetic resonance imaging. Eur. Radiol. 2018, 28, 3204–3214. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Wu, P.; Mu, W.C.; Yu, W.; Huang, S. Compact Broadband Planar Resonator with a Viaed Double Spiral for Robust Wireless Power Transfer. IEEE J. Electromagn. RF Microw. Med. Biol. 2021, 5, 329–339. [Google Scholar] [CrossRef]
- Ladd, M.E.; Bachert, P.; Meyerspeer, M.; Moser, E.; Nagel, A.M.; Norris, D.G.; Schmitter, S.; Speck, O.; Straub, S.; Zaiss, M. Pros and cons of ultra-high-field MRI/MRS for human application. Prog. Nucl. Magn. Reson. Spectrosc. 2018, 109, 1–50. [Google Scholar] [CrossRef]
- Griffiths, H. Magnetic induction tomography. Meas. Sci. Technol. 2001, 12, 1126–1131. [Google Scholar] [CrossRef]
- Seo, J.K.; Woo, E.J. Electrical Tissue Property Imaging at Low Frequency Using MREIT. IEEE Trans. Biomed. Eng 2014, 61, 1390–1399. [Google Scholar] [CrossRef]
- Xu, Y.; He, B. Magnetoacoustic tomography with magnetic induction (MAT-MI). Phys. Med. Biol. 2005, 50, 5175–5187. [Google Scholar] [CrossRef]
- Seo, J.; Woo, E. Magnetic resonance electrical impedance tomography (MREIT). SIAM Rev. 2011, 53, 40–68. [Google Scholar] [CrossRef]
- Cunningham, C.H.; Pauly, J.M.; Nayak, K.S. Saturated double-angle method for rapid B1+ mapping. Magn. Reson. Med. 2006, 55, 1326–1333. [Google Scholar] [CrossRef] [PubMed]
- Haacke, E.M.; Petropoulos, L.S.; Nilges, E.W.; Wu, D.H. Extraction of conductivity and permittivity using magnetic resonance imaging. Phys. Med. Biol. 1991, 36, 723–734. [Google Scholar] [CrossRef]
- Katscher, U.; Voigt, T.; Findeklee, C.; Vernickel, P.; Nehrke, K.; Dossel, O. Determination of Electric Conductivity and Local SAR Via B1 Mapping. IEEE Trans. Med. Imaging 2009, 28, 1365–1374. [Google Scholar] [CrossRef] [PubMed]
- Wen, H. Noninvasive quantitative mapping of conductivity and dielectric distributions using RF wave propagation effects in high-field MRI. In Medical Imaging 2003: Physics of Medical Imaging; SPIE: Bellingham, WA USA, 2003; Volume 5030, pp. 471–477. [Google Scholar]
- Hoult, D.I. The principle of reciprocity in signal strength calculations-A mathematical guide. Concepts Magn. Reson. 2000, 12, 173–187. [Google Scholar] [CrossRef]
- Gurler, N.; Ider, Y.Z. Gradient-based electrical conductivity imaging using phase. Magn. Reson. Med. 2017, 77, 137–150. [Google Scholar] [CrossRef] [PubMed]
- van Lier, A.L.; Raaijmakers, A.; Voigt, T.; Lagendijk, J.J.; Luijten, P.R.; Katscher, U.; van den Berg, C.A. Electrical Properties Tomography in the Human Brain at 1.5, 3, and 7T: A Comparison Study, EPT at 1.5, 3, and 7T. Magn. Reson. Med. 2014, 71, 354–363. [Google Scholar] [CrossRef]
- Mandija, S.; Sbrizzi, A.; Katscher, U.; Luijten, P.R.; van den Berg, C.A. Error analysis of helmholtz-based MR-electrical properties tomography, MR-Electrical Properties Tomography Reconstruction Errors. Magn. Reson. Med. 2018, 80, 90–100. [Google Scholar] [CrossRef]
- Shin, J.; Lee, J.; Kim, M.O.; Choi, N.; Seo, J.K.; Kim, D.H. Quantitative Conductivity Estimation Error due to Statistical Noise in Complex B Map. J. Korean Soc. Magn. Reson. Med. 2014, 18, 303. [Google Scholar] [CrossRef]
- Chen, Y.; Schönlieb, C.B.; Liò, P.; Leiner, T.; Dragotti, P.L.; Wang, G.; Rueckert, D.; Firmin, D.; Yang, G. AI-Based Reconstruction for Fast MRI—A Systematic Review and Meta-Analysis. Proc. IEEE 2022, 110, 224–245. [Google Scholar] [CrossRef]
- Mandija, S.; Meliadò, E.F.; Huttinga, N.R.F.; Luijten, P.R.; van den Berg, C.A.T. Opening a new window on MR-based Electrical Properties Tomography with deep learning. Sci. Rep. 2019, 9, 8895. [Google Scholar] [CrossRef]
- Jung, K.J.; Mandija, S.; Kim, J.H.; Ryu, K.; Jung, S.; Cui, C.; Kim, S.Y.; Park, M.; van den Berg, C.A.T.; Kim, D.H. Improving phase-based conductivity reconstruction by means of deep learning–based denoising of phase data for 3T MRI. Magn. Reson. Med. 2021, 86, 2084–2094. [Google Scholar] [CrossRef] [PubMed]
- Hampe, N.; Katscher, U.; van den Berg, C.A.T.; Tha, K.K.; Mandija, S. Investigating the challenges and generalizability of deep learning brain conductivity mapping. Phys. Med. Biol. 2020, 65, 135001. [Google Scholar] [CrossRef] [PubMed]
- Garcia Inda, A.J.; Huang, S.Y.; Imamoglu, N.; Yu, W. Physics-Coupled Neural Network Magnetic Resonance Electrical Property Tomography (MREPT) for Conductivity Reconstruction. IEEE Trans. Image Process. 2022, 31, 3463–3478. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Yu, W.; Huang, S.Y. An MR-Based Viscosity-Type Regularization Method for Electrical Property Tomography. Tomography 2017, 3, 50–59. [Google Scholar] [CrossRef]
- Thuerey, N.; Holl, P.; Mueller, M.; Schnell, P.; Trost, F.; Um, K. Physics-based Deep Learning. arXiv 2021, arXiv:2109.05237. [Google Scholar] [CrossRef]
- Garcia, A.; Huang, S.Y.; Imamoglu, N.; Yu, W. Machine-learning-enhanced stabilized cr-MREPT for noise-robust and artifact-reduced electrical properties reconstruction. In Proceedings of the 2020 IEEE International Conference on Computational Electromagnetics (ICCEM), Singapore, 24–26 August 2020; pp. 130–132. [Google Scholar] [CrossRef]
- Ahishakiye, E.; Gijzen, M.B.V.; Tumwiine, J.; Wario, R.; Obungoloch, J. A survey on deep learning in medical image reconstruction. Intell. Med. 2021, 1, 118–127. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Kelley, H.J. Gradient theory of optimal flight paths. Ars J. 1960, 30, 947–954. [Google Scholar] [CrossRef]
- Both, G.J.; Choudhury, S.; Sens, P.; Kusters, R. DeepMoD: Deep learning for model discovery in noisy data. J. Comput. Phys. 2021, 428, 109985. [Google Scholar] [CrossRef]
- Chen, Y.; Lu, L.; Karniadakis, G.E.; Negro, L.D. Physics-informed neural networks for inverse problems in nano-optics and metamaterials. Opt. Express 2020, 28, 11618–11633. [Google Scholar] [CrossRef]
- Garcia Inda, A.J.; Huang, S.Y.; Immamoglu, N.; Yu, W. Physics informed neural network (PINN) for noise-robust phase-based magnetic resonance electrical properties tomography. In Proceedings of the 2022 3rd URSI Atlantic and Asia Pacific Radio Science Meeting (AT-AP-RASC), Gran Canaria, Spain, 30 May–4 June 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Rahaman, N.; Baratin, A.; Arpit, D.; Draxler, F.; Lin, M.; Hamprecht, F.; Bengio, Y.; Courville, A. On the Spectral Bias of Neural Networks. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; Volume 97, pp. 5301–5310. [Google Scholar]
- Hafalir, F.S.; Oran, O.F.; Gurler, N.; Ider, Y.Z. Convection-Reaction Equation Based Magnetic Resonance Electrical Properties Tomography (cr-MREPT). IEEE Trans. Med. Imaging 2014, 33, 777–793. [Google Scholar] [CrossRef] [PubMed]
- Codina, R. Comparison of some finite element methods for solving the diffusion-convection-reaction equation. Comput. Methods Appl. Mech. Engrg. 1998, 156, 185–210. [Google Scholar] [CrossRef]
- Sun, X.; Lu, L.; Qi, L.; Mei, Y.; Liu, X.; Chen, W. A robust electrical conductivity imaging method with total variation and wavelet regularization. Magn. Reson. Imaging 2020, 69, 28–39. [Google Scholar] [CrossRef]
- Garcia, A.J.; Huang, S.; Yu, W. Region-specific regularization of convection-reaction Magnetic Resonance Electrical Property Tomography (MREPT) for improving the accuracy and noise-tolerance of EP reconstruction. In Proceedings of the ISMRM 26th Annual Meeting & Exhibition, Paris, France, 16–21 June 2018; p. 2286. [Google Scholar]
- Ider, Y.Z.; Akyer, M.N. Properties and implementation issues of phase based cr-MRECT for conductivity imaging. In Proceedings of the ISMRM & SMRT Virtual Conference & Exhibition, Online, 8–14 August 2020; p. 3190. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Gallo, O.; Frosio, I.; Kautz, J. Loss Functions for Image Restoration With Neural Networks. IEEE Trans. Comput. Imaging 2017, 3, 47–57. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Wallach, H., Larochelle, H., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; pp. 8024–8035. [Google Scholar]
- Pannell, J.J.; Rigby, S.E.; Panoutsos, G. Physics-informed regularisation procedure in neural networks: An application in blast protection engineering. Int. J. Prot. Struct. 2022, 13, 555–578. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Gosselin, M.C.; Neufeld, E.; Moser, H.; Huber, E.; Farcito, S.; Gerber, L.; Jedensjö, M.; Hilber, I.; Di Gennaro, F.; Lloyd, B.; et al. Development of a new generation of high-resolution anatomical models for medical device evaluation: The Virtual Population 3.0. Phys. Med. Biol. 2014, 59, 5287–5303. [Google Scholar] [CrossRef]
- Yildiz, G.; Ider, Y.Z. Use of dielectric padding to eliminate low convective field artifact in cr-MREPT conductivity images. Magn. Reson. Med. 2019, 81, 3168–3184. [Google Scholar] [CrossRef]
- Hancu, I.; Liu, J.; Hua, Y.; Lee, S.K. Electrical properties tomography: Available contrast and reconstruction capabilities. Magn. Reson. Med. 2019, 81, 803–810. [Google Scholar] [CrossRef]
- Stogryn, A. Equations for Calculating the Dielectric Constant of Saline Water (Correspondence). IEEE Trans. Microw. Theory Tech. 1971, 19, 733–736. [Google Scholar] [CrossRef]
- Kim, D.H.; Choi, N.; Gho, S.M.; Shin, J.; Liu, C. Simultaneous imaging of in vivo conductivity and susceptibility. Magn. Reson. Med. 2014, 71, 1144–1150. [Google Scholar] [CrossRef] [PubMed]
- Liao, Y.; Oros-Peusquens, A.M.; Lindemeyer, J.; Lechea, N.; Lucas, C.W.; Langen, K.J.; Shah, N.J. An MR technique for simultaneous quantitative imaging of water content, conductivity and susceptibility, with application to brain tumours using a 3T hybrid MR-PET scanner. Sci. Rep. 2019, 9, 88. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Tha, K.K.; Katscher, U.; Yamaguchi, S.; Stehning, C.; Terasaka, S.; Fujima, N.; Shirato, H. Noninvasive electrical conductivity measurement by MRI: A test of its validity and the electrical conductivity characteristics of glioma. Eur. Radiol. 2018, 28, 348–355. [Google Scholar] [CrossRef] [PubMed]
- Tha, K.K.; Kikuchi, Y.; Ishizaka, K.; Kamiyama, T.; Yoneyama, M.; Katscher, U. Higher Electrical Conductivity of Liver Parenchyma in Fibrotic Patients: Noninvasive Assessment by Electric Properties Tomography. J. Magn. Reson. Imaging 2021, 54, 1689–1691. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.K.; Bulumulla, S.; Hancu, I. Theoretical Investigation of Random Noise-Limited Signal-to-Noise Ratio in MR-Based Electrical Properties Tomography. IEEE Trans. Med Imaging 2015, 34, 2220–2232. [Google Scholar] [CrossRef]
- Wang, S.; Yu, X.; Perdikaris, P. When and why PINNs fail to train: A neural tangent kernel perspective. J. Comput. Phys. 2022, 449, 110768. [Google Scholar] [CrossRef]
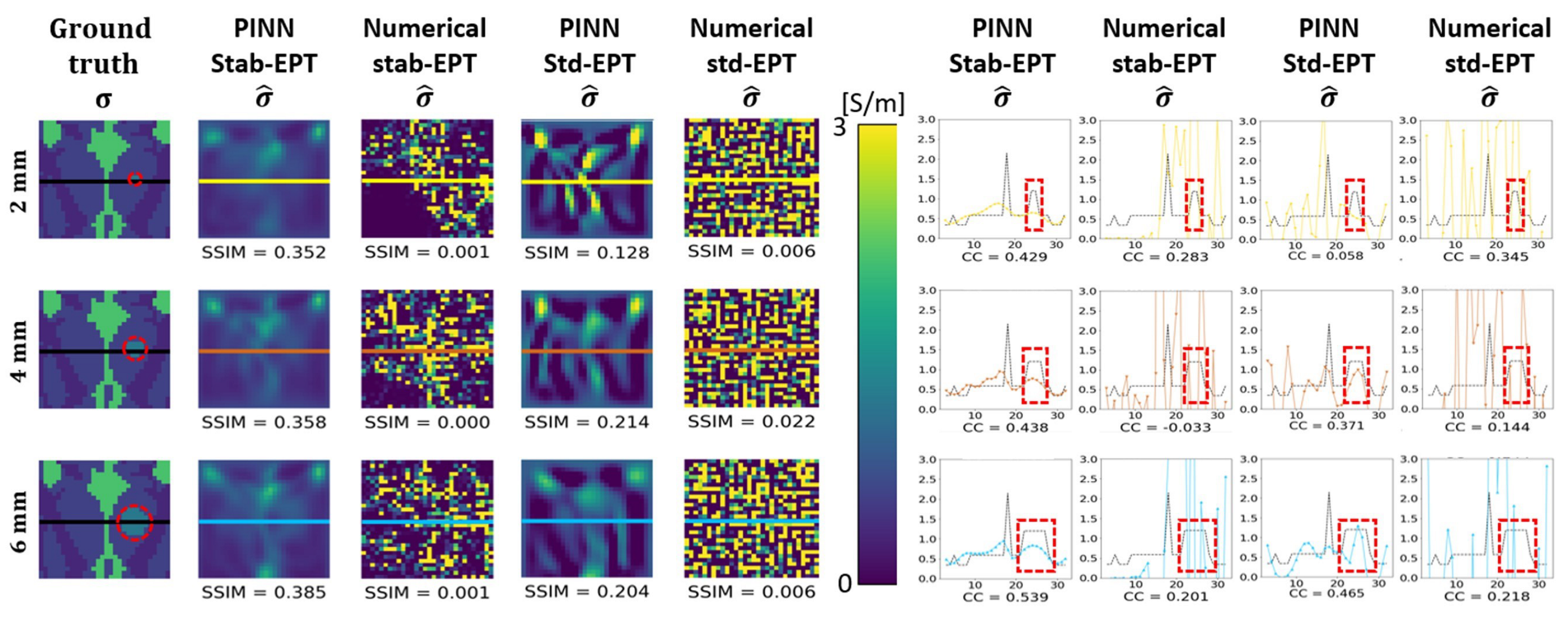
| Tissue | Ground Truth | PINN stab-EPT | Numerical stab-EPT | PINN std-EPT | Numerical std-EPT |
|---|---|---|---|---|---|
| CSF | 2.14 ± 0.00 | 1.04 ± 0.35 | 0.96 ± 11.1 | 1.00 ± 0.87 | 1.04 ± 4.08 |
| White matter | 0.34 ± 0.00 | 0.45 ± 0.12 | −4.67 ± 146 | 0.34 ± 0.63 | 0.32 ± 4.05 |
| Gray matter | 0.58 ± 0.00 | 0.60 ± 0.19 | 6.30 ± 245 | 0.48 ± 0.67 | 0.39 ± 4.07 |
| Tumor 2 mm | 1.20 ± 0.00 | 0.66 ± 0.01 | 0.91 ± 6.80 | 0.64 ± 0.09 | 1.63 ± 4.15 |
| Tumor 4 mm | 1.20 ± 0.00 | 0.73 ± 0.04 | 1.04 ± 3.37 | 0.82 ± 0.12 | 1.63 ± 4.90 |
| Tumor 6 mm | 1.20 ± 0.00 | 0.77 ± 0.06 | −0.60 ± 14.50 | 0.71 ± 0.44 | 0.46 ± 4.26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Inda, A.J.G.; Huang, S.Y.; İmamoğlu, N.; Qin, R.; Yang, T.; Chen, T.; Yuan, Z.; Yu, W. Physics Informed Neural Networks (PINN) for Low Snr Magnetic Resonance Electrical Properties Tomography (MREPT). Diagnostics 2022, 12, 2627. https://doi.org/10.3390/diagnostics12112627
Inda AJG, Huang SY, İmamoğlu N, Qin R, Yang T, Chen T, Yuan Z, Yu W. Physics Informed Neural Networks (PINN) for Low Snr Magnetic Resonance Electrical Properties Tomography (MREPT). Diagnostics. 2022; 12(11):2627. https://doi.org/10.3390/diagnostics12112627
Chicago/Turabian StyleInda, Adan Jafet Garcia, Shao Ying Huang, Nevrez İmamoğlu, Ruian Qin, Tianyi Yang, Tiao Chen, Zilong Yuan, and Wenwei Yu. 2022. "Physics Informed Neural Networks (PINN) for Low Snr Magnetic Resonance Electrical Properties Tomography (MREPT)" Diagnostics 12, no. 11: 2627. https://doi.org/10.3390/diagnostics12112627
APA StyleInda, A. J. G., Huang, S. Y., İmamoğlu, N., Qin, R., Yang, T., Chen, T., Yuan, Z., & Yu, W. (2022). Physics Informed Neural Networks (PINN) for Low Snr Magnetic Resonance Electrical Properties Tomography (MREPT). Diagnostics, 12(11), 2627. https://doi.org/10.3390/diagnostics12112627







