Mortality Prediction Utilizing Blood Biomarkers to Predict the Severity of COVID-19 Using Machine Learning Technique
Abstract
:1. Introduction
2. Methodology
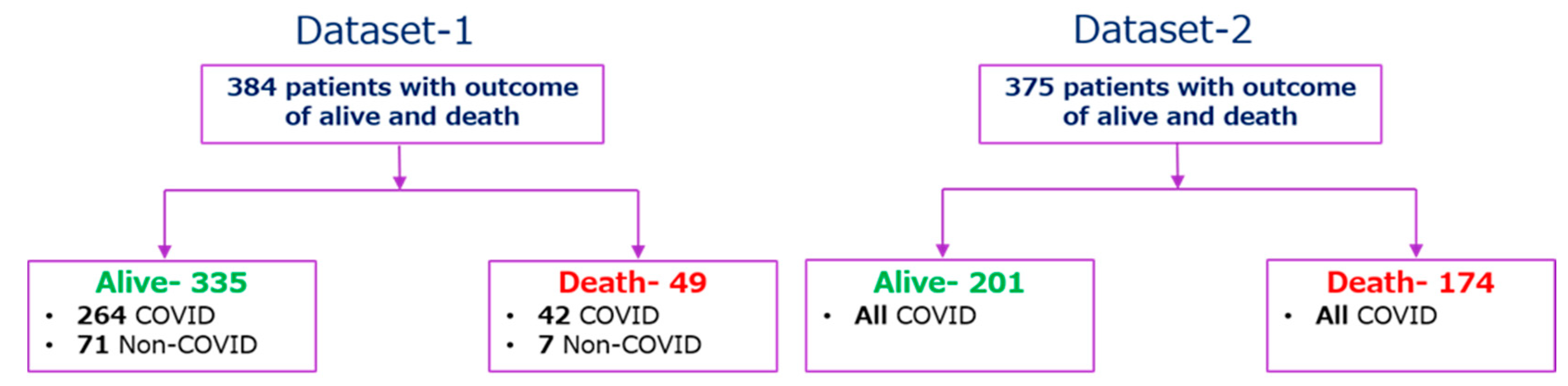
2.1. Study Population
2.2. Statistical Analysis
2.3. Data Preprocessing
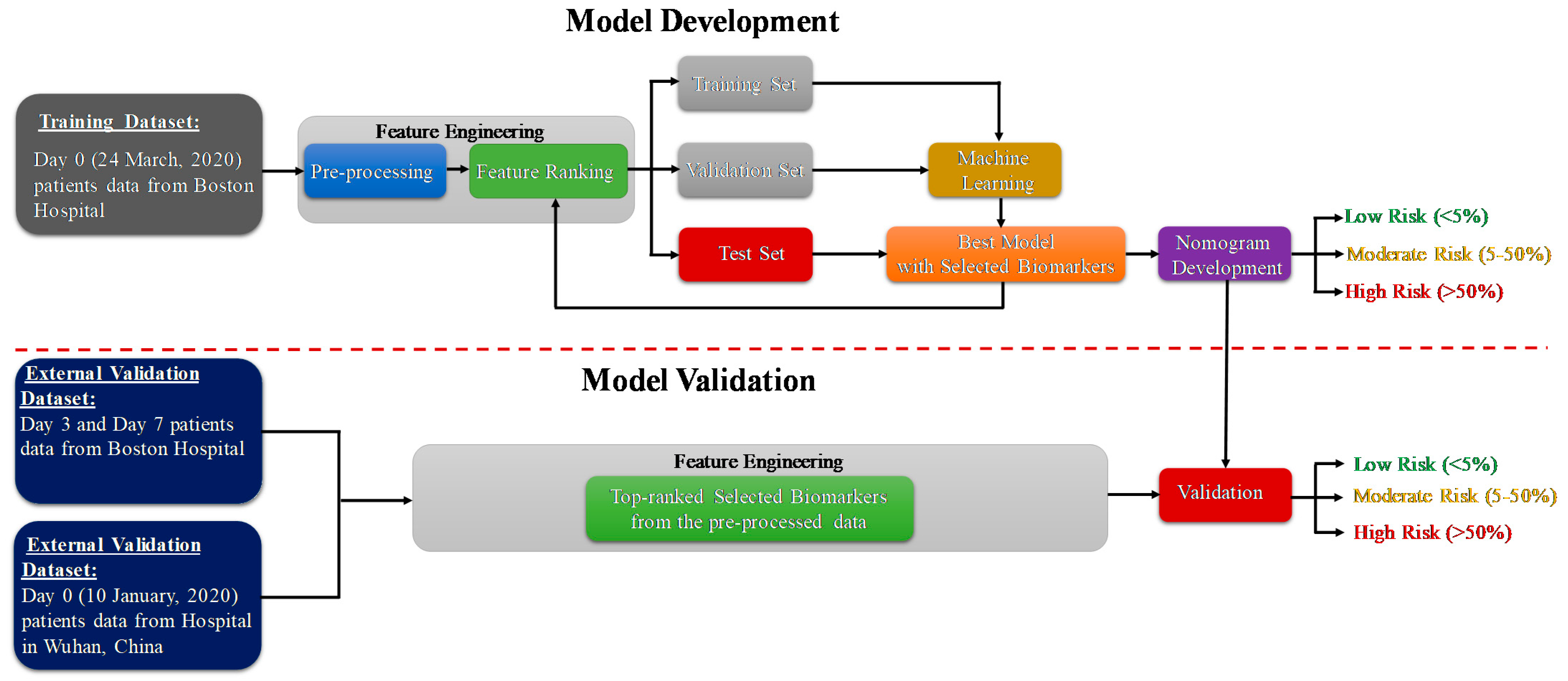
2.4. Development and Validation of Classification Model
2.5. Development and Validation of Logistic Regression-Based Nomogram
2.6. Nomogram-Based Scoring System
3. Results
3.1. Univariate and Multivariate Analysis Using Logistic Regression
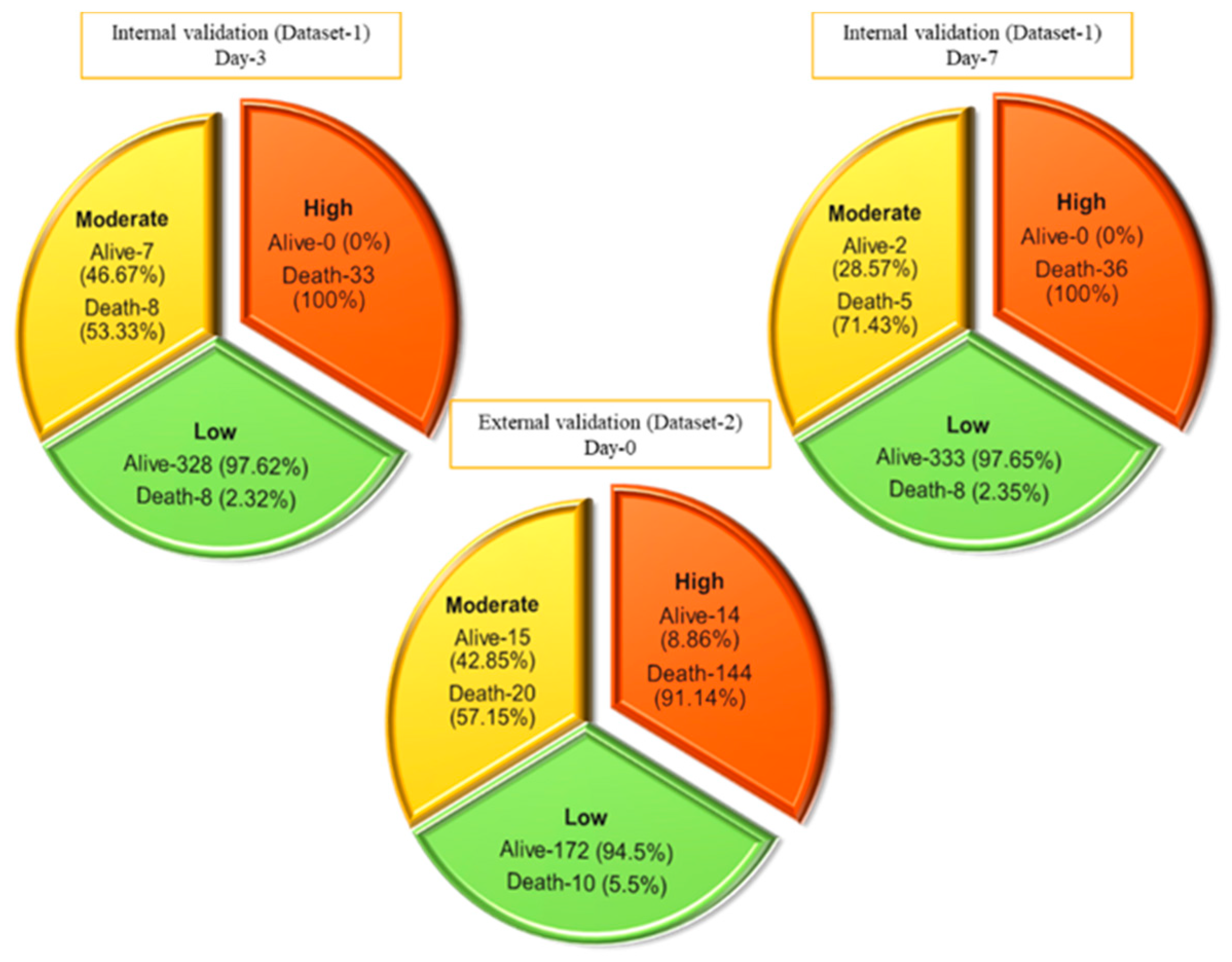
3.2. Nomogram-Based Scoring System
3.3. Performance Evaluation of the ALDCC Scoring Technique
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vaidyanathan, G. Coronavirus variants are spreading in India—What scientists know so far. Nature 2021, 593, 321–322. [Google Scholar] [CrossRef]
- Black, M.; Lee, A.; Ford, J. Vaccination against COVID-19 and inequalities–avoiding making a bad situation worse. Public Health Pract. 2021, 2, 100101. [Google Scholar] [CrossRef]
- Kluge, H.; McKee, M. COVID-19 vaccines for the European region: An unprecedented challenge. Lancet 2021, 397, 1689–1691. [Google Scholar] [CrossRef]
- COVID-19 Coronavirus Pandemic. Available online: https://www.worldometers.info/coronavirus/ (accessed on 19 April 2020).
- Huang, D.; Wang, T.; Chen, Z.; Yang, H.; Yao, R.; Liang, Z. A novel risk score to predict diagnosis with coronavirus disease 2019 (COVID-19) in suspected patients: A retrospective, multicenter, and observational study. J. Med. Virol. 2020, 92, 2709–2717. [Google Scholar] [CrossRef]
- Cai, Y.-Q.; Zhang, X.-B.; Zeng, H.-Q.; Wei, X.-J.; Zhang, Z.-Y.; Chen, L.-D.; Wang, M.-H.; Yao, W.-Z.; Huang, Q.-F.; Ye, Z.-Q. Prognostic Value of Neutrophil-to-Lymphocyte Ratio, Lactate Dehydrogenase, D-Dimer and CT Score in Patients with COVID-19. Res. Sq. 2020, 1–13. [Google Scholar] [CrossRef]
- Liu, Y.-P.; Li, G.-M.; He, J.; Liu, Y.; Li, M.; Zhang, R.; Li, Y.-L.; Wu, Y.-Z.; Diao, B. Combined use of the neutrophil-to-lymphocyte ratio and CRP to predict 7-day disease severity in 84 hospitalized patients with COVID-19 pneumonia: A retrospective cohort study. Ann. Transl. Med. 2020, 8, 635. [Google Scholar] [CrossRef]
- Zhang, C.; Qin, L.; Li, K.; Wang, Q.; Zhao, Y.; Xu, B.; Liang, L.; Dai, Y.; Feng, Y.; Sun, J. A novel scoring system for prediction of disease severity in COVID-19. Front. Cell. Infect. Microbiol. 2020, 10, 318. [Google Scholar] [CrossRef]
- Shang, Y.; Liu, T.; Wei, Y.; Li, J.; Shao, L.; Liu, M.; Zhang, Y.; Zhao, Z.; Xu, H.; Peng, Z. Scoring systems for predicting mortality for severe patients with COVID-19. EClinicalMedicine 2020, 24, 100426. [Google Scholar] [CrossRef]
- Initiative, C.-H.G. The COVID-19 host genetics initiative, a global initiative to elucidate the role of host genetic factors in susceptibility and severity of the SARS-CoV-2 virus pandemic. Eur. J. Hum. Genet. 2020, 28, 715. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, Y.; Huang, H.; Li, D.; Gu, D.; Lu, X.; Zhang, Z.; Liu, L.; Liu, T.; Liu, Y. Relationship between the ABO Blood Group and the COVID-19 Susceptibility. Clin. Infect. Dis. 2020, 73, 328–331. [Google Scholar] [CrossRef]
- Göker, H.; Karakulak, E.A.; Demiroğlu, H.; Ceylan, Ç.M.A.; Büyükaşik, Y.; Inkaya, A.Ç.; Aksu, S.; Sayinalp, N.; Haznedaroğlu, I.C.; Uzun, Ö. The effects of blood group types on the risk of COVID-19 infection and its clinical outcome. Turk. J. Med. Sci. 2020, 50, 679–683. [Google Scholar] [CrossRef]
- Leung, T.; Chan, A.; Chan, E.; Chan, V.; Chui, C.; Cowling, B.; Gao, L.; Ge, M.; Hung, I.; Ip, M. Short-and potential long-term adverse health outcomes of COVID-19: A rapid review. Emerg. Microbes Infect. 2020, 9, 2190–2199. [Google Scholar] [CrossRef] [PubMed]
- Zheng, K.I.; Feng, G.; Liu, W.Y.; Targher, G.; Byrne, C.D.; Zheng, M.H. Extrapulmonary complications of COVID-19: A multisystem disease? J. Med. Virol. 2021, 93, 323–335. [Google Scholar] [CrossRef]
- Imran, A.; Posokhova, I.; Qureshi, H.N.; Masood, U.; Riaz, M.S.; Ali, K.; John, C.N.; Hussain, M.I.; Nabeel, M. AI4COVID-19: AI enabled preliminary diagnosis for COVID-19 from cough samples via an app. Inform. Med. Unlocked 2020, 20, 100378. [Google Scholar] [CrossRef]
- Zhang, J.; Hao, Y.; Ou, W.; Ming, F.; Liang, G.; Qian, Y.; Cai, Q.; Dong, S.; Hu, S.; Wang, W. Serum interleukin-6 is an indicator for severity in 901 patients with SARS-CoV-2 infection: A cohort study. J. Transl. Med. 2020, 18, 1–8. [Google Scholar] [CrossRef]
- Grobler, C.; Maphumulo, S.C.; Grobbelaar, L.M.; Bredenkamp, J.C.; Laubscher, G.J.; Lourens, P.J.; Steenkamp, J.; Kell, D.B.; Pretorius, E. COVID-19: The rollercoaster of fibrin (ogen), d-dimer, von willebrand factor, p-selectin and their interactions with endothelial cells, platelets and erythrocytes. Int. J. Mol. Sci. 2020, 21, 5168. [Google Scholar] [CrossRef] [PubMed]
- Yan, L.; Zhang, H.-T.; Goncalves, J.; Xiao, Y.; Wang, M.; Guo, Y.; Sun, C.; Tang, X.; Jing, L.; Zhang, M. An interpretable mortality prediction model for COVID-19 patients. Nat. Mach. Intell. 2020, 2, 283–288. [Google Scholar] [CrossRef]
- Rahman, T.; Khandakar, A.; Kadir, M.A.; Islam, K.R.; Islam, K.F.; Mazhar, R.; Hamid, T.; Islam, M.T.; Kashem, S.; Mahbub, Z.B. Reliable tuberculosis detection using chest X-ray with deep learning, segmentation and visualization. IEEE Access 2020, 8, 191586–191601. [Google Scholar] [CrossRef]
- Tahir, A.; Qiblawey, Y.; Khandakar, A.; Rahman, T.; Khurshid, U.; Musharavati, F.; Islam, M.; Kiranyaz, S.; Chowdhury, M.E. Coronavirus: Comparing COVID-19, SARS and MERS in the eyes of AI. arXiv 2020, arXiv:2005.11524. [Google Scholar]
- Rahman, T.; Akinbi, A.; Chowdhury, M.E.; Rashid, T.A.; Şengür, A.; Khandakar, A.; Islam, K.R.; Ismael, A.M. COV-ECGNET: COVID-19 detection using ECG trace images with deep convolutional neural network. arXiv 2021, arXiv:2106.00436. [Google Scholar]
- Chowdhury, M.E.; Rahman, T.; Khandakar, A.; Mazhar, R.; Kadir, M.A.; Mahbub, Z.B.; Islam, K.R.; Khan, M.S.; Iqbal, A.; Al Emadi, N. Can AI help in screening viral and COVID-19 pneumonia? IEEE Access 2020, 8, 132665–132676. [Google Scholar] [CrossRef]
- Rahman, T.; Chowdhury, M.E.; Khandakar, A.; Islam, K.R.; Islam, K.F.; Mahbub, Z.B.; Kadir, M.A.; Kashem, S. Transfer learning with deep convolutional neural network (CNN) for pneumonia detection using chest X-ray. Appl. Sci. 2020, 10, 3233. [Google Scholar] [CrossRef]
- Chowdhury, M.E.; Rahman, T.; Khandakar, A.; Al-Madeed, S.; Zughaier, S.M.; Doi, S.A.; Hassen, H.; Islam, M.T. An early warning tool for predicting mortality risk of COVID-19 patients using machine learning. Cogn. Comput. 2021, 1–16. [Google Scholar] [CrossRef]
- Rahman, T.; Khandakar, A.; Qiblawey, Y.; Tahir, A.; Kiranyaz, S.; Kashem, S.B.A.; Islam, M.T.; Al Maadeed, S.; Zughaier, S.M.; Khan, M.S. Exploring the effect of image enhancement techniques on COVID-19 detection using chest X-ray images. Comput. Biol. Med. 2021, 132, 104319. [Google Scholar] [CrossRef]
- Banerjee, A.; Ray, S.; Vorselaars, B.; Kitson, J.; Mamalakis, M.; Weeks, S.; Baker, M.; Mackenzie, L.S. Use of machine learning and artificial intelligence to predict SARS-CoV-2 infection from full blood counts in a population. Int. Immunopharmacol. 2020, 86, 106705. [Google Scholar] [CrossRef]
- Proctor, E.A.; Dineen, S.M.; van Nostrand, S.C.; Kuhn, M.K.; Barrett, C.D.; Brubaker, D.K.; Yaffe, M.B.; Lauffenburger, D.A.; Leon, L.R. Coagulopathy signature precedes and predicts severity of end-organ heat stroke pathology in a mouse model. J. Thromb. Haemost. 2020, 18, 1900–1910. [Google Scholar] [CrossRef]
- Bhattacharyya, R.; Iyer, P.; Phua, G.C.; Lee, J.H. The interplay between coagulation and inflammation pathways in COVID-19-associated respiratory failure: A narrative review. Pulm. Ther. 2020, 6, 1–17. [Google Scholar] [CrossRef]
- Brinati, D.; Campagner, A.; Ferrari, D.; Locatelli, M.; Banfi, G.; Cabitza, F. Detection of COVID-19 infection from routine blood exams with machine learning: A feasibility study. J. Med. Syst. 2020, 44, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.S.; Hou, Y.; Vasovic, L.V.; Steel, P.A.; Chadburn, A.; Racine-Brzostek, S.E.; Velu, P.; Cushing, M.M.; Loda, M.; Kaushal, R. Routine laboratory blood tests predict SARS-CoV-2 infection using machine learning. Clin. Chem. 2020, 66, 1396–1404. [Google Scholar] [CrossRef]
- Tawsifur Rahman, A.K.; Hoque, M.E.; Ibtehaz, N.; Kashem, S.B.; Masud, R.; Shampa, L.; Hasan, M.M.; Islam, M.T.; Al-Madeed, S.; Zughaier, S.M.; et al. Development and Validation of an Early Scoring System for Prediction of Disease Severity in COVID-19 using Complete Blood Count Parameters. IEEE Access 2021, 9, 112565–112576. [Google Scholar]
- Vaid, A.; Somani, S.; Russak, A.J.; De Freitas, J.K.; Chaudhry, F.F.; Paranjpe, I.; Johnson, K.W.; Lee, S.J.; Miotto, R.; Richter, F. Machine Learning to Predict Mortality and Critical Events in a Cohort of Patients with COVID-19 in New York City: Model Development and Validation. J. Med. Internet Res. 2020, 22, e24018. [Google Scholar] [CrossRef]
- Aladağ, N.; Atabey, R.D. The role of concomitant cardiovascular diseases and cardiac biomarkers for predicting mortality in critical COVID-19 patients. Acta Cardiol. 2020, 76, 1–8. [Google Scholar] [CrossRef]
- de Terwangne, C.; Laouni, J.; Jouffe, L.; Lechien, J.R.; Bouillon, V.; Place, S.; Capulzini, L.; Machayekhi, S.; Ceccarelli, A.; Saussez, S. Predictive accuracy of COVID-19 world health organization (Who) severity classification and comparison with a bayesian-method-based severity score (epi-score). Pathogens 2020, 9, 880. [Google Scholar] [CrossRef]
- Liang, W.; Yao, J.; Chen, A.; Lv, Q.; Zanin, M.; Liu, J.; Wong, S.; Li, Y.; Lu, J.; Liang, H. Early triage of critically ill COVID-19 patients using deep learning. Nat. Commun. 2020, 11, 1–7. [Google Scholar] [CrossRef]
- Wang, C.; Deng, R.; Gou, L.; Fu, Z.; Zhang, X.; Shao, F.; Wang, G.; Fu, W.; Xiao, J.; Ding, X. Preliminary study to identify severe from moderate cases of COVID-19 using combined hematology parameters. Ann. Transl. Med. 2020, 8, 593. [Google Scholar] [CrossRef]
- McRae, M.P.; Simmons, G.W.; Christodoulides, N.J.; Lu, Z.; Kang, S.K.; Fenyo, D.; Alcorn, T.; Dapkins, I.P.; Sharif, I.; Vurmaz, D. Clinical decision support tool and rapid point-of-care platform for determining disease severity in patients with COVID-19. Lab Chip 2020, 20, 2075–2085. [Google Scholar] [CrossRef]
- Zhang, L.; Yan, X.; Fan, Q.; Liu, H.; Liu, X.; Liu, Z.; Zhang, Z. D-dimer levels on admission to predict in-hospital mortality in patients with COVID-19. J. Thromb. Haemost. 2020, 18, 1324–1329. [Google Scholar] [CrossRef] [PubMed]
- Hegde, H.; Shimpi, N.; Panny, A.; Glurich, I.; Christie, P.; Acharya, A. MICE vs. PPCA: Missing data imputation in healthcare. Inform. Med. Unlocked 2019, 17, 100275. [Google Scholar] [CrossRef]
- Filbin, M.R.; Mehta, A.; Schneider, A.M.; Kays, K.R.; Guess, J.R.; Gentili, M.; Fenyves, B.G.; Charland, N.C.; Gonye, A.L.; Gushterova, I. Plasma proteomics reveals tissue-specific cell death and mediators of cell-cell interactions in severe COVID-19 patients. BioRxiv 2020. [Google Scholar] [CrossRef]
- Tawsifur Rahman, F.A.A.-I.; Al-Mohannadi, F.S.; Mubarak, R.S.; Al-Hitmi, M.H.; Islam, K.R.; Khandaker, A.; Hssain, A.A.; al Maadeed, S.A.; Zughaier, S.M.; Chowdhury, M.E.H. Mortality-Severity-Prediction-Using-Blood-Biomarkers. Available online: https://github.com/tawsifur/Mortality-severity-prediction-using-blood-biomarkers (accessed on 5 June 2021).
- van Buuren, S.; Groothuis-Oudshoorn, K. mice: Multivariate imputation by chained equations in R. J. Stat. Softw. 2010, 45, 1–68. [Google Scholar] [CrossRef] [Green Version]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Khandakar, A.; Chowdhury, M.E.; Reaz, M.B.I.; Ali, S.H.M.; Hasan, M.A.; Kiranyaz, S.; Rahman, T.; Alfkey, R.; Bakar, A.A.A.; Malik, R.A. A Machine Learning Model for Early Detection of Diabetic Foot Using Thermogram Images. arXiv 2021, arXiv:2106.14207. [Google Scholar]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Keerthi, S.S.; Shevade, S.K.; Bhattacharyya, C.; Murthy, K.R.K. Improvements to Platt’s SMO algorithm for SVM classifier design. Neural Comput. 2001, 13, 637–649. [Google Scholar] [CrossRef]
- Guo, G.; Wang, H.; Bell, D.; Bi, Y.; Greer, K. KNN model-based approach in classification. In Proceedings of the OTM Confederated International Conferences “On the Move to Meaningful Internet Systems”, Rhodes, Greece, 21–25 October 2019. [Google Scholar]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y. Xgboost: Extreme Gradient Boosting; R Package Version 0.4-2; 2015; Volume 1, pp. 1–4. [Google Scholar]
- Sharaff, A.; Gupta, H. Extra-tree classifier with metaheuristics approach for email classification. In Advances in Computer Communication and Computational Sciences; Springer: Berlin/Heidelberg, Germany, 2019; pp. 189–197. [Google Scholar]
- Subasi, C. Logistic Regression Classifier. Available online: https://towardsdatascience.com/logistic-regression-classifier-8583e0c3cf9 (accessed on 26 April 2021).
- Anderson, R.P.; Jin, R.; Grunkemeier, G.L. Understanding logistic regression analysis in clinical reports: An introduction. Ann. Thorac. Surg. 2003, 75, 753–757. [Google Scholar] [CrossRef]
- Zlotnik, A.; Abraira, V. A general-purpose nomogram generator for predictive logistic regression models. Stata J. 2015, 15, 537–546. [Google Scholar] [CrossRef] [Green Version]
- Balachandran, V.P.; Gonen, M.; Smith, J.J.; DeMatteo, R.P. Nomograms in oncology: More than meets the eye. Lancet Oncol. 2015, 16, e173–e180. [Google Scholar] [CrossRef] [Green Version]
- Iasonos, A.; Schrag, D.; Raj, G.V.; Panageas, K.S. How to build and interpret a nomogram for cancer prognosis. J. Clin. Oncol. 2008, 26, 1364–1370. [Google Scholar] [CrossRef]
- Weng, Z.; Chen, Q.; Li, S.; Li, H.; Zhang, Q.; Lu, S.; Wu, L.; Xiong, L.; Mi, B.; Liu, D. ANDC: An early warning score to predict mortality risk for patients with coronavirus disease 2019. J. Transl. Med. 2020, 18, 1–10. [Google Scholar] [CrossRef]
- Jianfeng, X.; Daniel, H.; Hui, C.; Simon, T.A.; Shusheng, L.; Guozheng, W.; Yishan, W.; Hanyujie, K.; Laura, B.; Ruiqiang, Z. Development and External Validation of a Prognostic Multivariable Model on Admission for Hospitalized Patients with COVID-19. 2020. Available online: https://www.medrxiv.org/content/medrxiv/early/2020/03/30/2020.03.28.20045997.full.pdf (accessed on 1 June 2021).
- Zhang, B.; Zhou, X.; Qiu, Y.; Song, Y.; Feng, F.; Feng, J.; Song, Q.; Jia, Q.; Wang, J. Clinical characteristics of 82 cases of death from COVID-19. PLoS ONE 2020, 15, e0235458. [Google Scholar] [CrossRef] [PubMed]
- Al Youha, S.; Doi, S.A.; Jamal, M.H.; Almazeedi, S.; Al Haddad, M.; AlSeaidan, M.; Al-Muhaini, A.Y.; Al-Ghimlas, F.; Al-Sabah, S.K. Validation of the Kuwait Progression Indicator Score for predicting progression of severity in COVID19. MedRxiv 2020. [Google Scholar] [CrossRef]
- Chan, J.C.; Tsui, E.L.; Wong, V.C.; Group, H.A.S.C. Prognostication in severe acute respiratory syndrome: A retrospective time-course analysis of 1312 laboratory-confirmed patients in Hong Kong. Respirology 2007, 12, 531–542. [Google Scholar] [CrossRef] [PubMed]
- Assiri, A.; Al-Tawfiq, J.A.; Al-Rabeeah, A.A.; Al-Rabiah, F.A.; Al-Hajjar, S.; Al-Barrak, A.; Flemban, H.; Al-Nassir, W.N.; Balkhy, H.H.; Al-Hakeem, R.F. Epidemiological, demographic, and clinical characteristics of 47 cases of Middle East respiratory syndrome coronavirus disease from Saudi Arabia: A descriptive study. Lancet Infect. Dis. 2013, 13, 752–761. [Google Scholar] [CrossRef] [Green Version]
- Chen, R.; Liang, W.; Jiang, M.; Guan, W.; Zhan, C.; Wang, T.; Tang, C.; Sang, L.; Liu, J.; Ni, Z. Risk factors of fatal outcome in hospitalized subjects with coronavirus disease 2019 from a nationwide analysis in China. Chest 2020, 158, 97–105. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y.; Xiang, P.; Pu, L.; Xiong, H.; Li, C.; Zhang, M.; Tan, J.; Xu, Y.; Song, R. Neutrophil-to-lymphocyte ratio predicts severe illness patients with 2019 novel coronavirus in the early stage. MedRxiv 2020. [Google Scholar] [CrossRef] [Green Version]
- Huang, I.; Pranata, R. Lymphopenia in severe coronavirus disease-2019 (COVID-19): Systematic review and meta-analysis. J. Intensive Care 2020, 8, 1–10. [Google Scholar] [CrossRef]
- Han, X.; Ye, Q. Kidney involvement in COVID-19 and its treatments. J. Med. Virol. 2021, 93, 1387–1395. [Google Scholar] [CrossRef]
- Ok, F.; Erdogan, O.; Durmus, E.; Carkci, S.; Canik, A. Predictive values of blood urea nitrogen/creatinine ratio and other routine blood parameters on disease severity and survival of COVID-19 patients. J. Med. Virol. 2021, 93, 786–793. [Google Scholar] [CrossRef]
- Adamzik, M.; Broll, J.; Steinmann, J.; Westendorf, A.M.; Rehfeld, I.; Kreissig, C.; Peters, J. An increased alveolar CD4+ CD25+ Foxp3+ T-regulatory cell ratio in acute respiratory distress syndrome is associated with increased 30-day mortality. Intensive Care Med. 2013, 39, 1743–1751. [Google Scholar] [CrossRef]
- Lu, J.; Hu, S.; Fan, R.; Liu, Z.; Yin, X.; Wang, Q.; Lv, Q.; Cai, Z.; Li, H.; Hu, Y. ACP Risk Grade: A Simple Mortality Index for Patients with Confirmed or Suspected Severe Acute Respiratory Syndrome Coronavirus 2 Disease (COVID-19) during the Early Stage of Outbreak in Wuhan, China. SSRN J. 2020. [Google Scholar] [CrossRef]
- Ko, J.-H.; Park, G.E.; Lee, J.Y.; Lee, J.Y.; Cho, S.Y.; Ha, Y.E.; Kang, C.-I.; Kang, J.-M.; Kim, Y.-J.; Huh, H.J. Predictive factors for pneumonia development and progression to respiratory failure in MERS-CoV infected patients. J. Infect. 2016, 73, 468–475. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Wu, X.; Tian, Y.; Li, X.; Zhao, X.; Zhang, M. Dynamic changes and diagnostic and prognostic significance of serum PCT, hs-CRP and s-100 protein in central nervous system infection. Exp. Ther. Med. 2018, 16, 5156–5160. [Google Scholar] [CrossRef] [Green Version]
- Yildiz, B.; Poyraz, H.; Cetin, N.; Kural, N.; Colak, O. High sensitive C-reactive protein: A new marker for urinary tract infection, VUR and renal scar. Eur. Rev. Med. Pharmacol. Sci. 2013, 17, 2598–2604. [Google Scholar] [PubMed]
- Rahman, T. Early COVID-19 Mortality Risk Prediction. Available online: https://covid-19-risk-prediction.herokuapp.com/ (accessed on 1 June 2021).





| Variable/Features | Description |
|---|---|
| COVID | COVID status (tested positive prior to enrollment or during hospitalization): 0 = negative, 1 = positive |
| Age | Age: 1 = 20–34, 2 = 36–49, 3 = 50–64, 4 = 65–79, 5 = 80+ |
| BMI | Body mass index: 0 = <18.5 (underweight), 1 = 18.5–24.9 (normal), 2 = 25.0–29.9 (overweight), 3 = 30.0–39.9 (obese), 4 = ≥40 (severely obese), 5 = Unknown |
| Heart | Pre-existing heart disease—HEART-(coronary artery disease, congestive heart failure, valvular disease): 0 = No, 1 = Yes |
| Lung | Pre-existing lung disease—LUNG-(asthma, COPD, requiring home O, any chronic lung condition): 0 = No, 1 = Yes |
| Kidney | Pre-existing kidney disease—KIDNEY-(chronic kidney disease, baseline creatinine > 1.5, ESRD), 0 = No, 1 = Yes |
| Diabetes | Pre-existing diabetes—DIABETES- (pre-diabetes, insulin and non-insulin dependent diabetes): 0 = No, 1 = Yes |
| HTN | Pre-existing hypertension—HTN: 0 = No, 1 = Yes |
| Immunocompromised | Pre-existing immunocompromised condition—IMMUNO (active cancer, chemotherapy, transplant, immunosuppressant agents, aspenic): 0 = No, 1 = Yes |
| Resp_Symp | Respiratory symptoms—Symp_Resp (sore throat, congestion, productive or dry cough, shortness of breath or hypoxia, or chest pain): 0 = No, 1 = Yes |
| Fever_Sympt | Febrile symptom |
| GI_Symp | Any GI-related symptoms at presentation (abdominal pain, nausea, vomiting, diarrhea) |
| abs_neut | Absolute neutrophil count: 1 = 0–0.99, 2 = 1.0–3.99, 3 = 4.0–7.99, 4 = 8.0–11.99, 5 = 12+ |
| abs_lymph | Absolute lymphocyte count Day-0: 1 = 0–0.49, 2 = 0.50–0.99, 3 = 1.00–1.49, 4 = 1.50–1.99, 5 = 2+ |
| abs_mono | Absolute monocyte Day-0: 1 = 0–0.24, 2 = 0.25–0.49, 3 = 0.50–0.74, 4 = 0.75–0.99, 5 = 1.0+ |
| Creatinine | Creatinine: 1 = 0–0.79, 2 = 0.80–1.19, 3 = 1.20–1.79, 4 = 1.80–2.99, 5 = 3+ |
| CRP | C-reactive protein: 1 = 0–19.9, 2 = 20–59.0, 3 = 60–99.9, 4 = 100–179, 5 = 180+ |
| D-dimer | D-dimer: 1 = 0–499, 2 = 500–999, 3 = 1000–1999, 4 = 2000–3999, 5 = 4000+ |
| LDH | Lactate dehydrogenase: 1 = 0–200, 2 = 200–299, 3 = 300–399, 4 = 400–499, 5 = 500+ |
| Outcome | Outcome at 28 days: 1 = Death within 28 days; 2 = Intubated, ventilated, survived to 28 days; 3 = Non-invasive ventilation or high-flow nasal cannula; 4 = Hospitalized, supplementary O2 required; 5 = Hospitalized, no supplementary O2 required; 6 = Not hospitalized.Note: this study used ‘1′ for dead patients and ‘0′ for survived patients, which are created from, class 2–6. |
| (A) | ||||||
| Features | Survived (%) | Death (%) | Total | Method | Statistic | p-Value |
| Age (Year) | 335 (missing-0) | 49 (missing-0) | 384 (missing-0) | Chi-square test | X2 = 13.45 | <0.0001 |
| 1 (<34) | 36 (10.75%) | 0 (0%) | 36 (9.38%) | |||
| 2 (34–49) | 72 (21.49%) | 1 (2.04%) | 73 (19%) | |||
| 3 (50–64) | 105 (31.34%) | 6 (12.24%) | 111 (28.9%) | |||
| 4 (65–79) | 82 (24.48%) | 17 (34.69%) | 99 (25.78%) | |||
| 5 (above 80) | 40 (11.94%) | 25 (51.02%) | 65 (16.94%) | |||
| Lymphocyte count (lymphocyte/mcL) | 332 (missing-3) | 47 (missing-2) | 379 (missing-5) | Chi-square test | X2 = 12.34 | <0.0001 |
| 1 (0–0.49) | 38 (11.45%) | 16 (34.04%) | 54 (14.24%) | |||
| 2 (0.50–0.99) | 111 (33.43%) | 22 (46.81%) | 133 (35.09%) | |||
| 3 (1.00–1.49) | 103 (31.02%) | 5 (10.64%) | 108 (28.5%) | |||
| 4 (1.50–1.99) | 52 (15.66%) | 3 (6.38%) | 55 (14.51%) | |||
| 5 (above 2) | 28 (8.43%) | 1 (2.13%) | 29 (7.66%) | |||
| D-dimer (ng/mL) | 312 (missing-23) | 46 (missing-3) | 358 (missing-26) | Chi-square test | X2 = 6.7 | <0.0001 |
| 1 (0–499) | 50 (16.03%) | 1 (2.17%) | 51 (14.24%) | |||
| 2 (500–999) | 107 (34.29%) | 12 (26.09%) | 119 (33.24%) | |||
| 3 (1000–1999) | 93 (29.81%) | 14 (30.43%) | 107 (29.88%) | |||
| 4 (2000–3999) | 34 (10.90%) | 9 (19.57%) | 43 (12.08%) | |||
| 5 (above 4000) | 28 (8.97%) | 10 (21.74%) | 38 (10.56%) | |||
| Creatinine (mg/dL) | 334 (missing-1) | 47 (missing-2) | 381 (missing-3) | Chi-square test | X2 = 11.65 | <0.0001 |
| 1 (0–0.79) | 113 (33.83%) | 11 (23.40%) | 124 (32.54%) | |||
| 2 (0.80–1.19) | 155 (46.41%) | 13 (27.66%) | 168 (44.09%) | |||
| 3 (1.20–1.79) | 36 (10.78%) | 8 (17.02%) | 44 (11.54%) | |||
| 4 (1.80–2.99) | 16 (4.79%) | 7 (14.89%) | 23 (6.03%) | |||
| 5 (above 3) | 14 (4.19%) | 8 (17.02%) | 22 (5.8%) | |||
| CRP (mg/L) | 321 (missing-14) | 45 (missing-4) | 366 (missing-18) | Chi-square test | X2 = 7.86 | <0.0001 |
| 1 (0–19.9) | 68 (21.18%) | 4 (8.89%) | 72 (19.67%) | |||
| 2 (20–59) | 60 (18.69%) | 5 (11.11%) | 65 (17.76%) | |||
| 3 (60–99.9) | 64 (19.94%) | 8 (17.78%) | 72 (19.67%) | |||
| 4 (100–179) | 69 (21.50%) | 17 (37.78%) | 86 (23.5%) | |||
| 5 (above 180) | 60 (18.69%) | 11 (24.44%) | 71 (19.4%) | |||
| (B) | ||||||
| Features | Survived | Death | Total | Method | Statistic | p-Value |
| Frequency (%) | Frequency (%) | |||||
| Age (Year) | 201 (missing-0) | 174 (missing-0) | 375 (missing-0) | Chi-square test | X2 = 1.89 | <0.0001 |
| 1 (<34) | 36 (17.91%) | 2 (1.15%) | 38 (10.13%) | |||
| 2 (34–49) | 59 (29.35%) | 7 (4.02%) | 66 (17.60%) | |||
| 3 (50–64) | 63 (31.34%) | 47 (27.01%) | 110 (29.33%) | |||
| 4 (65–79) | 39 (19.40%) | 86 (49.43%) | 125 (33.33%) | |||
| 5 (above 80) | 4 (1.99%) | 32 (18.39%) | 36 (9.60%) | |||
| Lymphocyte count (lymphocytes/mcL) | 194 (missing-7) | 162 (missing-12) | 356 (missing-19) | Chi-square test | X2 = 8.23 | <0.0001 |
| 1 (0–0.49) | 8 (4.12%) | 66 (40.74%) | 74 (20.79%) | |||
| 2 (0.50–0.99) | 81 (41.75%) | 78 (48.15%) | 159 (44.66%) | |||
| 3 (1.00–1.49) | 61 (31.44%) | 15 (9.26%) | 76 (21.35%) | |||
| 4 (1.50–1.99) | 30 (15.46%) | 2 (1.23%) | 32 (8.99%) | |||
| 5 (above 2) | 14 (14%) | 1 (0.62%) | 15 (4.21%) | |||
| D-dimer (ng/mL) | 182 (missing-19) | 160 (missing-14) | 342 (missing-33) | Chi-square test | X2 = 7.22 | <0.0001 |
| 1 (0–499) | 79 (43.41%) | 7 (4.38%) | 86 (25.15%) | |||
| 2 (500–999) | 49 (26.92%) | 16 (10%) | 65 (19.01%) | |||
| 3 (1000–1999) | 36 (19.78%) | 19 (11.88%) | 55 (16.08%) | |||
| 4 (2000–3999) | 10 (5.49%) | 27 (16.88%) | 37 (10.82%) | |||
| 5 (above 4000) | 8 (4.40%) | 91 (56.88%) | 99 (28.95%) | |||
| Creatinine (mg/dL) | 193 (missing-8) | 163 (missing-11) | 356 (missing-19) | Chi-square test | X2 = 11.89 | <0.0001 |
| 1 (0–0.79) | 134 (69.43%) | 61 (37.42%) | 195 (54.78%) | |||
| 2 (0.80–1.19) | 44 (22.80%) | 67 (41.10%) | 111 (31.18%) | |||
| 3 (1.20–1.79) | 11 (5.70%) | 19 (11.66%) | 30 (8.43%) | |||
| 4 (1.80–2.99) | 0 (0%) | 10 (6.13%) | 10 (2.81%) | |||
| 5 (above 3) | 4 (2.07%) | 6 (3.68%) | 10 (2.81%) | |||
| CRP (mg/L) | 194 (missing-7) | 159 (missing-15) | 353 (missing-22) | Chi-square test | X2 = 7.01 | <0.0001 |
| 1 (0–19.9) | 100 (51.55%) | 5 (3.14%) | 105 (29.75%) | |||
| 2 (20–59) | 58 (29.90%) | 32 (20.13%) | 90 (25.50%) | |||
| 3 (60–99.9) | 17 (8.76%) | 30 (18.87%) | 47 (13.31%) | |||
| 4 (100–179) | 17 (8.76%) | 52 (32.70%) | 69 (19.55%) | |||
| 5 (above 180) | 2 (1.03%) | 40 (25.16%) | 42 (11.9%) | |||
| Machine Learning Classifier | Weighted Average (95% Confidence Interval) | Overall Accuracy | |||
|---|---|---|---|---|---|
| Precision | Sensitivity | F1-Score | Specificity | ||
| KNN | 0.88 ± 0.10 | 0.87 ± 0.16 | 0.88 ± 0.13 | 0.77 ± 0.08 | 0.88 ± 0.07 |
| Random Forest | 0.89 ± 0.11 | 0.88 ± 0.12 | 0.88 ± 0.12 | 0.77 ± 0.11 | 0.89 ± 0.05 |
| XGBoost | 0.87 ± 0.64 | 0.87 ± 0.42 | 0.86 ± 0.7 | 0.87 ± 0.2 | 0.87 ± 0.11 |
| SVM | 0.86 ± 0.03 | 0.85 ± 0.13 | 86 ± 0.03 | 0.86 ± 0.5 | 0.86 ± 0.07 |
| Extra-tree | 0.90 ± 0.024 | 0.89 ± 0.015 | 0.90 ± 0.01 | 0.90 ± 0.025 | 0.89 ± 0.012 |
| Logistic Regression | 0.92 ± 0.03 | 0.91 ± 0.03 | 0.92 ± 0.03 | 0.78 ± 0.04 | 0.91 ± 0.03 |
| (A) | |||||||||
| Features | AUC | Accuracy | Precision | Recall | F1 Score | Specificity | |||
| Age | 0.81 | 0.85 ± 0.04 | 0.86 ± 0.03 | 0.85 ± 0.04 | 0.85 ± 0.04 | 0.56 ± 0.05 | |||
| Lymphocyte count | 0.71 | 0.72 ± 0.10 | 0.75 ± 0.08 | 0.72 ± 0.06 | 0.72 ± 0.07 | 0.55 ± 0.17 | |||
| D-Dimer | 0.65 | 0.66 ± 0.08 | 0.67 ± 0.13 | 0.66 ± 0.04 | 0.65 ± 0.07 | 0.80 ± 0.14 | |||
| Creatinine | 064 | 0.62 ± 0.02 | 0.64 ± 0.02 | 0.62 ± 0.08 | 0.61 ± 0.06 | 0.80 ± 0.04 | |||
| CRP | 0.61 | 0.57 ± 0.05 | 0.57 ± 0.05 | 0.57 ± 0.04 | 0.57 ± 0.04 | 0.59 ± 0.09 | |||
| HTN | 0.61 | 0.65 ± 0.04 | 0.65 ± 0.04 | 0.65 ± 0.13 | 0.65 ± 0.07 | 0.66 ± 0.10 | |||
| Kidney | 0.60 | 0.54 ± 0.09 | 0.54 ± 0.08 | 0.54 ± 0.11 | 0.54 ± 0.09 | 0.50 ± 0.10 | |||
| Heart | 0.60 | 0.61 ± 0.09 | 0.69 ± 0.06 | 0.61 ± 0.06 | 0.56 ± 0.06 | 0.28 ± 0.14 | |||
| Abs Neutrophil | 0.59 | 0.61 ± 0.011 | 0.62 ± 0.09) | 0.61 ± 0.014 | 0.60 ± 0.10 | 0.48 ± 0.14 | |||
| GI_Symp | 0.58 | 0.57 ± 0.03 | 0.57 ± 0.03 | 0.57 ± 0.05 | 0.56 ± 0.04 | 0.71 ± 0.03 | |||
| (B) | |||||||||
| Features | Overall Accuracy | Weighted Performance with 95% CI | Confusion Matrix | ||||||
| Death | Alive | ||||||||
| Precision | Recall | F1 Score | Specificity | TP | FP | FN | TN | ||
| Top 1 feature | 0.85 ± 0.04 | 0.86 ± 0.03 | 0.85 ± 0.04 | 0.85 ± 0.04 | 0.56 ± 0.05 | 25 | 24 | 34 | 301 |
| Top 2 features | 0.91 ± 0.03 | 0.92 ± 0.03 | 0.91 ± 0.03 | 0.91 ± 0.03 | 0.76 ± 0.04 | 36 | 13 | 22 | 313 |
| Top 3 features | 0.91 ± 0.03 | 0.92 ± 0.03 | 0.91 ± 0.03 | 0.91 ± 0.03 | 0.78 ± 0.04 | 37 | 12 | 22 | 313 |
| Top 4 features | 0.9 ± 0.03 | 0.91 ± 0.03 | 0.9 ± 0.03 | 0.9 ± 0.03 | 0.74 ± 0.04 | 35 | 14 | 24 | 311 |
| Top 5 features | 0.92 ± 0.03 | 0.93 ± 0.02 | 0.92 ± 0.03 | 0.93 ± 0.03 | 0.83 ± 0.04 | 40 | 9 | 20 | 315 |
| Top 6 features | 0.92 ± 0.03 | 0.93 ± 0.03 | 0.92 ± 0.03 | 0.92 ± 0.03 | 0.81 ± 0.04 | 39 | 10 | 21 | 314 |
| Top 7 features | 0.91 ± 0.03 | 0.92 ± 0.03 | 0.91 ± 0.03 | 0.91 ± 0.03 | 0.78 ± 0.04 | 37 | 12 | 23 | 312 |
| Top 8 features | 0.91 ± 0.03 | 0.92 ± 0.03 | 0.91 ± 0.03 | 0.92 ± 0.03 | 0.8 ± 0.04 | 38 | 11 | 22 | 313 |
| Top 9 features | 0.92 ± 0.03 | 0.93 ± 0.03 | 0.92 ± 0.03 | 0.92 ± 0.03 | 0.8 ± 0.04 | 38 | 11 | 20 | 315 |
| Top 10 features | 0.91 ± 0.03 | 0.92 ± 0.03 | 0.91 ± 0.03 | 0.92 ± 0.03 | 0.78 ± 0.04 | 37 | 12 | 21 | 314 |
| Outcome | Coef. | Std. Err. | z | p > |z| | [95% Conf. Interval] | |
|---|---|---|---|---|---|---|
| Age | 1.90473 | 0.49970 | 3.81 | 0.000 | 0.92533 | 2.88412 |
| Lymphocyte count | −1.96463 | 0.47123 | −4.17 | 0.000 | −2.88822 | −1.04103 |
| D-Dimer | −1.50833 | 0.57196 | −2.64 | 0.008 | −2.62936 | −0.38732 |
| CRP | 0.70930 | 0.44818 | 1.58 | 0.114 | −0.169129 | 1.58772 |
| Creatinine | −0.24677 | 0.40469 | −0.61 | 0.542 | −1.03995 | 0.54641 |
| _cons | −0.76069 | 2.53057 | −0.30 | 0.764 | −5.72051 | 4.19914 |
| Paper | Patient Count | Patient Condition | Methodology in the Paper | Reported Performance |
|---|---|---|---|---|
| Weng et al. [55] | 301 patients | Confirmed COVID-19 | A nomogram was constructed to predict the death probability of COVID-19 patients. Age, neutrophil-to-lymphocyte ratio, d-dimer and C-reactive protein obtained on admission were identified as predictors of mortality for COVID-19 patients by LASSO. | The nomogram demonstrated good calibration and discrimination with the area under the curve (AUC) of 0.921 and 0.975 for the derivation and validation cohort, respectively. |
| Jianfeng Xie et al. [56] | 299 patients and external validation with 145 patient | Confirmed COVID-19 | Logistic regression analysis with the outcome variable defined as mortality. | Discrimination of the model was excellent in both internal (c = 0.89) and external (c = 0.98) validation. |
| Yan et al. [18] | 485 patients | Confirmed COVID-19 | Logistic regression-based machine learning tools selected three biomarkers that predict the mortality of individual patients | 90% accuracy for mortality prediction. |
| Zhang et al. [57] | 82 Patients | Confirmed COVID-19 | The association between the different clinical variables and the time from initial symptom to death was evaluated using Spearman’s rank correlation coefficient. | Most of the death cases were male (65.9%). More than half of dead patients were older than 60 years (80.5%) and the median age was 72.5 years. |
| Youha et al. [58] | 752 patients | Confirmed COVID-19 | Association of scores with documented hard endpoints (ICU admission or death) were assessed using binary logistic regression. | The area under the curve was equal to 90.4% |
| Proposed Study | 384 patients for Internal validation and 375 patients for external validation | Confirmed COVID-19 and Non-COVID-19 | Different ML classifier and developed a nomogram with the best performed model. | For the internal (Day-3 and Day-7) and external validation cohort, the area under the curves (AUCs) were 0.987, 0.999, and 0.992, respectively. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, T.; Al-Ishaq, F.A.; Al-Mohannadi, F.S.; Mubarak, R.S.; Al-Hitmi, M.H.; Islam, K.R.; Khandakar, A.; Hssain, A.A.; Al-Madeed, S.; Zughaier, S.M.; et al. Mortality Prediction Utilizing Blood Biomarkers to Predict the Severity of COVID-19 Using Machine Learning Technique. Diagnostics 2021, 11, 1582. https://doi.org/10.3390/diagnostics11091582
Rahman T, Al-Ishaq FA, Al-Mohannadi FS, Mubarak RS, Al-Hitmi MH, Islam KR, Khandakar A, Hssain AA, Al-Madeed S, Zughaier SM, et al. Mortality Prediction Utilizing Blood Biomarkers to Predict the Severity of COVID-19 Using Machine Learning Technique. Diagnostics. 2021; 11(9):1582. https://doi.org/10.3390/diagnostics11091582
Chicago/Turabian StyleRahman, Tawsifur, Fajer A. Al-Ishaq, Fatima S. Al-Mohannadi, Reem S. Mubarak, Maryam H. Al-Hitmi, Khandaker Reajul Islam, Amith Khandakar, Ali Ait Hssain, Somaya Al-Madeed, Susu M. Zughaier, and et al. 2021. "Mortality Prediction Utilizing Blood Biomarkers to Predict the Severity of COVID-19 Using Machine Learning Technique" Diagnostics 11, no. 9: 1582. https://doi.org/10.3390/diagnostics11091582
APA StyleRahman, T., Al-Ishaq, F. A., Al-Mohannadi, F. S., Mubarak, R. S., Al-Hitmi, M. H., Islam, K. R., Khandakar, A., Hssain, A. A., Al-Madeed, S., Zughaier, S. M., & Chowdhury, M. E. H. (2021). Mortality Prediction Utilizing Blood Biomarkers to Predict the Severity of COVID-19 Using Machine Learning Technique. Diagnostics, 11(9), 1582. https://doi.org/10.3390/diagnostics11091582








