Prediction of Incidental Osteoporotic Fractures at Vertebral-Specific Level Using 3D Non-Linear Finite Element Parameters Derived from Routine Abdominal MDCT
Abstract
1. Introduction
2. Materials and Methods
2.1. Subjects
2.2. Image Acquisition
2.3. MDCT-Derived BMD Calculation
2.4. Finite Element Modelling and ANALYSIS
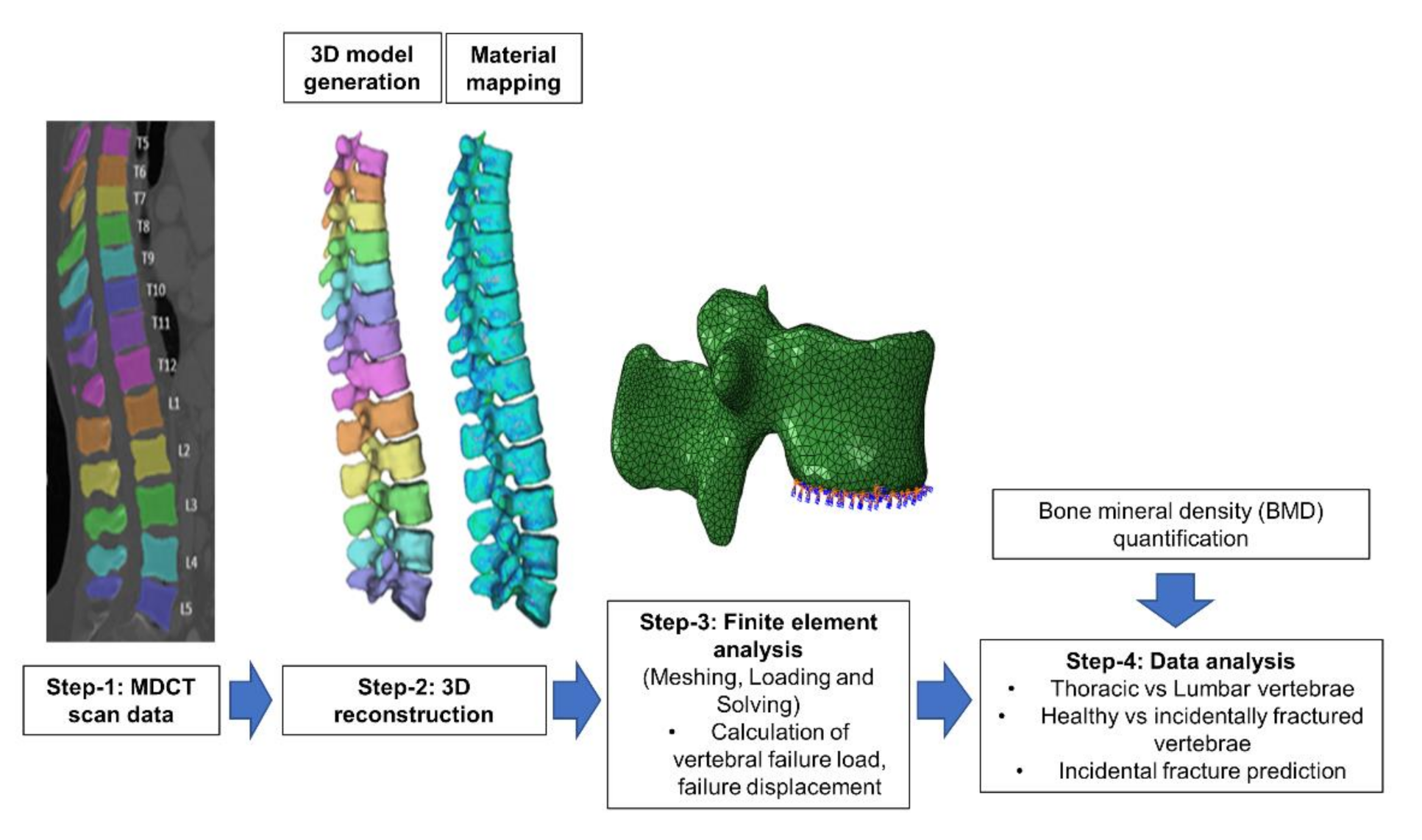
2.4.1. Image Segmentation and Meshing
2.4.2. 3D Reconstruction and Meshing
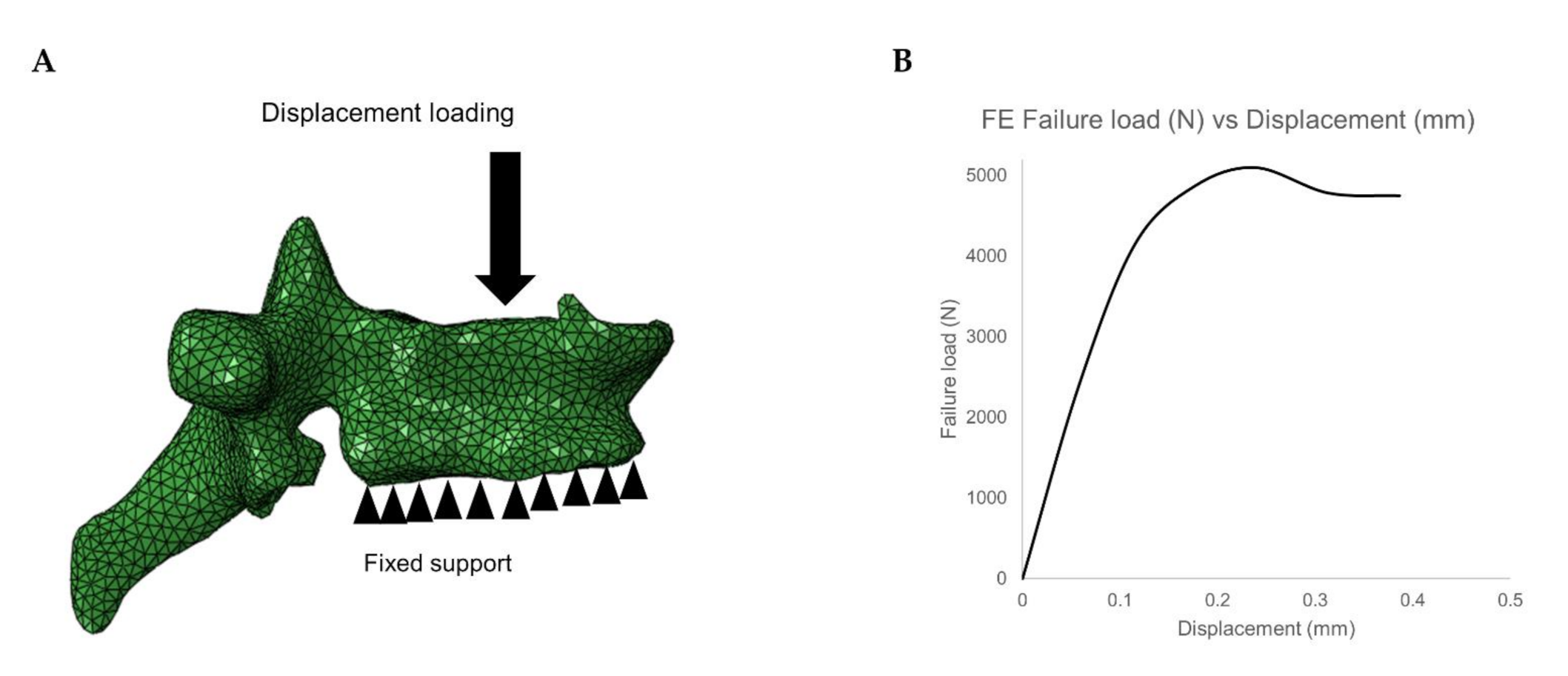
2.4.3. Finite Element Analysis
2.5. Statistical Analysis
3. Results
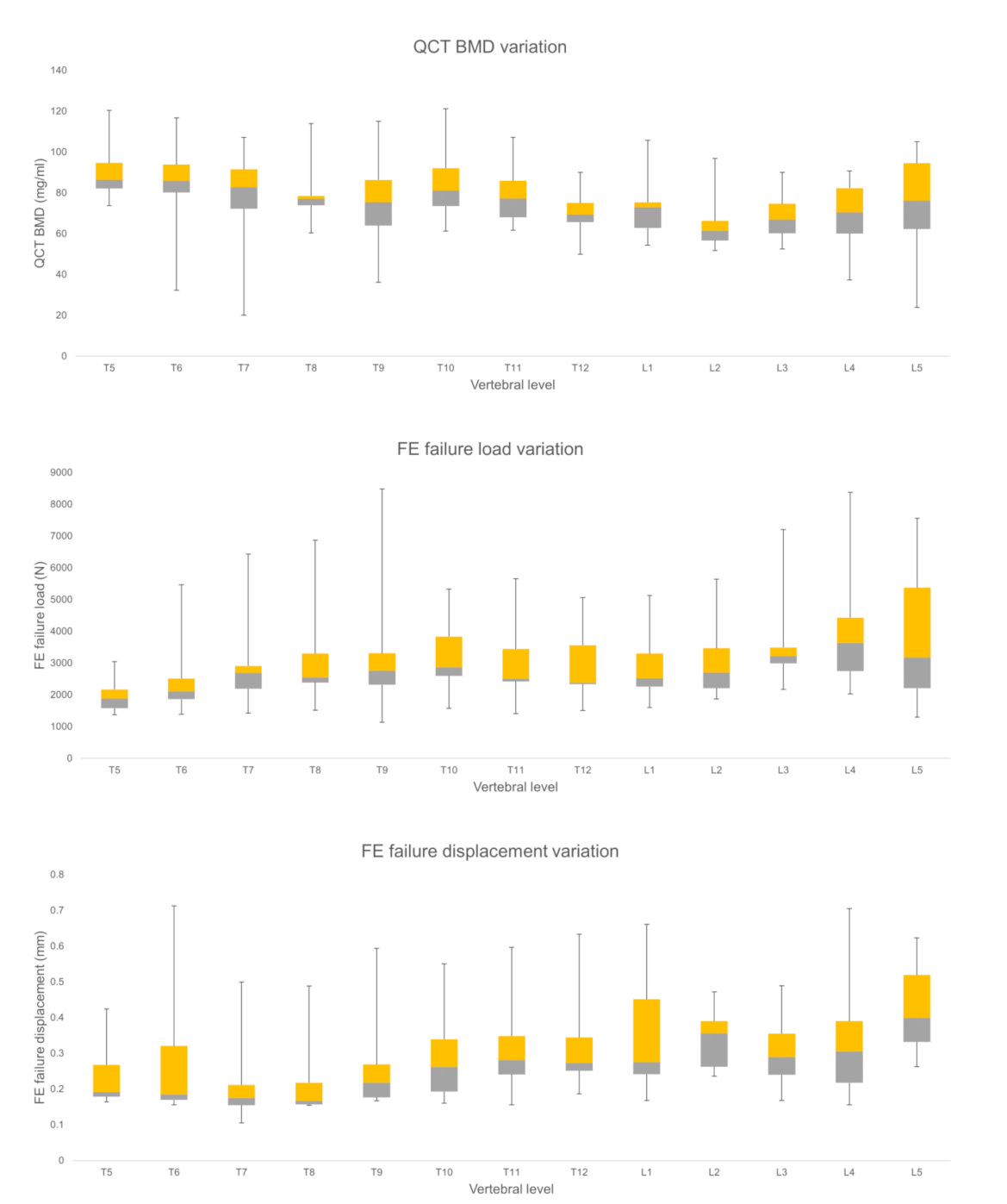
3.1. Comparison of FE and BMD Parameters for Thoracic and Lumbar Region
3.2. Comparison of FE and BMD Parameters for Healthy and Incidentally Fractured Vertebrae
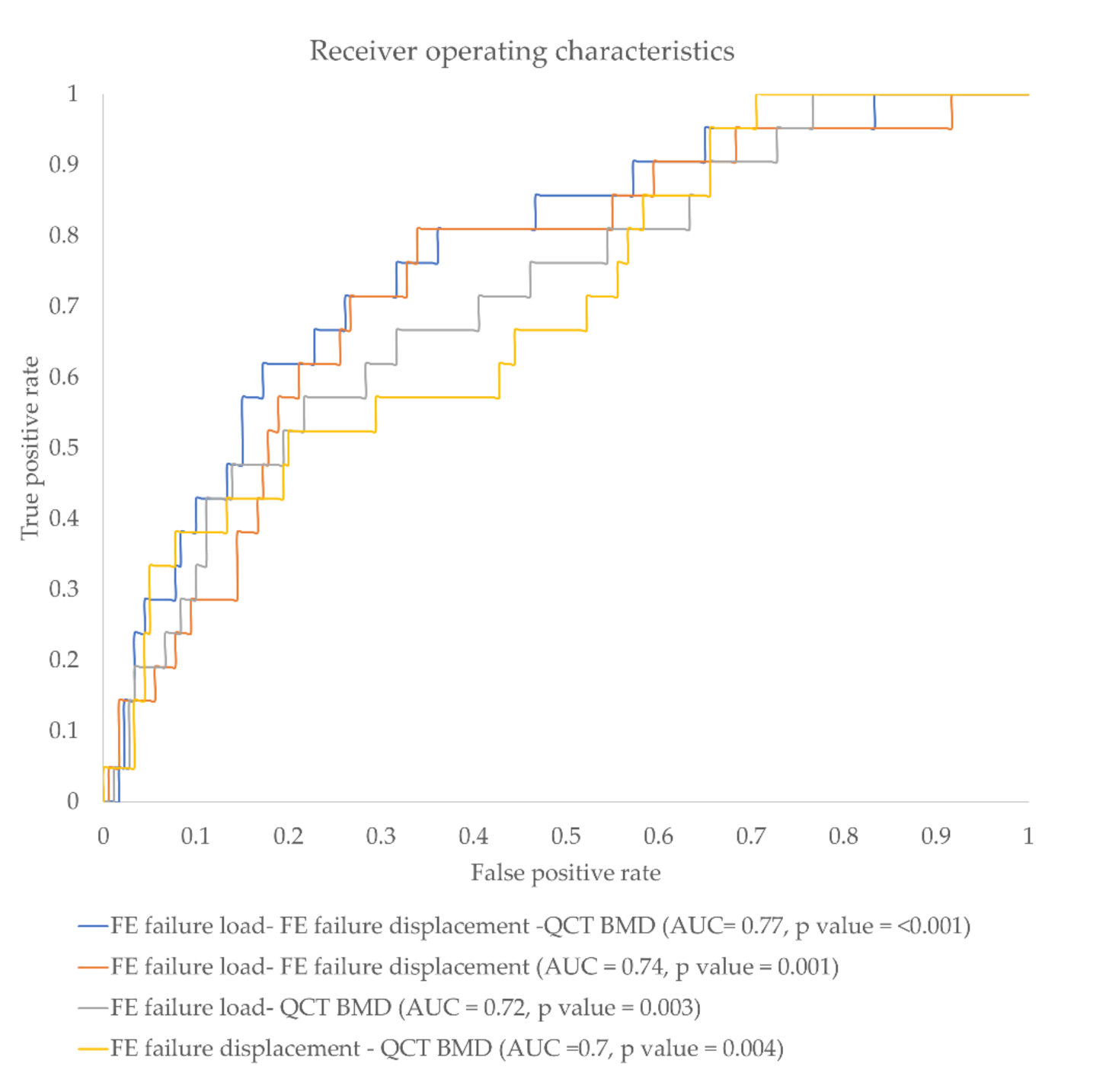
3.3. Incidental Fracture Prediction Using Different FE and BMD Parameter Combination
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 3D | Three-dimensional |
| aBMD | Areal bone mineral density |
| AUC | Area under the curve |
| BMD | Bone mineral density |
| CT | Computed tomography |
| DXA | Dual-energy X-ray absorptiometry |
| F | Incidentally fractured vertebrae |
| FE | Finite elements |
| H | Healthy vertebrae |
| HU | Hounsfield Units |
| K | Normalized ratio parameter |
| Kdisplacement | Normalized FE failure displacement ratio |
| Kload | Normalized FE failure load ratio |
| KBMD | Normalized BMD ratio |
| K(displacement)g | Normalized global FE failure displacement ratio |
| K(load)g | Normalized global FE failure load ratio |
| K(BMD)g | Normalized global BMD ratio |
| L | Lumbar region |
| MDCT | Multi detector computed tomography |
| PACS | Picture archiving and communication system |
| QCT | Quantitative computed tomography |
| ROC | Receiver operating characteristic |
| ROI | Region of interest |
| SD | Standard deviation |
| T | Thoracic region |
References
- Kanis, J.A. Diagnosis of Osteoporosis and Assessment of Fracture Risk. Lancet 2002, 359, 1929–1936. [Google Scholar] [CrossRef]
- Reginster, J.Y.; Burlet, N. Osteoporosis: A still increasing prevalence. Bone 2006, 38, 4–9. [Google Scholar] [CrossRef]
- Tu, K.N.; Lie, J.D.; Wan, C.K.V.; Cameron, M.; Austel, A.G.; Nguyen, J.K.; Van, K.; Hyun, D. Osteoporosis: A review of treatment options. Pharm. Ther. 2018, 43, 92–104. [Google Scholar]
- Drake, M.T.; Clarke, B.L.; Lewiecki, E.M. The pathophysiology and treatment of osteoporosis. Clin. Ther. 2015, 37, 1837–1850. [Google Scholar] [CrossRef] [PubMed]
- Borgström, F.; Karlsson, L.; Ortsäter, G.; Norton, N.; Halbout, P.; Cooper, C.; Lorentzon, M.; McCloskey, E.V.; Harvey, N.C.; Javaid, M.K.; et al. Fragility fractures in Europe: Burden, management and opportunities. Arch. Osteoporos. 2020, 15. [Google Scholar] [CrossRef] [PubMed]
- Hernlund, E.; Svedbom, A.; Ivergård, M.; Compston, J.; Cooper, C.; Stenmark, J.; McCloskey, E.V.; Jönsson, B.; Kanis, J.A. Osteoporosis in the European Union: Medical management, epidemiology and economic burden: A report prepared in collaboration with the International Osteoporosis Foundation (IOF) and the European Federation of Pharmaceutical Industry Associations (EFPIA). Arch. Osteoporos. 2013, 8. [Google Scholar] [CrossRef] [PubMed]
- Arpitha, A.; Rangarajan, L. Computational techniques to segment and classify lumbar compression fractures. Radiol. Med. 2020, 125, 551–560. [Google Scholar] [CrossRef]
- Rajasekaran, S.; Kanna, R.M.; Shetty, A.P. Management of thoracolumbar spine trauma an overview. Ind. J. Orthop. 2015, 49, 72–82. [Google Scholar] [CrossRef]
- Blake, G.M.; Fogelman, I. An update on dual-energy X-Ray absorptiometry. Semin. Nucl. Med. 2010, 40, 62–73. [Google Scholar] [CrossRef][Green Version]
- Imai, K. Aging and disease analysis of vertebral bone strength, fracture pattern, and fracture location: A validation study using a computed tomography-based nonlinear finite element analysis. Aging Dis. 2015, 6, 180–187. [Google Scholar] [CrossRef]
- Pickhardt, P.J.; Graffy, P.M.; Zea, R.; Lee, S.J.; Liu, J.; Sandfort, V.; Summers, R.M. Automated abdominal CT imaging biomarkers for opportunistic prediction of future major osteoporotic fractures in asymptomatic adults. Radiology 2020, 200466. [Google Scholar] [CrossRef] [PubMed]
- Baum, T.; Müller, D.; Dobritz, M.; Rummeny, E.J.; Link, T.M.; Bauer, J.S. BMD measurements of the spine derived from sagittal reformations of contrast-enhanced MDCT without dedicated software. Eur. J. Radiol. J. 2011, 80, 140–145. [Google Scholar] [CrossRef] [PubMed]
- Löffler, M.T.; Sollmann, N.; Mei, K.; Valentinitsch, A.; Noël, P.B.; Kirschke, J.S.; Baum, T. X-ray-based quantitative osteoporosis imaging at the spine. Osteoporos. Int. 2019, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Baum, T.; Muller, D.; Dobritz, M.; Wolf, P.; Rummeny, E.J.; Link, T.M.; Bauer, J.S. Converted lumbar BMD values derived from sagittal reformations of contrast-enhanced MDCT predict incidental osteoporotic vertebral fractures. Calcif. Tissue Int. 2012, 90, 481–487. [Google Scholar] [CrossRef] [PubMed]
- Schuit, S.C.E.; Van Der Klift, M.; Weel, A.E.A.M.; De Laet, C.E.D.H.; Burger, H.; Seeman, E.; Hofman, A.; Uitterlinden, A.G.; Van Leeuwen, J.P.T.M. Fracture incidence and association with bone mineral density in elderly men and women: The Rotterdam study. Bone 2004, 34, 195–202. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, H.; Moreira-Gonçalves, D.; Coriolano, H.J.A.; Duarte, J.A. Bone quality: The determinants of bone strength and fragility. Sport. Med. 2014, 44, 37–53. [Google Scholar] [CrossRef]
- Allaire, B.T.; Lu, D.; Johannesdottir, F.; Kopperdahl, D.; Keaveny, T.M.; Jarraya, M.; Guermazi, A. Prediction of incident vertebral fracture using CT-based finite element analysis. Osteoporos. Int. 2018, 30, 323–331. [Google Scholar] [CrossRef]
- Crawford, R.P.; Cann, C.E.; Keaveny, T.M. Finite element models predict in vitro vertebral body compressive strength better than quantitative computed tomography. Bone 2003, 33, 744–750. [Google Scholar] [CrossRef]
- Lee, D.C.; Varela, A.; Kostenuik, P.J.; Ominsky, M.S.; Keaveny, T.M. Finite element analysis of denosumab treatment effects on vertebral strength in ovariectomized cynomolgus monkeys. J. Bone Miner. Res. 2016, 31, 1586–1595. [Google Scholar] [CrossRef]
- Zysset, P.K.; Dall’Ara, E.; Varga, P.; Pahr, D.H. Finite element analysis for prediction of bone strength. Bonekey Rep. 2013. [Google Scholar] [CrossRef]
- Chevalier, Y.; Pahr, D.; Allmer, H.; Charlebois, M.; Zysset, P. Validation of a voxel-based FE method for prediction of the uniaxial apparent modulus of human trabecular bone using macroscopic mechanical tests and nanoindentation. J. Biomech. 2007, 40, 3333–3340. [Google Scholar] [CrossRef] [PubMed]
- Nithin M., R.; Subburaj, K.; Dieckmeyer, M.; Jan S, K.; Noel, P.B.; Baum, T. MDCT-based Vertebral Bone Strength Prediction using Finite Element Analysis: How low can we go? Front. Endocrinol. (Lausanne) 2020, 1–4. [Google Scholar] [CrossRef]
- Anitha, D.; Subburaj, K.; Kopp, F.K.; Mei, K.; Foehr, P.; Burgkart, R.; Sollmann, N.; Maegerlein, C.; Kirschke, J.S.; Noel, P.B.; et al. Effect of statistically iterative image reconstruction on vertebral bone strength prediction using bone mineral density and finite element modeling: A preliminary study. J. Comput. Assist. Tomogr. 2019, 43, 61–65. [Google Scholar] [CrossRef] [PubMed]
- Chevalier, Y.; Quek, E.; Borah, B.; Gross, G.; Stewart, J.; Lang, T.; Zysset, P. Biomechanical effects of teriparatide in women with osteoporosis treated previously with alendronate and risedronate: Results from quantitative computed tomography-based finite element analysis of the vertebral body. Bone 2010, 46, 41–48. [Google Scholar] [CrossRef] [PubMed]
- Kopperdahl, D.L.; Aspelund, T.; Hoffmann, P.F.; Sigurdsson, S.; Siggeirsdottir, K.; Harris, T.B.; Gudnason, V.; Keaveny, T.M. Assessment of incident spine and hip fractures in women and men using finite element analysis of CT scans. J. Bone Miner. Res. 2014, 29, 570–580. [Google Scholar] [CrossRef] [PubMed]
- Anitha, D.; Thomas, B.; Jan, K.S.; Subburaj, K. Risk of vertebral compression fractures in multiple myeloma patients: A finite-element study. Medicine (United States) 2017, 96. [Google Scholar] [CrossRef]
- Anitha, D.P.; Baum, T.; Kirschke, J.S.; Subburaj, K. Effect of the intervertebral disc on vertebral bone strength prediction: A finite-element study. Spine. J. 2019, 000, 1–7. [Google Scholar] [CrossRef]
- Imai, K.; Ohnishi, I.; Matsumoto, T.; Yamamoto, S.; Nakamura, K. Assessment of vertebral fracture risk and therapeutic effects of alendronate in postmenopausal women using a quantitative computed tomography-based nonlinear finite element method. Osteoporos. Int. 2009, 20, 801–810. [Google Scholar] [CrossRef]
- Wang, X.; Sanyal, A.; Cawthon, P.M.; Palermo, L.; Jekir, M.; Christensen, J.; Ensrud, K.E.; Cummings, S.R.; Orwoll, E.; Black, D.M.; et al. Prediction of new clinical vertebral fractures in elderly men using finite element analysis of CT scans. J. Bone Miner. Res. 2012, 27, 808–816. [Google Scholar] [CrossRef]
- Valentinitsch, A.; Trebeschi, S.; Alarcón, E.; Baum, T.; Kaesmacher, J.; Zimmer, C.; Lorenz, C.; Kirschke, J.S. Regional analysis of age-related local bone loss in the spine of a healthy population using 3D voxel-based modeling. Bone 2017, 103, 233–240. [Google Scholar] [CrossRef]
- Genant, H.K.; Wu, C.Y.; van Kuijk, C.; Nevitt, M.C. Vertebral fracture assessment using a semiquantitative technique. J. Bone Miner. Res. 1993, 8, 1137–1148. [Google Scholar] [CrossRef] [PubMed]
- Huber, M.B.; Carballido-Gamio, J.; Bauer, J.S.; Baum, T.; Eckstein, F.; Lochmüller, E.M.; Majumdar, S.; Link, T.M. Proximal femur specimens: Automated 3D trabecular bone mineral density analysis at multidetector CT–Correlation with biomechanical strength measurement. Radiology 2008, 247, 472–481. [Google Scholar] [CrossRef] [PubMed]
- Rayudu, N.M.; Dieckmeyer, M.; T Loffler, M.; Noel, P.B.; Korschke, J.S.; Baum, T.; Karupppasamy, S. Predicting vertebral bone strength using finite element analysis for opportunistic osteoporosis screening in routine MDCT scans. Front. Endocrinol. (Lausanne) 2020, 11, 1046. [Google Scholar] [CrossRef] [PubMed]
- Mei, K.; Kopp, F.K.; Bippus, R.; Köhler, T.; Schwaiger, B.J.; Gersing, A.S.; Fehringer, A.; Sauter, A.; Münzel, D.; Pfeiffer, F.; et al. Is multidetector CT-based bone mineral density and quantitative bone microstructure assessment at the spine still feasible using ultra-low tube current and sparse sampling? Eur. Radiol. 2017, 27, 5261–5271. [Google Scholar] [CrossRef] [PubMed]
- Löffler, M.T.; Sekuboyina, A.; Jacob, M.E.A.; Grau, A.; Scharr, A.; El Husseini, M.; Kallweit, M.; Zimmer, C.; Baum, T.; Kirschke, J.S. A vertebral segmentation dataset with fracture grading. Radiol. Intell. 2020, 2, e190138. [Google Scholar]
- Rho, J.Y.; Hobatho, M.C.; Ashman, R.B. Relations of mechanical properties to density and CT numbers in human bone. Med. Eng. Phys. 1995, 17, 347–355. [Google Scholar] [CrossRef]
- Goulet, R.W.; Goldstein, S.A.; Ciarelli, M.J.; Kuhn, J.L.; Brown, M.B.; Feldkamp, L.A. The relationship between the structural and orthogonal compressive properties of trabecular bone. J. Biomech. 1994, 27. [Google Scholar] [CrossRef]
- Keyak, J.H. Improved prediction of proximal femoral fracture load using nonlinear finite element models. Med. Eng. Phys. 2001, 23, 165–173. [Google Scholar] [CrossRef]
- Keller, T.S. Predicting the compressive mechanical behavior of bone. J. Biomech. 1994, 27, 1159–1168. [Google Scholar] [CrossRef]
- Anitha, D.; Mei, K.; Dieckmeyer, M.; Kopp, F.K.; Sollmann, N.; Zimmer, C.; Kirschke, J.S.; Noel, P.B.; Baum, T.; Subburaj, K. MDCT-based finite element analysis of vertebral fracture risk: What dose is needed? Clin. Neuroradiol. 2019, 29, 645–651. [Google Scholar] [CrossRef]
- Imai, K.; Ohnishi, I.; Bessho, M.; Nakamura, K. Nonlinear finite element model predicts vertebral bone strength and fracture site. Spine (Phila. Pa. 1976). 2006, 31, 1789–1794. [Google Scholar] [CrossRef] [PubMed]
- Rayudu, N.M.; Anitha, D.P.; Mei, K.; Zoffl, F.; Kopp, F.K.; Sollmann, N.; Löffler, M.T.; Kirschke, J.S.; Noël, P.B.; Subburaj, K.; et al. Low-dose and sparse sampling MDCT-based femoral bone strength prediction using finite element analysis. Arch. Osteoporos. 2020, 15, 17. [Google Scholar] [CrossRef] [PubMed]
- Anitha, D.; Subburaj, K.; Mei, K.; Kopp, F.K.; Foehr, P.; Noel, P.B.; Kirschke, J.S.; Baum, T. Effects of dose reduction on bone strength prediction using finite element analysis. Sci. Rep. 2016, 6, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, L.J.; Russo, G.A. Spinal Evolution; Been, E., Gómez-Olivencia, A., Kramer, P.A., Eds.; Springer: New York, NY, USA, 2019; ISBN 9783030193485. [Google Scholar]
- Kang, K.S.; Song, K.S.; Lee, J.S.; Yang, J.J.; Song, I.S. Comparison of radiographic and computed tomographic measurement of pedicle and vertebral body dimensions in Koreans: The ratio of pedicle transverse diameter to vertebral body transverse diameter. Eur. Spine J. 2011, 20, 414–421. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Chandran, M.; Rayudu, N.; Anitha, D.; Duraisamy, S.; Magsombol, B.; Dce, N.; Subburaj, K. Normalized FE-predicted failure load: A potentially better tool to classify osteoporotic fragility fracture risk than BMD alone in post-menopausal chinese women. In Proceedings of the ASBMR 2019 Annual Meeting, Orlando, FL, USA, 20–23 September 2019; pp. 1–3. [Google Scholar]
- Valentinitsch, A.; Trebeschi, S.; Kaesmacher, J.; Lorenz, C.; Löffler, M.T.; Zimmer, C.; Baum, T.; Kirschke, J.S. Opportunistic osteoporosis screening in multi-detector CT images via local classification of textures. Osteoporos. Int. 2019, 30, 1275–1285. [Google Scholar] [CrossRef] [PubMed]
- Taylor, W.R.; Roland, E.; Ploeg, H.; Hertig, D.; Klabunde, R.; Warner, M.D.; Hobatho, M.C.; Rakotomanana, L.; Clift, S.E. Determination of orthotropic bone elastic constants using FEA and modal analysis. J. Biomech. 2002, 35, 767–773. [Google Scholar] [CrossRef]
- Duchemin, L.; Mitton, D.; Jolivet, E.; Bousson, V.; Laredo, J.D.; Skalli, W.; Mitton, D.; Jolivet, E.; Bousson, V.; Laredo, J.D.; et al. Computer methods in biomechanics and biomedical engineering an anatomical subject-specific FE-model for hip fracture load prediction an anatomical subject-specific FE-model for hip fracture load prediction. Comput. Methods Biomech. Biomed. Engin. 2008, 11, 105–111. [Google Scholar] [CrossRef]
- Muehlematter, U.J.; Mannil, M.; Becker, A.S.; Vokinger, K.N.; Finkenstaedt, T.; Osterhoff, G.; Fischer, M.A.; Guggenberger, R. Vertebral body insufficiency fractures: Detection of vertebrae at risk on standard CT images using texture analysis and machine learning. Eur. Radiol. 2018, 29, 2207–2217. [Google Scholar] [CrossRef]
| Inclusion Criteria | Exclusion Criteria |
|---|---|
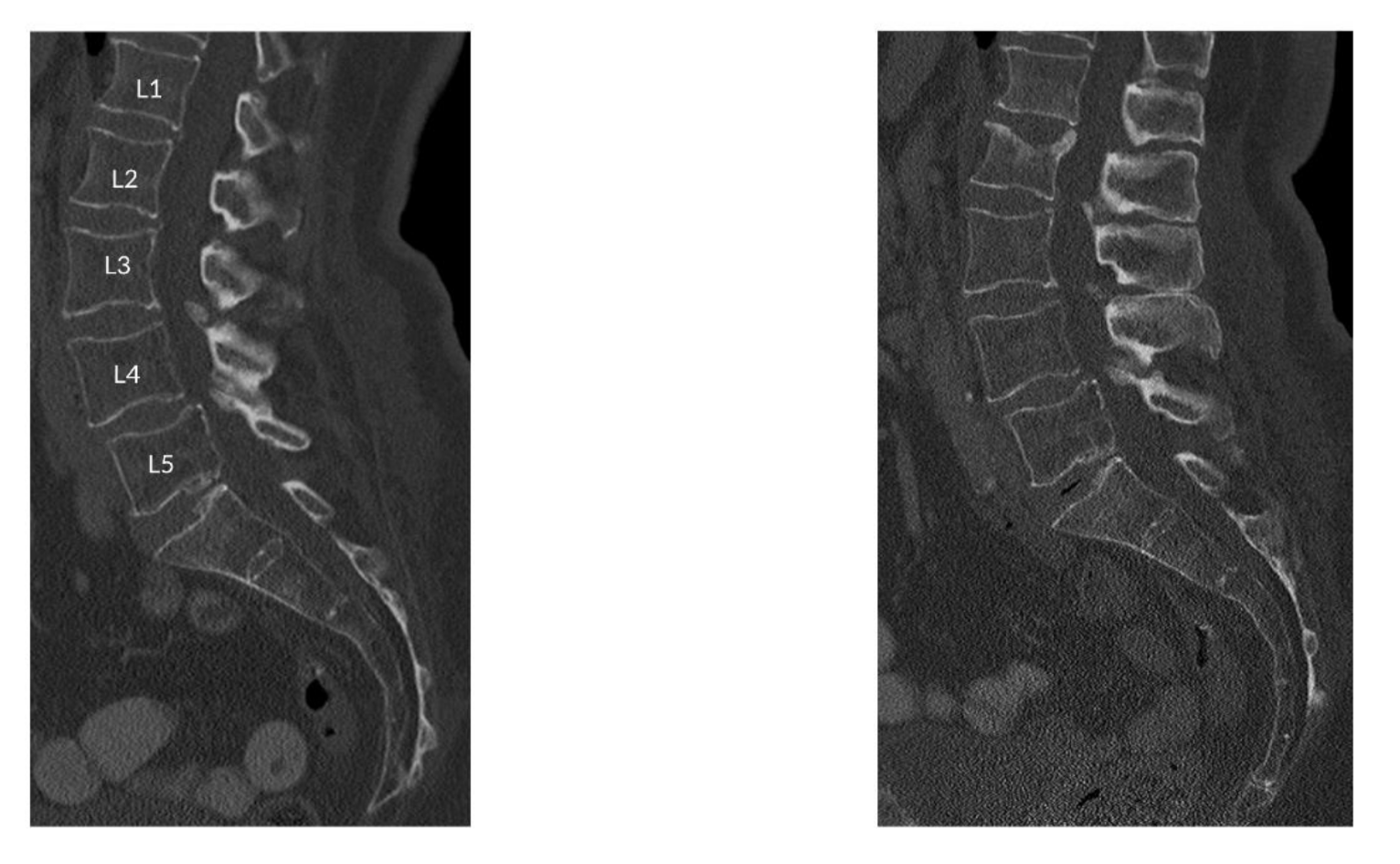
| Baseline thoracic and abdominal MDCT exams at the same single MDCT scanner with a specific protocol | History of bone diseases, including hematologic and metabolic disorders, aside from osteoporosis |
| Follow-up thoracic and abdominal MDCT exams with incidental osteoporotic vertebral fracture | Bone metastases |
| Availability of sagittal image reformations of the spine at baseline and follow-up MDCT |
| Material Properties | Unit | Mapping Relations |
|---|---|---|
| Apparent density (ρapp) [35] | Kg/m3 | ρapp = 47 + 1.122 × HU HU—Hounsfield unit |
| Ash density (ρash) [36] | Kg/m3 | ρash = 0.6 × ρapp |
| Elastic modulus (E) [35] | MPa | Ez = −349 + 5.82 × ρapp Ex = Ey = 0.333 Ez Z—axial direction of the vertebra |
| Shear modulus (G) [18] | MPa | Gxy = 0.121 Ez Gxz = Gyz = 0.157 Ez |
| Poisson ratio (V) [18] | Constant | Vxy = 0.381 Vxy = Vyz = 0.104 |
| Maximum principal stress limit (σ) [38] | MPa | σ = 137 × ρash 1.88, ρash < 0.317 σ = 114 × ρash 1.72, ρash > 0.317 |
| Plastic strain (εAB) [37] | No unit | εAB = −0.00315 + 0.0728 ρash |
| Minimum principal stress limit (σmin) [37] | MPa | σmin = 65.1 × ρash 1.93 |
| Normalized Ratio Parameter (Local) | Healthy (Mean ± sd) | Fractured (Mean ± sd) | p-Value |
| FE Failure load | 1.01 ± 0.22 | 0.87 ± 0.19 | 0.005 * |
| FE Failure displacement | 0.98 ± 0.32 | 1.18 ± 0.47 | 0.045 * |
| BMD | 1.01 ± 0.16 | 0.92 ± 0.13 | 0.037 * |
| Normalized Ratio Parameter (Global) | Healthy (Mean ± sd) | Fractured (Mean ± sd) | p-Value |
| FE Failure load | 1.00 ± 0.31 | 0.85 ± 0.18 | 0.003 * |
| FE Failure displacement | 0.92 ± 0.36 | 1.12 ± 0.62 | 0.171 |
| BMD | 1.14 ± 0.27 | 1.03 ± 0.19 | 0.054 |
| Normalized Ratio Parameter Combination | p-Value | AUC |
|---|---|---|
| FE failure load ratio and FE failure displacement ratio | <0.001 * | 0.74 |
| FE failure load ratio and Qct BMD ratio | 0.003 * | 0.72 |
| Qct BMD and FE failure displacement ratio | 0.004 * | 0.70 |
| FE failure load ratio, FE failure displacement ratio, and Qct BMD ratio | <0.001 * | 0.77 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeung, L.Y.; Rayudu, N.M.; Löffler, M.; Sekuboyina, A.; Burian, E.; Sollmann, N.; Dieckmeyer, M.; Greve, T.; Kirschke, J.S.; Subburaj, K.; et al. Prediction of Incidental Osteoporotic Fractures at Vertebral-Specific Level Using 3D Non-Linear Finite Element Parameters Derived from Routine Abdominal MDCT. Diagnostics 2021, 11, 208. https://doi.org/10.3390/diagnostics11020208
Yeung LY, Rayudu NM, Löffler M, Sekuboyina A, Burian E, Sollmann N, Dieckmeyer M, Greve T, Kirschke JS, Subburaj K, et al. Prediction of Incidental Osteoporotic Fractures at Vertebral-Specific Level Using 3D Non-Linear Finite Element Parameters Derived from Routine Abdominal MDCT. Diagnostics. 2021; 11(2):208. https://doi.org/10.3390/diagnostics11020208
Chicago/Turabian StyleYeung, Long Yu, Nithin Manohar Rayudu, Maximilian Löffler, Anjany Sekuboyina, Egon Burian, Nico Sollmann, Michael Dieckmeyer, Tobias Greve, Jan S. Kirschke, Karupppasamy Subburaj, and et al. 2021. "Prediction of Incidental Osteoporotic Fractures at Vertebral-Specific Level Using 3D Non-Linear Finite Element Parameters Derived from Routine Abdominal MDCT" Diagnostics 11, no. 2: 208. https://doi.org/10.3390/diagnostics11020208
APA StyleYeung, L. Y., Rayudu, N. M., Löffler, M., Sekuboyina, A., Burian, E., Sollmann, N., Dieckmeyer, M., Greve, T., Kirschke, J. S., Subburaj, K., & Baum, T. (2021). Prediction of Incidental Osteoporotic Fractures at Vertebral-Specific Level Using 3D Non-Linear Finite Element Parameters Derived from Routine Abdominal MDCT. Diagnostics, 11(2), 208. https://doi.org/10.3390/diagnostics11020208