Abstract
During image segmentation tasks in computer vision, achieving high accuracy performance while requiring fewer computations and faster inference is a big challenge. This is especially important in medical imaging tasks but one metric is usually compromised for the other. To address this problem, this paper presents an extremely fast, small and computationally effective deep neural network called Stripped-Down UNet (SD-UNet), designed for the segmentation of biomedical data on devices with limited computational resources. By making use of depthwise separable convolutions in the entire network, we design a lightweight deep convolutional neural network architecture inspired by the widely adapted U-Net model. In order to recover the expected performance degradation in the process, we introduce a weight standardization algorithm with the group normalization method. We demonstrate that SD-UNet has three major advantages including: (i) smaller model size (23x smaller than U-Net); (ii) 8x fewer parameters; and (iii) faster inference time with a computational complexity lower than 8M floating point operations (FLOPs). Experiments on the benchmark dataset of the Internatioanl Symposium on Biomedical Imaging (ISBI) challenge for segmentation of neuronal structures in electron microscopic (EM) stacks and the Medical Segmentation Decathlon (MSD) challenge brain tumor segmentation (BRATs) dataset show that the proposed model achieves comparable and sometimes better results compared to the current state-of-the-art.
1. Introduction
Biomedical image segmentation is the process of identifying important image components and it is a basic task in biomedical image processing which provides the basis for further and other image processing in a variety of clinical applications [1]. Some of these applications include the segmentation and quantification of gray and white matter tissues from magnetic resonance imaging brain scans for identifying various neurological diseases [2]. It usually employs partitioning a set of image pixels into subsets where the pixels in each subset are related [3]. Identifying vital information about the shapes and volumes of biological organs is very necessary and one of the most difficult tasks in biomedical image analysis [4]. In the past few years, convolutional neural networks (CNNs) have been successfully used in completing various computer vision tasks such as image classification [5,6,7], object detection [8], segmentation [9,10,11,12], action recognition [13,14], and tracking [15,16]. After outperforming state-of-the-art in image classification, researchers started paying attention to applying CNNs in structured prediction problems such as pose estimation [15] and semantic segmentation. Semantic segmentation [10,11,17,18,19] has become a major area of interest for researchers from multiple disciplines working on various types of images from biomedical to outdoor scene datasets. Automated segmentation of biomedical images could be difficult when there are large shape and size variations of the anatomy between patients as well as low contrast to surrounding tissues [20]. However, there is a rising need for automatic segmentation of medical images as a result of the complexity of manually segmenting them and recent advances have led to easier segmentation using CNNs [9,21]. One of the most significant contributions to biomedical image segmentation with CNNs is the U-Net architecture [9]. The U-Net model is very popular in biomedical image segmentation due to its ability to segment images efficiently with a very limited amount of labeled training data. Variants of U-Net have also been successfully implemented in various kinds of vision tasks. U-Net has been used with pixel-wise regression and applied to pansharpening [22]. TernausNet [23] initializes the encoder path of the architecture with weights obtained from a VGG11 [7] model pretrained on ImageNet [24] data. Attention U-Net [25] extends the standard U-Net with a proposed attention gate (AG) model for medical imaging that automatically learns to focus on target structures of varying shapes and sizes.
In recent times, there has been an increased need to implement deep learning solutions on mobile handheld devices, embedded systems or any computer with low computational budgets. A major reason why this is a challenging feat is the fact that CNNs are over-parameterized [26] and they usually require larger computing power and storage capacity for training and inference. Deep learning researchers have proposed several techniques that require pruning or quantization of weights of models pretrained on large image datasets [27,28,29,30]. Others have focused on training compact models from scratch [31,32,33] by factorizing standard convolution layers into depthwise separable convolution layers for cheaper computations.
This paper presents a similar technique used in these compact architectures also known as mobilenet architectures with the goal of training the U-Net model with fewer parameters requiring smaller storage space, less computational requirements, and faster inference. However, depthwise separable convolutions are known to have degraded performance in terms of accuracy compared to standard convolution layers. Weight standardization combined with group normalization is therefore implemented on weights of each input layer to recover its accuracy loss. This new architecture is referred to as the SD-UNet. The performance of SD-UNet is evaluated on the ISBI challenge dataset for the segmentation of neuronal structures in EM stacks and further demonstrates its robustness on brain tumor segmentation tasks on the Medical Segmentation Decathlon (MSD) challenge brain tumor segmentation dataset.
1.1. Motivation
There have been major shifts in technology over the past decade and the most significant of them is the migration from desktop or laptop computers to mobile and handheld devices. This means that people are naturally leaning towards deep learning solutions using their mobile devices. There is a need to develop applications that require less memory storage and low computation and battery power. Latency usually comes about as a result of time for transferring data over networks and the number of computations required by the deep learning model. Performing tasks that require low latency like timely identification and segmentation of biomedical images require data to be immediately available. Most companies and researchers currently rely on retrieving data stored on a network server or distributed on other devices usually leading to huge overhead costs especially during deployment. This also makes it difficult to continuously update training data in order to improve the efficiency of the deep neural network. The energy required by deep CNNs usually exceeds the limited on-chip memory of mobile and handheld devices, so they are sometimes supplemented with off-chip memory, which consumes a significant amount of energy. To overcome such limitations, we introduce a new variant of the U-Net architecture, the SD-UNet for efficient segmentation of biomedical images on devices with low computational budgets.
1.2. Contributions
The contributions of this paper can be summarized as follows:
- We propose the use of depthwise separable convolution layers to replace all standard CNN layers except the first CNN layer in the original U-Net model
- Depthwise separable convolution layers are known to achieve lower performance compared to standard convolution layers. We demonstrate that performance drop due to the process can be recovered with a method of weight standardization and group normalization.
- SD-UNet model has 8x fewer parameters and requires 23x less storage space. The computational complexity or number of floating point operations (FLOPs) required by SD-UNet is 8x less than is required by the original U-Net model and shows great performance on the segmentation of biomedical images.
2. Related Work
In this section, we describe in detail the major previous works that motivated our work.
2.1. Depthwise Separable Convolutions
Depthwise separable convolutions were initially introduced by [34] and then later implemented by [31,35]. Depthwise separable convolution is a form of factorization which factorizes a standard convolution into a depthwise convolution and a pointwise convolution (1 × 1 convolution). A standard convolution layer works by applying a convolution kernel to all of the channels of the input image and takes a weighted sum of the input pixels covered by the kernel sliding across all input channels of the image. This means that for a standard convolution, no matter how many input channels are available, the output channel is one. However, in depthwise separable convolutions, features are only learned from the input channels so the output layer has the same number of channels as the input.
This is known as depthwise convolution followed by a pointwise (1 × 1) convolution layer which computes the weighted sum of all output channels into a single output (Figure 1 and Figure 2).
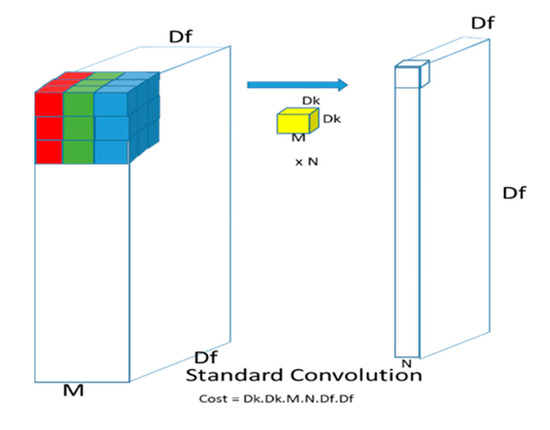
Figure 1.
Standard Convolution.
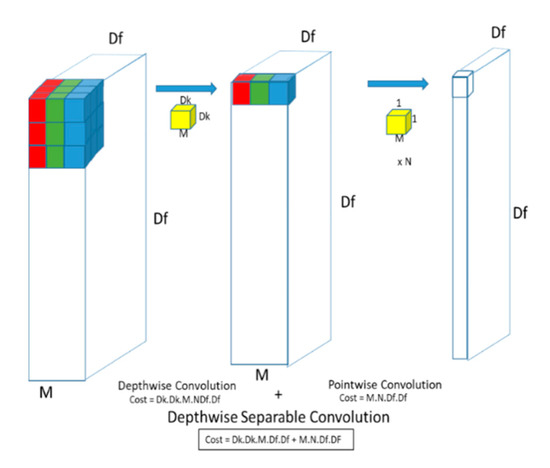
Figure 2.
Depthwise Separable Convolution.
The cost of a standard convolution is given by:
where Df, is the feature map size with M input channels and Dk is the size of the kernel with N output channels. The total cost of a depthwise separable convolution is also given by:
which is the sum of the separable and the pointwise convolutions. Some deep networks [31,32,33] are able to reduce computation to 8 or 9 times as compared to standard convolutions by using 3 × 3 depthwise separable convolutions.
2.2. Batch and Group Normalization
Batch normalization (BN) [36] has been a widely adopted technique over the years and has proven to be very effective in several deep learning tasks. BN makes use of the mean and variance computed within a mini-batch of data to normalize its features during activations. BN standardizes activations to have zero mean and unit variance. The major advantages of BN include allowing faster convergence in fewer training iterations, providing some level of regularization, thereby reducing the generalization error. One major setback of BN, however, is that it requires significantly large batch sizes to work effectively. In applications that require high-resolution images for computations like object detection and image segmentation, BN does not work efficiently due to computational limitations. Group normalization (GN) [37] was therefore introduced as a layer that divides channels into groups and computes the mean and standard deviation over these groups of channels for each example during training (Figure 3). GN does not exploit batch dimensions. This allows it to perform better than BN with smaller mini-batch sizes (usually less than 32).
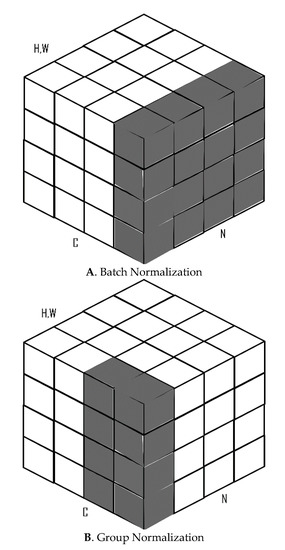
Figure 3.
Difference between BN (A) and GN (B) as in a feature map tensor with the height and width dimensions (H, W), C as the channel axis and N as the batch axis.
2.3. Weight Standardization
Weight standardization (WS) [38] is another method of normalization which is applied to the input weights of the convolution layer, unlike BN and GN, which are implemented on the output layer or the activations (Figure 4). The main aim of WS is to standardize gradients during backpropagation. Experiments have shown that a combination of WS and GN achieves performances that are comparable to BN with large batch sizes. Given a standard convolution layer and assuming its bias term to be 0,
with as the layer weights and the convolution operation. corresponds to the number of output channels and the number of input channels in the kernel region of the output channels, respectively. Instead of optimizing the loss on the original weights, as in BN, WS represents the weights as a function of , and optimizes the loss, on . So that:
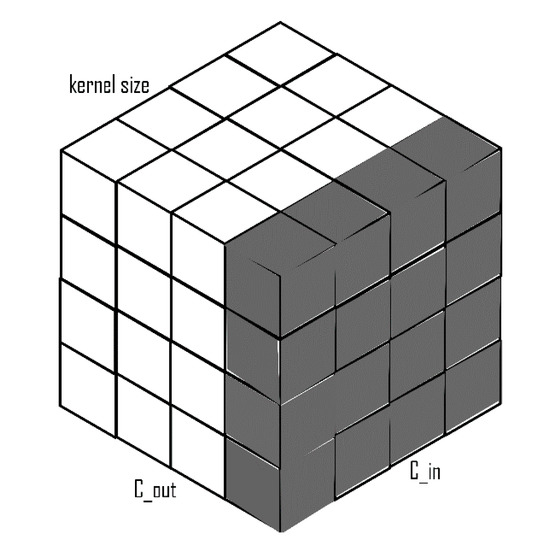
Figure 4.
Weight standardization with C_out as the number of output channels, C_in as the number of input channels x kernel size.
Using stochastic gradient descent (SGD),
where is mean of the weights, is the standard deviation
Therefore:
2.4. Fully Convolutional Networks (FCNs)
The most fundamental idea behind FCNs [10] is that they are only made up of locally connected layers (convolution, pooling, and upsampling) without fully connected or dense layers. This tends to reduce the time required for computation and the number of parameters. It also means that an FCN will work regardless of the input image size. FCNs are typically made up of:
- Downsampling/Contraction/Encoding Path: On this path, the model extracts and interprets the contextual information on the input image.
- Upsampling/Expanding/Decoding Path: The specific localization or construction of segmentation maps from the extracted context in the encoding path.
- Skip Connections/Bottlenecks: Combines information from encoding and decoding paths by summing feature maps
2.5. U-Net
The U-Net architecture is designed as an improvement of the FCN architecture specifically for the segmentation of medical images. The major difference between U-Net and FCN is U-Net is symmetrical and the bottleneck layers that combine information from the encoding and decoding paths do so by concatenating the feature maps whereas they are summed in the FCN architecture. The encoding path of U-Net is made of four blocks each containing two 3 × 3 unpadded convolutions with a ReLu activation layer and a 2 × 2 max-pooling layer. The number of feature channels is also doubled after each downsampling step but the size of feature maps is reduced due to max-pooling. The decoding path contains 2 × 2 upsampling with 3 × 3 standard convolutions. Each convolution is followed by a concatenation of features from corresponding layers in the encoding path. This helps to transfer the localization information that is learned during downsampling from the encoding to the decoding path.
3. Materials and Methods
In this section, we outline the proposed technique, describe the SD-UNet architecture and experiments conducted.
3.1. WS with Depthwise Separable Convolutions
WS has been proposed to be implemented on the weights of standard convolutions. In this study, in order to reduce the number of parameters and required computations in the U-Net model, the standard convolution layers are replaced with depthwise separable layers. WS is now implemented on the weights of the depthwise (3 × 3) convolution layers only so that,
where = weights of the depthwise layer and,
WS achieves a better and smoother loss curve during training [38] and also helps improve model accuracy as shown in Figure 10 and Table 3.
3.2. SD-UNet (Proposed Architecture)
SD-UNet follows a similar architecture as U-Net with a few modifications. Except for the first convolution layer which has a standard convolution, all other convolution layers are made of depthwise separable convolution layers. The encoding is made up of 5 blocks:
- Block1: A standard convolution layer, a ReLu activation function, and a GN layer
- Block2 and Block3: One SD-UNet block and a max-pooling layer. An SD-UNet block is made up of two depthwise separable convolution layers, two activation layers, and one GN layer (Figure 5).
 Figure 5. Components of one SD-UNet Block.
Figure 5. Components of one SD-UNet Block. - Block4: One SD-UNet block, a dropout layer to introduce regularization [39], and a max-pooling layer. All depthwise (3 × 3) convolution layers are weight standardized.
- Block5: A final depthwise separable layer with a dropout layer.
Upsampling is performed on the decoding path with a size of 2 in order to recover the size of the segmentation map. The decoding path of SD-UNet is made of a mixture of depthwise separable convolutions and SD-UNet blocks. It also consists of 5 Blocks:
- Block1: A depthwise separable convolution layer with its features concatenated with the dropout layer from Block4 of the encoding path.
- Blocks 2, 3, 4: An SD-UNet block and a depthwise separable layer concatenated with corresponding blocks from the encoding path
- Block 5: Two SD-UNet blocks and two depthwise separable layers with the last one as the final prediction layer (Figure 6).
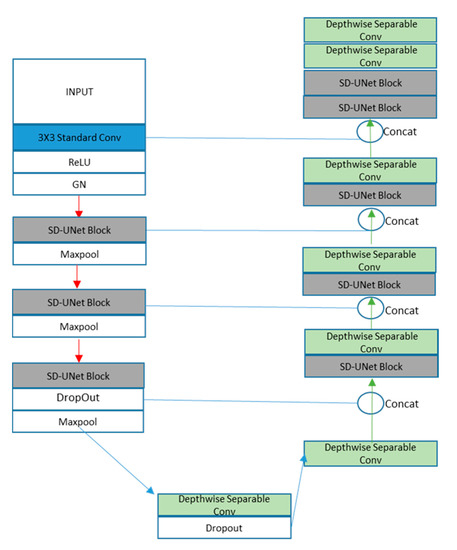 Figure 6. SD-UNet Architecture.
Figure 6. SD-UNet Architecture.
3.3. Setup
The training was based on the Keras with a Tensorflow backend as the deep learning framework on a work station enabled with an NVidia Tesla K40c GPU (12GB memory) and Intel ® Xeon (R) CPU E5-2603 V4 @ 1.70 GHz with 12CPUs. CuDNN 7.0 library was used with the benchmark function enabled to ensure that the fastest algorithms are used.
3.4. Datasets
The datasets used to evaluate the performance of SD-UNet are the ISBI challenge dataset for the segmentation of neuronal structures in electron microscopic (EM) stacks [40,41] and the MSD challenge brain tumor segmentation dataset [42].
3.4.1. ISBI Challenge Dataset
The training data is a set of 30 sections from a serial section transmission electron microscopy (ssTEM) data set of the Drosophila first instar larva ventral nerve cord (VNC). The microcube measures 2 × 2 × 1.5 microns approx., with a resolution of 4 × 4 × 50 nm/pixel. The corresponding binary labels are provided in an in-out fashion, i.e., white for the pixels of segmented objects and black for the rest of the pixels (which correspond mostly to the membranes) (Figure 7).
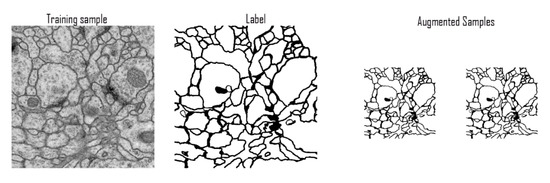
Figure 7.
Samples of ISBI training data.
3.4.2. MSD Challenge Brain Tumor Segmentation (BRATs) Dataset
The Medical Segmentation Decathlon (MDS) Dataset is a challenge that contains 10 large datasets for medical image segmentation. In our experiments, the Brain Tumor Segmentation (BRATs) subset of the dataset is used to evaluate and compare the performance of SD-UNet. This dataset contains a subset of data obtained from BRATs challenge datasets of 2016 and 2017 [43,44,45]. Multiparametric magnetic resonance imaging (MRI) scans from 750 patients diagnosed with either glioblastoma or lower-grade glioma were also added. The MRI sequences include volumes of native (T1) and post-Gadolinium (Figure 8).
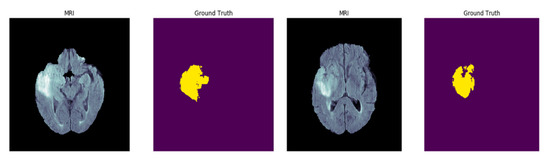
Figure 8.
Sample magnetic resonance imaging (MRI) images and their ground truth labels from the Brain Tumor Segmentation (BRATs) dataset.
(Gd) contrast T1-weighted (T1-Gd), native T2-weighted (T2), and T2 fluid attenuated inversion recovery (T2-FLAIR) as the input channels (modality) collected for segmenting sub-regions of brain tumors which include the edema (swelling around the tumor), enhancing (Gadolinium contrast-enhanced regions), and non-enhancing (not enhanced by Gadolinium contrast) tumors with a background (no tumor) as the output channels (labels) during training.
3.4.3. Data Pre-Processing
The resolution of the images of the ISBI challenge EM stacks is originally 512 × 512 but was resized to 256 × 256 due to computational limitations. Data augmentation techniques were used due to the small number of available training images. A smaller number of images might lead to a concept known as overfitting where a trained model performs very well on training data but performs poorly on new test data. These augmentation techniques included horizontal flip, zoom range, height and width shift range. The number of images of the EM stacks dataset after augmentation increased to 120. The resolution of images in the BRATs dataset (240 × 240) was also reduced to 144 × 144. Center cropping and normalization of data to ensure 0 mean and unit variance was also employed and the original 3D slices converted to 2D slices for training and testing of SD-UNet. In all, there are 75,020 MRI image samples. For training and testing, we split the images into 62,930 training, 4960 for validation, and 7130 for testing.
3.5. Optimization
The Adam [46] optimization algorithm was used to train the network with a learning rate of 0.0001 and 0.00001 on the EM stacks and BRATs data respectively. The loss used in training on the EM stacks dataset was based on binary cross-entropy loss. On the BRATs dataset, the loss was a weighted sum of negative dice loss and binary cross-entropy loss algorithms.
3.6. Performance Metrics
In this section, the major performance metrics used in evaluating the performance of SD-UNet on the datasets are explained in detail.
3.6.1. Accuracy (AC)
Accuracy measures the percentage of correct predictions in any given image and is given by:
where TP = number of true positives, TN = number of true negatives, FP = number of false positives, FN = number of false negatives
3.6.2. Intersection over Union (IOU)
The IOU or the Jaccard Index measures the percentage of overlap between the ground truth labels and the predicted outputs and is given by:
where GT = ground truth labels, PO = predicted outputs.
3.6.3. Sorensen-Dice Co-Efficient (Dice Co-Eff)
Dice Co-Eff Measures the Percentage of Repeated Overlaps between Ground Truth and Predicted Images and Is Different from Iou Which Takes Account of True Positives Only Once (Equation (10)). It is given by:
3.6.4. Maximal Foreground-Restricted Rand Score (VRand)
VRand is defined with the intuition that given a predicted segmentation S and a ground truth T, two randomly chosen pixels belong to the same segment in S and the same segment in T with a certain probability [40] and is given by a weighted mean. The weighted mean is a combination of the Rand split score, which is the probability that two randomly chosen pixels are part of the same segment in S, given that they are of the same segment in T and the merge score, which is the probability that two randomly chosen pixels are part of the same segment in T, given that they belong to the same segment in S.
3.6.5. Maximal Foreground-Restricted Information Theoretic Score (VInfo)
VInfo is an alternative of VRand that measures similarity between predicted segmentation S and ground truth T. It is also the weighted mean of the information-theoretic split score and the information-theoretic mean score. It should be noted that VRand and VInfo are both the official metrics used by the ISBI challenge organizers while Dice Co-Eff is the metric used by the MSD challenge organizers with all scripts publicly available on their websites.
3.6.6. Floating Point Operations Per Second (FLOPs)
FLOPs are simply a measure of the number of multiplications and additions of floating point numbers required to be performed by a computing device’s processor. Convolutional neural networks require such floating point operations and FLOPs are the standard metric used to measure them.
4. Results
Experiments measuring the computational requirements of SD-UNet, its inference speed, and segmentation performance on the mentioned datasets are conducted in this section.
4.1. Ablation Study
An extensive ablation study is performed to evaluate the performance of the proposed model and to support the final design decisions made in this study. Four different modifications are made to the architecture design and they include:
- U-Net (GN = 32)—Original U-Net architecture with GN only with 32 groups.
- U-Net (depthwise + BN)—U-Net architecture with depthwise separable layers replacing standard convolution layers and BN layers only
- U-Net (depthwise + GN)—U-Net architecture with depthwise separable layers replacing standard convolution layers and GN layers only
- SD-UNet (depthwise + BN + WS)—Proposed SD-UNet based on BN, WS, and depthwise separable convolutions
The performance of these modifications is reported alongside the original U-Net architecture, the proposed SD-UNet based on GN in Table 1, Table 2 and Table 3.

Table 1.
Computational comparison of SD-UNet and other models.

Table 2.
Comparison of results on the ISBI challenge dataset.

Table 3.
Performance comparison between U-Net and SD-UNet.
4.2. Computational Results
SD-UNet is measured for its computational requirements in FLOPs, storage requirements, a number of parameters, and inference speed and compared with the original U-Net model. In terms of computational complexity, SD-UNet requires approximately 8× fewer FLOPs compared to U-Net as does all other modifications that have depthwise separable convolution layers. Additionally, SD-UNet is approximately 81 milliseconds faster than U-Net in prediction speed for an input dimension of 256 × 256 × 1 on a single NVidia Tesla K40C GPU device. SD-UNet is also 23× smaller. U-Net (depthwise + GN=32) achieves the fastest inference on a single test image with 87 milliseconds but is still 3x the size of SD-UNet (Table 1).
4.3. Results on ISBI Challenge Dataset
SD-UNet is seen to achieve comparable performance in terms of accuracy, mean IOU and Dice co-efficient, while being more computationally efficient than the original U-Net model. U-Net (GN = 32) achieves higher than all the reported models. However, it obtains the slowest prediction time and is 19× bigger in size than SD-UNet. Moreover, the difference in mean IOU and dice co-efficient is quite negligible considering tradeoffs against computational demands, storage requirements, and inference speed. Segmentation results were submitted to the ISBI challenge website and SD-UNet achieved maximal foreground-restricted Rand score after thinning: 0.914200251 and maximal foreground-restricted information theoretic score after thinning: 0.967836631 and has since been published on the available leaders’ board on the challenge website (available online: http://brainiac2.mit.edu/isbi_challenge/, accessed on 16 February 2020). A visual sample of segmentation results is shown in Figure 9.
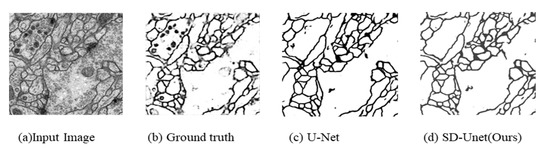
Figure 9.
Sample Segmentation on electron microscopy dataset. (a) Input image; (b) Ground truth; (c) U-Net; (d) SD-Unet (Ours).
4.4. Results on BRATs Dataset
U-Net and SD-UNet are trained from scratch for only four epochs and their mean dice scores on validation data compared alongside their inference speed. The choice of a smaller number of epochs is due to the ability of the Adam optimization algorithm reaching a minimum quickly and each epoch runs 1000 iterations over the dataset. SD-UNet achieves a better loss and mean dice co-efficient compared to the U-Net model. Its inference speed is also faster on a single Tesla K40C gpu device. The training curve in Figure 10 also shows that WS with GN also significantly improves the training loss and obtains a smoother curve. Pixel wise, accuracy has been accepted as a general metric but is not necessarily the best form of performance evaluation mostly due to class imbalance. This means that accuracy could be very high or very low depending on the scale of pixel imbalance that exists in the dataset and, therefore, is not necessarily always correlated with the Dice coefficient which measures the difference in the overlap between each pixel in an image and its prediction. The Dice coefficient is not dependent on the balance of data and is more accurate compared to pixel accuracy. Sample tumor segmentation visualizations are shown in Figure 11 and it is interesting to note that while SD-UNet achieves comparable performance with U-Net on large tumor segmentations, it significantly outperforms U-Net on smaller tumor segmentations.
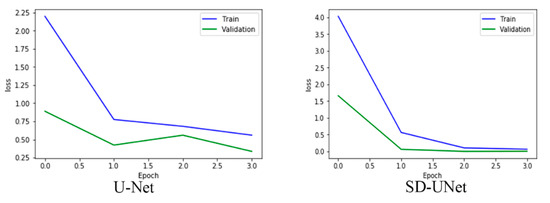
Figure 10.
SD-UNet shows a faster convergence and improved loss during training.

Figure 11.
Sample Segmentation results on sample images from our test split. SD-UNet significantly performs better than U-Net on smaller tumors. The green-colored regions are simply a function of the plots that specify edges and show regions around the segmentation that are not part of the background.
5. Discussion and Conclusions
Biomedical image segmentation is an important preliminary step in the identification of tissues in image scans to aid in illness diagnosis, treatment, and general analysis. Early diagnosis is necessary to help in preventing complications that may arise due to late detections. However, with the increasing availability of large biomedical data, the workload on neurologists, radiologists, and other experts in the field has also increased. To help provide easier, accurate and timely detections, several deep learning methods have been proposed and most have chalked great successes in these tasks. The U-Net architecture is one such model that is widely accepted among researchers for biomedical image segmentation tasks.
In recent times, mobile handheld devices have been enabled with processing functionalities that were only imaginable for large computers in the past. However, deep learning applications require even higher computations. This makes it very challenging to deploy deep learning applications on handheld or embedded devices. The U-Net architecture, for instance, requires over 62M FLOPs and over 370 megabytes (Mb) of storage space which are really high demands. Moreover, not much attention has been paid to applying deep learning methods on resource-constrained devices in areas of biomedical imaging.
In this study, Stripped-Down UNet (SD-UNet), has been presented for the segmentation of biomedical data on devices with limited computational budgets. The SD-UNet architecture makes use of depthwise separable convolutions (Figure 6). However, the disadvantage of depthwise convolutions compared to standard convolutions is lower accuracy performance. It is highlighted that the problem of expected performance degradation is resolved by introducing the weight standardization algorithm with the group normalization method.
Our findings show that the proposed architecture is only 15.8 Mb in size which is 23× smaller than the U-Net and requires 8× less computational complexity (less than 8M FLOPs) (Table 1) while maintaining decent accuracy results. This means that SD-UNet can be deployed on embedded devices and any handheld device with a low computational ability such as mobile phones. Based on the results from the experiments done on the benchmark dataset of the ISBI challenge for segmentation of neuronal structures in electron microscopic (EM) stacks and the MSD challenge brain tumor segmentation (BRATs) dataset, it is seen that SD-UNet performs impressively on biomedical images. Test results on MRI scans on the BRATs dataset set show that SD-UNet achieves an average dice score of 82.75, which is in agreement with the ground truth data labeled by neuroradiologists with a dice score between 75.0 and 85.0 [45]. Additionally, SD-UNet is shown to have faster inference speed on test data and is conducive for situations where quick and accurate segmentation results are required.
Furthermore, in the absence of experts for different unforeseen reasons, being able to deploy SD-UNet on a device such as a mobile phone could help anybody in obtaining segmentation results given the availability of images. SD-UNet’s robustness is also demonstrated during test results to perform significantly better than the original UNet architecture on smaller brain tumor segmentations and can be extended to other tasks such as lung cancer detection in CT scans, skin lesions detection, breast cancer detection, and many other similar biomedical applications.
There are a few cases, however, where dice scores on test images fall under 75.0 (Figure 12). These may be due to factors relating to data preprocessing and hyperparameter tuning. In future work, the authors intend to continue research into designing deep architectures that require even fewer computations and target work on embedded devices as well while achieving higher test results. SD-UNet will also be applied to different kinds of biomedical data for further testing of its performance.
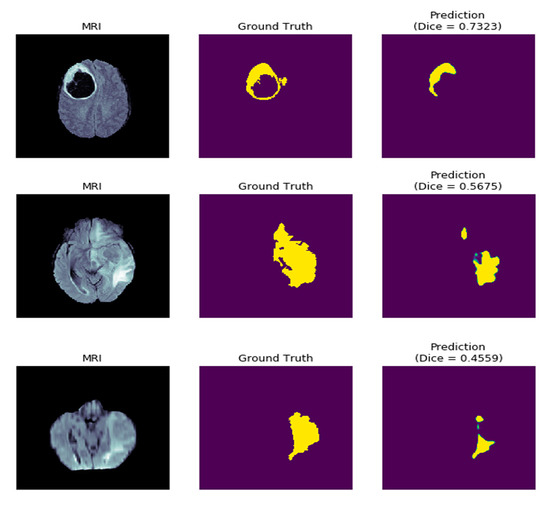
Figure 12.
Sample SD-UNet poorly segmented tumors in the test dataset.
Author Contributions
Conceptualization, P.K.G.; methodology, P.K.G and E.A.A.; validation, Y.L., T.Z., and Z.L.; formal analysis, P.K.G. and Y.L.; investigation, E.A.A., P.T.Y. and F.E.; resources, Y.L.; data curation, P.K.G. and F.E; writing—original draft preparation, P.K.G. and E.A.A; writing—review and editing, T.Z, Z.L., P.T.Y., and F.E.; visualization, P.K.G. and E.A.A.; supervision, Y.L., T.Z., and Z.L.; project administration, Y.L.; funding acquisition, Y.L. All authors have read and agreed to the published version of the manuscript. All authors have contributed substantially to this study.
Funding
This work was supported by the National Natural Science Foundation of China (61876010, 61806013, 61906005); Chaoyang Postdoctoral Foundation of Beijing (2019zz-35).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Wismüller, A.; Vietze, F.; Behrends, J.; Meyer-Baese, A.; Reiser, M.; Ritter, H. Fully automated biomedical image segmentation by self-organized model adaptation. Neural Netw. 2004, 17, 1327–1344. [Google Scholar] [CrossRef]
- Chen, C.; Ozolek, J.A.; Wang, W.; Rohde, G. A General System for Automatic Biomedical Image Segmentation Using Intensity Neighborhoods. Int. J. Biomed. Imaging 2011, 2011, 1–12. [Google Scholar] [CrossRef]
- Aganj, I.; Harisinghani, M.G.; Weissleder, R.; Fischl, B. Unsupervised Medical Image Segmentation Based on the Local Center of Mass. Sci. Rep. 2018, 8, 13012. [Google Scholar] [CrossRef]
- Hesamian, M.H.; Jia, W.; He, X.; Kennedy, P. Deep Learning Techniques for Medical Image Segmentation: Achievements and Challenges. J. Digit. Imaging 2019, 32, 582–596. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Adv. Neural Inf. Process. 2012, 1097–11059. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556, 1–14. [Google Scholar]
- Davis, J.W.; Sharma, V. Simultaneous detection and segmentation of pedestrians using top-down and bottom-up processing. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition Processing, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. Form. Asp. Compon. Softw. 2015, 9351, 234–241. [Google Scholar]
- Shelhamer, E.; Long, J.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 640–651. [Google Scholar] [CrossRef]
- Badrinarayanan, V.; Badrinarayanan, V.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Hu, R.; Dollar, P.; He, K.; Darrell, T.; Girshick, R. Learning to Segment Every Thing 2017. Available online: http://openaccess.thecvf.com/content_cvpr_2018/papers/Hu_Learning_to_Segment_CVPR_2018_paper.pdf (accessed on 18 February 2020).
- Simonyan, K.; Zisserman, A. Two-Stream Convolutional Networks for Action Recognition in Videos. Available online: http://papers.nips.cc/paper/5353-two-stream-convolutional (accessed on 18 February 2020).
- Ehsani, K.; Bagherinezhad, H.; Redmon, J.; Mottaghi, R.; Farhadi, A. Who Let the Dogs Out? Modeling Dog Behavior from Visual Data. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, AL, USA, 18–22 June 2018; pp. 4051–4060. [Google Scholar]
- Iqbal, U.; Milan, A.; Gall, J. PoseTrack: Joint Multi-Person Pose Estimation and Tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 2011–2020. [Google Scholar]
- Kehl, W.; Tombari, F.; Ilic, S.; Navab, N. Real-Time 3D Model Tracking in Color and Depth on a Single CPU Core. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), City of Honolulu, HI, USA, 21–26 July 2017; pp. 465–473. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J.; Malik, J. Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 24–27 June 2014; pp. 580–587. [Google Scholar]
- Li, J.; Wu, Y.; Zhao, J.; Guan, L.; Ye, C.; Yang, T. Pedestrian detection with dilated convolution, region proposal network and boosted decision trees. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 4052–4057. [Google Scholar]
- Sun, W.; Wang, R. Fully Convolutional Networks for Semantic Segmentation of Very High Resolution Remotely Sensed Images Combined With DSM. IEEE Geosci. Remote. Sens. Lett. 2018, 15, 474–478. [Google Scholar] [CrossRef]
- Roth, H.R.; Shen, C.; Oda, H.; Oda, M.; Hayashi, Y.; Misawa, K.; Mori, K. Deep learning and its application to medical image segmentation. Med Imaging Technol. 2018, 36, 63–71. [Google Scholar]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; Van Der Laak, J.A.; Van Ginneken, B.; Sánchez, C.I. A survey on deep learning in medical image analysis. Med Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef]
- Yao, W.; Zeng, Z.; Lian, C.; Tang, H. Pixel-wise regression using U-Net and its application on pansharpening. Neurocomputing 2018, 312, 364–371. [Google Scholar] [CrossRef]
- Iglovikov, V.; Shvets, A. TernausNet: U-Net with VGG11 Encoder Pre-Trained on ImageNet for Image Segmentation 2018. arXiv 2018, arXiv:1801.05746. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Oktay, O.; Schlemper, J.; Le Folgoc, L.; Lee, M.C.H.; Heinrich, M.; Misawa, K.; Mori, K.; McDonagh, S.; Hammerla, N.Y.; Kainz, B.; et al. Attention U-Net: Learning Where to Look for the Pancreas 2018. Available online: https://arxiv.org/abs/1804.03999 (accessed on 18 February 2020).
- Denil, M.; Shakibi, B.; Dinh, L.; Ranzato, M.; de Freitas, N. Predicting Parameters in Deep Learning. Available online: https://papers.nips.cc/paper/5025-predicting-parameters-in-deep-learning.pdf (accessed on 18 February 2020).
- LeCun, Y.; Denker, J.S.; Solla, S.A. Optimal Brain Damage. Adv. Neural Inf. Process. Syst. 1990, 2, 598–605. [Google Scholar]
- Hassibi, B.; Stork, D.G. Second Order Derivaties for Network Prunning: Optimal Brain Surgeon. Available online: https://authors.library.caltech.edu/54983/3/647-second-order-derivatives-for-network-pruning-optimal-brain-surgeon(1).pdf (accessed on 15 February 2020).
- Alvarez, J.M.; Salzmann, M. Compression-aware Training of Deep Networks 2017. Available online: http://papers.nips.cc/paper/6687-compression-aware-training-of-deep-networks (accessed on 17 February 2020).
- Han, S.; Mao, H.; Dally, W.J. Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization, and Huffman Coding. Available online: https://arxiv.org/abs/1510.00149 (accessed on 17 February 2020).
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. Available online: https://arxiv.org/abs/1704.04861 (accessed on 18 February 2020).
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition 2018, Salt Lake City, AL, USA, 18–22 June 2018; pp. 6848–6856. [Google Scholar]
- Qin, Z.; Zhang, Z.; Chen, X.; Peng, Y. FD-MobileNet: Improved MobileNet with a Fast Downsampling Strategy. 2018. Available online: https://ieeexplore.ieee.org/abstract/document/8451355 (accessed on 17 February 2020).
- Sifre, L. Rigid-Motion Scattering for Image Classification. Ph.D. Thesis, Ecole Polytechnique, Palaiseau, France, 2014. CMAP Rigid-Motion Scattering For Image Classification. Available online: https://www.di.ens.fr/data/publications/papers/phd_sifre.pdf (accessed on 17 February 2020).
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26July 2017; pp. 1800–1807. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. Available online: https://arxiv.org/abs/1502.03167 (accessed on 17 February 2020).
- Wu, Y.; He, K. Group Normalization. Formal Asp. Compon. Softw. 2018, 11217 LNCS, 3–19. [Google Scholar]
- Qiao, S.; Wang, H.; Liu, C.; Shen, W.; Yuille, A. Weight Standardization. Available online: https://arxiv.org/abs/1903.10520 (accessed on 18 February 2020).
- Srivastava, N.; Hinton, A.; Sutskever, K.I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2017, 15, 1929–1958. [Google Scholar]
- Arganda-Carreras, I.; Turaga, S.C.; Berger, D.R.; Cireşan, D.; Giusti, A.; Gambardella, L.M.; Schmidhuber, J.; Laptev, D.; Dwivedi, S.; Buhmann, J.M.; et al. Crowdsourcing the creation of image segmentation algorithms for connectomics. Front. Neuroanat. 2015, 9, 898. [Google Scholar] [CrossRef]
- Cardona, A.; Saalfeld, S.; Preibisch, S.; Schmid, B.; Cheng, A.; Pulokas, J.; Tomancak, P.; Hartenstein, V. An integrated micro- and macroarchitectural analysis of the Drosophila brain by computer-assisted serial section electron microscopy. PLoS Boil. 2010, 8, e1000502. [Google Scholar] [CrossRef] [PubMed]
- Simpson, A.; Antonelli, M.; Bakas, S.; Bilello, M.; Farahani, K.; Van Ginneken, B.; Kopp-Schneider, A.; Landman, B.A.; Litjens, G.; Menze, B.; et al. A Large Annotated Medical Image Dataset for the Development and Evaluation of Segmentation Algorithms. Available online: https://arxiv.org/abs/1902.09063 (accessed on 18 February 2020).
- Bakas, S.; Reyes, M.; Jakab, A.; Bauer, S.; Rempfler, M.; Cromo, A.; Shinohara, R.T.; Berger, C.; Ha, S.M.; Rozycki, M.; et al. Identifying the Best Machine Learning Algorithms for Brain Tumor Segmentation, Progression Assessment, and Overall Survival Prediction in the BRATS Challenge. Available online: https://arxiv.org/abs/1811.02629 (accessed on 17 February 2020).
- Bakas, S.; Akbari, H.; Sotiras, A.; Bilello, M.; Rozycki, M.; Kirby, J.; Freymann, J.B.; Farahani, K.; Davatzikos, C. Advancing The Cancer Genome Atlas glioma MRI collections with expert segmentation labels and radiomic features. Sci. Data 2017, 4, 170117. [Google Scholar] [CrossRef]
- Menze, B.H.; Jakab, A.; Bauer, S.; Kalpathy-Cramer, J.; Farahani, K.; Kirby, J.; Burren, Y.; Porz, N.; Slotboom, J.; Wiest, R.; et al. The multimodal brain tumor image segmentation benchmark (BRATS). IEEE Trans. Med Imaging 2015, 34, 1993–2024. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. Available online: https://arxiv.org/abs/1412.6980 (accessed on 17 February 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
