Formamide Adsorption at the Amorphous Silica Surface: A Combined Experimental and Computational Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Approach
2.2. Computational Approach
3. Results
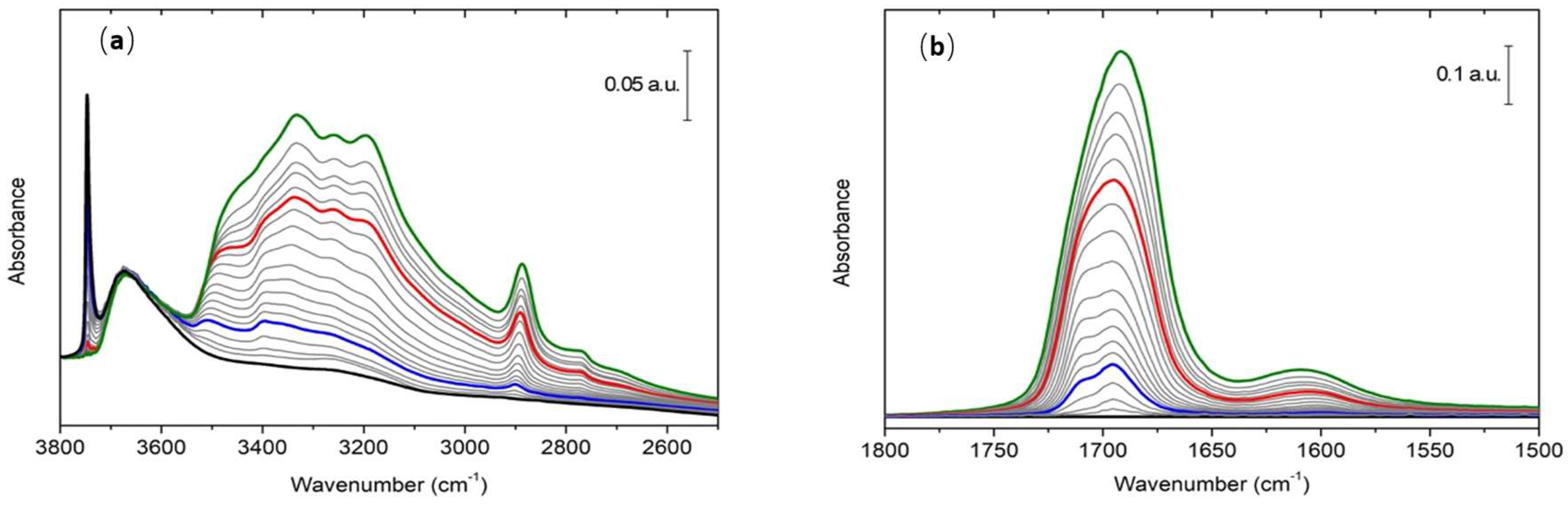
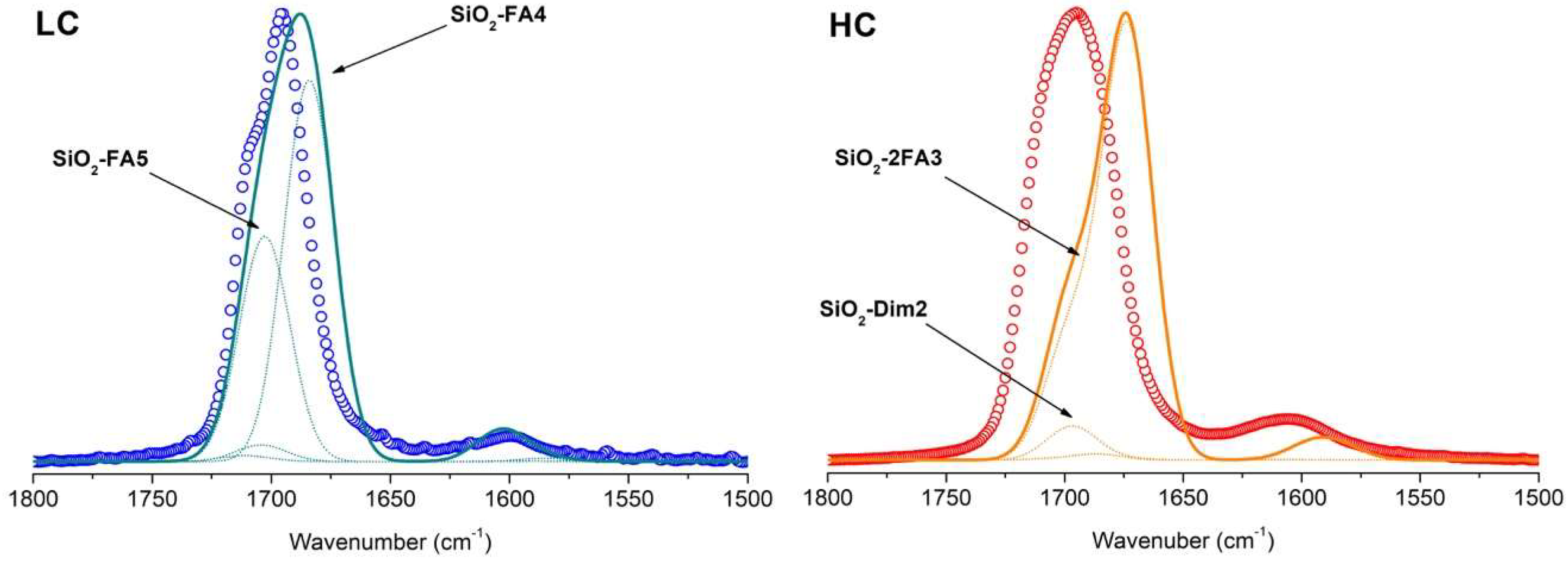
3.1. FTIR of Formamide Adsorbed on A50
3.2. Simulation of Formamide-A50 Adducts
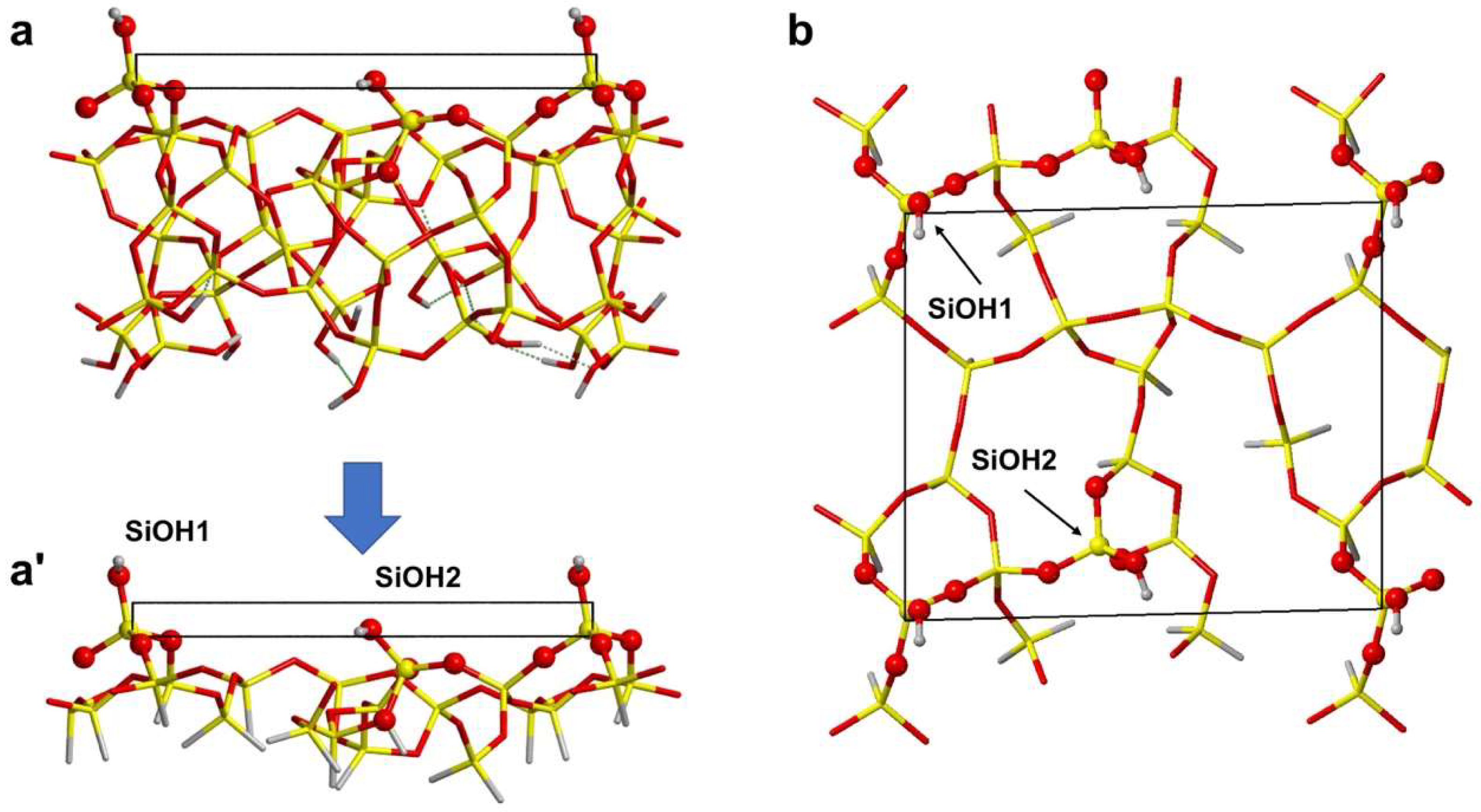
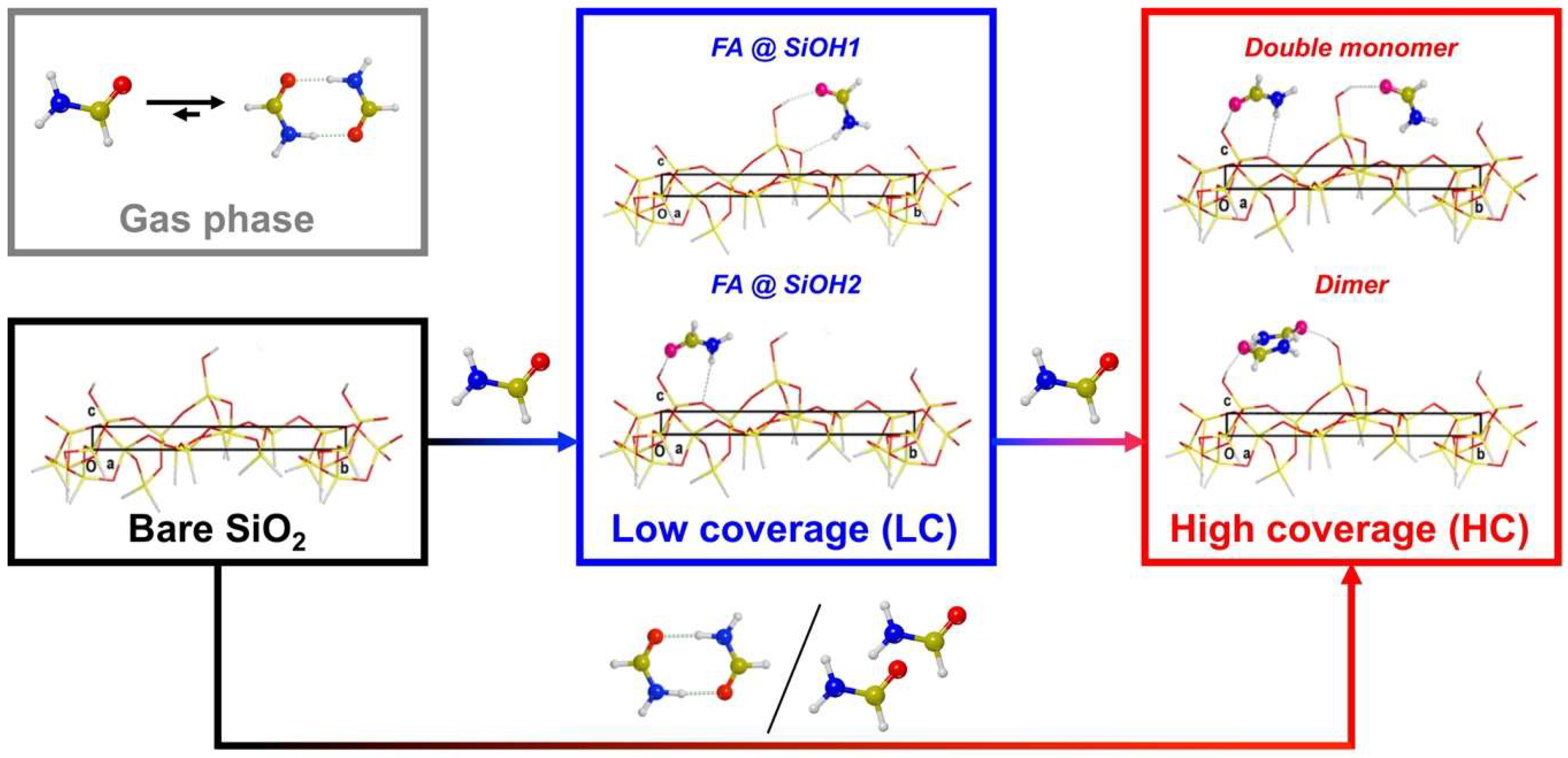
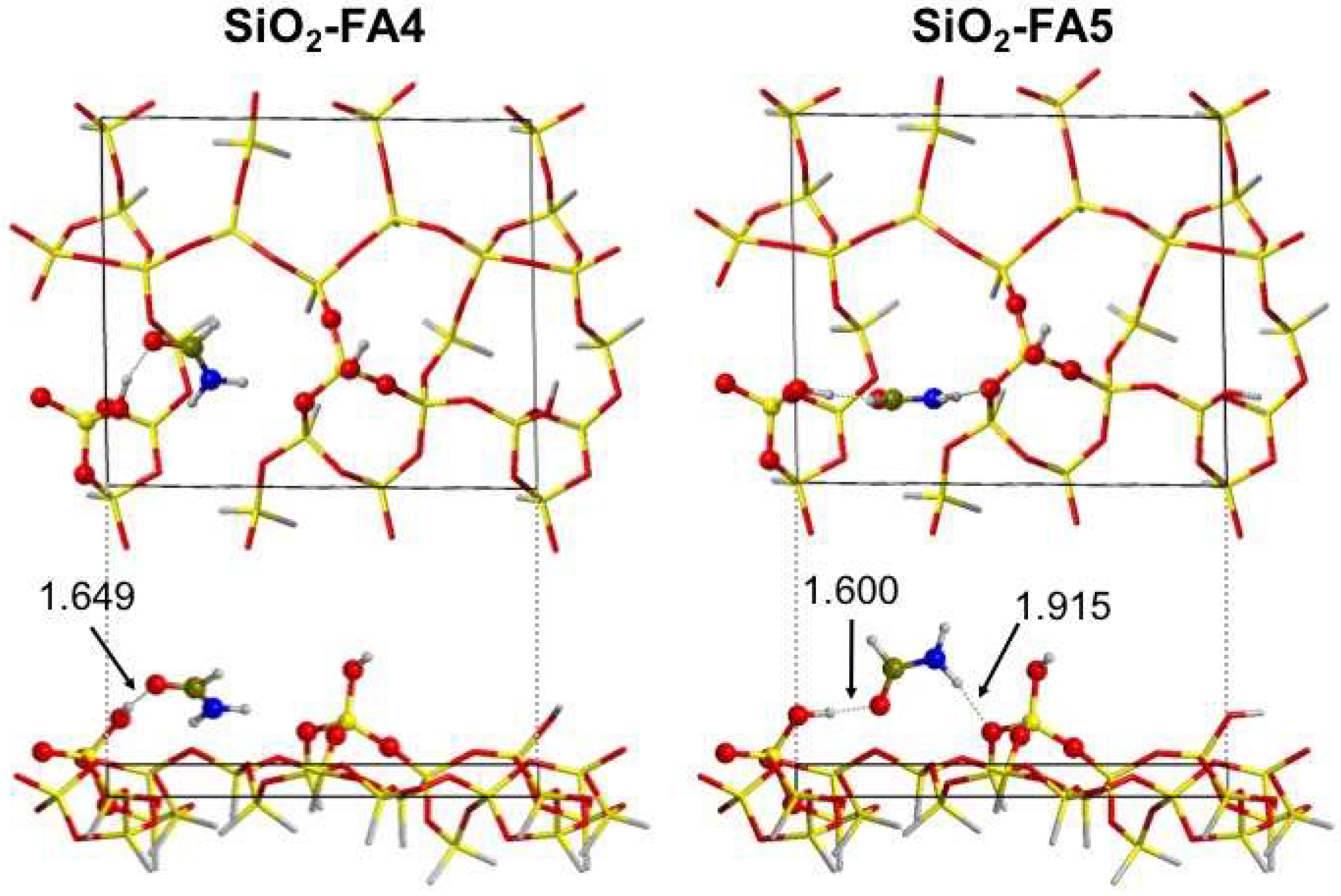
3.2.1. Low Coverage Models
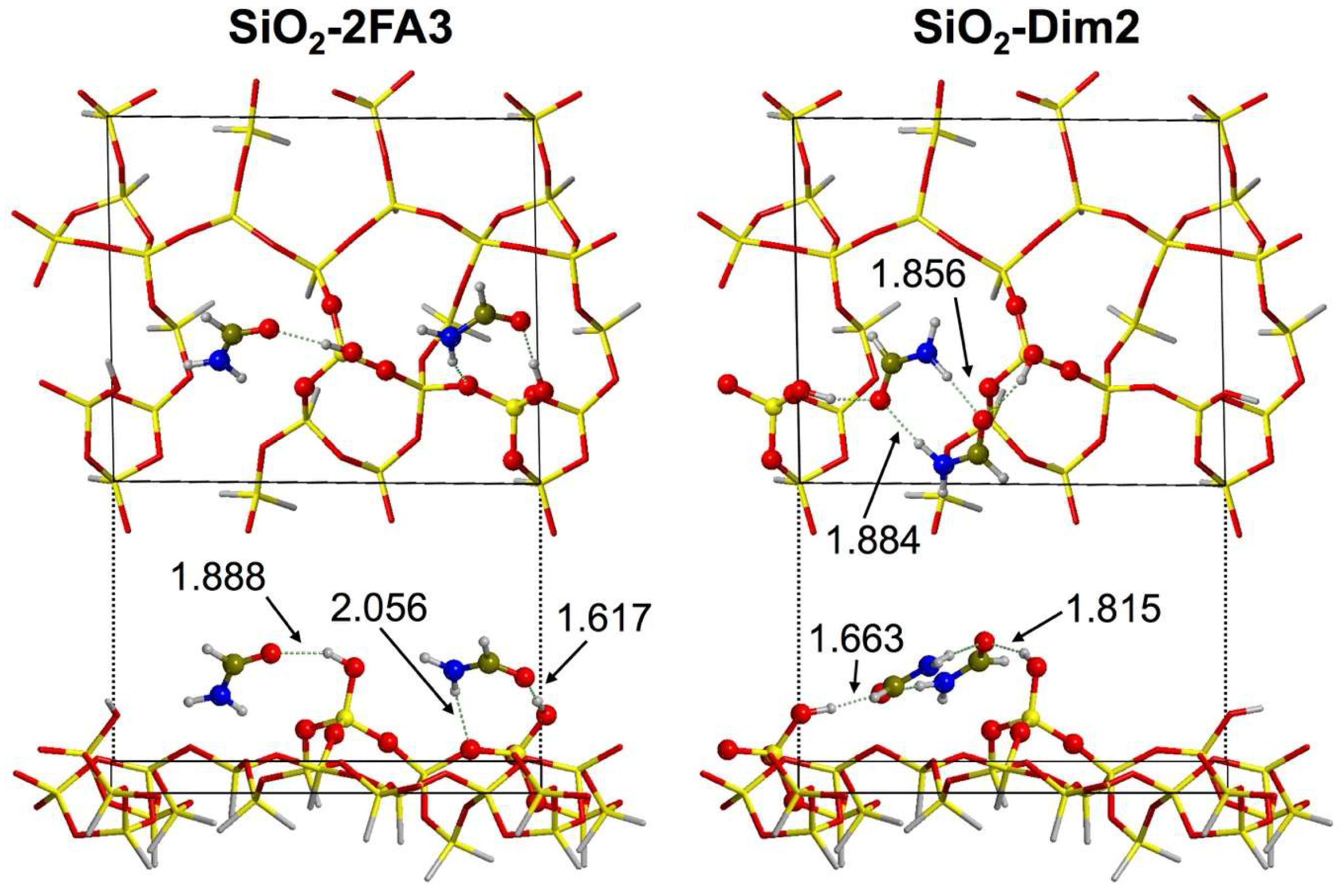
3.2.2. High-Coverage Models
3.3. Simulation of FTIR Spectra of Formamide-A50 Adducts: Comparison with Experimental Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Whitesides, G.M. Reinventing chemistry. Angew. Chem. Int. Ed. 2015, 54, 3196–3209. [Google Scholar] [CrossRef] [PubMed]
- Kahane, C.; Ceccarelli, C.; Faure, A.; Caux, E. Detection of formamide, the simplest but crucial amide, in a solar-type protostar. Astrophys. J. 2013, 763, L38. [Google Scholar] [CrossRef]
- Saladino, R.; Crestini, C.; Neri, V.; Brucato, J.R.; Colangeli, L.; Ciciriello, F.; Di Mauro, E.; Costanzo, G. Synthesis and Degradation of Nucleic Acid Components by Formamide and Cosmic Dust Analogues. ChemBioChem 2005, 6, 1368–1374. [Google Scholar] [CrossRef] [PubMed]
- Aladino, R.; Botta, G.; Bizzarri, B.M.; Di Mauro, E.; Garcia-Ruiz, J.M. A Global Scale Scenario for Prebiotic Chemistry: Silica-Based Self-Assembled Mineral Structures and Formamide. Biochemistry 2016, 55, 2806–2811. [Google Scholar] [CrossRef] [PubMed]
- Saladino, R.; Crestini, C.; Costanzo, G.; DiMauro, E. Advances in the prebiotic synthesis of nucleic acids bases: Implications for the origin of life. Curr. Org. Chem. 2004, 8, 1425–1443. [Google Scholar] [CrossRef]
- Rotelli, L.; Trigo-Rodríguez, J.M.; Moyano-Cambero, C.E.; Carota, E.; Botta, L.; Di Mauro, E.; Saladino, R. The key role of meteorites in the formation of relevant prebiotic molecules in a formamide/water environment. Sci. Rep. 2016, 6, 38888. [Google Scholar] [CrossRef] [PubMed]
- Senanayake, S.D.; Idriss, H. Photocatalysis and the origin of life: Synthesis of nucleoside bases from formamide on TiO2(001) single surfaces. Proc. Natl. Acad. Sci. USA 2006, 103, 1194–1198. [Google Scholar] [CrossRef] [PubMed]
- Saladino, R.; Crestini, C.; Neri, V.; Ciciriello, F.; Costanzo, G.; Di Mauro, E. Origin of informational polymers: The concurrent roles of formamide and phosphates. ChemBioChem 2006, 7, 1707–1714. [Google Scholar] [CrossRef] [PubMed]
- Saladino, R.; Crestini, C.; Pino, S.; Costanzo, G.; Di Mauro, E. Formamide and the origin of life. Phys. Life Rev. 2012, 9, 84–104. [Google Scholar] [CrossRef] [PubMed]
- Saladino, R.; Crestini, C.; Costanzo, G.; Negri, R.; Di Mauro, E. A possible prebiotic synthesis of purine, adenine, cytosine, and 4(3H)-pyrimidinone from formamide: Implications for the origin of life. Bioorg. Med. Chem. 2001, 9, 1249–1253. [Google Scholar] [CrossRef]
- Muir, J.M.R.; Idriss, H. Formamide reactions on rutile TiO2(011) surface. Surf. Sci. 2009, 603, 2986–2990. [Google Scholar] [CrossRef]
- Ferus, M.; Nesvorný, D.; Šponer, J.; Kubelík, P.; Michal, R.; Shestivská, V.; Sponer, J.E.; Civiš, S. High-energy chemistry of formamide: A unified mechanism of nucleobase formation. Proc. Natl. Acad. Sci. USA 2015, 112, 657–662. [Google Scholar]
- Rimola, A.; Costa, D.; Sodupe, M.; Lambert, J.F.; Ugliengo, P. Silica surface features and their role in the adsorption of biomolecules: Computational modeling and experiments. Chem. Rev. 2013, 113, 4216–4313. [Google Scholar] [CrossRef] [PubMed]
- Rimola, A.; Fabbiani, M.; Sodupe, M.; Ugliengo, P.; Martra, G. How Does Silica Catalyze the Amide Bond Formation under Dry Conditions? Role of Specific Surface Silanol Pairs. ACS Catal. 2018, 8, 4558–4568. [Google Scholar] [CrossRef]
- Lambert, J.F. Adsorption and polymerization of amino acids on mineral surfaces: A review. Orig. Life Evol. Biosph. 2008, 38, 211–242. [Google Scholar] [CrossRef] [PubMed]
- Lambert, J.-F.; Jaber, M.; Georgelin, T.; Stievano, L. A comparative study of the catalysis of peptide bond formation by oxide surfaces. Phys. Chem. Chem. Phys. 2013, 15, 13371–13380. [Google Scholar] [CrossRef] [PubMed]
- Martra, G.; Deiana, C.; Sakhno, Y.; Barberis, I.; Fabbiani, M.; Pazzi, M.; Vincenti, M. The formation and self-assembly of long prebiotic oligomers produced by the condensation of unactivated amino acids on oxide surfaces. Angew. Chem. Int. Ed. 2014, 53, 4671–4674. [Google Scholar] [CrossRef] [PubMed]
- Corno, M.; Delle Piane, M.; Monti, S.; Moreno-Couranjou, M.; Choquet, P.; Ugliengo, P. Computational Study of Acidic and Basic Functionalized Crystalline Silica Surfaces as a Model for Biomaterial Interfaces. Langmuir 2015, 31, 6321–6331. [Google Scholar] [CrossRef] [PubMed]
- Musso, F.; Sodupe, M.; Corno, M.; Ugliengo, P. H-bond features of fully hydroxylated surfaces of crystalline silica polymorphs: A periodic B3LYP study. J. Phys. Chem. C 2009, 113, 17876–17884. [Google Scholar] [CrossRef]
- Garofalini, S.H. Molecular dynamics computer simulations of silica surface structure and adsorption of water molecules. J. Non-Cryst. Solids 1990, 120, 1–12. [Google Scholar] [CrossRef]
- Tosoni, S.; Civalleri, B.; Pascale, F.; Ugliengo, P. Hydroxylated crystalline edingtonite silica faces as models for the amorphous silica surface. J. Phys. Conf. Ser. 2008, 117. [Google Scholar] [CrossRef]
- Tielens, F.; Gervais, C.; Lambert, J.F.; Mauri, F.; Costa, D. Ab initio study of the hydroxylated surface of amorphous silica: A representative model. Chem. Mater. 2008, 20, 3336–3344. [Google Scholar] [CrossRef]
- Ugliengo, P.; Sodupe, M.; Musso, F.; Bush, I.J.; Orlando, R.; Dovesi, R. Realistic models of hydroxylated amorphous silica surfaces and MCM-41 mesoporous material simulated by large-scale periodic B3LYP calculations. Adv. Mater. 2008, 20, 4579–4583. [Google Scholar] [CrossRef]
- Delle Piane, M.; Corno, M.; Ugliengo, P. Does dispersion dominate over H-bonds in drug-surface interactions? The case of silica-based materials as excipients and drug-delivery agents. J. Chem. Theory Comput. 2013, 9, 2404–2415. [Google Scholar] [CrossRef] [PubMed]
- Mardyukov, A.; Sánchez-Garcia, E.; Rodziewicz, P.; Doltsinis, N.L.; Sander, W. Formamide dimers: A computational and matrix isolation study. J. Phys. Chem. A 2007, 111, 10552–10561. [Google Scholar] [CrossRef] [PubMed]
- Alessandrini, S.; Puzzarini, C. Structural and Energetic Characterization of Prebiotic Molecules: The Case Study of Formamide and Its Dimer. J. Phys. Chem. A 2016, 120, 5257–5263. [Google Scholar] [CrossRef] [PubMed]
- Erba, A.; Baima, J.; Bush, I.; Orlando, R.; Dovesi, R. Large-Scale Condensed Matter DFT Simulations: Performance and Capabilities of the CRYSTAL Code. J. Chem. Theory Comput. 2017, 13, 5019–5027. [Google Scholar] [CrossRef] [PubMed]
- Dovesi, R.; Erba, A.; Orlando, R.; Zicovich-Wilson, C.M.; Civalleri, B.; Maschio, L.; Rérat, M.; Casassa, S.; Baima, J.; Salustro, S. Quantum-mechanical condensed matter simulations with CRYSTAL. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1360. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Nada, R.; Nicholas, J.B.; McCarthy, M.I.; Hess, A.C. Basis sets for ab initio periodic Hartree-Fock studies of zeolite/adsorbate interactions: He, Ne, and Ar in silica sodalite. Int. J. Quantum Chem. 1996, 60, 809–820. [Google Scholar] [CrossRef]
- Schäfer, A.; Huber, C.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
- Antony, J.; Grimme, S. Density functional theory including dispersion corrections for intermolecular interactions in a large benchmark set of biologically relevant molecules. Phys. Chem. Chem. Phys. 2006, 8, 5287–5293. [Google Scholar] [CrossRef] [PubMed]
- Dovesi, R.; Saunders, V.R.; Roetti, C.; Orlando, R.; Zicovich-Wilson, C.M.; Pascale, F.; Civalleri, B.; Doll, K. CRYSTAL17 User’s Manual. 2017. Available online: http://www.crystal.unito.it/Manuals/crystal17.pdf (accessed on 20 September 2018).
- Lendvay, G.; Mayer, I. Some difficulties in computing BSSE-corrected potential surfaces of chemical reactions. Chem. Phys. Lett. 1998, 297, 365–373. [Google Scholar] [CrossRef]
- Sugawara, Y.; Hamada, Y.; Masamichi, T. Vibration-rotation Spectra of Formamide. Bull. Chem. Soc. Jpn. 1983, 56, 1045–1050. [Google Scholar] [CrossRef]
- Crocellà, V.; Cerrato, G.; Magnacca, G.; Morterra, C. Adsorption of Acetone on Nonporous and Mesoporous Silica. J. Phys. Chem. C 2009, 113, 16517–16529. [Google Scholar] [CrossRef]
- Crocellà, V.; Cerrato, G.; Morterra, C. On the adsorption/reaction of acetone on pure and sulfate-modified zirconias. Phys. Chem. Chem. Phys. 2013, 15, 13446. [Google Scholar] [CrossRef] [PubMed]
- Lamberti, C.; Zecchina, A.; Groppo, E.; Bordiga, S. Probing the surfaces of heterogeneous catalysts by in situ IR spectroscopy. Chem. Soc. Rev. 2010, 39, 4951. [Google Scholar] [CrossRef] [PubMed]
| Model | ΔEc (ΔE disp) | ΔHc | ΔGc | p |
|---|---|---|---|---|
| SiO2-FA1 | −69.9 (−18.8) | −62.8 | −13.3 | 0.03 |
| SiO2-FA2 | −44.0 (−28.1) | −38.1 | 8.6 | 0.00 |
| SiO2-FA3 | −68.0 (−26.4) | −60.7 | −9.6 | 0.01 |
| SiO2-FA4 | −80.5 (−27.4) | −74.2 | −21.3 | 0.67 |
| SiO2-FA5 | −63.3 (−15.6) | −56.8 | −19.3 | 0.30 |
| Model | ΔEc (ΔE disp) | ΔHc | ΔGc | p |
|---|---|---|---|---|
| SiO2-2FA1 | −57.6 (−28.4) | −50.1 | −1.7 | 0.00 |
| SiO2-2FA2 | −56.4 (−20.4) | −49.2 | −6.3 | 0.01 |
| SiO2-2FA3 | −67.3 (−16.9) | −59.9 | −17.9 | 0.91 |
| SiO2-Dim1 | −46.8 (−24.2) | −39.9 | 7.2 | 0.00 |
| SiO2-Dim2 | −73.5 (−24.1) | −64.7 | −12.0 | 0.08 |
| SiO2-Dim3 | −51.7 (−19.3) | −43.4 | 2.3 | 0.00 |
| SiO2-Dim4 | −58.5 (−21.3) | −49.4 | −1.5 | 0.00 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Signorile, M.; Salvini, C.; Zamirri, L.; Bonino, F.; Martra, G.; Sodupe, M.; Ugliengo, P. Formamide Adsorption at the Amorphous Silica Surface: A Combined Experimental and Computational Approach. Life 2018, 8, 42. https://doi.org/10.3390/life8040042
Signorile M, Salvini C, Zamirri L, Bonino F, Martra G, Sodupe M, Ugliengo P. Formamide Adsorption at the Amorphous Silica Surface: A Combined Experimental and Computational Approach. Life. 2018; 8(4):42. https://doi.org/10.3390/life8040042
Chicago/Turabian StyleSignorile, Matteo, Clara Salvini, Lorenzo Zamirri, Francesca Bonino, Gianmario Martra, Mariona Sodupe, and Piero Ugliengo. 2018. "Formamide Adsorption at the Amorphous Silica Surface: A Combined Experimental and Computational Approach" Life 8, no. 4: 42. https://doi.org/10.3390/life8040042
APA StyleSignorile, M., Salvini, C., Zamirri, L., Bonino, F., Martra, G., Sodupe, M., & Ugliengo, P. (2018). Formamide Adsorption at the Amorphous Silica Surface: A Combined Experimental and Computational Approach. Life, 8(4), 42. https://doi.org/10.3390/life8040042








