Intrinsic Properties of tRNA Molecules as Deciphered via Bayesian Network and Distribution Divergence Analysis
Abstract
1. Introduction
2. Materials and Methods
3. Results
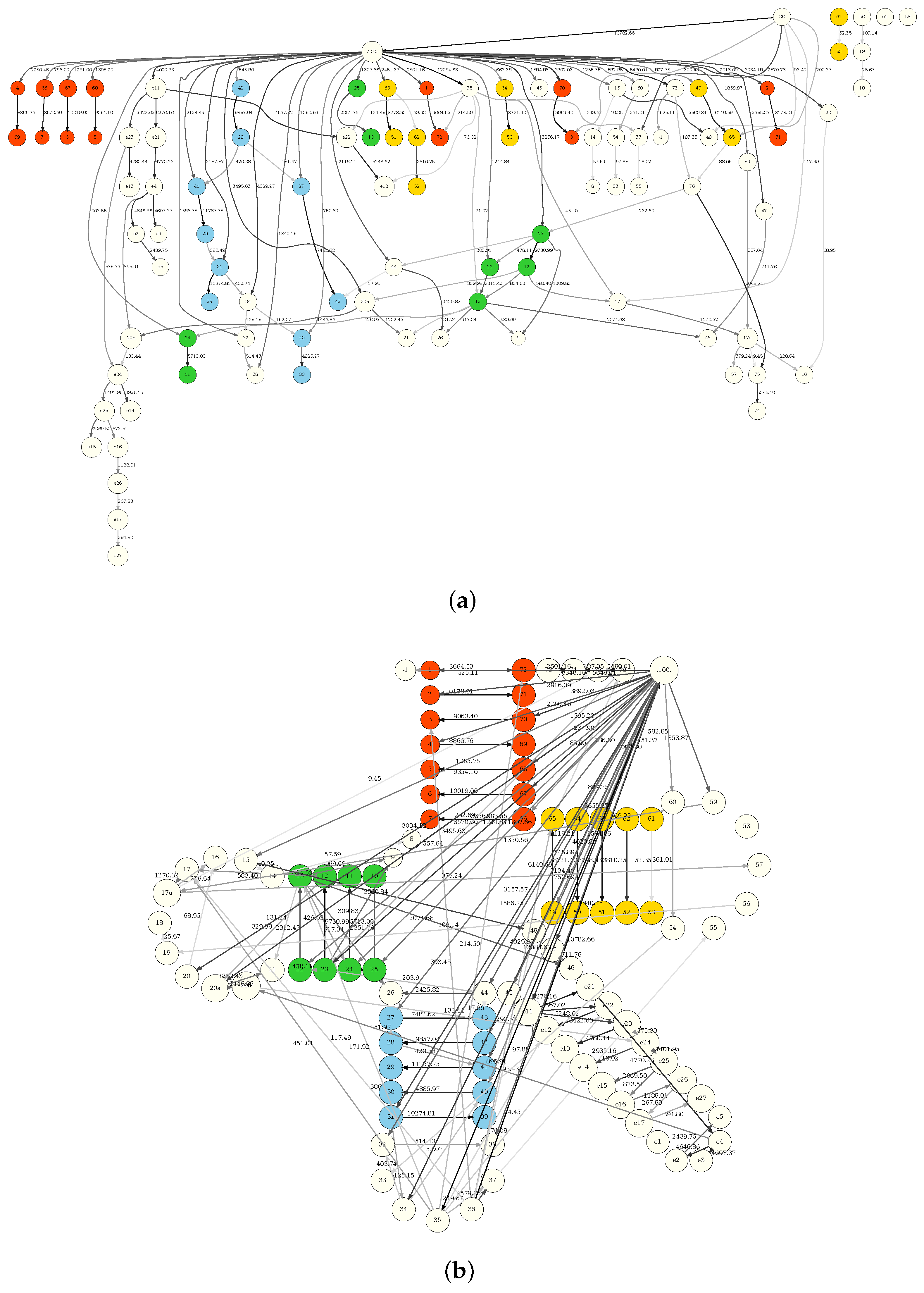
3.1. Structural Information
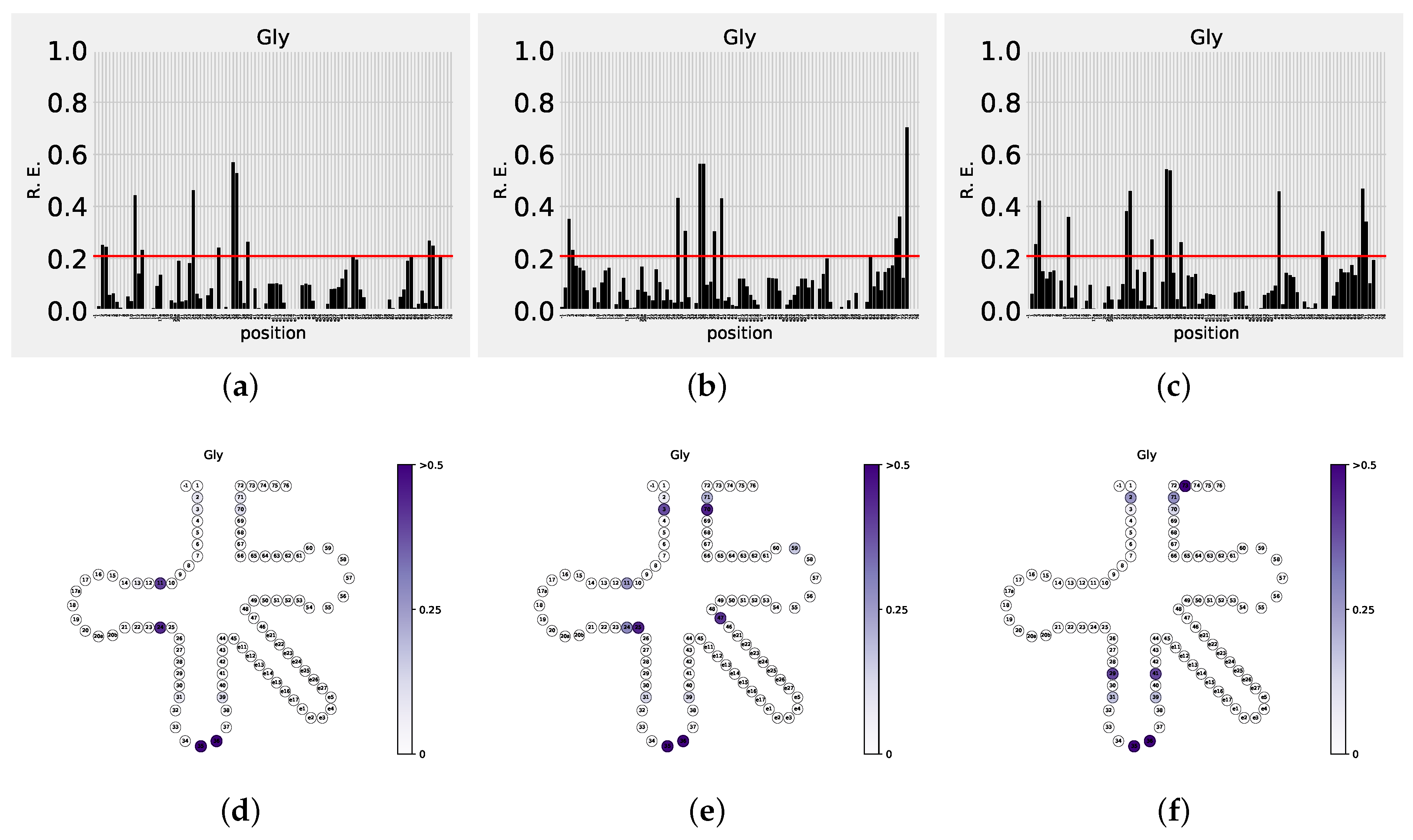
3.2. Amino Acids Specificity
3.3. Identification, in the Three Domains of Life, of the tRNA Amino Acid Specificity Identity Determinants
4. Discussion and Future Directions
- (1)
- Build the BNs for the tRNA sub- and super-classes of interest. Visually compare and contrast topologies. Interpret the intra-tRNA features (dependencies between the positions, pairwise and more complex) and inter-tRNA class differences.
- (2)
- In parallel, use measures of distribution divergence to identify aa class-specific tRNA identity positions.
- (3)
- For such positions, go back to the results of (1) to identify and interpret dependencies between these positions and other tRNA sites.
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Schimmel, P. Development of tRNA synthetases and connection to genetic code and disease. Protein Sci. 2008, 17, 1643–1652. [Google Scholar] [CrossRef] [PubMed]
- Giegé, R.; Eriani, G. Transfer RNA Recognition and Aminoacylation by Synthetases. In eLS; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Eriani, G.; Karam, J.; Jacinto, J.; Richard, E.M.; Geslain, R. MIST, a Novel Approach to Reveal Hidden Substrate Specificity in Aminoacyl-tRNA Synthetases. PLoS ONE 2015, 10, e0130042. [Google Scholar] [CrossRef] [PubMed]
- Cvetesic, N.; Gruic-Sovulj, I. Synthetic and editing reactions of aminoacyl-tRNA synthetases using cognate and non-cognate amino acid substrates. Methods 2017, 113, 13–26. [Google Scholar] [CrossRef] [PubMed]
- Sapienza, P.; Li, L.; Williams, T.; Lee, A.; Carter, C.W., Jr. An Ancestral Tryptophanyl-tRNA Synthetase Precursor Achieves High Catalytic Rate Enhancement without Ordered Ground-State Tertiary Structures. ACS Chem. Biol. 2016, 11, 1661–1668. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Rodriguez, L.; Erdogan, O.; Jimenez-Rodriguez, M.; Gonzalez-Rivera, K.; Williams, T.; Li, L.; Weinreb, V.; Collier, M.; Chandrasekaran, S.; Ambroggio, X.; et al. Functional Class I and II Amino Acid-activating Enzymes Can Be Coded by Opposite Strands of the Same Gene. J. Biol. Chem. 2015, 290, 19710–19725. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Macnamara, L.; Leuchter, J.; Alexander, R.; Cho, S. MD Simulations of tRNA and Aminoacyl-tRNA Synthetases: Dynamics, Folding, Binding, and Allostery. Int. J. Mol. Sci. 2015, 16, 15872–15902. [Google Scholar] [CrossRef] [PubMed]
- Adrion, J.; White, P.; Montooth, K. The Roles of Compensatory Evolution and Constraint in Aminoacyl tRNA Synthetase Evolution. Mol. Biol. Evol. 2016, 33, 152–161. [Google Scholar] [CrossRef] [PubMed]
- Fang, P.; Guo, M. Structural characterization of human aminoacyl-tRNA synthetases for translational and nontranslational functions. Methods 2017, 113, 83–90. [Google Scholar] [CrossRef] [PubMed]
- Datt, M.; Sharma, A. Novel and unique domains in aminoacyl-tRNA synthetases from human fungal pathogens Aspergillus niger, Candida albicans and Cryptococcus neoformans. BMC Genom. 2014, 15, 1609. [Google Scholar] [CrossRef] [PubMed]
- Amiram, M.; Haimovich, A.; Fan, C.; Wang, Y.; Aerni, H.; Ntai, I.; Moonan, D.; Ma, N.; Rovner, A.; Hong, S.; et al. Evolution of translation machinery in recoded bacteria enables multi-site incorporation of nonstandard amino acids. Nat. Biotechnol. 2015, 33, 1272–1279. [Google Scholar] [CrossRef] [PubMed]
- Terasaka, N.; Iwane, Y.; Geiermann, A.; Goto, Y.; Suga, H. Recent developments of engineered translational machineries for the incorporation of non-canonical amino acids into polypeptides. Int. J. Mol. Sci. 2015, 16, 6513–6531. [Google Scholar] [CrossRef] [PubMed]
- Perli, E.; Fiorillo, A.; Giordano, C.; Pisano, A.; Montanari, A.; Grazioli, P.; Campese, A.; Di Micco, P.; Tuppen, H.; Genovese, I.; et al. Short peptides from leucyl-tRNA synthetase rescue disease-causing mitochondrial tRNA point mutations. Hum. Mol. Genet. 2016, 25, 903–915. [Google Scholar] [CrossRef] [PubMed]
- Rodin, A.; Gogoshin, G.; Litvinenko, A.; Boerwinkle, E. Exploring genetic epidemiology data with Bayesian networks. In Handbook of Statistics; Rao, C., Chakraborty, R., Eds.; Elsevier: St. Louis, MI, USA, 2012; Volume 28, pp. 53–76. [Google Scholar]
- Gogoshin, G.; Boerwinkle, E.; Rodin, A. New Algorithm and Software (BNOmics) for Inferring and Visualizing Bayesian Networks from Heterogeneous Big Biological and Genetic Data. J. Comput. Biol. 2017, 24, 340–356. [Google Scholar] [CrossRef] [PubMed]
- Juhling, F.; Morl, M.; Hartmann, R.; Sprinzl, M.; Stadler, P.; Putz, J. tRNAdb 2009: Compilation of tRNA sequences and tRNA genes. Nucleic Acids Res. 2009, 37, D159–D162. [Google Scholar] [CrossRef] [PubMed]
- Quigley, G.; Rich, A. Structural domains of transfer RNA molecules. Science 1976, 194, 796–806. [Google Scholar] [CrossRef] [PubMed]
- Heckerman, D. A Tutorial on Learning with Bayesian Networks; MSRFF-TR-95-06; Microsoft Research: Redmond, WA, USA, 1995. [Google Scholar]
- Pearl, J. Causality: Models, Reasoning, and Inference; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2009. [Google Scholar]
- Zhang, X.; Branciamore, S.; Gogoshin, G.; Rodin, A.S.; Riggs, A.D. Analysis of high-resolution 3D intrachromosomal interactions aided by Bayesian network modeling. Proc. Natl. Acad. Sci. USA 2017, 114, E10359–E10368. [Google Scholar] [CrossRef] [PubMed]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 2002, 37, 145–151. [Google Scholar] [CrossRef]
- Sprinzl, M.; Horn, C.; Brown, M.; Ioudovitch, A.; Steinberg, S. Compilation of tRNA sequences and sequences of tRNA genes. Nucleic Acids Res. 1998, 26, 148–153. [Google Scholar] [CrossRef] [PubMed]
- Laslett, D.; Canback, B. ARAGORN, a program to detect tRNA genes and tmRNA genes in nucleotide sequences. Nucleic Acids Res. 2004, 32, 11–16. [Google Scholar] [CrossRef] [PubMed]
- Giegé, R.; Sissler, M.; Florentz, C. Universal rules and idiosyncratic features in tRNA identity. Nucleic Acids Res. 1998, 26, 5017–5035. [Google Scholar] [CrossRef] [PubMed]
- Galili, T.; Gingold, H.; Shaul, S.; Benjamini, Y. Identifying the ligated amino acid of archaeal tRNAs based on positions outside the anticodon. RNA 2016, 22, 1477–1491. [Google Scholar] [CrossRef] [PubMed]
- Zamudio, G.; Jose, M. Identity Elements of tRNA as Derived from Information Analysis. Orig. Life Evol. Biosph. 2017. [Google Scholar] [CrossRef] [PubMed]
- Rodin, A.; Litvinenko, A.; Klos, K.; Morrison, A.; Woodage, T.; Coresh, J.; Boerwinkle, E. Use of wrapper algorithms coupled with a random forests classifier for variable selection in large-scale genomic association studies. J. Comput. Biol. 2009, 16, 1705–1718. [Google Scholar] [CrossRef] [PubMed]
- Saffarian, A.; Giraud, M.; Touzet, H. Modeling alternate RNA structures in genomic sequences. J. Comput. Biol. 2015, 22, 190–204. [Google Scholar] [CrossRef] [PubMed]
- Mustoe, A.; Liu, X.; Lin, P.; Al-Hashimi, H.; Fierke, C.; Brooks, C.L., Jr. Noncanonical secondary structure stabilizes mitochondrial tRNA(Ser(UCN)) by reducing the entropic cost of tertiary folding. J. Am. Chem. Soc. 2015, 137, 3592–3599. [Google Scholar] [CrossRef] [PubMed]
- Velandia-Huerto, C.; Berkemer, S.; Hoffmann, A.; Retzlaff, N.; Marroquin, L.C.R.; Hernandez-Rosales, M.; Stadler, P.; Bermudez-Santana, C. Orthologs, turn-over, and remolding of tRNAs in primates and fruit flies. BMC Genom. 2016, 17, 617. [Google Scholar] [CrossRef] [PubMed]
- Schimmel, P. The emerging complexity of the tRNA world: Mammalian tRNAs beyond protein synthesis. Nat. Rev. Mol. Cell Biol. 2018, 19, 45–58. [Google Scholar] [CrossRef] [PubMed]
- Koonin, E.; Novozhilov, A. Origin and Evolution of the Universal Genetic Code. Annu. Rev. Genet. 2017, 51, 45–52. [Google Scholar] [CrossRef] [PubMed]
- Carter, C.W., Jr.; Wills, P. Interdependence, Reflexivity, Fidelity, Impedance Matching, and the Evolution of Genetic Coding. Mol. Biol. Evol. 2017, 35, 269–286. [Google Scholar] [CrossRef] [PubMed]
- Wills, P.; Carter, C.W., Jr. Insuperable problems of the genetic code initially emerging in an RNA world. Biosystems 2017. [Google Scholar] [CrossRef]
- Di Giulio, M. The aminoacyl-tRNA synthetases had only a marginal role in the origin of the organization of the genetic code: Evidence in favor of the coevolution theory. J. Theor. Biol. 2017, 432, 14–24. [Google Scholar] [CrossRef] [PubMed]
- Di Giulio, M. Some pungent arguments against the physico-chemical theories of the origin of the genetic code and corroborating the coevolution theory. J. Theor. Biol. 2017, 414, 1–4. [Google Scholar] [CrossRef] [PubMed]


| Amino Acid | Confirmed | Low Significance | Suggested | Domain |
|---|---|---|---|---|
| 2-71; 3-70; 4-69; 9; 12-23; 13-22 | Arc | |||
| 20a; 30-40; 35; 36; 44; 47 | ||||
| Ala | 2-71; 3-70; 4-69; 20; 64; 73 | 17; 20a; 29-41; 35; 36; 44; 51-63 | Bac | |
| 3-70 | 2-71; 4-69; 5-68; 9; 12-23; 13-22; 20a; 27-43 | Euk | ||
| 29-41; 31-39; 32; 35; 36; 38; 59 | ||||
| 4-69; 20; 35; 36; 73 | Arc | |||
| Arg | 20; 20A; | 38; 73 | 4-69; 5-68; 20a; 35; 36 | Bac |
| 4-69; 15; 20; 35; 36; 48; 71 | Euk | |||
| 2-71; 3-70; 9; 11-24; 12-23; 17; 17a | Arc | |||
| 20a; 22; 31-39; 34; 35; 36; 37 | ||||
| 46; 47; 51-63; 59; 73 | ||||
| Asn | 73 | 1-72; 2-71; 3-70; 12-23; 31-39 | Bac | |
| 32; 34; 35; 36; 51-63 | ||||
| 2-71; 4-69; 13-22; 17; 27-43; 29-41 | Euk | |||
| 31-39; 34; 35; 36; 38; 49-65 | ||||
| 50-64; 51-63; 59; 73 | ||||
| 2-71; 3-70; 6-67; 11-24; 12-23; 13-22; 17a | Arc | |||
| 20b; 20a; 20; 25; 28-42; 34; 35 | ||||
| 36; 44; 46; 47; 49-65; 64; 73 | ||||
| Asp | 25; 38; 73 | 2-71; 10 | 11-24; 20a; 31-39; 34; 35; 36 | Bac |
| 43; 44; 50-64; 51-63; 65 | ||||
| 9-12-23; 25; 38; 73 | 10 | 1-72; 11-24; 13-22; 20a; 26; 28-42 | Euk | |
| 29-41; 31-39; 34; 35; 36; 46 | ||||
| 47; 49-65; 50-64; 59; 63; 71 | ||||
| 3-70; 4-69; 5-68; 12-23; 13-22; 17 | Arc | |||
| 17a; 20; 21; 24; 27-43; 34 | ||||
| 35; 36; 45; 46; 47; 73 | ||||
| Cys | 2-71; 3-70; 13-22; 46; 73 | 15; 48 | 12-23; 17; 29-41; 34; 35; 36 | Bac |
| 43; 45; 47; 51-63; 71 | ||||
| 12-23; 73 | 20a | 2-71; 3-70; 6-67; 7-66; 9; 13-22; | Euk | |
| 26; 29-41; 31-39; 34; 35; 36; 37 | ||||
| 38; 51-63; 59; 68; 69 | ||||
| 1-72; 2-71; 3-70; 4-69; 11-24; 12-23; 13-22 | Arc | |||
| 17; 17a; 20b; 20a; 25; 34; 35 | ||||
| 36; 37; 44; 46; 47; 73 | ||||
| Gln | 1-72; 38; 73 | 2-71; 3-70; 10-25; 37 | 12-23; 13-22; 20a; 34; 35; 36 | Bac |
| 44; 45; 46; 51-63; 65 | ||||
| 2-71; 3-70; 6-67; 7-66; 11-24; 12-23 | Euk | |||
| 13-22; 26; 29-41; 31-39; 34; 35 | ||||
| 36; 44; 46; 47; 52-62; 73 | ||||
| 2-71; 3-70; 11-24; 12-23; 13-22; 17a; 20a; 20b | Arc | |||
| 25; 34; 35; 36; 46; 47; 49-65 | ||||
| Glu | 11-24; 13; 46; 47; 71 | 1-72; 22; 33; 37 | 3-70; 4-69; 5-68; 7-66; 9; 12-23 | Bac |
| 17; 20a; 30-40; 34; 35; 36 | ||||
| 38; 45; 49-65; 51-63 | ||||
| 1-72; 2-71; 3-70; 5-68; 11-24; 12-23 | Euk | |||
| 13-22; 25; 26; 31-39; 34; 35 | ||||
| 36; 38; 47; 59 | ||||
| 2-71; 3-70; 11-24; 13-22 | Arc | |||
| 31-39; 35; 36; 49-65 | ||||
| Gly | 2-71; 3-70; 73 | 1-72; 10-25 | 29-41; 31-39; 35; 36; 63 | Bac |
| 2-71; 3-70 | 73 | 11-24; 25; 31-39; 35; 36; 47; 59 | Euk | |
| -1; 2-71; 3-70; 5-68; 11-24; 12-23 | Arc | |||
| 34; 35; 36; 37; 50-64; 73 | ||||
| His | -1; 73 | 2-71; 3-70; 4-69; 6-67; 31-39 | Bac | |
| 32; 34; 35; 36; 38; 63 | ||||
| -1; 73 | 2-71; 9; 11-24; 12-23; 13-22; 26 | Euk | ||
| 30-40; 31-39; 32; 34; 35; 36 | ||||
| 37; 38; 44; 45; 46; 47 | ||||
| 2-71; 3-70; 11-24; 12-23; 29-41; 31-39 | Arc | |||
| 34; 35; 36; 37; 46; 73 | ||||
| Ile | 12-23; 29-41 | 4-69; 24; 37; 38; 73 | 3-70; 6-67; 13-22; 20a; 27-43; 28-42 | Bac |
| 34; 35; 36; 44; 51-63 | ||||
| 4-69; 17; 20a; 28-42; 29-41 | Euk | |||
| 30-40; 34; 35; 36; 60 | ||||
| 1-72; 2-71; 9; 11-24; 17; 17a; 20 | Arc | |||
| 20b; 27-43; 31-39; 34; 35; 36; 37 | ||||
| 47; 51-63; 57; 64; 73 | ||||
| Ini | 2-71; 3-70; 32 | 33; 37 | 1-72; 5-68; 6-67; 11-24; 12-23; 17a | Bac |
| 26; 27-43; 29-41; 31-39; 34; 35 | ||||
| 36; 44; 57; 59; 73 | ||||
| 1-72; 2-71; 3-70; 4-69; 5-68; 6-67; 7-66 | Euk | |||
| 12-23; 20; 20a; 22; 27-43; 29-41; 31-39 | ||||
| 33; 34; 35; 36; 38; 46; 51-63 | ||||
| 54; 59; 60; 73 | ||||
| 2-71; 3-70; 4-69; 5-68; 9; e11 | Arc | |||
| 12-23; 13-22; 20a; 20b; e21; 31-39 | ||||
| 35; 36; 37; 44; ; 46 | ||||
| Leu | 20A; 73 | 20; 38; | 2-71; e5; 9; e11; 12-23; 13-22; 15; 20a; 21 | Bac |
| e21; 35; 36; 44; ; 46; 47; 48; 73 | ||||
| 4-69; e5; e11; 12-23; 13-22; 20a | Euk | |||
| 20b; e21; 29-41; 35; 36; 37 | ||||
| 44; ; 45; 47; 49-65; 68 | ||||
| 2-71; 3-70; 4-69; 9; 11-24; 12-23; 22 | Arc | |||
| 31-39; 34; 35; 36; 37; 46; 73 | ||||
| Lys | 73? | 4-69; 5-68; 7-66; 12-23; 20a; 26 | Bac | |
| 31-39; 34; 35; 36; 73 | ||||
| 2-71; 7-66; 9; 12-23; 13-22; 17; 20a; 29-41 | Euk | |||
| 31-39; 34; 35; 36; 44; 59; 70 | ||||
| 31-39; 34; 35; 36; 37; 73 | Arc | |||
| Met | 73 | 4-69; 5-68; 38 | 31-39; 34; 35; 36; 71 | Bac |
| 20 | 73 | 1-72; 12-23; 31-39; 34; 35; 36; 60; 64 | Euk | |
| 9; 12-23; 13-22; 20; 20a; 34; 35 | Arc | |||
| 36; 37; 45; 46; 47; 73 | ||||
| Phe | 27-43; 31-39; 44; 45; 59 | 20?; 28-42; 30-40; 37; 39?; 43?; 60; 73? | 3-70; 12-23; 17; 20a; 34; 35 | Bac |
| 36; 39; 43; 51-63; 73 | ||||
| 20; 31-39; 37 | 73? | 2-71; 4-69; 5-68; 6-67; 9; 12-23 | Euk | |
| 13-22; 17; 20a; 29-41; 34; 35 | ||||
| 36; 51-63; 59; 60; 73 | ||||
| 2-71; 3-70; 6-67; 11-24; 12-23; 13-22 | Arc | |||
| 17a; 25; 35; 36; 37; 46 | ||||
| Pro | 72; 73 | 15; 48 | 1-72; 2-71; 3-70; 17a; 35 | Bac |
| 36; 37; 44; 59 | ||||
| 2-71; 11-24; 12-23; 13-22; 20a; 25 | Euk | |||
| 26; 27-43; 29-41; 31-39; 32; 35 | ||||
| 36; 37; 38; 49-65; 73 | ||||
| 3-70; 4-69; 7-66; 9; 10-25; e11; 11-24; 12-23 | Arc | |||
| 13-22; 14; 15; 16; 17a; 17; 20b; 20 | ||||
| 20a; 21; e21; 27-43; 28-42; 31-39; 34; 35 | ||||
| 36; 37; 44; ; 48; 49-65; 50-64; 59 | ||||
| 67; 68; 72; 73 | ||||
| Sec | 2-71; 3-70; 4-69; 5-68; e5; 7-66 | 1-72; e2; e3; e4; 6-67; 12-23; e12; e13 | 14; 15; 16; 20a; 29-41; 31-39; 34; 35 | Bac |
| 8; 9; 10-25; 11-24; e11; e17 | 13-22; 20; e22; e23 | 36; ; 59; 63; 64; 66; 68 | ||
| e21; e27; 45; 48; 73; e24; e25 | ||||
| e26; 50-64; 64?; 66?; 68? | ||||
| 2-71; 4-69; 5-68; 9; 10-25; e11; 14; 20a | Euk | |||
| e21; 21; 23; 26; 27-43; 28-42; 29-41; 31-39 | ||||
| 34; 35; 36; 38; 44; ; 46; 47 | ||||
| 48; 49-65; 50-64; 51-63; 59; 66; 67; 73 | ||||
| 2-71; 4-69; 5-68; e11; 12-23; e21; 22; 24 | Arc | |||
| 35; 36; 44; ; 46; 47; 73 | ||||
| Ser | 2-71; 3-70; e4-69;11; e21; 44; 73 | 11-24 | 5-68; 12-23; 13-22; 20a; 20b; 35 | Bac |
| e4; e5?;e12; e13; e14; e15; e16; e22 | 36; ; 46; 47; 51-63; 59 | |||
| e23; e24; e25; e26; 69? e2; e3; | ||||
| e11; e21; e2; e3; e4; e12; e13; e22; e23 | 4-69; 13-22; 20a; 23; 27-43; 35; 36; 44 | Euk | ||
| ; 46; 47; 49-65; 51-63; 59; 73 | ||||
| 2-71; 3-70; 11-24; 12-23; 35 | Arc | |||
| 36; 37; 46; 73 | ||||
| Thr | 2-71; 3-70 | 1-72; 73 | 20a; 35; 36 | Bac |
| 1-72 | 31-39; 35; 36; 73 | Euk | ||
| 2-71; 3-70; 6-67; 22; 27-43 | Arc | |||
| 31-39; 34; 35; 36; 50-64 | ||||
| Trp | 1-72; 3-70; 73 | 2-71; 5-68; 9 | 15; 20a; 29-41; 31-39; 34; 35; 36; 48 | Bac |
| 2-71; 15; 20a; 31-39; 34; 35 | Euk | |||
| 36; 43; 48; 52-62; 65 | ||||
| 1-72; 4-69; 9; 12-23; 13-22; 31-39; 34 | Arc | |||
| 35; 36; 37; 46; 47; 51-63; 73 | ||||
| Tyr | 73 | e5; 6-67; 10-25; e11; 12-23; 13-22; 17; 20 | Bac | |
| 20a; 20b; e21; 27-43; 28-42; 31-39; 34; 35 | ||||
| 36; 44; ; 46; 59; 71 | ||||
| 1-72 | 73 | 12-23; 17; 27-43; 28-42; 31-39 | Euk | |
| 34; 35; 36; 51-63; 70 | ||||
| 2-71; 3-70; 4-69; 5-68; 6-67; 11-24; 12-23 | Arc | |||
| 20a; 30-40; 31-39; 35; 36; 47 | ||||
| Val | 73 | 3-70; 4-69 | 13-22; 35; 36 | Bac |
| 3-70; 11-24; 12-23; 13-22; 27-43 | Euk | |||
| 31-39; 35; 36; 38; 60 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Branciamore, S.; Gogoshin, G.; Di Giulio, M.; Rodin, A.S. Intrinsic Properties of tRNA Molecules as Deciphered via Bayesian Network and Distribution Divergence Analysis. Life 2018, 8, 5. https://doi.org/10.3390/life8010005
Branciamore S, Gogoshin G, Di Giulio M, Rodin AS. Intrinsic Properties of tRNA Molecules as Deciphered via Bayesian Network and Distribution Divergence Analysis. Life. 2018; 8(1):5. https://doi.org/10.3390/life8010005
Chicago/Turabian StyleBranciamore, Sergio, Grigoriy Gogoshin, Massimo Di Giulio, and Andrei S. Rodin. 2018. "Intrinsic Properties of tRNA Molecules as Deciphered via Bayesian Network and Distribution Divergence Analysis" Life 8, no. 1: 5. https://doi.org/10.3390/life8010005
APA StyleBranciamore, S., Gogoshin, G., Di Giulio, M., & Rodin, A. S. (2018). Intrinsic Properties of tRNA Molecules as Deciphered via Bayesian Network and Distribution Divergence Analysis. Life, 8(1), 5. https://doi.org/10.3390/life8010005





