Enrichment of Circular Code Motifs in the Genes of the Yeast Saccharomyces cerevisiae
Abstract
1. Introduction
2. Method
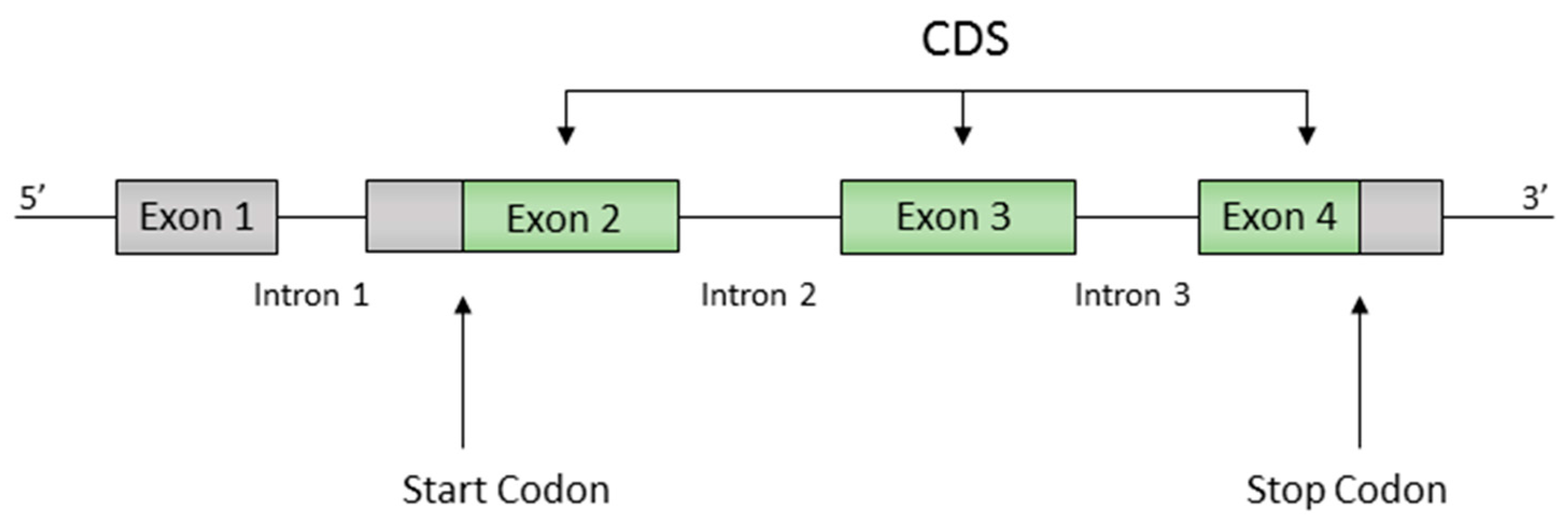
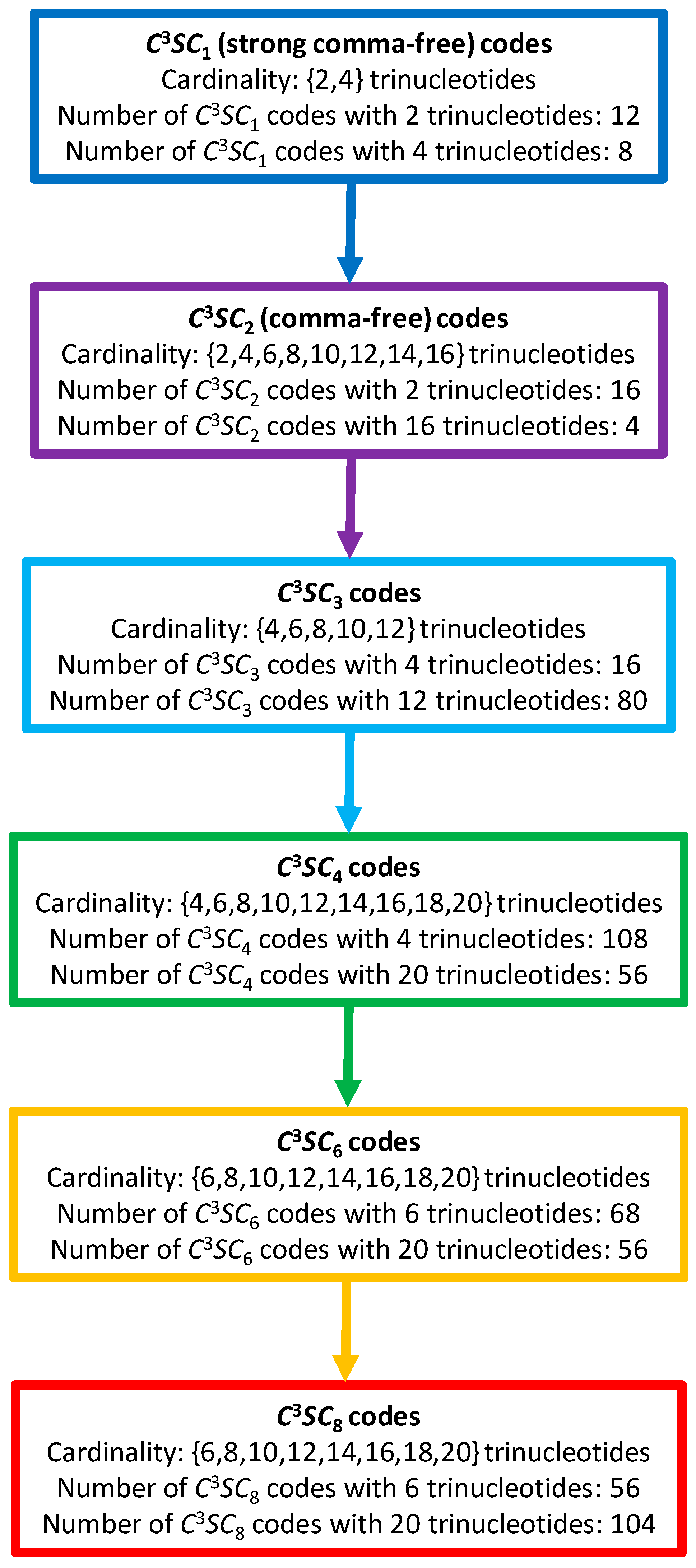
2.1. Definitions
- (i)
- The code is circular.
- (ii)
- The graph is acyclic.
2.2. Definition of Motifs and Random Motifs
- (i)
- has a cardinality equal to 20 trinucleotides;
- (ii)
- The total number of each nucleotide , , and in is equal to 15 (note that );
- (iii)
- has no stop trinucleotides and no periodic trinucleotides ;
- (iv)
- is not a circular code. Its associated graph is cyclic ( being not shown).
2.3. Statistical Analysis of Motifs in the Genome of S. cerevisiae
2.4. Statistical Analysis of Motifs in the Three Frames of S. cerevisiae Genes
2.5. Statistical Analysis of S. cerevisiae Genes with Motifs
2.6. Software Development
2.7. Genome S. cerevisiae
3. Results
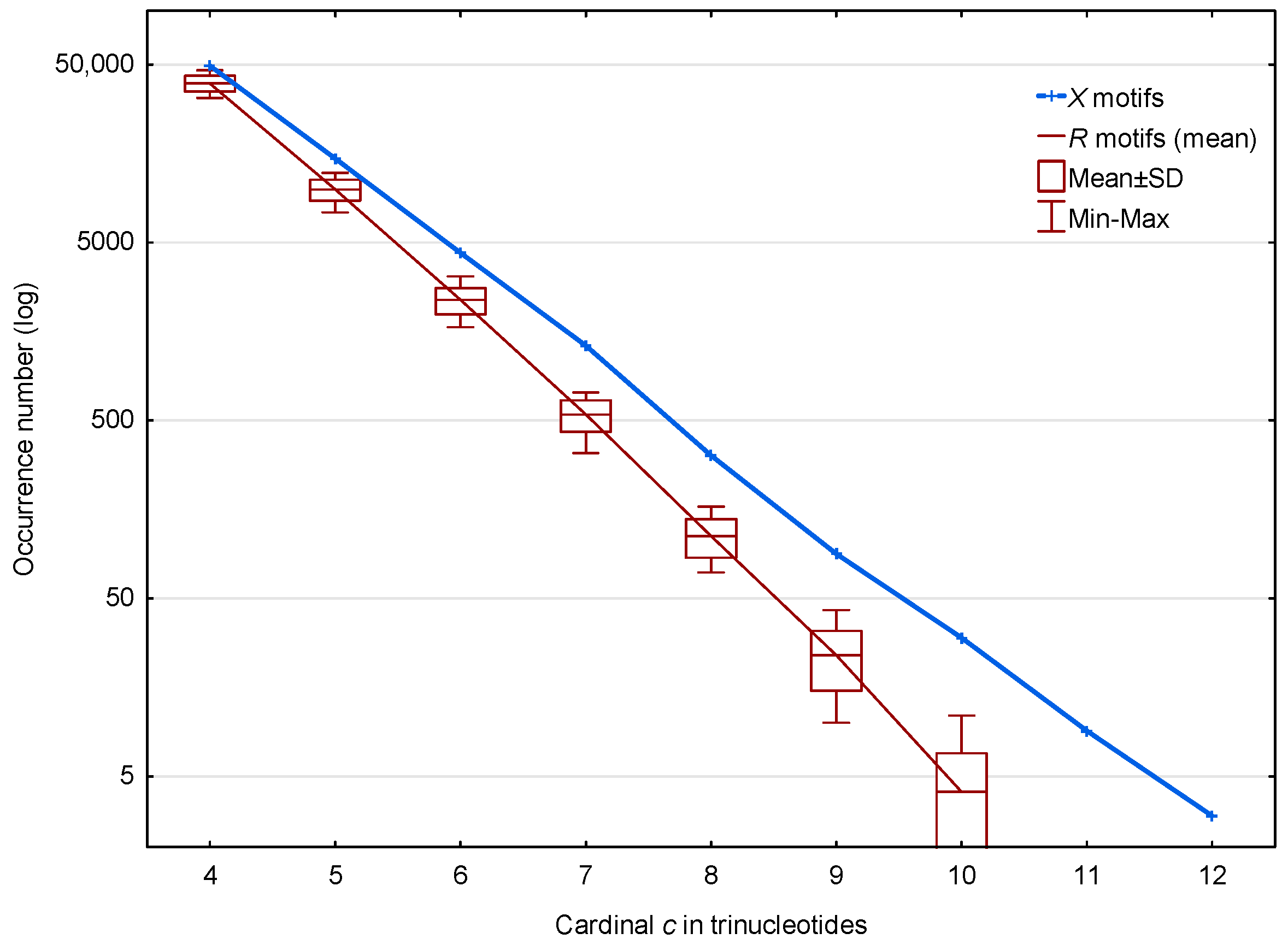
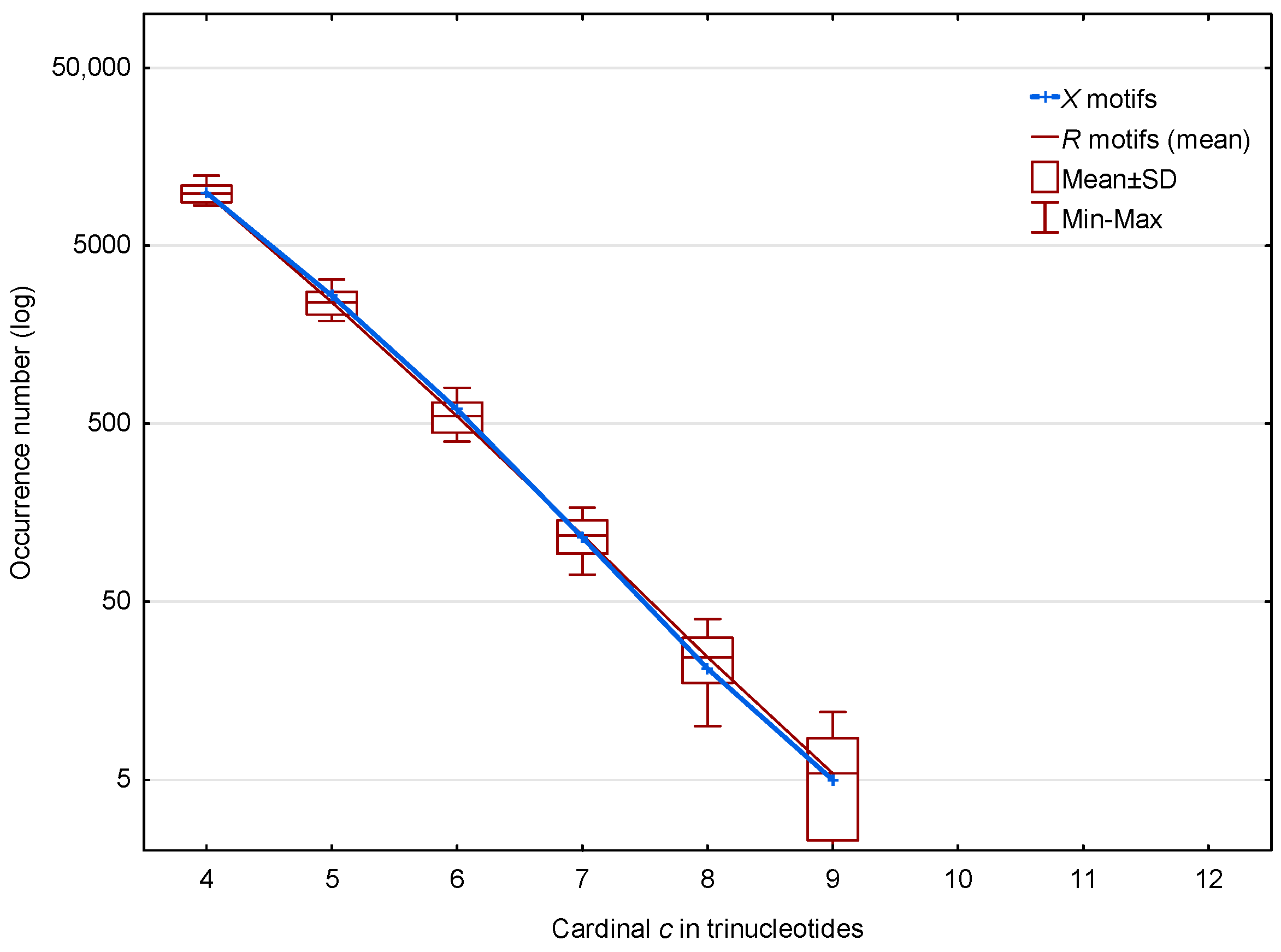
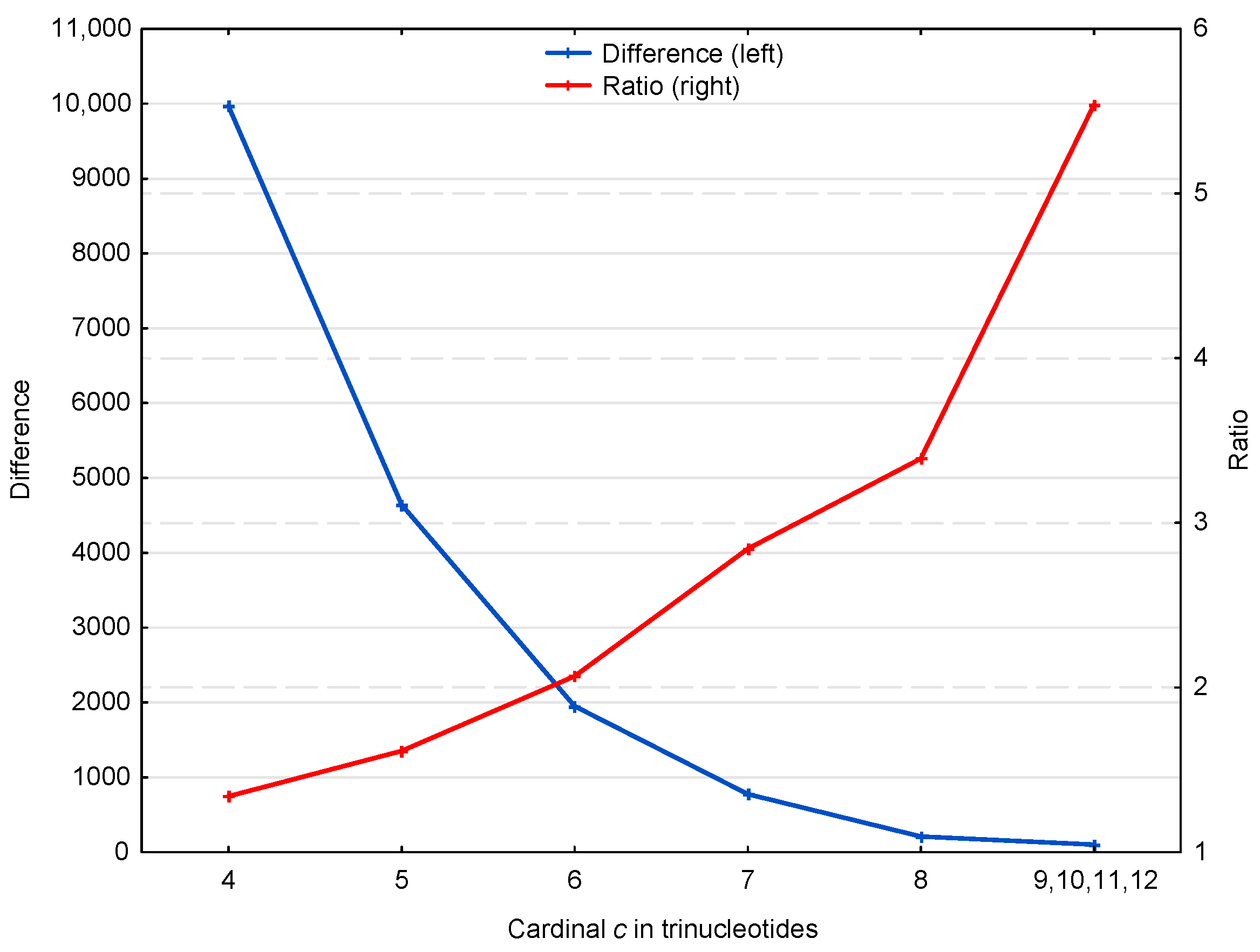
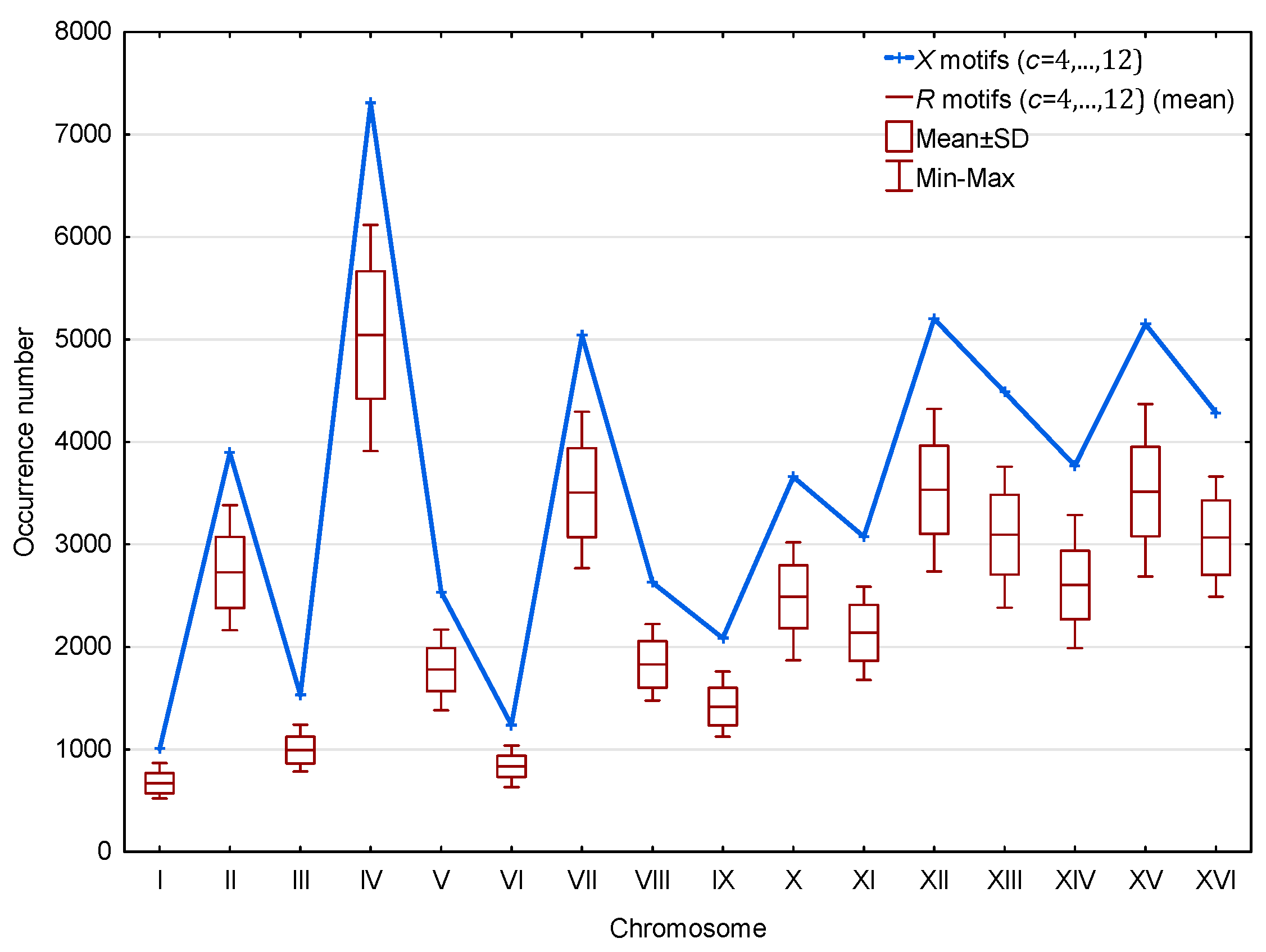
3.1. Occurrence Number of Motifs in the Genome of S. cerevisiae
3.1.1. Occurrence Number of Motifs in the Non-Coding Regions of S. cerevisiae
3.1.2. Occurrence Number of Motifs in the Genes of S. cerevisiae
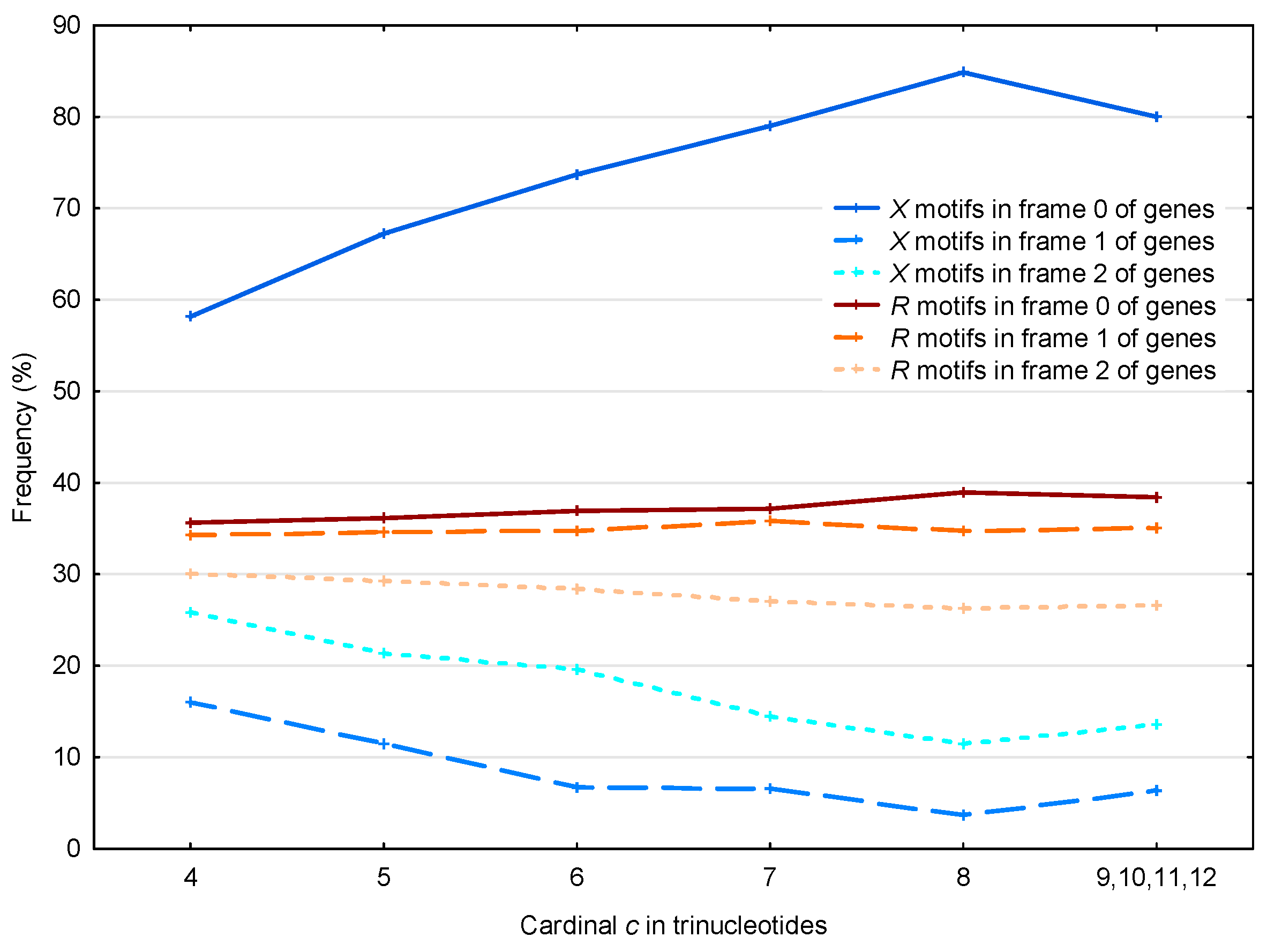
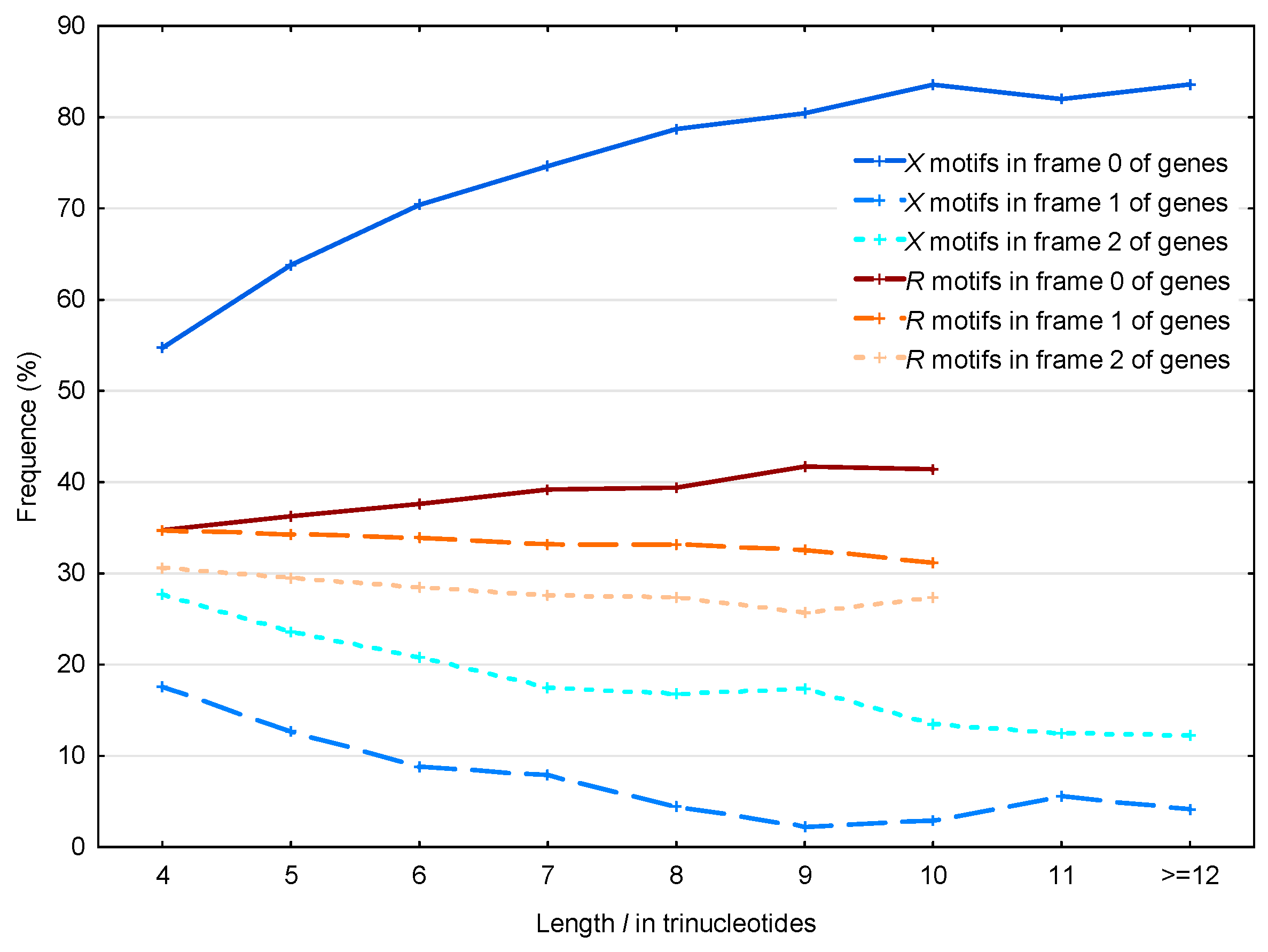
3.2. Occurrence Number of Motifs in the Three Frames of S. cerevisiae Genes
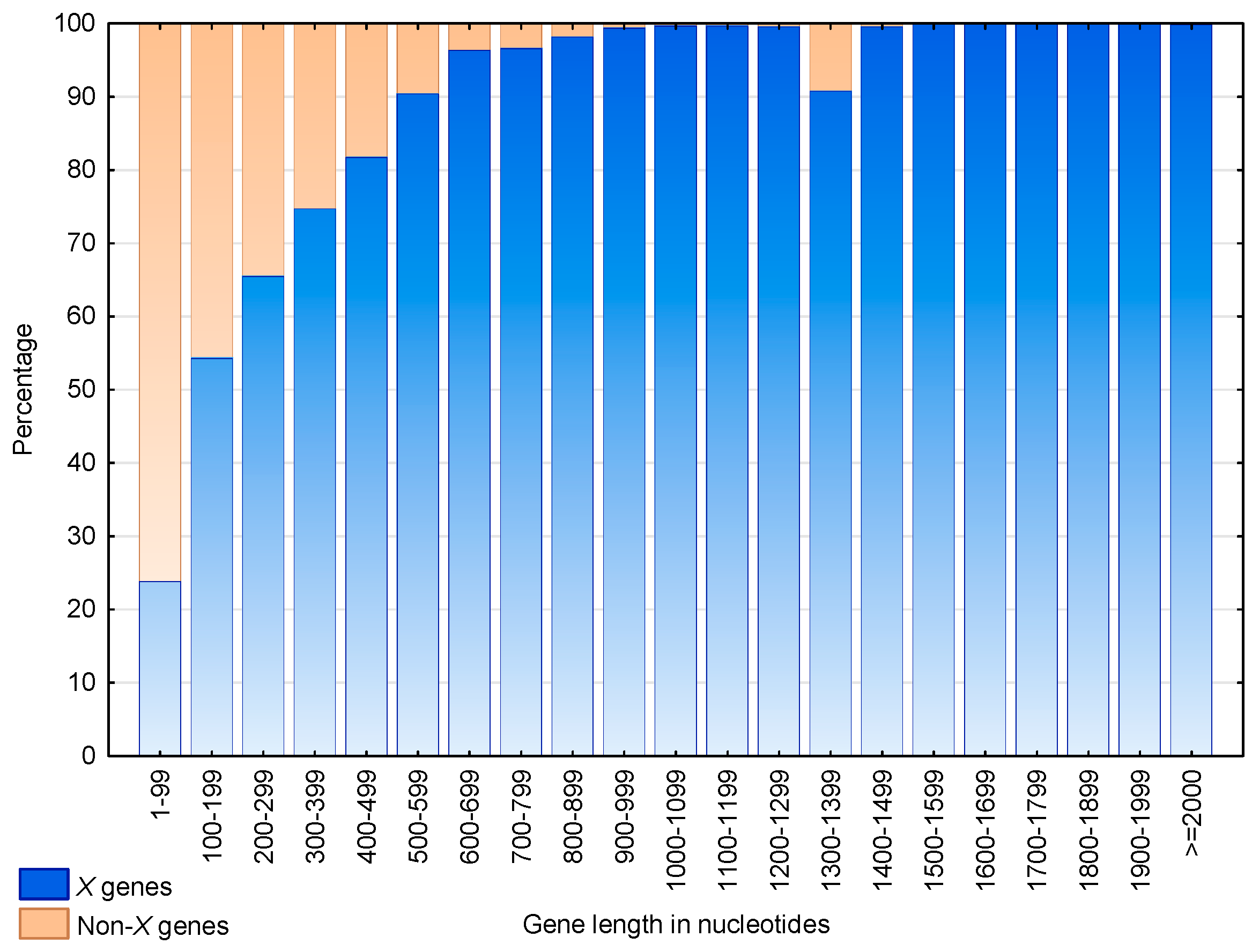
3.3. Identification of S. cerevisiae Genes
3.4. Trinucleotide Composition in the Motifs of S. cerevisiae Genes
4. Conclusions
Author Contributions
Conflicts of Interest
Appendix A. Random Codes
- (i)
- has a cardinality equal to 20 trinucleotides;
- (ii)
- The total number of each nucleotide , , and in is equal to 15;
- (iii)
- has no stop trinucleotides and no periodic trinucleotides ;
- (iv)
- is not a circular code. Its associated graph is cyclic ( being not shown).
References
- Michel, C.J. The maximal C3 self-complementary trinucleotide circular code X in genes of bacteria, archaea, eukaryotes, plasmids and viruses. Life 2017, 7, 20. [Google Scholar] [CrossRef] [PubMed]
- Michel, C.J. The maximal C3 self-complementary trinucleotide circular code X in genes of bacteria, eukaryotes, plasmids and viruses. J. Theor. Biol. 2015, 380, 156–177. [Google Scholar] [CrossRef] [PubMed]
- Arquès, D.G.; Michel, C.J. A complementary circular code in the protein coding genes. J. Theor. Biol. 1996, 182, 45–58. [Google Scholar] [CrossRef] [PubMed]
- Michel, C.J.; Pirillo, G. Dinucleotide circular codes. ISRN Biomath. 2013, 2013, 538631. [Google Scholar] [CrossRef][Green Version]
- Fimmel, E.; Michel, C.J.; Strüngmann, L. Diletter circular codes over finite alphabets. Math. Biosci. 2017, 294, 120–129. [Google Scholar] [CrossRef] [PubMed]
- Michel, C.J.; Pirillo, G.; Pirillo, M.A. A relation between trinucleotide comma-free codes and trinucleotide circular codes. Theor. Comput. Sci. 2008, 401, 17–26. [Google Scholar] [CrossRef]
- Michel, C.J.; Pirillo, G. Identification of all trinucleotide circular codes. Comput. Biol. Chem. 2010, 34, 122–125. [Google Scholar] [CrossRef] [PubMed]
- Fimmel, E.; Michel, C.J.; Strüngmann, L. n-Nucleotide circular codes in graph theory. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150058. [Google Scholar] [CrossRef] [PubMed]
- Souciet, J.L.; Génolevures Consortium GDR CNRS 2354. Ten years of the Génolevures Consortium: A brief history. C. R. Biol. 2011, 334, 580–584. [Google Scholar] [CrossRef] [PubMed]
- Goffeau, A.; Barrell, B.G.; Bussey, H.; Davis, R.W.; Dujon, B.; Feldmann, H.; Galibert, F.; Hoheisel, J.D.; Jacq, C.; Johnston, M.; et al. Life with 6000 genes. Science 1996, 274, 563–567. [Google Scholar] [CrossRef]
- Hellerstedt, S.T.; Nash, R.S.; Weng, S.; Paskov, K.M.; Wong, E.D.; Karra, K.; Engel, S.R.; Cherry, J.M. Curated protein information in the Saccharomyces genome database. Database 2017. [Google Scholar] [CrossRef] [PubMed]
- Bussoli, L.; Michel, C.J.; Pirillo, G. On conjugation partitions of sets of trinucleotides. Appl. Math. 2012, 3, 107–112. [Google Scholar] [CrossRef]
- El Soufi, K.; Michel, C.J. Unitary circular code motifs in genomes of eukaryotes. Biosystems 2017, 153, 45–62. [Google Scholar] [CrossRef] [PubMed]
- Arquès, D.G.; Fallot, J.-P.; Michel, C.J. An evolutionary model of a complementary circular code. J. Theor. Biol. 1997, 185, 241–253. [Google Scholar] [CrossRef] [PubMed]
- Bahi, J.M.; Michel, C.J. A stochastic gene evolution model with time dependent mutations. Bull. Math. Biol. 2004, 66, 763–778. [Google Scholar] [CrossRef] [PubMed]
- Bahi, J.M.; Michel, C.J. A stochastic model of gene evolution with chaotic mutations. J. Theor. Biol. 2008, 255, 53–63. [Google Scholar] [CrossRef] [PubMed]
- Kellis, M.; Birren, B.W.; Lander, E.S. Proof and evolutionary analysis of ancient genome duplication in the yeast Saccharomyces cerevisiae. Nature 2004, 428, 617–624. [Google Scholar] [CrossRef] [PubMed]
- Crick, F.H.; Brenner, S.; Klug, A.; Pieczenik, G. A speculation on the origin of protein synthesis. Orig. Life 1976, 7, 389–397. [Google Scholar] [CrossRef] [PubMed]
- Eigen, M.; Schuster, P. The Hypercycle. A principle of natural self-organization. Part C: The realistic hypercycle. Naturwissenschaften 1978, 65, 341–369. [Google Scholar] [CrossRef]
- Shepherd, J.C.W. Method to determine the reading frame of a protein from the purine/pyrimidine genome sequence and its possible evolutionary justification. Proc. Natl. Acad. Sci. USA 1981, 78, 1596–1600. [Google Scholar] [CrossRef] [PubMed]
- Ikehara, K. Origins of gene, genetic code, protein and life: Comprehensive view of life systems from a GNC-SNS primitive genetic code hypothesis. J. Biosci. 2002, 27, 165–186. [Google Scholar] [CrossRef] [PubMed]
- Trifonov, E.N. Translation framing code and frame-monitoring mechanism as suggested by the analysis of mRNA and 16S rRNA nucleotide sequences. J. Mol. Biol. 1987, 194, 643–652. [Google Scholar] [CrossRef]
- Fimmel, E.; Michel, C.J.; Strüngmann, L. Strong comma-free codes in genetic information. Bull. Math. Biol. 2017, 79, 1796–1819. [Google Scholar] [CrossRef] [PubMed]
- Koonin, E.V. Frozen accident pushing 50: Stereochemistry, expansion, and chance in the evolution of the genetic code. Life 2017, 7, 22. [Google Scholar] [CrossRef] [PubMed]
- Fimmel, E.; Michel, C.J.; Strüngmann, L. Self-complementary circular codes in pairing genetic processes. 2017; submitted. [Google Scholar]
- Michel, C.J. Circular code motifs in transfer and 16S ribosomal RNAs: A possible translation code in genes. Comput. Biol. Chem. 2012, 37, 24–37. [Google Scholar] [CrossRef] [PubMed]
- Michel, C.J. Circular code motifs in transfer RNAs. Comput. Biol. Chem. 2013, 45, 17–29. [Google Scholar] [CrossRef] [PubMed]
- El Soufi, K.; Michel, C.J. Circular code motifs in the ribosome decoding center. Comput. Biol. Chem. 2014, 52, 9–17. [Google Scholar] [CrossRef] [PubMed]
- El Soufi, K.; Michel, C.J. Circular code motifs near the ribosome decoding center. Comput. Biol. Chem. 2015, 59, 158–176. [Google Scholar] [CrossRef] [PubMed]
- Lobanov, M.Y.; Klus, P.; Sokolovsky, I.V.; Tartaglia, G.G.; Galzitskaya, O.V. Non-random distribution of homo-repeats: Links with biological functions and human diseases. Sci. Rep. 2016, 6, 1–11. [Google Scholar] [CrossRef] [PubMed]

| Chr | Gene Name | Gene Start | Gene End | Gene Length | Motif Start | Motif End | Motif Length | Motif |
|---|---|---|---|---|---|---|---|---|
| VIII | YHR131C | 365,340 | 367,892 | 2553 | 365,358 | 365,489 | 132 | |
| XVI | YPL190C | 185,317 | 187,725 | 2409 | 187,303 | 187,428 | 126 | |
| XVI | YPL158C | 252,034 | 254,310 | 2277 | 252,241 | 252,363 | 123 | |
| XVI | YPR042C | 650,435 | 653,662 | 3228 | 650,504 | 650,611 | 108 | |
| VII | YGL150C | 221,104 | 225,573 | 4470 | 224,830 | 224,934 | 105 | |
| II | YBR150C | 541,209 | 544,493 | 3285 | 541,446 | 541,550 | 105 | |
| XI | YKR072C | 576,435 | 578,123 | 1689 | 576,471 | 576,572 | 102 | |
| XII | YLR114C | 374,944 | 377,238 | 2295 | 375,259 | 375,360 | 102 |
| Frame 1 | Frame 2 | Total | |
|---|---|---|---|
| TAA | 64,458 | 91,661 | 156,119 |
| TAG | 51,774 | 37,366 | 89,140 |
| TGA | 69,568 | 115,459 | 185,027 |
| Total | 185,800 | 244,486 | 430,286 |
| Genes with Motifs | Non- Genes | Total | |||||
|---|---|---|---|---|---|---|---|
| Verified genes | 5262 | 5082 | 4758 | 4388 | 4013 | 121 | 5383 |
| Uncharacterized genes | 449 | 348 | 266 | 221 | 174 | 97 | 546 |
| Dubious genes | 404 | 247 | 133 | 61 | 32 | 269 | 673 |
| Transposable elements | 60 | 60 | 60 | 59 | 59 | 29 | 89 |
| Total | 6175 | 5737 | 5217 | 4729 | 4278 | 516 | 6691 |
| Motifs | Verified Genes | |||
|---|---|---|---|---|
| Number | % | Number | % | |
| AAC | 9796 | 6.33 | 48,354 | 6.27 |
| AAT | 13,228 | 8.55 | 71,108 | 9.22 |
| ACC | 5245 | 3.39 | 24,307 | 3.15 |
| ATC | 7569 | 4.89 | 33,049 | 4.29 |
| ATT | 12,117 | 7.84 | 58,617 | 7.60 |
| CAG | 4350 | 2.81 | 24,378 | 3.16 |
| CTC | 2499 | 1.62 | 10,475 | 1.36 |
| CTG | 4121 | 2.66 | 20,695 | 2.68 |
| GAA | 15,353 | 9.93 | 90,008 | 11.68 |
| GAC | 9125 | 5.90 | 39,699 | 5.15 |
| GAG | 7935 | 5.13 | 38,265 | 4.96 |
| GAT | 14,132 | 9.14 | 74,274 | 9.64 |
| GCC | 4896 | 3.17 | 23,549 | 3.05 |
| GGC | 3992 | 2.58 | 18,951 | 2.46 |
| GGT | 9004 | 5.82 | 44,365 | 5.76 |
| GTA | 4623 | 2.99 | 23,497 | 3.05 |
| GTC | 5132 | 3.32 | 21,884 | 2.84 |
| GTT | 8538 | 5.52 | 42,051 | 5.46 |
| TAC | 5983 | 3.87 | 28,452 | 3.69 |
| TTC | 6997 | 4.52 | 34,862 | 4.52 |
| Total | 154,635 | 100.00 | 770,840 | 100.00 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Michel, C.J.; Nguefack Ngoune, V.; Poch, O.; Ripp, R.; Thompson, J.D. Enrichment of Circular Code Motifs in the Genes of the Yeast Saccharomyces cerevisiae. Life 2017, 7, 52. https://doi.org/10.3390/life7040052
Michel CJ, Nguefack Ngoune V, Poch O, Ripp R, Thompson JD. Enrichment of Circular Code Motifs in the Genes of the Yeast Saccharomyces cerevisiae. Life. 2017; 7(4):52. https://doi.org/10.3390/life7040052
Chicago/Turabian StyleMichel, Christian J., Viviane Nguefack Ngoune, Olivier Poch, Raymond Ripp, and Julie D. Thompson. 2017. "Enrichment of Circular Code Motifs in the Genes of the Yeast Saccharomyces cerevisiae" Life 7, no. 4: 52. https://doi.org/10.3390/life7040052
APA StyleMichel, C. J., Nguefack Ngoune, V., Poch, O., Ripp, R., & Thompson, J. D. (2017). Enrichment of Circular Code Motifs in the Genes of the Yeast Saccharomyces cerevisiae. Life, 7(4), 52. https://doi.org/10.3390/life7040052




