Ecology and Evolution in the RNA World Dynamics and Stability of Prebiotic Replicator Systems
Abstract
:1. Introduction
- Ecological diversity—maintaining the coexistence of a sufficient number of different species (replicators, sequences, genotypes, etc.) in light of the Gause-principle (see later), which poses a strict limit on the number of coexisting species based on the number of regulating factors.
- Ecological stability—maintaining dynamical stability in a given set of coexistent species against external perturbations.
- Evolutionary stability—maintaining an adequate amount of information (a critical diversity of replicator species) from generation to generation and avoiding information decay (diversity reduction) in spite of frequent mutations and the lack of error correction.
2. The Three Pillars of Prebiotics
2.1. Maintaining Diversity
2.2. Ecological Stability
2.3. Evolutionary Stability
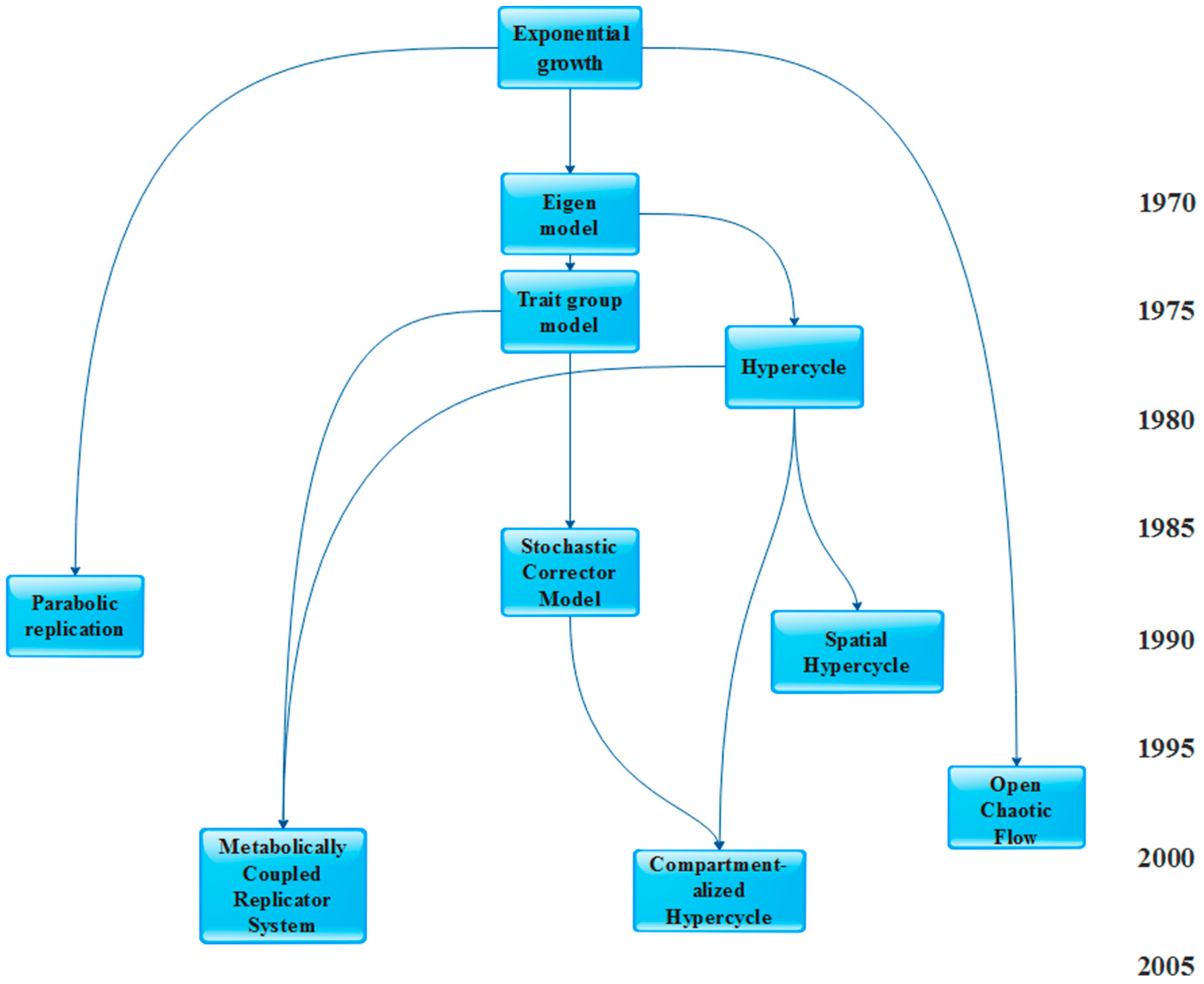
3. Models of Prebiotic Systems
- The Parabolic replicators (PR) model [17]
3.1. Models Assuming no Structure
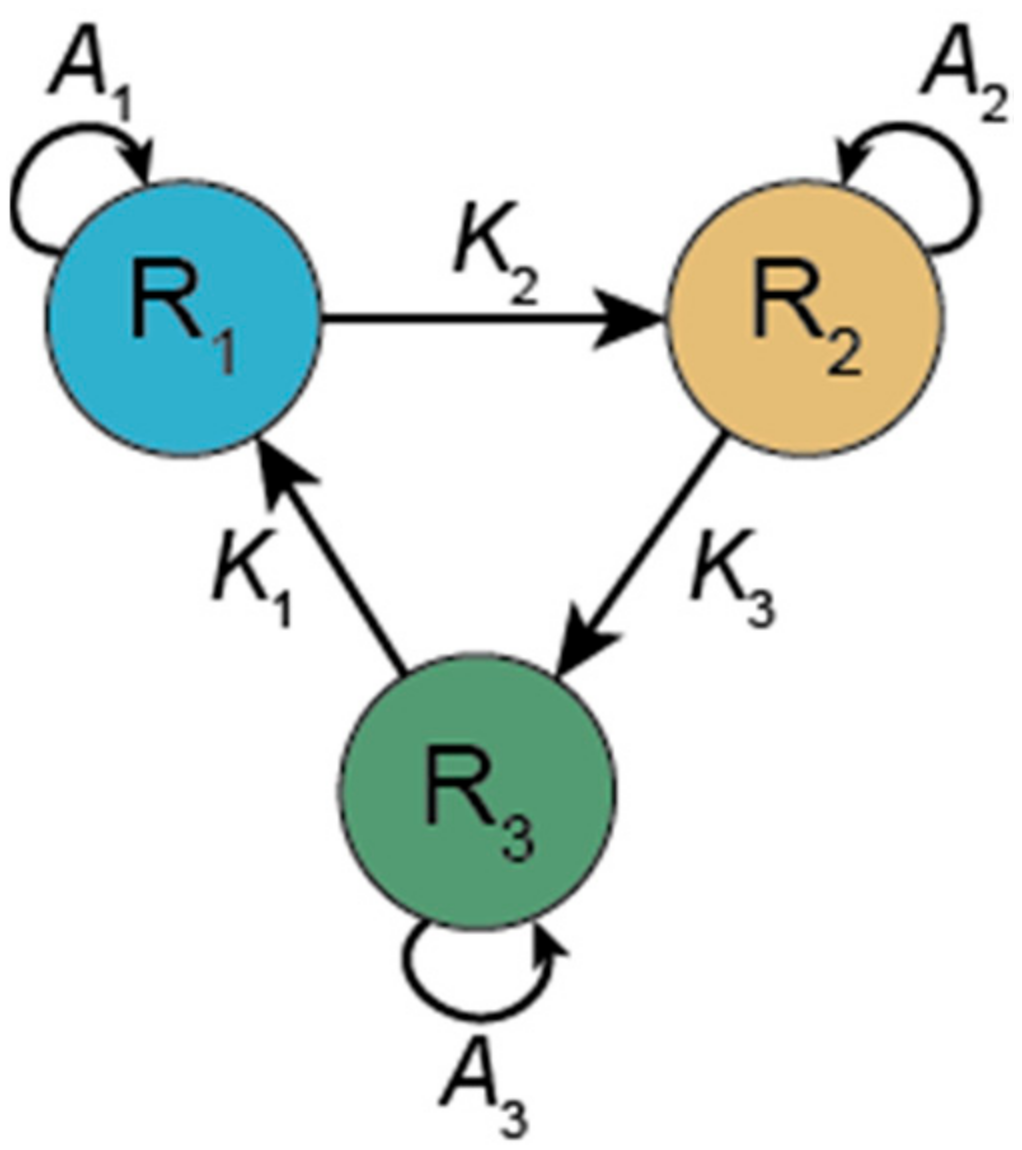
3.1.1. Hypercycle (HC)
3.1.2. Parabolic Replicators (PR)
3.2 Models Assuming Structure
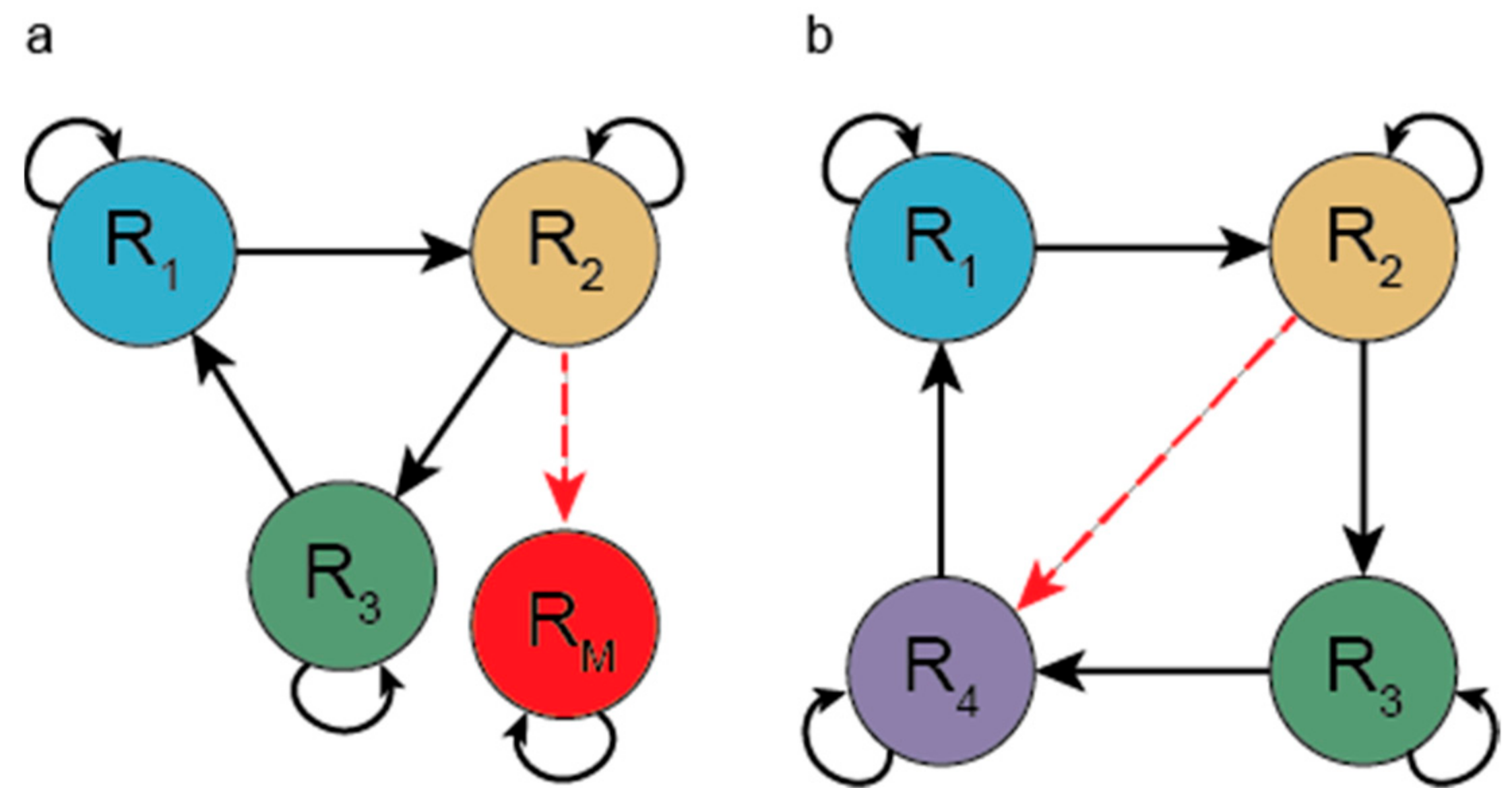
3.2.1. Spatial Hypercycle (SHC) and Compartmentalized Hypercycle (CHC)
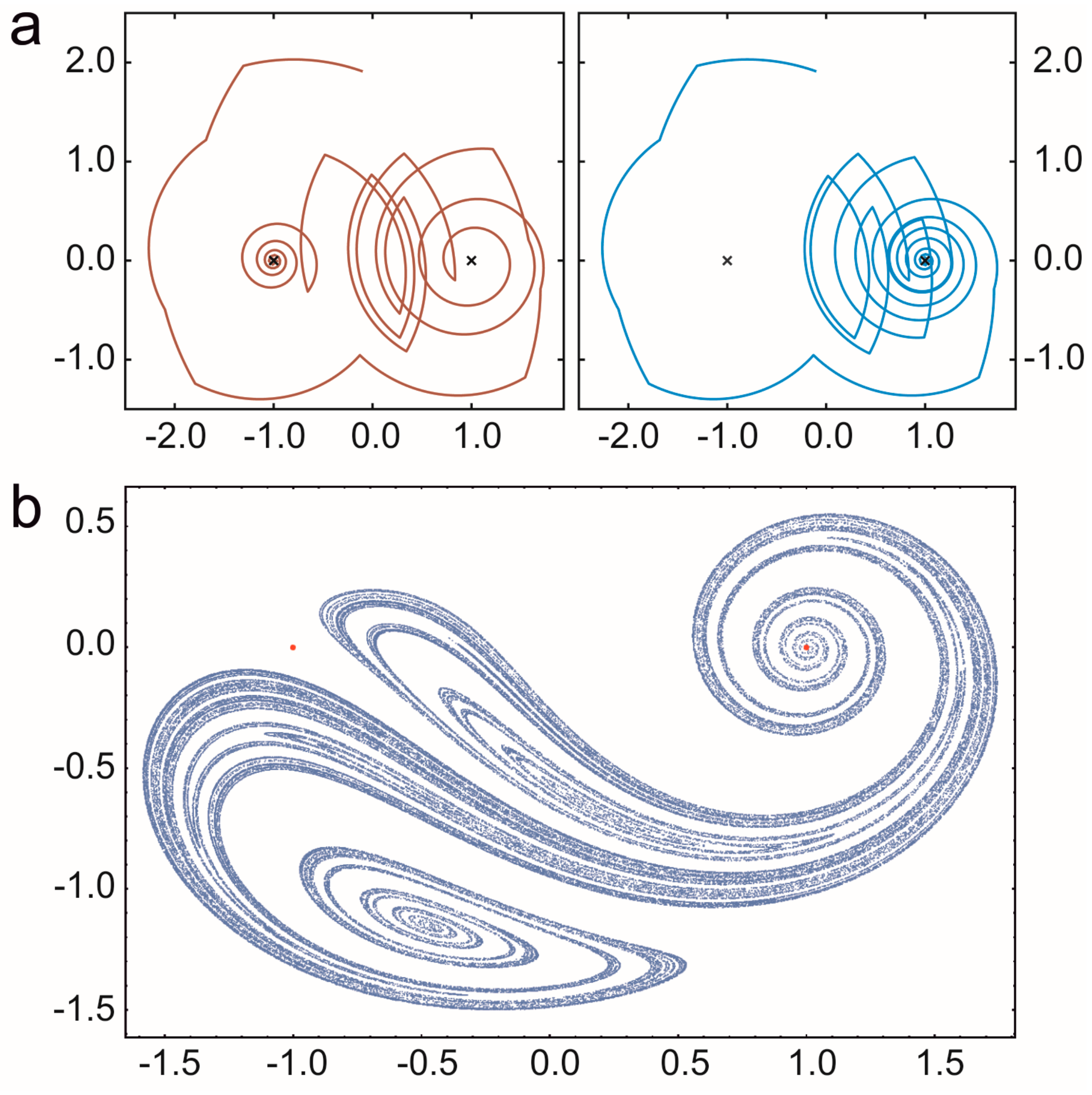
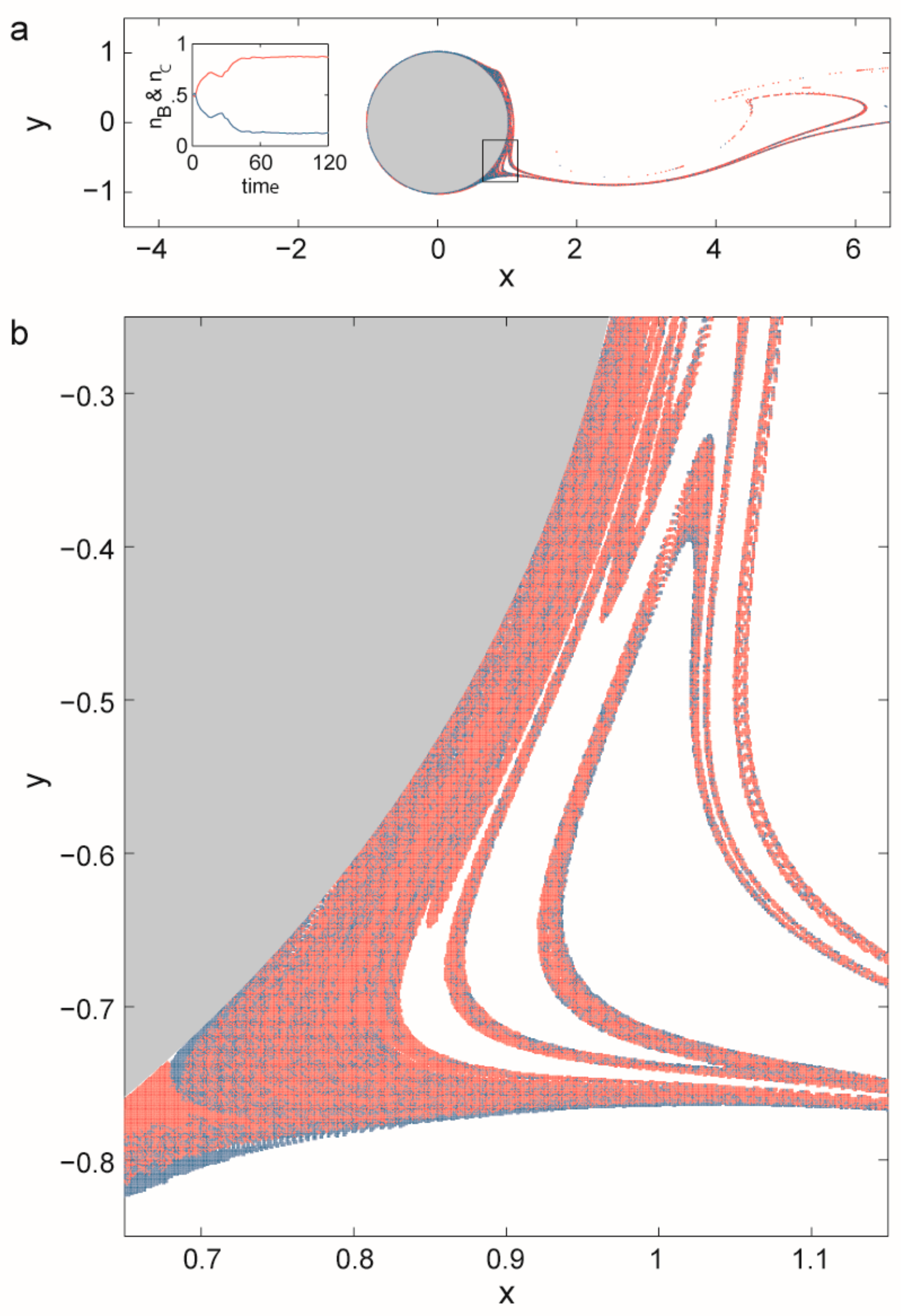
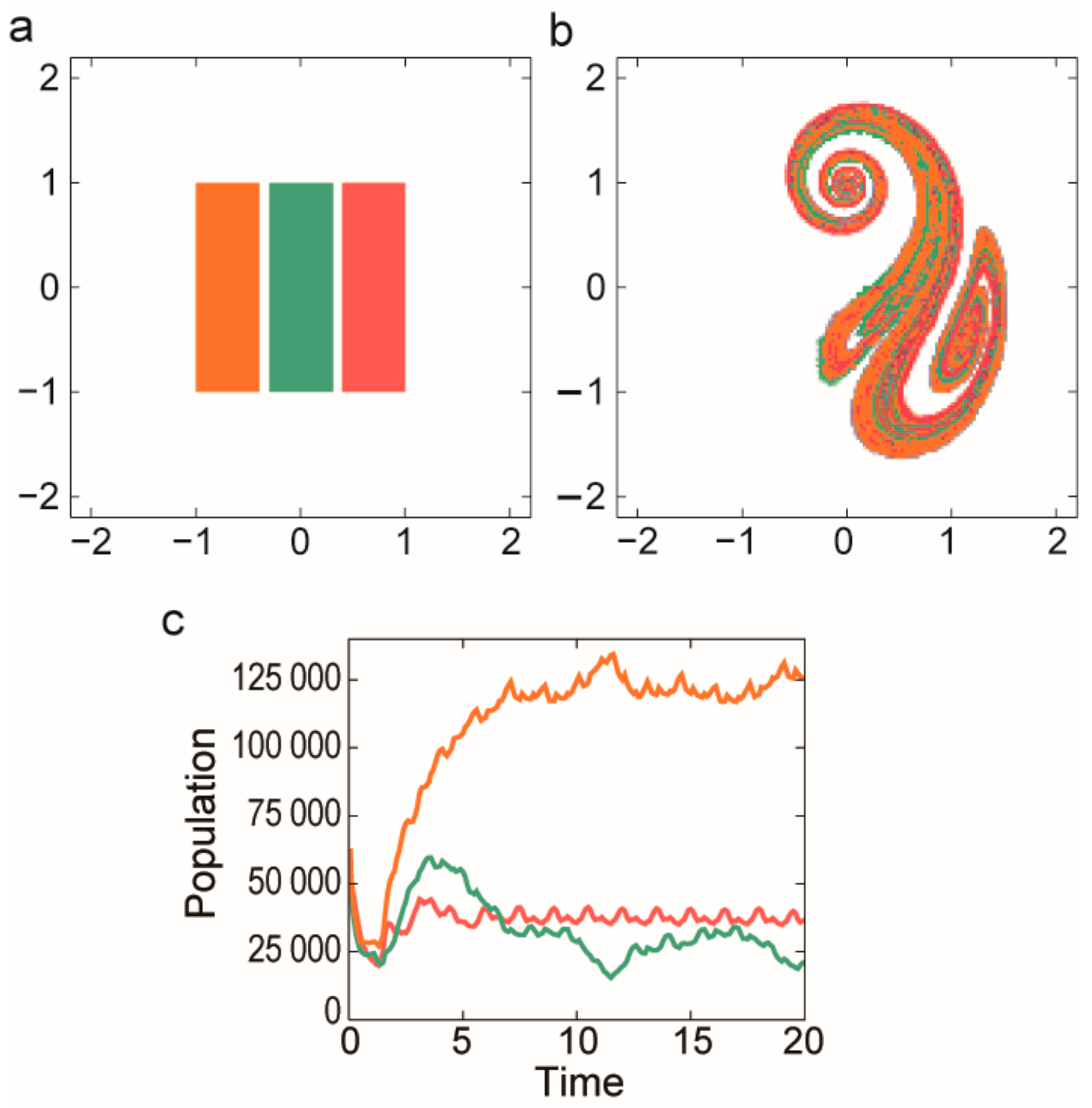
3.2.2. Coexistence in Open Chaotic Flow (OCF)
3.2.3. Trait Group Model and Kin Selection (TGM)
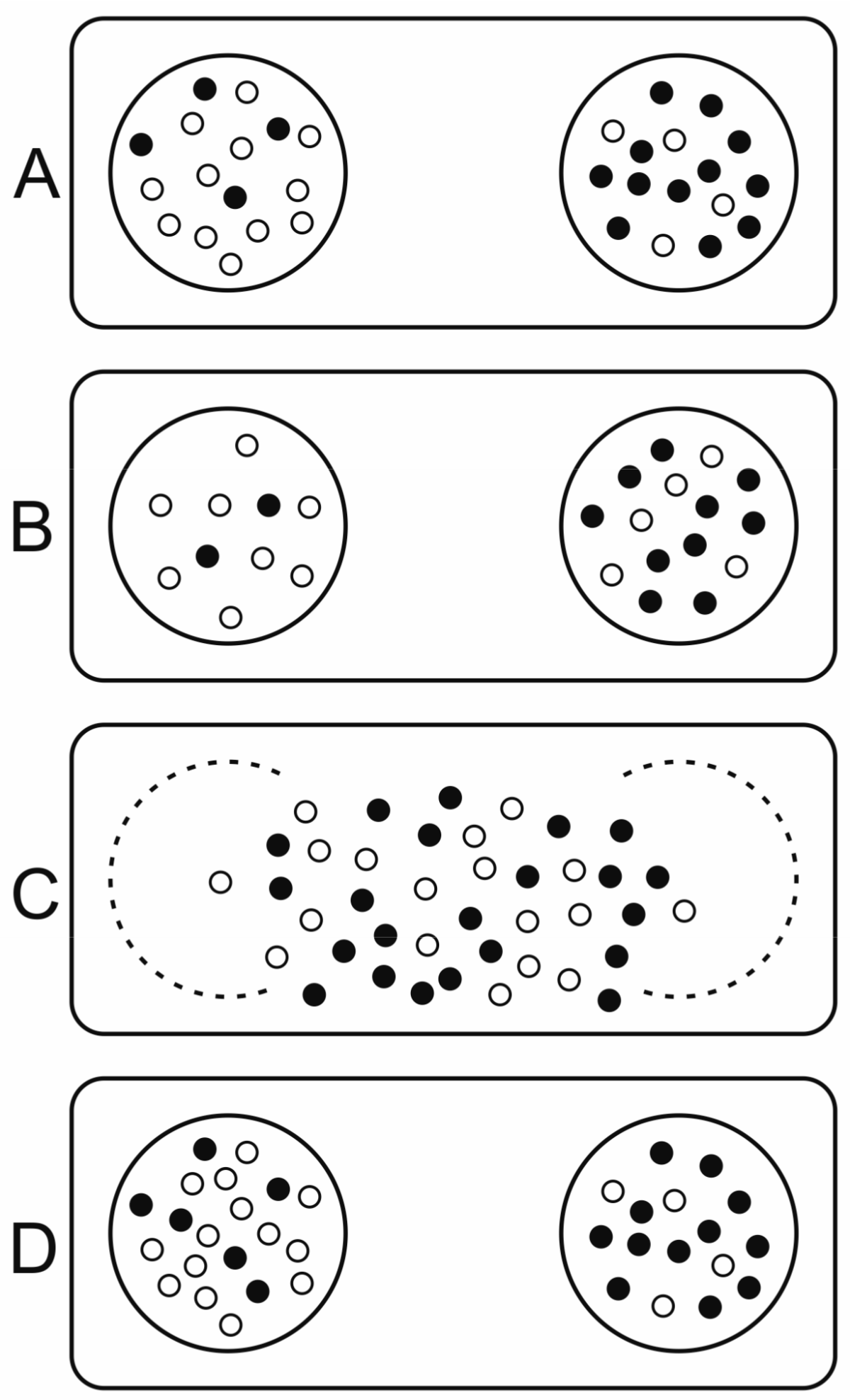
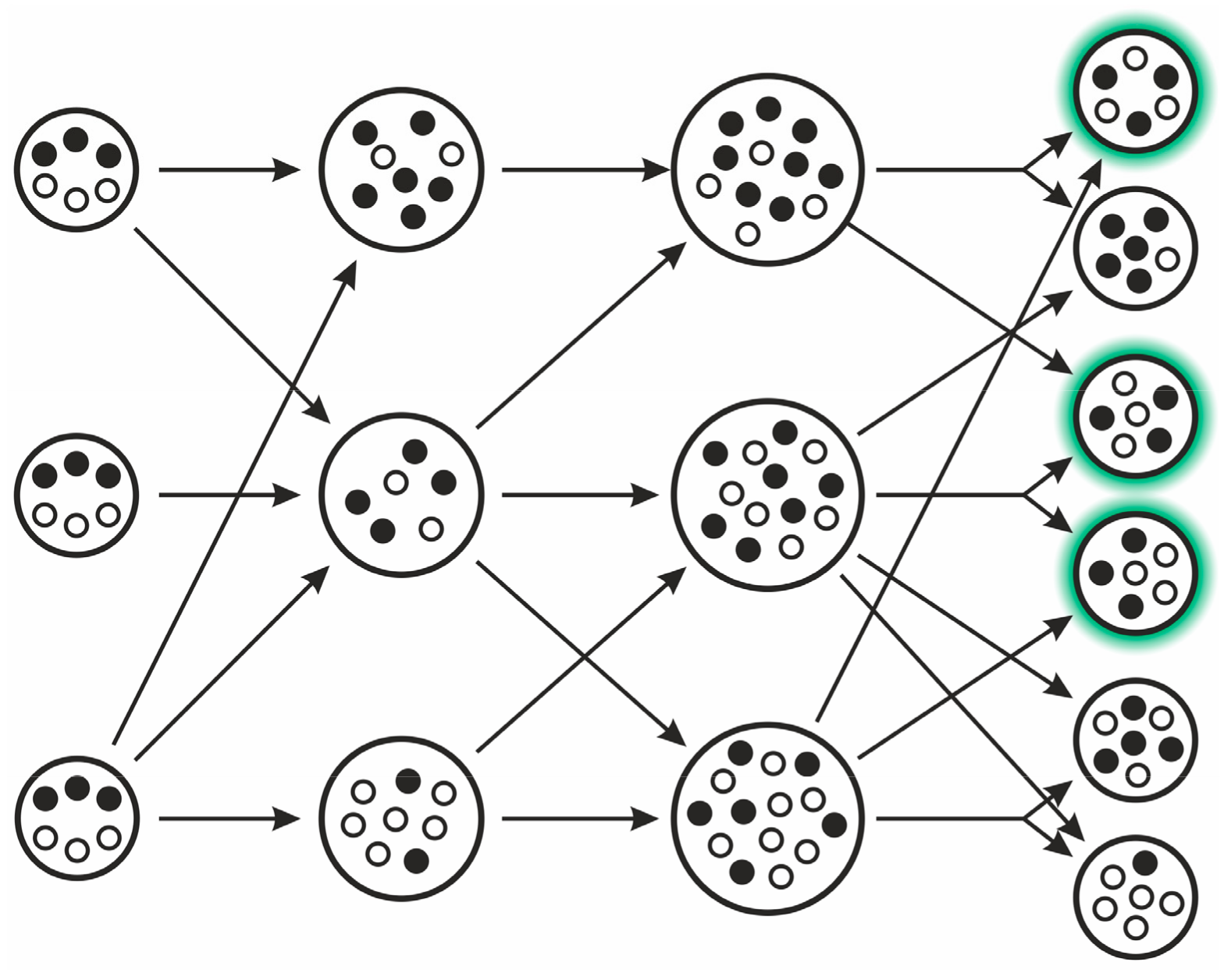
3.2.4. Stochastic Corrector Model (SCM)
- Template replicators replicate independently within vesicles (they are not hypercyclically coupled), competing for shared resources (nucleotides, enzymes, space).
- Replicators contribute to a common good (e.g., metabolism) such that they affect the selection of the whole group, thus compartment fitness (group replication rate) depends on composition.
- Replicators are essential: a group can only replicate if both replicator types are present.
- The redistribution of molecules during fission is not biased by any replicator type but is random for each molecule, hence they will follow a hypergeometric distribution in the offspring.
- Compartment size is relatively small and fission happens before equilibrium is reached in cells.
- Replicator migration (or other transposon-effects) from one compartment to another is negligible.
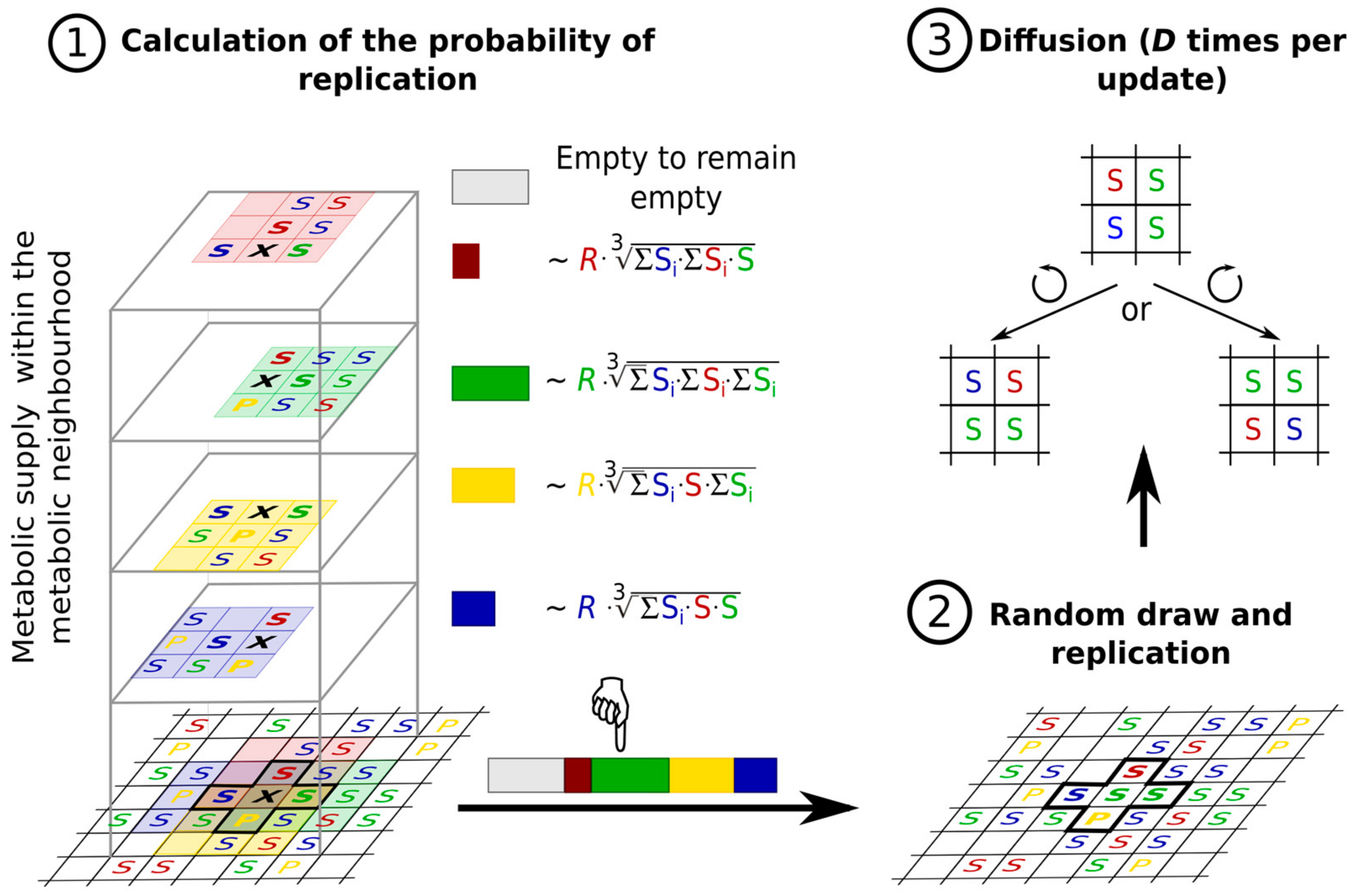
3.2.5. Metabolically Coupled Replicator System (MCRS)
The Concept of a Metabolically Coupled RNA World
- the replicase function is given: any RNA sequence is capable of producing a copy of itself by template replication if it has a sufficient concentration of monomers at its disposal.
- all the members of the metabolic replicator set are indispensable in running a simple metabolic reaction network (metabolism) producing the monomers; if any one replicator type is missing from the set, monomers are not produced at all and the system goes extinct.
- the replicators are attached to a 2D mineral surface on which their horizontal mobility is limited; replicators leaving the surface are lost to the system (replicator “death”).
- nutrient compounds (external initial substrates of the metabolic reaction network) are supplied from the third spatial dimension in excess.
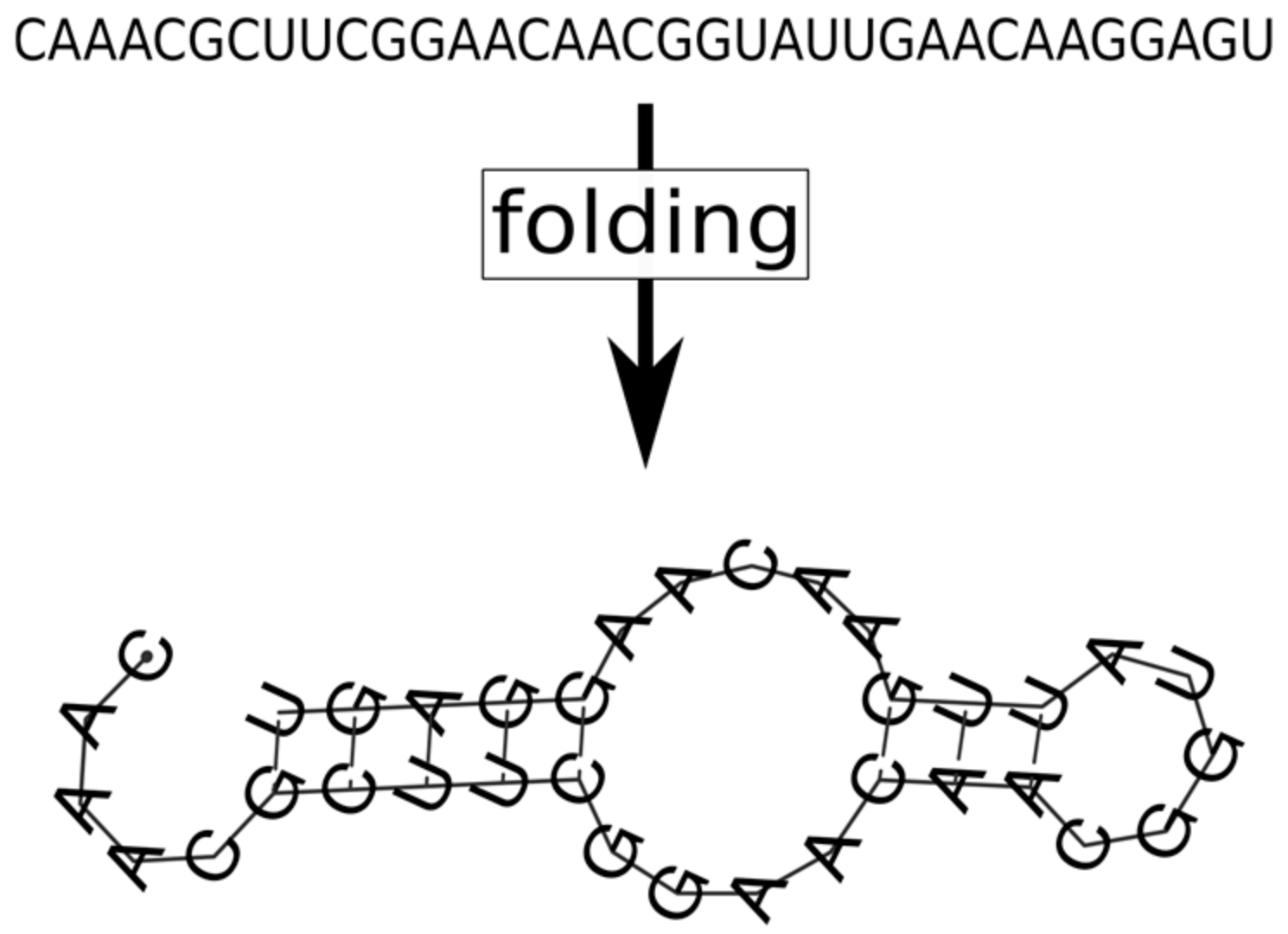
- the metabolites (substrates and products of the reactions that the replicators catalyse) are also attached to the surface, on which they may diffuse to a certain distance d before either being detached from the surface and lost, or used in a metabolic reaction or in replication (Figure 8).
- the metabolic contribution to the probability of a certain replicator being copied is dependent on the local ribozyme composition of its metabolic neighbourhood (i.e., within the distance d defining the metabolic neighbourhood of the focal replicator); only metabolically complete neighbourhoods (which have at least one copy of each essential ribozyme) allow for replication.
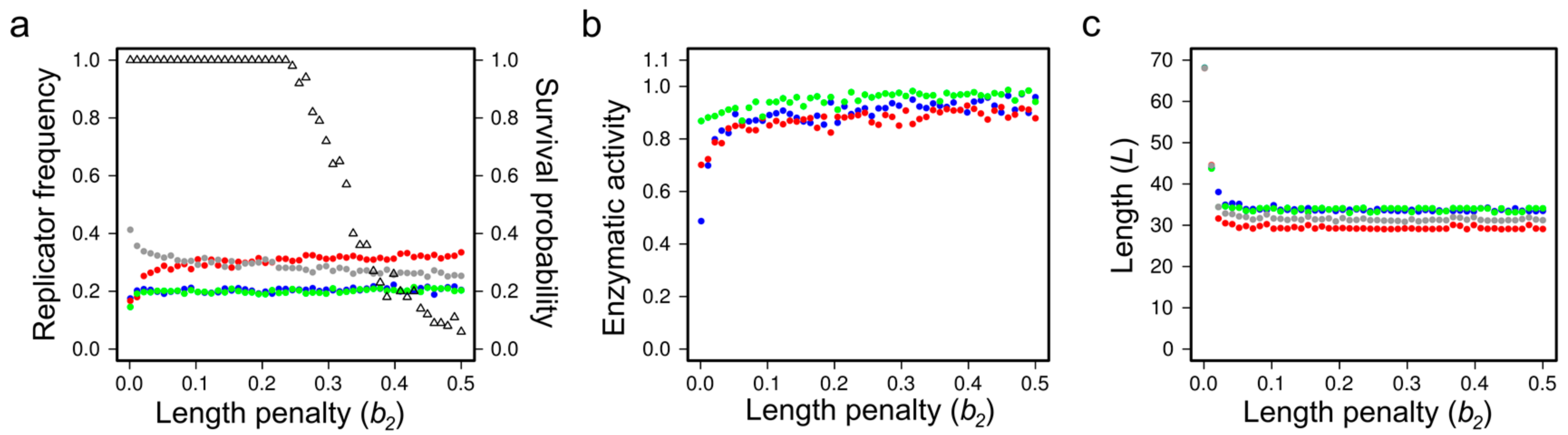
- the metabolically active set of ribozyme replicators may have enzymatically inactive parasites, i.e., replicators which do not contribute to monomer production but use the monomers produced by the cooperating replicators for their own replication.
Replicator Diversity and Ecological Stability in MCRS Models
Evolutionary Stability and Evolvability in MCRS Models
4. Discussion
- the stochastic corrector model (SCM), as long as the origin and the maintenance of compartments coupled to replicator population growth are explained;
- the parabolic replicator (PR) model and its dynamical homologue, the open chaotic flow (OCF) model, with the future addition of a scenario for the appearance of a selection regime; and
- the metabolically coupled replicator system (MCRS) model, which meets all the criteria for maintaining diversity and being robust both in the ecological and the evolutionary sense but only for a limited number of replicators as yet.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Eigen, M. Selforganization of matter and the evolution of biological macromolecules. Naturwissenscaften 1971, 10, 465–523. [Google Scholar] [CrossRef]
- Maynard Smith, J.; Szathmáry, E. The Major Transition in Evolution; W.H. Freeman: Oxford, UK, 1995. [Google Scholar]
- Szathmáry, E.; Maynard Smith, J. The origin of genetic system. Abstr. Bot. 1993, 17, 10. [Google Scholar]
- Watson, R.A.; Szathmáry, E. How can evolution learn? Trends Ecol. Evol. 2016, 31, 147–157. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Vladar, H.P.; Santos, M.; Szathmáry, E. Grand views of evolution. Trends Ecol. Evol. 2016, 32, 324–334. [Google Scholar] [CrossRef] [PubMed]
- Zachar, I.; Szathmáry, E. A new replicator: A theoretical framework for analysing replication. BMC Biol. 2010, 8, 21. [Google Scholar] [CrossRef] [PubMed]
- Segré, D.; Lancet, D.; Kedem, O.; Pilpel, Y. Graded autocatalytic replication domain (grad): Kinetic analysis of self-replication in mutually catalytic sets. Orig. Life Evol. Biosph. 1998, 28, 501–514. [Google Scholar] [CrossRef] [PubMed]
- Segré, D.; Ben-Eli, D.; Lancet, D. Compositional genomes: Prebiotic information transfer in mutually catalytic noncovalent assemblies. Proc. Natl. Acad. Sci. USA 2000, 97, 4112–4117. [Google Scholar] [CrossRef] [PubMed]
- Lancet, D.; Shenhav, B. Compositional lipid protocells: Reproduction without polynucleotides. In Protocells: Bridging Nonliving and Living Matter; Rasmussen, S., Bedau, M.A., Chen, L., Deamer, D., Krakauer, D.C., Packard, N.H., Stadler, P.F., Eds.; MIT Press: Cambridge, MA, USA, 2009; pp. 233–252. [Google Scholar]
- Kauffman, S.A. Autocatalytic sets of proteins. J. Theor. Biol. 1986, 119, 1–24. [Google Scholar] [CrossRef]
- Nghe, P.; Hordijk, W.; Kauffman, S.A.; Walker, S.I.; Schmidt, F.J.; Kemble, H.; Yeates, J.A.; Lehman, N. Prebiotic network evolution: Six key parameters. Mol. Biosyst. 2015, 11, 3206–3217. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W. Autocatalytic sets: From the origin of life to the economy. BioScience 2013, 63, 877–881. [Google Scholar]
- Vasas, V.; Szathmáry, E.; Santos, M. Lack of evolvability in self-sustaining autocatalytic networks constraints metabolism-first scenarios for the origin of life. Proc. Natl. Acad. Sci. USA 2010, 107, 1470–1475. [Google Scholar] [CrossRef] [PubMed]
- Vasas, V.; Fernando, C.; Szilágyi, A.; Zachár, I.; Santos, M.; Szathmáry, E. Primordial evolvability: Impasses and challenges. J. Theor. Biol. 2015, 381, 29–38. [Google Scholar] [CrossRef] [PubMed]
- Meszéna, G.; Gyllenberg, M.; Pásztor, L.; Metz, J.A.J. Competitive exclusion and limiting similarity: A unified theory. Theor. Popul. Biol. 2006, 69, 68–87. [Google Scholar] [CrossRef] [PubMed]
- Szilágyi, A.; Zachar, I.; Szathmáry, E. Gause’s principle and the effect of resource partitioning on the dynamical coexistence of replicating templates. PLoS Comput. Biol. 2013, 9, e1003193. [Google Scholar] [CrossRef] [PubMed]
- Szathmáry, E.; Gladkih, I. Sub-exponential growth and coexistence of non-enzymatically replicating templates. J. Theor. Biol. 1989, 138, 55–58. [Google Scholar] [CrossRef]
- Chesson, P. Multispecies competition in variable environments. Theor. Popul. Biol. 1994, 45, 227–276. [Google Scholar] [CrossRef]
- Levins, R. Coexistence in a variable environment. Am. Nat. 1979, 114, 765–783. [Google Scholar] [CrossRef]
- Szilágyi, A.; Meszéna, G. Coexistence in a fluctuating environment by the effect of relative nonlinearity: A minimal model. J. Theor. Biol. 2010, 267, 502–512. [Google Scholar] [CrossRef] [PubMed]
- Maynard Smith, J. Evolution and the Theory of Games; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Eigen, M.; Schuster, P. The hypercycle. A principle of natural self-organisation part a: Emergence of the hypercycle. Naturwissenscaften 1977, 64, 541–565. [Google Scholar] [CrossRef]
- Cronhjort, M.B.; Blomberg, C. Hypercycles versus parasites in a two dimensional partial differential equations model. J. Theor. Biol. 1994, 169, 31–49. [Google Scholar] [CrossRef]
- Cronhjort, M.B. Hypercycles versus parasites in the origin of life: Model dependence in spatial hypercycle systems. Orig. Life Evol. Biosph. 1995, 25, 227–233. [Google Scholar] [CrossRef] [PubMed]
- Boerlijst, M.C.; Hogeweg, P. Spiral wave structure in pre-biotic evolution: Hypercycles stable against parasites. Physica D 1991, 48, 17–28. [Google Scholar] [CrossRef]
- Boerlijst, M.C.; Hogeweg, P. Selfstructuring and selection: Spiral waves as a substrate for evolution. In Artificial Life; Langton, C.G., Taylor, C., Farmer, J.D., Rasmussen, S., Eds.; Addison-Wesley: Redwood City, CA, USA, 1991; Volume 2, pp. 255–276. [Google Scholar]
- Zintzaras, E.; Santos, M.; Szathmáry, E. “Living” under the challenge of information decay: The stochastic corrector model versus hypercycles. J. Theor. Biol. 2002, 217, 167–181. [Google Scholar] [CrossRef] [PubMed]
- Szathmáry, E.; Demeter, L. Group selection of early replicators and the origin of life. J. Theor. Biol. 1987, 128, 463–486. [Google Scholar] [CrossRef]
- Grey, D.; Hutson, V.; Szathmáry, E. A re-examination of the stochastic corrector model. Proc. R. Soc. Lond. Ser. B 1995, 262, 29–35. [Google Scholar] [CrossRef]
- Hubai, A.G.; Kun, Á. Maximal gene number maintainable by stochastic correction—The second error threshold. J. Theor. Biol. 2016, 405, 29–35. [Google Scholar] [CrossRef] [PubMed]
- Károlyi, G.; Péntek, Á.; Scheuring, I.; Tél, T.; Toroczkai, Z. Chaotic flow: The physics of species coexistence. Proc. Natl. Acad. Sci. USA 2000, 97, 13661–13665. [Google Scholar] [CrossRef] [PubMed]
- Károlyi, G.; Scheuring, I.; Czárán, T. Metabolic network dynamics in open chaotic flow. Chaos 2002, 12, 460–469. [Google Scholar] [CrossRef] [PubMed]
- Czárán, T.; Szathmáry, E. Coexistence of replicators in prebiotic evolution. In The Geometry of Ecological Interactions; Dieckmann, U., Law, R., Metz, J.A.J., Eds.; Cambridge University Press: Cambridge, UK, 2000; pp. 116–134. [Google Scholar]
- Könnyű, B.; Czárán, T.; Szathmáry, E. Prebiotic replicase evolution in a surface-bound metabolic system: Parasites as a source of adaptive evolution. BMC Evolut. Biol. 2008, 8, 267. [Google Scholar] [CrossRef] [PubMed]
- Könnyű, B.; Czárán, T. The evolution of enzyme specificity in the metabolic replicator model of prebiotic evolution. PLoS ONE 2011, 6, e20931. [Google Scholar] [CrossRef] [PubMed]
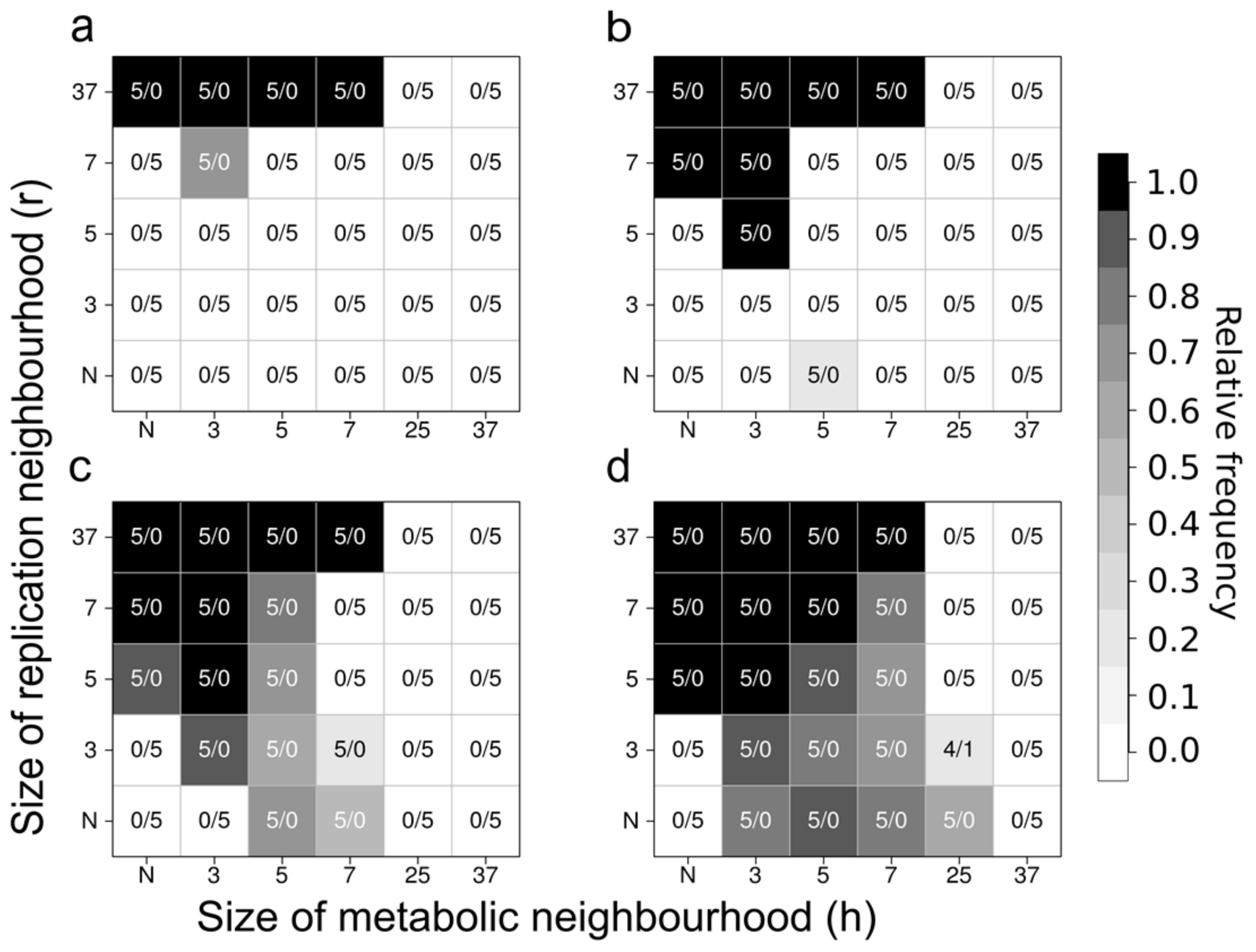
- Könnyű, B.; Czárán, T. Spatial aspects of prebiotic replicator coexistence and community stability in a surface-bound rna world model. BMC Evolut. Biol. 2013, 13, 204. [Google Scholar] [CrossRef] [PubMed]
- Czárán, T.; Könnyű, B.; Szathmáry, E. Metabolically coupled replicator systems: Overview of an rna-world model concept of prebiotic evolution on mineral surfaces. J. Theor. Biol. 2015, 381, 39–54. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Könnyű, B.; Szilágyi, A.; Czárán, T. In silico ribozyme evolution in a metabolically coupled rna population. Biol. Direct 2015, 10, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Wilson, D.S. A theory of group selection. Proc. Natl. Acad. Sci. USA 1975, 72, 143–146. [Google Scholar] [CrossRef] [PubMed]
- Matsumura, S.; Kun, Á.; Ryckelynck, M.; Coldren, F.; Szilágyi, A.; Jossinet, F.; Rick, C.; Nghe, P.; Szathmáry, E.; Griffiths, A.D. Transient compartmentalization of rna replicators prevents extinction due to parasites. Science 2016, 354, 1293–1296. [Google Scholar] [CrossRef] [PubMed]
- Eigen, M.; Schuster, P. The hypercycle. A principle of natural self-organisation part b: The abstract hypercycle. Naturwissenschaften 1978, 65, 7–41. [Google Scholar] [CrossRef]
- Eigen, M.; Schuster, P. The hypercycle. A principle of natural self-organisation part c: The realistic hypercycle. Naturwissenschaften 1978, 65, 341–369. [Google Scholar] [CrossRef]
- Eigen, M.; Schuster, P. The Hypercycle: A Principle of Natural Self-Organization; Springer: Berlin, Germany, 1979. [Google Scholar]
- Drake, J.W.; Charlesworth, B.; Charlesworth, D.; Crow, J.F. Rates of spontaneous mutation. Genetics 1998, 148, 1667–1686. [Google Scholar] [PubMed]
- Orgel, L.E. Molecular replication. Nature 1992, 358, 203–209. [Google Scholar] [CrossRef] [PubMed]
- Maynard Smith, J. Models of evolution. Proc. R. Soc. Lond. Ser. B 1983, 219, 315–325. [Google Scholar] [CrossRef]
- Szilágyi, A.; Kun, Á.; Szathmáry, E. Local neutral networks help maintain inaccurately replicating ribozymes. PLoS ONE 2014, 9, e109987. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kun, Á.; Szilágyi, A.; Könnyű, B.; Boza, G.; Zachár, I.; Szathmáry, E. The dynamics of the rna world: Insights and challenges. Ann. N. Y. Acad. Sci. 2015, 1341, 75–95. [Google Scholar] [CrossRef] [PubMed]
- Kun, Á.; Santos, M.; Szathmáry, E. Real ribozymes suggest a relaxed error threshold. Nat. Genet. 2005, 37, 1008–1011. [Google Scholar] [CrossRef] [PubMed]
- Szathmáry, E. On the propagation of a conceptual error concerning hypercycles and cooperation. J. Syst. Chem. 2013, 4, 1. [Google Scholar] [CrossRef]
- Hofbauer, J. A difference equation model for the hypercycle. SIAM J. Appl. Math. 1984, 44, 762–772. [Google Scholar] [CrossRef]
- Schuster, P.; Sigmund, K.; Wolff, R. Dynamical systems under constant organization. Iii. Cooperative and competitive behavior of hypercycles. J. Differ. Equ. 1979, 32, 357–368. [Google Scholar] [CrossRef]
- Hofbauer, J.; Schuster, P.; Sigmund, K. Competition and cooperation in catalytic selfreplication. J. Math. Biol. 1981, 11, 155–168. [Google Scholar] [CrossRef]
- Hofbauer, J. A general cooperation theorem for hypercycles. Monatshefte Mathematik 1981, 91, 233–240. [Google Scholar] [CrossRef]
- Hofbauer, J.; Schuster, P.; Sigmund, K.; Wolff, R. Dynamical systems under constant organization ii: Homogeneous growth functions of degree p = 2. SIAM J. Appl. Math. 1980, 38, 282–304. [Google Scholar] [CrossRef]
- Schuster, P.; Sigmund, K.; Wolff, R. Dynamical systems under constant organization i. Topological analysis of a family of non-linear differential equations—A model for catalytic hypercycles. Bull. Math. Biol. 1978, 40, 743–769. [Google Scholar] [PubMed]
- Guillamon, A.; Fontich, E.; Sardanyés, J. Bifurcations analysis of oscillating hypercycles. J. Theor. Biol. 2015, 387, 23–30. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hofbauer, J.; Mallet-Paret, J.; Smith, H.L. Stable periodic solutions for the hypercycle system. J. Dyn. Differ. Equ. 1991, 3, 423–436. [Google Scholar] [CrossRef]
- Stadler, P.F.; Nuño, J.C. The influence of mutation on autocatalytic reaction networks. Math. Biosci. 1994, 122, 127–160. [Google Scholar] [CrossRef]
- Nuño, J.C.; Andrade, M.A.; Morán, F.; Montero, F. A model of an autocatalytic network formed by error-prone self-replicative species. Bull. Math. Biol. 1993, 55, 385–415. [Google Scholar] [CrossRef]
- Sardanyés, J.; Duarte, J.; Januário, C.; Martins, N. Topological entropy of catalytic sets: Hypercycles revisited. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 795–803. [Google Scholar] [CrossRef]
- Sardanyés, J. Error threshold ghosts in a simple hypercycle with error prone self-replication. Chaos Solitons Fract. 2008, 35, 313–319. [Google Scholar] [CrossRef]
- García-Tejedor, A.; Morán, F.; Montero, F. Influence of the hypercyclic organization on the error threshold. J. Theor. Biol. 1987, 127, 393–402. [Google Scholar] [CrossRef]
- García-Tejedor, A.; Sanz-Nuño, J.C.; Olarrea, J.; de la Rubia, F.J.; Montero, F. Influence of the hypercycle on the error threshold: A stochastic approach. J. Theor. Biol. 1988, 134, 431–443. [Google Scholar] [CrossRef]
- Silvestre, D.A.M.M.; Fontanari, J.F. The information capacity of hypercycles. J. Theor. Biol. 2008, 254, 804–806. [Google Scholar] [CrossRef] [PubMed]
- Campos, P.R.A.; Fontanari, J.F.; Stadler, P.F. Error propagation in the hypercycle. Phys. Rev. E 2000, 61, 2996–3002. [Google Scholar] [CrossRef]
- Szathmáry, E. Simple growth laws and selection consequences. Trends Ecol. Evol. 1991, 6, 366–370. [Google Scholar] [CrossRef]
- Hofbauer, J. Competitive exclusion of disjoint hypercycles. Z. Phys. Chem. 2002, 216, 35–39. [Google Scholar] [CrossRef]
- Boerlijst, M.C.; Hogeweg, P. Attractors and spatial patterns in hypercycles with negative interactions. J. Theor. Biol. 1995, 176, 199–210. [Google Scholar] [CrossRef]
- Bresch, C.; Niesert, U.; Harnasch, D. Hypercycles, parasites and packages. J. Theor. Biol. 1980, 85, 399–405. [Google Scholar] [CrossRef]
- Maynard Smith, J. Hypercycles and the origin of life. Nature 1979, 280, 445–446. [Google Scholar] [CrossRef]
- Mills, D.R.; Peterson, R.E.; Spiegelman, S. An extracellular darwinian experiment with a self-duplicating nucleic acid molecule. Proc. Natl. Acad. Sci. USA 1967, 58, 217–224. [Google Scholar] [CrossRef] [PubMed]
- Levisohn, R.; Spiegelman, S. Further extracellular darwinian experiments with replicating rns molecules: Diverse variants isolated under different selective conditions. Proc. Natl. Acad. Sci. USA 1969, 63, 805–811. [Google Scholar] [CrossRef] [PubMed]
- Szostak, N.; Wasik, S.; Blazewicz, J. Hypercycle. PLOS Comput. Biol. 2016, 12, e1004853. [Google Scholar] [CrossRef] [PubMed]
- Von Kiedrowski, G. A self-replicating hexadeoxynucleotide. Angew. Chem. Int. Ed. 1986, 25, 932–935. [Google Scholar] [CrossRef]
- Von Kiedrowski, G. Minimal replicator theory i.: Parabolic versus exponential growth. Bioorg. Chem. Front. 1993, 3, 113–146. [Google Scholar]
- Von Kiedrowski, G. Molekulare prinzipen der artifiziellen selbsreplikation. In Gene, Neurone, Qubits and co. Unsere Welt der Informationen; Ganten, D., Ed.; Hirzel Verlag: Stuttgart, Germany, 1999; pp. 123–145. [Google Scholar]
- Varga, Z.; Szathmáry, E. An extremum principle for parabolic competition. Bull. Math. Biol. 1997, 59, 1145–1154. [Google Scholar] [CrossRef]
- Darwin, C. On the Origin of Species by Means of Natural Selection, or Preservation of Favoured Races in the Struggle for Life; John Murray: London, UK, 1859. [Google Scholar]
- Lifson, S.; Lifson, H. A model of prebiotic replication: Survival of the fittest versus extinction of the unfittest. J. Theor. Biol. 1999, 199, 425–433. [Google Scholar] [CrossRef] [PubMed]
- Scheuring, I.; Szathmáry, E. Survival of replicators with parabolic growth tendency and exponential decay. J. Theor. Biol. 2001, 212, 99–105. [Google Scholar] [CrossRef] [PubMed]
- Von Kiedrowski, G.; Szathmáry, E. Selection versus coexistence of parabolic replicators spreading on surfaces. Selection 2000, 1, 173–179. [Google Scholar] [CrossRef]
- Vespalcová, Z.; Holden, A.V.; Brindley, J. The effect of inhibitory connections in a hypercycle: A study of the spatio-temporal evolution. Phys. Lett. A 1995, 197, 147–156. [Google Scholar] [CrossRef]
- Boerlijst, M.C.; Hogeweg, P. Spatial gradients enhance persistence of hypercycles. Phys. D 1995, 88, 29–39. [Google Scholar] [CrossRef]
- Kim, P.-J.; Jeong, H. Spatio-temporal dynamics in the origin of genetic information. Phys. D Nonlinear Phenom. 2005, 203, 88–99. [Google Scholar] [CrossRef]
- Tél, T. Transient chaos. In Directions in Chaos; World Scientific: Singapore, 1990; Volume 3, pp. 149–211. [Google Scholar]
- Toroczkai, Z.; Károlyi, G.; Péntek, Á.; Tél, T.; Grebogi, C. Advection of active particles in open chaotic flows. Phys. Rev. Lett. 1998, 80, 500–503. [Google Scholar] [CrossRef]
- Scheuring, I.; Károlyi, G.; Toroczkai, Z.; Tél, T.; Péntek, Á. Competing populations in flows with chaotic mixing. Theor. Popul. Biol. 2003, 63, 77–90. [Google Scholar] [CrossRef]
- Scheuring, I.; Czárán, T.; Szabó, P.; Károlyi, G.; Toroczkai, Z. Spatial models of prebiotic evolution: Soup before pizza? Orig. Life Evol. Biosph. 2003, 33, 319–355. [Google Scholar] [CrossRef] [PubMed]
- Wilson, D.S. Structured demes and the evolution of group-advantageous traits. Am. Nat. 1977, 111, 157–185. [Google Scholar] [CrossRef]
- Maynard Smith, J. Group selection. Quart. Rev. Biol. 1976, 51, 277–283. [Google Scholar]
- Hamilton, W.D. Genetical evolution of social behaviour i and ii. J. Theor. Biol. 1964, 7, 1–52. [Google Scholar] [CrossRef]
- Cohen, D.; Eshel, I. On the founder effect and the evolution of altruistic traits. Theor. Popul. Biol. 1976, 10, 276–302. [Google Scholar] [CrossRef]
- Szathmáry, E. Natural selection and dynamical coexistence of defective and complementing virus segments. J. Theor. Biol. 1992, 157, 383–406. [Google Scholar] [CrossRef]
- Szathmáry, E. The eukaryotic cell as an information integrator. Endocytobiosis Cell Res. 1986, 3, 113–132. [Google Scholar]
- Szathmáry, E. The emergence, maintenance, and transitions of the earliest evolutionary units. Oxf. Surv. Evol. Biol. 1989, 6, 169–205. [Google Scholar]
- Szathmáry, E. The integration of the earliest genetic information. Trends Ecol. Evol. 1989, 4, 200–204. [Google Scholar] [CrossRef]
- Joyce, G.F. The antiquity of rna-based evolution. Nature 2002, 418, 214–220. [Google Scholar] [CrossRef] [PubMed]
- Santos, M.; Zintzaras, E.; Szathmáry, E. Origin of sex revisited. Orig. Life Evol. Biosph. 2003, 33, 405–432. [Google Scholar] [CrossRef] [PubMed]
- Gánti, T. Az Élet Princípiuma (The Principle of Life); Gondolat: Budapest, Hungary, 1971. [Google Scholar]
- Gánti, T. The Principles of Life; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Gánti, T. Chemoton Theory; Kluwer Academic/Plenum Publishers: New York, NY, USA, 2003. [Google Scholar]
- Zachar, I.; Fedor, A.; Szathmáry, E. Two different template replicators coexisting in the same protocell: Stochastic simulation of an extended chemoton model. PLoS ONE 2011, 6, e21380. [Google Scholar] [CrossRef] [PubMed]
- Szathmáry, E. Toward major evolutionary transitions theory 2.0. Proc. Natl. Acad. Sci. USA 2015, 112, 10104–10111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wochner, A.; Attwater, J.; Coulson, A.; Holliger, P. Ribozyme-catalyzed transcription of an active ribozyme. Science 2011, 332, 209–212. [Google Scholar] [CrossRef] [PubMed]
- Attwater, J.; Wochner, A.; Holliger, P. In-ice evolution of rna polymerase ribozyme activity. Nat. Chem. 2013, 5, 1011–1018. [Google Scholar] [CrossRef] [PubMed]
- Horning, D.P.; Joyce, G.F. Amplification of rna by an rna polymerase ribozyme. Proc. Natl. Acad. Sci. USA 2016, 113, 9786–9791. [Google Scholar] [CrossRef] [PubMed]
- Chumachenko, N.V.; Novikov, Y.; Yarus, M. Rapid and simple ribozymic aminoacylation using three conserved nucleotides. J. Am. Chem. Soc. 2009, 131, 5257–5263. [Google Scholar] [CrossRef] [PubMed]
- Ruiz-Mirazo, K.; Briones, C.; de la Escosura, A. Prebiotic systems chemistry: New perspectives for the origins of life. Chem. Rev. 2014, 114, 285–366. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.; Higgs, P.G. Origin of self-replicating biopolymers: Autocatalytic feedback can jump-start the rna world. J. Mol. Evol. 2009, 69, 541. [Google Scholar] [CrossRef] [PubMed]
- Benner, S.A.; Kim, H.-J.; Carrigan, M.A. Asphalt, water, and the prebiotic synthesis of ribose, ribonucleosides, and rna. Acc. Chem. Res. 2012, 45, 2025–2034. [Google Scholar] [CrossRef] [PubMed]
- Szostak, N.; Synak, J.; Borowski, M.; Wasik, S.; Blazewicz, J. Simulating the origins of life: The dual role of rna replicases as an obstacle to evolution. PLoS ONE 2017, 12, e0180827. [Google Scholar] [CrossRef] [PubMed]
- Takeuchi, N.; Hogeweg, P. Multilevel selection in models of prebiotic evolution ii: A direct comparison of compartmentalization and spatial self-organization. PLoS Comput. Biol. 2009, 5, e1000542. [Google Scholar] [CrossRef] [PubMed]
- Toffoli, T.; Margolus, N. Cellular Automata Machines: A New Environment for Modelling; MIT Press: Cambridge, MA, USA, 1987. [Google Scholar]
- Könnyű, B.; Czárán, T. Phenotype/genotype sequence complementarity and prebiotic replicator coexistence in the metabolically coupled replicator system. BMC Evol. Biol. 2014, 14, 234. [Google Scholar] [CrossRef] [PubMed]
- Tél, T.; Károlyi, G.; Péntek, Á.; Scheuring, I.; Toroczkai, Z.; Grebogi, C.; Kadtke, J. Chaotic advection, diffusion, and reactions in open flows. Chaos Interdiscip. J. Nonlinear Sci. 2000, 10, 89–98. [Google Scholar] [CrossRef] [PubMed]
- Tél, T.; de Moura, A.; Grebogi, C.; György, K. Chemical and biological activity in open flows: A dynamical system approach. Phys. Rep. 2005, 413, 91–196. [Google Scholar] [CrossRef]
- Priye, A.; Yu, Y.; Hassan, Y.A.; Ugaz, V.M. Synchronized chaotic targeting and acceleration of surface chemistry in prebiotic hydrothermal microenvironments. Proc. Natl. Acad. Sci. USA 2017, 114, 1275–1280. [Google Scholar] [CrossRef] [PubMed]
- Lorenz, R.; Bernhart, S.; Honer zu Siederdissen, C.; Tafer, H.; Flamm, C.; Stadler, P.; Hofacker, I. Viennarna package 2.0. Algorithms Mol. Biol. 2011, 6, 26. [Google Scholar] [CrossRef] [PubMed]
- Higgs, P.; Wu, M. The importance of stochastic transitions for the origin of life. Orig. Life Evol. Biosph. 2012, 42, 453–457. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.; Higgs, P. The origin of life is a spatially localized stochastic transition. Biol. Direct 2012, 7, 42. [Google Scholar] [CrossRef] [PubMed]
- Takeuchi, N.; Hogeweg, P.; Kaneko, K. The origin of a primordial genome through spontaneous symmetry breaking. Nat. Commun. 2017, 8, 250. [Google Scholar] [CrossRef] [PubMed]
- Yarus, M. Life from an Rna World: The Ancestor Within; Harvard University Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Gil, R.; Silva, F.J.; Peretó, J.; Moya, A. Determination of the core of a minimal bacterial gene set. Microbiol. Mol. Biol. Rev. 2004, 68, 518–537. [Google Scholar] [CrossRef] [PubMed]
| Structure/Time | Discrete Time | Continuous Time | |
|---|---|---|---|
| Without structure (only global interactions) | - | QS, HC, PR | |
| With structure (global and local interactions) | Compartmentalized | SCM | CHC, TGM |
| Spatial | MCRS | SHC, CM |
| Diversity-Maintaining Ability | Ecological Stability | Evolutionary Stability | Evolvability | |
|---|---|---|---|---|
| HC | An arbitrary number of sequences can coexist if there is no population stochasticity; otherwise some species can be lost. | The cooperative nature of organization ensures that, given high enough catalytic aid, the system is stable. | Selfish parasites and short-cut mutants can destroy the system. | No |
| SHC | Due to the importance of local interaction, the number of potentially coexisting sequences is limited. | The cooperative nature of organization ensures that, given high enough catalytic aid, the system is stable. | The organization is stable against selfish parasites but short-cut mutants could still take over. The system still cannot evolve new hypercycle members. | No |
| CHC | The number of sequences is limited due to the random assortment into daughter cells. | The cooperative nature of organization ensures that, given high enough catalytic aid, the system is stable. | Group selection can probably maintain existing diversity but the system still cannot evolve new hypercycle members. | N/A |
| PR | An arbitrary number of sequences can coexist at arbitrarily small concentrations. | The continuous advantage of rarity of any replicator ensures coexistence at any external parameter combination. |
| No |
| SCM | N/A | N/A |
| Yes |
| OCF | An arbitrary number of sequences can coexist at arbitrarily small concentrations but locally dense populations (the concentration at the boundary of fractals can be very high). | The continuous advantage of rarity for any replicator ensures the coexistence at any external parameter combination. |
| No |
| MCRS | A limited number of ribozyme replicators coexist in a highly robust system. | Advantage of rarity due to the mandatory metabolic cooperation of all replicator species maintains stability across the parameter space. |
| Yes |
| TGM | N/A | N/A |
| Yes |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szilágyi, A.; Zachar, I.; Scheuring, I.; Kun, Á.; Könnyű, B.; Czárán, T. Ecology and Evolution in the RNA World Dynamics and Stability of Prebiotic Replicator Systems. Life 2017, 7, 48. https://doi.org/10.3390/life7040048
Szilágyi A, Zachar I, Scheuring I, Kun Á, Könnyű B, Czárán T. Ecology and Evolution in the RNA World Dynamics and Stability of Prebiotic Replicator Systems. Life. 2017; 7(4):48. https://doi.org/10.3390/life7040048
Chicago/Turabian StyleSzilágyi, András, István Zachar, István Scheuring, Ádám Kun, Balázs Könnyű, and Tamás Czárán. 2017. "Ecology and Evolution in the RNA World Dynamics and Stability of Prebiotic Replicator Systems" Life 7, no. 4: 48. https://doi.org/10.3390/life7040048
APA StyleSzilágyi, A., Zachar, I., Scheuring, I., Kun, Á., Könnyű, B., & Czárán, T. (2017). Ecology and Evolution in the RNA World Dynamics and Stability of Prebiotic Replicator Systems. Life, 7(4), 48. https://doi.org/10.3390/life7040048





