Abstract
In 1957, Francis Crick et al. suggested an ingenious explanation for the process of frame maintenance. The idea was based on the notion of comma-free codes. Although Crick’s hypothesis proved to be wrong, in 1996, Arquès and Michel discovered the existence of a weaker version of such codes in eukaryote and prokaryote genomes, namely the so-called circular codes. Since then, circular code theory has invariably evoked great interest and made significant progress. In this article, the codon distributions in maximal comma-free, maximal self-complementary and maximal self-complementary circular codes are discussed, i.e., we investigate in how many of such codes a given codon participates. As the main (and surprising) result, it is shown that the codons can be separated into very few classes (three, or five, or six) with respect to their frequency. Moreover, the distribution classes can be hierarchically ordered as refinements from maximal comma-free codes via maximal self-complementary codes to maximal self-complementary circular codes.
1. Introduction
The genetic code as it is today is a product of a long evolutionary process. It can be seen as a kind of dictionary that translates information from the world of nucleic acids into the world of proteins. As such, it is involved in the transmission of information, the translation process, and thus, plays an essential role in the process that defines the central dogma of molecular biology. During this process, degeneracy is one of the most conserved features of the genetic code. It can be postulated that this is for a good reason, since degeneracy is the fundamental ingredient in any error-detecting and error-correcting system [1,2]. Therefore, for example, the self-referential model for the formation of the code is based on an original regionalization of characters through the concerted superposition of the two components of the encodings. With this approach, the degeneracy of the genetic code and clusters of similar amino acids corresponding to similar triplets should be explained [3].
The preservation of the genetic information is impossible without an error-correcting system (this can even be proven by the methods of information theory) and cannot be guaranteed just by DNA replication. There are different hypotheses for how such error-correction may happen. In [4], the so-called ambush hypothesis is examined. According to this hypothesis, off-frame stops terminate frameshifted translation, potentially decreasing energy and resource waste on nonfunctional proteins. Moreover, codons with more potential to form hidden stops (off-frame stops) have greater usage frequency and bias in their favor among synonymous codons. In [5], a model of an amino acid composed of a constant part and of a variable part is considered, and it was concluded that the kinetic energetic disturbance caused by the substitution of the variable part of an amino acid is minimized. In [6], error prevention and mitigation as forces in the evolution of genes and genomes are postulated.
Errors in the translation process can occur in several ways, e.g., mutation of the genetic information or insertion/deletion of nucleotides. In the late 1950s, biologists tripped over another essential source of errors, the so-called frameshift problem: a sequence of nucleotides can be translated correctly into a chain of amino acids only when it is read in the correct frame. The first reaction to this problem was the new concept of “codes without commas”, nowadays called comma-free codes, suggested by Crick, Griffith and Orgel [7]. They hypothesized that only a subset of codons is actually used for the translation. The strong property of such codes is the immediate detection of the wrong reading frame. Each out-of-frame codon in a sequence of codons from a comma-free code is outside the code and has therefore no meaning. In particular, the use of a comma-free code would re-establish the correct reading frame within a window of three nucleotide bases. Unfortunately, after the discovery of the standard genetic code lexicon by Nirenberg and Matthaei [8] (see also Khorana [9]), it became clear that the elegant theory of Crick et al. is not valid in the form proposed. For instance, the trinucleotide TTT, an excluded trinucleotide in a comma-free code, codes phenylalanine [8].
The motivation to study comma-free codes again came after the discovery of so-called circular codes, which are a weaker version of comma-free codes. In Arquès and Michel [10], a set of 20 codons was identified by statistical analysis of genes of prokaryotes and eukaryotes. These 20 codons appear preferentially in the correct reading frame and have the property of detecting frame shifts not immediately, but eventually. In fact, at most 13 consecutive nucleotides in a sequence of codons from the code are enough to detect the correct reading frame. In 2015, by quantifying the approach used in 1996 and by applying massive statistical analysis of gene taxonomic groups, the circular code detected in 1996 was rediscovered extensively in genes of prokaryotes and eukaryotes and now also identified in the genes of plasmids and viruses [11]. The codes discovered by Arquès and Michel in nature have even more interesting properties. With each codon, its anticodon is also in the code (self-complementarity), and they also have the error detection property in frame 1 and 2 (-property). Such codes are called self-complementary codes and have been completely classified in [10,12] and [13]. A weaker version of such codes are self-complementary circular codes, which are self-complementary, but cannot recognize if the reading-frame is shifted by one or two bases. Any comma-free code, self-complementary -code or self-complementary circular code can contain at most 20 codons (see, e.g., [14]), and all such maximal codes have been completely classified by computer calculations: there are exactly 216 maximal self-complementary codes, exactly 408 maximal comma-free codes and exactly 528 maximal self-complementary circular codes (see [10,14,15,16,17,18]). None of the maximal comma-free codes, however, can be self-complementary.
In the present work, we first discuss some ancient genetic codes, e.g., the primeval code, the RNY code, SNS code and the NNS code, that have been postulated in several theories about the evolution of the genetic code as a predecessor of the current standard genetic code (see [19,20,21,22,23,24]). This is by far not a complete list of such hypothesized codes, but serves as a motivating list of examples based on biological concepts, the RNY code being the most important one, since it has been statistically observed in genes on the two-letter alphabet . We show that all of these ancient genetic codes that used only some of the 64 codons always contain a large comma-free code that codes for almost all of the amino acids involved. This shows that in predecessors of the current genetic code, Crick’s hypothesis on the usage of a comma-free code was much more likely and could have been true. However, nowadays, the genetic code has become too complex to use such strong codes (in the sense of having strong error-detecting properties, i.e., recognizing a frameshift immediately), and therefore, nature moved on to the weaker circular codes. Thus, it is very likely that the circular codes have evolved from the comma-free codes in some way. In this article, we give some hints for this hypothesis, which would shed more light on the evolutionary development of the genetic code and why it is as it is.
We consider the three classes of codes: maximal comma-free, maximal self-complementary circular and maximal self-complementary codes. For each codon, except for the excluded , we calculate how many codes of the three classes considered it can appear in; this is called the frequency class number of the codon with respect to a class of codes. After preparing definitions (see Section 2), the main results of the article are presented in Section 3. Surprisingly, it turns out that for each of the above classes of codes, there are very few frequency class numbers of codons with respect to it (see also [16,17] for the data). It is even more surprising that the frequency classes of codons for self-complementary codes are refinements of the classes for comma-free codes, and those for self-complementary circular codes are refinements for the corresponding classes of self-complementary codes. Thus, the number of different frequency classes of codons increases parallel to the decrease of error-detecting properties of the codes. The fact that the frequency classes of the codons for maximal self-complementary codes are refinements of the classes for maximal comma-free codes is a strong hint that the maximal self-complementary codes used in the current genetic code could have evolved from the maximal comma-free codes, which were very likely used in earlier times, since these two classes of codes are disjoint. This means that there is no obvious mathematical reason for this refinement property.
Our results strengthen the supposition that the modern codes originated from ancient (self-complementary) comma-free codes (see [23,24]) and, as a consequence, a weaker version of the Crick et al. theory.
2. Definitions and Notations
The genetic code is written with words of three letters, called codons, built over an alphabet:
of four letters, nucleotide bases uracil (thymine), cytosine, adenine and guanine, in short and In recent studies, e.g., [11,12,14,18,25], the structure of certain sub-codes of the genetic code that are assumed to play a role in nature were investigated. The first class of codes was suggested by Crick et al. in [7].
Definition 1.
A trinucleotide code is called comma-free if any given two codons , any sub-codon of the concatenation , except themselves, does not belong to X. We will call a trinucleotide comma-free code X maximal if it contains exactly 20 codons.
Being comma-free means that a frameshift of one or two bases is detected after reading of three nucleotide bases (see Figure 1). We would like to mention at this point that our point of view of the frameshift problem is an information theoretical point of view. In living cells, a frameshift is of course also “detected” because of the mistranslated protein product that is produced and its potential phenotypic consequences.

Figure 1.
For comma-free codes, a frameshift is detected immediately. All codons highlighted in gray in the second and the third row are not in the code.
Clearly, a comma-free code cannot contain the periodical codons , , or since, for example, a frame shift in a sequence of adenines could not be detected. Moreover, for any codon from a comma-free code, the shifted codons and cannot be in the same code. For instance, if is in the code, then and must not be in the same code, because they appear in frameshift 1 and 2 of the:
The two shift operations are commonly denoted by and , i.e., and for any codon (see, for instance, [12]). Thus, any comma-free code can at most contain one codon out of the three and and similarly for any other codon. Thus, the maximal number of codons in a comma-free code is , as required in the above Definition 1.
Maximal comma-free codes have been completely classified by computer calculations, and it turned out that there are exactly 408 such codes (see [15]).
At this point, we would like to discuss some examples of ancient codes, i.e., genetic code tables that were suggested as a predecessor of the current standard genetic code in some theory about the evolution of the genetic code. These codes coded only for a few amino acids and very often also used only some of the codons and not all. Surprisingly, most of these codes contained a large comma-free sub-code that codes for almost all of the amino acids or were even themselves comma-free. Note that any comma-free code can code for at most 13 amino acids ([16]; see also Table 4 in [26]), while a circular code can code for at most 18 amino acids [27].
Example 1.
- In the generalized co-evolution theory by Di Giulio [20,21], the SNS code (the letter S stands here for the strong nucleotide bases C or G, in contrast to weak nucleotide bases A or T) was suggested and consists of the following codons coding for the seven amino acids valine, glutamine, alanine, asparagine, glycine and serine:It contains the comma-free sub-code:which is as large as possible (of size 10), because there are two codons of the form in , and four codons have a cyclically-equivalent codon in the code. It codes for all but one amino acid, namely alanine.
- In the generalized co-evolution theory by Di Giulio [20,21], the NNS code was suggested and consists of the following codons coding for the seven amino acids valine, glutamine, alanine, asparagine, glycine and serine plus the stop signal:It contains the comma-free sub-code:which is as large as possible (of size 11) and codes for all except one amino acid, namely alanine, and the stop signal.
- The RNY code [19] consists of the eight amino acids glycine, threonine, asparagine, serine, valine, arginine, isoleucine and alanine and the 16 codons:This code is comma-free.
- The theory of Jolivet and Rothen [22] yields another primeval code, which codes for the amino acids tyrosine, alanine, phenylalanine, arginine, valine, asparagine, aspartate, leucine, glutamate, glycine, glutamine and isoleucine:The code is even a code (see below). Moreover, it contains a comma-free sub-code of size 11 (as large as possible) that codes for all amino acids, except for two, namely alanine and arginine:
As mentioned in the Introduction, this list of examples of predecessor codes is by far not complete, and most of these codes are based on biological concepts. The most important code is the RNY code [19], which has also been statistically observed in genes on the two-letter alphabet . It is comma-free, and it was already shown in [10] that the RNY code can be also constructed by looking at the preferential frame of the RNY codons in genes. In fact, in [10], the authors assigned to each codon a preferential frame (which then led to the discovery of the first maximal self-complementary -code), and taking the average frame of the RNY codons, it was pointed out by the authors that this is in fact Frame 0 (see [10], Table 3a–c and the corresponding discussion).
As we can see, the ancient codes discussed in the above Example 1 always contain a large sub-code that is comma-free and encodes almost all of the amino acids used in the code. This is impossible in the current standard genetic code, as we have seen above.
Since Crick’s hypothesis on the usage of comma-free codes consequently had to fail in nature, the next class of codes that was investigated is the class of maximal self-complementary codes.
Definition 2.
We will call a set of codons a trinucleotide circular code if any word over the alphabet written on a circle has at most one decomposition into words from X. By word written on a circle, it is intended that after the last letter, the word starts again (from its first letter). We will call a trinucleotide circular code X maximal if it contains exactly 20 codons.
Circular codes do not allow the detection a frameshift immediately as comma-free codes do, but eventually, after a few codons (see Figure 2). Thus, it is obvious that any comma-free code is also circular.
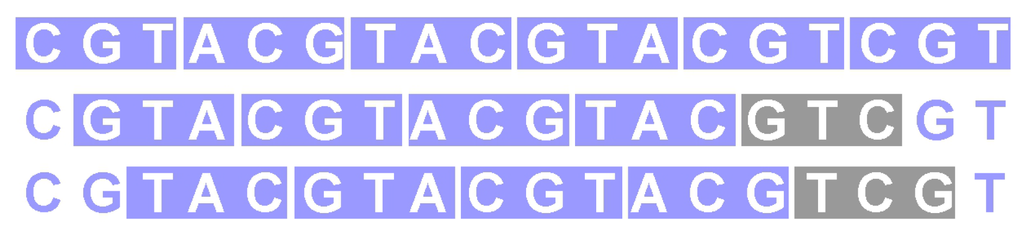
Figure 2.
For circular codes, a frameshift is detected after a few codons. The codons highlighted in gray in the second and the third row are not in the code.
The first maximal circular code that was found in nature by Arquès and Michel [10] is:
The code had even stronger properties. The first one says that the code is not just error-detecting in the normal reading frame, but also in shifts 1 and 2.
Definition 3.
Let . We will say that X is a code if X, as well as and are circular, where and .
Moreover, the code found by Arquès and Michel was also invariant under forming the anticodons of its members.
Definition 4.
Let . We will call X self-complementary if with each codon , its anticodon is also in X.
Again, computer calculations showed that there are exactly 528 maximal self-complementary circular codes containing exactly 216 maximal self-complementary codes (see [10,13,28]).
In the recent investigations of comma-free and circular codes, the group of permutations (bijective transformations) of bases played a significant role (see, for example, [12,29]). Recall that a permutation of the bases from is just a bijective shuffling of the bases. Formally, the symmetric group on the set is defined as:
with the group operation of function composition. Bijective transformations π: → can be applied componentwise to x ∈ 3 and, thus, induce a bijective map 3 → 3 which we will denote also by π. Hence, π systematically exchanges bases in a codon or sequence of codons, and there are exactly 24 such transformations. The complementing map plays a very essential role:
with
which assigns to each basis its complementary basis. An important property of permutations is the following (see [12,29]):
However, self-complementarity is not always preserved, but is by eight of the 24 permutations. These permutations, among which we find the complementing map c, were characterized in [12] and form a subgroup of the symmetric group . Finally, the so-called reversing permutation, which reverses a codon, i.e., , also preserves self-complementarity (see [12]). Note that the anticodon of a codon x can be expressed as . Thus, we have:
We would like to draw the reader to very interesting works by Seligmann [30,31,32,33] that are related to the bijective transformations . In fact, it was shown by Seligmann that parts of actual DNA and RNA sequences are replicated by systematic exchanges of nucleotides, i.e., by applying one of the 24 bijective transformations to it. These sequences are called swinger sequences, and convergence between swinger sequences detected are based on classical PCR sequencing methods.
3. Distribution of Codons in Maximal Error-Detecting Codes
In this section, we will mainly consider three classes of error-detecting and error-correcting codes that have appeared in the development and theory of the genetic code: the class of all maximal comma-free codes, the class of all maximal circular self-complementary codes and the class of all maximal self-complementary codes. We are interested in the frequency of codons appearing in such codes, i.e., we will determine for each codon the number of codes from the above three classes in which it appears. We start with the following:
Definition 5.
Let be a codon, and let be either the class of all maximal comma-free codes, or the class of all maximal circular self-complementary codes, or the class of all maximal self-complementary codes. Then:
denotes the number of codes K from the class , such that x belongs to K. The number is called the frequency class number of x with respect to .
A first easy observation is that for any codon x and any of the above classes , the frequency number of x with respect to is the same as the frequency number of the anticodon with respect to , as well as that of the reversed codon of x with respect to (for comma-free codes this follows from Equations (2) and (3) above):
Moreover, by the maximality of the codes in all of the above classes, we also have:
for all codons x and classes , , . Recall that and are the circular permutations of x.
We now show all equivalence numbers of codons with respect to the three classes of codes , and . Recall first that there are exactly 408 maximal comma-free codes and that clearly any codon contained in a comma-free code either consists of three different bases or has exactly two identical bases. Thus, the cases in the following theorem cover all possible codons.
Theorem 6.
Let be a codon and the class of all maximal comma-free codes. Then, the following statements are true:
- If with and , then:
- If or with and , then:
- If with and , then:
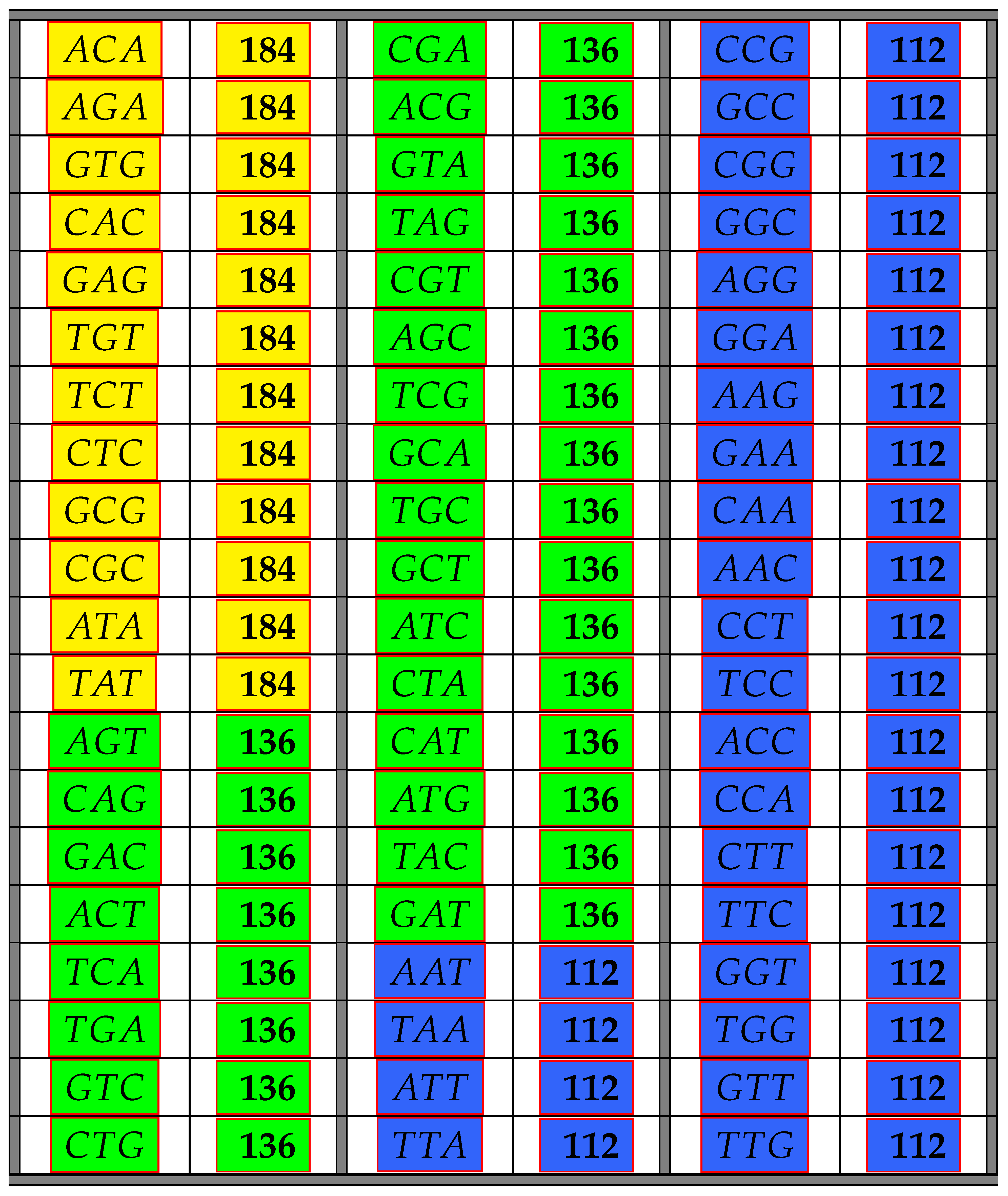
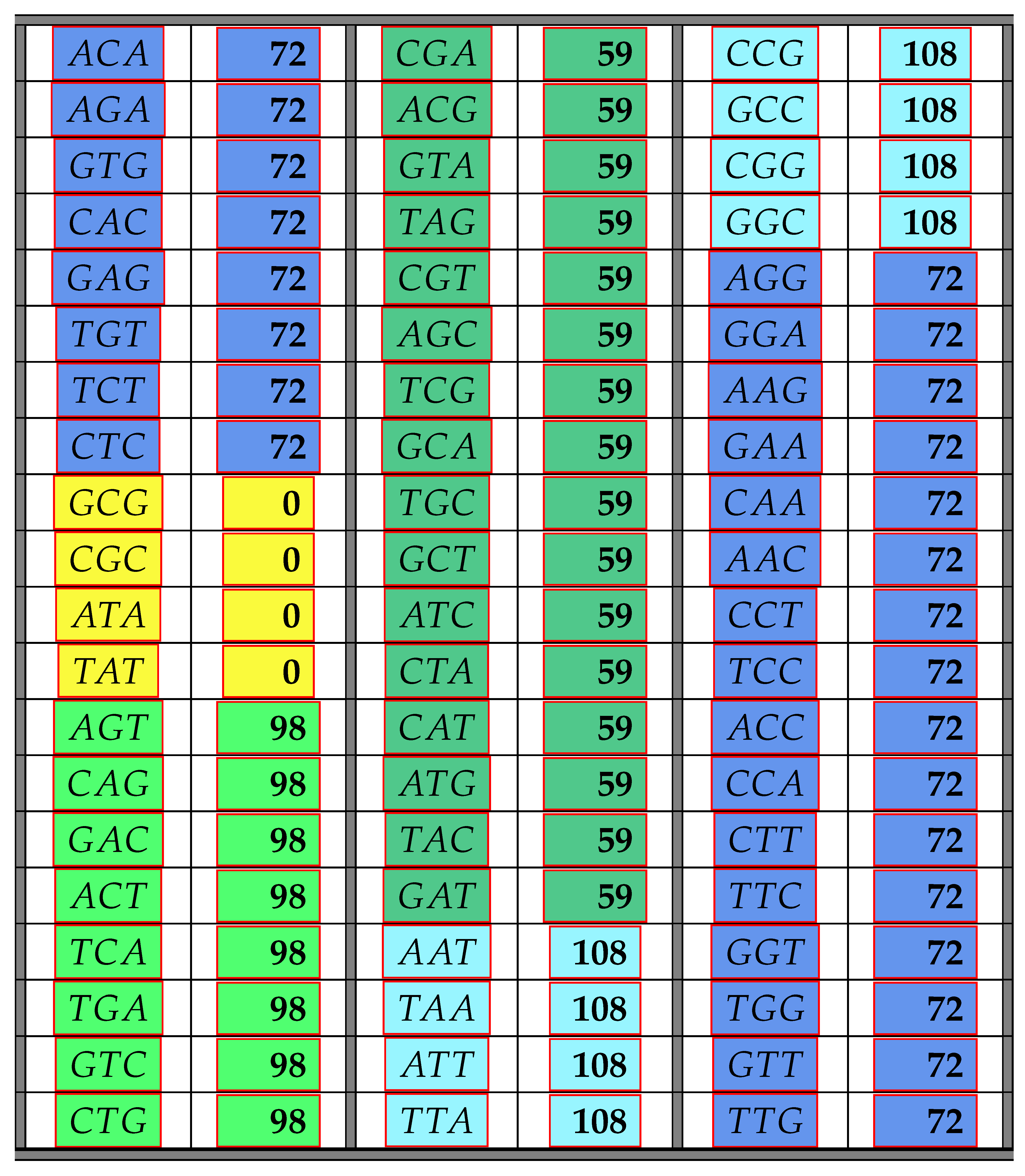
The following Table 1 illustrates the result from the above Theorem 6 showing the frequency class numbers of codons with respect to . Recall that the trivial codons can never be part of any error-detecting system; hence, there are only 60 codons shown in the next table. Codons colored in the same color have the same frequency class number.

Table 1.
The table shows all non-trivial codons and their frequency class number with respect to maximal comma-free codes. Codons colored in the same color have the same frequency class number.
Theorem 6 was obtained by computer calculations, but proofs of some parts of Theorem 6 can be found in Appendix A. However, it is easy to see why there are only three different frequency class numbers. The reason for this is of a group theoretic nature. Since any permutation carries a maximal comma-free code into a maximal comma-free code, it follows that for any codon , we have . Thus, all codons consisting of three different bases must have the same frequency class number with respect to . Moreover, those with two identical bases in positions 1 and 3 must have the same frequency class number, and finally, the codons with two identical bases in positions 1 and 2, as well as in positions 2 and 3 must have the same frequency class numbers. The latter follows from Equation (4).
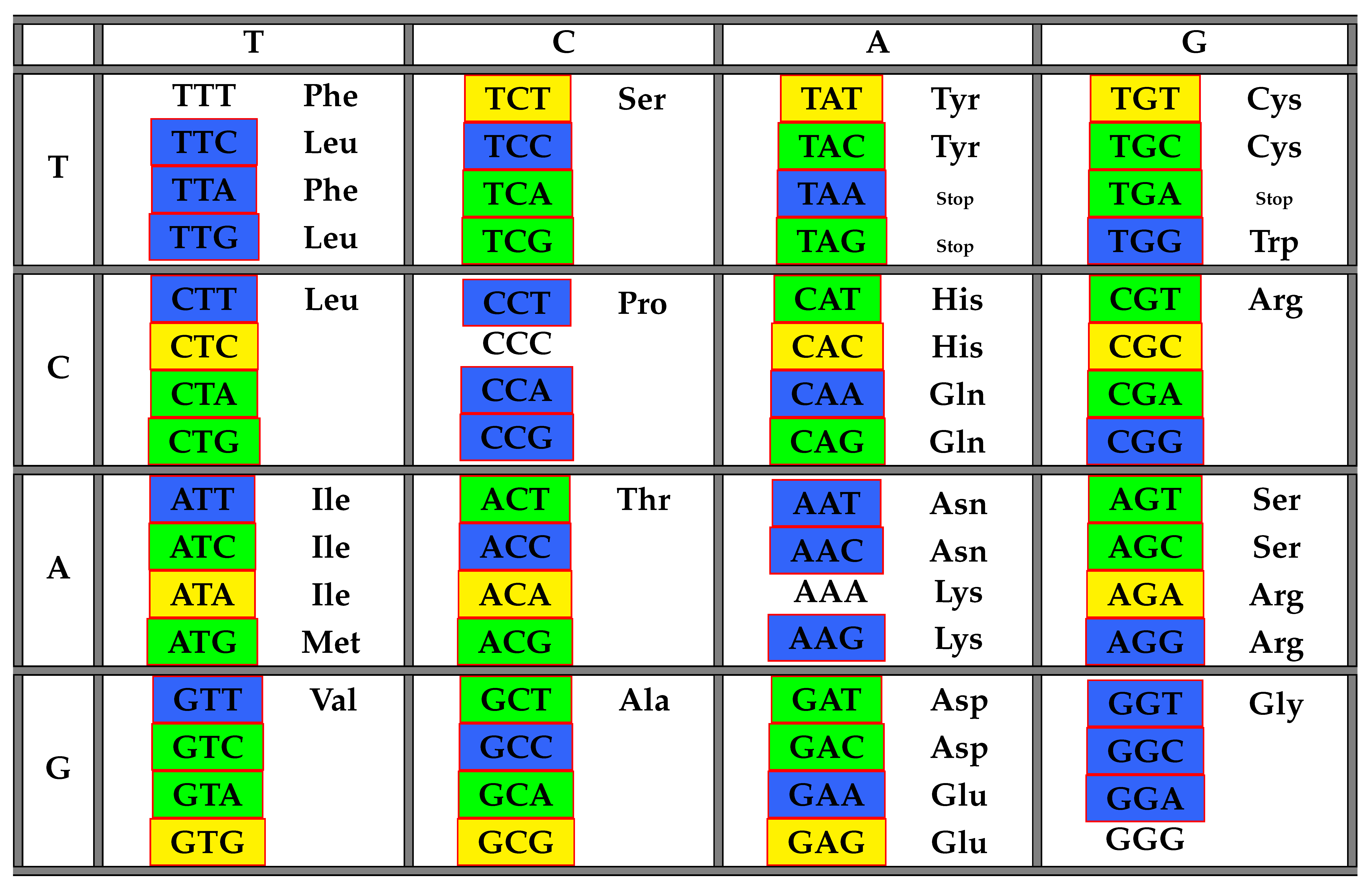
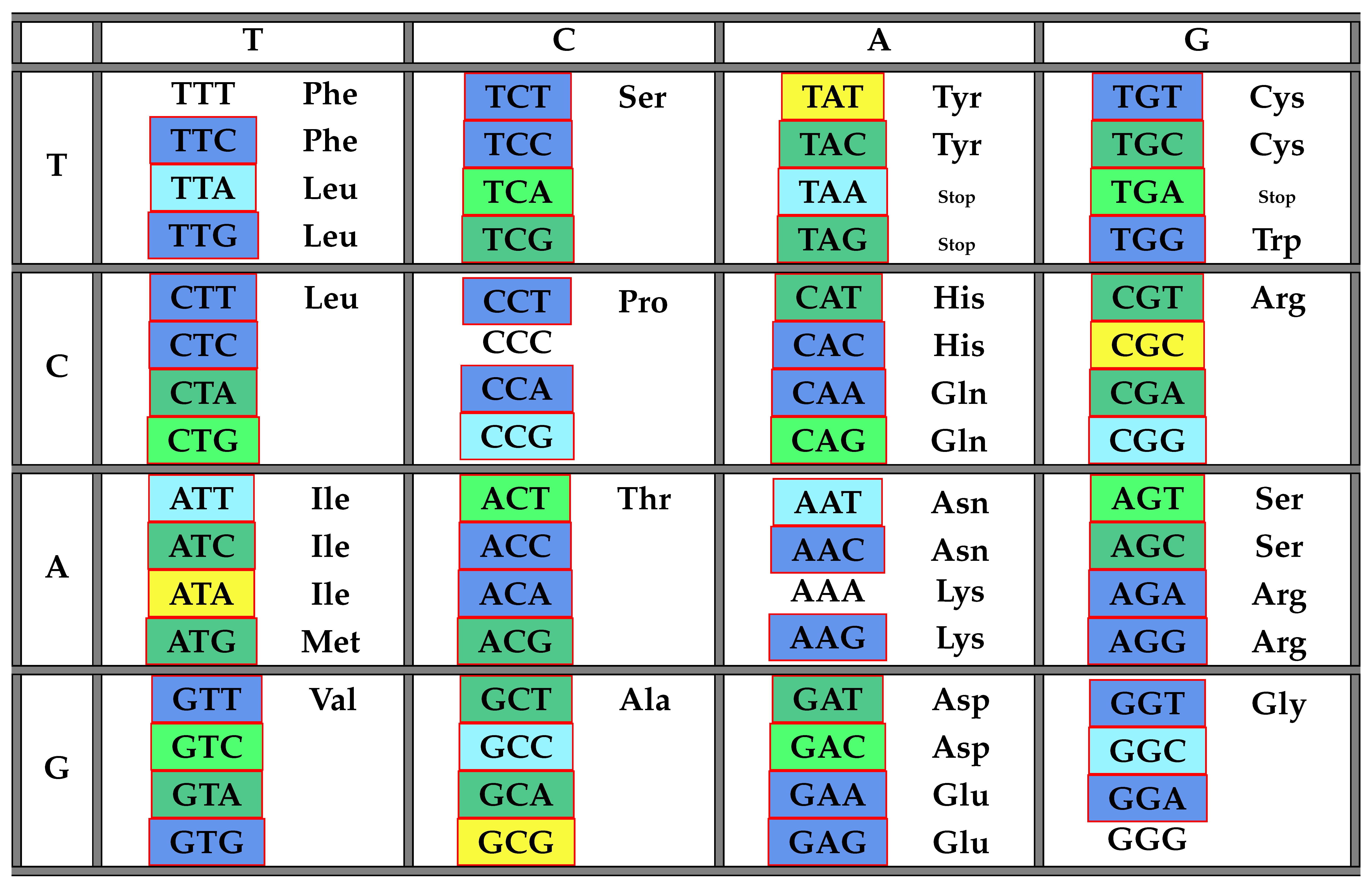
The following Table 2 illustrates the result from Theorem 6 above showing the distribution of codons with respect to in the standard genetic code table.

Table 2.
The table of codons and their frequency numbers with respect to the class of all maximal comma-free codes. The class 184 is highlighted in yellow, 112 in blue and 136 in green.
The next theorem gives the same characterization of frequency numbers with respect to the class of maximal circular self-complementary codes. Note that the number of such codes is exactly 528. Moreover, note that any codon has either two identical bases, and then, the third basis is the complementary one (Cases (1) and (2) in the next theorem), or the third basis is not the complementary one (Cases (3) and (4) below), or the codon has three different bases and in these cases, two of them must be complementary to each other (Cases (5) and (6)). Thus, the case distinction in the following theorem covers all possible codons.
Theorem 7.
Let be a codon and the class of all maximal circular self-complementary codes. Then, the following holds:
- If with , then:
- If or with , then:
- If or with , , then:
- If with , , , then:
- If x= with ., then:
- If or with , , , then:
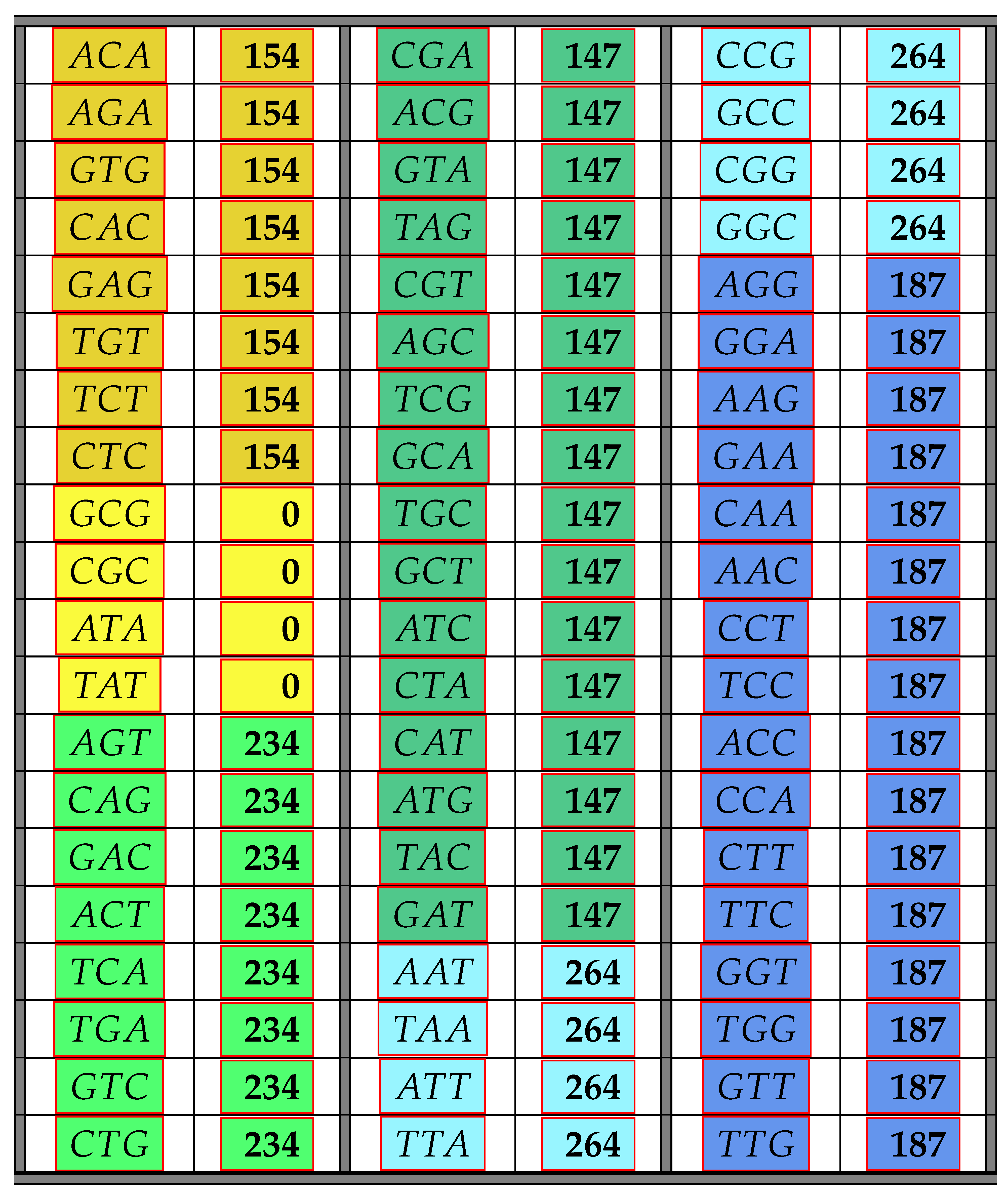
The following Table 3 illustrates the result from Theorem 7 above showing the frequency class numbers of codons with respect to . Again, recall that the trivial codons can never be part of any error-detecting system; hence, there are only 60 codons shown in the next table.

Table 3.
The table shows all non-trivial codons and their frequency class number with respect to maximal circular self-complementary codes.
As for Theorem 6, the results of Theorem 7 were found by computer calculations, but a mathematical proof of some parts of the theorem can be found in Appendix B. Again, group theory shows why there are only a few different frequency class numbers. However, this time, there are only eight transformations that carry self-complementary circular codes into self-complementary circular codes. These eight transformations were classified as the dihedral group L in [12]. Thus, for these eight transformations and any codon , we have . Thus, all codons consisting of three different bases must have the same frequency class number with respect to if they can be mapped onto each other by a permutation from L. The same holds for those codons with two identical bases in two out of the three positions.
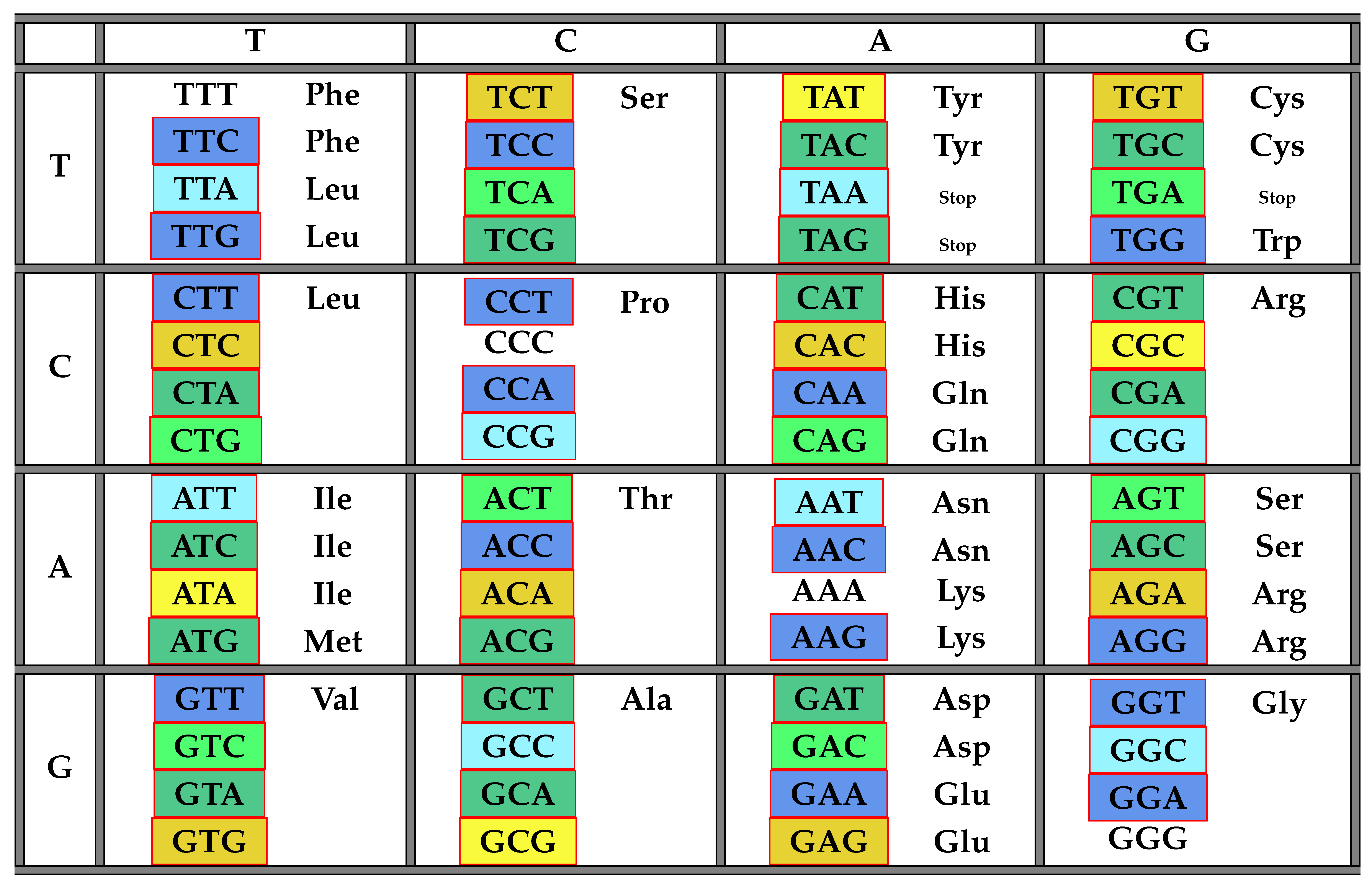
The following Table 4 illustrates the result from Theorem 7 above showing the distribution of codons with respect to in the standard genetic code table.

Table 4.
The table of codons and their frequency numbers with respect to the class of all maximal circular self-complementary codes. The class 264 is highlighted in light blue, 187 in dark blue, 234 in light green, 154 in light yellow, 147 in dark green and 0 in dark yellow.
A surprising fact is that the frequency class numbers of codons with respect to the class of all maximal circular self-complementary codes is a refinement of the frequency class numbers of codons with respect to the class of all maximal comma-free codes. This is not at all clear, since the two classes and are disjoint. No maximal comma-free code is self-complementary. We will come back to this point after the next theorem and its illustration.
We finally show the frequency class numbers of codons with respect to the class of all maximal self-complementary codes. Note that the number of such codes is exactly 216. Moreover, note that as above, the case distinction in the following theorem covers all possible codons.
Theorem 8.
Let be a codon and the class of all maximal self-complementary codes. Then, the following holds:
- If or with , then:
- If with , then:
- If or or with , , , then:
- If with , , , then:
- If or with , , , then:
As for Theorems 6 and 7, the results in Theorem 8 were discovered by computer calculation; however, some parts of the above theorem are proven in Appendix C. As for Theorem 7, the action of the dihedral group L on the set explains why there are only a few different frequency classes.
The following Table 5 and Table 6 illustrate the result from the above Theorem 8 showing the frequency class numbers of codons with respect to and their distribution in the standard genetic code table. Recall once more that the trivial codons can never be part of any error-detecting system; hence, there are only 60 codons shown in the next table.

Table 5.
The table shows all non-trivial codons and their frequency class number with respect to maximal self-complementary codes.

Table 6.
The table of codons and their frequency numbers with respect to the class of all maximal self-complementary codes. The class 108 is highlighted in light blue, 72 in dark blue, 98 in light green, 59 in dark green and 0 in dark yellow.
Since the maximal self-complementary codes are a subset of the set of maximal circular self-complementary codes, it is clear that the splitting of codons with respect to their frequency class numbers cannot be significantly different. Nevertheless, as we can see, it is not completely the same. The Classes (3) and (4) from Theorem 7 merge to one class in Theorem 8 (Class (3)), due to the additional -property. Thus, the frequency class numbers of codons with respect to the class is a refinement of the ones with respect to the class .
4. Results, Discussion and Conclusions
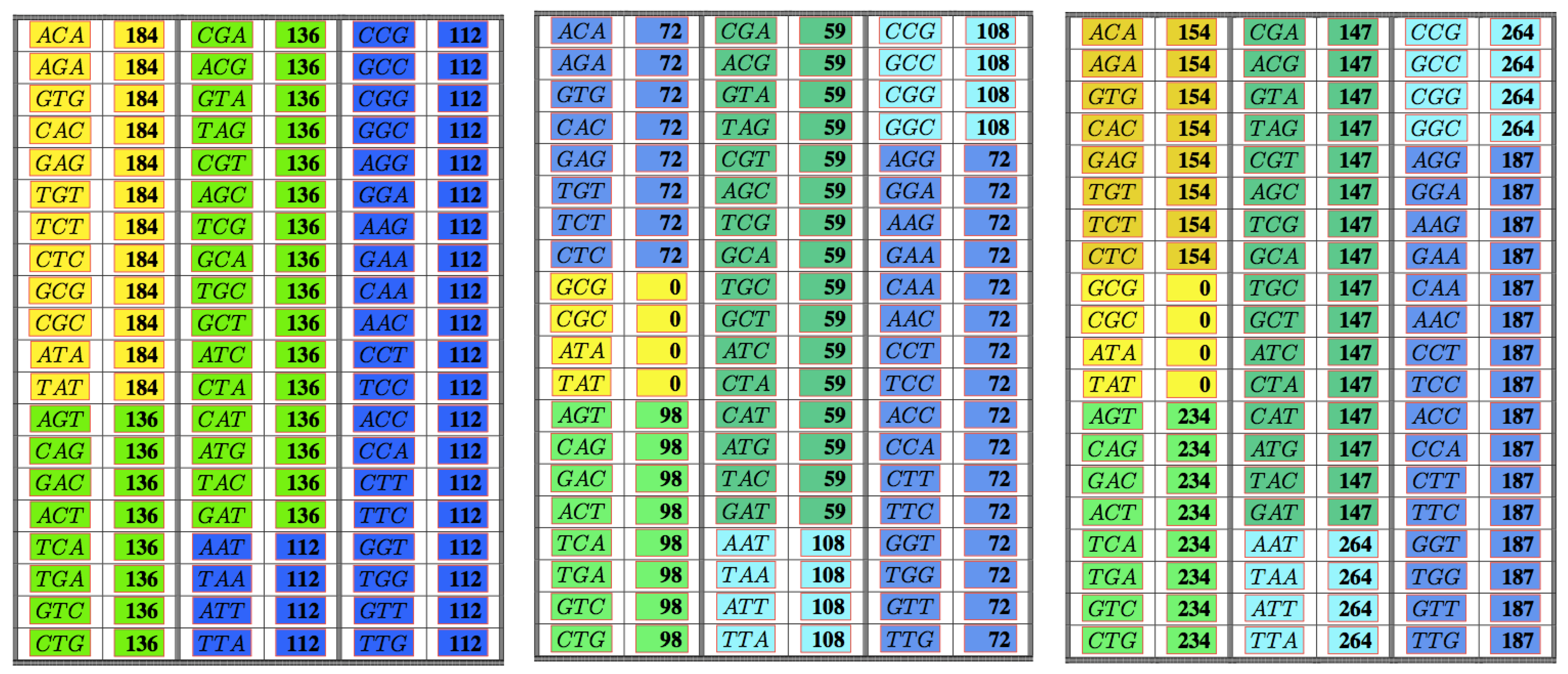
In this work, we have investigated the frequency class numbers of codons with respect to the three important classes of error-detecting codes that play a role in the theory of the genetic code: the class of all maximal comma-free codes, the class of all maximal self-complementary codes and finally, the class of all maximal self-complementary circular codes. The results show two surprising facts. Firstly, for each of the classes , and , there are only very few frequency class numbers of codons. Secondly, the frequency class numbers yield partitions of the set of codons that become finer when passing from the class via the class to the class (see the Table 7 below for a visualization of this refinement).

Table 7.
The table shows all non-trivial codons with their frequency class number with respect to the classes , and .
The existence of only a few frequency class numbers for each of the classes , and is explained by a mathematical theory using group theory. Moreover, parts of the main Theorems 6–8 are given in the Appendix. The main result, however, is the refinement property shown in the table above. Since the class of maximal self-complementary codes is a subclass of the class of all maximal self-complementary circular codes, the refinement property of the corresponding frequency class numbers is a consequence. However, the first refinement from the class of all maximal comma-free codes to the class of all maximal self-complementary codes is a surprise. No maximal comma-free code is self-complementary; hence, the two classes and (even and ) are disjoint. That the frequency class numbers with respect to are still a refinement of the frequency class numbers with respect to is a clear hint at a relation between the two classes of codes and supports the theory that the genetic code in its present form evolved from earlier ancient codes in a way that stronger error-detecting and error-correcting properties were weakened to codes that still allow error-detection and error-correction, but in a less effective form. Ancient codes used less codons and coded for less amino acids; hence, comma-free codes that detect a frameshift in a reading window of only three bases, hence immediately, could be incorporated. As soon as the genetic codes got more complex involving all codons and coding for a larger number of amino acids, the weaker circular codes that detect frameshifts eventually and in a larger reading window (of 13 nuclear bases) had to take over the error-detection and error-correction function.
Appendix A. Proof of Theorem 6
Proof.
Clearly, any codon is either of the form , or , or , or with all different, i.e., either the codons consist of three different nucleic bases or two bases are identical. Thus, Cases (1)–(3) of Theorem 6 form a complete case distinction. Moreover, since any bijective transformation , as well as the reversing transformation preserve comma-freeness, it is obvious that any two codons must have the same frequency class numbers , provided they can be mapped onto each other by such transformations. We now first prove that this is indeed the case in all three cases of Theorem 6.
- (1)
- Let be two codons of the form and with , such that and . Obviously, the bijective transformation with:maps x onto .
- (2)
- Let be two codons of the form and with , such that and . As above, the bijective transformation with:maps x onto . The same holds for codons of the form and . Finally, if are of the form and , then we use the reversing map concatenated with the following map σ to map x onto :
- (3)
- Let be two codons of the form and with , such that and . Similar to the other two cases, we define the bijective transformation the following way:
We have thus shown that there are only three possible frequency numbers for codons with respect to the class of maximal comma-free codes. The exact values of these frequency class numbers have been found by computer calculations. However, for Case (3), we even have a proof. Given a codon with all different, it is readily seen that the shifted codons and are of the same form. Thus, we have . Equation (5) implies that . Moreover, there is a relation between the frequency numbers of codons from Case (1) and Case (2). Given a codon from Case (1) the shifted codons and are codons of the form described in Case (2). Thus, it follows that:
In particular, if , then . ☐
Appendix B. Proof of Theorem 7
Proof.
It is easy to see that the cases described in Theorem 7 give a complete case distinction for the set of codons . In fact, any such codon has to be of one of the forms described in (1)–(6). As in the proof of Theorem 6, it suffices to show that codons of the same form can be mapped onto each other by some bijective transformation or the reversing transformation in order to show that the corresponding frequency class numbers are the same. However, since we are dealing with the class of all maximal self-complementary circular codes, we need to find bijective transformations that preserve self-complementarity. These permutations have been classified in [12] as a subgroup L of the permutation group . In fact, the group L consists of the following eight transformations:
where:
We now show that indeed in any of the cases of Theorem 7, (1)–(6), we can find such a permutation π from L.
- (1)
- If and , then either (in case ) or one of the three permutations (in case ) does the job.
- (2)
- As in Case (1), either the identity or one of the three permutations does the job in combination with the reversing transformation .
- (3)–(6)
- Similarly to Cases (1) and (2), one can define permutations in L that do the job.
Moreover, as in the proof of Theorem 6, one can show that the frequency class numbers - from the Cases (1)–(6) of Theorem 7 satisfy the following equations:
In particular, it follows that . ☐
Appendix C. Proof of Theorem 8
Proof.
As in the proof of Theorem 7, we can show that the cases in Theorem 8 form a complete case distinction and that the frequency class numbers are the same for codons of the same forms described in (1)–(5) of Theorem 7. The exact values are once more determined by computer calculations. In fact, we have for the frequency class numbers to from the cases of Theorem 8 that:
In particular, we have and . ☐
Acknowledgments
The authors would like to thank Simone Giannerini, Diego Gonzalez, Markus Gumbel and Christian Michel for many stimulating and helpful discussions on the subject.
Author Contributions
Both authors have equally contributed to the work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Freeland, S.J.; Knight, R.D.; Landweber, L.F.; Hurst, L.D. Early fixation of an optimal genetic code. Mol. Biol. Evol. 2000, 17, 511–518. [Google Scholar] [CrossRef] [PubMed]
- Jestin, J.L.; Kempf, A. Degeneracy in the genetic code: How and why? Genes Genomes Genom. 2007, 1, 100–103. [Google Scholar]
- Guimarães, R.C. The self-referential genetic code is biologic and includes the error mini-mization property. Orig. Life Evol. Biosph. 2015, 45, 69–75. [Google Scholar] [CrossRef] [PubMed]
- Seligmann, H.; Pollock, D.D. The ambush hypothesis: Hidden stop codons prevent off-frame gene reading. DNA Cell Biol. 2004, 23, 701–705. [Google Scholar] [CrossRef] [PubMed]
- Guilloux, A.; Jestin, J.-L. The genetic code and its optimization for kinetic energy conservation in polypeptide chains. Bio. Syst. 2012, 109, 141–144. [Google Scholar] [CrossRef] [PubMed]
- Warnecke, T.; Hurst, L.D. Error prevention and mitigation as forces in the evolution of genes and genomes. Nat. Rev. Genet. 2011, 12, 875–881. [Google Scholar] [CrossRef] [PubMed]
- Crick, F.; Griffith, J.S.; Orgel, L.E. Codes without commas. Proc. Natl. Acad. Sci. USA 1957, 43, 416–421. [Google Scholar] [CrossRef] [PubMed]
- Nirenberg, M.W.; Matthaei, J.H. The dependence of cell-free protein synthesis in E. coli upon naturally occurring or synthetic polyribonucleotides. Proc. Natl. Acad. Sci. USA 1961, 47, 1588–1602. [Google Scholar] [CrossRef] [PubMed]
- Khorana, H.G. Polynucleotide synthesis and the genetic code. Federation Proc. 1965, 24, 1473–1487. [Google Scholar] [CrossRef]
- Arquès, D.G.; Michel, C.J. A complementary circular code in the protein coding genes. J. Theor. Biol. 1996, 182, 45–58. [Google Scholar] [CrossRef] [PubMed]
- Michel, C.J. The maximal C3 self-complementary trinucleotide circular code X in genes of bacteria, eukaryotes, plasmids and viruses. J. Theor. Biol. 2015, 380, 156–177. [Google Scholar] [CrossRef] [PubMed]
- Fimmel, E.; Giannerini, S.; Gonzalez, D.; Strüngmann, L. Circular codes, symmetries and transformations. J. Math. Biol. 2015, 70, 1623–1644. [Google Scholar] [CrossRef] [PubMed]
- Lacan, J.; Michel, C.J. Analysis of a circular code model. J. Theor. Biol. 2001, 213, 159–170. [Google Scholar] [CrossRef] [PubMed]
- Michel, C.J.; Pirillo, G. Identification of all trinucleotide circular codes. Comput. Biol. Chem. 2010, 34, 122–125. [Google Scholar] [CrossRef] [PubMed]
- Golomb, S.W.; Gordon, B.; Welch, L.R. Comma-free codes. Can. J. Math. 1958, 10, 202–209. [Google Scholar] [CrossRef]
- Keller, V. Fehlerkorrigierende genetische Codes. Bachelor’s Thesis, University of Applied Sciences Mannheim, Mannheim, Germany, 2014. [Google Scholar]
- Lemegne, L. Trinucleotide maximal circular self-complementary genetic codes and their symmetries. Bachelor’s Thesis, University of Applied Sciences Mannheim, Mannheim, Germany, 2015. [Google Scholar]
- Michel, C.J.; Pirillo, G.; Pirillo, M.A. A relation between trinucleotide comma-free codes and trinucleotide circular codes. Theor. Comput. Sci. 2012, 401, 17–26. [Google Scholar] [CrossRef]
- Eigen, M.; Schuster, P. The Hypercycle. A principle of natural self-organization. Part C: The realistic hypercycle. Naturwissenschaften 1978, 65, 341–369. [Google Scholar] [CrossRef]
- Di Giulio, M. An Extension of the coevolution theory of the origin of the genetic code. Biol. Direct 2008, 3. [Google Scholar] [CrossRef] [PubMed]
- Di Giulio, M. A blind empiricism against the coevolution theory of the genetic code. J. Mol. Evol. 2001, 53, 724–732. [Google Scholar] [CrossRef] [PubMed]
- Jolivet, R.; Rothen, F. Peculiar symmetry of DNA sequences and evidence suggesting its evolutionary origin in a primeval genetic code. Exo-/Astro- Biol. 2001, 496, 173–176. [Google Scholar]
- Josè, M.V.; Morgado, E.R.; Govezensky, T. An extended RNA code and its relationship to the standard genetic code: an algebraic and geometrical approach. Bull. Math. Biol. 2007, 69, 215–243. [Google Scholar] [CrossRef] [PubMed]
- Shepherd, J.C.W. Method to determine the reading frame of a protein from the purine/pyrimidine genome sequence and its possible evolutionary justification. Proc. Natl Acad. Sci. USA 1981, 78, 1596–1600. [Google Scholar] [CrossRef] [PubMed]
- Fimmel, E.; Strüngmann, L. On the hierarchy of trinucleotide n-circular codes and their corresponding amino acids. J. Theor. Biol. 2015, 364, 113–120. [Google Scholar] [CrossRef] [PubMed]
- Michel, C.J. A genetic scale of reading frame coding. J. Theor. Biol. 2014, 355, 83–94. [Google Scholar] [CrossRef] [PubMed]
- Michel, C.J.; Pirillo, G. A permuted set of a trinucleotide circular code coding the 20 amino acids in variant nuclear codes. J. Theor. Biol. 2013, 319, 116–121. [Google Scholar] [CrossRef] [PubMed]
- Bussilo, L.; Michel, C.J.; Pirillo, G. On conjugation partitions of sets of trinucleotides. Appl. Math. 2012, 3, 107–112. [Google Scholar] [CrossRef]
- Michel, C.J.; Seligmann, H. Bijective transformation circular codes and nucleotide exchanging RNA transcription. Biosystems 2014, 118, 39–50. [Google Scholar] [CrossRef] [PubMed]
- Seligmann, H. Species radiation by DNA replication that systematically exchanges nucleotides? J. Theor. Biol. 2014, 363, 216–222. [Google Scholar] [CrossRef] [PubMed]
- Seligmann, H. Mitochondrial swinger replication: DNA replication systematically exchanging nucleotides and short 16S ribosomal DNA swinger inserts. Bio. Syst. 2014, 125, 22–31. [Google Scholar] [CrossRef] [PubMed]
- Seligmann, H. Sharp switches between regular and swinger mitochondrial replication: 16S rDNA systematically exchanging nucleotides A<->T+C<->G in the mitogenome of Kamimuria wangi. Mitochondrial DNA 2015. [Google Scholar] [CrossRef]
- Seligmann, H. Systematic exchanges between nucleotides: Genomic swinger repeats and swinger transcription in human mitochondria. J. Theor. Biol. 2015, 384, 70–77. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).