O₂ and Other High-Energy Molecules in Photosynthesis: Why Plants Need Two Photosystems

Abstract

The energetics of photosynthesis in plants have been re-analyzed in a framework that represents the relatively high energy of O₂ correctly. Starting with the photon energy exciting P680 and “loosening an electron”, the energy transfer and electron transport are represented in a comprehensive, self-explanatory sequence of redox energy transfer and release diagrams. The resulting expanded Z-scheme explicitly shows charge separation as well as important high-energy species such as O₂, Tyr_Z˙, and P680⁺˙, whose energies are not apparent in the classical Z-scheme of photosynthesis. Crucially, the energetics of the three important forms of P680 and of P700 are clarified. The relative free energies of oxidized and reduced species are shown explicitly in kJ/mol, not encrypted in volts. Of the chemical energy produced in photosynthesis, more is stored in O₂ than in glucose. The expanded Z-scheme introduced here provides explanatory power lacking in the classical scheme. It shows that P680* is energetically boosted to P680⁺˙ by the favorable electron affinity of pheophytin and that Photosystem I (PSI) has insufficient energy to split H₂O and produce O₂ because P700* is too easily ionized. It also avoids the Z-scheme’s bewildering implication, according to the “electron waterfall” concept, that H₂O gives off electrons that spontaneously flow to chlorophyll while releasing energy. The new analysis explains convincingly why plants need two different photosystems in tandem: (i) PSII mostly extracts hydrogen from H₂O, producing PQH₂ (plastoquinol), and generates the energetically expensive product O₂; this step provides little energy directly to the plant; (ii) PSI produces chemical energy for the organism, by pumping protons against a concentration gradient and producing less reluctant hydrogen donors. It also documents that electron transport and energy transfer occur in opposite directions and do not involve redox voltages. The analysis makes it clear that the high-energy species in photosynthesis are unstable, electron-deficient species such as P680⁺˙ and Tyr_Z˙, not putative high-energy electrons.

1. Introduction

Photosynthesis, the light-enabled synthesis of biomolecules from much simpler precursors, is a fascinating and obviously important process. For plants, the overall reaction is usually summarized as the production of glucose and oxygen,

6 H₂O + 6 CO₂ → C₆H₁₂O₆ + 6 O₂
Δ_rG^o’ = +2870 kJ/mol, Δ_rG^o = +2875 kJ/mol = Δ_rG^o”.

(1)

where a double prime indicates Alberty’s pH 7 biochemical standard conditions [1], a single prime conventional pH 7 biochemical standard conditions [2], and the absence of a prime chemical standard conditions (e.g., at pH 0); their differences are usually insignificant in this work. The solar energy is captured in a first step, the light reaction, which includes

12 H₂O + 12 NADP⁺ → 12 NADPH + 12 H⁺ + 6 O₂
Δ_rG^o’ = +2640 kJ/mol, Δ_rG^o” = +2600 kJ/mol,

(2)

as well as ATP production (“photophosphorylation”):

~18 (ADP + P_i) → ~18 (ATP + H₂O)  Δ_rG^o’ ≈ +540 kJ/mol.

(3)

In the subsequent light-independent reaction, products of Equation (2), 12 NADPH + 12 H⁺, a biochemical equivalent of 12 H₂ [2,3], go on to transfer hydrogen to 6 CO₂ molecules to form carbohydrates like C₆H₁₂O₆ (plus 6 H₂O), with the needed moderate energy boosts provided by hydrolysis of the ATP molecules from Equation (3). Descriptions of the historical path towards the current understanding of photosynthesis can be found in excellent books [2,4] and articles [5,6,7,8].

Traditionally, the reactions in Equations (1) and (2) have been viewed as the production of energy-rich organic molecules, glucose and NADPH [2,9,10,11,12,13,14]. We have shown that the energetic aspect of this view is incorrect: The high-energy molecule among the products is O₂ with its relatively weak double bond [15], while glucose and NADPH are only of moderate energy [3]. O₂ shows its high energy in a myriad of strongly exothermic reactions with any of millions of organic molecules and many inorganic species, not only when forming CO₂ and H₂O, but also CO, formaldehyde, ethanol, acetic acid, glucose, SiO₂, SO₂, etc. [3,15]. The conclusion that O₂ is a high-energy product making the reaction in Equation (2) unfavorable can be confirmed by considering an analogous reaction without O₂ production:

12 H₂ + 12 NADP⁺ → 12 NADPH + 12 H⁺
Δ_rG^o’ = −204 kJ/mol, Δ_rG^o” = −252 kJ/mol,

(4)

where free energy would be released.

In the most common representation of the energetics of oxygenic photosynthesis, the Z-scheme [2,4,12,13,16,17,18,19,20] (see Supplementary Material Figure S1), O₂ often seems to be shown at very low energy [2,13,18], which cannot be correct [3,15]. Rectifying this problem was the original motivation for the present study. The resulting critical analysis also revealed that other high-energy molecules have been missing from the Z-scheme. In particular, the charged species in the important initial charge-separation process, emphasized in conceptual descriptions of photosynthesis [2,13,17,21], are absent from the Z-scheme. Furthermore, the labeling of the redox potentials in the Z-scheme inconsistently switches between reduced and oxidized species, or it shows conjugate redox species at different redox potentials (e.g., 2 H₂O and O₂ + 4 H⁺) [2,13,18]. The Z-scheme is easily misinterpreted as a diagram of energies of specific chemical species or electrons [4,20]. It incorrectly suggests that electrons spontaneously flow from H₂O to ground-state chlorophyll, perplexingly releasing energy, before they are excited by photon energy. In this work, these problems (for a full listing see the SI) will be rectified, most importantly in a more comprehensive and intuitive diagram of relative free energies that contains the important high-energy species explicitly and is self-explanatory. In particular, it shows the energy boost by ionization of chlorophyll that enables Photosystem II (PSII) [22] to split water and produce O₂, while the corresponding boost in Photosystem I (PSI) would be insufficient.

This analysis leads to a clear answer to the long-standing question why plants have two different photosystems working in tandem. Some textbooks just state this fact without explanation [2]. while others propose rationalizations that are unconvincing [12]. For instance, an ‘explanation’ that PSII is needed because it is hard to remove electrons from H₂O [12] immediately requires the next explanation of why it is hard to remove electrons from H₂O, e.g., compared to ubiquinol, QH₂, the hydrogenated form of ubiquinone (coenzyme Q), which also features two O–H bonds that are broken when ubiquinol is oxidized. Experts declare [23] that “ancestor cyanobacteria had to evolve the capability to use two photosystems working in series in order to accumulate the energy of two photons”, which is an insufficient explanation since PSI already accumulates the energy of four photons, and since two photons in two Photosystems I in series, or two Photosystems II in series, could not achieve the needed net (i.e., formal) hydrogen transfer from H₂O into NADPH. Our analysis reveals that photosynthesis in plants requires two distinct outcomes, each associated with a different photosystem: (i) PSII makes hydrogen from H₂O available via plastoquinol for eventual bonding to CO₂ and production of carbohydrates, (CH₂O)_n, and other biomolecules, while more of the photon energy ends up in O₂ than in plastoquinol; and (ii) PSI converts solar energy into chemical energy in the organism, for instance stored first in H⁺ gradients and then in ATP; this occurs most prominently in “cyclic electron transport”, whose net effect is summarized by Equation (3) [2]. PSI also produces a less reluctant hydrogen donor, NADPH. As a “side effect” of the first process, the biosphere (rather than the specific organism) is supplied with chemical energy in the form of atmospheric O₂, a high-energy molecule [3,15]. The opposing flows of energy and electrons [3] in photosynthesis and their implications for the misguided concept of “high-energy electrons” are discussed.

Before the outlined analysis, we provide a brief discussion of photosynthesis in the context of the laws of thermodynamics. Energy transport in antenna chlorophylls [4] is outside the scope of this paper.

2. Results

2.1. The Laws of Thermodynamics and Photosynthesis

The central energy boost in photosynthesis is sometimes treated implicitly as if the increase in the free energy of the plant is equal to the photon energy, Δ_rG = E_photon. However, this is not exactly what the laws of thermodynamics tell us, as outlined in the following paragraphs. Fortunately, the relative error is small.

The first law for the internal-energy change resulting from a process involving a closed system,

ΔU = w + q

(5)

implies that energy is transferred either as work w or as heat q between the system and the surroundings. Work is usually generated by a force acting through a macroscopic distance. Heat is transferred through contact between bodies of different temperature, radiative heating, or friction (see Figure S2). Light energy from the sun is radiative heat [24]. This means that solar photon energy is heat and disproves a textbook statement [2] that heat is not a source of energy for cells.

The second law of thermodynamics states categorically that for a process occurring in a closed system at constant T and P [25],

ΔG < w_ele.

(6)

Since no external electrical energy is used to drive photosynthesis, w_ele ≤ 0 and the second law requires ΔG < 0 at constant T and P. How is it possible, then, that G increases in photosynthesis? The answer is found in the violation of the constant-T condition when heat is transferred from the sun at 5800 K to a leaf at 300 K. An analysis of photon emission and absorption [26,27] (see the SI, e.g., Equations (S37b) and (S42)) shows that the global entropy change in both emission and absorption is positive and allows for,

Δ_rG < 0.92 E_photon > 0.

(7)

This means that in the primary reaction in photosynthesis, Δ_rG can be positive up to 0.92 E_photon ≈ +180 kJ/(mol photons). The factor of 0.92 in Equation (7) is slightly lower than the famous Carnot efficiency limit of (1−T_leaf/T_sun) = 0.95, as required: Like traditional heat engines, photosynthesis cannot fully convert heat (photon energy) to work [14,28,29,30,31] (note that Δ_rG is equal to electrical work under suitable conditions) [32]. Nevertheless, due to the high temperature of the sun, the discrepancy between E_photon and the maximum Δ_rG in Equation (7) is small and can usually be ignored. More specific models of photon absorption by chlorophyll [33] yield even lower, more stringent limits to the conversion of photon energy into free energy by the plant.

2.2. Misconceptions from Redox Potentials

Redox potentials (i.e., standard reduction potentials) are shown on the vertical axis in the Z-scheme and widely used in the quantitative description of photosynthesis. This section provides the link between redox potentials and the free-energy differences needed in our analysis as well as a critical discussion mostly intended for readers who have grown accustomed to redox potentials without being aware of their limitations. It explains why a different energy scheme of photosynthesis is desirable. Novices can ignore this historical detour and skip to Section 2.5. to learn the energetics of photosynthesis directly in terms of meaningful individual free energies G^o’ of molecules and ions in kJ/mol, and their robust differences Δ_hrG^o’ in half reactions, as developed and shown in the figures below.

Redox potentials are given in volts, while energies in biochemical reactions should have units of kJ/mol. This use of inapplicable units obscures the understanding of bioenergetics. It conjures up an image of voltages that drive electric currents carried by high-energy electrons [18,34]; this is misleading, as shown in the following using the redox reaction “between Pheo and Q_A”, i.e.,

Pheo⁻˙ + Q_A → Pheo + Q_A⁻˙  Δ_rG^o’ = −35 kJ/mol

(8)

as an example (see after Section 4. for short descriptions of Pheo and Q_A; the raised dot indicates a radical). The redox potentials are E^o’_{Pheo, Pheo-·} = −0.505 V and E^o’_{QA, QA-·} = −0.144 V [35]:

• There is no voltage or electric potential difference [36] of [−0.144 V − (−0.505 V)] = 0.36 V between the locations of Pheo and Q_A in PSII, nor an associated electric field acting on electrons. The redox potential of E^o’_{Pheo, Pheo-·} = −0.505 V depends on the free energies of both Pheo and Pheo⁻˙, and E^o’_{QA, QA-·} = −0.144 V on those of both Q_A and Q_A⁻˙ (see Equations (S63) and (S57)). Since Q_A and Q_A⁻˙ are not simultaneously present in a given PSII, there is no physical basis for predicting a static voltage of 0.36 V. When Pheo⁻˙ sits at a distance d from Q_A, the electric potential difference is roughly −e/d, which is unrelated to the redox-potential difference of 0.36 V. As in simple batteries, where positively charged ions move to the positive electrode [32], the movement of charged species in redox processes is not determined by electric fields or voltages but by free-energy (e.g., bond-energy) differences. An example of a redox reaction occurring without a voltage [37] is shown in Figure S5a and Equation (S95). The predicted voltage exists only if conductive electrodes, see Figures S5b–d and S6, are immersed into (or connected via salt bridges to) half cells each containing the reduced and conjugate oxidized species simultaneously in similar amounts.
• The energy release in a redox reaction such as Pheo⁻˙ + Q_A → … cannot be attributed to electron transfer from a high-energy donor to a lower-energy acceptor [3]. It is shown in the SI (see Equation (S52)) that the acceptor accepting the electron must be of high enough energy for the reaction to be spontaneous (Δ_rG^o’ < 0), since that acceptor (Q_A in our example) is a reactant.

A redox potential E^o’ in volts can be formally converted to a free-energy difference in kJ/mol using the well-known relation,

Δ_hr,tG^o’ = −ν_e F E^o’

(9)

with the stoichiometric coefficient ν_e of the electrons transferred in the half reaction (see the SI, e.g., Equation (S94)) and Faraday’s constant F. Here, the index “_hr” refers to a half reaction, and the second subscript “_t” to the traditional description (see the SI). When the Z-scheme is interpreted as an energy diagram [4,20], the free energy on the vertical axis is usually Δ_hr,tG^o’/ν_e, at least implicitly. Redox potentials in V correspond directly to free-energy differences in eV.

Redox potentials are commonly shown as pseudo energy levels [18], prominently so in the Z-scheme [4,20], but the “redox-potential (free) energy” Δ_hr,tG^o’ obtained from a redox potential according to Equation (9) is the free energy neither of one specific chemical species nor of electrons:

• A redox potential depends on the bond and hydration energies of at least two chemical species [32], the oxidized and reduced molecules or ions in the half reaction, see Figure S3b, (as well as on the ionization energy for cations and the electron affinity of anions).
• Redox-potential energies are not energy levels of electrons. For instance, the electron energy in the electrodes of two separate electrochemical half cells connected only by a wire of negligible resistance is equal even when the half-cell redox potentials differ [3]. The energy of an electron in a half reaction depends on its environment and presents a difficult problem even in simple metal electrodes (keywords: work function, Fermi level, inner/outer/surface potentials) [38]; it would be even more challenging to analyze for electrons in molecules. ‘Free’ electrons are only intermediates and do not show up in the overall redox reaction such as Pheo⁻˙ + Q_A → Pheo + Q_A⁻˙. Therefore, the energetics of batteries [32] and biochemical reactions [3] can be analyzed without requiring quantification of the unknown free energy of ‘free’ electrons.

What has nonetheless made redox potentials useful parameters is their formal relation to the free energy of reaction, Δ_rG^o’, see Equations (S92) and (S93). Thus, one can make quantitative predictions of Δ_rG^o’ from given empirical redox potentials, but they do not explain anything.

2.3. Why Electrons Move without Redox Voltages

The concept of redox voltages seems to provide an easy explanation for electron transport, but it is not valid. Why, then, do electrons move in an electron transport chain? The answer in the framework of classical thermodynamics refers to a reduction in Gibbs free energy: The electrons move so as to reduce the free energy by enabling a spontaneous chemical reaction with Δ_rG < 0. Note that the reaction is not spontaneous because of the electron transfer, but because of the lower free energy of products relative to the reactants, due to stronger bonds, higher entropy, more favorable electron affinity for anions, lower ionization energy for cations, and/or more favorable hydration [32]. This is an energy-reduction argument that is quite simple and intuitive.

What thermodynamics really says is this: If electrons undergo net transport, it must be in the direction that ensures ΔG < w_ele = 0. This is a direct result of the second law of thermodynamics in the form of the inequality of Clausius evaluated at constant T and P [32]. This analysis correctly predicts that, referring to the reaction in Equation (8), the reactants may remain kinetically trapped for an indefinite amount of time, but if Pheo + Q_A⁻˙ form by electron transfer, they will not undergo a net reverse reaction.

A somewhat more mechanistic and microscopic picture acknowledges that the electrons can move back and forth but will prefer to remain in relatively lower-free-energy Q_A⁻˙ rather than higher-energy Pheo⁻˙, resulting in a net transformation of Pheo⁻˙ to Q_A⁻˙. Correspondingly, Δ_rG^o determines products of ratios of forward to reverse rate constants, k_f/k_r, even in an open system (see Equation (S110)). In the simplest case of an elementary reaction [39],

$$\frac{k_f}{k_r}={\left(\frac{mol}{L}\right)}^{\Delta \nu }K={\left(\frac{mol}{L}\right)}^{\Delta \nu }\exp \left(-\frac{{\Delta }_r{G}^o}{RT}\right)$$

(10)

2.4. Misconceptions about Electron Donors

Good electron donors such as P680*, the excited state of the chlorophyll dimer at the center of Photosystem II, are mentioned prominently in textbook analyses of photosynthesis (for a brief description of this and other redox-active species in photosynthesis see the list after Section 4). It is easy to misunderstand what a statement like “P680* is an excellent electron donor” [2] really means. The half reaction in which an electron is donated is invariably energetically uphill (endergonic): No neutral stable chemical species reduces its free energy by giving off an electron, not even lithium metal, a strong reducing agent high up in a plot of −E^o with its very negative E^o = −3.04 V but still with Δ_hrG^o = +119 kJ/mol > 0 for Li(s) → Li⁺(aq) + e⁻(g) [32]. Ionization of P700* to P700⁺˙ requires input of >250 kJ/mol, so P700* is not a spontaneous electron emitter either.

For a neutral species in photosynthesis to “act as an electron donor” means (i) ionization or (ii) loss of a hydrogen atom. Case (i), ionization, is equivalent to having a bound electron ripped off, which invariably requires energy input; as a simple example from introductory science, consider an isolated hydrogen atom in its ground state: for it to act as an electron donor, 13.6 eV = 1312 kJ/mol of energy has to be put in (an endothermic process). Case (ii), loss of a hydrogen atom from a molecule, means loss of the bond to the H-atom. Since bonds stabilize molecules and reduce their energy, loss of a bond by an electron donor means an energy increase; a simple example is presented in Figure S4. For instance, when an O–H bond in Tyr_Z is broken and the H-atom is given off (as a proton plus electron), high-energy Tyr_Z˙ is formed. Even many singly negatively charged species (e.g., chloride or Pheo⁻˙ ions) give off their extra electron only if energy is put in (corresponding to the electron affinity of single atoms and the lowest unfilled molecular orbital (LUMO) binding energy of uncharged molecules).

“P680* is an excellent electron donor” means that P680* requires less energy input to give off its electron than many other electron donors; or equivalently, that when its electron is taken up by an average electron acceptor, the overall redox reaction reduces the system free energy and can be spontaneous. We could say colloquially that the electron in P680* is relatively ‘loose’.

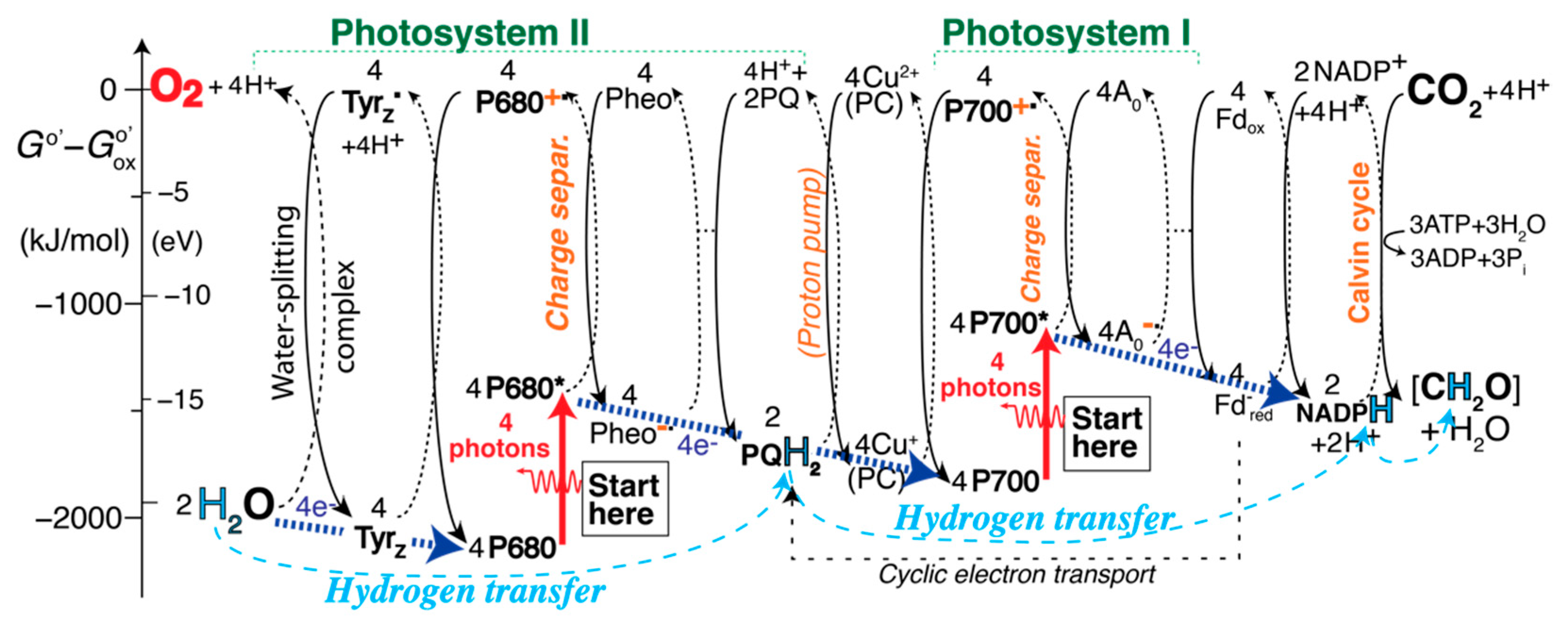
2.5. The Self-Explanatory Expanded Z (EZ)-Scheme: Processes in Photosystem II (PSII)

The energy flow and chemical transformation in Photosystem II can be represented in a sequence of redox energy transfer and release (RETAR) diagrams [3] as shown in Figure 1. More energy is released in a reduction (downward arrow on a solid curved line) than is consumed in the oxidation (upward arrow on a dashed curved line) to which it is coupled in the redox reaction, which is therefore spontaneous. The relation between the free-energy change Δ_hrG^o’ associated with a curved arrow and the corresponding standard reduction potential E^o’ in the traditional Z-scheme is,

Δ_hrG^o’ = −ν_e F (E^o’+ 4.28 V),

(11)

as derived in the SI (see Equation (S61)). An individual curved arrow is often associated with the transfer of one electron (ν_e = 1).

The first part of the expanded Z-scheme (EZ-scheme for short) of photosynthesis, shown in Figure 1, explains every step in PSII naturally: A photon excites P680, the chlorophyll dimer at the center of Photosystem II with an absorption maximum near 680 nm, to P680*, a state with a ‘loosened’ electron. (Four photons exciting four P680 are shown, because this is the number needed to generate one O₂ molecule.) Pheophytin (“Pheo”) takes the loosened electron from P680*, turning it into P680⁺˙, which is high in energy for two reasons: because of the absorbed photon and because of the energy transferred from Pheo as it is reduced to Pheo⁻˙. The generation of P680⁺˙ and Pheo⁻˙ is charge separation, emphasized [2,13,17,21] because it prevents the undesirable conversion of P680* directly back to P680, which would just produce heat. Pheo taking up one electron is a fast process since it requires no co-reactant (unlike Tyr_Z˙ also requiring H⁺ to form Tyr_Z, or NADP⁺ requiring a second electron and a proton to form NADPH). Note that the reverse reaction of P680⁺˙ and Pheo⁻˙ would be energetically uphill and is therefore not spontaneous.

The diagram shows, to the left of center, how the high-energy electron-deficient P680⁺˙ rips an electron off of Tyr_Z, turning it into Tyr_Z˙ plus a proton. The high-energy, electron-deficient Tyr_Z˙ in turn rips an electron off of H₂O, mediated by the Mn₄CaO₅ water-splitting complex (also known as the oxygen-evolving complex or OEC), and combines with H⁺ back to Tyr_Z. When this has happened four times (dissociating two H₂O molecules) in a full Kok(-Joliot) cycle of the water-splitting complex, four H⁺ ions and one O₂ molecule have been generated; [6] while the exact mechanism of the cycle is not currently known [8,21,40,41], as indicated in Figure 1 it must involve four (semi)stable intermediate states S₀ to S₃ and the unstable state S₄, which reflect increasing oxidation states of Mn and deprotonated H₂O generated using the energy transferred four times from P680⁺˙ [6]. The high-energy intermediates P680⁺˙, Tyr_Z˙, and S₄ are needed to generate the high-energy product, O₂.

On the right side of the diagram, Pheo⁻˙ gets oxidized back to Pheo by Q_A spontaneously reducing the overall free energy and its oxidation state to Q_A⁻˙ [35], which in turn gets oxidized back to Q_A by Q_B reducing the overall free energy and its oxidation state (towards Q_BH₂, in two steps). All of these redox processes are spontaneous because the free-energy reduction in the reduction half reaction is larger than the free-energy increase in the oxidation.

In the end, this process has effectively or formally moved four H atoms (or four protons and four electrons) from two H₂O to two Q_BH₂, restored ground-state P680, and pumped four protons from the stroma to the lumen of the chloroplast:

2 H₂O_lumen + (2 Q_B + 4 H⁺_stroma) → (O₂ + 4 H⁺_lumen) + 2 Q_BH₂.

(12)

The produced quinols (hydrogenated quinones) [2,35] are still much too low in free energy to transfer hydrogen to CO₂ spontaneously:

12 Q_BH₂ + 6 CO₂ → 12 Q_B + C₆H₁₂O₆ + 6 H₂O  Δ_rG^o” = +1100 kJ/mol

(13)

12 PQH₂ + 6 CO₂ → 12 PQ + C₆H₁₂O₆ + 6 H₂O  Δ_rG^o” = +1260 kJ/mol

(14)

where PQH₂ is plastoquinol, the free form of Q_BH₂. The large positive values of Δ_rG^o” in Equations (13) and (14) [35] make it clear why the further energy boost in Photosystem I is needed. The photon energy in PSII was mostly consumed to generate O₂, a relatively weakly bonded, high-energy product [3,15]. The free-energy change in the water-splitting and O₂-generating half reaction is easy to analyze using G^o’ values of H₂O(l), O₂, and H⁺(aq) from Table S1 in ref. [3] (with stoichiometric coefficients of 2, 1, and 4, respectively):

Δ_hrG^o’^(ORR) = 2 × (−875.5) kJ/mol − (−463.5 kJ/mol + 4 × 170 kJ/mol) = −1968 kJ/mol.

(15)

The sign here is opposite from that of the oxidation indicated by the left-most dashed curved arrow in Figure 1, since Δ_hrG^o’ by definition applies to the reduction reaction. It may be noted that this diagram does not prove that O₂ is a high-energy molecule; other analyses [3,15] comparing the bonding in O₂ with that in other molecules, without H⁺ involved, are needed to make this point convincingly. Nevertheless, O₂ showing up high above H₂O in the diagram is clearly compatible with O₂ being energy-rich.

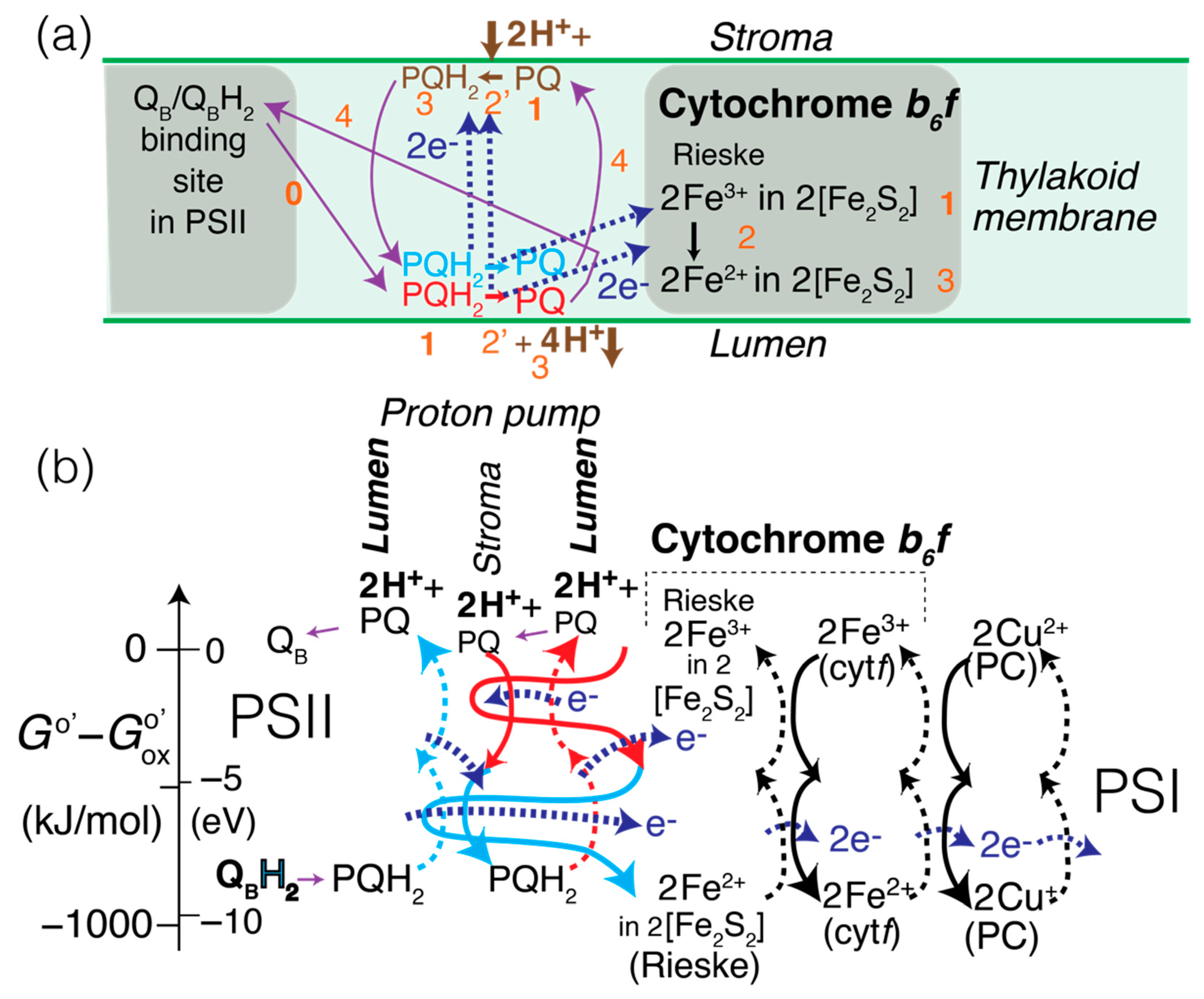
2.6. Processes Involving Cytochrome b₆f, in the EZ-Scheme

Next, Q_BH₂ needs to be reoxidized to Q_B + 2 H⁺ for the water-splitting process in PSII to be able to occur again. After being released from PSII into the thylakoid membrane (quinones are relatively hydrophobic), Q_BH₂ is recognized as plastoquinol, PQH₂, the protonated form of plastoquinone. PQH₂ is central to a “Q-cycle” proton pump [2] associated with cytochrome b₆f, whose function it is to move protons across the membrane from stroma (low [H⁺], pH = 8) to lumen (high [H⁺], pH = 5). The free energy put in to push the protons against a concentration gradient and electric potential is stored as chemical energy directly benefitting the organism; it is converted to chemical energy stored in ATP by the H⁺-flow-driven ATP synthase [2].

The Q-cycle is a complex process with three (rather than the normal two) coupled half reactions. In full versions of the Z-scheme, this complexity is reflected in unusual apparent energy increases (involving forms of cytochrome b subscripted “₆” or “_L//H”) rather than the usual downward trend [16]. A cartoon of the cycle (in spatial, not energetic terms) in the thylakoid membrane is shown in Figure 2a. The free-energy diagram of the Q-cycle in Figure 2b is color-coded to indicate that PQH₂ undergoes two electron transfers (two red, stacked dashed curved upward arrows), one to Fe³⁺ in a [Fe₂S₂] (or 2Fe-2S) cluster of the Rieske protein, and the other to PQ at the other (stroma) side of the membrane. Concomitantly, PQH₂ releases its H-atoms as protons into the lumen, while PQ picks up one proton from the stroma, forming PQH˙. To indicate that it is the substantial energy reduction of Fe³⁺ in [Fe₂S₂] that drives the whole process, its curved downward arrow in Figure 2b is expanded horizontally to cover the two other redox processes involved. Next, a second PQH₂ (again at the lumen side) undergoes the analogous electron and proton releases, but in addition to a second reduction of Fe³⁺ in a [Fe₂S₂] cluster it now reduces the PQH˙ at the lumen side fully to PQH₂ (again with a proton removed from the stroma). In short, the uphill proton-pumping redox reaction, with coupling through electron transfer via hemes at the center of the membrane,

(PQH₂)_{lumen side} + PQ_{stroma side} + 2 H⁺_stroma
→ PQ_{lumen side} + 2 H⁺_lumen + (PQH₂)_{stroma side}

(16)

is driven by being coupled with energetically downhill

(PQH₂)_{lumen side} + 2 [Fe³⁺₂S₂] (Rieske)
→ PQ_{lumen side} + 2 H⁺_lumen + 2 [Fe²⁺Fe³⁺S₂] (Rieske).

(17)

The reactions are coupled by (PQH₂)_{lumen side} passing one electron to Fe³⁺ in [Fe₂S₂] and one to PQ_{stroma side} + 2 H⁺_stroma, so more realistically each of the two (PQH₂)_{lumen side} contributes half to the first and half to the second reaction shown. All PQH₂ are at the same energy, so the slightly higher energy of the protons in the lumen relative to the stroma shows at the top of the diagram in Figure 2b.

The electron transport from left to right and free-energy flow from right to left through cytochrome b₆f continues in Figure 2b with regular redox pairs: The reduced iron–sulfur cluster in a Rieske protein is oxidized by Fe³⁺ in cytochrome b₆f reducing to Fe²⁺, which in turn is reoxidized by Cu²⁺ in plastocyanin reducing to Cu⁺.

2.7. Processes Involving Photosystem I (PSI) in the EZ-Scheme

Plastocyanin is water-soluble and diffuses to PSI, where its copper center is oxidized back to Cu²⁺ with energy provided by P700⁺˙ when the process continues as shown in Figure 3. Photon energy absorbed by P700 (a chlorophyll dimer with an absorption maximum near 700 nm) loosens an electron, forming excited P700*, which is easily ionized and raised in energy to P700⁺˙ by chlorophyll A₀, which gives off energy by taking up the loosened electron and forming A₀⁻˙. A₀ is quickly restored by reduction of A₁. Next in the diagram, three dots indicate two regular redox steps that have been skipped for brevity because their redox energy cycles are analogous to others shown. These involve two [Fe₄S₄] or 4Fe-4S clusters that cycle between Fe³⁺ and Fe²⁺, just like the third cluster, which is shown in the figure. Fe²⁺ in [Fe₄S₄] is cycled back to Fe³⁺ by reduction of Fe³⁺ in an [Fe₂S₂] cluster in ferredoxin, a soluble protein. Reduced ferredoxin can initiate cyclic electron transport, which is discussed further below, or be oxidized back to Fe³⁺ by redox reaction with NADP⁺, which is catalyzed by ferredoxin–NADP⁺ reductase (FNR) [2].

2.8. “Hydrogenation” (Reduction) of CO₂ to Carbohydrates

The EZ-scheme concludes in Figure 3, on the right, with the restoration of NADP⁺ and carbohydrate [CH₂O] synthesis by transfer of hydrogen to CO₂, in the Calvin cycle (greatly simplified). The curved orange arrows indicate that ATP hydrolysis is needed to make the redox reaction spontaneous. The surprising status of CO₂ among the higher-energy species here is explained in terms of bond energies in the SI. In short, the reduced species, [CH₂O] + H₂O, have two more electron-pair bonds than CO₂ + 4 H⁺(aq) and therefore appear lower in energy; the ionization energy of a hydrogen atom in water at pH 7, +170 kJ/mol (see Figure S4b) [3], also raises the energy of the reduced species. (In terms of energy per electron-pair bond, which is generally a more meaningful measure of the energetics of molecules [15], CO₂ and [CH₂O] are actually very similar, see also the SI, Equation (S113).) Hypothetical energy-releasing reactions of CO₂ + 4 H⁺ with various reduced species in PSI, see Equations (S114) and (S115), confirm the inferred energetic status of CO₂ + 4 H⁺.

2.9. Cyclic Electron Transport

In cyclic electron transport, PSI runs the Q-cycle proton pump without O₂ production. This is shown in Figure S9. The details of how ferredoxin is reduced by a quinone needed in the Q-cycle are possibly not fully understood. This process exclusively produces chemical energy directly for the plant, stored in a proton concentration gradient that is utilized for ATP synthesis. It is thus unlike O₂ production in PSII, which does not directly benefit the plant, and unlike true photo-synthesis producing carbohydrates by transfer of hydrogen to CO₂.

2.10. The Complete EZ-Scheme of Oxygenic Photosynthesis

Figure 1, Figure 2 and Figure 3 show the EZ-scheme broken up into three pieces for clarity. The full sequence of reactions is displayed in Figure S10. A simplified, more compact version is shown in Figure 4, with charge separation in the photosystems, generation of high-energy oxygen, and the Calvin cycle still included; only the Kok cycle and the complicated proton pump are not shown in an intelligible manner. Straight blue arrows at the bottom trace out the familiar Z-scheme of the reduced species, which is, however, greatly expanded by inclusion of the energetics of the high-energy oxidized species shown at the top.

2.11. Vertical Shifts in the EZ-Scheme

In a redox energy transfer and release diagram, the “column” for a given half reaction can be shifted up or down without changing the energy released in reduction and the energy used in oxidation. For instance, while the free energies of P680, P680*, and P680⁺˙ are fixed relative to each other, they are not in a fixed relation to the free energy of Pheo, which, however, is fixed relative to Pheo⁻˙.

When comparing the bond energies of molecules [15] and ionization energies in water [32], the free atoms are a natural reference point. They were chosen as the zero point of the energies in Figure S11, which shows the higher energy of P680⁺˙ compared to P700⁺˙ more clearly but looks more disjointed than Figure 4. For many species, the thermodynamic data needed for Figure S11 are not easily available. If we set the free energies of all the oxidized species to zero as in Figure 4, a relatively smooth diagram results in which the reduced species trace out the familiar Z-scheme.

2.12. An Alternative EZ-Scheme: Energy Flow

An alternative version of the comprehensive EZ-scheme is presented in Figure 5 and Figure S12. It again takes advantage of the mentioned free choice of the vertical displacement of each half-reaction column in order to make various energetics comparisons easier. Neutral reduced molecules are shown guided by bond-energy diagrams [3,15], as in Figure S11, while ionic reduced species are aligned with their right neighbors for a simpler diagram. With ground-state P680 and P700 assigned the same energy, the easier ionization of P700* to P700⁺˙, compared to P680* to P680⁺˙ [42], becomes more apparent than in Figure 4. The relative energies of the “active bonds” in the hydrogen carriers H₂O, Tyr_Z, Q_BH₂/PQH₂, NADPH + H⁺, and [CH₂O] + H₂O match bond-energy considerations outlined in Section 3.7. below. The red arrows at the top indicate energy flow from PSII to the water-splitting complex and into high-energy O₂, and from PSI to the proton pump (and thus, eventually, to ATP). Ancillary energy flow is marked by thinner dashed red arrows; for instance, the energy boost of P680* to P680⁺˙ comes from the right. While energy transfer is not the main function of photosynthesis, the crucial net or formal hydrogen transfer from H₂O to carbohydrate marked at the bottom of the diagram can occur only if the intervening redox reactions, enabled by photon absorption, release free energy.

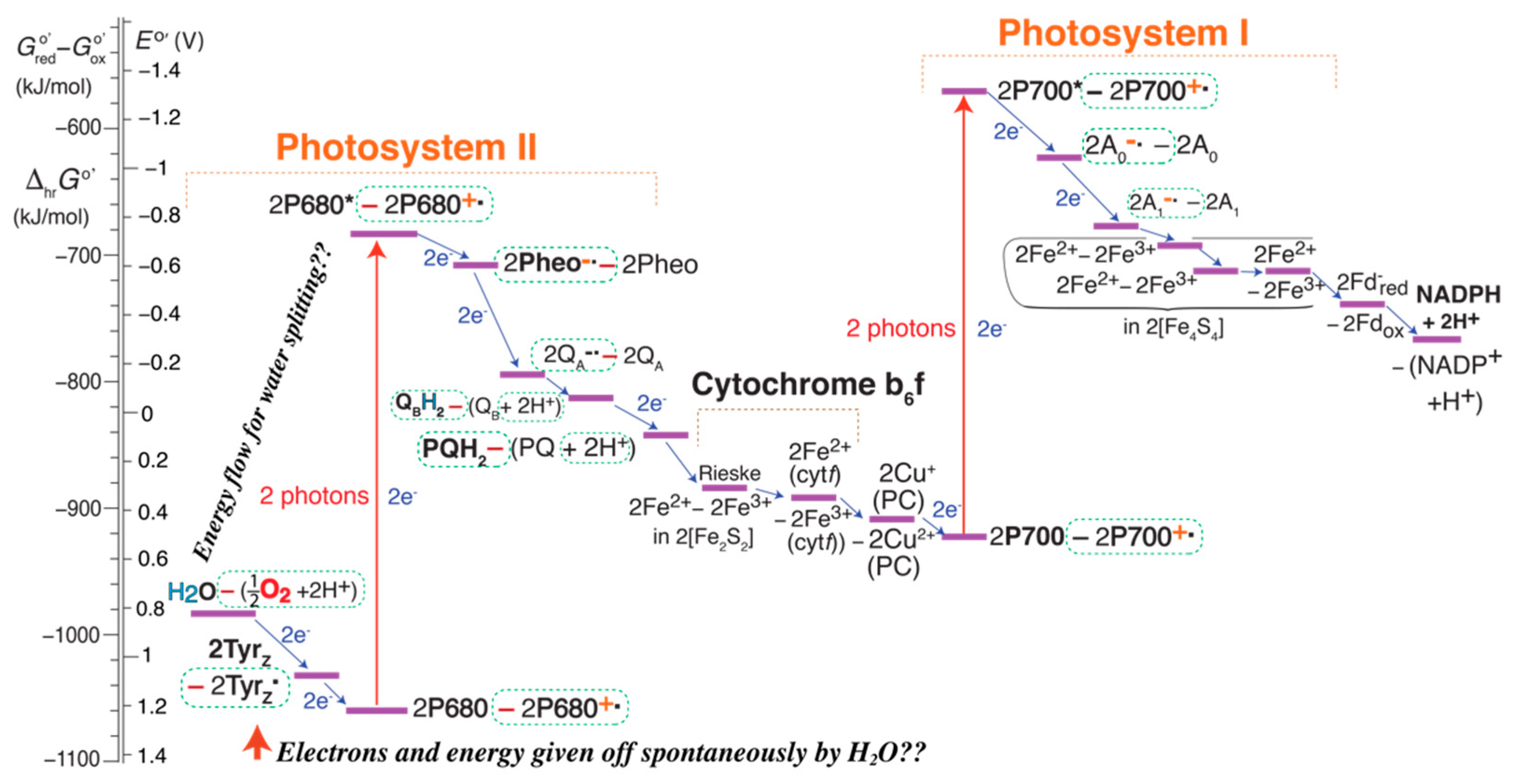
2.13. The Corrected Z-Scheme

The EZ-scheme helps clarify the original Z-scheme and makes it clear how the Z-scheme can be made more consistent and meaningful. Each pseudo-energy-level in the Z-scheme indicates the free-energy difference between products and reactants in a reduction half reaction (see ref. [3] and Figure S3b), i.e., between reduced and oxidized species. This is indicated in Figure 6; for brevity, the symbol G^o has been omitted for all species. For instance, “H₂O—(½ O₂ + 2 H⁺)” means

G^o_H2O—(½ G^o_O2 + 2 G^o’_H⁺).

(18)

While some references have shown both oxidized and reduced species in the Z-scheme, they usually left out protons, even though these are crucial electron acceptors [3], and used the division slash instead of the minus sign between reduced and oxidized species [35]. Previously missing species such as O₂, Tyr_Z˙, P680⁺˙, P700⁺˙, and Pheo⁻˙ all show up in the corrected Z-scheme in Figure 6. Nevertheless, the high energies of the former three are still not directly obvious, unlike in the EZ-schemes of Figure 4 and Figure 5.

3. Discussion

3.1. The Superiority of the EZ-Scheme

The EZ-scheme shown in Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 and Figure S12 eliminates the mentioned shortcomings of the Z-scheme: It displays charge separation and the two sources of the high energy of P680⁺˙ (the absorbed photon and Pheo) explicitly; it shows O₂ correctly at high energy; it explicitly shows both reduced and oxidized species; it demonstrates that PSI has insufficient energy to split water and produce O₂ because P700* is easier to ionize than P680* [42], which also clarifies why P700 is shifted up relative to P680 in the traditional Z-scheme and why two photosystems are needed; it shows the energy flow from P680⁺˙ to H₂O needed for water splitting and explains that electrons move from H₂O to Tyr_Z˙ because the coupled reduction of the latter and oxidation of the former has ΔG < 0; it makes clear that the process starts with the absorption of a photon; it shows that 2 × 4 photons are needed per O₂ produced; it can represent pure energy transfer (see Figures S7 and S8); the “energy levels” represent the (relative) energies of chemical species [3] rather than energy differences that are easily misinterpreted; it explains the Q-cycle proton pump and includes the Kok and Calvin cycles.

3.2. PSI Has Too Little Energy for Water Splitting, Due to Low Ionization Energy

The physical difference between PSII and PSI is not apparent from the traditional Z-scheme, where PSI is shifted up, without an intuitively meaningful explanation. The EZ-scheme, by contrast, makes clear why: the upshift in E^o’ corresponds to a smaller Δ_hrG^o’, which is due to a smaller energy difference between P700⁺˙ and P700, compared to P680⁺˙ and P680. This difference between the energy differences is directly apparent in the EZ-scheme of Figure 5 and Figure S12. The energy of P700⁺˙ relative to ground-state P700 is the sum of the absorbed photon energy and the ionization energy of P700* (to P700⁺˙), and an analogous statement applies to P680⁺˙. Since the absorbed-photon energies differ only by about (700−680)/700 = 3% or ~10 kJ/mol, the main energetic difference between P680* and P700* is the ~80-kJ/mol smaller ionization energy of the latter, which has been attributed to differences in the protein atomic charges [42]. As a result of this reduced ionization energy, the ionized form P700⁺˙ has too little energy to split water and generate O₂. In a traditional E^o’ diagram, this is indicated by an E^o’ value < 0.82 V for P700–P700⁺˙.

This analysis shows that a textbook statement [2] to the effect that P680* is an excellent electron donor misses an important point and needs to be qualified. P700*, being more easily ionized, is actually a more excellent electron donor, but it must be pointed out that this is not always an advantage. For instance, it is the reason why P700* after donating an electron has too little energy to split water and produce O₂.

3.3. Little of the Energy of the Photons Absorbed by PSII Directly Benefits the Plant

We argue that most of the energy of the photons absorbed by PSII is used to produce high-energy dioxygen, which leaves the leaf and therefore does not benefit the plant directly. What the water-splitting PSII produces within the plant is plastoquinol, PQH₂, which is a rather low-energy molecule, in part due to aromatic stabilization. Consider that the reaction of 12 PQH₂ with 6 CO₂ to glucose and water, Equation (14), would be strongly uphill energetically, by Δ_rG^o” = +1260 kJ/mol. We can compare this with much less unfavorable hydrogenation of CO₂ from H₂

12 H₂ + 6 CO₂ → C₆H₁₂O₆ + 6 H₂O
Δ_rG^o = +31 kJ/mol, Δ_rG^o” = +27 kJ/mol

(19)

and with the spontaneous, energy-releasing reaction that CO₂ could undergo with the products of PSI, i.e., NADPH and ATP:

12 NADPH + 12H⁺ + 12 ATP + 6 CO₂ → 12 NADP⁺ + C₆H₁₂O₆ + 12 ADP + 12 P_i
Δ_rG^o’ < −125 kJ/mol, Δ_rG^o” < −90 kJ/mol.

(20)

This demonstrates that PSI provides significant energy for the organism, while PSII does not. A literature claim ([2], p. 779) that “the percentage of the photon’s energy conserved in PQH₂ … is 30%” incorrectly attributes the energy of O₂ [3,15] to PQH₂. This energy is not intrinsic to PQH₂ and would not be available in an anaerobic environment, while the energy of O₂ could be released by reaction with any organic molecule, H₂, H₂S, C(s), P₄(s), S₈(s), or Fe(s). That PQH₂ is a relatively low energy species is confirmed by the observation that it has no energy-releasing reaction with any organic biomolecule:

12 PQH₂ + 12 (CH₃)₂C=O → 12 PQ + 12 (CH₃)₂CHOH
Δ_rG^o” = +922 kJ/mol

(21)

12 PQH₂ + 12 pyruvate → 12 PQ + 12 lactate
Δ_rG^o” = +695 kJ/mol

(22)

12 PQH₂ + 12 oxaloacetate → 12 PQ + 12 malate
Δ_rG^o” = +635 kJ/mol

(23)

12 PQH₂ → 12 PQ + 12 H₂  Δ_rG^o” = +1230 kJ/mol

(24)

12 PQH₂ + 12 fumarate → 12 PQ + 12 succinate
Δ_rG^o” = +200 kJ/mol

(25)

Even a C=C double bond as a fairly high-energy co-reactant in Equation (25) is not sufficient to make the reaction spontaneous. Only biochemical reactions of PQH₂ with certain Fe- or Cu-containing species or with O₂ are spontaneous.

3.4. Two Photosystems Because of the High Energy of O₂

The function of processes in Photosystem II is not conversion of solar to chemical energy, but setting the stage for the synthesis of organic molecules: taking H-atoms (as H⁺ + e⁻) from H₂O in order to (formally) transfer them to CO₂ and eventually produce glucose and other biomolecules. This has been appreciated by some authors (though others see the function differently [4], e.g., in energizing electrons [43]). What has rarely been recognized is that the photon energy in Photosystem II is essentially used up to make the high-energy molecule O₂, a “waste product” that does not directly benefit the organism. Therefore oxygen-producing organisms need a second photosystem, PSI, to generate chemical energy for the organism, for instance in the form of ATP.

3.5. Photosynthesis with Only One Photosystem

As a test of our understanding of the need for two photosystems in oxygenic photosynthesis, it is instructive to compare with anoxygenic microbial photosynthesis. As predicted by our analysis, without the high energetic cost of O₂ production, a single photosystem is sufficient here.

Photoorganoheterotrophs (such as the heliobacteria or some filamentous anoxygenic phototrophs, also known as green non-sulfur bacteria [4,12,17]) utilize organic C and H (e.g., of acetate, succinate, or pyruvate) rather than CO₂ and H₂O as their carbon and hydrogen sources. These organisms only need to convert given organic molecules into carbohydrates, which requires relatively little energy, e.g.,

3 CH₃COOH → C₆H₁₂O₆   Δ_rG^o = +271 kJ/mol.

(26)

This reaction is 10 times less endergonic than the glucose production in plants according to Equation (1). The single microbial photosystem can use photon energy to produce ATP that can make slightly endergonic reactions like Equation (26) spontaneous, analogous to the reaction between NADPH + H⁺ and CO₂ in Equation (20), which would be slightly endergonic without ATP hydrolysis.

Some photolithoautotrophs use H₂ (e.g., purple non-sulfur bacteria in photoautotrophic mode) or H₂S (purple or green sulfur bacteria) [4,17] as their source of hydrogen to produce glucose. According to Equation (19), synthesis of glucose from H₂ and CO₂ without O₂ production is only slightly exergonic, Δ_rG^o = +31 kJ/mol, and from H₂S and CO₂ it only requires a moderate amount of energy input,

6 CO₂ + 12 H₂S → C₆H₁₂O₆ + 6 H₂O + 1.5 S₈
Δ_rG^o = +426 kJ/mol.

(27)

Because of the relatively weak bonds in H₂S compared to H₂O and because these reactions do not produce high-energy O₂, a single photosystem is sufficient to supply the few hundred kilojoules that are needed per mole of glucose produced.

3.6. Photon Energy Stored in O₂ vs. Glucose

The net result of photosynthesis is mostly the synthesis of glucose and oxygen according to Equation (1). It had long been assumed that the required input of +2875 kJ/mol is chemical energy stored in the bonds of glucose [2,14]. We have shown that this is incorrect: due to its weak double bond, O₂ is a high-energy molecule, while glucose is only of moderate energy [3,15]. This can be confirmed by comparing the total bond-formation energies (enthalpies) of the four species involved:

6 H₂O(l) + 6 CO₂ vs. C₆H₁₂O₆ + 6 O₂

(28)

Bond-formation energies:

6(−971) + 6(−1608) vs. −9672 + 6 (−498) kJ/mol

(29)

−5826 + (−9648) vs. −9672 + (−2988) kJ/mol.

(30)

These data show that the oxygen molecules are the least negative, i.e., highest, in energy among the four different species.

The analysis just presented tends to assign an only moderately negative (i.e., a relatively high) energy to molecules with few bonds or atoms. A more meaningful comparison can be made in terms of the average energy of two electron-pair bonds (in kJ/mol) in the molecules because the number of electron pair bonds is the same in reactants and products (if O₂ is assigned its usual bond order of two); then a reaction will occur spontaneously from reactants with weak bonds to products with stronger bonds [15]. The following data comparing the energies of pairs of electron-pair bonds

H₂O(l)  CO₂ vs. C₆H₁₂O₆  O₂
2 electron-pair bonds: −971 −804  −806 −498 kJ/mol

(31)

confirm that O₂ is the highest-energy species in the reaction. It is interesting to note in Equations (30) and (31) that the total energy of the 24 electron-pair bonds in 6 CO₂ and C₆H₁₂O₆ is essentially the same.

The average energy per electron-pair bond in the reactants of Equation (31) is −860 kJ/mol. The energy of glucose is by 24/2 × (860 − 804) = 672 kJ/mol, that of 6 O₂ by 6 × (860 − 498) = 2172 kJ/mol higher than that of the reactants. Thus, 76% of the energy of the products can be assigned to O₂, as usual [15]. The corresponding analysis in terms of free energies, with similar results, is shown in the SI (Equation (S116)). Overall, more than 3/4 of the chemical energy produced in photosynthesis is stored in O₂ rather than glucose.

3.7. Energetics of H₂O Relative to O₂ and QH₂

The photosynthesis reaction of Equation (1) is energetically uphill because of the relatively strong bonds in the reactant H₂O and the relatively weak double bond of the product O₂, while according to Equation (30), the 24 electron-pair bonds in 6 CO₂ and glucose essentially balance each other out energetically. The energy contributions of H₂O and O₂ can be reasonably separated by considering the energetics of Equation (1) if it produced a hypothetical O₂′ molecule with a more typical pair-of-electron-pair bond strength of −806 kJ/mol, which would be within ±2 kJ/mol (i.e., within ± 0.3%) of ½ CO₂ and the average for glucose (see Equation (31)) and still weaker than in ½ CH₄ (−815 kJ/mol) and 2 H₂ (−872 kJ/mol). With oxygen’s experimentally observed entropic free-energy contribution of 498 − 464 = 34 kJ/mol, the free energy of the hypothetical O₂′ is −772 kJ/mol, 308 kJ/mol below the actual −464 kJ/mol of O₂. Accordingly, O₂ not being weakly bonded would make the photosynthesis reaction of Equation (1) less unfavorable by 6 × (−308 kJ/mol) = −1848 kJ/mol. The remaining free-energy difference of 2875 − 1848 = 1027 kJ/mol can be attributed to the relatively strong bonds in 6 H₂O compared to glucose, CO₂, and O₂′. This value of 1027 kJ/mol is similar to the 1260 kJ/mol required for glucose synthesis from PQH₂ and CO₂ according to Equation (14) and justifies placing 2 H₂O and 2 PQH₂ at approximately the same energy in Figure 5. This confirms quantitatively that most of the chemical energy derived from the photons absorbed by PSII does not end up in the hydrogen carrier produced, PQH₂, but in O₂.

3.8. Photosynthetic Efficiency: Is It Meaningful?

It is tempting to try to quantify the efficiency of photosynthesis, for instance by calculating the ratio of the free-energy increase during glucose production according to Equation (1) to the total photon energy absorbed by the leaf or the total solar energy impinging on the leaf [26,36]. We propose in the following that from biological and chemical-energy standpoints the analysis may be misguided due to incorrect assumptions about the function of photosynthesis, its reactions, and where the photon energy is stored.

From a biological perspective, the primary function of photosynthesis is not energy conversion but synthesis of biomolecules, as the term photosynthesis properly indicates. For instance, trees produce wood not to store chemical energy but to expose leaves in a broad canopy to direct sunlight, keep them out of the reach of large herbivores, etc. In fact, most of the chemical energy produced in oxygenic photosynthesis is stored not in biomass but in O₂ with its relatively weak double bond [15]. The examples of algal blooms and desert plants show that scarcity of nutrients or water, rather than of photon energy, often limit plant growth, so optimization of photosynthetic efficiency may not be critical to the plant.

Quantitative analyses of the efficiency of photosynthesis mostly focus on glucose production according to Equation (1). They overlook that most of the chemical energy is stored in the co-product O₂ [3,15] and, therefore, does not benefit the plant directly, and that photosynthesis can occur without glucose production, producing ATP for the organism according to Equation (3), e.g., using cyclic electron transport. This means that the result of the traditional efficiency calculation may not be really meaningful in a bioenergetics context.

3.9. Challenging the Paradigm of Electron Transport as Energy Transport

Traditional explanations of photosynthesis, most notably the Z-scheme, as well as of aerobic respiration have emphasized electron transport and equated it with energy flow, implicitly by red-hot electrons shown flowing through a cell [2] or explicitly when “high-energy electrons” [16,18,34,43] are invoked. According to a widely held view exemplified by Goodsell [43], photosynthesis “uses the energy of … photons to create high-energy electrons”, which are “used to power the pumping of hydrogen ions across the membrane” or transferred to NADPH. This interpretation is encapsulated in the widely quoted aphorism: “What drives life is thus a little electric current, kept up by the sunshine” [44]. In the following sections, these concepts are discussed critically, confirming the conclusion that what really drives complex life is chemical energy stored in relatively weak bonds, mostly in O₂ [3], kept up by the sunshine.

3.9.1. No “High-Energy Electrons” in Photosynthesis

The idea that photons produce high-energy electrons does not stand up to critical analysis. For instance, Figure 1 and chemical intuition shows that the unstable radical P680⁺˙ generated with the help of photon energy is energy-rich, but it is electron-deficient compared to P680 and P680*. Therefore, P680⁺˙ does not release a putative high-energy electron; in fact, it is an electron acceptor.

The misguided concept of “high-energy electrons” is linked by the erroneous “electron waterfall” [18,34] interpretation of a step in the Z-scheme as a high-energy donor passing an electron to a low-energy acceptor. In fact, the free energy released during a redox reaction represented by a step in the Z-diagram depends on the free energies of two donor and two acceptor species, as shown in the SI, and it is larger in magnitude the higher the energy of the actual acceptor of the electron (Equation (S52)). The absurdity of the traditional “electron waterfall” interpretation becomes apparent when one applies it to the left end of the Z-scheme in Figure 6 and Figure S1, where it leads to the unreasonable proposition that electrons flow spontaneously from H₂O via the OEC and tyrosine to ground-state chlorophyll and release energy in the process.

To the right of each photosystem, the implications of the conventional Z-scheme are unclear. For instance, it suggests (see Figure S1) spontaneous, energy-releasing electron transfer from Pheo to Q_A and then Q_B. However, Pheo is an electron acceptor, not an electron donor, so the suggested electron transfer does not occur between these species. The EZ-scheme is much superior in providing a self-explanatory diagram of energy absorption, transfer and release, and the associated electron transport in photosynthesis. It shows the relative free energies of all the molecules and ions involved, which reflect not nebulous electron affinities but bond, ionization, and solvation energies—in other words, chemical energy of molecules and ions [32].

Finally, high-energy electrons are supposedly transferred to NADPH; [45,46] this is often invoked to explain the large heat release (comparable with H₂ on a molar basis) when NADH, a close analogue of NADPH, reacts with O₂ [3]. However, this misassigns the energy of O₂ to NADH [3]. Analyzing other reactions of NAD(P)H, we have shown that it is only of moderate energy [3].

3.9.2. Energy Flow Runs Counter to Electron Flow

We had previously pointed out that electron flow runs opposite to energy flow in electron-transport chains [3]. Figure 5, as well as a careful analysis of Figure 1, Figure 2, Figure 3 and Figure 4, confirms that while electrons flow from left to right, energy flows from right to left (and up when photons are absorbed). For instance, energy clearly flows from high-energy, unstable P680⁺˙ to the left to split low-energy, stable H₂O, while electrons flow to the right. In any of the redox pairs without photon energy input in the Z- or EZ-scheme, the reduction, on the right, releases more free energy than the oxidation, to the left, takes up, so energy arguably flows from right to left. For instance, P680⁺˙ transfers energy into Tyr_Z˙ + H⁺, from right to left.

Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5, in agreement with basic chemical intuition, show that electron-carrying (reduced) species, such as stable P680 and Tyr_Z, are generally lower in energy than their oxidized counterparts, such as the electron-deficient, high-energy, unstable radicals P680⁺˙ and Tyr_Z˙ + H⁺. Similarly, ionization of Cu⁺ to Cu²⁺ in plastocyanin or of Fe²⁺ to Fe³⁺ in ferredoxin requires energy input but removes an electron. Thus, it is the net movement of oxidized, high-energy species, which are deficient in electrons, that generally represents energy flow. This confirms that the energy transferred is not carried by the transported electrons.

3.9.3. Hydrogen Transfer, Not Electron Transport, as the Main Function of Photosynthesis

At and above the college level, photosynthesis has traditionally been explained in terms of electron transport [2,9,18,43], but it is not always clarified explicitly why an organism needs electron transport. We argue that the main function of photosynthesis is the (formal) transfer of hydrogen atoms from water to carbon dioxide in order to form carbohydrates (CH₂O)_n and other biomolecules (photosynthesis). As highlighted at the bottom of Figure 4 and Figure 5, in PSII, H atoms are effectively (i.e., formally) transferred from H₂O into PQH₂, in PSI from PQH₂ into NADPH + H⁺, and in the Calvin cycle from 3 (NADPH + H⁺) into the three-carbon sugar glyceraldehyde 3-phosphate, C₃H₅O₃PO₃H. In many steps along this path, instead of an actual H-atom, H⁺ and e⁻ are transferred separately. Thus, distinct electron transport does occur, but only locally, over short distances within the thylakoid membrane. On a larger scale, H-atoms bound in molecules or ions of various oxidation states are transported in photosynthesis, not electrons as in a wire. Diffusion of plastoquinol, plastocyanin, or ferredoxin is not associated with any definable electron current. In the cell medium, electrical current is usually carried by protons and other ions, not by distinct electrons.

3.9.4. The Bicycle Chain: An Analogy for Electron Transport

Electron flow is often taken as an implicit marker of a series of spontaneous redox processes. It is sometimes said that a reaction, or in the quote above life itself, is driven by electron transport. This is as true as saying that a bicycle is propelled by its chain. Just like the chain is actually driven by the pedaling cyclist, the electrons are driven by the free-energy difference between high-energy reactants and low-energy products, which are often due to differences in bond energies—in short, chemical energy [15,32].

In this author’s view, the transfer of hydrogen to CO₂ to form biomolecules is the main function of photosynthesis, and electron transfer is only a means to that end. To present electron transport as the functional purpose of photosynthesis is like saying that the purpose of a bicycle ride is to move the chain, rather than to transport the rider.

3.10. Synopsis: A Valid Description of Energy and Hydrogen Flow in Photosynthesis

Casting aside historical misconceptions, the flow of energy, electrons, and hydrogen in photosynthesis can be cogently summarized based on the EZ-scheme as shown in Figure 4 and Figure 5: Photon energy excites the chlorophyll dimer P680 in Photosystem II to P680*, whose loosened electron can be taken up by pheophytin, a chlorophyll without Mg. It converts to pheophytin⁻˙ and gives off the LUMO binding energy of the added electron, turning P680* into the high-energy, electron-deficient radical P680⁺˙ (charge separation). Unstable P680⁺˙ quickly returns to the ground state, P680, by ripping an electron off tyrosine_Z, breaking an O–H bond and generating the unstable, high-energy Tyr_Z˙ radical and a proton. Tyr_Z˙ recovers its electron from H₂O by means of the Mn₄CaO₅ water-splitting complex. The energy released by P680⁺˙ returning to ground-state P680 four times is used to split 2 H₂O and generate O₂, a high-energy molecule, after four photons have been absorbed. Returning to pheophytin⁻˙, we find that its additional electron is taken up by an even more avid electron acceptor, PSII-bound quinone Q in site A, to form Q_A⁻˙ and then by quinone Q in site B, which in two such steps with two protons forms stable Q_BH₂. Overall in PSII, four H-atoms have been formally transferred from 2 H₂O to 2 Q_BH₂, a reluctant hydrogen donor that cannot generate carbohydrates, (CH₂O)_n, from CO₂, while photon energy has been stored in the weak double bond of O₂.

For this process to occur again, Q_B has to be recovered from Q_BH₂. This is achieved with photon energy absorbed by P700 in PSI and transferred to plastoquinol PQH₂, the free form of Q_BH₂, via P700⁺˙, diffusing soluble plastocyanin, cytochrome b₆f and its Rieske protein. The electrons taken from Q_BH₂ are transported in the opposite direction between these species. Through coupled redox reactions of 2 PQH₂ and the Rieske protein, protons are pumped through the thylakoid membrane, storing some of the photon energy in a proton gradient that drives ATP synthesis. The electron given off in the formation of P700⁺˙ is taken up by the acceptor A₀. Since P700* is easier to ionize than P680*, A₀ does not need to release as much energy as pheophytin when it accepts the electron. After several electron-transport redox steps, which include soluble ferredoxin that can diffuse to ferredoxin–NADP⁺ reductase, this allows for the reduction of NADP⁺ to NADPH + H⁺, a biochemical analogue of H₂ that gives off hydrogen atoms more easily upon oxidation than does PQH₂. This allows NADPH + H⁺ to transfer hydrogen to CO₂ in the Calvin cycle and form carbohydrates, (CH₂O)_n, helped along by hydrolysis of several ATP molecules.

Summarizing the essential points even more succinctly: photon absorption in PSII helps generate the high-energy electron acceptor P680⁺˙, which can split water to form high-energy O₂ while H-atoms are in effect transferred (as protons plus electrons) to form plastoquinol. The latter subsequently performs proton transport for ATP synthesis driven by energy passed down from light-generated, electron-deficient P700⁺˙ generated in PSI. Electrons given off in the formation of P700⁺˙ eventually combine with NADP⁺ and H⁺ to form NADPH, which in turn transfers H atoms to CO₂ to form carbohydrates in the Calvin cycle.

4. Conclusions

In this paper, it has been highlighted that oxygenic photosynthesis in plants does not produce high-energy organic molecules or high-energy electrons, but has two other functions: (i) making hydrogen from H₂O available for bonding to CO₂ and thus synthesis of carbohydrates and other biomolecules; (ii) converting solar energy into chemical energy stored in ATP. Step (i) requires production of the unavoidable high-energy “waste product” O₂. The photon energy absorbed by Photosystem II is essentially used up to produce O₂. Step (ii) includes “cyclic electron transport”, which is known to not involve carbohydrate but only chemical-energy production. The new analysis explains convincingly why plants need two photosystems: (i) PSII to extract hydrogen from H₂O, generating not only the low-energy hydrogen carrier PQH₂ but also the energetically expensive product O₂; this step provides little energy directly to the plant; (ii) PSI to produce stored chemical energy and eventually ATP as well as a hydrogen carrier of moderate free energy, NADPH. Fully consistent with our analysis, anoxygenic photosynthesis, e.g., transferring hydrogen from H₂S or H₂ to CO₂ without O₂ production, requires only one photosystem. Important aspects of oxygenic photosynthesis, e.g., charge separation by generation of Pheo⁻˙ and high-energy P680⁺˙, which had previously been described only in words, have been represented in an energy diagram for the first time. Others, such as the major energy boost from 680* to P680⁺˙ provided by the “electron affinity” (LUMO binding energy) of Pheo, have been completely missing from textbooks. That the crucial difference in the ionization energies of P680* and P700* results in P700⁺˙ having too little energy to split water and generate O₂ has also not been much emphasized. Unlike the traditional Z-scheme, which encodes energy differences on a shifted scale and in volts, the comprehensive EZ-scheme of photosynthesis introduced here shows free-energy differences explicitly, in kJ/mol. This is made possible by the use of individual free energies in this work, while conventional electrochemical thermodynamics, due to its arbitrary choice of the zero point of energy, can only predict relative redox energy differences. Our analysis has pointed out that the Z-scheme as traditionally presented shows O₂ incorrectly as a low-energy species, does not explain why electrons move from H₂O into tyrosine and chlorophyll, misses important high-energy species, and does not include the Kok and Calvin cycles. All these shortcomings have been addressed in the self-explanatory EZ-scheme, which also documents the counterflow of electrons and energy in photosynthesis and thus disproves the notion of high-energy electrons transporting energy.