Natural Selection beyond Life? A Workshop Report
Abstract
1. Introduction: Why Investigate “Natural Selection beyond Life”?
2. Natural Selection in Protobiotic Systems?
3. Natural Selection in the Context of Physical Phenomena
4. Natural Selection as a Framework
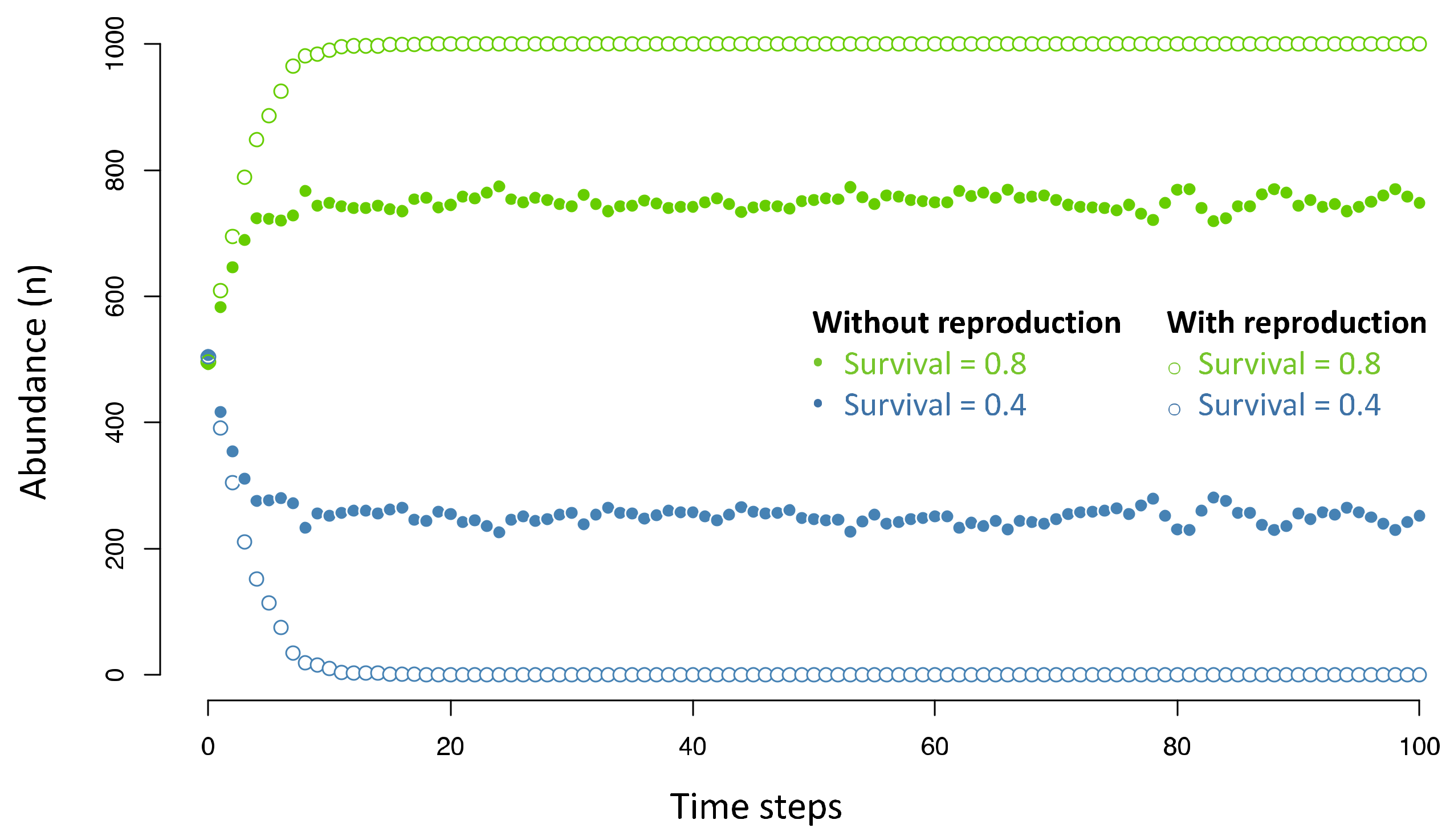
4.1. The Conditions of Natural Selection
4.2. The Signatures of Natural Selection
5. Conclusions: Individuality beyond Life?
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Neander, K. The Teleological Notion of ‘Function’. Australas. J. Philos. 1991, 69, 454–468. [Google Scholar] [CrossRef]
- Millikan, R.G. Language, Thought, and Other Biological Categories; MIT Press: Cambridge, MA, USA, 1984. [Google Scholar]
- Lewontin, R.C. The Units of Selection. Annu. Rev. Ecol. Syst. 1970, 1, 18. [Google Scholar] [CrossRef]
- Dawkins, R. The Selfish Gene; Oxford University Press: Oxford, UK, 1976. [Google Scholar]
- Kirby, S. The evolution of language. In Oxford Handbook of Evolutionary Psychology; Dunbar, R., Barret, L., Eds.; Oxford Univeristy Press: Oxford, UK, 2007; pp. 669–681. [Google Scholar]
- Spiegelman, S.; Haruna, I.; Holland, I.B.; Beaudreau, G.; Mills, D. The Synthesis of a Self-Propagating and Infectious Nucleic Acid with a Purified Enzyme. Proc. Natl. Acad. Sci. USA 1965, 54, 919–927. [Google Scholar] [CrossRef]
- Bartel, D.P.; Szostak, J.W. Isolation of New Ribozymes from a Large Pool of Random Sequences. Science 1993, 261, 1411–1418. [Google Scholar] [CrossRef] [PubMed]
- Pace, N.R.; Brown, J.W. Evolutionary Perspective on the Structure and Function of Ribonuclease, P, a Ribozyme. J. Bacteriol. 1995, 177, 1919–1928. [Google Scholar] [CrossRef] [PubMed]
- Cech, T.R.; Zaug, A.J.; Grabowski, P.J. In Vitro Splicing of the Ribosomal RNA Precursor of Tetrahymena: Involvement of a Guanosine Nucleotide in the Excision of the Intervening Sequence. Cell 1981, 27, 487–496. [Google Scholar] [CrossRef]
- Guerrier-Takada, C.; Gardiner, K.; Marsh, T.; Pace, N.; Altman, S. The RNA Moiety of Ribonuclease P Is the Catalytic Subunit of the Enzyme. Cell 1983, 35, 849–857. [Google Scholar] [CrossRef]
- Johnston, W.K.; Unrau, P.J.; Lawrence, M.S.; Glasner, M.E.; Bartel, D.P. RNA-Catalyzed RNA Polymerization: Accurate and General RNA-Templated Primer Extension. Science 2001, 292, 1319–1325. [Google Scholar] [CrossRef]
- Attwater, J.; Wochner, A.; Holliger, P. In-Ice Evolution of RNA Polymerase Ribozyme Activity. Nat. Chem. 2013, 5, 1011–1018. [Google Scholar] [CrossRef]
- Joyce, G.F.; Szostak, J.W. Protocells and RNA Self-Replication. Cold Spring Harb. Perspect. Biol. 2018, 10, a034801. [Google Scholar] [CrossRef]
- Lee, D.H.; Granja, J.R.; Martinez, J.A.; Severin, K.; Ghadiri, M.R. A Self-Replicating Peptide. Nature 1996, 382, 525–528. [Google Scholar] [CrossRef]
- Ashkenasy, G.; Jagasia, R.; Yadav, M.; Ghadiri, M.R. Design of a Directed Molecular Network. Proc. Natl. Acad. Sci. USA 2004, 101, 10872–10877. [Google Scholar] [CrossRef]
- Lincoln, T.A.; Joyce, G.F. Self-Sustained Replication of an RNA Enzyme. Science 2009, 323, 1229–1232. [Google Scholar] [CrossRef]
- Vaidya, N.; Manapat, M.L.; Chen, I.A.; Xulvi-Brunet, R.; Hayden, E.J.; Lehman, N. Spontaneous Network Formation among Cooperative RNA Replicators. Nature 2012, 491, 72–77. [Google Scholar] [CrossRef] [PubMed]
- Arsène, S.; Ameta, S.; Lehman, N.; Griffiths, A.D.; Nghe, P. Coupled Catabolism and Anabolism in Autocatalytic RNA Sets. Nucleic Acids Res. 2018, 46, 9660–9666. [Google Scholar] [CrossRef] [PubMed]
- Schulman, R.; Yurke, B.; Winfree, E. Robust Self-Replication of Combinatorial Information via Crystal Growth and Scission. Proc. Natl. Acad. Sci. USA 2012, 109, 6405–6410. [Google Scholar] [CrossRef] [PubMed]
- Zeravcic, Z.; Brenner, M.P. Self-Replicating Colloidal Clusters. Proc. Natl. Acad. Sci. USA 2014, 111, 1748–1753. [Google Scholar] [CrossRef] [PubMed]
- Sadownik, J.W.; Mattia, E.; Nowak, P.; Otto, S. Diversification of Self-Replicating Molecules. Nat. Chem. 2016, 8, 264–269. [Google Scholar] [CrossRef]
- Segre, D.; Ben-Eli, D.; Lancet, D. Compositional Genomes: Prebiotic Information Transfer in Mutually Catalytic Noncovalent Assemblies. Proc. Natl. Acad. Sci. USA 2002, 97, 4112–4117. [Google Scholar] [CrossRef]
- Vasas, V.; Szathmary, E.; Santos, M. Lack of Evolvability in Self-Sustaining Autocatalytic Networks Constraints Metabolism-First Scenarios for the Origin of Life. Proc. Natl. Acad. Sci. USA 2010, 107, 1470–1475. [Google Scholar] [CrossRef] [PubMed]
- Vasas, V.; Fernando, C.; Santos, M.; Kauffman, S.; Szathmáry, E. Evolution before Genes. Biol. Direct 2012, 7, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Bruylants, G.; Bartik, K.; Reisse, J. Prebiotic Chemistry: A Fuzzy Field. Comptes Rendus Chim. 2011, 14, 388–391. [Google Scholar] [CrossRef]
- Sutherland, J.D. Opinion: Studies on the Origin of Life—The End of the Beginning. Nat. Rev. Chem. 2017, 1, 0012. [Google Scholar] [CrossRef]
- Heams, T. Infravies—Le Vivant Sans Frontières; Seuil: Paris, France, 2019. [Google Scholar]
- Jeancolas, C.; Malaterre, C.; Nghe, P. Thresholds in Origin of Life Scenarios. Iscience 2020, 23, 101756. [Google Scholar] [CrossRef] [PubMed]
- Malaterre, C.; Chartier, J.-F. Beyond Categorical Definitions of Life: A Data-Driven Approach to Assessing Lifeness. Synthese 2021, 198, 4543–4572. [Google Scholar] [CrossRef]
- Schrödinger, E. What Is Life? The Physical Aspect of the Living Cell; Cambridge University Press: Cambridge, UK, 1944. [Google Scholar]
- Glansdorff, P.; Prigogine, I. Thermodynamic Theory of Structure, Stability and Fluctuations; Wiley-Interscience: London, UK, 1971. [Google Scholar]
- Prigogine, I.; Nicolis, G.; Babloyantz, A. Thermodynamics of Evolution. Phys. Today 1972, 25, 23–28. [Google Scholar] [CrossRef]
- Nicolis, G.; Prigogine, I. Self-Organization in Nonequilibrium Systems: From Dissipative Structures to Order through Fluctuations; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Pross, A. Stability in Chemistry and Biology: Life as a Kinetic State of Matter. Pure Appl. Chem. 2005, 77, 1905–1921. [Google Scholar] [CrossRef]
- England, J. Every Life Is on Fire: How Thermodynamics Explains the Origins of Living Things, 1st ed.; Basic Books: New York, NY, USA, 2020; ISBN 978-1-5416-9901-4. [Google Scholar]
- Bénard, M.H. Les Tourbillons Cellulaires Dans Une Nappe Liquide Transportant de La Chaleur Par Convection En Régime Permanent. Ann. de Chim. et de Phys. 1901, 23, 62–144. [Google Scholar]
- Rayleigh, L. Convection Currents in a Horizontal Layer of Fluid. Philos. Mag. Ser. 1916, 32, 529–546. [Google Scholar] [CrossRef]
- Goldbeter, A. Dissipative Structures in Biological Systems: Bistability, Oscillations, Spatial Patterns and Waves. Phil. Trans. R. Soc. A. 2018, 376, 20170376. [Google Scholar] [CrossRef]
- Allen, P.M. Evolution, Population Dynamics, and Stability. Proc. Natl. Acad. Sci. USA 1976, 73, 665–668. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Sumpter, D.J.T. Mathematical Modeling Reveals Spontaneous Emergence of Self-Replication in Chemical Reaction Systems. J. Biol. Chem. 2018, 293, 18854–18863. [Google Scholar] [CrossRef] [PubMed]
- Zeravcic, Z.; Brenner, M.P. Spontaneous Emergence of Catalytic Cycles with Colloidal Spheres. Proc. Natl. Acad. Sci. USA 2017, 114, 4342–4347. [Google Scholar] [CrossRef] [PubMed]
- Cross, M.C.; Hohenberg, P.C. Pattern Formation Outside of Equilibrium. Rev. Mod. Phys. 1993, 65, 851–1112. [Google Scholar] [CrossRef]
- Landauer, R. Inadequacy of Entropy and Entropy Derivatives in Characterizing the Steady State. Phys. Rev. A 1975, 12, 636–638. [Google Scholar] [CrossRef]
- Gyllenberg, M.; Service, R. Necessary and Sufficient Conditions for the Existence of an Optimisation Principle in Evolution. J. Math. Biol. 2011, 62, 359–369. [Google Scholar] [CrossRef] [PubMed]
- Bouchard, F. Causal Processes, Fitness, and the Differential Persistence of Lineages. Philos. Sci. 2008, 75, 560–570. [Google Scholar] [CrossRef]
- Bourrat, P. From Survivors to Replicators: Evolution by Natural Selection Revisited. Biol. Philos. 2014, 29, 517–538. [Google Scholar] [CrossRef]
- Doolittle, W.F. Making the Most of Clade Selection. Philos. Sci. 2017, 84, 275–295. [Google Scholar] [CrossRef][Green Version]
- Papale, F. Evolution by Means of Natural Selection without Reproduction: Revamping Lewontin’s Account. Synthese 2020, 198, 10429–10455. [Google Scholar] [CrossRef]
- Bissette, A.J.; Fletcher, S.P. Mechanisms of Autocatalysis. Angew. Chem. Int. Ed. 2013, 52, 12800–12826. [Google Scholar] [CrossRef] [PubMed]
- Blokhuis, A.; Lacoste, D.; Nghe, P. Universal Motifs and the Diversity of Autocatalytic Systems. Proc. Natl. Acad. Sci. USA 2020, 117, 25230–25236. [Google Scholar] [CrossRef] [PubMed]
- Godfrey-Smith, P. Darwinian Populations and Natural Selection; Oxford Univeristy Press: Oxford, UK, 2009. [Google Scholar]
- Matthen, M.; Ariew, A. Two Ways of Thinking About Fitness and Natural Selection. J. Philos. 2002, 99, 55–83. [Google Scholar] [CrossRef]
- Ariew, A.; Lewontin, R.C. The Confusions of Fitness. Br. J. Philos. Sci. 2004, 55, 347–363. [Google Scholar] [CrossRef]
- Clarke, E. The Problem of Biological Individuality. Biol. Theory 2010, 14, 312–325. [Google Scholar] [CrossRef]
- Van Valen, L.M. Energy and Evolution. Evol. Theory 1979, 1, 179–229. [Google Scholar]
- Clarke, E. A Levels-of-Selection Approach to Evolutionary Individuality. Biol. Philos. 2016, 31, 893–911. [Google Scholar] [CrossRef]
- Huneman, P. Individuality as a Theoretical Scheme. I. Formal and Material Concepts of Individuality. Biol. Theory 2014, 9, 361–373. [Google Scholar] [CrossRef]
- Guay, A.; Pradeu, T. Introduction: Progressive Steps toward a Unified Conception of Individuality across the Sciences. In Individuals across the Sciences; Guay, A., Pradeu, T., Eds.; Oxford Univeristy Press: Oxford, UK, 2016; pp. 1–22. [Google Scholar]
- Maynard Smith, J.; Szathmáry, E. The Major Transitions in Evolution; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Michod, R.E. Darwinian Dynamics; Princeton University Press: Princeton, NJ, USA, 1999. [Google Scholar]
- Okasha, S. Multilevel Selection and the Major Transitions in Evolution. Philos. Sci. 2005, 72, 1013–1025. [Google Scholar] [CrossRef]
- Bourrat, P. Levels, Time and Fitness in Evolutionary Transitions in Individuality. Philos. Theory Biol. 2015, 7, 17. [Google Scholar] [CrossRef]
- Price, G.R. Selection and Covariance. Nature 1970, 227, 520–521. [Google Scholar] [CrossRef] [PubMed]
- Rice, S.H. A Stochastic Version of the Price Equation Reveals the Interplay of Deterministic and Stochastic Processes in Evolution. BMC Evol. Biol. 2008, 8, 262. [Google Scholar] [CrossRef]
- Luque, V.J. One Equation to Rule Them All: A Philosophical Analysis of the Price Equation. Biol. Philos. 2017, 32, 97–125. [Google Scholar] [CrossRef]
- Day, T.; Parsons, T.; Lambert, A.; Gandon, S. The Price Equation and Evolutionary Epidemiology. Phil. Trans. R. Soc. B 2020, 375, 20190357. [Google Scholar] [CrossRef]
- Gardner, A. Price’s Equation Made Clear. Phil. Trans. R. Soc. B 2020, 375, 20190361. [Google Scholar] [CrossRef]
- Lehtonen, J.; Okasha, S.; Helanterä, H. Fifty Years of the Price Equation. Phil. Trans. R. Soc. B 2020, 375, 20190350. [Google Scholar] [CrossRef] [PubMed]
- van Veelen, M. The Problem with the Price Equation. Phil. Trans. R. Soc. B 2020, 375, 20190355. [Google Scholar] [CrossRef] [PubMed]
- Price, G.R. The Nature of Selection. J. Theor. Biol. 1995, 175, 389–396. [Google Scholar] [CrossRef]
- Okasha, S. Evolution and the Levels of Selection; Clarendon Press: Oxford, UK, 2006. [Google Scholar]
- Bourrat, P. Transitions in Evolution: A Formal Analysis. Synthese 2021, 198, 3699–3731. [Google Scholar] [CrossRef]
- Glymour, B. Cross-Unit Causation and the Identity of Groups. Philos. Sci. 2017, 84, 717–736. [Google Scholar] [CrossRef]
- Bourrat, P. Facts, Conventions, and the Levels of Selection, Cambridge Elements, Philosophy of Biology; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Krakauer, D.; Bertschinger, N.; Olbrich, E.; Flack, J.C.; Ay, N. The Information Theory of Individuality. Theory Biosci. 2020, 139, 209–223. [Google Scholar] [CrossRef] [PubMed]
- Flack, J.C. Coarse-Graining as a Downward Causation Mechanism. Phil. Trans. R. Soc. A 2017, 375, 20160338. [Google Scholar] [CrossRef]
- Sachs, J.L.; Mueller, U.G.; Wilcox, T.P.; Bull, J.J. The Evolution of Cooperation. Q. Rev. Biol. 2004, 79, 135–160. [Google Scholar] [CrossRef]
- Levin, S.R.; Gandon, S.; West, S.A. The Social Coevolution Hypothesis for the Origin of Enzymatic Cooperation. Nat. Ecol. Evol. 2020, 4, 132–137. [Google Scholar] [CrossRef]
- Earnshaw-Whyte, E. Increasingly Radical Claims about Heredity and Fitness. Philos. Sci. 2012, 79, 396–412. [Google Scholar] [CrossRef]
- Bourrat, P. How to Read “Heritability” in the Recipe Approach to Natural Selection. Br. J. Philos. Sci. 2015, 66, 883–903. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Charlat, S.; Ariew, A.; Bourrat, P.; Ferreira Ruiz, M.; Heams, T.; Huneman, P.; Krishna, S.; Lachmann, M.; Lartillot, N.; Le Sergeant d'Hendecourt, L.; et al. Natural Selection beyond Life? A Workshop Report. Life 2021, 11, 1051. https://doi.org/10.3390/life11101051
Charlat S, Ariew A, Bourrat P, Ferreira Ruiz M, Heams T, Huneman P, Krishna S, Lachmann M, Lartillot N, Le Sergeant d'Hendecourt L, et al. Natural Selection beyond Life? A Workshop Report. Life. 2021; 11(10):1051. https://doi.org/10.3390/life11101051
Chicago/Turabian StyleCharlat, Sylvain, André Ariew, Pierrick Bourrat, María Ferreira Ruiz, Thomas Heams, Philippe Huneman, Sandeep Krishna, Michael Lachmann, Nicolas Lartillot, Louis Le Sergeant d'Hendecourt, and et al. 2021. "Natural Selection beyond Life? A Workshop Report" Life 11, no. 10: 1051. https://doi.org/10.3390/life11101051
APA StyleCharlat, S., Ariew, A., Bourrat, P., Ferreira Ruiz, M., Heams, T., Huneman, P., Krishna, S., Lachmann, M., Lartillot, N., Le Sergeant d'Hendecourt, L., Malaterre, C., Nghe, P., Rajon, E., Rivoire, O., Smerlak, M., & Zeravcic, Z. (2021). Natural Selection beyond Life? A Workshop Report. Life, 11(10), 1051. https://doi.org/10.3390/life11101051






