On the Design of a Class of Rotary Compressors Using Bayesian Optimization
Abstract
:1. Introduction
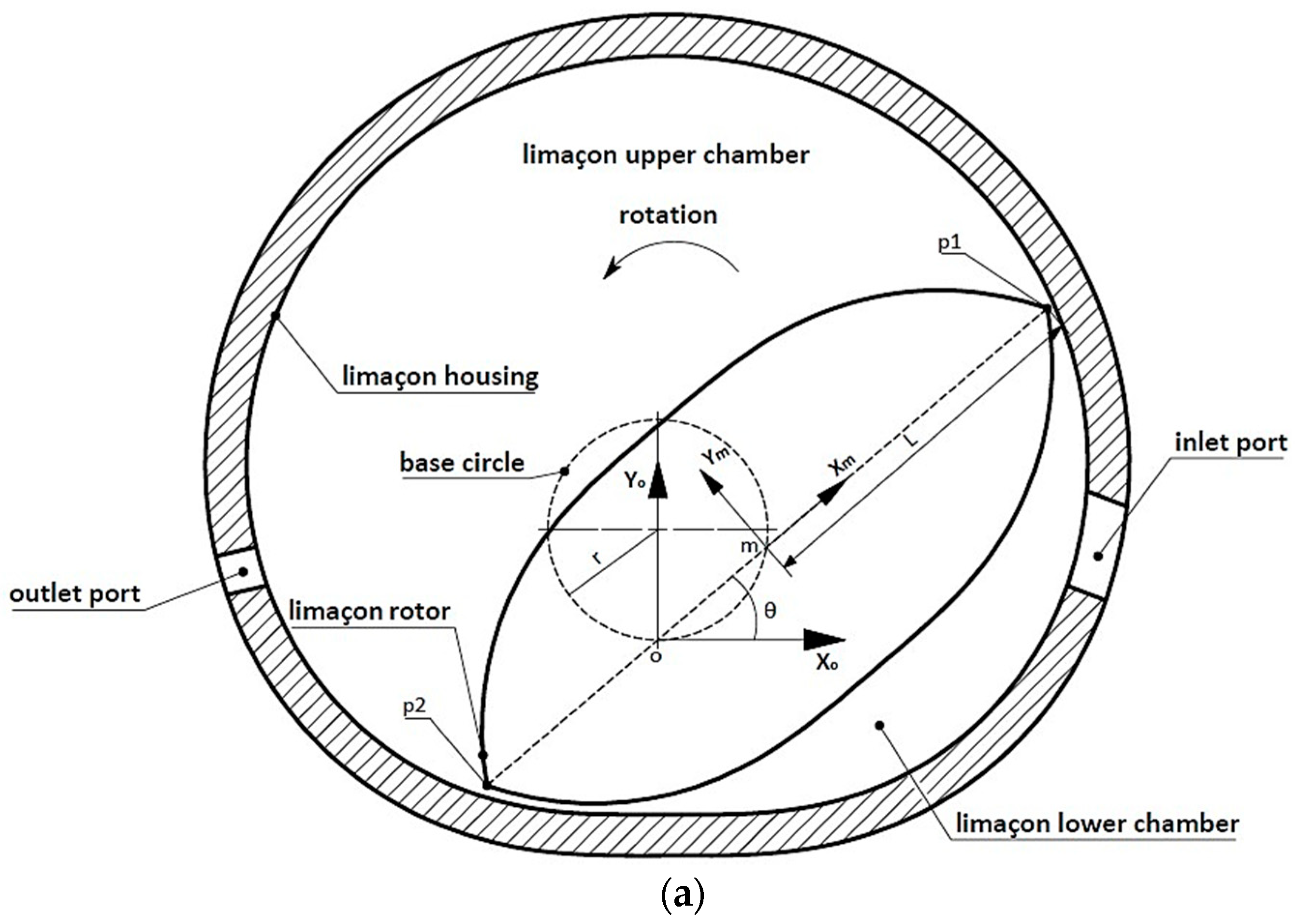
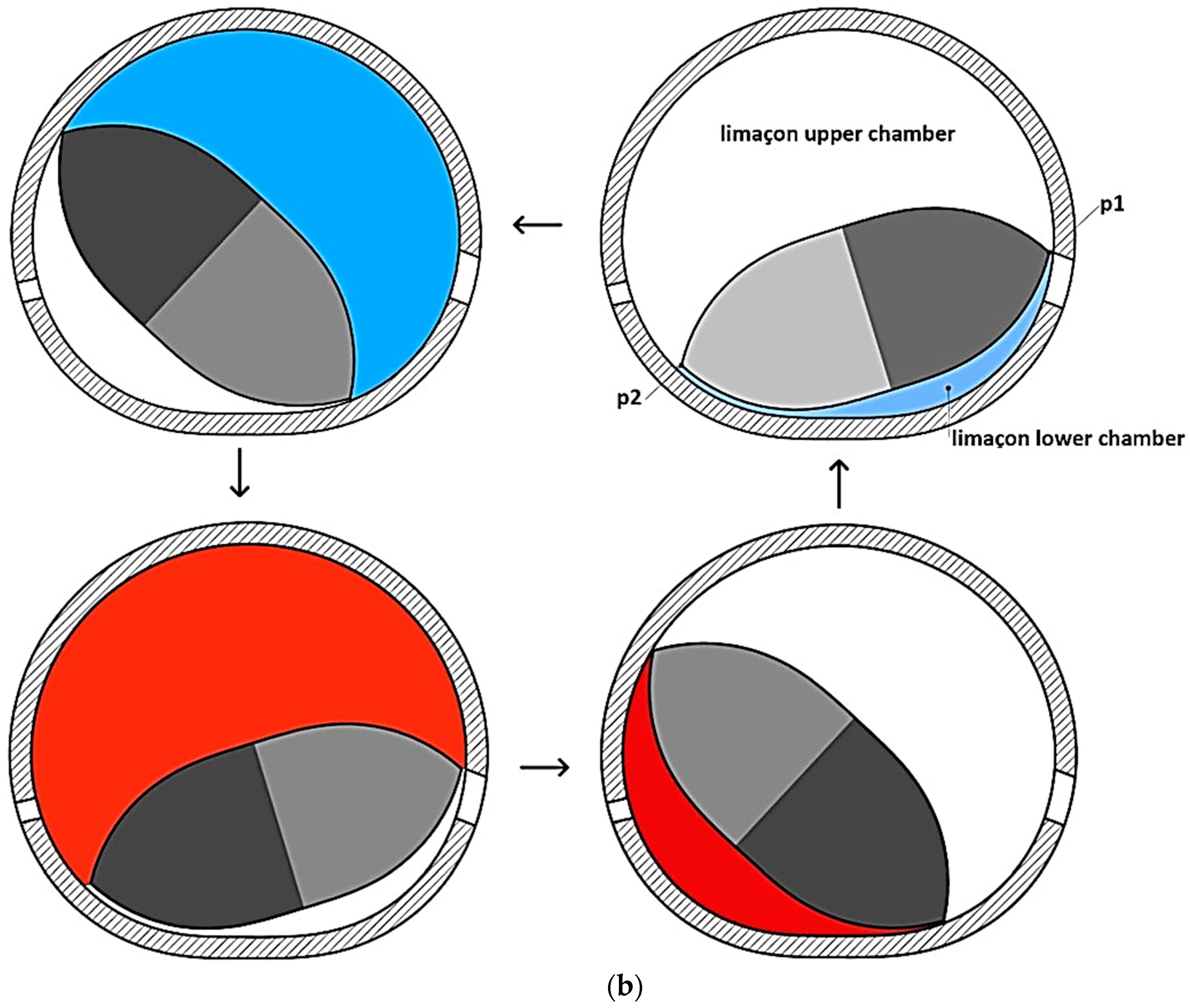
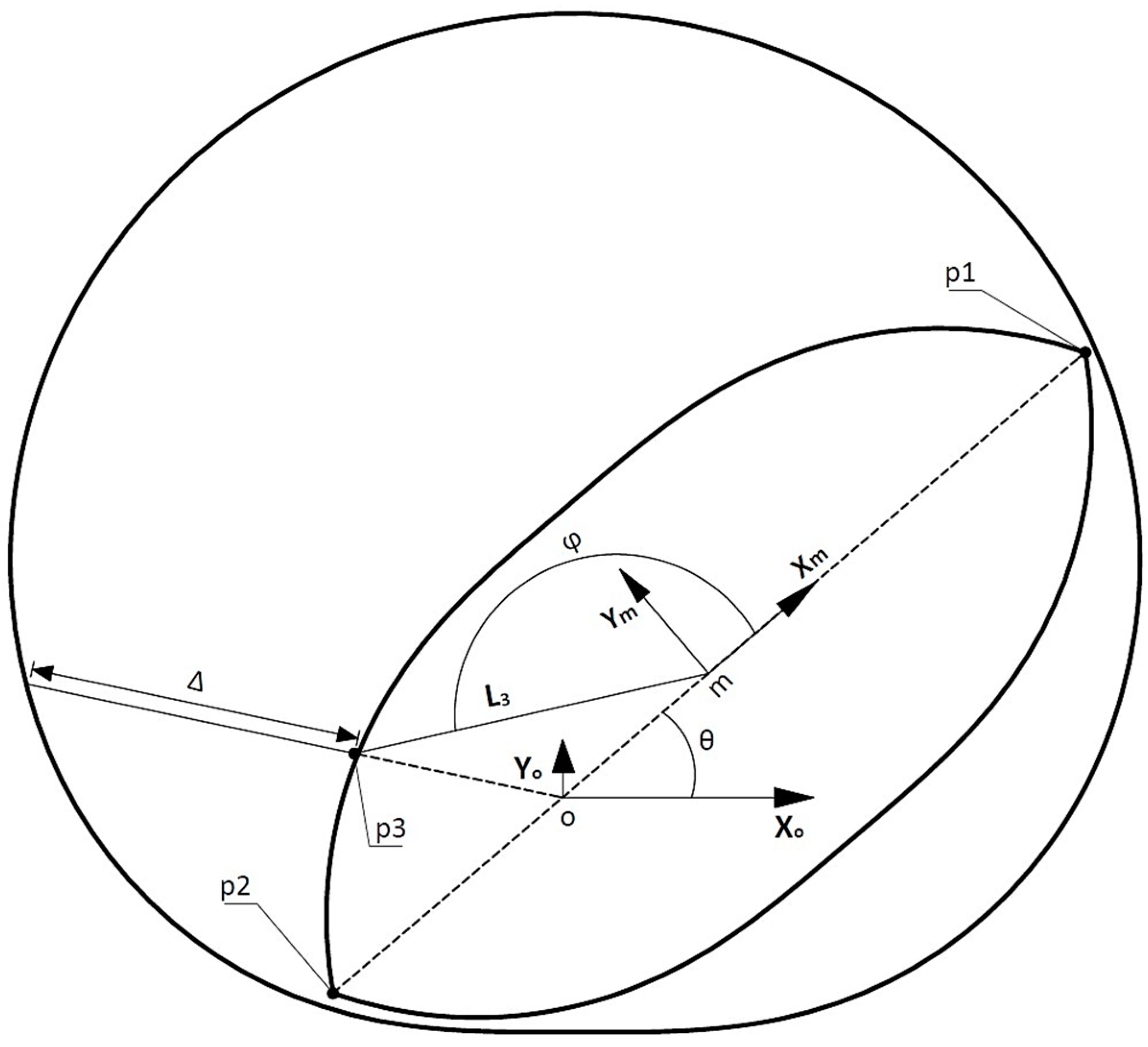
2. Geometric Characteristics of the Limaçon Compressor
3. Mathematical Model
3.1. Mass Flow Rate through the Inlet Port
3.2. Mass Flow Rate through the Discharge Valve
3.3. Side and Apex Leakage
3.4. Thermodynamic Model
3.5. Simulation of the Limaçon Compressor
3.6. Performance Indices
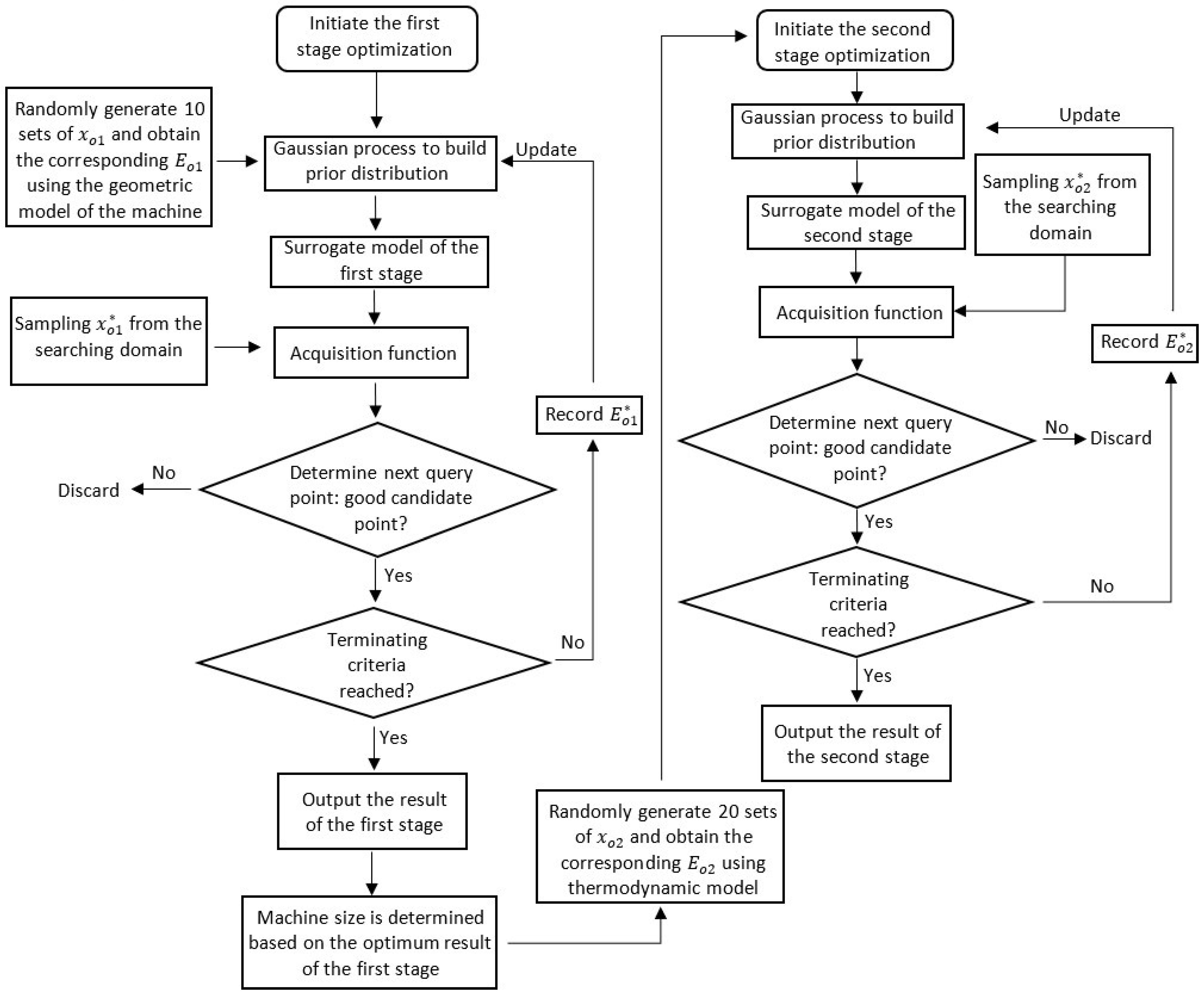
4. Optimization Process
4.1. Bayesian Optimization Method
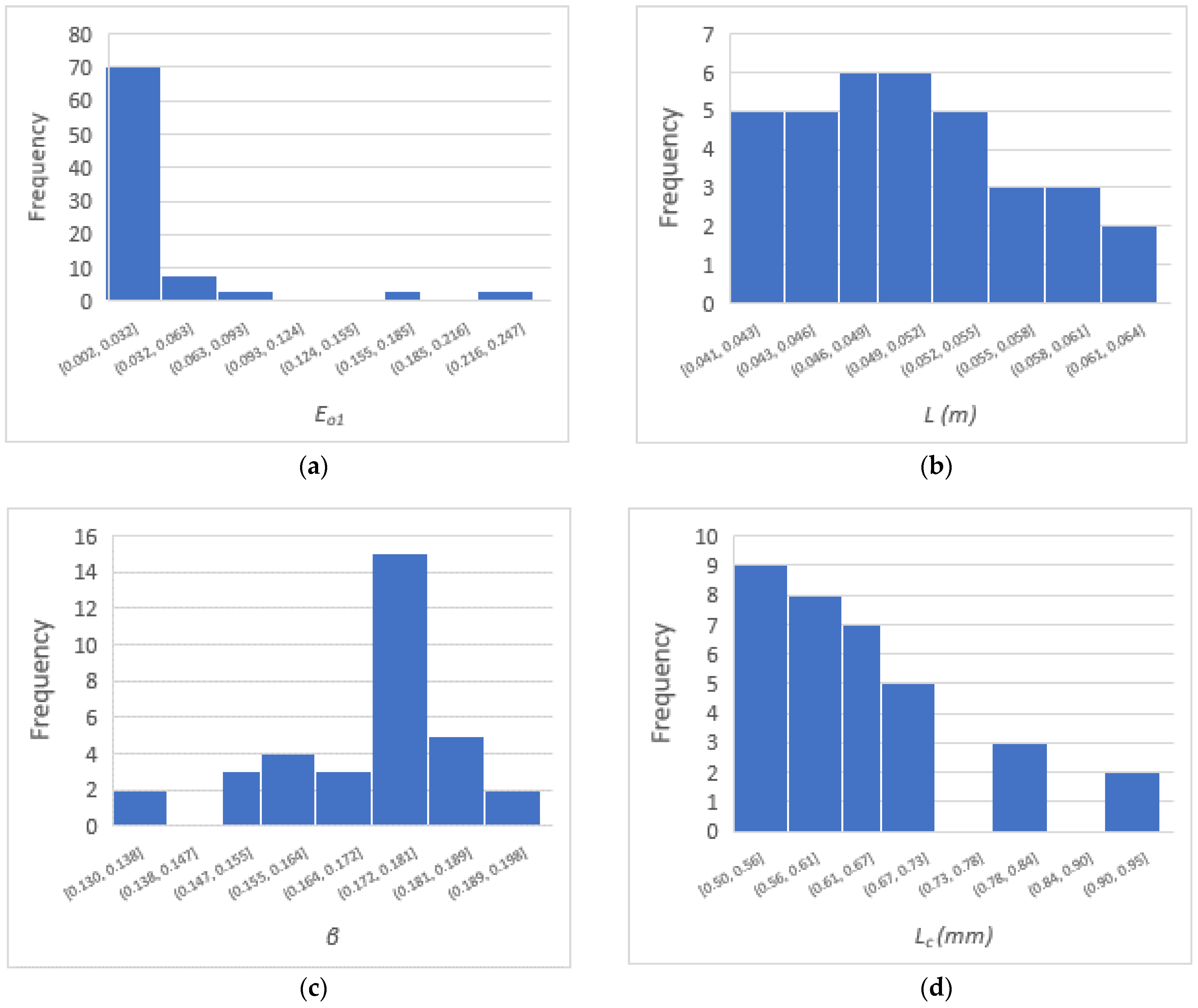
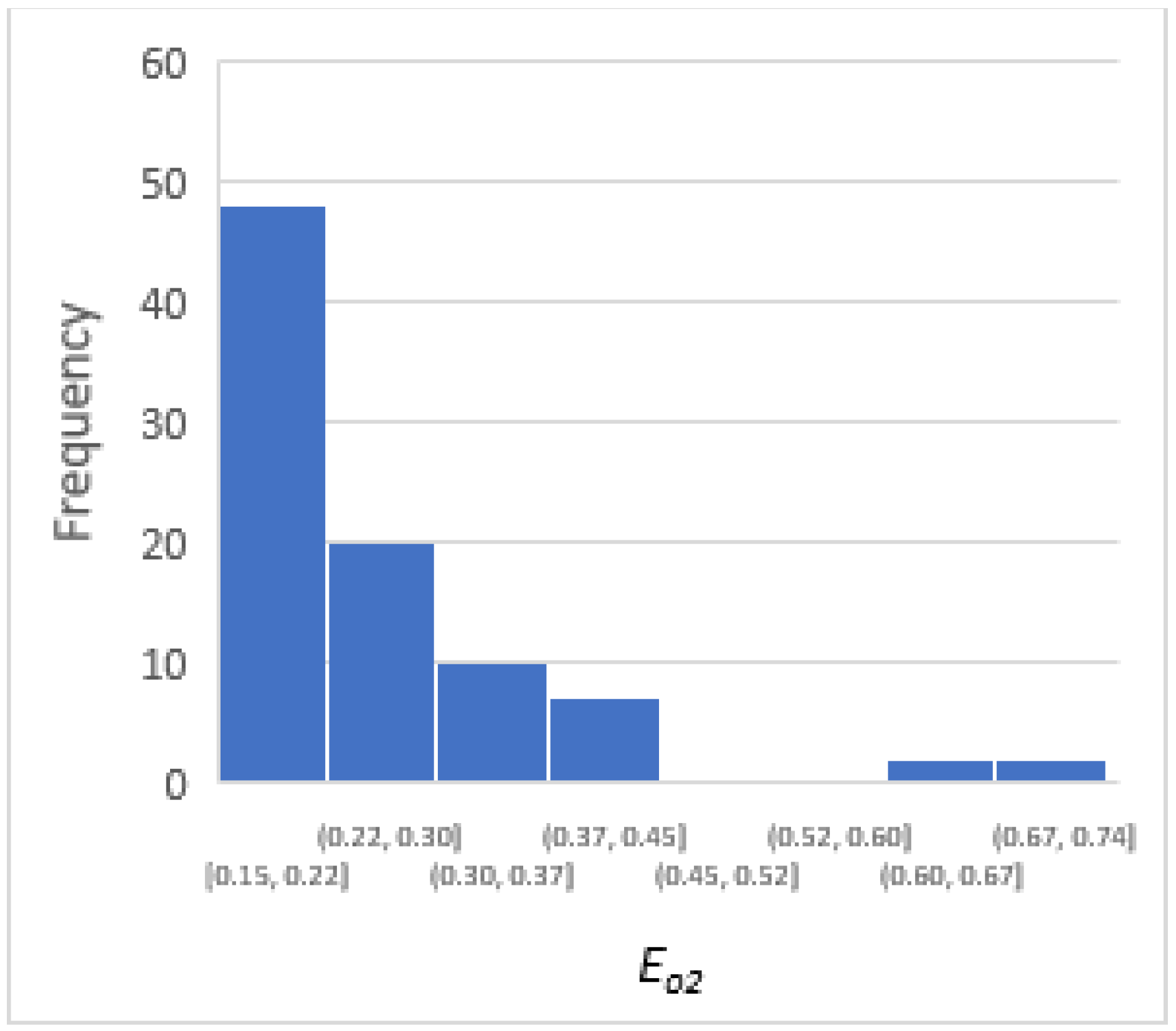
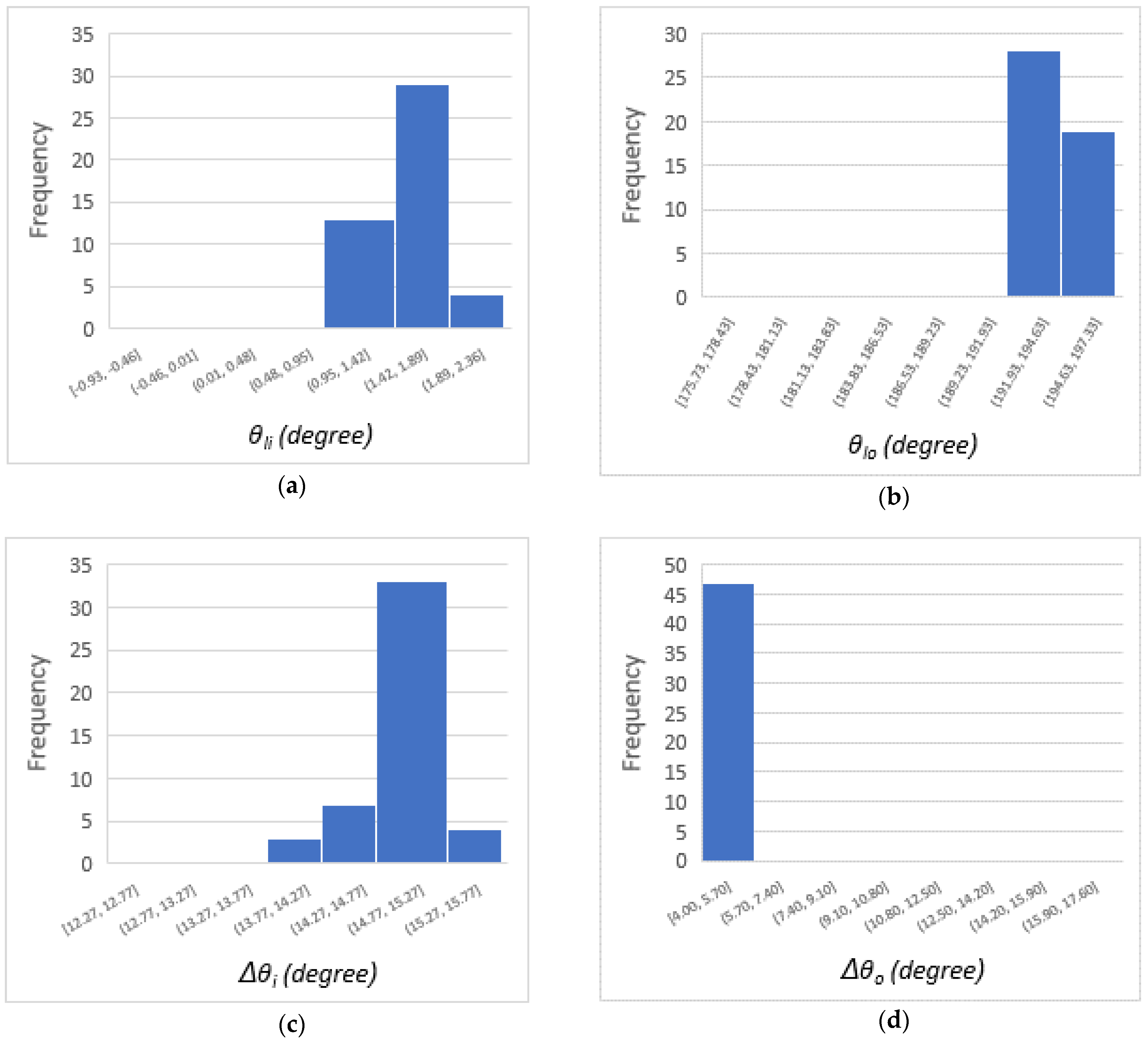
4.2. Two-Stage Optimization
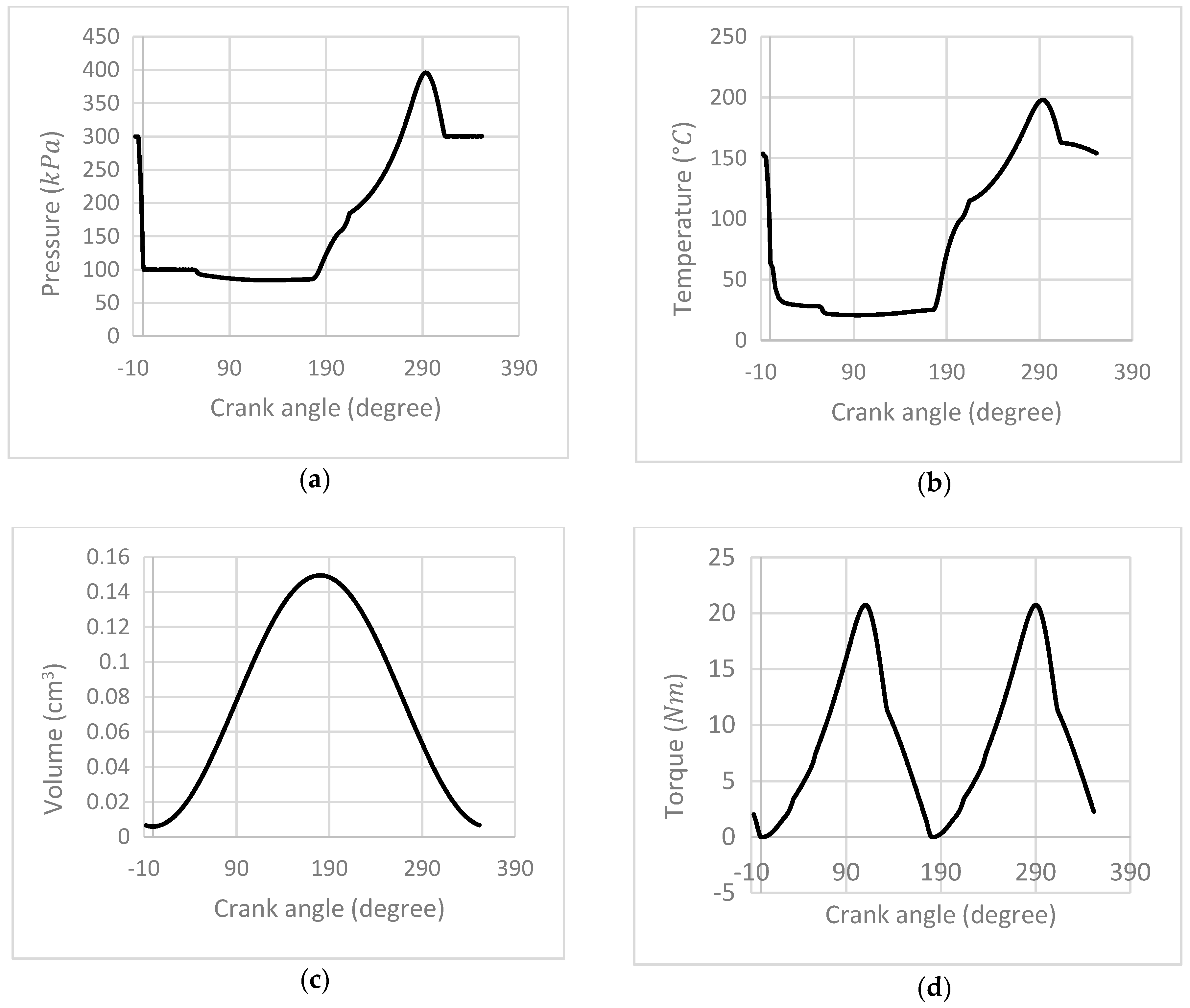
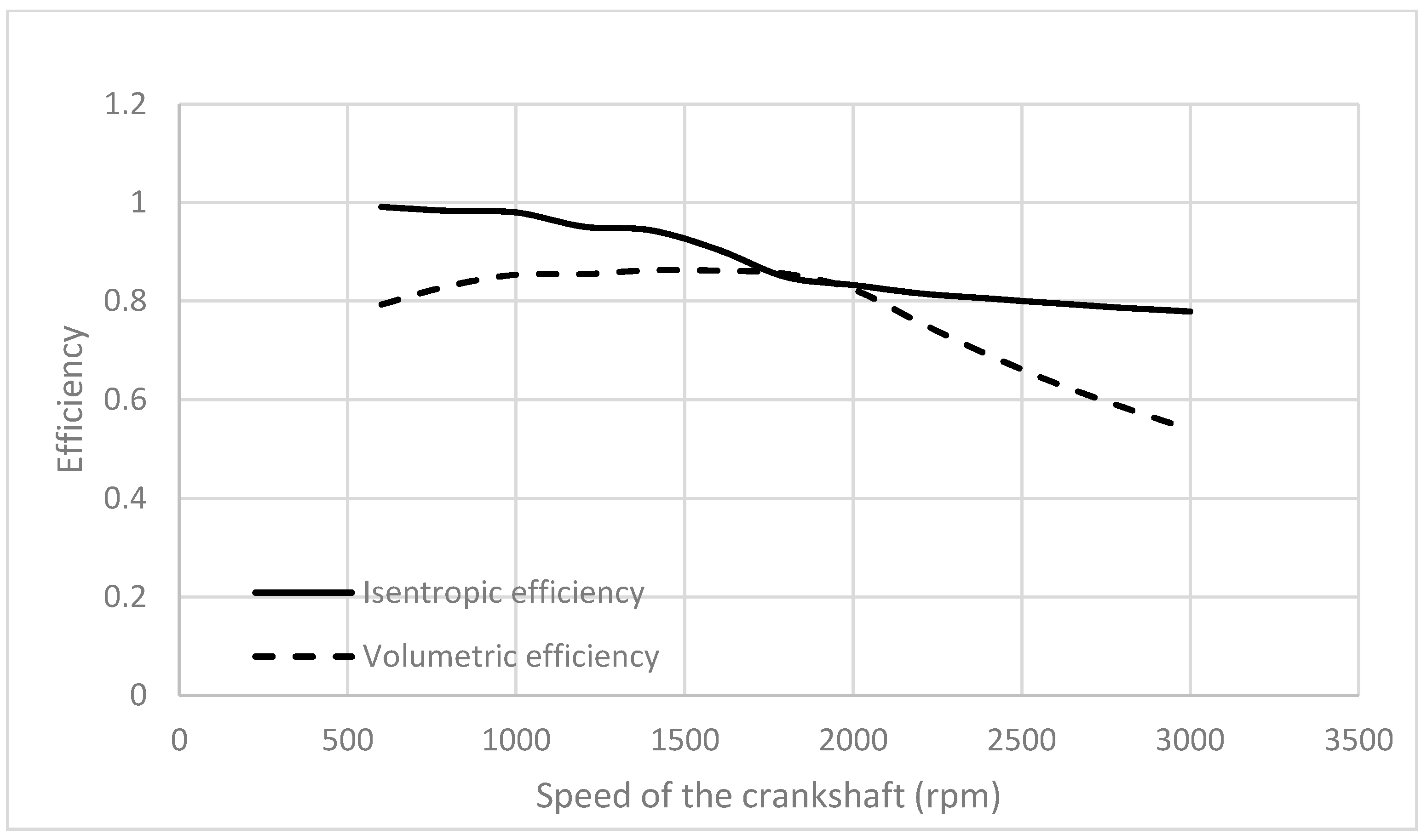
5. Numerical Illustration
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ooi, K. Design optimization of a rolling piston compressor for refrigerators. Appl. Therm. Eng. 2005, 25, 813–829. [Google Scholar] [CrossRef]
- Liu, Y.; Hung, C.; Chang, Y. Design optimization of scroll compressor applied for frictional losses evaluation. Int. J. Refrig. 2010, 33, 615–624. [Google Scholar] [CrossRef]
- Sultan, I.; Kalim, A. Improving reciprocating compressor performance using a hybrid two-level optimisation approach. Eng. Comput. 2011, 28, 616–636. [Google Scholar] [CrossRef]
- Phung, T.H.; Sultan, I.A. Geometric Design of the Limaçon-to-Circular Fluid Processing Machine. J. Mech. Des. 2021, 143, 103501. [Google Scholar] [CrossRef]
- Cavazzini, G.; Giacomel, F.; Ardizzon, G.; Casari, N.; Fadiga, E.; Suman, A.; Pinelli, M. CFD-based optimization of scroll compressor design and uncertainty quantification of the performance under geometrical variations. Energy 2020, 209, 118382. [Google Scholar] [CrossRef]
- Silva, E.; Dutra, T. Piston trajectory optimization of a reciprocating compressor. Int. J. Refrig. 2021, 121, 159–167. [Google Scholar] [CrossRef]
- Aw, K.T.; Ooi, K.T. A Review on Sliding Vane and Rolling Piston Compressors. Machines 2021, 9, 125. [Google Scholar] [CrossRef]
- Pelikan, M.; Goldberg, D.E.; Cantú-Paz, E. BOA: The Bayesian optimization algorithm. In Proceedings of the Genetic and Evolutionary Computation Conference, Orlando, FL, USA, 13–17 July 1999; Volume 1, pp. 525–532. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian optimization of machine learning algorithms. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NA, USA, 3–6 December 2012; pp. 2951–2959. [Google Scholar]
- Frazier, P.I.; Wang, J. Bayesian optimization for materials design. In Information Science for Materials Discovery and Design; Lookman, T., Alexander, F.J., Rajan, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 45–75. [Google Scholar]
- Torun, H.; Swaminathan, M.; Kavungal Davis, A.; Bellaredj, M. A Global Bayesian Optimization Algorithm and Its Application to Integrated System Design. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2018, 26, 792–802. [Google Scholar] [CrossRef]
- Griffiths, R.R.; Hernández-Lobato, J.M. Constrained Bayesian optimization for automatic chemical design. arXiv 2017, arXiv:1709.05501. [Google Scholar]
- Letham, B.; Karrer, B.; Ottoni, G.; Bakshy, E. Constrained Bayesian Optimization with Noisy Experiments. Bayesian Anal. 2019, 14, 495–519. [Google Scholar] [CrossRef]
- Hickish, B.; Fletcher, D.; Harrison, R. Investigating Bayesian Optimization for rail network optimization. Int. J. Rail Transp. 2019, 8, 307–323. [Google Scholar] [CrossRef] [Green Version]
- Sultan, I.A. The Limaçon of Pascal: Mechanical Generation and Utilization for Fluid Processing. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2005, 219, 813–822. [Google Scholar] [CrossRef] [Green Version]
- Sultan, I.A. Profiling Rotors for Limaçon-to-Limaçon Compression-Expansion Machines. J. Mech. Des. 2006, 128, 787–793. [Google Scholar] [CrossRef]
- Sultan, I.A. A Surrogate Model for Interference Prevention in the Limaçon-to-Limaçon Machines. Eng. Comput. 2007, 24, 437–449. [Google Scholar] [CrossRef]
- Sultan, I.A. Inverse geometric design for a class of rotary positive displacement machines. Inverse Probl. Sci. Eng. 2008, 16, 127–139. [Google Scholar] [CrossRef]
- Sultan, I.A.; Schaller, C. Optimum Positioning of Ports in the Limaçon Gas Expanders. J. Eng. Gas Turbines Power 2011, 133. [Google Scholar] [CrossRef]
- Sultan, I.A. Optimum design of limaçon gas expanders based on thermodynamic performance. Appl. Therm. Eng. 2012, 39, 188–197. [Google Scholar] [CrossRef]
- Phung, T.; Sultan, I.; Appuhamillage, G. On the apex seal analysis of limaçon positive displacement machines. Mech. Mach. Theory 2018, 127, 126–145. [Google Scholar] [CrossRef]
- Tuymer, W.J.; Machu, E.H. Compressor valves. In Compressor Handbook; Hanlon, P.C., Ed.; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Noè, U.; Husmeier, D. On a new improvement-based acquisition function for Bayesian optimization. arXiv 2018, arXiv:1808.06918. [Google Scholar]
- Cuevas, C.; Lebrun, J.; Lemort, V.; Winandy, E. Characterization of a scroll compressor under extended operating conditions. Appl. Therm. Eng. 2010, 30, 605–615. [Google Scholar] [CrossRef]
- Pan, X.; Tian, C.; Wu, S.; Xing, Z.; Pan, S. Experimental study of the swing compressor with no valves. Appl. Therm. Eng. 2019, 163, 114274. [Google Scholar] [CrossRef]
- Shakya, P.; Ooi, K. Introduction to Coupled Vane compressor: Mathematical modelling with validation. Int. J. Refrig. 2020, 117, 23–32. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Chen, Z.; Tan, Q. Geometric model and pressurization analysis on a novel sliding vane compressor with an asymmetrical cylinder profile. Int. J. Refrig. 2021, 129, 175–183. [Google Scholar] [CrossRef]


| Geometric Parameters | Values |
|---|---|
| Half-length of the rotor-chord, | |
| Axial length of the rotor, | |
| Rotor clearance, | |
| Side clearance, | |
| Aspect ratio, | |
| Leading edge of inlet port, | |
| Leading edge of outlet port, | |
| Angular width of inlet port, | |
| Angular width of outlet port, | |
| Length of inlet port, | |
| Length of outlet port, |
| Parameters | Value | |
|---|---|---|
| Speed of the crankshaft | ||
| Temperature at inlet port, | ||
| Pressure at inlet port, | ||
| Pressure at outlet port, | ||
| Clearance volume factor, | ||
| Cut-off angle of the suction process, | ||
| Weighting factors | ||
| Design Variable | Lower Limit | Upper Limit |
|---|---|---|
| Half chord length, | ||
| Aspect ratio, | ||
| Rotor clearance, | ||
| Leading edge of inlet port, | ||
| Leading edge of outlet port, | ||
| Angular width of inlet port, | ||
| gular width of outlet port, | ||
| Length of inlet port, | ||
| Length of outlet port, |
| Objective Parameters | Required Value | Obtained Value |
|---|---|---|
| Volume ratio, | ||
| Induced volume per suction process, | ||
| Rotor-housing clearance, |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, K.; Phung, T.H.; Sultan, I.A. On the Design of a Class of Rotary Compressors Using Bayesian Optimization. Machines 2021, 9, 219. https://doi.org/10.3390/machines9100219
Lu K, Phung TH, Sultan IA. On the Design of a Class of Rotary Compressors Using Bayesian Optimization. Machines. 2021; 9(10):219. https://doi.org/10.3390/machines9100219
Chicago/Turabian StyleLu, Kui, Truong H. Phung, and Ibrahim A. Sultan. 2021. "On the Design of a Class of Rotary Compressors Using Bayesian Optimization" Machines 9, no. 10: 219. https://doi.org/10.3390/machines9100219
APA StyleLu, K., Phung, T. H., & Sultan, I. A. (2021). On the Design of a Class of Rotary Compressors Using Bayesian Optimization. Machines, 9(10), 219. https://doi.org/10.3390/machines9100219







