Comprehensive Parameters Identification and Dynamic Model Validation of Interior-Mount Line-Start Permanent Magnet Synchronous Motors
Abstract
:1. Introduction
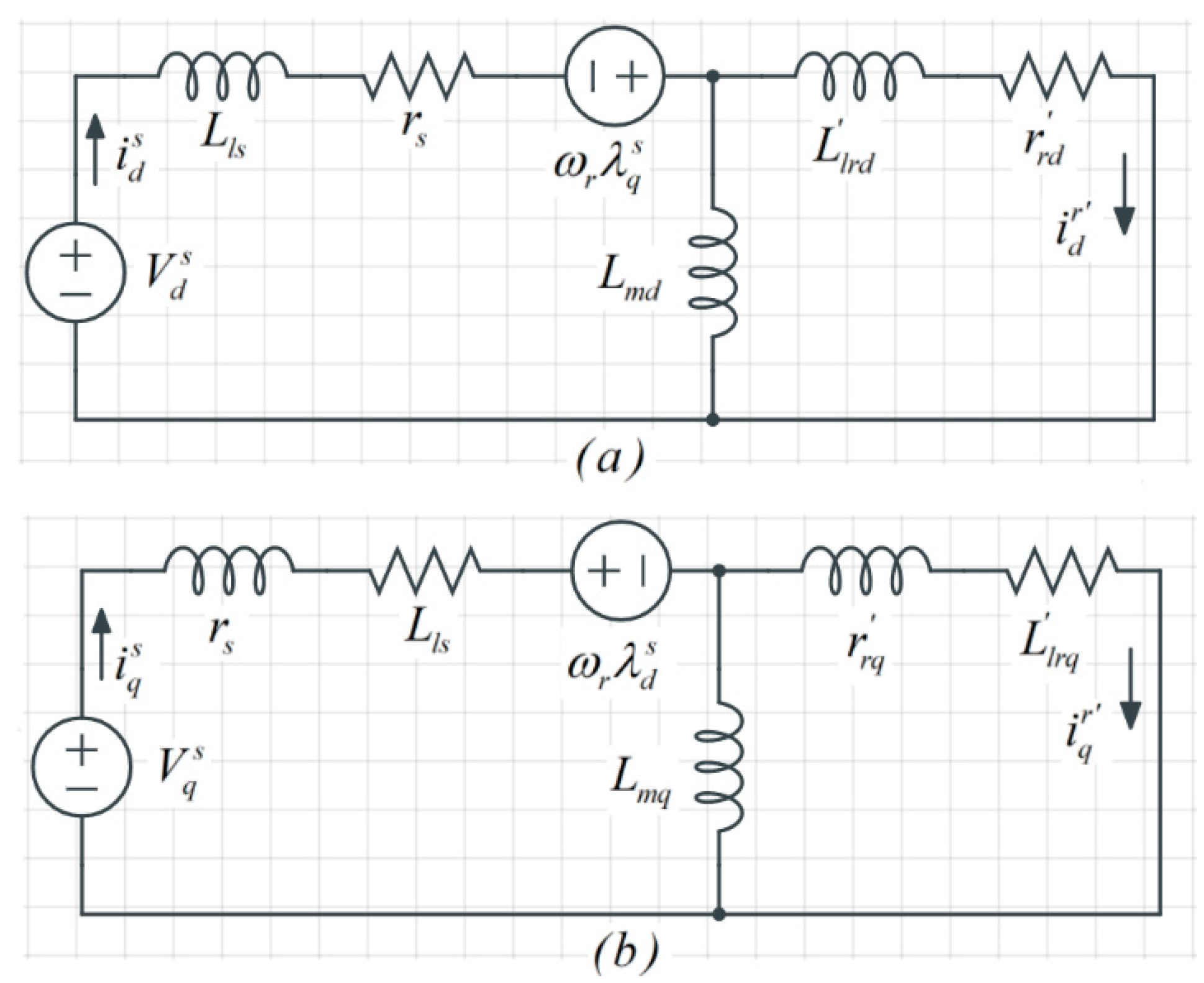
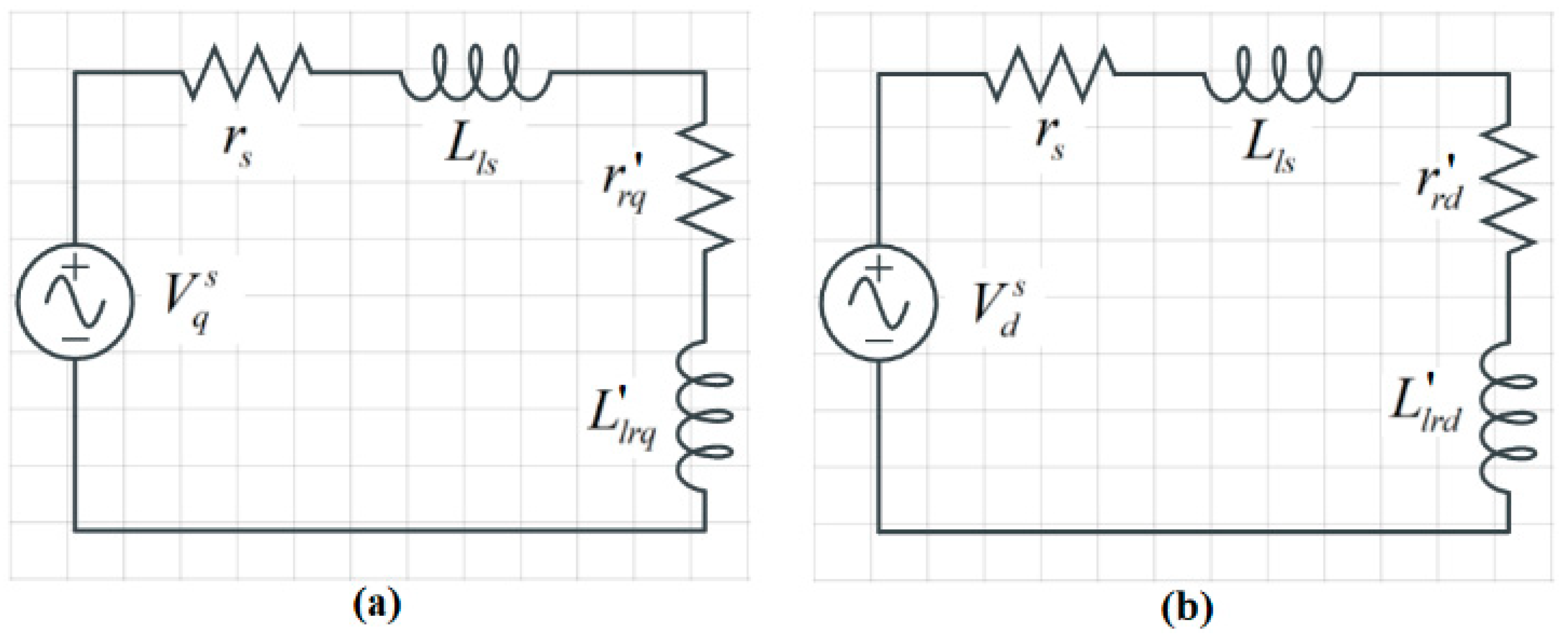
2. Mathematical Model of LSPMSM
3. LSPMSM Parameters Measurement Using Different Experimental Tests
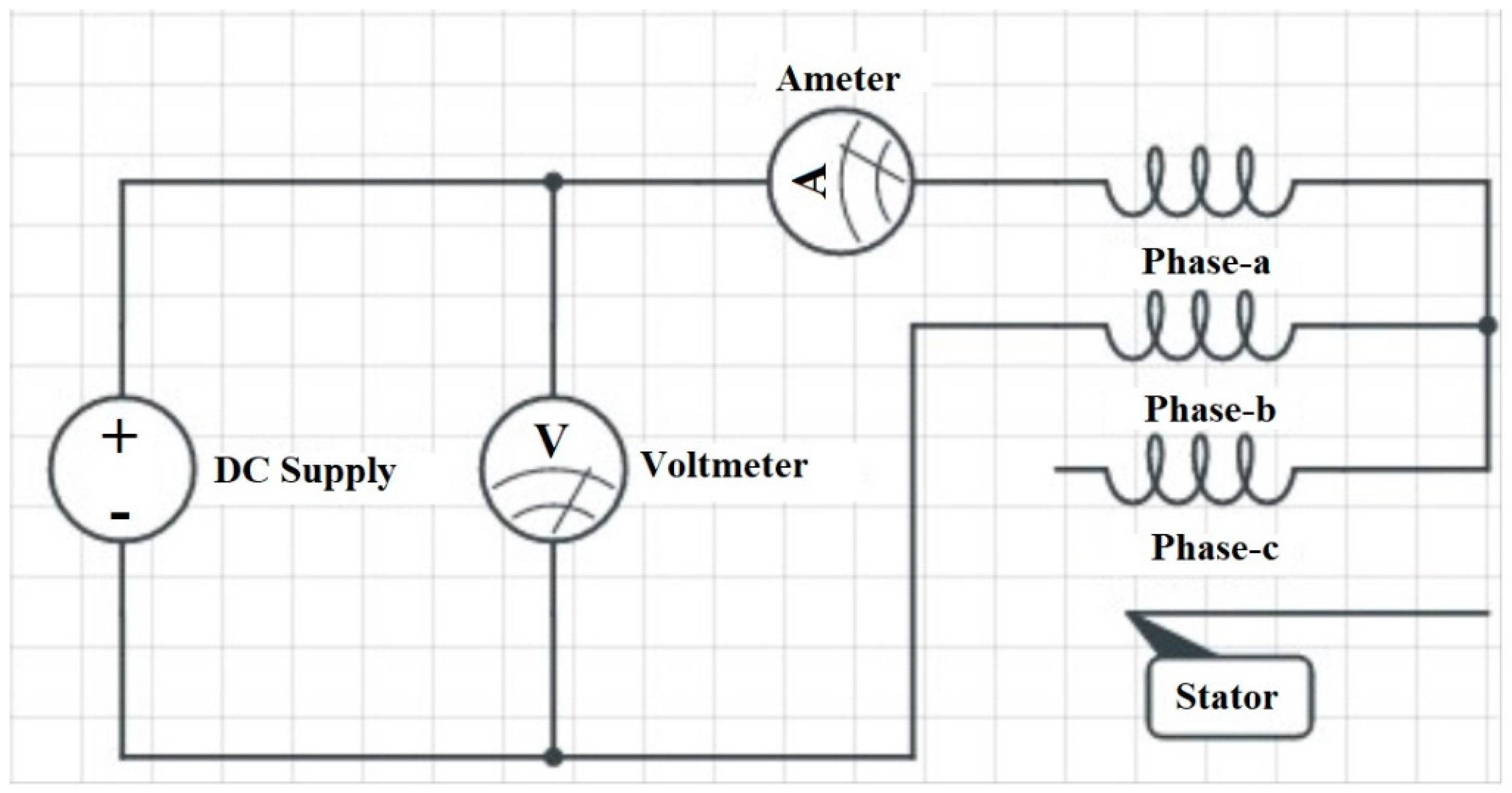
3.1. DC Test
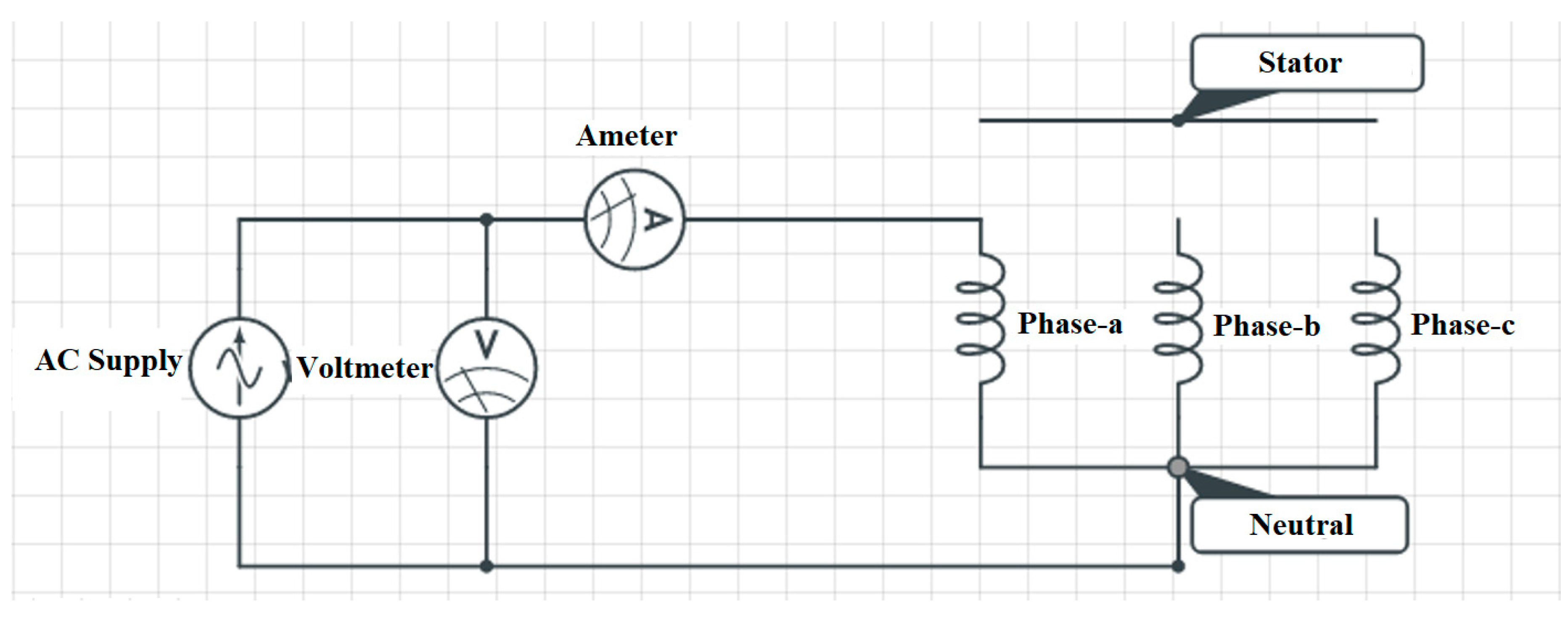
3.2. Single Phase AC Test (Rotor Not Included)
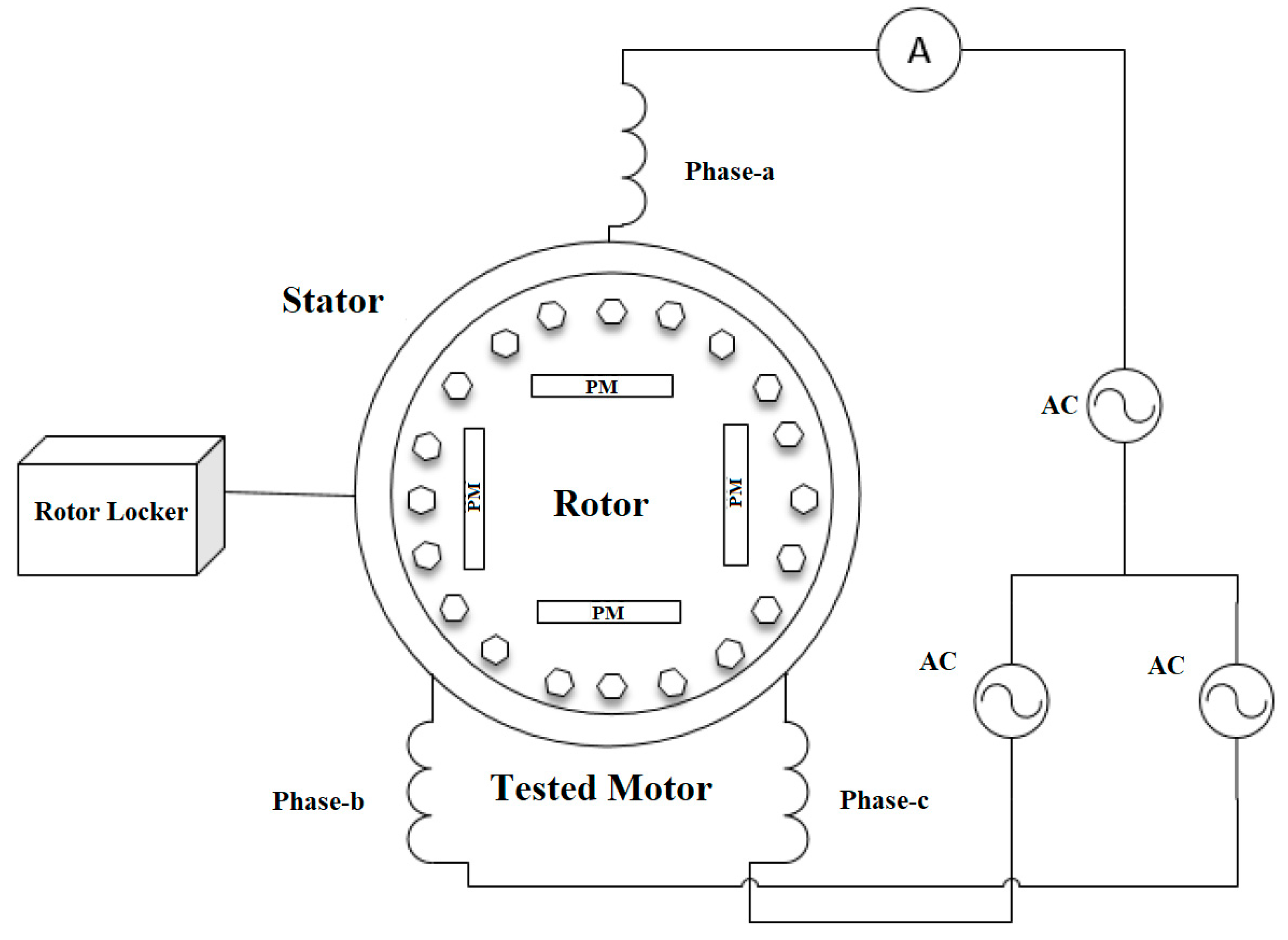
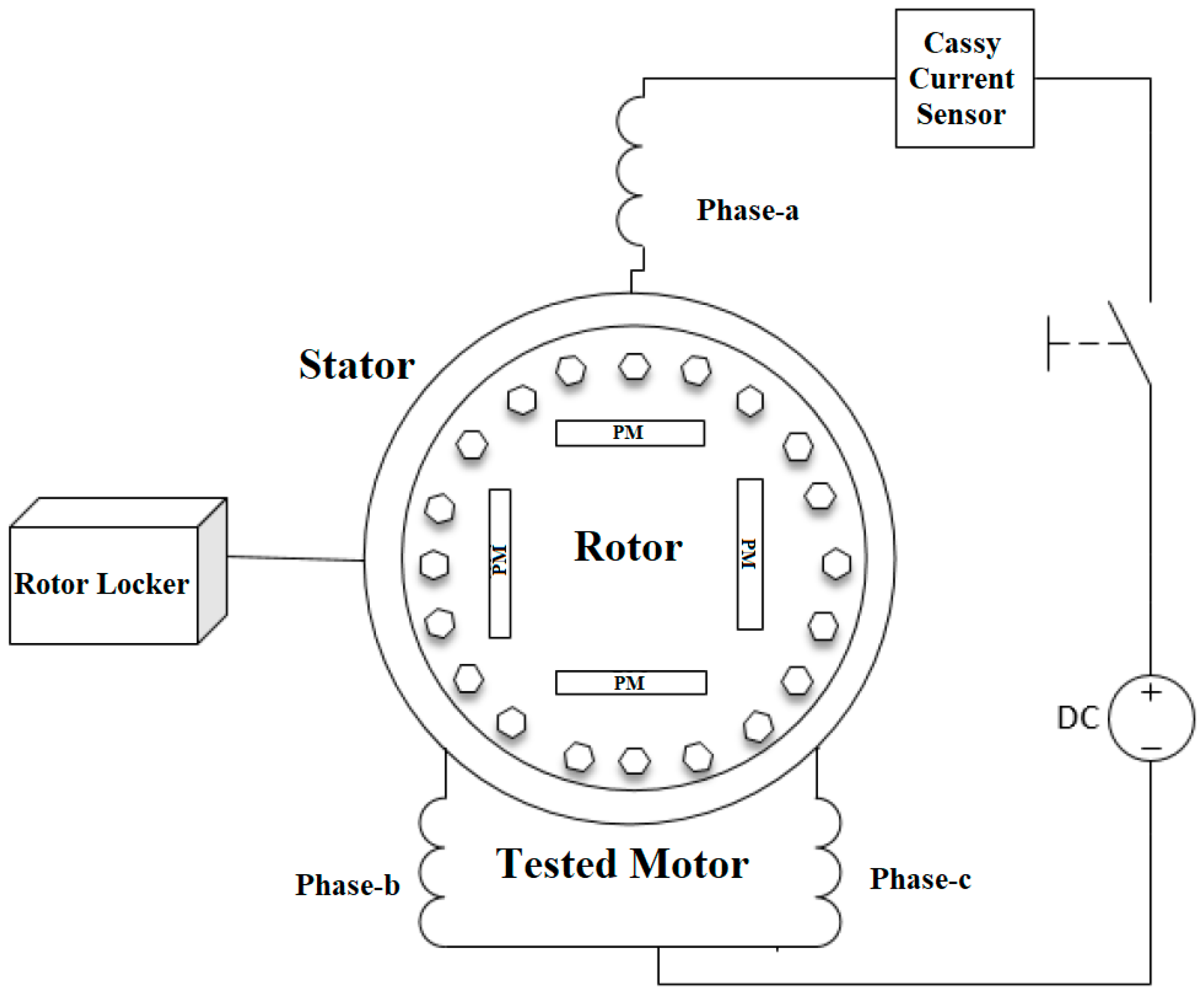
3.3. Locked Rotor Test
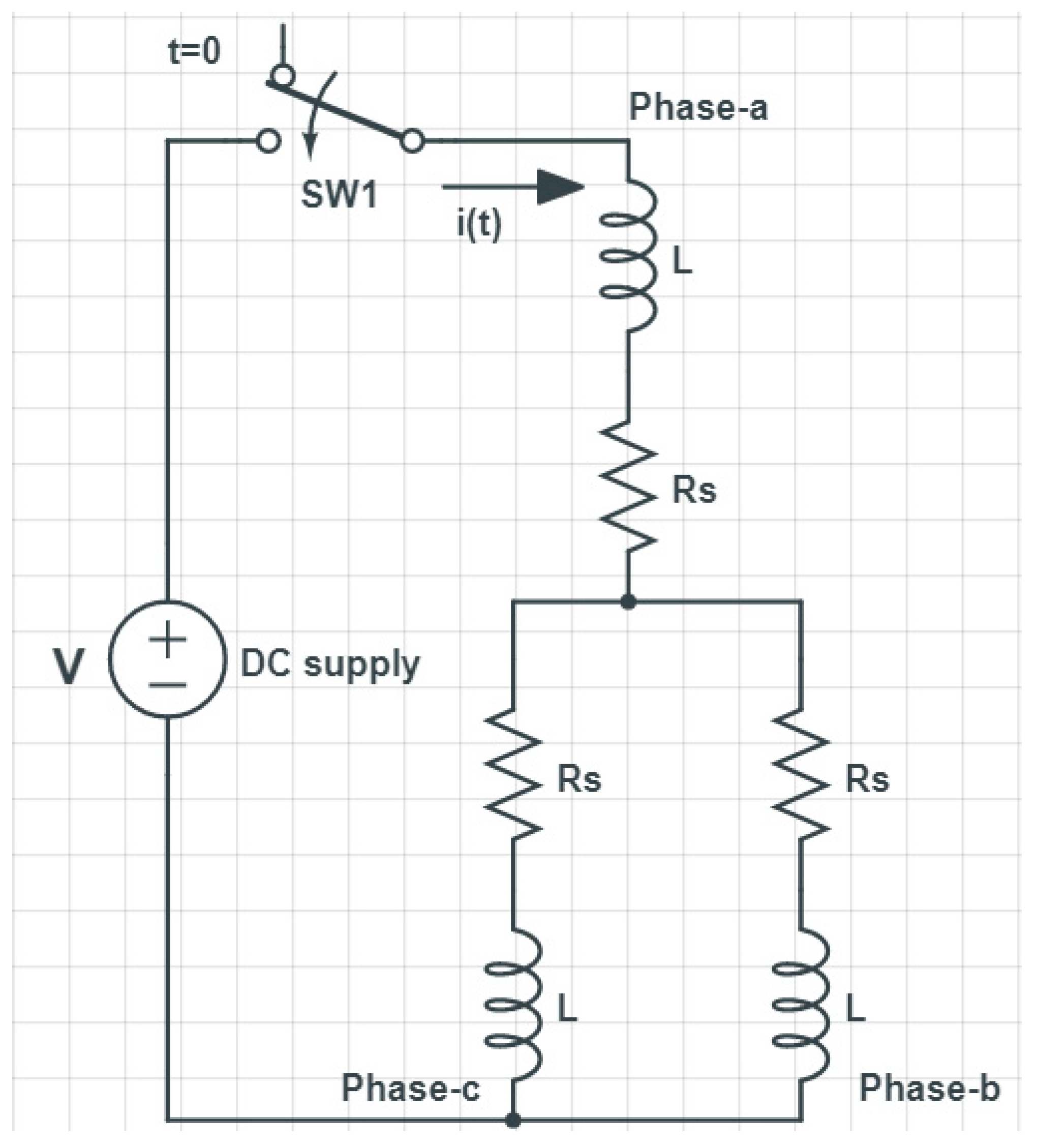
3.4. DC Step Test
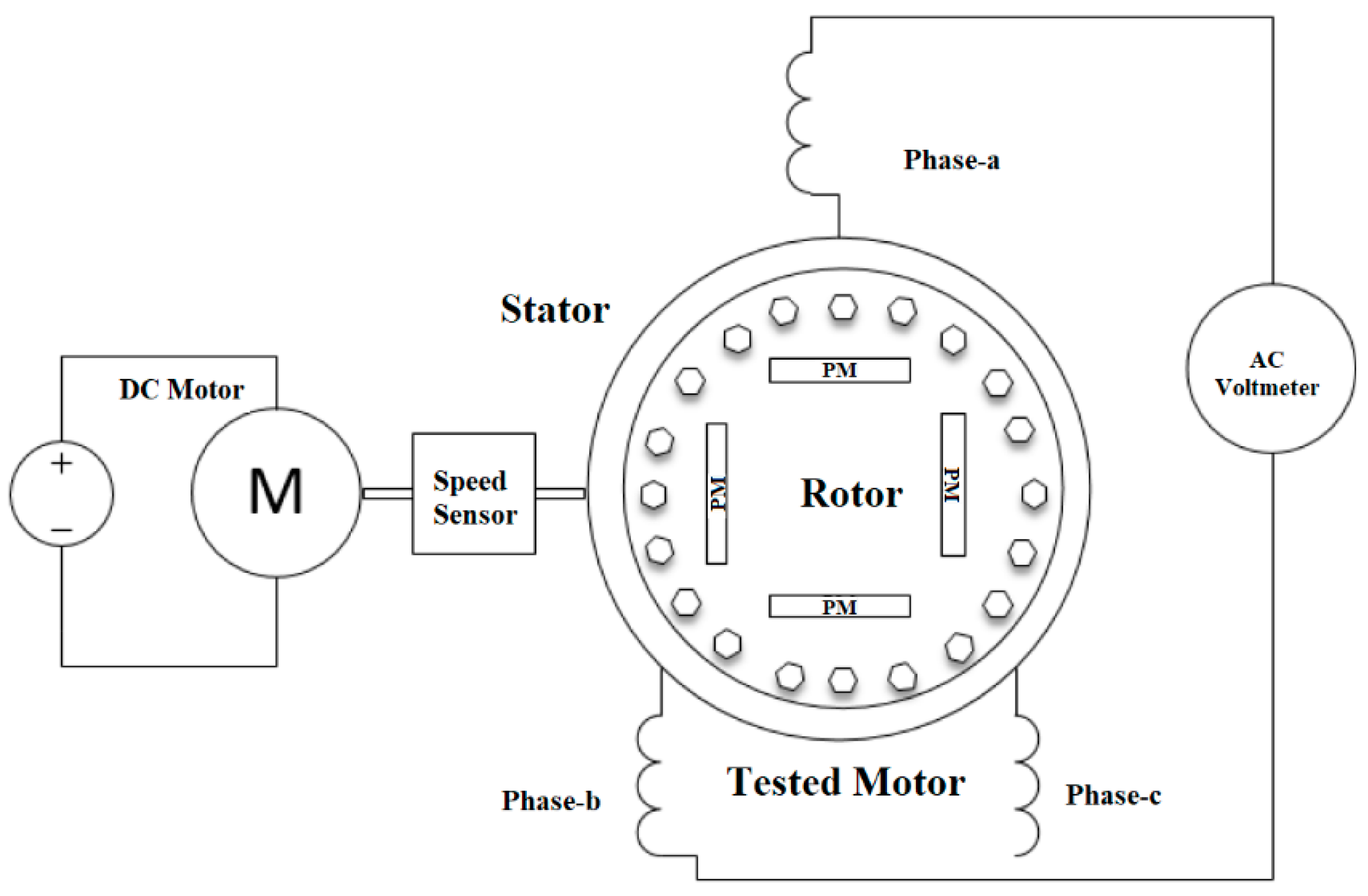
3.5. Open-Circuit Test
4. Results and Discussion
4.1. DC Test Results
4.2. Single Phase AC Test (Rotor Not Included) Results
4.3. Block Rotor Test Results
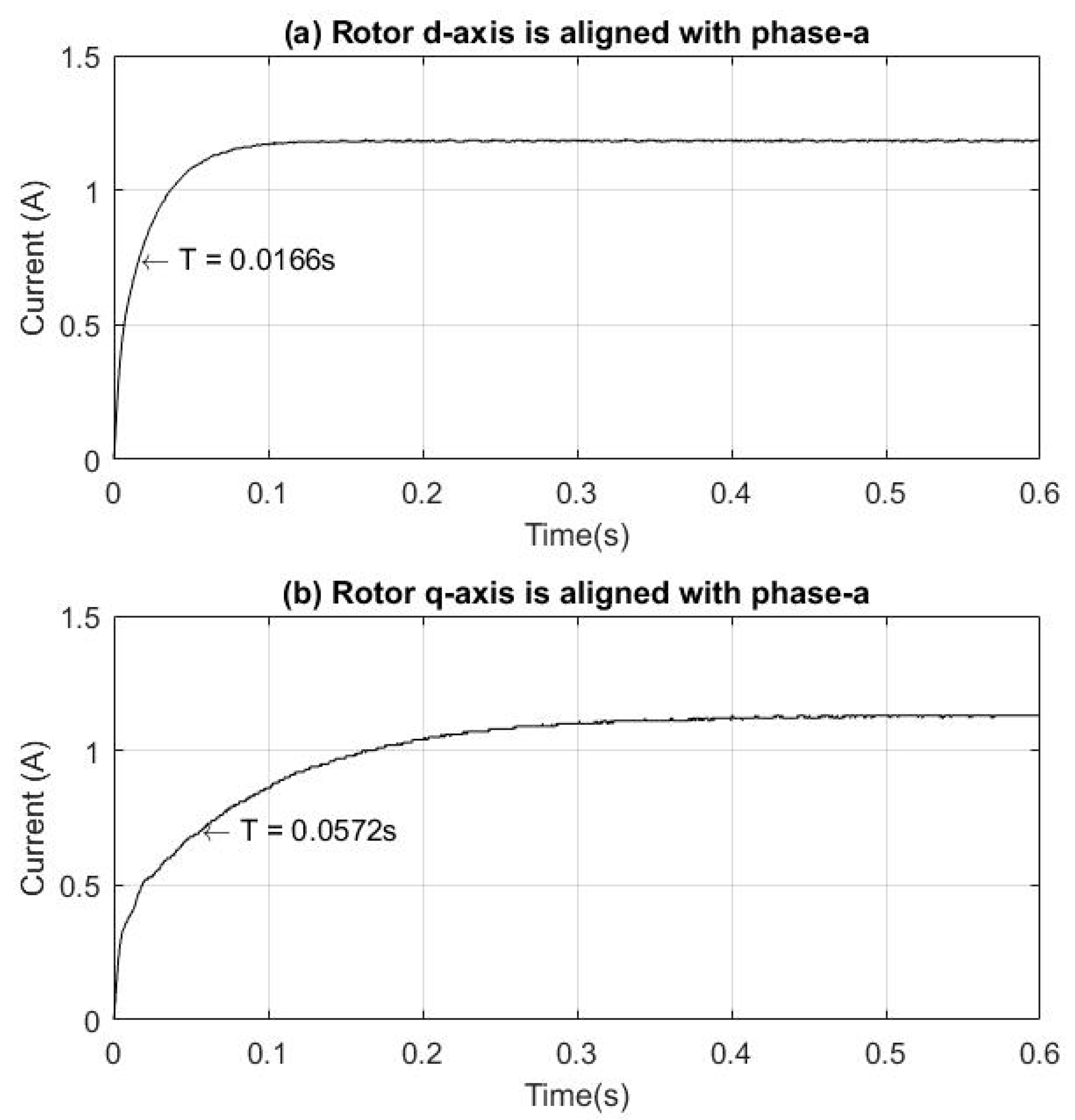
4.4. DC Step Test Results
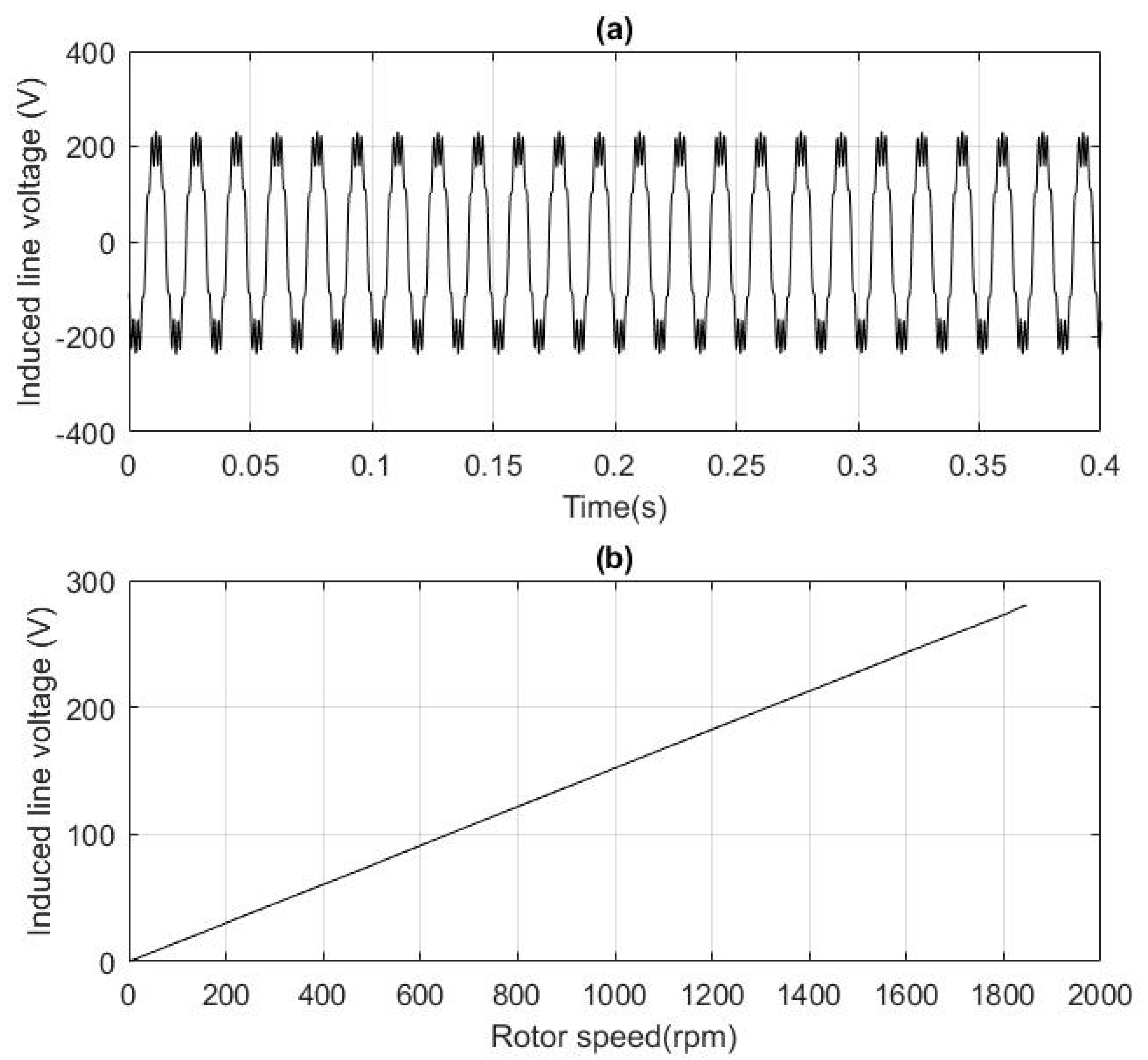
4.5. Open-Circuit Test Results
4.6. Summary of Parameter Measurement Results
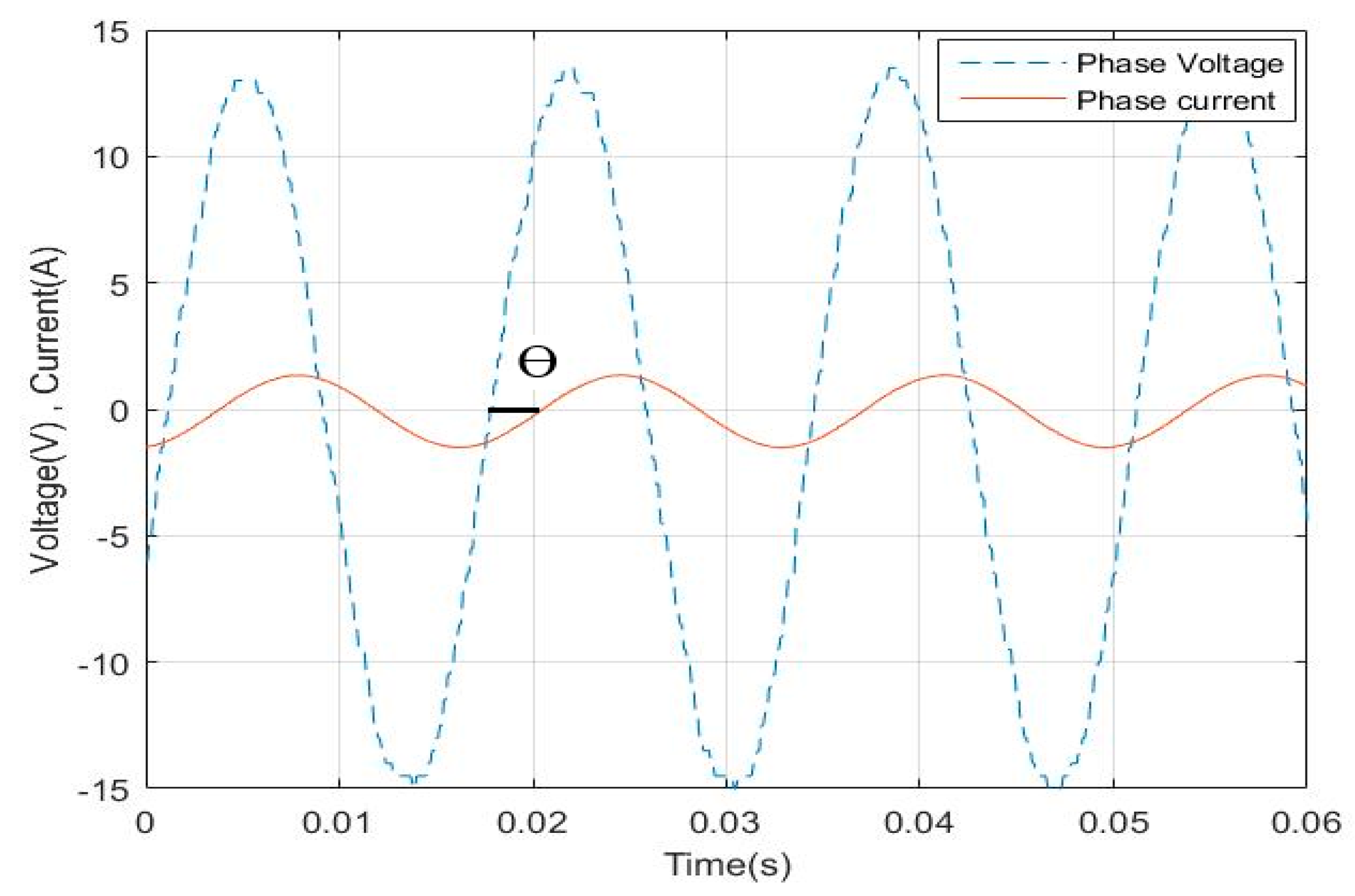
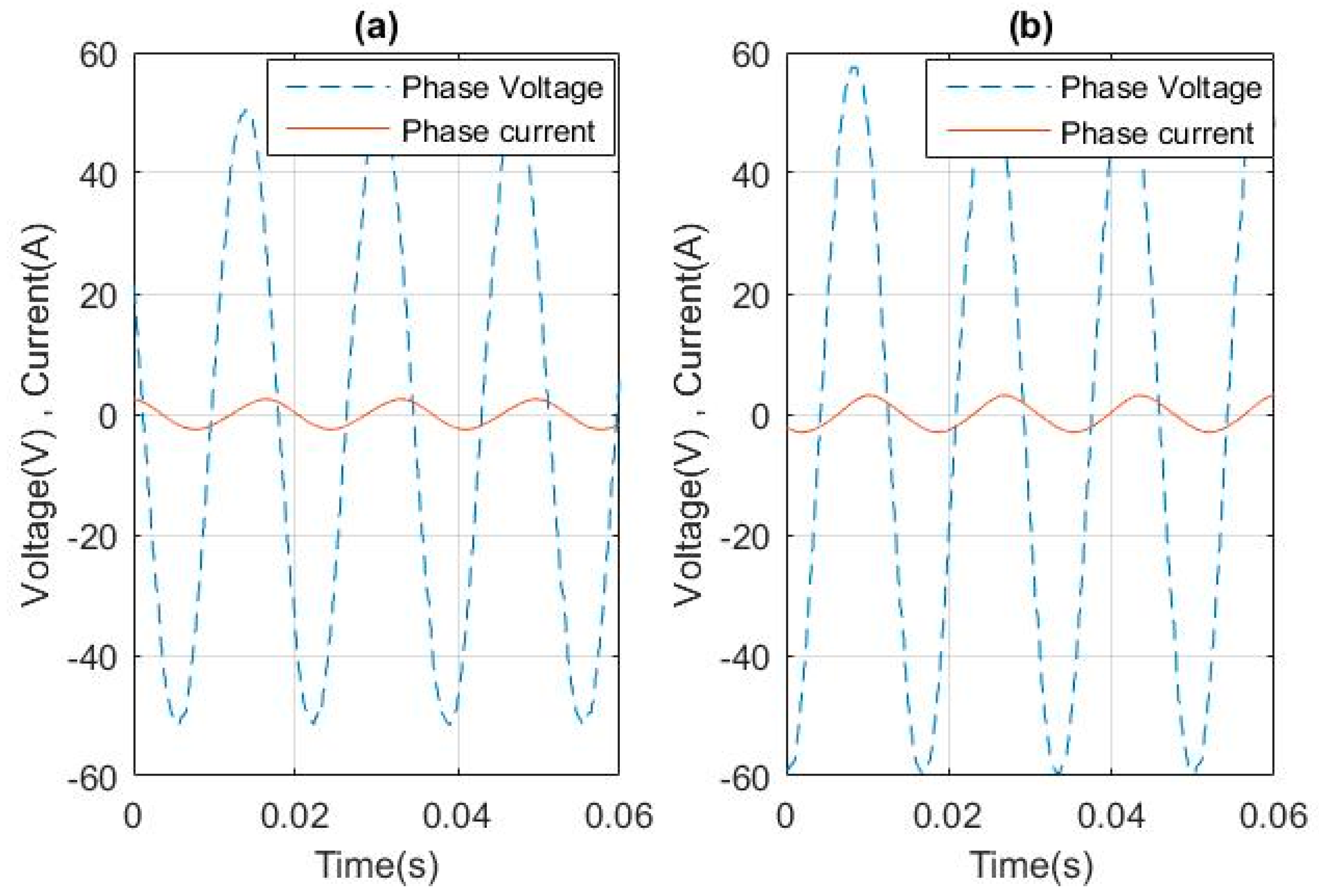
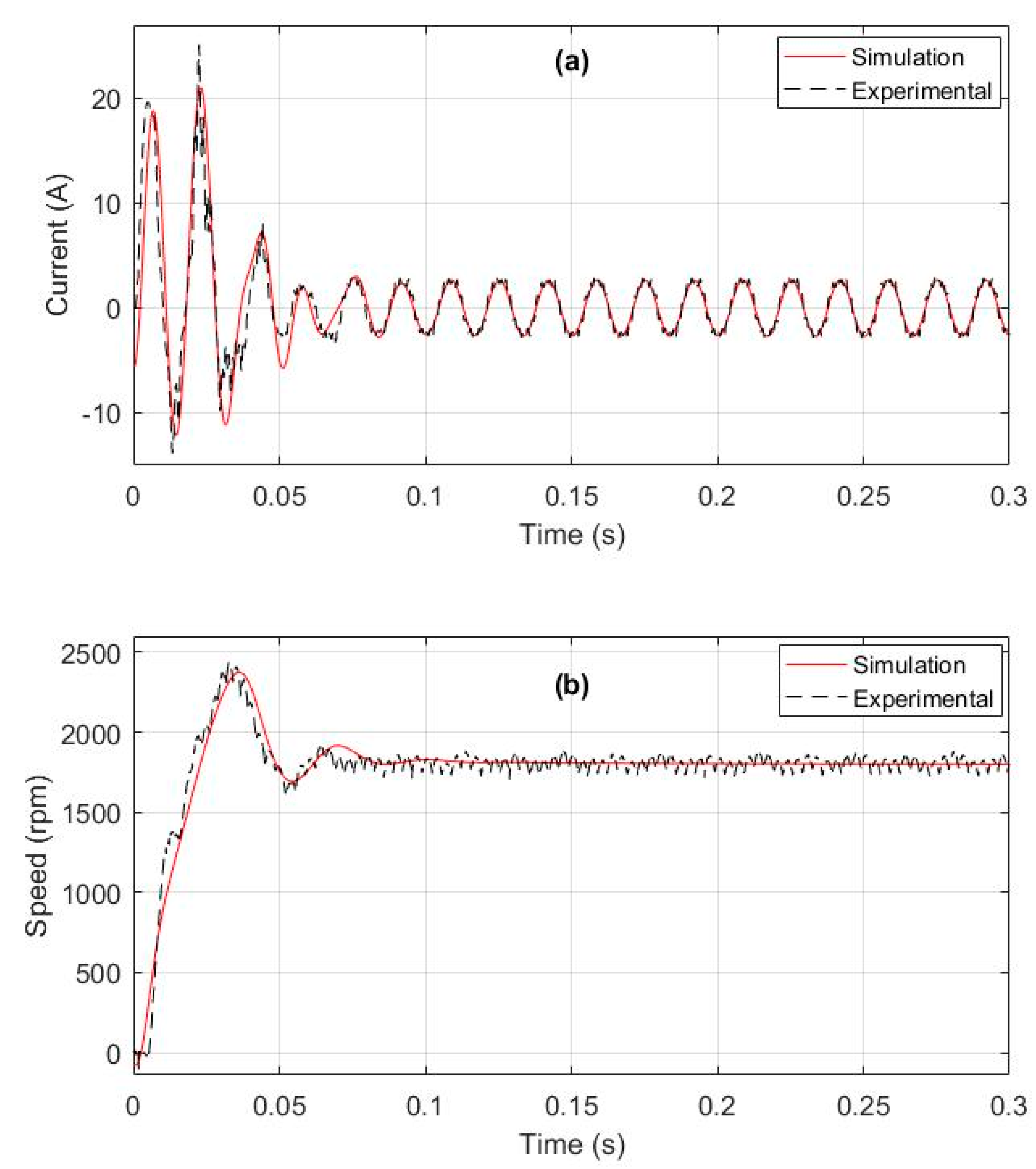
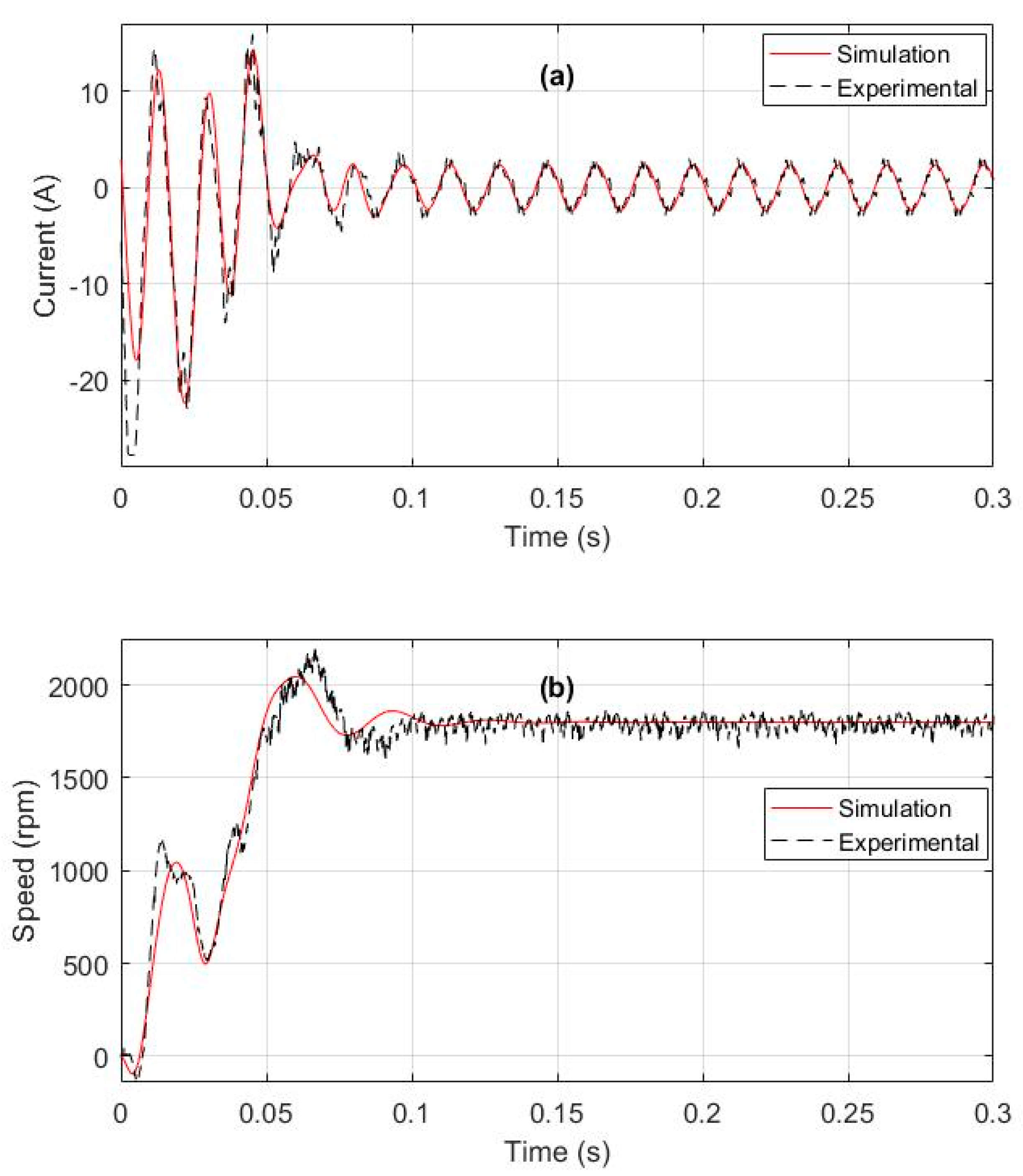
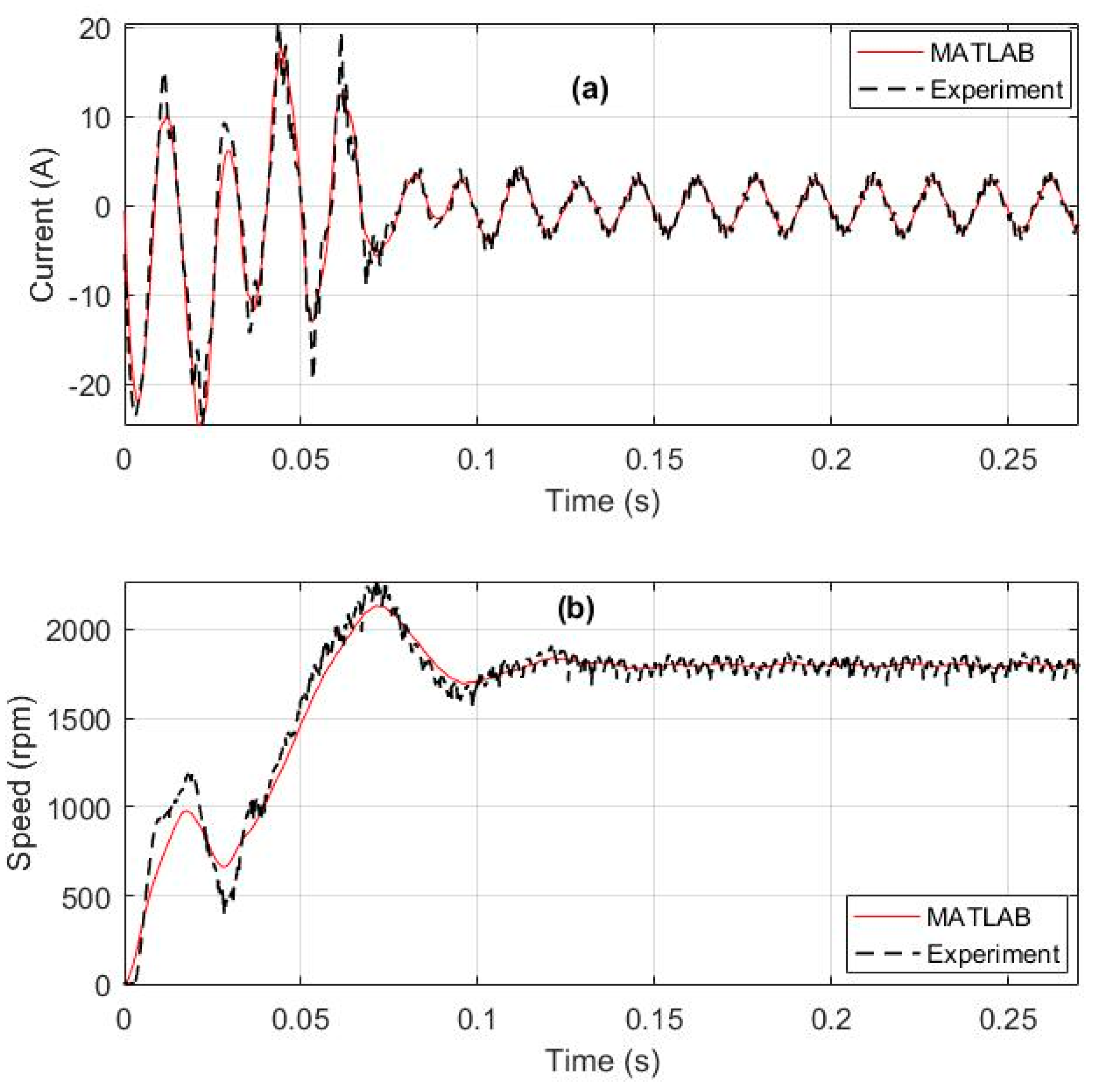
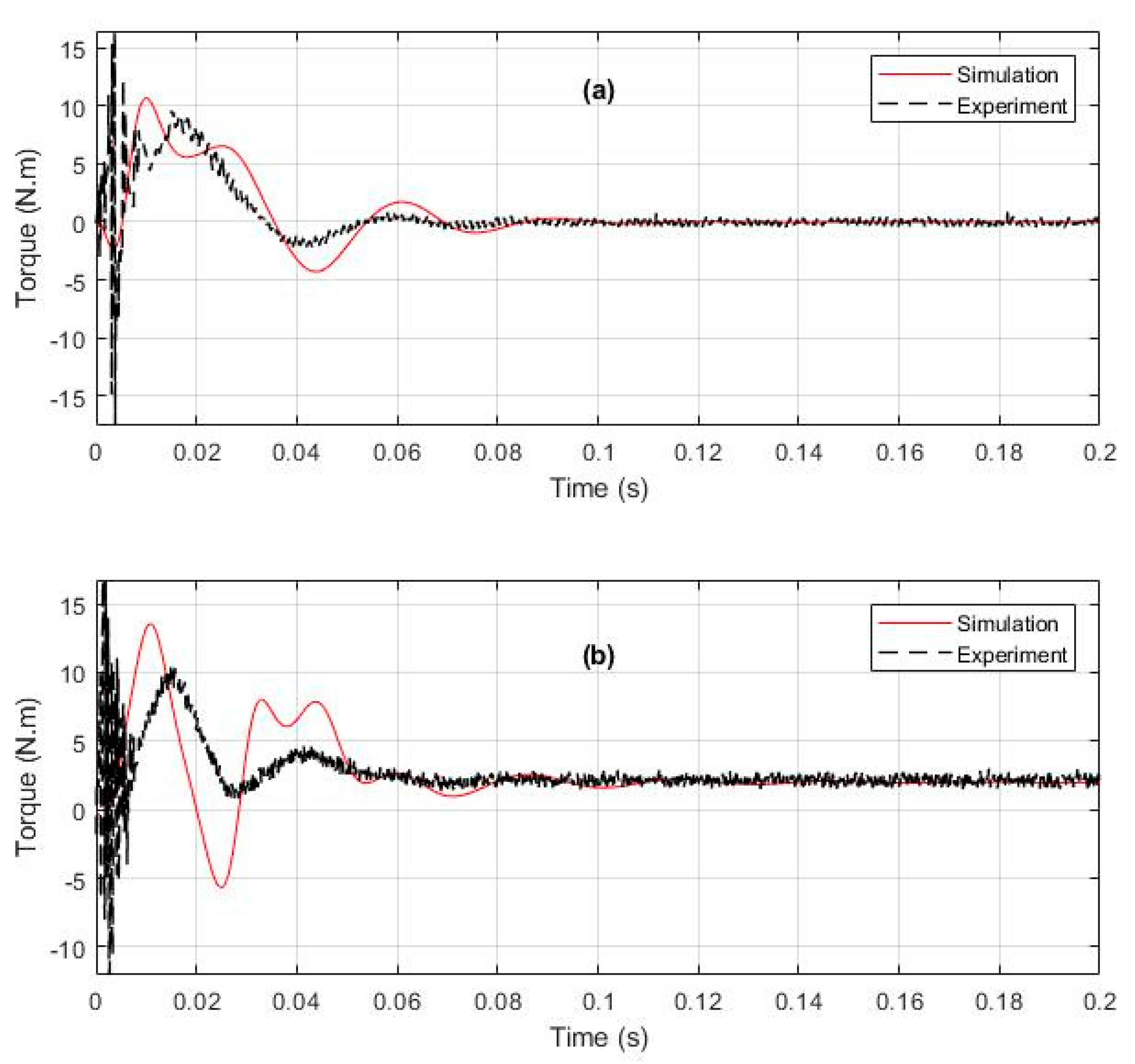
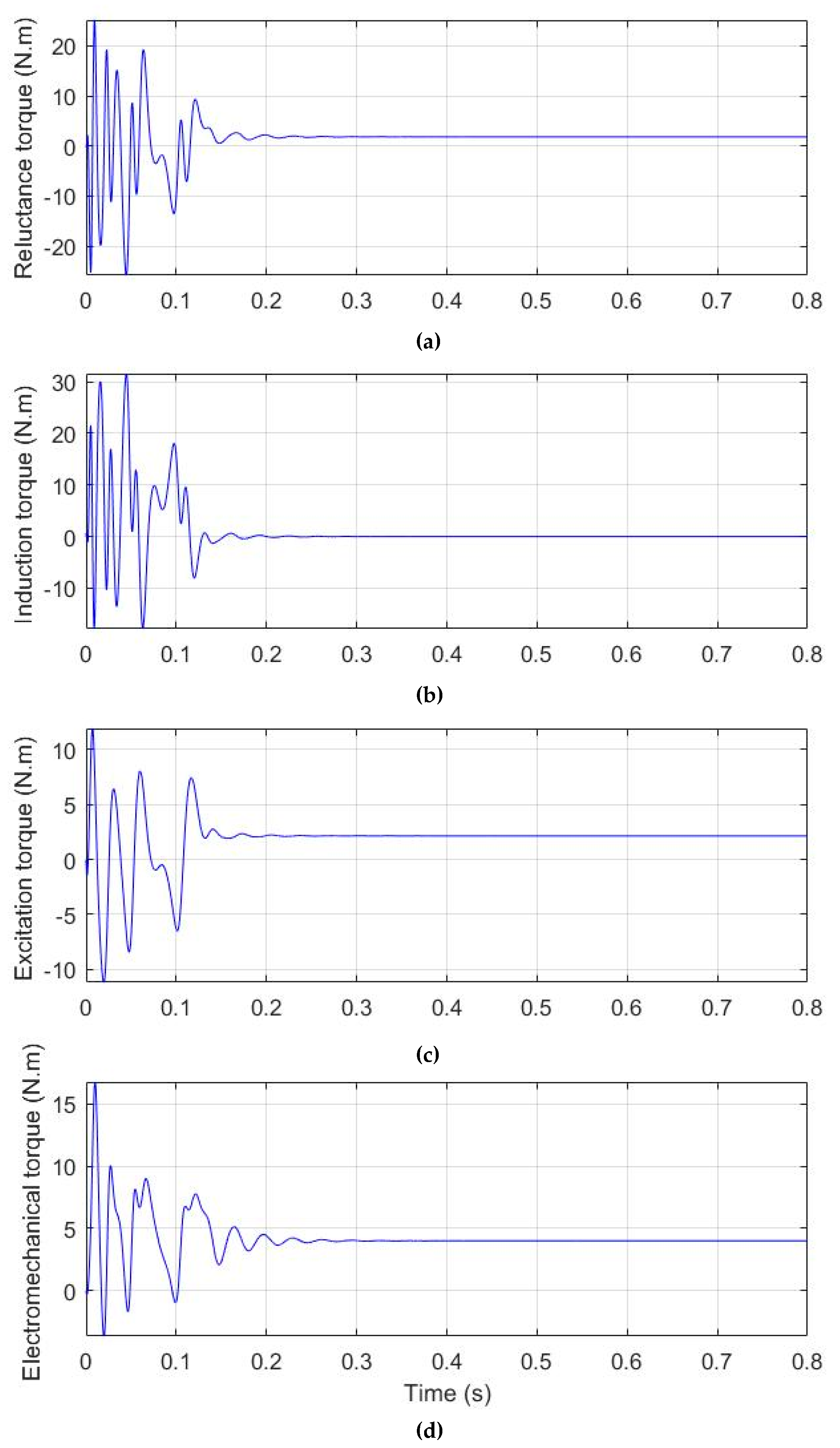
5. Parameters/Dynamic Model Testing and Validation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, G.; Ma, J.; Shen, J.-X.; Wang, Y. Optimal design and experimental verification of a line-start permanent magnet synchronous motor. In Proceedings of the 2008 International Conference on Electrical Machines and Systems, Wuhan, China, 17–20 October 2008; pp. 3232–3236. [Google Scholar]
- Takegami, T.; Hasegawa, M.; Tsuboi, K.; Hirotsuka, I.; Nakamura, M. Basic characteristics of a single-phase line-start permanent magnet synchronous motor. In Proceedings of the 2011 International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011; pp. 1–4. [Google Scholar]
- Nedelcu, S.; Tudorache, T.; Ghita, C. Influence of design parameters on a line start permanent magnet machine characteristics. In Proceedings of the 2012 13th International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Brasov, Romania, 24–26 May 2012; pp. 565–571. [Google Scholar]
- Hu, Y.; Guan, Z.; Yan, X. Calculation on the Rotor Slot Leakage Reactance of Line-Start Permanent Magnet Synchronous Motor. In Proceedings of the 2012 Sixth International Conference on Electromagnetic Field Problems and Applications, Dalian, China, 19–21 June 2012; pp. 1–4. [Google Scholar]
- De Almeida, A.T.; Ferreira, F.J.; Baoming, G. Beyond induction motors—Technology trends to move up efficiency. IEEE Trans. Ind. Appl. 2014, 50, 2103–2114. [Google Scholar] [CrossRef]
- De Almeida, A.T.; Ferreira, F.J.; Quintino, A. Technical and economical considerations on super high-efficiency three-phase motors. In Proceedings of the 2012 IEEE/IAS 48th Industrial & Commercial Power Systems Technical Conference (I&CPS), Louisville, KY, USA, 20–24 May 2012; pp. 1–13. [Google Scholar]
- Debruyne, C.; Polikarpova, M.; Derammelaere, S.; Sergeant, P.; Pyrhonen, J.; Desmet, J.J.; Lieven, V. Evaluation of the efficiency of line-start permanent-magnet machines as a function of the operating temperature. IEEE Trans. Ind. Electron. 2014, 61, 4443–4454. [Google Scholar] [CrossRef]
- Sarani, E.; Vaez-Zadeh, S. Design Procedure and Optimal Guidelines for Overall Enhancement of Steady State and Transient Performances of Line Start Permanent Magnet Motors. IEEE Trans. Energy Convers. 2017, 32, 885–894. [Google Scholar] [CrossRef]
- Iyer, K.L.V.; Lu, X.; Mukherjee, K.; Kar, N.C. A novel two-axis theory-based approach towards parameter determination of line-start permanent magnet synchronous machines. IEEE Trans. Magn. 2012, 48, 4208–4211. [Google Scholar] [CrossRef]
- Marcic, T.; Stumberger, B.; Stumberger, G. Differential-evolution-based parameter identification of a line-start IPM synchronous motor. IEEE Trans. Ind. Electron. 2014, 61, 5921–5929. [Google Scholar] [CrossRef]
- Ji, X.; Noguchi, T. Off-line parameter identification of interior permanent magnet motor by searching minimum point of current norm characteristics. In Proceedings of the 2014 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Ischia, Italy, 18–20 June 2014; pp. 279–284. [Google Scholar]
- Jing, D. Computational Analysis of a Permanent Magnet Synchronous Machine Using Numerical Techniques. Ph.D. Thesis, Department of Electrical & Computer Engineering, National University of Singapore, Singapore, 2005. [Google Scholar]
- Maraaba, L.; Al-Hamouz, Z.; Milhem, A.; Abido, M. Modelling of interior-mount LSPMSM under asymmetrical stator winding. IET Electr. Power Appl. 2018, 12, 693–700. [Google Scholar] [CrossRef]
- Yamamoto, S.; Ara, T. Determination of direct and quadrature axes inductances of reluctance motors taking into account cross saturation. IEEJ Trans. Ind. Appl. 2004, 123, 911–917. [Google Scholar] [CrossRef]
- Yamamoto, S.; Kano, T.; Yamaguchi, Y.; Ara, T. A method to determine direct-and quadrature-axis inductances of permanent magnet synchronous motors. Electr. Eng. Jpn. 2010, 171, 41–50. [Google Scholar] [CrossRef]
- Jedryczka, C.; Wojciechowski, R.M.; Demenko, A. Finite element analysis of the asynchronous torque in LSPMSM with non-symmetrical squirrel cage winding. Int. J. Appl. Electromagn. Mech. 2014, 46, 367–373. [Google Scholar] [CrossRef]
- Lazăr, F.; Simion, A.; Livadaru, L.; Daniel, I. FEM analysis of a 3 kW line-start permanent magnet synchronous machine. In Proceedings of the 2014 International Conference and Exposition on Electrical and Power Engineering (EPE), Iasi, Romania, 16–18 October 2014; pp. 402–405. [Google Scholar]
- Mehrjou, M.R.; Mariun, N.; Karami, M.; Misron, N.; Radzi, M.A.M. Performance analysis of line-start permanent magnet synchronous motor in presence of rotor fault. In Proceedings of the 2014 IEEE Student Conference on Research and Development, Batu Ferringhi, Malaysia, 16–17 December 2014; pp. 1–4. [Google Scholar]
- Ghoroghchian, F.; Aliabad, A.D.; Amiri, E.; Poudel, B. Line start permanent magnet synchronous motor with dual magnetic polarity. In Proceedings of the 2017 IEEE International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017; pp. 1–6. [Google Scholar]
- Takahashi, A.; Kikuchi, S.; Mikami, H.; Ide, K.; Binder, A. dq Space vector analysis for line-starting permanent magnet synchronous motors. In Proceedings of the 2012 XXth International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; pp. 136–142. [Google Scholar]
- Elistratova, V.; Hecquet, M.; Brochet, P.; Vizireanu, D.; Dessoude, M. Analytical approach for optimal design of a line-start internal permanent magnet synchronous motor. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–7. [Google Scholar]
- Ahmed, S.; Tremelling, D.; Kim, H.; Zhang, Z.; Frank, N.; McElveen, R. Modeling, simulation and performance evaluation of cage rotor permanent magnet motor fed by variable speed drive. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–6. [Google Scholar]
- Kemmetmuller, W.; Faustner, D.; Kugi, A. Modeling of a permanent magnet synchronous machine with internal magnets using magnetic equivalent circuits. IEEE Trans. Magn. 2014, 50, 1–14. [Google Scholar]
- Lu, X.; Iyer, K.L.V.; Mukherjee, K.; Kar, N.C. Development of a novel magnetic circuit model for design of premium efficiency three-phase line start permanent magnet machines with improved starting performance. IEEE Trans. Magn. 2013, 49, 3965–3968. [Google Scholar] [CrossRef]
- Isfahani, A.H.; Vaez-Zadeh, S.; Hasanzadeh, S. An educational toolbox for performance analysis of line-start permanent magnet synchronous motors. Comput. Appl. Eng. Educ. 2014, 22, 452–462. [Google Scholar] [CrossRef]
- Ong, C.-M. Dynamic Simulation of Electric Machinery: Using Matlab/Simulink; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1998; Volume 5. [Google Scholar]
- Lu, X.; Iyer, K.; Mukherjee, K.; Kar, N.C. A Novel Two-Axis Theory-Based Experimental Approach Towards Determination of Magnetization Characteristics of Line-Start Permanent Magnet Synchronous Machines. IEEE Trans. Magn. 2013, 49, 4733–4737. [Google Scholar] [CrossRef]
- Soreshjani, M.H.; Ghafari, A.; Haghparast, M. Direct Torque and Flux Controlled Space Vector Modulated (DTFC-SVM) Based on Fuzzy Logic Controller for Line-Start Permanent Magnet Synchronous and Permanent Magnet Synchronous Machines. J. Control Eng. Appl. Inform. 2014, 16, 75–83. [Google Scholar]
- Motors, P.M.S. Educational Bench of Line-Start Permanent Magnet Synchronous Motors Part I: Operating Point Of Permanent Magnet. In Proceedings of the 4th International Conference on Interdisciplinarity in Education ICIE’09, Vilnius, Lithuania, 21–22 May 2009. [Google Scholar]
- Stoia, D.; Cernat, M.; Hameyer, H.; Ban, D. Line-start permanent magnet synchronous motors analysis and design. In Proceedings of the 15th International Conference on Electrical Drives and Power Electronics, EDPE 2009, Dubrovnik, Croatia, 12–14 October 2009. [Google Scholar]
- Kinnunen, J. Direct-on-Line Axial Flux Permanent Magnet Synchronous Generator Static and Dynamic Performance; Lappeenrannan teknillinen yliopisto: Lappeenranta, Finnland, 2007. [Google Scholar]
- Maraaba, L.S.; AlHamouz, Z.M.; Abido, M. Mathematical Modeling, Simulation and Experimental Testing of Interior-mount LSPMSM under Stator Inter-Turn Fault. IEEE Trans. Energy Convers. 2018. [Google Scholar] [CrossRef]
- Rahman, K.M.; Hiti, S. Identification of machine parameters of a synchronous motor. IEEE Trans. Ind. Appl. 2005, 41, 557–565. [Google Scholar]
- Haque, M.; Rahman, M. Dynamic model and parameter measurement of interior permanent magnet synchronous motor. In Proceedings of the 2006 Australasian Universities Power Engineering Conference (AUPEC’06), Melbourne, Australia, 10–13 December 2006; pp. 10–13. [Google Scholar]
- Cavagnino, A.; Lazzari, M.; Profumo, F.; Tenconi, A. Axial flux interior PM synchronous motor: parameters identification and steady-state performance measurements. IEEE Trans. Ind. Appl. 2000, 36, 1581–1588. [Google Scholar]
- Marcic, T.; Stumberger, G.; Stumberger, B.; Hadziselimovic, M.; Virtic, P. Determining parameters of a line-start interior permanent magnet synchronous motor model by the differential evolution. IEEE Trans. Magn. 2008, 44, 4385–4388. [Google Scholar] [CrossRef]
- Sonnaillon, M.O.; Bisheimer, G.; Angelo, C.D.; García, G.O. Automatic induction machine parameters measurement using standstill frequency-domain tests. IET Electr. Power Appl. 2007, 1, 833–838. Available online: http://digital-library.theiet.org/content/journals/10.1049/iet-epa_20060512 (accessed on 22 November 2018). [CrossRef]
- Chapman, S. Electric Machinery Fundamentals; Tata McGraw-Hill Education: New York, NY, USA, 2005. [Google Scholar]
- Zeni, R. Investigation of the Sensorless Capability of an Induction Motor with Intentionally Created Saliency. Simulations and Measurements. Master’s Thesis, Department of Industrial Engineering, University degli Studi di Padova, Padova, Italy, 2013. [Google Scholar]
- Ayasun, S.; Nwankpa, C.O. Induction motor tests using MATLAB/Simulink and their integration into undergraduate electric machinery courses. IEEE Trans. Educ. 2005, 48, 37–46. [Google Scholar] [CrossRef]
- Okoro, O.I. Dynamic and Thermal Modelling of Induction Machine with Non-Linear Effects; Kassel University Press: Kassel, Germany, 2002. [Google Scholar]
- Bobek, V. Pmsm electrical parameters measurement. Free. Semicond. 2013. [Google Scholar]
- Cisneros-Gonzalez, M.; Hernandez, C.; Escarela-Perez, R.; Arjona, M. Determination of equivalent-circuit parameters of a synchronous generator based on the standstill DC decay test and a hybrid optimization method. Electr. Power Compon. Syst. 2011, 39, 645–659. [Google Scholar] [CrossRef]
- Ohm, D.Y. Dynamic Model of PM Synchronous Motors; Drivetech, Inc.: Blacksburg, Virginia, 2000; Volume 16, Available online: www.drivetechinc.com (accessed on 22 November 2018).
- Lu, X. Dual Benefits of Adding Damper Bars in PMSMs for Electrified Vehicles: Improved Machine Dynamics and Simplified Integrated Charging. Ph.D. Thesis, Department of Electrical & Computer Engineering, University of Windsor, Windsor, ON, Canada, 2014. [Google Scholar]
- Institute of Electrical and Electronics Engineers. IEEE Standard Test Procedure for Polyphase Induction Motors and Generators; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2004. [Google Scholar]






| Parameter | Value |
|---|---|
| Mean air gap radius | 37.35 mm |
| Number of poles | 4 |
| Air gap width | 0.3 mm |
| Permanent magnet thickness | 3 mm |
| Stack length | 80 mm |
| Number of turns per stator phase | 86 × 4 |
| Rotor bar resistivity | 2.655 × 10−8 Ω·m |
| Rotor end ring resistance | 1 × 10−5 Ω |
| Angle between two adjacent rotor bars | 18 degrees |
| Number of bars | 20 |
| Permanent magnet flux density | 1.25 T |
| Machine rated power | 1 hp |
| Moment of inertia | 0.001586 kg·m2 |
| Rated voltage | 400 Vrms |
| Rated frequency | 60 Hz |
| Rated speed | 1800 rpm |
| Bar length | 80 mm |
| Bar cross-sectional area | 27 mm2 |
| 5.3 | 0.495 | 5.35353 |
| 6.61 | 0.62 | 5.33064 |
| 7.56 | 0.71 | 5.32394 |
| 8.443 | 0.8 | 5.27687 |
| 9.53 | 0.89 | 5.35393 |
| 5.3 | 0.495 | 5.35353 |
| 10.96 | 1.03 | 5.3203 |
| 11.94 | 1.14 | 5.2368 |
| 12.72 | 1.19 | 5.3445 |
| 13.91 | 1.293 | 5.3789 |
| 14.93 | 1.394 | 5.3550 |
| 10.96 | 1.03 | 5.3203 |
| Average Value | 5.3274 |
| (Deg) | ||||
|---|---|---|---|---|
| 15.31 | 1.529 | 56.6329 | 5.5071 | 0.0221 |
| 17.71 | 1.7687 | 56.6329 | 5.5071 | 0.0221 |
| 21.154 | 2.108 | 56.6329 | 5.5193 | 0.0222 |
| 23.811 | 2.363 | 56.6329 | 5.5421 | 0.0223 |
| 26.98 | 2.671 | 56.6329 | 5.5555 | 0.0223 |
| 29.44 | 2.9 | 55.9442 | 5.6849 | 0.0223 |
| 15.31 | 1.529 | 56.6329 | 5.5071 | 0.0221 |
| Average Value | 5.5527 | 0.0222 |
| (deg) | ||||||
|---|---|---|---|---|---|---|
| 0.722 | 13.59 | 50.20 | 12.048 | 14.465 | 6.4955 | 0.0161 |
| 1.036 | 20.19 | 50.20 | 12.462 | 14.962 | 6.9102 | 0.0174 |
| 1.493 | 29.16 | 50.20 | 12.502 | 15.010 | 6.9502 | 0.0175 |
| 1.79 | 36.18 | 50.20 | 12.916 | 15.506 | 7.3632 | 0.0188 |
| 2.55 | 48.997 | 50.20 | 12.273 | 14.735 | 6.7204 | 0.0168 |
| Average Value | 6.8879 | 0.0173 |
| (deg) | Xiq (Ω) | (H) | ||||
|---|---|---|---|---|---|---|
| 0.74 | 15.97 | 45.412 | 14.993 | 15.210 | 9.4407 | 0.0180 |
| 1.05 | 22.52 | 45.412 | 14.984 | 15.202 | 9.4321 | 0.0180 |
| 1.5 | 33.38 | 45.412 | 15.621 | 15.848 | 10.069 | 0.0197 |
| 2.11 | 41.85 | 45.412 | 13.925 | 14.127 | 8.3731 | 0.0152 |
| 2.51 | 50.69 | 45.412 | 14.177 | 14.3825 | 8.6243 | 0.0158 |
| Average Value | 9.187 | 0.0173 |
| V (v) | τ (s) | R (Ω) | Ld (H) |
|---|---|---|---|
| 1.4 | 0.0163 | 7.991 | 0.0868 |
| 3.2 | 0.0171 | 7.991 | 0.0910 |
| 5.07 | 0.0188 | 7.991 | 0.1001 |
| 7.15 | 0.0172 | 7.991 | 0.0916 |
| 9.43 | 0.0166 | 7.991 | 0.0884 |
| 10 | 0.0178 | 7.9912 | 0.0948 |
| 10.5 | 0.01811 | 7.991 | 0.0964 |
| 11 | 0.01889 | 7.991 | 0.1006 |
| Average Value | 0.09376 |
| V (v) | τ (s) | R (Ω) | Lq (H) |
|---|---|---|---|
| 1.76 | 0.0524 | 7.991 | 0.2791 |
| 3.44 | 0.0515 | 7.991 | 0.2743 |
| 5.6 | 0.0513 | 7.991 | 0.2732 |
| 7.2 | 0.0529 | 7.991 | 0.2818 |
| 9.02 | 0.0572 | 7.991 | 0.3047 |
| 9.7 | 0.056 | 7.991 | 0.2983 |
| 10.3 | 0.0501 | 7.991 | 0.2669 |
| 10.8 | 0.053 | 7.991 | 0.2823 |
| Average Value | 0.2826 |
| 418 | 63.1 | 0.58850 |
| 494 | 74.5 | 0.58792 |
| 536 | 81.2 | 0.59059 |
| 630 | 95.7 | 0.59219 |
| 697 | 106 | 0.59288 |
| 1308 | 199 | 0.59311 |
| 1404 | 213.4 | 0.59254 |
| 1506 | 228.8 | 0.59227 |
| 1601 | 243.4 | 0.59268 |
| 1701 | 258.3 | 0.59199 |
| 1800 | 272.8 | 0.59083 |
| 1847 | 280.9 | 0.59289 |
| Average Value | 0.59153 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| (Ω) | 5.5525 | (H) | 0.0173 |
| (H) | 0.0222 | (mH) | 71.496 |
| (Ω) | 6.8879 | (mH) | 260.355 |
| (H) | 0.01735 | (Wb) | 0.591538 |
| (Ω) | 9.1879 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maraaba, L.S.; Al-Hamouz, Z.M.; Milhem, A.S.; Twaha, S. Comprehensive Parameters Identification and Dynamic Model Validation of Interior-Mount Line-Start Permanent Magnet Synchronous Motors. Machines 2019, 7, 4. https://doi.org/10.3390/machines7010004
Maraaba LS, Al-Hamouz ZM, Milhem AS, Twaha S. Comprehensive Parameters Identification and Dynamic Model Validation of Interior-Mount Line-Start Permanent Magnet Synchronous Motors. Machines. 2019; 7(1):4. https://doi.org/10.3390/machines7010004
Chicago/Turabian StyleMaraaba, Luqman S., Zakariya M. Al-Hamouz, Abdulaziz S. Milhem, and Ssennoga Twaha. 2019. "Comprehensive Parameters Identification and Dynamic Model Validation of Interior-Mount Line-Start Permanent Magnet Synchronous Motors" Machines 7, no. 1: 4. https://doi.org/10.3390/machines7010004
APA StyleMaraaba, L. S., Al-Hamouz, Z. M., Milhem, A. S., & Twaha, S. (2019). Comprehensive Parameters Identification and Dynamic Model Validation of Interior-Mount Line-Start Permanent Magnet Synchronous Motors. Machines, 7(1), 4. https://doi.org/10.3390/machines7010004






