Robust Control of Small Turbojet Engines
Abstract
1. Introduction
2. Modeling the iSTC-21v Engine with Uncertainties
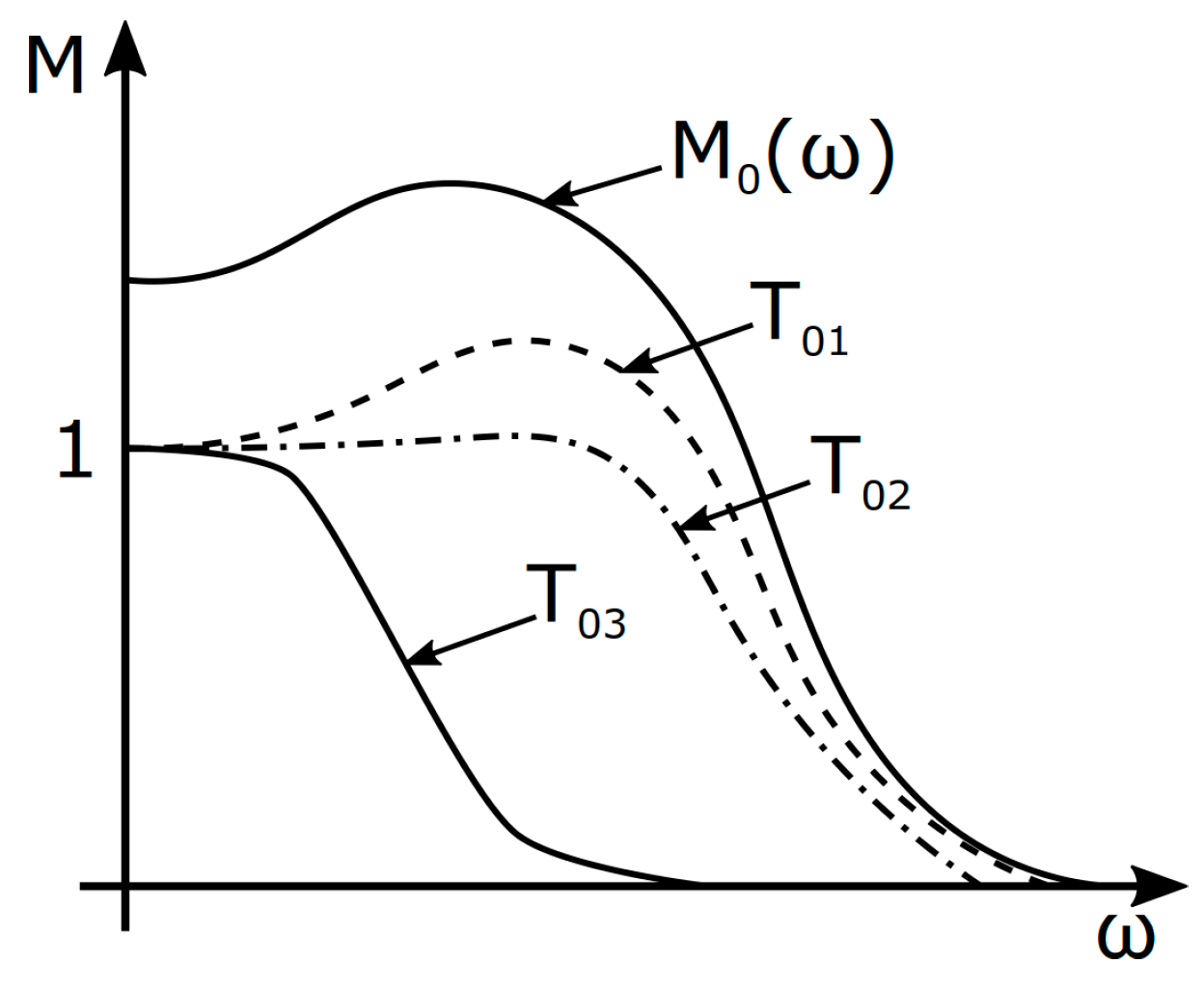
- F0 (s) represents the nominal model of the dynamic system, in this case a small turbojet engine described in Equation (2).
- wa(s) represents the transfer function of the additive uncertainty.
- wm(s) represents the transfer function of the multiplicative form of uncertainty.
- δ(s) represents the absolute value of the uncertainty in the interval: <−1,1>.
3. Robust Control Design
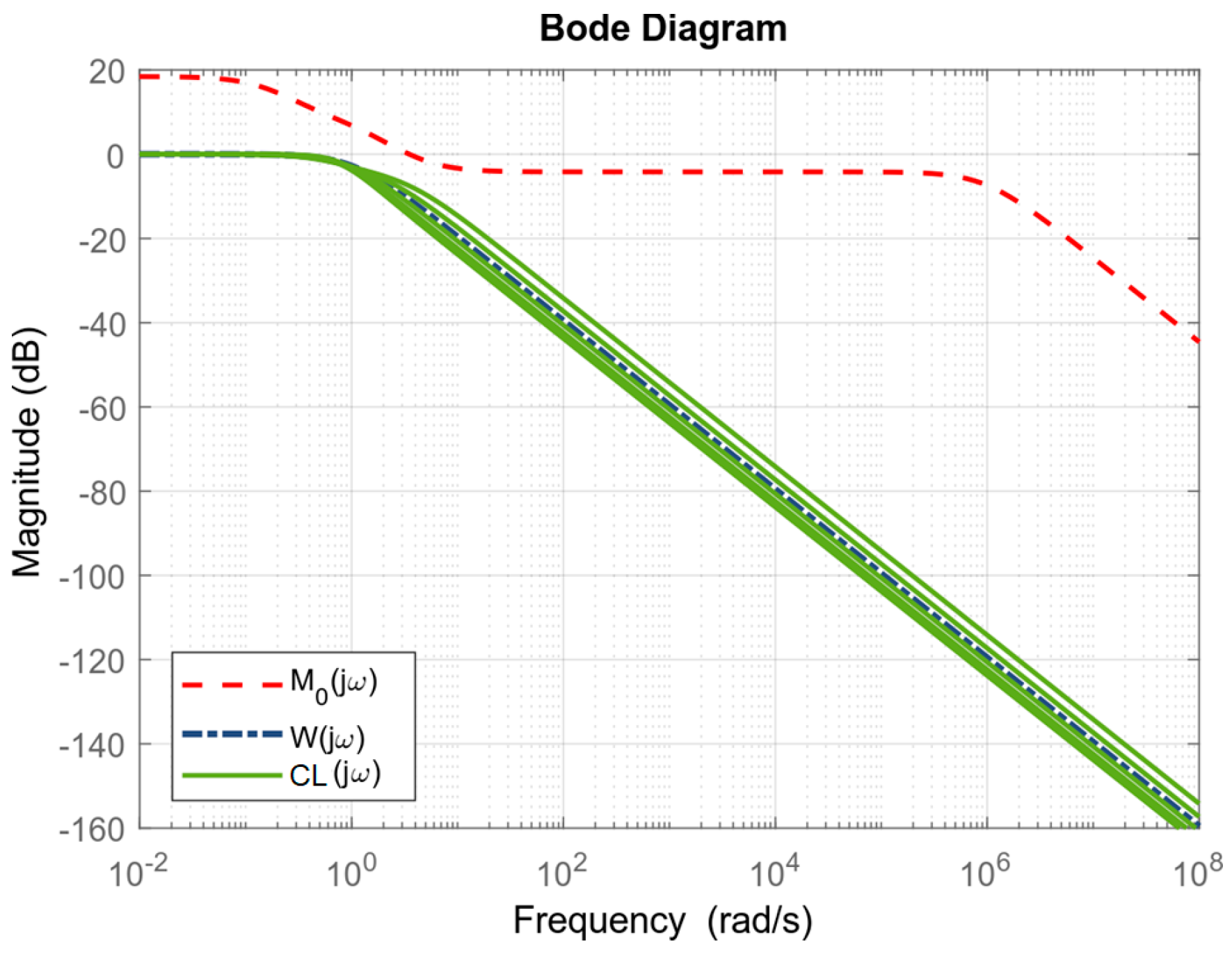
3.1. The Small Gain Theory
3.2. H-Infinity Control
3.2.1. Loop Shaping
3.2.2. Mixed Sensitivity
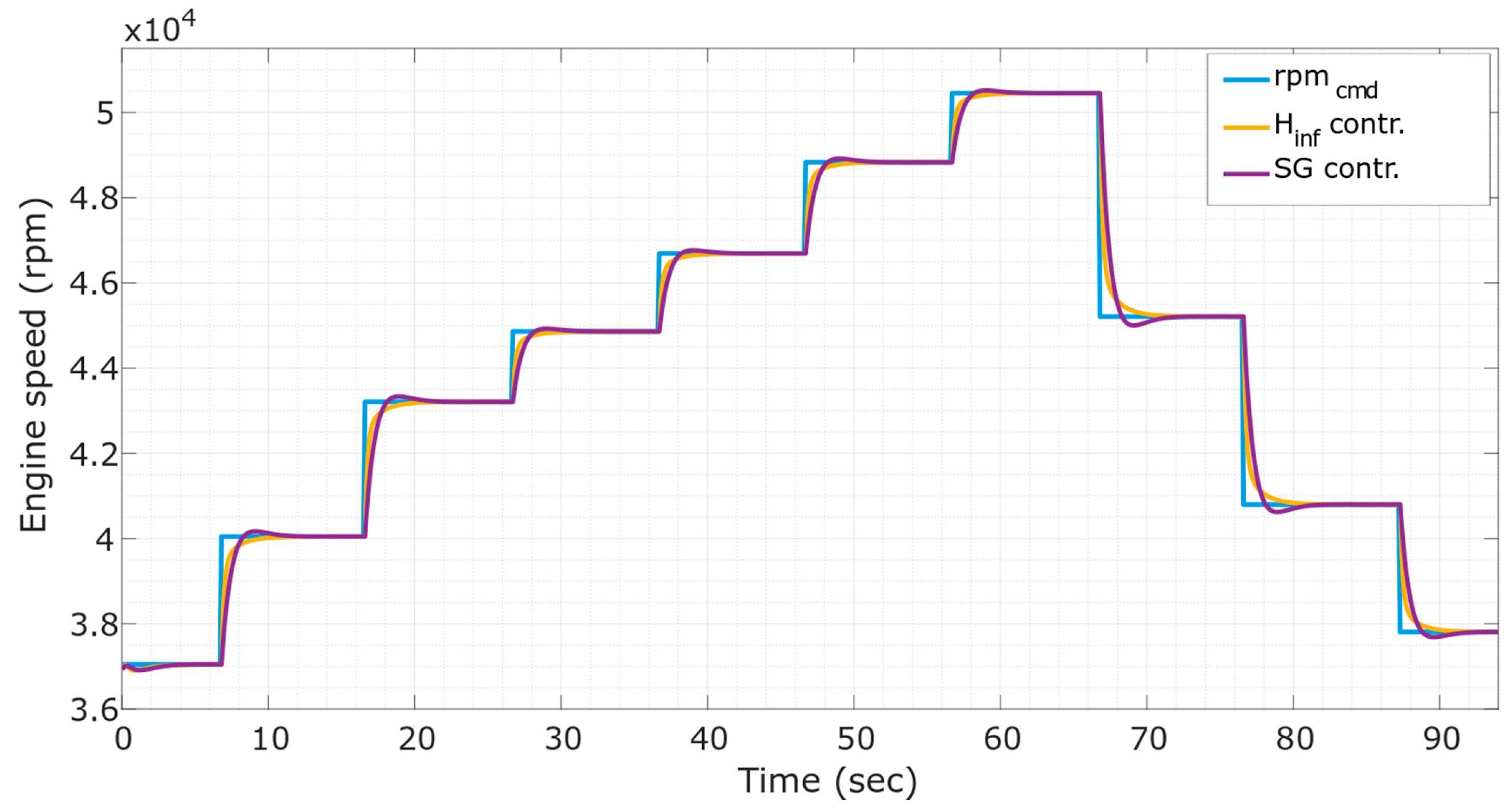
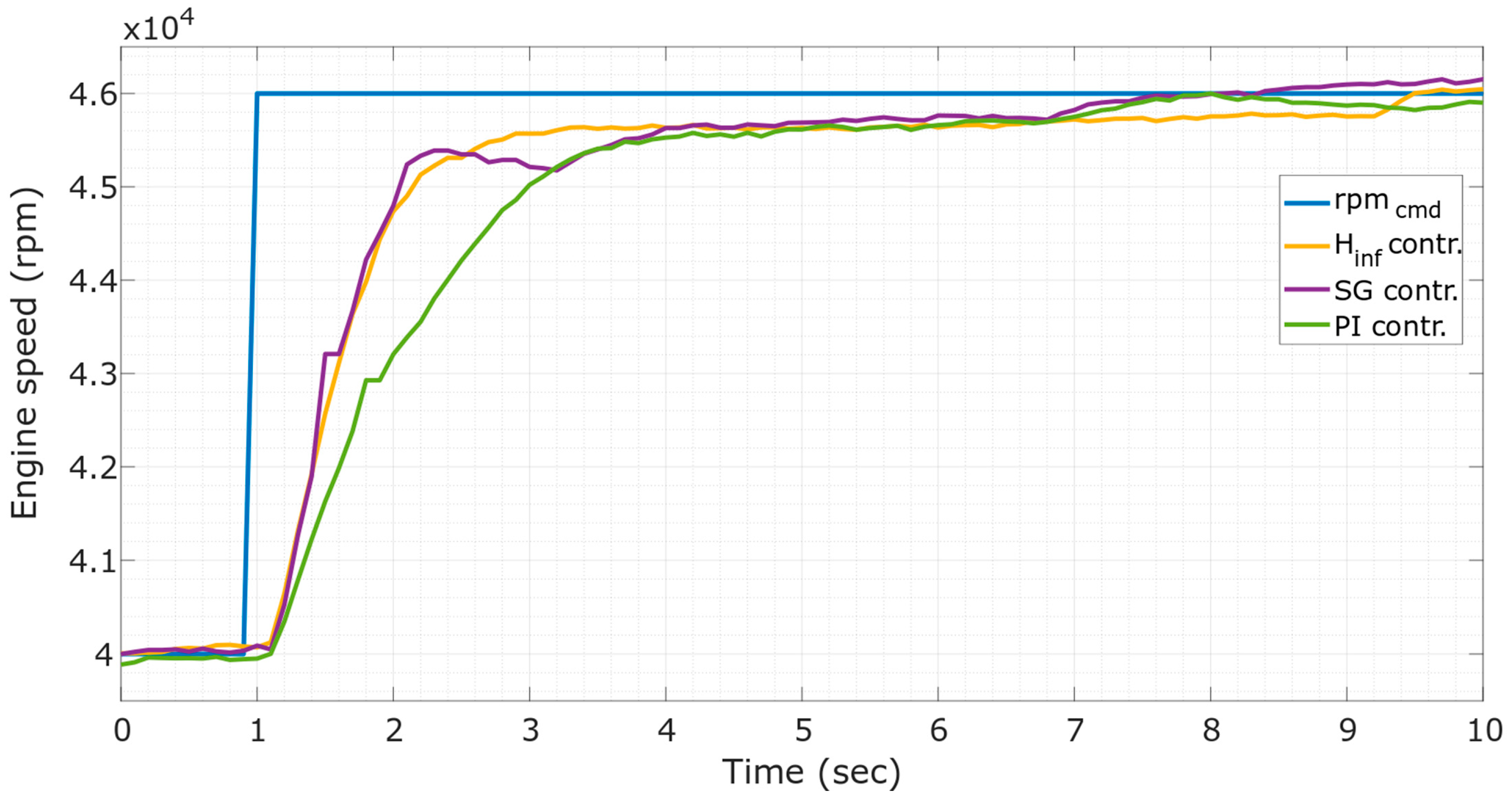
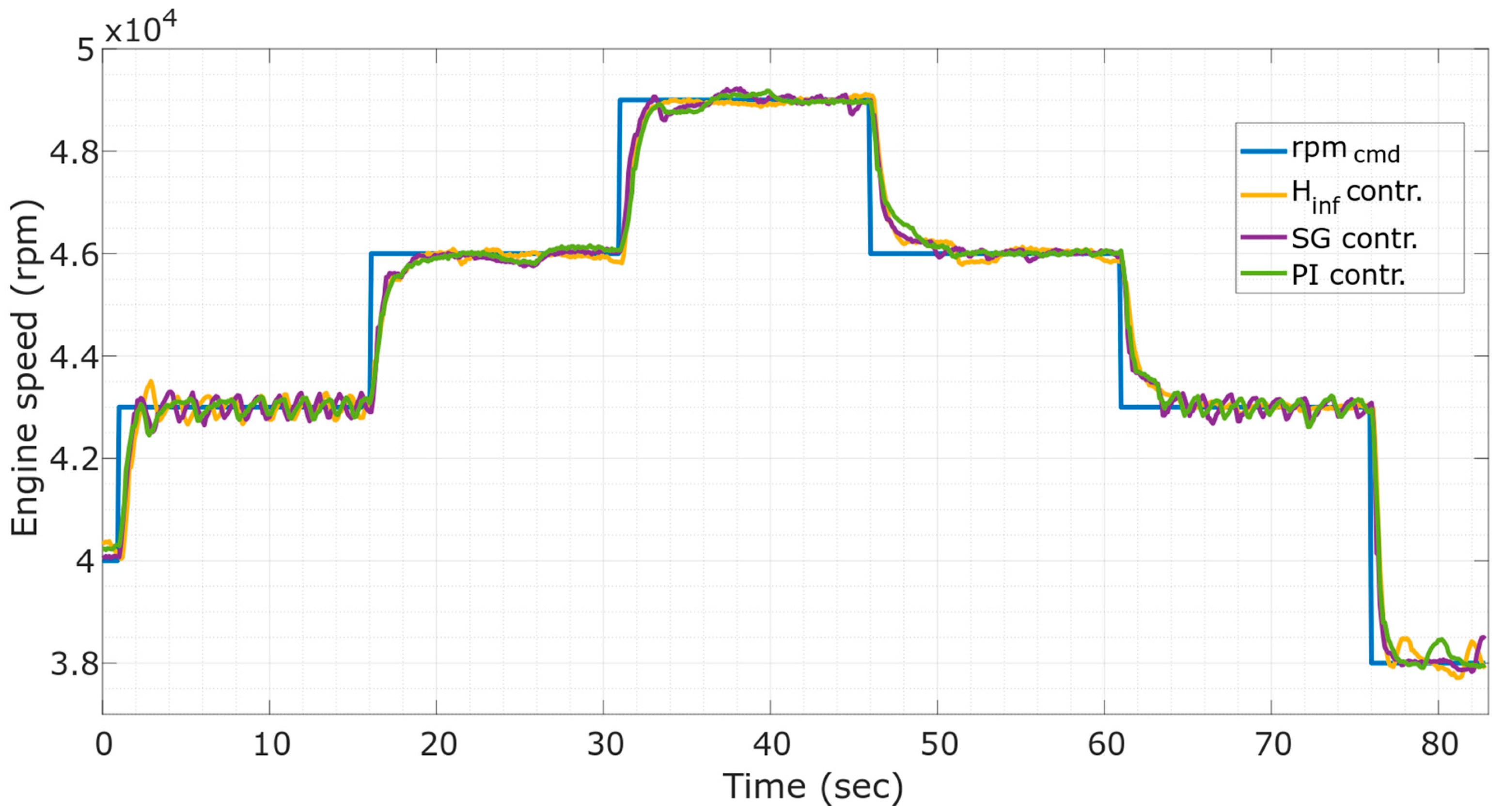
4. Simulation and Experimental Results
5. Conclusions and Discussion
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| ARX | Auto regressive Model with Exogenous Input |
| C* | The C Star Algorithm for Aircraft Attitude Control |
| EGT | Exhaust Gas Temperature |
| FADEC | Full Authority Digital Engine Control |
| FF | Fuel Flow |
| H-inf | H Infinity Method |
| iSTC-21v | Intelligent Small Turbo-Compressor Engine -21 with Variable Exhaust Nozzle |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MAAE | Maximum Absolute Error |
| MAAPE | Maximum Absolute Percentage Error |
| n | The Speed of the Engine |
| NARX | Non Linear Autoregressive Model with Exogenous Input |
| OP | Operational Point |
| PID | Proportional Integral Derivative Controller |
| RPM | Revolutions per Minute |
| SG | Small Gain Controller |
| T1C | Temperature on the Compressor Inlet |
| T3C | Temperature on the Compressor Outlet |
References
- Jaw, L.; Mattingly, J. Aircraft Engine Controls: Design, System Analysis, and Health Monitoring; AIAA Education Series; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2009; ISBN 978-1-60086-705-7. [Google Scholar]
- Gu, D.W.; Petkov, P.; Konstantinov, M.M. Robust Control Design with MATLAB®; Advanced Textbooks in Control and Signal Processing; Springer: London, UK, 2014; ISBN 978-1-4471-4682-7. [Google Scholar]
- Zhou, K.; Doyle, J. Essentials of Robust Control; Prentice Hall Modular Series; Prentice Hall: Upper Saddle River, NJ, USA, 1998; ISBN 978-0-13-525833-0. [Google Scholar]
- Green, M.; Limebeer, D. Linear Robust Control; Dover Books on Electrical Engineering; Dover Publications: Mineola, NY, USA, 2013; ISBN 978-0-486-26509-4. [Google Scholar]
- Vesely, V.; Harsanyi, L. Robust Control: Applications (Robustné Riadenie: Aplikácie); Slovak Technical University in Bratislava STU: Bratislava, Slovak, 2015; ISBN 978-80-227-4339-6. [Google Scholar]
- Főző, L.; Andoga, R.; Madarász, L.; Kolesár, J.; Judičák, J. Description of an intelligent small turbo-compressor engine with variable exhaust nozzle, in with variable exhaust nozzle. In Proceedings of the IEEE 13th International Symposium on Applied Machine Intelligence and Informatics (SAMI), Herl’any, Slovakia, 22–24 January 2015; pp. 22–24. [Google Scholar]
- Alikhani, H.R.; Motlagh, M.M. Aero Engine Multivariable Robust Control. Tech. J. Eng. Appl. Sci. 2016, 5, 228–232. [Google Scholar]
- Baniassadi, A.; Markazi, A.H.D.; Karami, M. Robust control of a gas turbine with wiener model uncertainty. Indian J. Sci. Technol. 2012, 5, 3584–3592. [Google Scholar]
- Peng, J.; Zhang, Z.; Feng, F. H∞ Optimal Control of Aero engine Distributed Control System with Packet Dropout Compensator. Procedia Eng. 2011, 15, 618–623. [Google Scholar] [CrossRef]
- Kolmanovsky, I.V.; Jaw, L.C.; Merrill, W.; Van, H.T. Robust control and limit protection in aircraft gas turbine engines. In Proceedings of the 2012 IEEE International Conference on Control Applications (CCA), Dubrovnik, Croatia, 3–5 October 2012; pp. 812–819, ISBN 978-1-4673-4503-3. [Google Scholar] [CrossRef]
- Kratz, J.; Yedavalli, R.K. A Riccati equation based robust control design with application to a gas turbine engine leading toward distributed control. In Proceedings of the 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, OH, USA, 28–30 July 2014; p. 3639. [Google Scholar] [CrossRef]
- Najimi, E.; Ramezani, M.H. Robust control of speed and temperature in a power plant gas turbine. ISA Trans. 2012, 51, 304–308. [Google Scholar] [CrossRef] [PubMed]
- Turso, J.; Litt, J. Intelligent, Robust Control of Deteriorated Turbofan Engines via Linear Parameter Varing Quadratic Lyapunov Function Design. In Proceedings of the AIAA 1st Intelligent Systems Technical Conference, Chicago, IL, USA, 20–22 September 2004; p. 6363. [Google Scholar] [CrossRef]
- Pan, M.; Zhang, K.; Chen, Y.H.; Huang, J. A New Robust Tracking Control Design for Turbofan Engines: H∞/Leitmann Approach. Appl. Sci. 2017, 7, 439. [Google Scholar] [CrossRef]
- Marcos, A. Revisiting the aircraft C∗ control law: A comparison between classical and structured H-infinity designs. In Proceedings of the 2017 IEEE Conference on Control Technology and Applications (CCTA), Mauna Lani, HI, USA, 27–30 August 2017; pp. 2114–2119, ISBN 978-1-5090-2182-6. [Google Scholar] [CrossRef]
- Garcia, G.A.; Kashmiri, S.; Shukla, D. Nonlinear control based on H-infinity theory for autonomous aerial vehicle. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 336–345, ISBN 978-1-5090-4495-5. [Google Scholar] [CrossRef]
- You, S.S.; Lim, T.W.; Kim, J.Y.; Choi, H.S. Robust control synthesis for dynamic vessel positioning. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2017, 231, 98–108. [Google Scholar] [CrossRef]
- Bayas, A.; Škrjanc, I.; Sáez, D. Design of fuzzy robust control strategies for a distributed solar collector field. Appl. Soft Comput. 2018, 71, 1009–1019. [Google Scholar] [CrossRef]
- Wang, X.; Yaz, E.E.; Schneider, S.C.; Yaz, Y.I. H2−H∞ control of discrete-time nonlinear systems using the state-dependent Riccati equation approach. Syst. Sci. Control Eng. 2017, 5, 215–223. [Google Scholar] [CrossRef]
- Andoga, R.; Főző, L.; Judičák, J.; Bréda, R.; Szabo, S.; Rozenberg, R.; Džunda, M. Intelligent Situational Control of Small Turbojet Engines. Int. J. Aerosp. Eng. 2018, 2018, 8328792. [Google Scholar] [CrossRef]
- Főző, L.; Andoga, R.; Beneda, K.; Kolesár, J. Effect of operating point selection on non-linear experimental identification of iSTC–21v and TKT–1 small turbojet engines. Period. Polytech. Transp. Eng. 2017, 45, 141–147. [Google Scholar] [CrossRef]
- Komjáty, M.; Főző, L.; Andoga, R. Experimental identification of a small turbojet engine with variable exhaust nozzle. In Proceedings of the 2015 16th IEEE International Symposium on Computational Intelligence and Informatics (CINTI), Budapest, Hungary, 19–21 November 2015; pp. 65–69, ISBN 978-1-4673-8519-0. [Google Scholar]
- Madarász, L.; Andoga, R.; Češkovič, M.; Laššák, M.; Šmelko, M.; Főző, L. Advanced Approaches in Modeling of Complex Electromechanical Systems. In Proceedings of the CINTI 2011: 12th IEEE International Symposium on Computational Intelligence and Informatics, Budapest, Hungary, 21–22 November 2011; pp. 541–544, ISBN 978-1-4577-0043-9. [Google Scholar]
- Nyulászi, L.; Madarász, L. Experimental Identification of the Small Turbojet Engine MPM-20. In Proceedings of the CINTI 2014: 15th IEEE International Symposium on Computational Intelligence and Informatics, Budapest, Hungary, 19–21 November 2014; pp. 497–501, ISBN 978-1-4799-5338-7. [Google Scholar]
- Mackenroth, U. Robust Control Systems: Theory and Case Studies; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-662-09775-5. [Google Scholar]
- Glover, K.; McFarlane, D. Robust stabilization of normalized coprime factor plant descriptions with H/sub infinity/-bounded uncertainty. IEEE Trans. Autom. Control 1989, 34, 821–830. [Google Scholar] [CrossRef]
- Precup, R.-E.; David, R.-C.; Petriu, E.M. Grey wolf optimizer algorithm-based tuning of fuzzy control systems with reduced parametric sensitivity. IEEE Trans. Ind. Electron. 2017, 64, 527–534. [Google Scholar] [CrossRef]
- Várkonyi, T.A.; Tar, J.; Rudas, I. Improved stabilization for robust fixed point transformations-based controllers. J. Adv. Comput. Intell. Intell. Inform. 2013, 17, 418–424. [Google Scholar] [CrossRef]
- Lacerda, M.J.; Tognetti, E.S.; Oliveira, R.C.; Peres, P.L. A new approach to handle additive and multiplicative uncertainties in the measurement for LPV filtering. Int. J. Syst. Sci. 2016, 47, 1042–1053. [Google Scholar] [CrossRef]


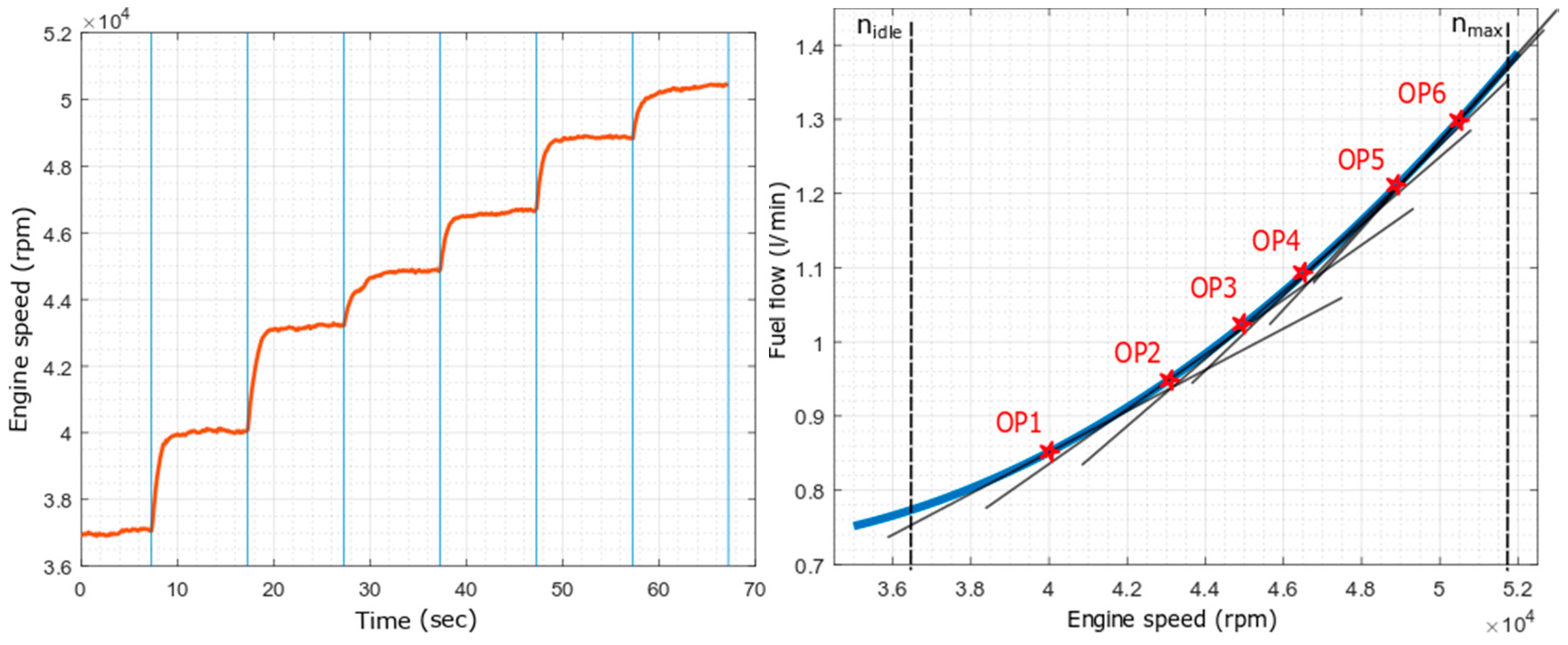
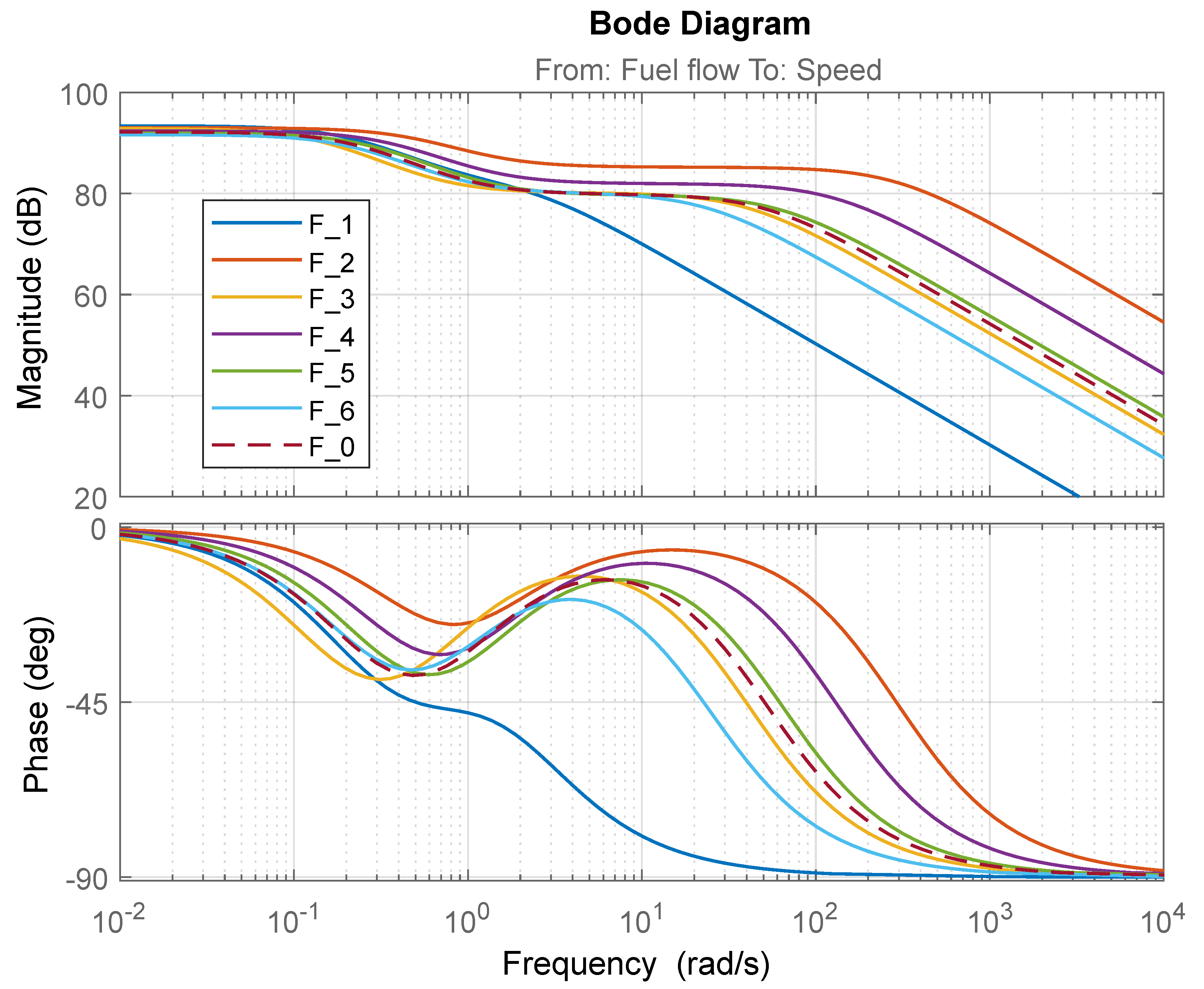
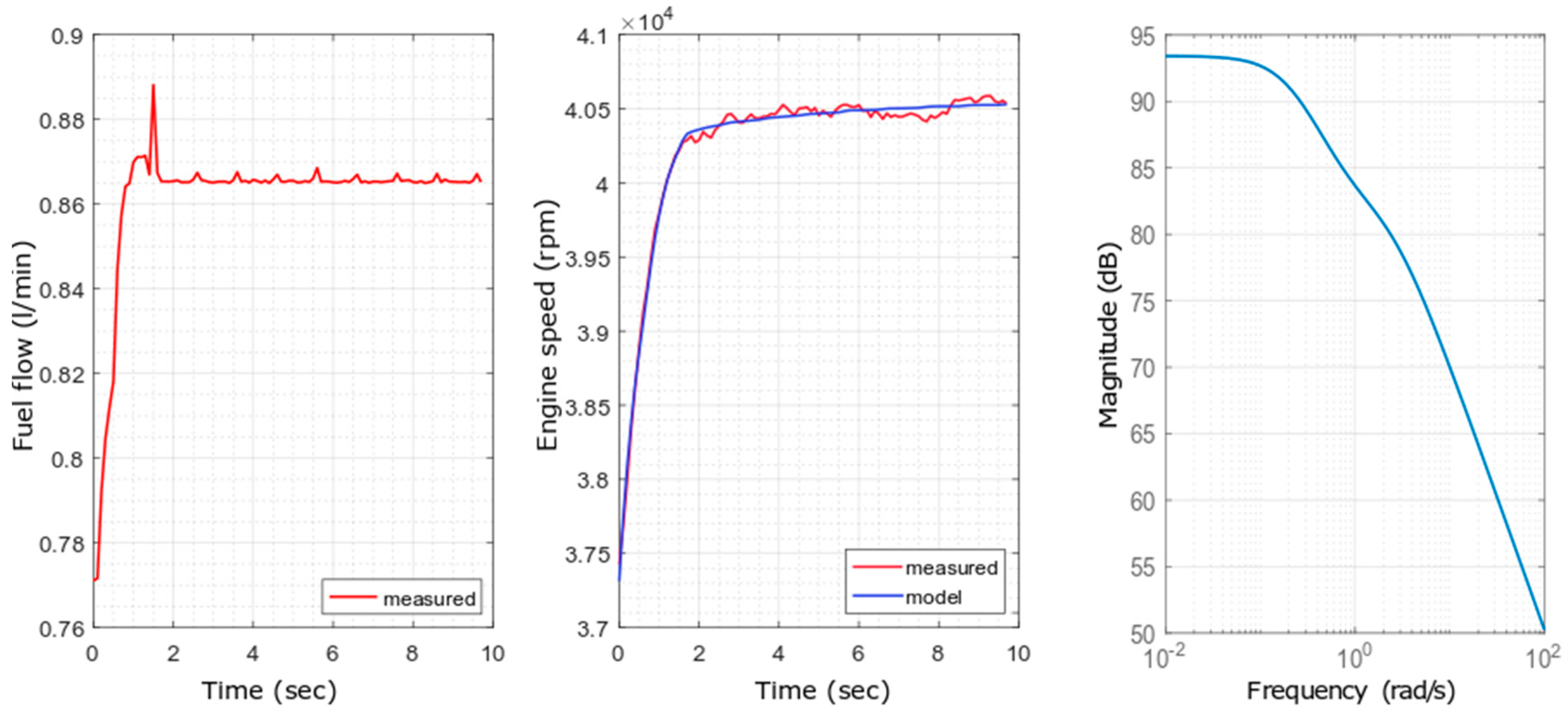

| Operational Point (OP) | MAE (rpm) | MAPE (%) | MAAE (rpm) | MAAPE (%) | Individual Transfer Functions Fi(s) |
|---|---|---|---|---|---|
| 1. | 37.3312 | 0.2714 | 109.9996 | 0.0931 | |
| 2. | 76.3130 | 0.1778 | 621.0031 | 1.4112 | |
| 3. | 35.1434 | 0.0778 | 132.2502 | 0.2889 | |
| 4. | 34.1676 | 0.0721 | 175.5602 | 0.3669 | |
| 5. | 37.7333 | 0.0762 | 110.1576 | 0.2215 | |
| 6. | 30.8231 | 0.0607 | 187.9138 | 0.3676 |
| Controller | Discrete Transfer Function Controllers—Sample Time: 0.01 s |
|---|---|
| SG | |
| PI |
| Transition State | Steady State | |||||
|---|---|---|---|---|---|---|
| Controller | Settling Time (sec) | Max. Overshoot (%) | MAE (RPM) | MAPE (%) | MAAE (RPM) | MAAPE (%) |
| SG | 5.115 | 0.435 | 111.805 | 0.245 | 284.405 | 0.615 |
| 2.7833 | 0.788 | 101.532 | 0.2347 | 285.4147 | 0.6507 | |
| PI | 3.244 | 0.8215 | 157.3056 | 0.3594 | 396.0219 | 0.89 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andoga, R.; Főző, L.; Kovács, R.; Beneda, K.; Moravec, T.; Schreiner, M. Robust Control of Small Turbojet Engines. Machines 2019, 7, 3. https://doi.org/10.3390/machines7010003
Andoga R, Főző L, Kovács R, Beneda K, Moravec T, Schreiner M. Robust Control of Small Turbojet Engines. Machines. 2019; 7(1):3. https://doi.org/10.3390/machines7010003
Chicago/Turabian StyleAndoga, Rudolf, Ladislav Főző, Radovan Kovács, Károly Beneda, Tomáš Moravec, and Michal Schreiner. 2019. "Robust Control of Small Turbojet Engines" Machines 7, no. 1: 3. https://doi.org/10.3390/machines7010003
APA StyleAndoga, R., Főző, L., Kovács, R., Beneda, K., Moravec, T., & Schreiner, M. (2019). Robust Control of Small Turbojet Engines. Machines, 7(1), 3. https://doi.org/10.3390/machines7010003






