Nonlinear Model Predictive Control Using Robust Fixed Point Transformation-Based Phenomena for Controlling Tumor Growth
Abstract
1. Introduction
2. System Model
3. Control Algorithm
3.1. The Nonlinear Model Predictive Controller
3.2. The Robust Fixed Point Transformations Based Controller
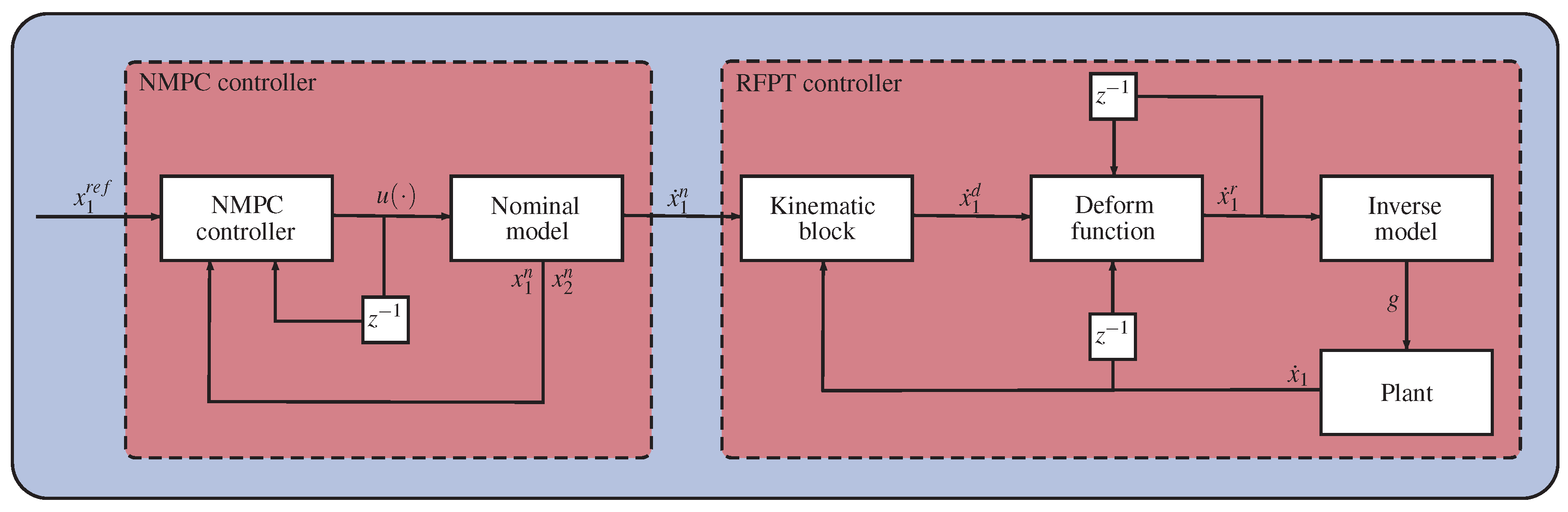
3.3. The Combined Approach
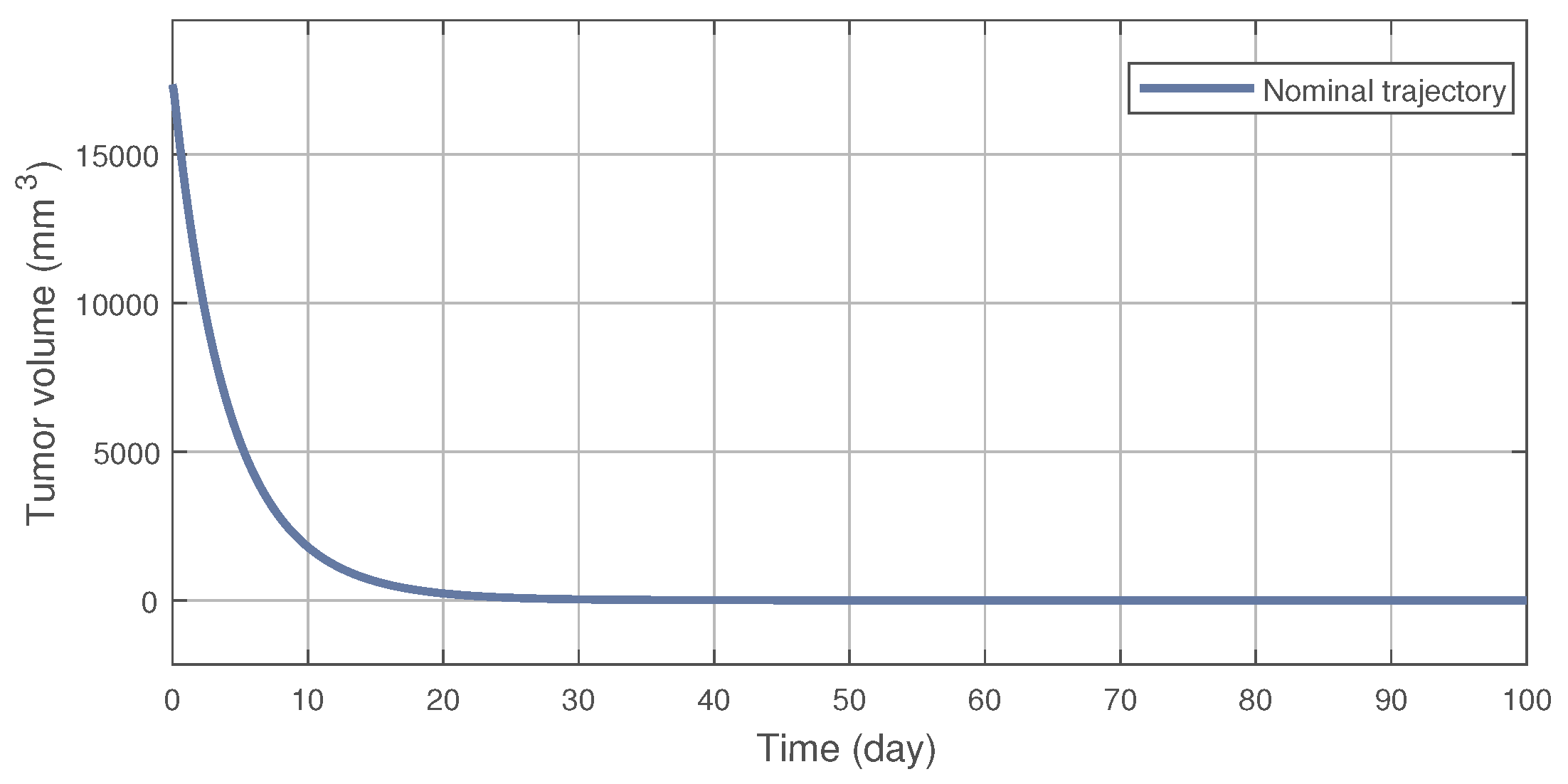
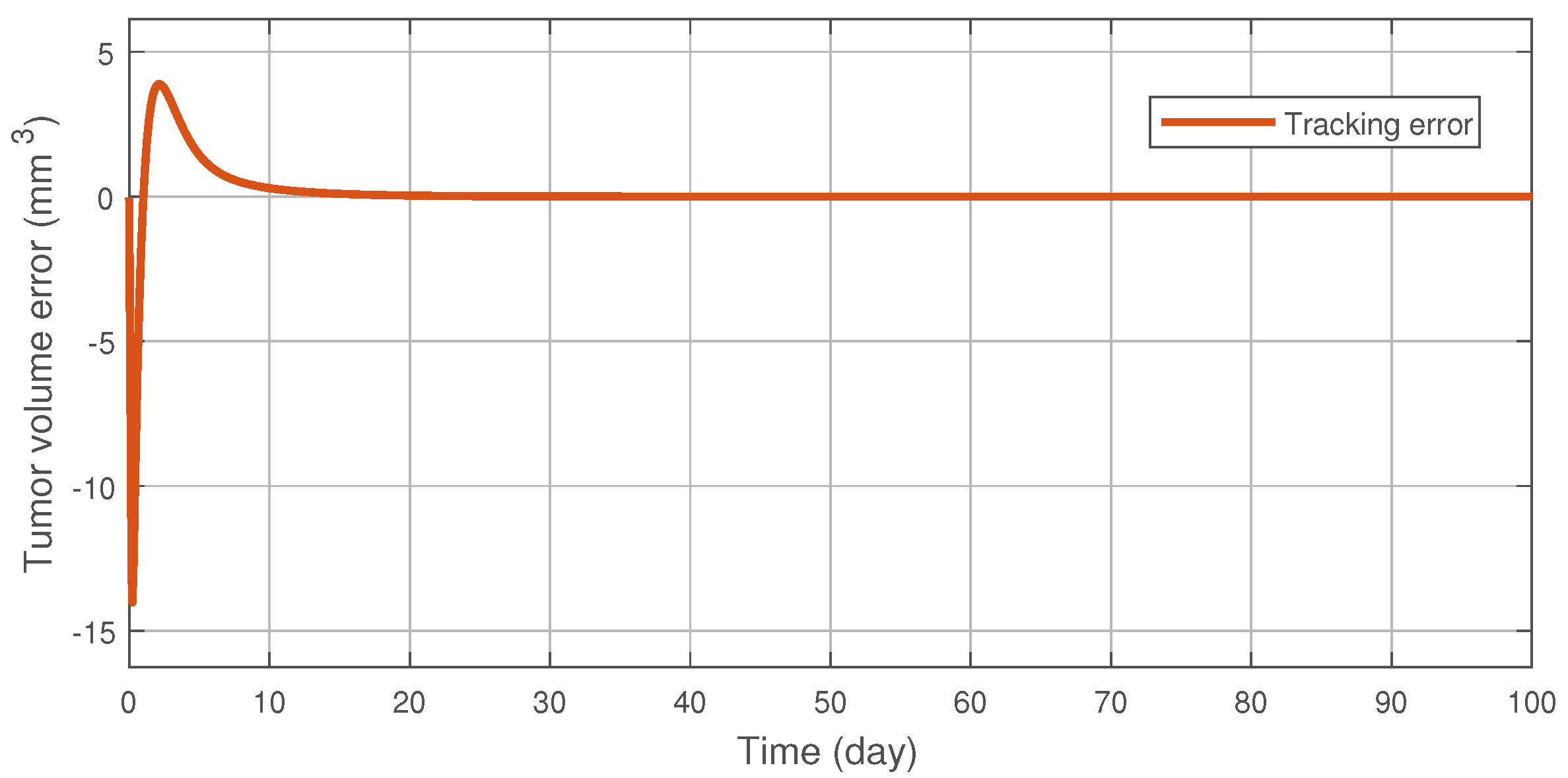
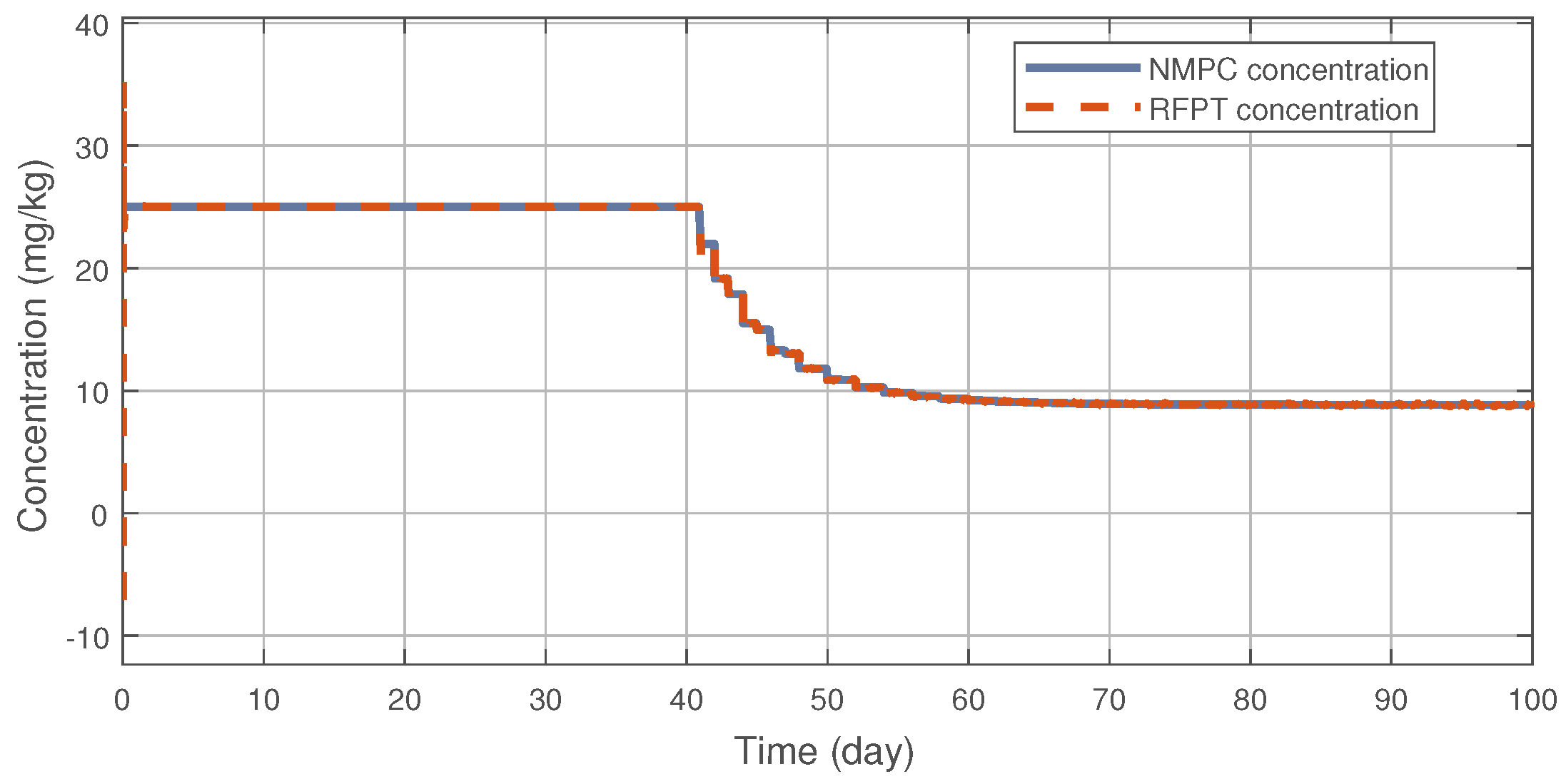
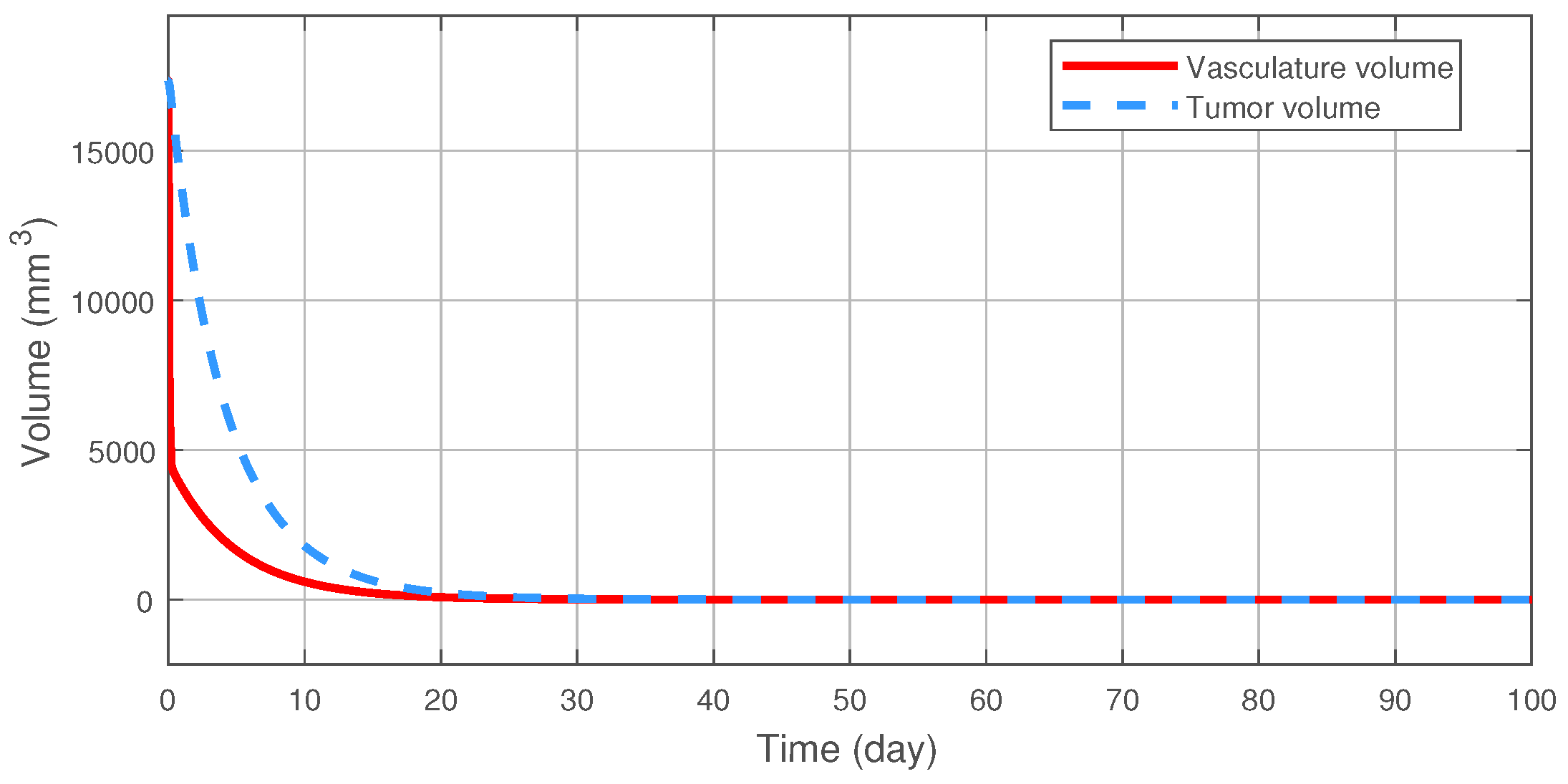
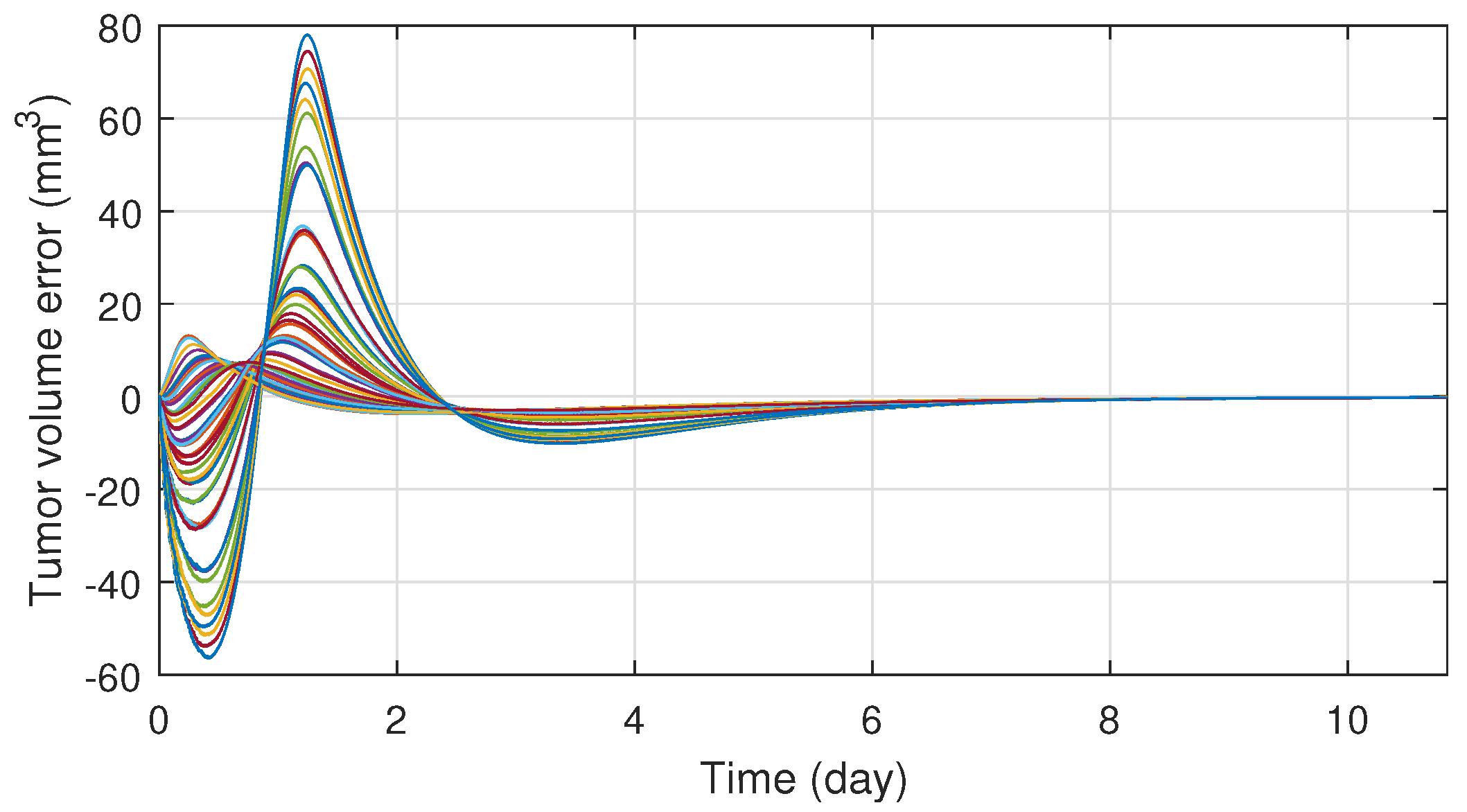
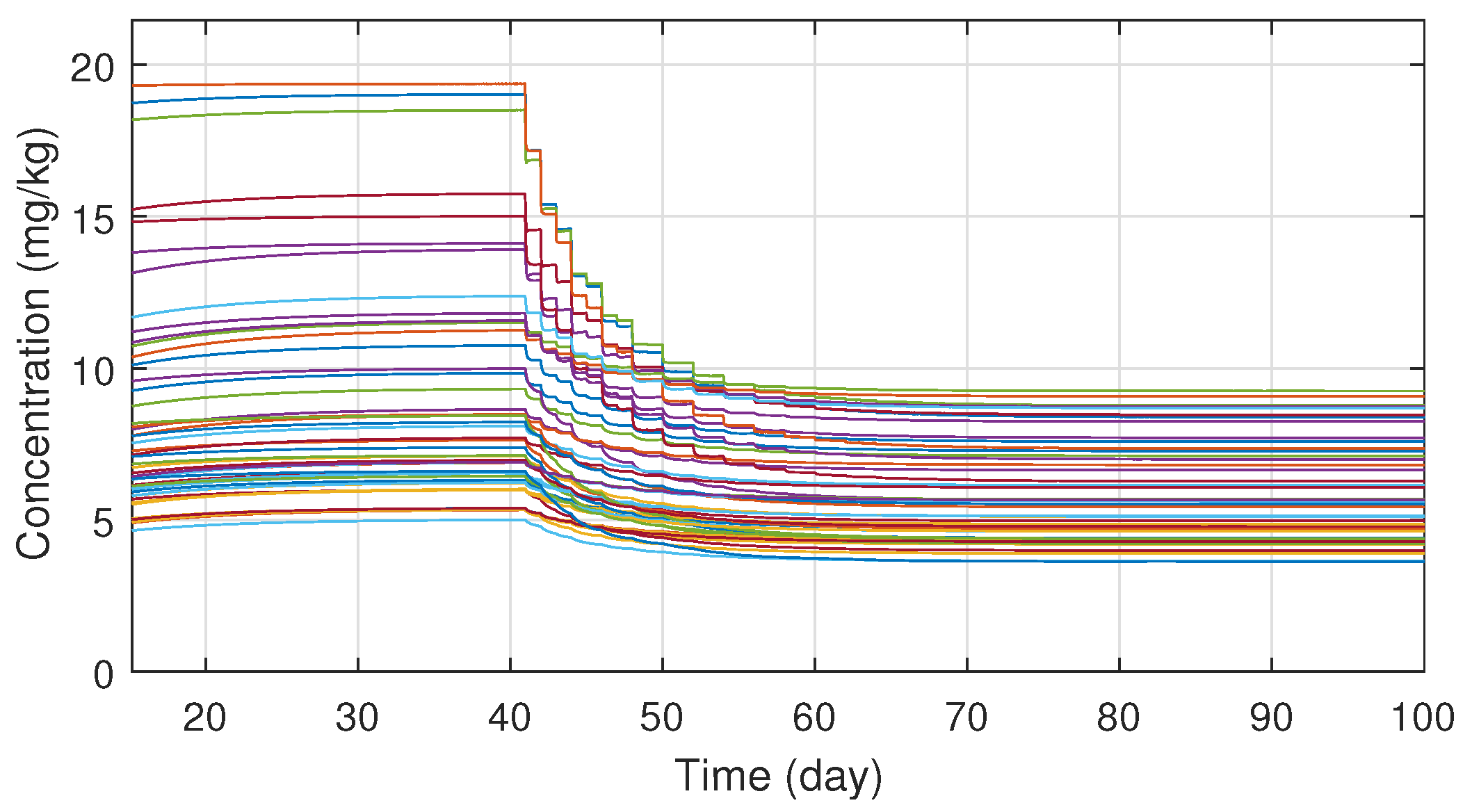
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ionescu, C.M.; Copot, D. Guided closed loop control of analgesia: Are we there yet? In Proceedings of the 2017 IEEE 21st International Conference on Intelligent Engineering Systems (INES), Larnaca, Cyprus, 20–23 October 2017; p. 137142. [Google Scholar]
- Kovács, L. A robust fixed point transformation-based approach for type 1 diabetes control. Nonlinear Dyn. 2017, 89, 2481–2493. [Google Scholar] [CrossRef]
- Churilov, A.; Medvedev, A.; Shepeljavyi, A. Mathematical model of testosterone regulation by pulse-modulated feedback. In Proceedings of the 2007 IEEE International Conference on Control Applications, Singapore, 1–3 October 2007. [Google Scholar]
- Malvezzi, M.; Carioli, G.; Bertuccio, P.; Rosso, T.; Boffetta, P.; Levi, F.; Vecchia, C.L.; Negri, E. European cancer mortality predictions for the year 2016 with focus on leukaemias. Ann. Oncol. 2016, 27, 725–731. [Google Scholar] [CrossRef] [PubMed]
- Hanhfeldt, P.; Panigrahy, D.; Folkman, J.; Hlatky, L. Tumor development under angiogenic signaling: A dynamical theory of tumor growth, treatment response, and postvascular dormancy. Cancer Res. 1999, 59, 4770–4775. [Google Scholar]
- Sapi, J.; Drexler, D.A.; Kovacs, L. Parameter optimization of H infinity controller designed for tumor growth in the light of physiological aspects. In Proceedings of the 2013 IEEE 14th International Symposium on Computational Intelligence and Informatics (CINTI), Budapest, Hungary, 19–21 November 2013. [Google Scholar]
- Drexler, D.A.; Sápi, J.; Kovács, L. Positive nonlinear control of tumor growth using angiogenic inhibition. IFAC-PapersOnLine 2017, 50, 15068–15073. [Google Scholar] [CrossRef]
- Czako, B.G.; Kosi, K. Novel method for quadcopter controlling using nonlinear adaptive control based on robust fixed point transformation phenomena. In Proceedings of the 2017 IEEE 15th International Symposium on Applied Machine Intelligence and Informatics (SAMI), Košice, Slovakia, 26–28 January 2017. [Google Scholar]
- Szeles, A.; Drexler, D.A.; Sapi, J.; Harmati, I.; Kovacs, L. Model-based angiogenic inhibition of tumor growth using feedback linearization. In Proceedings of the 52nd IEEE Conference on Decision and Control, Lorence, Italy, 10–13 December 2013. [Google Scholar]
- Czakó, B.; Sápi, J.; Kovács, L. Model-based optimal control method for cancer treatment using model predictive control and robust fixed point method. In Proceedings of the 2017 IEEE 21st International Conference on Intelligent Engineering Systems (INES), Bratislava, Slovakia, 20–23 October 2017; p. 271276. [Google Scholar]
- Kovács, L.; Eigner, G.; Tar, J.K.; Rudas, I. Robust Fixed Point Transformation based Proportional-Derivative Control of Angiogenic Tumor Growth. IFAC-PapersOnLine 2018, 51, 894–899. [Google Scholar] [CrossRef]
- Świerniak, A. Comparison of six models of antiangiogenic therapy. Appl. Math. 2009, 36, 333–348. [Google Scholar] [CrossRef]
- Döme, B.; Hendrix, M.J.; Paku, S.; Tóvári, J.; Tímár, J. Alternative Vascularization Mechanisms in Cancer. Am. J. Pathol. 2007, 170, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Csercsik, D.; Sápi, J.; Gönczy, T.; Kovács, L. Bi-compartmental modelling of tumor and supporting vasculature growth dynamics for cancer treatment optimization purpose. In Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, Australia, 12–15 December 2017. [Google Scholar]
- Drexler, D.A.; Sápi, J.; Kovács, L. A minimal model of tumor growth with angiogenic inhibition using bevacizumab. In Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, Australia, 12–15 December 2017. [Google Scholar]
- Ledzewicz, U.; Schattler, H. A Synthesis of Optimal Controls for a Model of Tumor Growth under Angiogenic Inhibitors. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 12–15 December 2005. [Google Scholar]
- Sápi, J.; Drexler, D.A.; Harmati, I.; Sápi, Z.; Kovács, L. Qualitative analysis of tumor growth model under antiangiogenic therapy—choosing the effective operating point and design parameters for controller design. OCAM 2015, 37, 848–866. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Kerrigan, E.C.; van Wyk, E.J.; Falugi, P. Tube-based robust nonlinear model predictive control. Int. J. Robust. Nonlinear 2011, 21, 1341–1353. [Google Scholar] [CrossRef]
- Grüne, L.; Pannek, J. Nonlinear Model Predictive Control; Springer: London, UK, 2011. [Google Scholar]
- Tar, J.K.; Bitó, J.; Nádai, L.; Machado, J.T. Robust Fixed Point Transformations in Adaptive Control Using Local Basin of Attraction. Acta Polytech. Hung. 2009, 6, 21–37. [Google Scholar]
- Tar, J.K.; Rudas, I.J. Geometric Approach to Nonlinear Adaptive Control. In Proceedings of the 2007 4th International Symposium on Applied Computational Intelligence and Informatics, Timisoara, Romania, 17–18 May 2007. [Google Scholar]
- Nádai, L.; Rudas, I.J.; Tar, J.K. System and Control Theory with Especial Emphasis on Nonlinear Systems; Typotex: Budapest, Hungary, 2012. [Google Scholar]
| b | d | e | |
|---|---|---|---|
| 0.192 | 5.85 | 0.00873 | 0.66 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Czakó, B.; Kovács, L. Nonlinear Model Predictive Control Using Robust Fixed Point Transformation-Based Phenomena for Controlling Tumor Growth. Machines 2018, 6, 49. https://doi.org/10.3390/machines6040049
Czakó B, Kovács L. Nonlinear Model Predictive Control Using Robust Fixed Point Transformation-Based Phenomena for Controlling Tumor Growth. Machines. 2018; 6(4):49. https://doi.org/10.3390/machines6040049
Chicago/Turabian StyleCzakó, Bence, and Levente Kovács. 2018. "Nonlinear Model Predictive Control Using Robust Fixed Point Transformation-Based Phenomena for Controlling Tumor Growth" Machines 6, no. 4: 49. https://doi.org/10.3390/machines6040049
APA StyleCzakó, B., & Kovács, L. (2018). Nonlinear Model Predictive Control Using Robust Fixed Point Transformation-Based Phenomena for Controlling Tumor Growth. Machines, 6(4), 49. https://doi.org/10.3390/machines6040049






