A Methodology for the Lightweight Design of Modern Transfer Machine Tools

Abstract

This paper deals with a modern design approach via finite elements in the definition of the main structural elements (rotary table and working unit) of an innovative family of transfer machine tools. Using the concepts of green design and manufacture, as well as sustainable development thinking, the paper highlights the advantages derived from their application in this specific field (i.e., the clever use of lightweight materials to allow ruling out high-consumption hydraulic pump systems). The design is conceived in a modular way, so that the final solution can cover transfers from four to 15 working stations. Two versions of the machines are examined. The first one has a rotary table with nine divisions, which can be considered as a prototype: this machine has been studied in order to set up the numerical predictive model, then validated by experimental tests. The second one, equipped with a rotary table with 15 divisions, is the biggest of the range: this machine has been entirely designed with the aid of the previously developed numerical model. The loading input forces for the analyses have been evaluated experimentally via drilling operations carried out on a three-axis CNC unit. The definition of the design force made it possible to accurately assess both the rotary table and the working units installed in the machine.

1. Introduction: Green Design Applied to Machine Tools

In order to be competitive in today’s business world, more and more companies have to plan their activities by thinking about energy consumption and resource saving. The themes of green design are compelling in the modern design of machine tools. In practical aspects, up to 10 years ago the goal of machine tool manufacturers was to improve the performance of machine tools in terms of availability, reliability, dimensional accuracy, and precision. To achieve these targets, machine tools have become increasingly complex and automated in their design. These changes resulted in increasing energy requirements, which lead to rising power costs and limited access to resources (particularly fossil fuels), and run counter to increasing environmental consciousness among customers and stricter government regulations. For instance, specifications for the purchase of machine tools set out by automotive companies have dedicated chapters dealing with energy consumption and the correct design of electrical motors, compressed air circuit, hydraulic pumps, etc., in order to optimize the energy-related costs and the environmental impact of the production. Under the label of “energy management”, the following points are usually found:

• No compressed-air motors should be used;
• It is not allowed to use compressed air for blowing functions, for cleaning or cooling;
• Drive systems for pumping liquids, such as hydraulic pumps shall have the option to control the input power according to the working requirements;
• Pumps shall fulfill the criteria according to the EC regulation no. 641/2009 [1];
• The power rating of the electric motors is to be adjusted to the mechanical power requirement of the machine. If a bigger motor has to be selected because of a performance grading, oversizing cannot overcome 30%;
• The characteristics and design of the motors must be adjusted to the working conditions. The motors must be designed for an on-period covering the entire mission time. The performance shall be measured so that the motor is used for up to maximum 85% of its performance range;
• The supplier shall indicate and offer potential optimization strategies for energy saving and recovery.

Machine tool energy consumption may be reduced in any of the four areas of its life cycle: (i) manufacturing (design and production of the parts), (ii) transportation (design for assembly/disassembly to allow standard transport), (iii) use (energy used to produce parts), or (iv) end of life (recycled materials). The most important phases are (i) and (iii): design-level changes are able to provide the greatest flexibility and therefore potentially offer the best opportunities for energy savings. The modern approach to the metal cutting operations such as the use of Minimal Quantity Lubrication (MQL) or the dry cutting [2,3,4,5,6,7,8,9,10,11,12] are able to dramatically cut consumption by nearly eliminating the impact of cutting fluids. Just for reference, it is possible to compare the need for a Ø = 12 mm standard drill in the presence of emulsion at p = 30 bar coolant pressure and for a MQL drill: 900 L/h versus 15 mL/h. Furthermore, the presence of the emulsion needs a dedicated system for the filtration of the fluid from the chips and of volumetric (high consumption) pumps to supply the high-pressure internal coolant. A breakdown of the consumption, split between the different power units in a machining center, is shown in Figure 1.

Based on this scenario, a new line of drilling/milling machines has been conceived in order to fulfill the aforementioned requirements. Particularly, the main topics of the new solution can be summarized as follows:

• High dynamic performances: the idea is to build the main structural parts from lightweight materials, in order to maximize the ratio between the “chip to chip time” and the servo-motor consumption. An accurate design of the components must be carried out, in order to warrant adequate stiffness of the structure, which in turn leads to dimensional accuracy of the workpiece;
• Accurate selection of the CNC motors for the movements of the axis (as a rule of thumb, a maximum motor oversize of 30% is allowed in modern design);
• Elimination of the high-consumption hydraulic system.

A new family of transfer machine tools has been designed by Giuliani, based on the guidelines mentioned above. A high performance torque motor is mounted on each transfer machine: it makes it possible to reach high values of torque with limited energy consumption. Every component involved in the motion of the transfer is designed to be as light as possible, according to the required stiffness, to preserve the required tolerances on the finished parts. Each transfer machine consists of a number of machining stations being equipped with a three-axis reconfigurable tooling unit. The three-axis unit geometry has been recently redesigned, in order to improve its performance: this optimization is based on the reduction of the carriage weight, achieved using aluminum alloys, rather than cast iron for these parts, while keeping the stiffness of the parts unchanged. The MQL machining approach has been followed as well, to achieve both energy and coolant saving.

Leveraging the concepts of green design and manufacture, as well as sustainable development thinking, the paper highlights the advantages derived from their application in this specific field: Two versions of the machines are examined. The first one, with nine divisions, which can be considered as a prototype: this machine has been studied in order to set up the numerical predictive model, then validated by experimental tests. The second one, equipped with a bigger rotary table with 15 divisions, has been entirely designed with the aid of the previously developed numerical model. To the best of the authors’ knowledge, limited to the case of transfer machine tools, no works based on the same approach are currently available in the literature.

2. Setup of the FE Models for the Transfer Machine with Nine Divisions

2.1. Experimental Determination of the Operating Loads

The three-axis unit has been designed, so that it is able to efficiently withstand a spindle thrust force in the order of F = 1 kN. This reference value has been chosen, following a preliminary experimental campaign, aimed at the estimation of the maximum thrust forces during the most frequent as well as the most demanding machining operations on the workpiece. In particular, a highly critical task, in terms of the load acting on the transfer, is drilling a hole under an MQL strategy. The outcome of the experiment was that 1 kN could be regarded as a proper threshold, considering for instance the drilling of a 7-mm hole on a round bar made of 16MnCrS5 steel or of a 12-mm hole on a CuZn39Pb3 brass component. In all the studied cases, which can be considered within the conventional applications of the transfer machine, the most recommended values of feed rate have been selected, also based on [13]. The estimated reference force F is going to be assumed in the following numerical analyses, in order to calculate the displacements of the transfer machine under load application.

2.2. Experimental Characterization of the Stiffness of the Reference Transfer

The transfers involved in the investigation consist of two tables (Figure 2), whose outer diameter is D_out = 1680 mm. The lower one spins around the y-axis, actuated by the torque motor; whereas the upper one is fixed to the frame and supports the three-axis units. In the following, they will be referred to as the “rotating table” and “fixed table,” Respectively. Supports are bolted under the rotating table in a number equal to the workstations. Each support carries a pneumatic vise that enables to safely grip the workpiece. The mechanical group described above is fixed to the ground at the base of the column.

Some experimental measurements have been carried out, in order to evaluate the vertical displacements of the supports of the Transfer Machine with nine divisions, when a vertical load is applied on a support along y-axis: the measured displacements would then be useful for the validation of the numerical model. Three dial gauges with a resolution of 0.01 mm have been placed at the positions shown in Figure 3.

Then, a mass m = 50 kg has been applied on the support object of investigation. The position of each dial gauge and the position of the mass are shown in Figure 4. The experimental data are shown in

Table 1. Dial gauge readings.

Position	Δy (mm)
1	−0.06
2	−0.02
3	−0.04

.

2.3. Tuning of the Stiffness Parameter of the FE Model

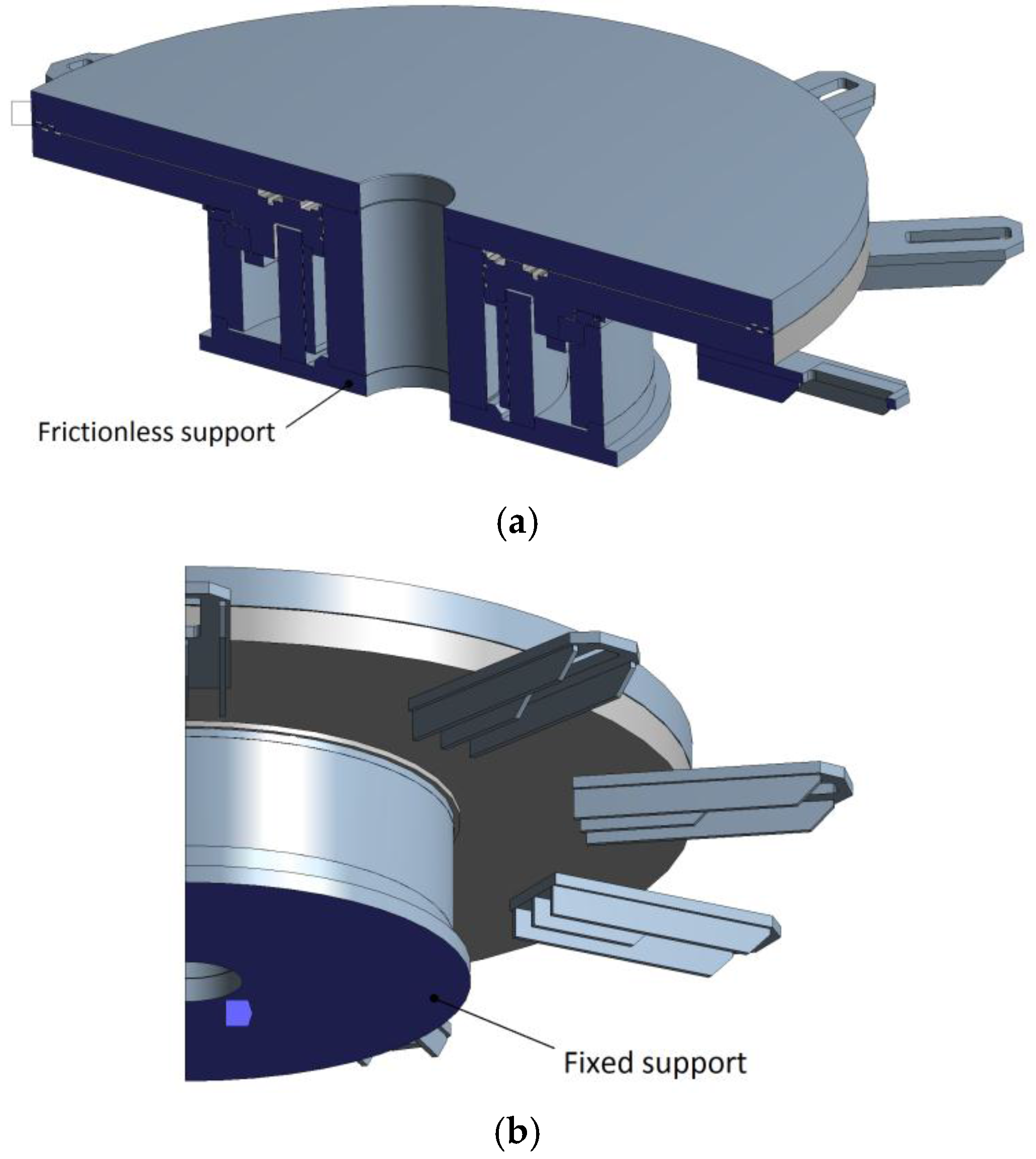
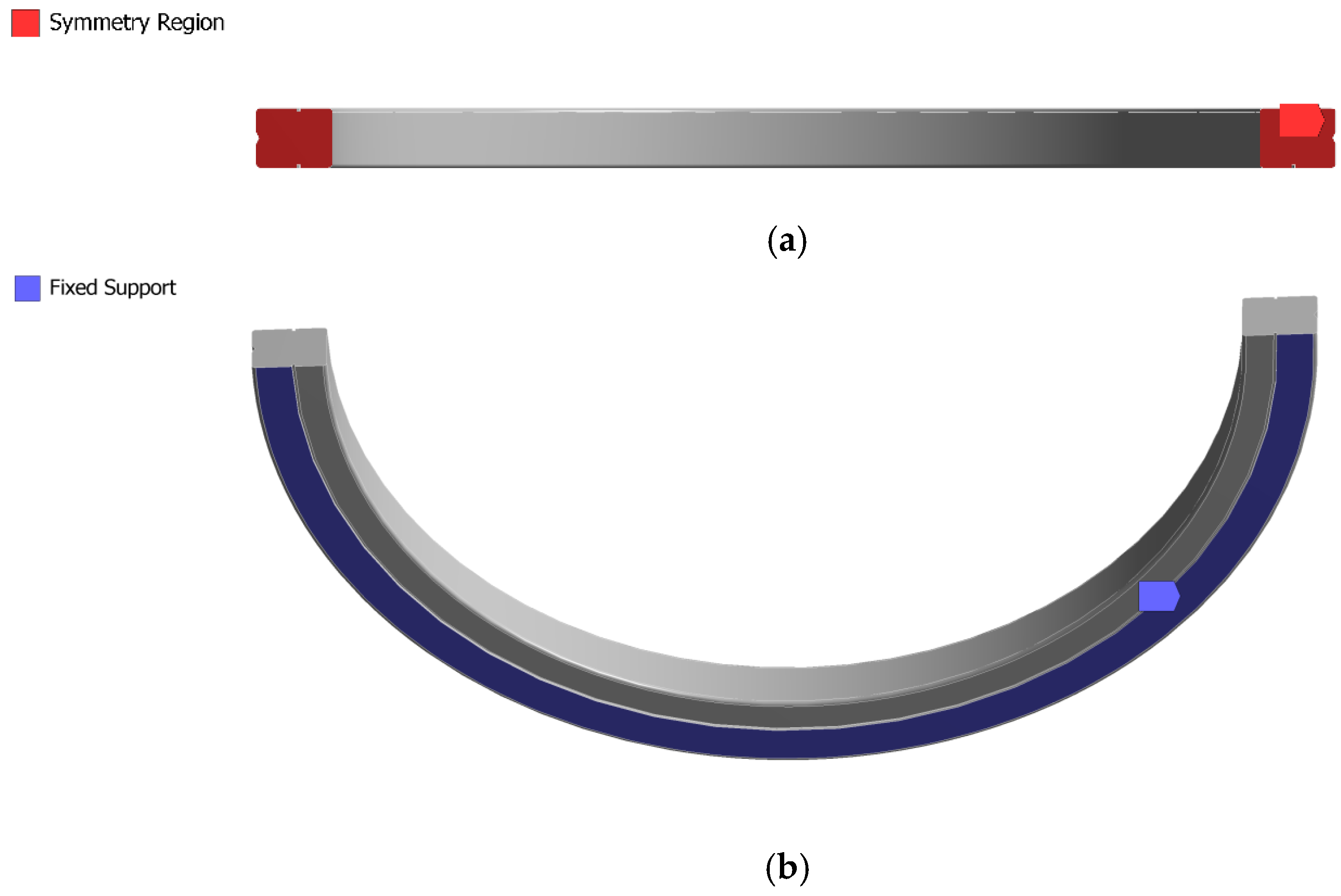
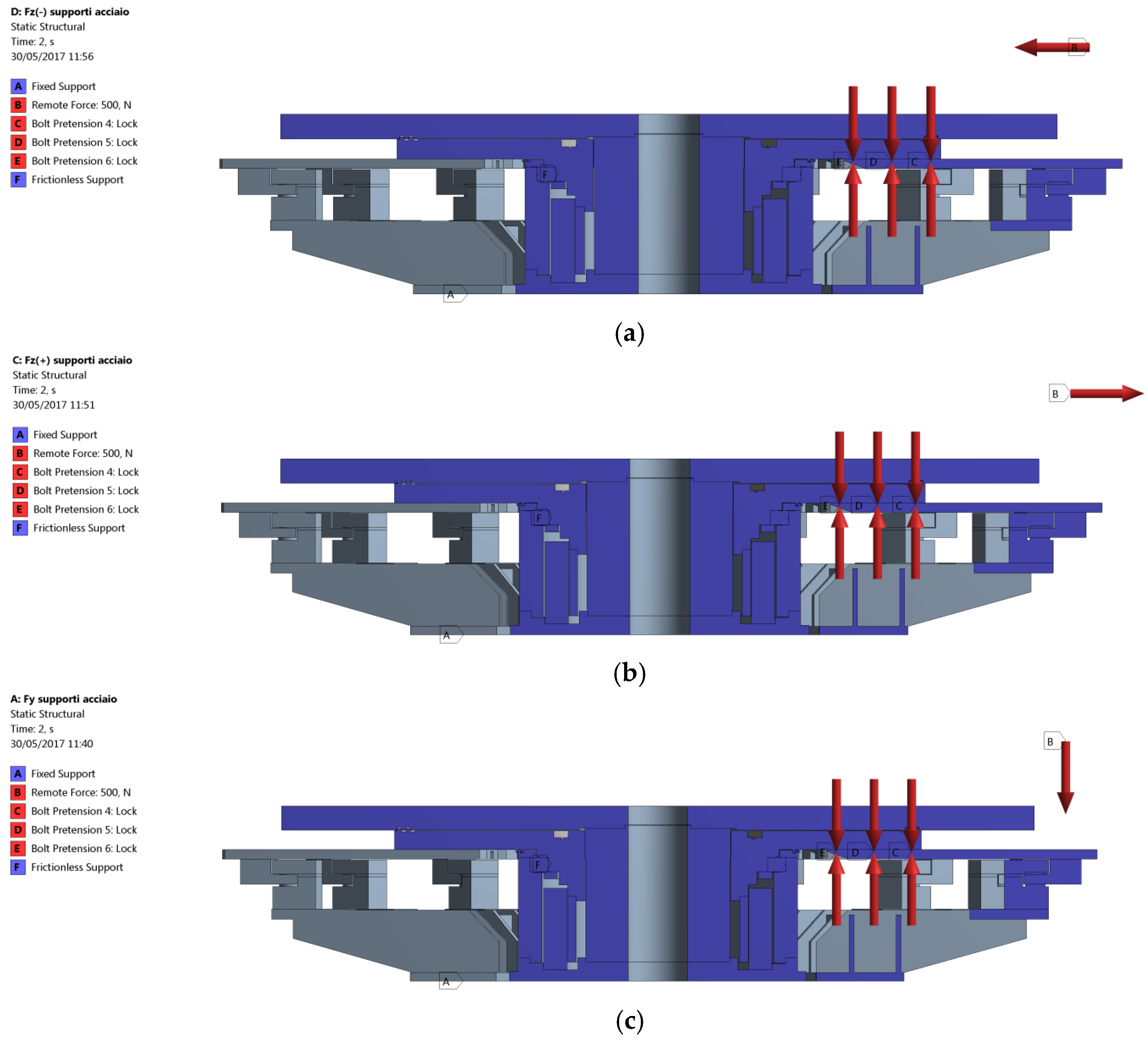
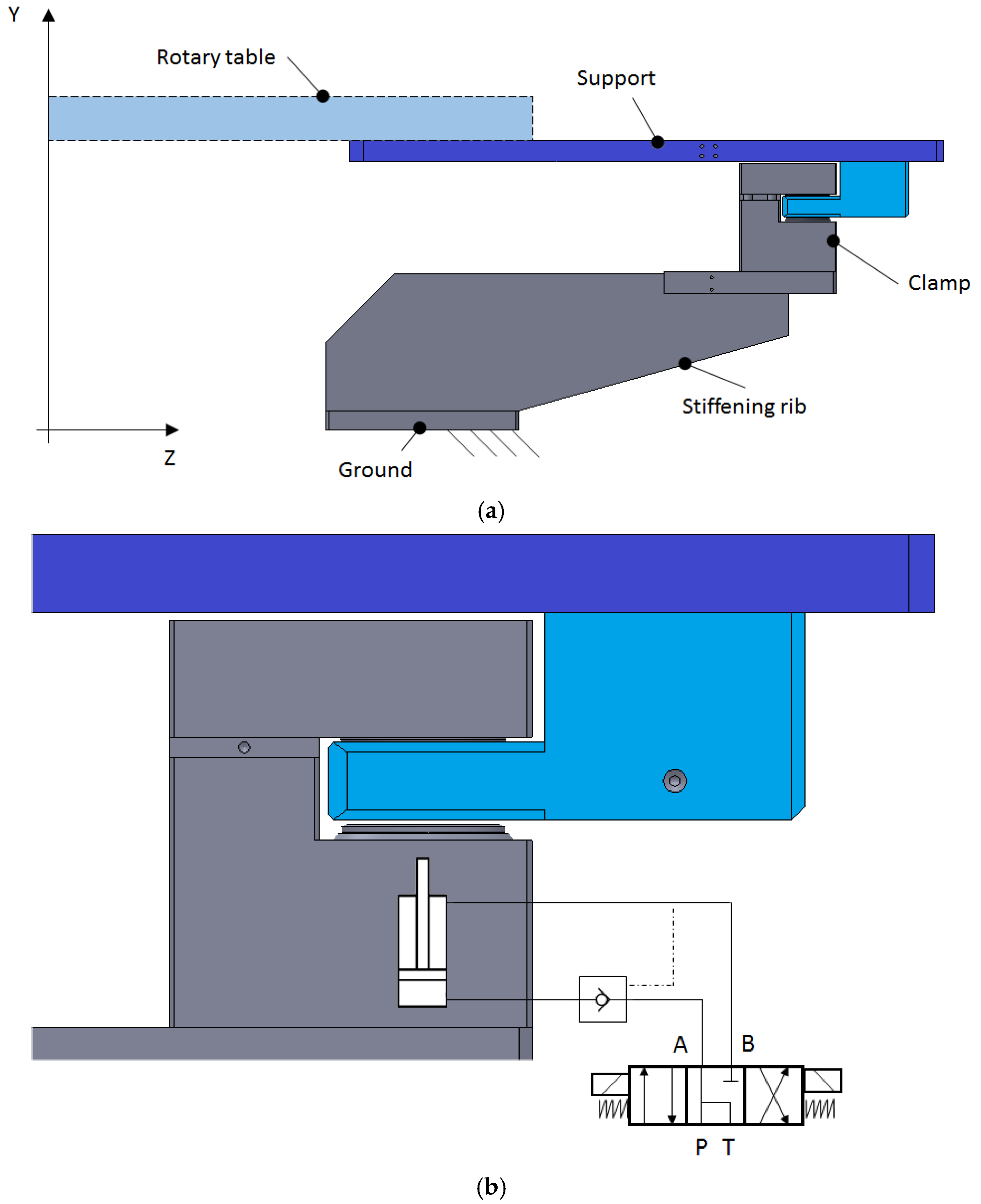
At first, the CAD geometry of the Transfer Machine with nine divisions has been simplified, in order to reduce the computational effort without significantly affecting the accuracy of the results: it must be remarked that the accurate evaluation of the stresses at notches or joints is beyond the scope of the present analysis. In fact, previous investigations carried out on similar machines showed that no significant stresses are generated on the key components of the frame during operation. Hence, the present analysis focuses just on the stiffness performance of the structure. Due to geometrical and loading symmetry conditions, a half of the geometry has been considered. A frictionless support has been applied on the symmetry plane, as shown in Figure 5a, in order to enforce the symmetry condition. Moreover, the base of the column has been constrained by means of a fixed support (Figure 5b): in the actual application, such a surface is constrained to the lower part of the frame, which can be considered perfectly rigid.

The materials assigned to the parts are AlMg0.7Si (E = 69.5 GPa, ν = 0.33) for the rotating table and a structural steel (E = 200 GPa, ν = 0.30) for any other part. The geometry has been meshed with SOLID187 tetrahedral and hexahedral elements, for a total node count n ≈ 95,000. All the contacts in the model are set as bonded, assuming a pure penalty formulation and a normal stiffness factor controlled by the software (FKN = 1, [14,15]). The applied force F_y is calculated according to Equation (1), where term 2 in the denominator is due to the symmetry of the model.

$$F_y=\frac{9.81\times 50}{2}=245.25\mathrm{N}$$

(1)

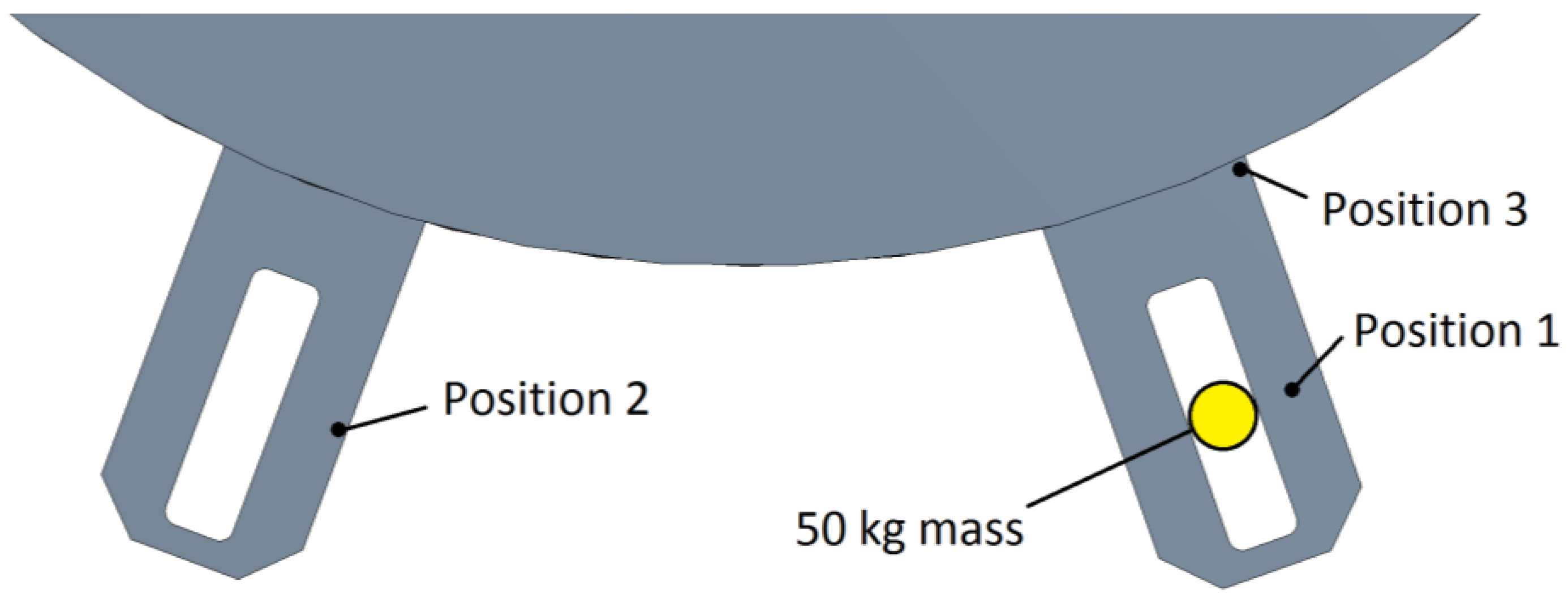
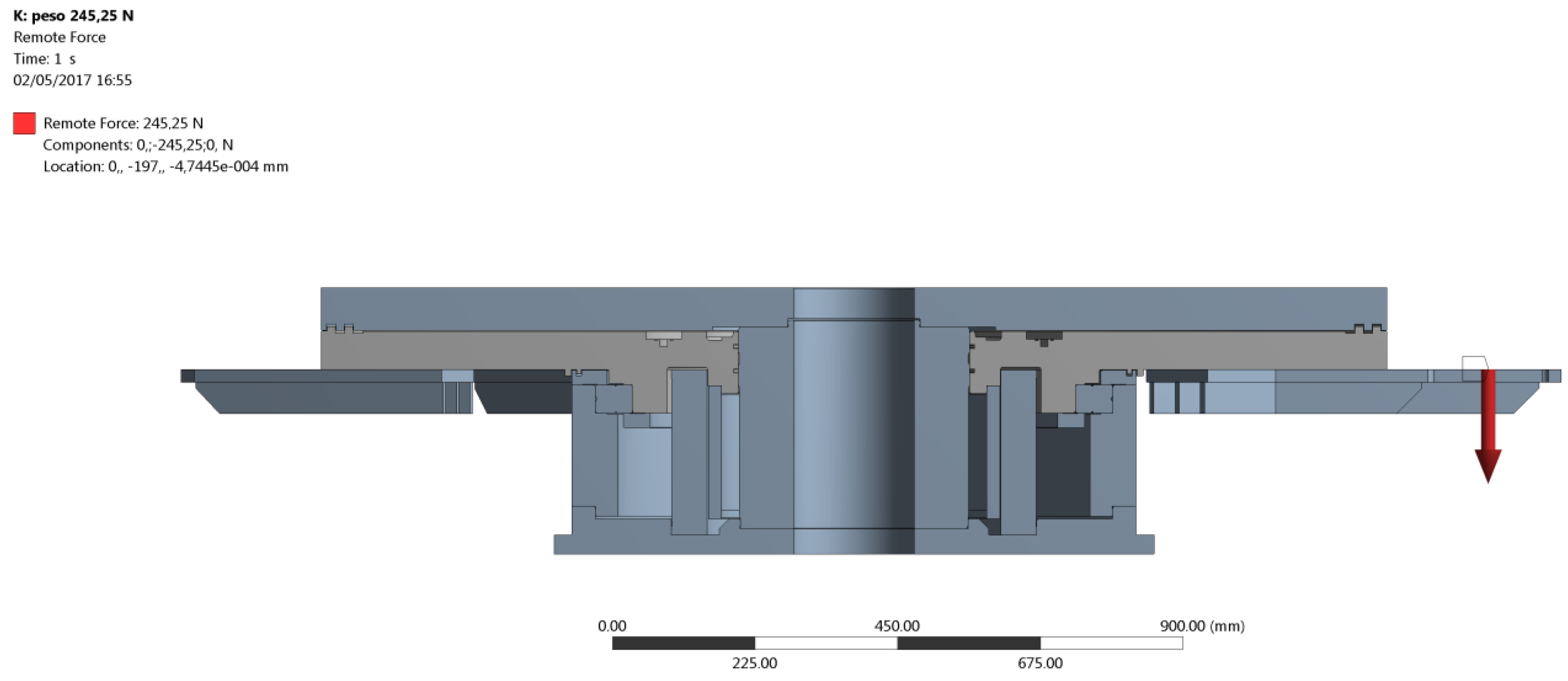
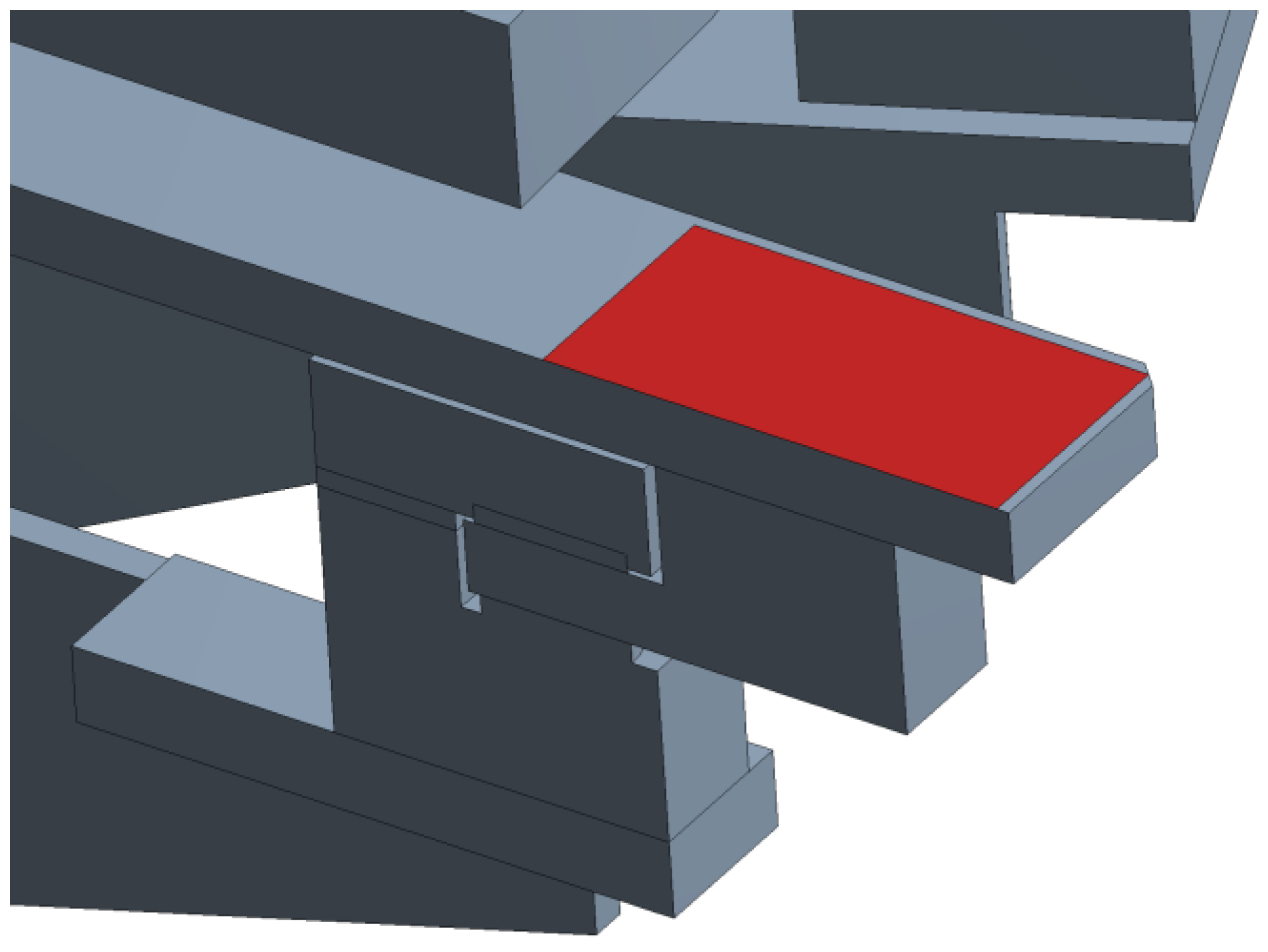
F_y acts on the upper surface of the reference support, as shown in Figure 6.

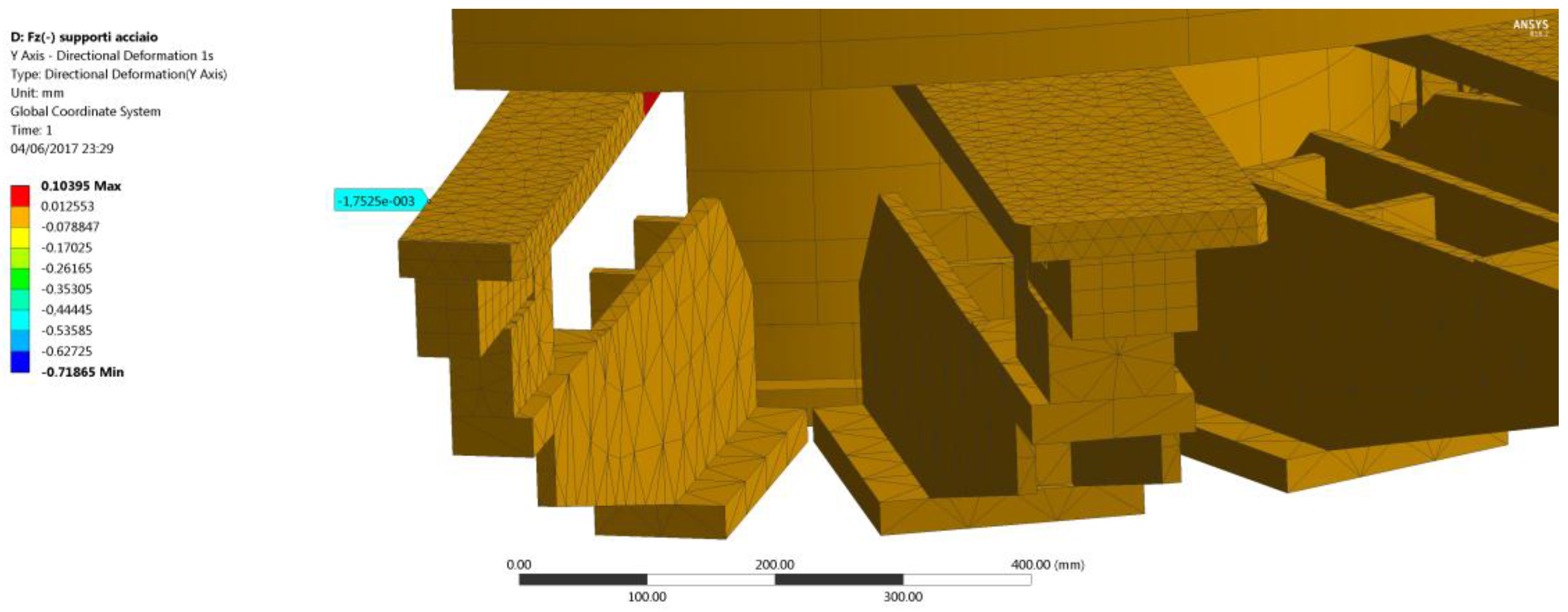
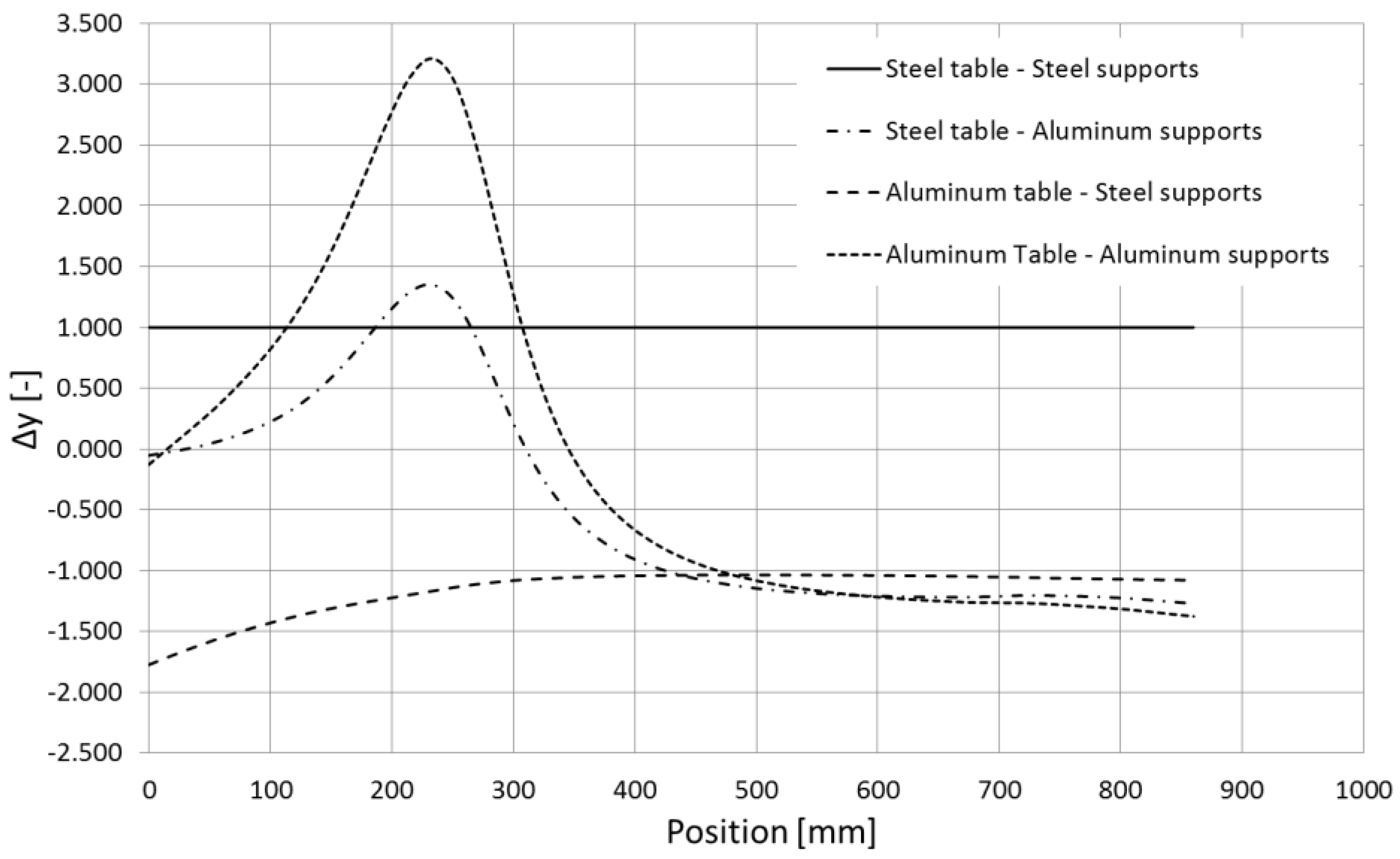
The displacements yielded by the numerical simulation and measured at the same positions of the dial gauges, are shown in Figure 7 and summarized in

Table 2. FEM displacements and percentage errors with respect to the experimental data.

Position	ΔyFEM (mm)	Δyexp (mm)	Error (-)
1	−0.051	−0.060	−15%
2	−0.016	−0.020	−20%
3	−0.031	−0.040	−22.5%

, along with the percentage error with respect to the experimental ones.

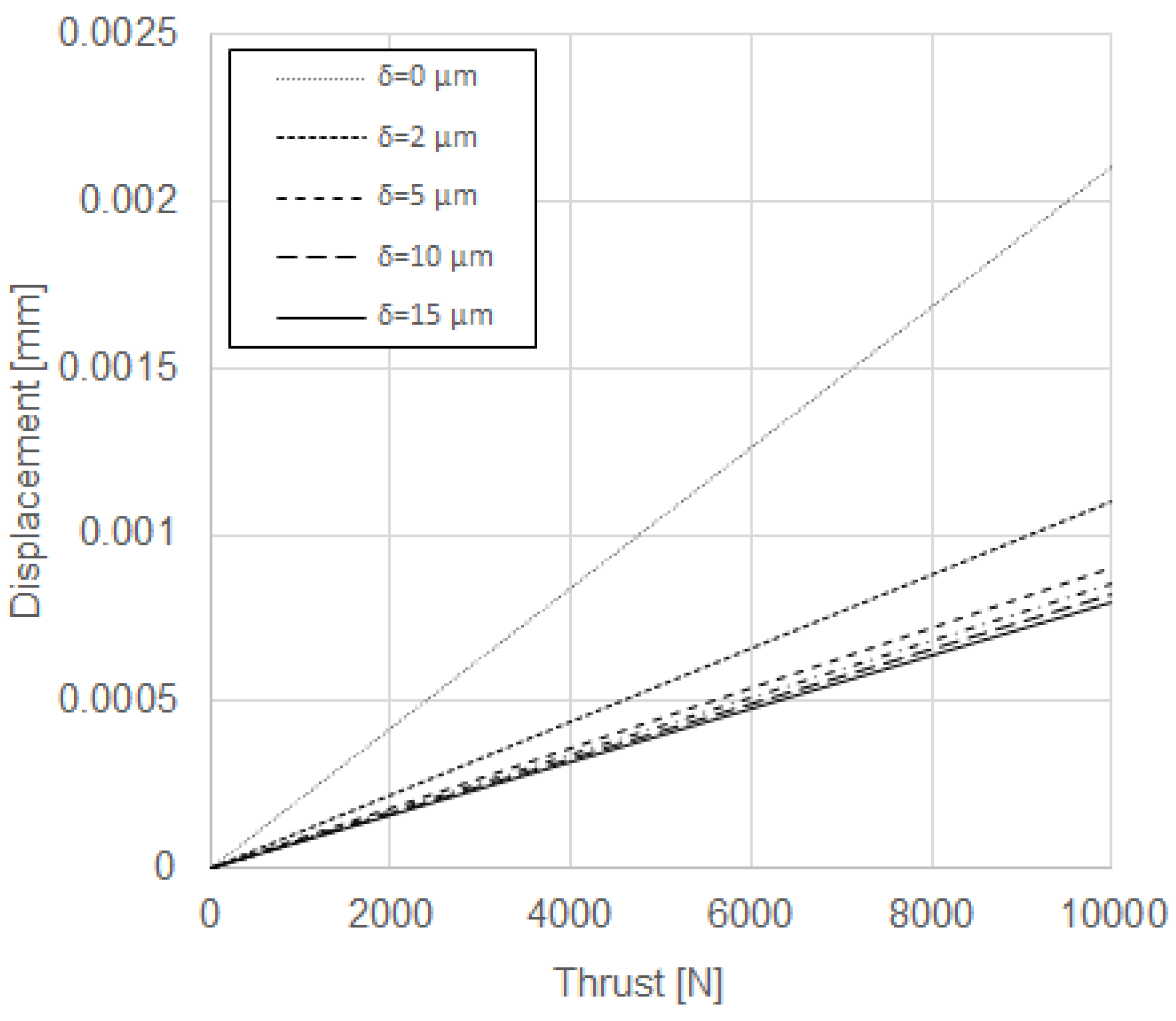
The results reveal that the numerical model, defined according to the basic settings reported above, is stiffer than the actual machine: hence, it has been decided to improve the model, by tuning the key parameters that affect its stiffness. The rotating table is supported by a double-row angular contact roller bearing. In the previous analysis, the bearing has been modeled as a unique ring made of steel: this approximation leads to overestimating its stiffness. Therefore, it has been decided to model the bearing by means of a single ring made of an elastic, isotropic material, whose Young’s modulus has to be determined upfront by the following steps. First, (i) a FE analysis of the ring alone is prepared, by assuming its elastic modulus as a parameter and the ring is constrained, replicating the actual application and loaded by an axial thrust; (ii) the displacement of the force application surface is recorded; (iii) the experimental displacement provided by the bearing manufacturer is read-in. 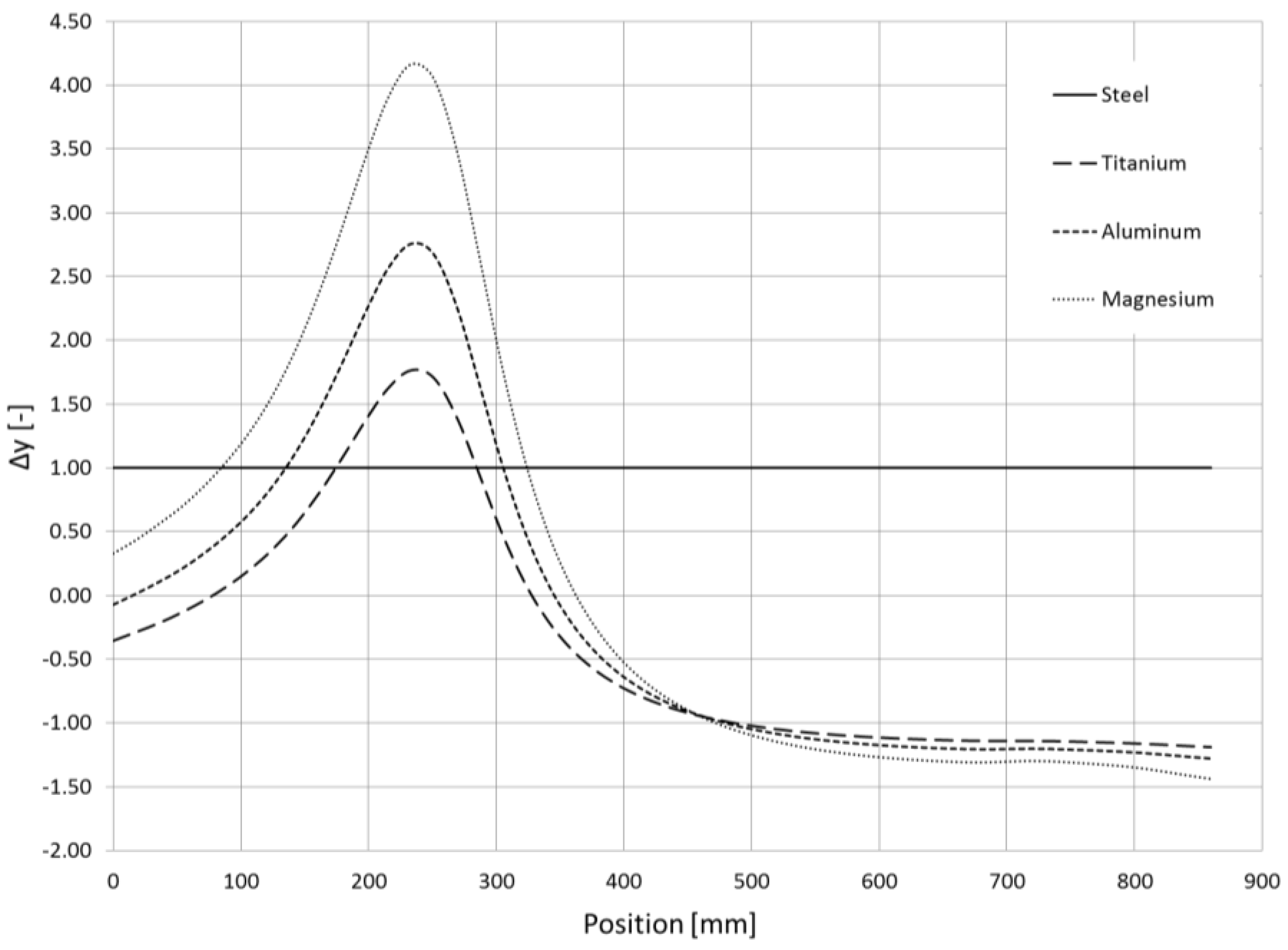The manufacturer usually provides plots like that shown in Figure 8, where several curves express the axial displacement of the bearing as a function of the applied thrust load. Each curve is relevant to a value of the assembly preload δ of the bearing: for the present application, δ = 15 μm; (iv) the Young’s modulus of the ring is adjusted until the FE calculated displacement matches the experimental axial displacement for given axial thrust.

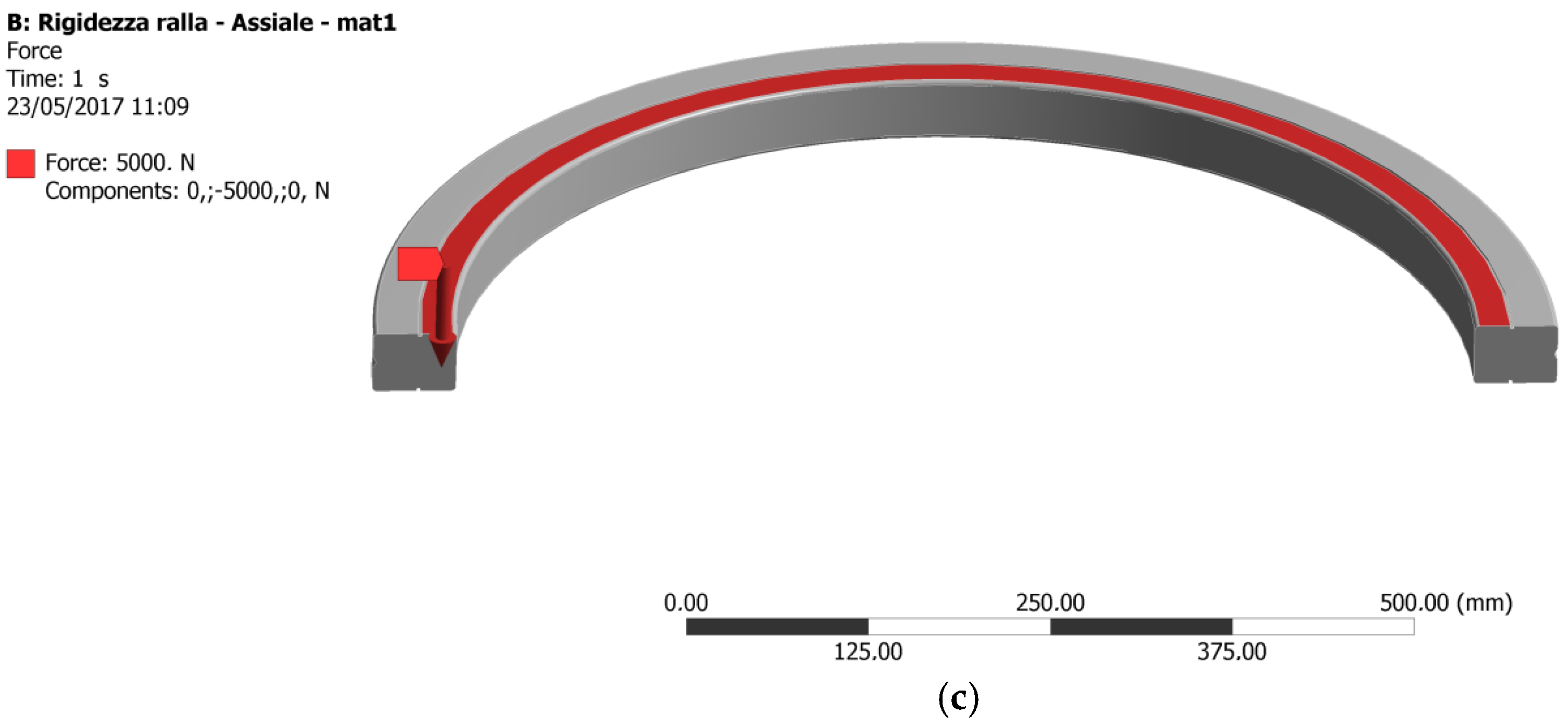
The static structural analysis has been carried out on a half-ring geometry, as shown in Figure 9a: the ring has been constrained with a fixed support on its lower external surface Figure 9b; the upper inner surface of the ring has been loaded with a 10 kN load (Figure 9c).

As explained above, a set of FE analyses have been run varying the input parameter (equivalent Young’s modulus of the ring) until the displacement of the loaded surface equaled 8.5 × 10⁻⁴ mm, which is the value reported in Figure 8 for a thrust load of 10 kN and a preload of 15 μm. Such a displacement value was reached by setting an equivalent Young’s modulus of E_ring = 39 GPa. 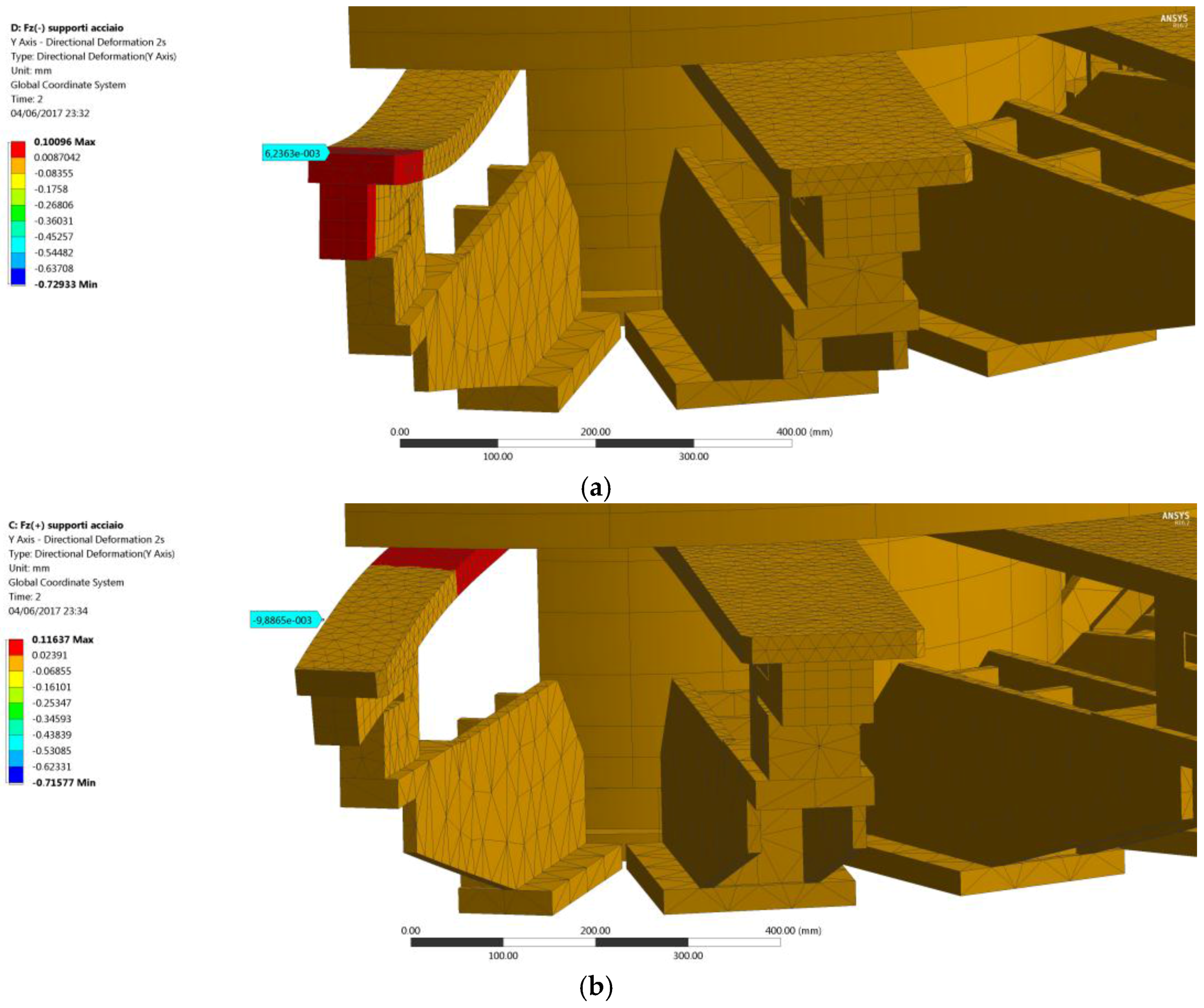Then, a finite element analysis (FEA) of the whole Transfer Machine with nine divisions, including the ring with the above specified E_ring, was run. The displacements at the reference points (Figure 10) are substantially unvaried with respect to the previous simulation, with differences smaller than 1 μm in terms of displacement. Therefore, another modification had to be made to the numerical model in order to make it more consistent to the actual machine stiffness.

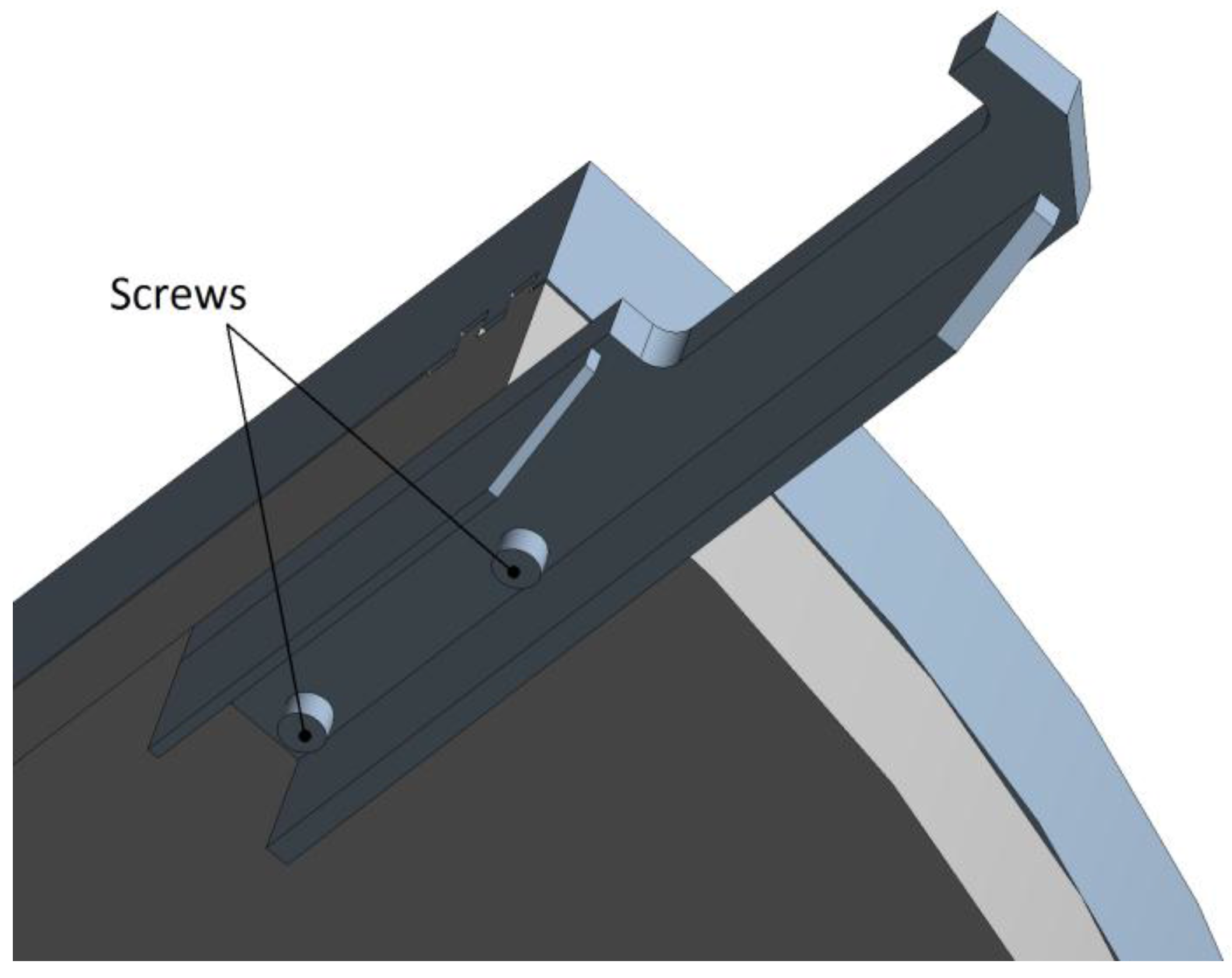
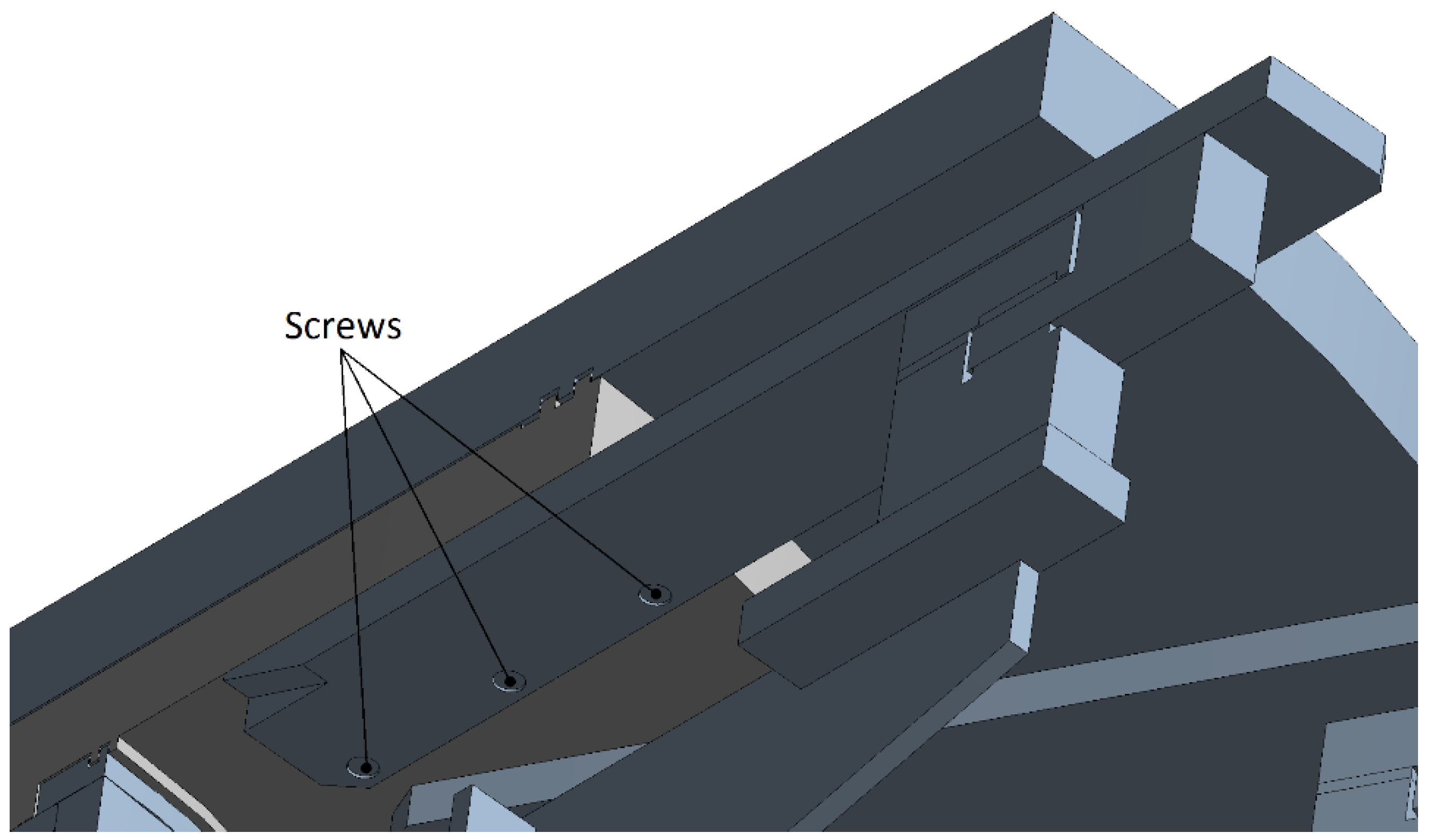
Since a correct estimate of the stiffness of a complex assembly is often related to an accurate modeling of its mechanical joints [16,17,18], the contact conditions between the support and the rotating table have been modified in order to achieve a more accurate FE model. Hence, the bonded contact between the rotary table and the support has been replaced by a set of four M12 12.9 class screws (Figure 11): this bolt pattern replicates that being actually used on the Transfer Machine with nine divisions. The screws have been modeled as solids, and the axial preload has been imposed by the bolt preload tool available in the Ansys Workbench environment.

The contact at the interface between the support and the rotating table, as well as the one between the underhead of the screws and the support, has been set as frictional, with a friction coefficient μ = 0.2 [19]. The contact formulation has been set as pure penalty with a normal stiffness factor controlled by the software (FKN = 1). The terminal portion of the shank and the “threaded” hole on the rotating table have been joined by means of a bonded contact. The analysis has been divided into two steps: at the first step, a preload of F_i = 70 kN has been assigned to each screw: this preload is calculated, based on a tightening torque T = 106 Nm and oiled surfaces, μ_m = 0.10 [20,21,22,23], as for the company’s assembly specification. 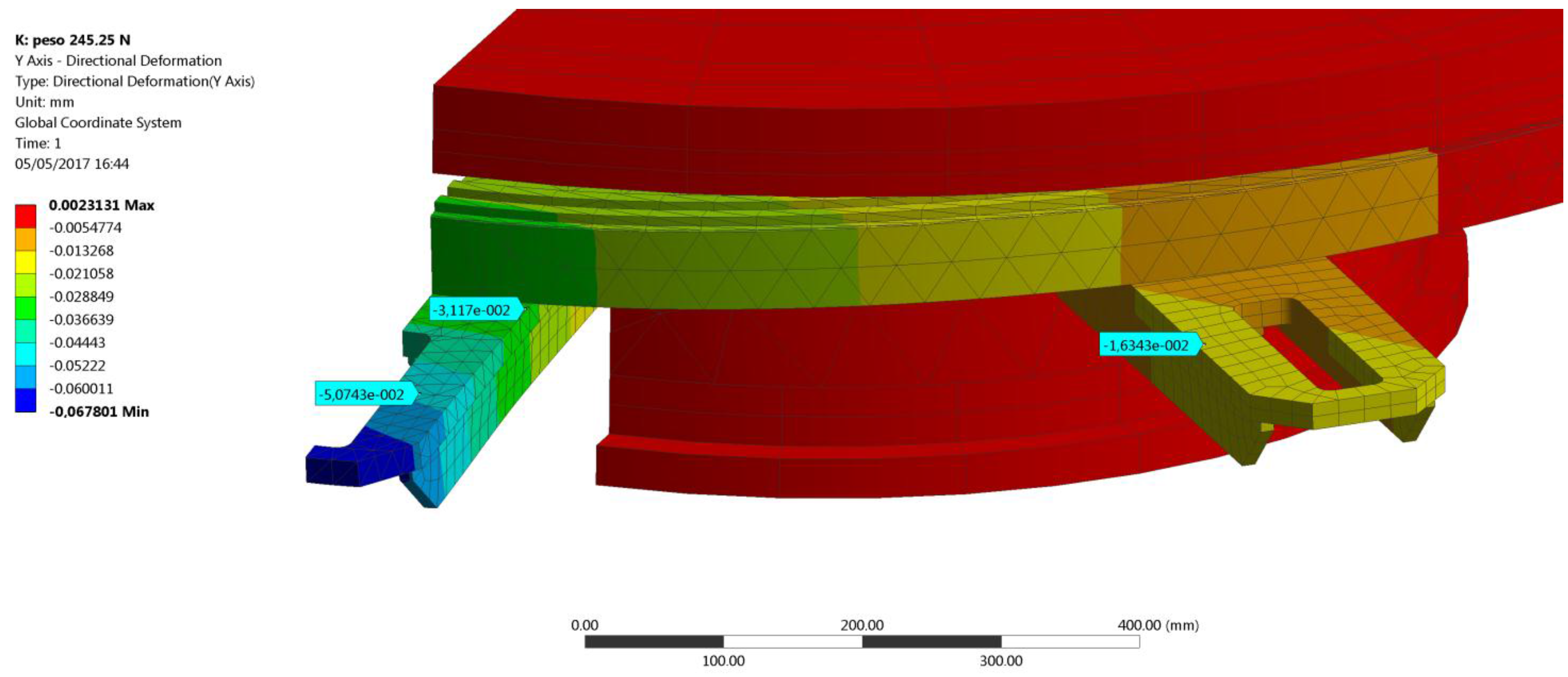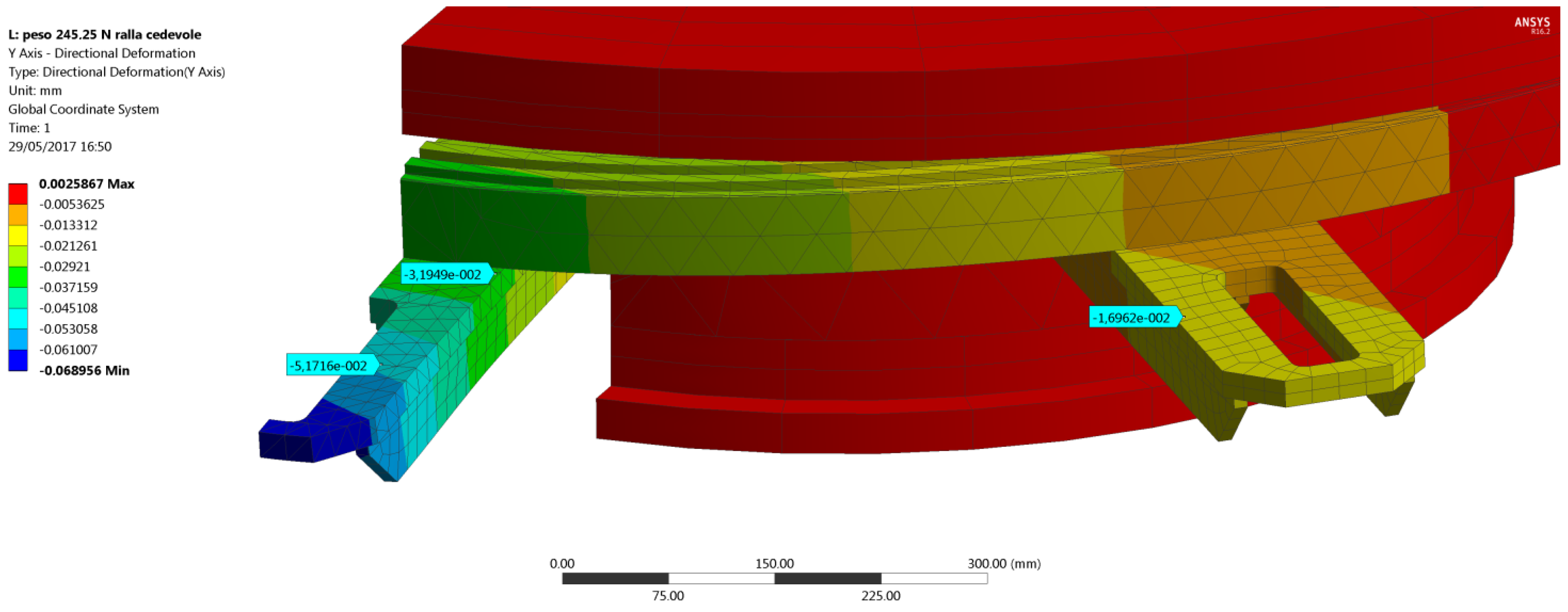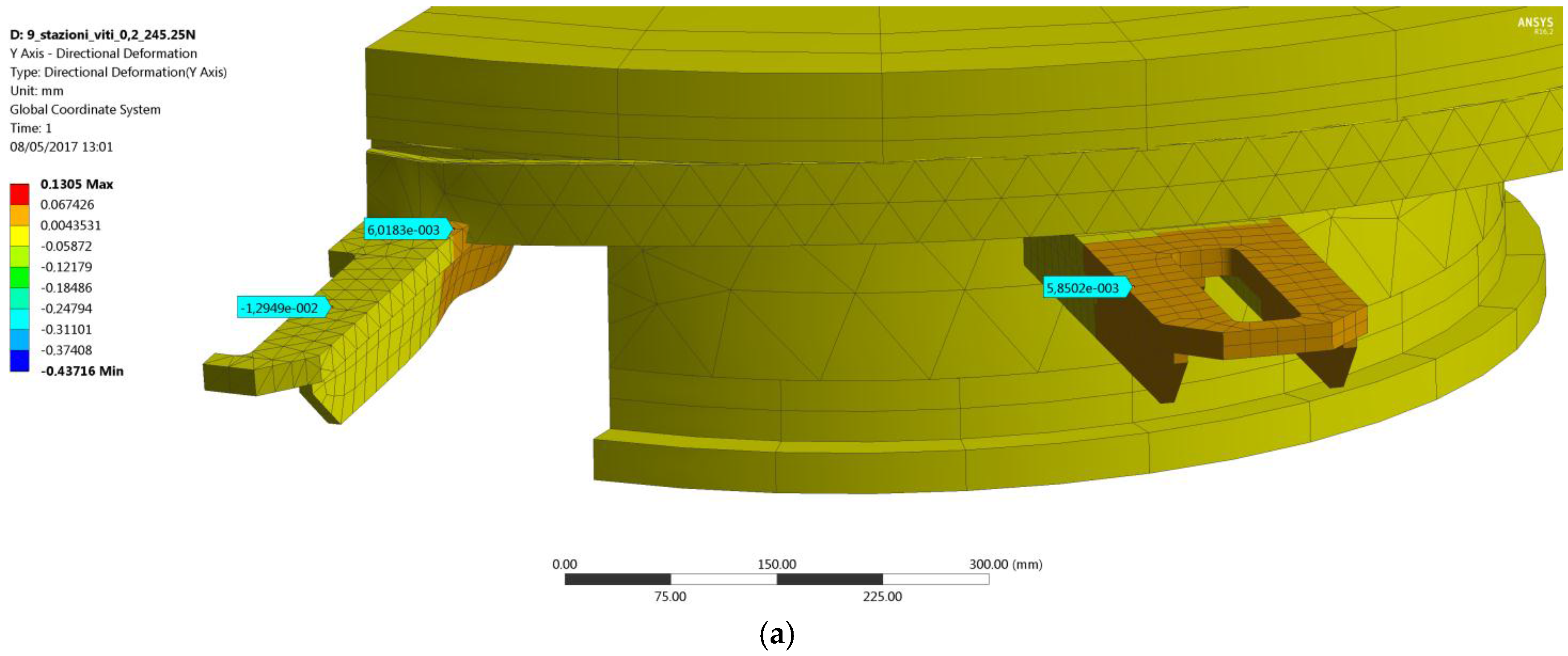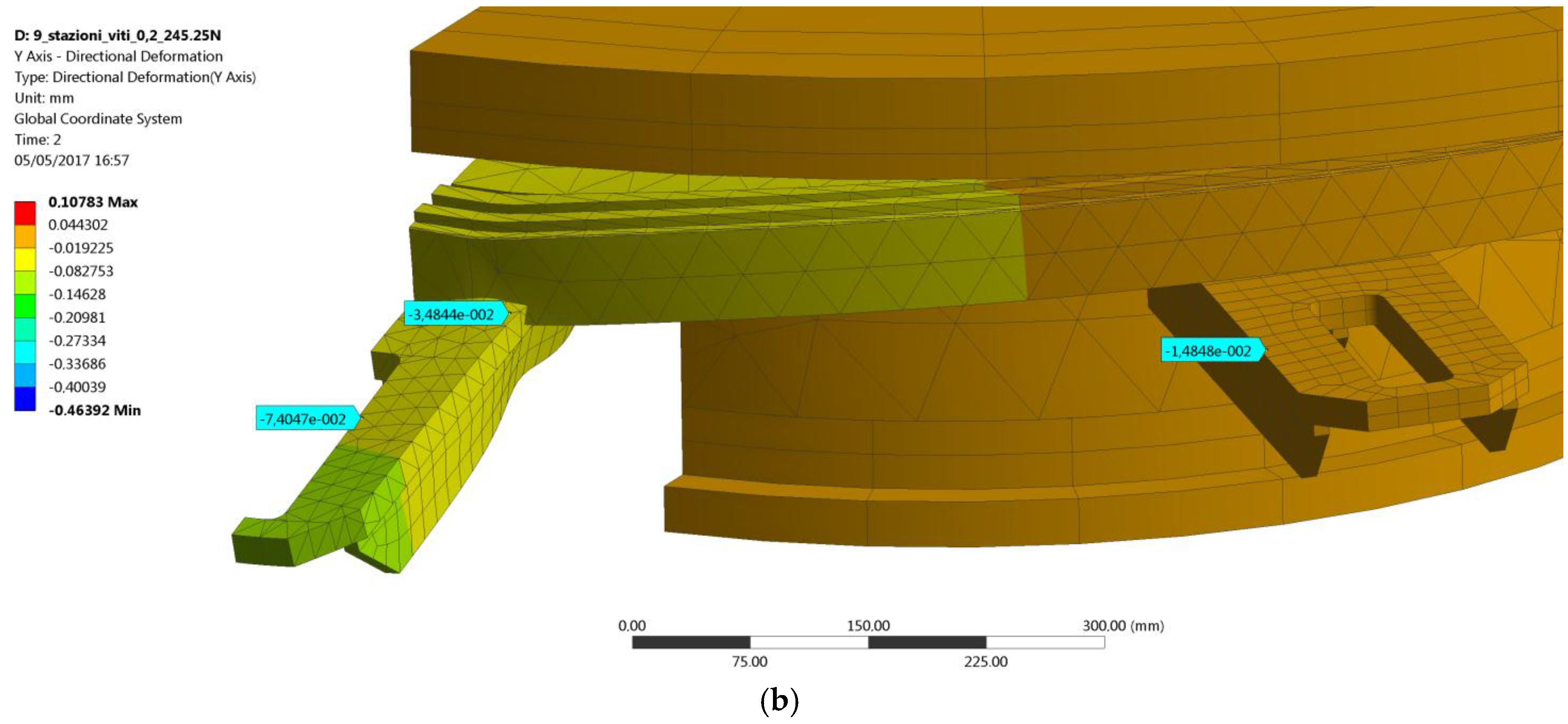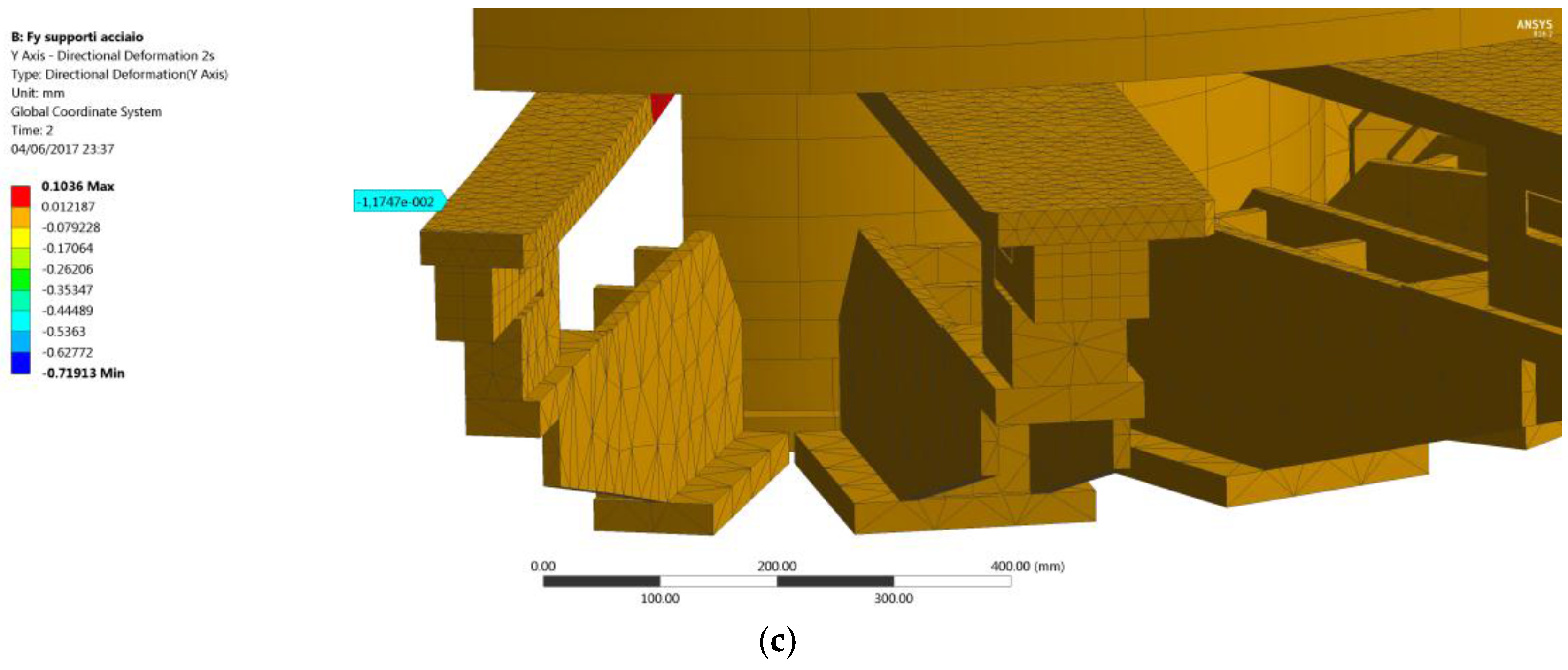The displacements retrieved at this step are shown in Figure 12a. A vertical force F = 245.25 N has been added at the second step of the analysis with the bolt preload still acting (lock option set as active in the Ansys WB bolt preload tool). The difference between the displacements recorded at the end of the second step (Figure 12b) and at the end of the first step gives the displacements due to the effect of the external load only, as explained by Equation (2):

$$\Delta y_{FEM}=\Delta y_{step2}-\Delta y_{step1}.$$

(2)

Looking at the data in

Table 3. FE displacements of the modified model at the end of the two steps, Δy_FEM and errors with respect to the experimental data.

Position	Δystep1 (mm)	Δystep2 (mm)	ΔyFEM (mm)	Δyexp (mm)	Error (-)
1	−0.013	−0.074	−0.061	−0.060	+1.7%
2	+0.006	−0.015	−0.021	−0.020	+5%
3	+0.006	−0.035	−0.041	−0.040	+2.5%

, relevant to the new FE model, the maximum absolute value of the percentage error is 5% and it is normalized with respect to the displacement at position 2, which is not located on the loaded support but on the adjacent one. Conversely, the errors recorded at the loaded support are of a small entity and stay lower than 3%. In light of the results above, the FE model can now be deemed as validated.

2.4. Modal Analysis

Based on the settings reported in the previous sections, considering the bolts as bonded contacts with a reduced stiffness, a modal analysis has been carried out in order to predict the first five modes of vibration of the assembly. The natural frequencies are reported in

Table 4. FE calculated natural frequencies of the Transfer Machine with nine divisions.

Mode #	f (Hz)
1	80.742
2	81.723
3	89.092
4	117.83
5	143.57

and the first two modes are shown in Figure 13a,b.

The natural frequencies and the associated modes reported above will be useful for a vibration assessment, which should take the following points into account: (i) the match between the deformation induced by the generic excitation force and one of the modes shown above; (ii) the match between the frequency of the excitation force and the frequency of the relevant mode. The source of excitation could either be due to the movement of the carriages or to the cutting operation itself. (iii) A further point is the energy associated to the source of excitation: e.g., it must be carefully assessed if the energy associated to the cutting operation is high enough to bring the structure into resonation, provided that there is compatibility between the modes and frequencies. All these checks have been carried out in a separate study [24].

3. Structural Design of the Transfer Machine with 15 Divisions

3.1. FEA and Structural Optimization

The Transfer Machine with 15 divisions is represented in Figure 14: it has six more divisions, thus, if compared to the same machine with nine divisions, a greater diameter (D_out = 2940 mm) and one more component (stiffening rib) under the support.

The analysis takes three different load scenarios into account: two radial drilling operations along x-axis, positively or negatively oriented, and a vertical (y-axis) downwards drilling operation. The purpose of the study is to determine the displacement of the component being clamped under the machining conditions. The same FEM settings validated on the Transfer Machine with nine divisions have been adopted for the analysis of the same machine with 15 divisions, where the same bearing and joining techniques are utilized (see also below). After geometry simplification, the model has been treated again as a symmetrical structure. The materials assigned to the transfer are AlMg0.7Si (E = 69.5 GPa, ν = 0.33) for the rotating table and a generic structural steel (E = 200 GPa, ν = 0.30) for all other components. The geometry has been meshed with SOLID187 tetrahedral and hexahedral elements, for a total node count n ≈ 160,000. Every contact between the parts has been set as bonded, except the one between the reference support and the rotating table, which is obtained by means of a set of screws. In particular, the Transfer Machine with 15 divisions has a screw pattern made of six M12 12.9 classes, instead of the four-screw pattern utilized in the same machine with nine divisions, as shown in Figure 15. The modeling strategy is the same adopted for the machine with nine divisions.

Three types of machining scenarios have been studied, so three different simulations had to be performed. Each load has been simulated by a remote force F₁ = 500 N acting on the upper surface of a support. Symmetry has been enforced as described above. In order to better approximate the actual area of force application (roughly corresponding to the contact area between the vise and the support) a portion of surface has been isolated by a division line (red area in Figure 16) and the machining force applied thereof. The point of application of the force is the center of gravity of the clamped lock, as shown in Figure 17.

Figure 18 shows the displacements along the y-axis due to the sole bolt preload, whereas Figure 19 displays the values of y-axis displacement for the three load scenarios. The flagged spot always represents the projection of the center of gravity of the clamped lock on the support: the displacements measured at this point in the three different load cases are summarized in

Table 5. FE displacements under different machining conditions for the Transfer Machine with 15 divisions.

Machining Condition	Δystep1 (mm)	Δystep2 (mm)	ΔyFEM (mm)	Δyexp (mm)	Error (-)
Fz (−)	−0.002	+0.006	+0.008	-	-
Fz (+)	−0.002	−0.010	−0.008	-	-
Fy (−)	−0.002	−0.012	−0.010	−0.01	0%

, along with the calculation of the displacements caused by the sole external loads (the displacement due to the bolt preload has been ruled out by applying Equation (2)).

The greatest displacement on the reference point is caused by the force Fy (−) (Δy = 0.01 mm), while both Fz (−) and Fz (+) cause a displacement of 0.008 mm. The result reported in Table 5, for the Fy (−) load case only, has been compared with the experimental outcome, retrieved by means of the test setup shown in Figure 20. The FEA outcome perfectly matches the experimental result. It is noteworthy that the vertical displacement of the Transfer Machine with 15 divisions is less than 17% of that for the same machine with nine divisions, under the same loading condition of vertical downwards drilling, even though the first has a much larger (and thus more flexible) rotary table. Such an outcome has been achieved thanks to a dynamic stiffening system developed by the authors. In fact, the stiffening ribs do not spin around the y-axis together with the rotary table; they are instead fixed to the ground. The ribs and the supports at the outer diameter of the rotary table (Figure 21a: in blue shades the moving parts) are clamped together just for the machining time, by means of a hydraulic clamp whose operating principle is quite the same of a disc brake (Figure 21b). This simple device allows for keeping the rotary table comparatively light, as well as achieving enough bending stiffness when needed.

In order to assess the possibility of further weight savings on the moving parts, further FEA have been run by changing the material assigned to the supports: e.g., lightweight alloys: aluminum, titanium, and magnesium. The comparison between the different solutions has been made in the case of Fy (−).The vertical displacements have been sampled along the path illustrated in Figure 22. The results in terms of vertical displacement for different choices of the support material, normalized with respect to the steel support are shown in the plot of Figure 23, whereas Figure 24 shows the displacements obtained with different materials combinations of the support and of the rotary table, normalized with respect to the steel-steel combination.

As can be appreciated by looking at Figure 23, besides Ti-alloys, which would have been impractical due to cost and manufacturing reasons, both Al-alloy and Mg-alloy supports negatively affect the bending stiffness of the assembly, especially at the outer edge where machining operations take place: a steel support is therefore the best option. On the other hand, looking at Figure 24, it can be seen that a combination of Al-alloy table and steel support would not be much more compliant than the base case with both components made of steel. The displacement at the outer end would increase by just 10⁻³ mm, should the lighter construction be adopted.

Based on these premises, an aluminum alloy has been chosen for the construction of the rotary table, whereas the supports have been built of steel.

3.2. Modal Analysis

Based on the settings reported in the previous sections for the Transfer Machine with nine divisions, a modal analysis has been carried out in order to determine the first five modes of vibration of the same machine with 15 divisions. The natural frequencies are reported in

Table 6. FE calculated natural frequencies of the Transfer Machine with 15 divisions.

Mode #	f (Hz)
1	123.74
2	147.61
3	154.31
4	154.97
5	155.01

and the first two modes are shown in Figure 25a,b.

4. Discussion

In light of the results presented in the previous sections, some general guidelines for the structural design of a modern transfer machine tool can be drawn.

• Different FE modeling strategies lead to different predictions in terms of the overall stiffness of the assembly. The following considerations stem from the results illustrated at Section 2.3: (i) the accurate modeling of the bearing stiffness has little or no impact on the stiffness prediction provided by FEA. Therefore, this component can be even modeled as a single body with the elastic properties of steel without significantly affecting the accuracy of the results; (ii) the accurate modeling of the bolt pattern has conversely a significant effect on the stiffness of the FE model. As a rule of thumb, at preliminary analysis stage, or when the bolt preload tool cannot be used, a bonded contact with a pure penalty formulation and a normal stiffness factor set at FKN = 1.5 × 10⁻³ has been proven to provide results close to the case of bolt modeling. The FKN parameter has to be fine-tuned based on the actual application.
• Other rather complex components, such as roller monoguides, ballscrews and the like can be represented with a good accuracy in terms of stiffness, by replacing them with homogeneous, isotropic elastic single bodies, whose elastic modulus and Poisson’s ratio shall be tuned by means of preliminary FEA. However, it must be observed that the loading scheme adopted in the tuning FEA must be properly chosen in order to properly reproduce the actual load scenario in the machine service conditions.
• The bigger, 15-division transfer, needs some stiffness raisers, so as to match the performance of the same machine with nine divisions. For instance, a rib, which is fixed to the ground, helps increase the flexural stiffness of the rotary table–supports assembly. The rib stiffness kicks in just during the machining time, by means of a hydraulic clamp device developed by the authors. Such an arrangement allows for achieving a twofold task: (i) proper stiffness is warranted during machining; (ii) the moving parts are kept as light as possible, thus shrinking the chip-to-chip time. The advantage in terms of stiffness may be appreciated considering that, despite its larger size, the maximum displacement of the transfer machine with 15 divisions is approximately one-fourth of the displacement of the corresponding machine with nine divisions for given vertical load, measured at the same reference point.
• With regard to the 15-division transfer, some FEAs have been performed in order to work out the most favorable combination between the materials for the construction of the supports and of the rotary table. This combination turned out to be the one comprising an aluminum alloy table and steel supports. No significant loss in terms of flexural stiffness has been observed with respect to the base case with all steel components.
• Based on the outcomes of the modal analysis, should any loading condition lead to instability, this issue could be overcome and the system optimized by locally modifying the stiffness of the elements and/or the distribution of the masses.

5. Conclusions

An experimentally validated numerical model for transfer machine tools has been defined, which allows for forecasting the structural as well as the vibrational response of this kind of machine under typical operating loads. The models helped develop a bigger machine, evaluating different scenarios in terms of materials and design solutions. Through this approach, it has also been possible to optimize the structure in terms of flexural stiffness at a very early stage of the design. A proper choice of the materials and the introduction of an ad hoc designed stiffening solution made it possible to achieve even greater stiffness than with the smaller machine, thus ensuring the desired manufacturing tolerance of the finished parts. This choice will ultimately lead to higher speed and a more efficient machine whose performance is aligned with the values of green design.