Perception, Planning, Control, and Coordination for Autonomous Vehicles
Abstract
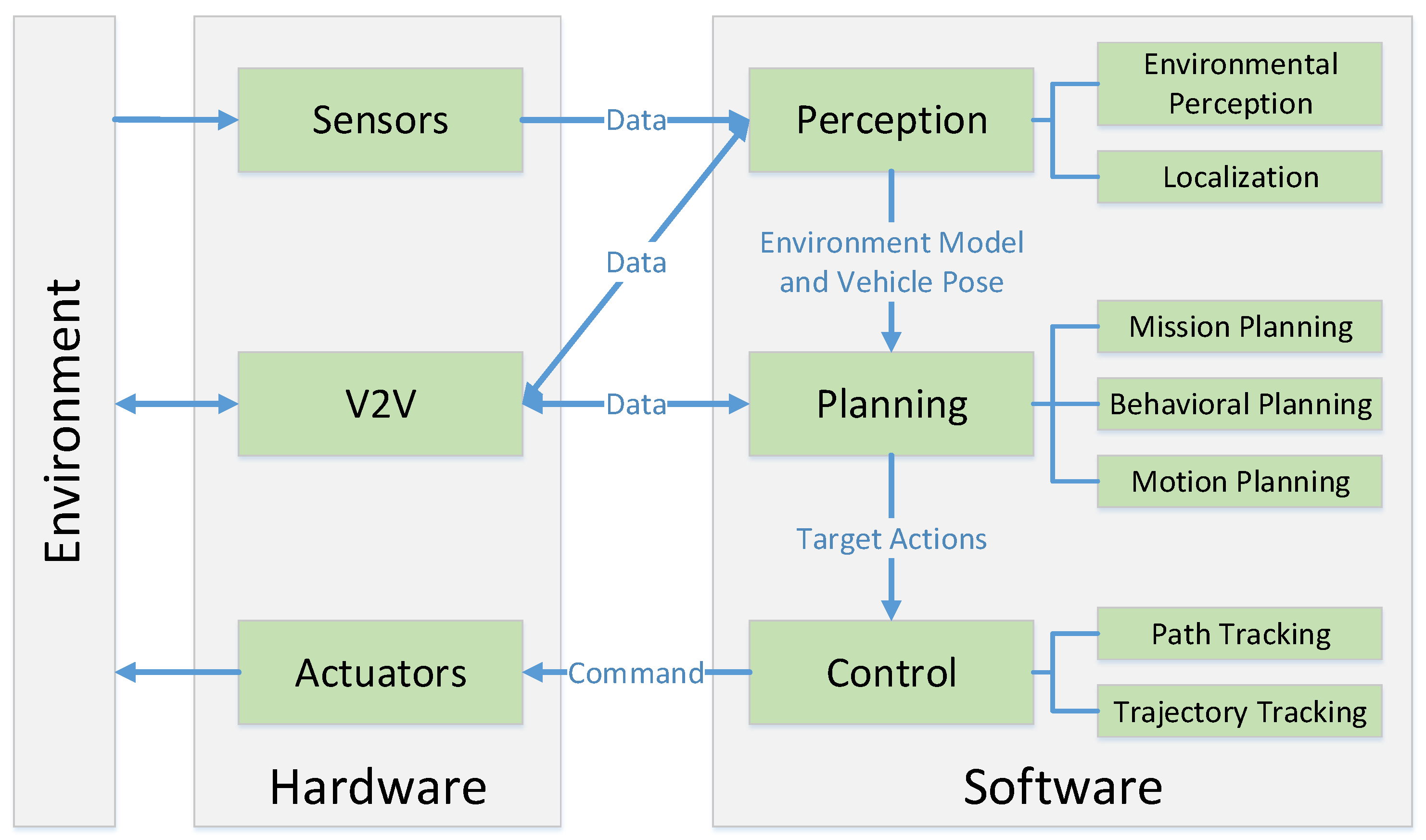
:1. Introduction
2. Perception
2.1. Environmental Perception
2.1.1. LIDAR
Representation
Segmentation Algorithms
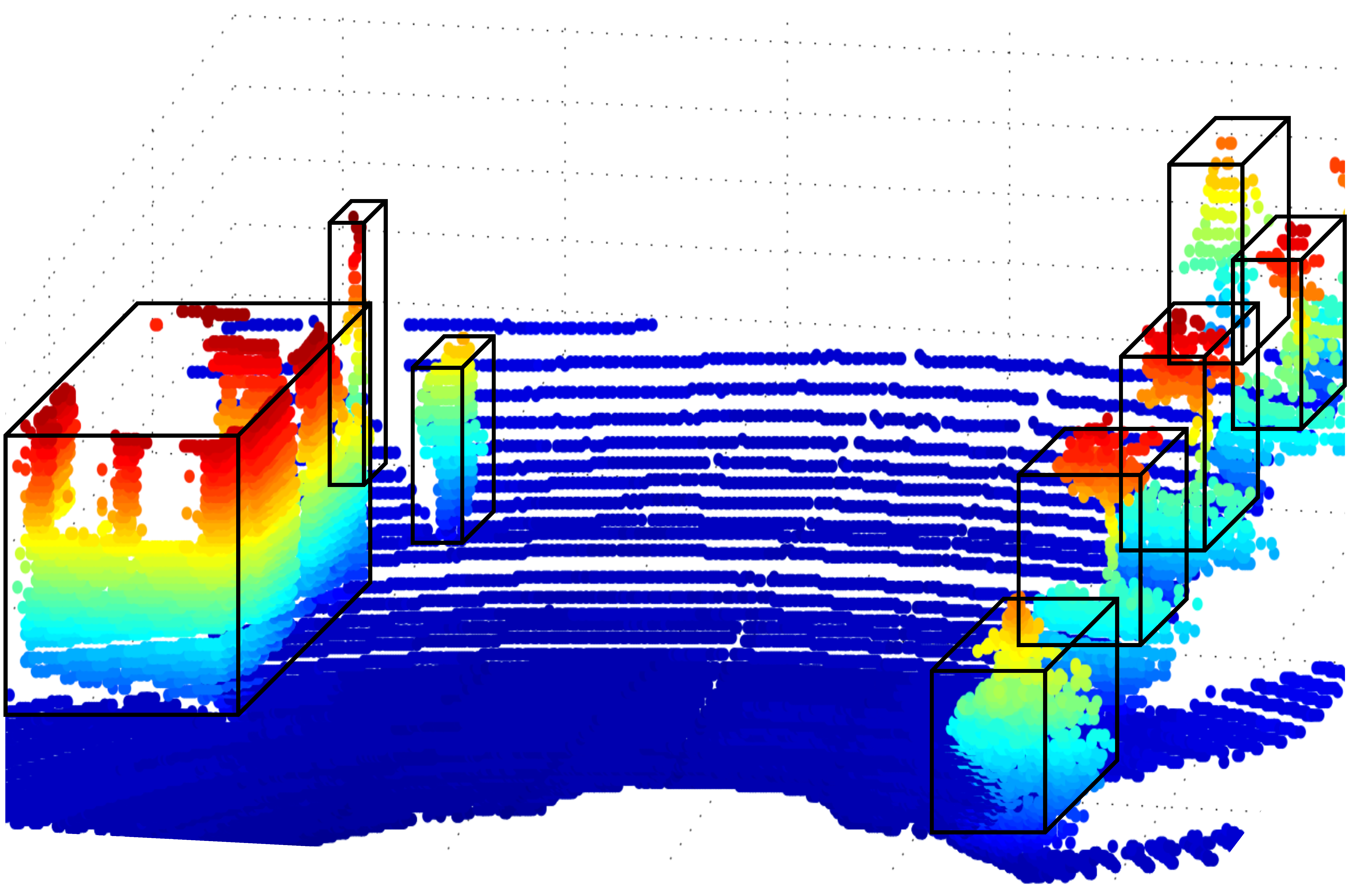
Detection Algorithm
2.1.2. Vision
Lane Line Marking Detection
Road Surface Detection
On-Road Object Detection
2.1.3. Fusion
2.2. Localization
3. Planning
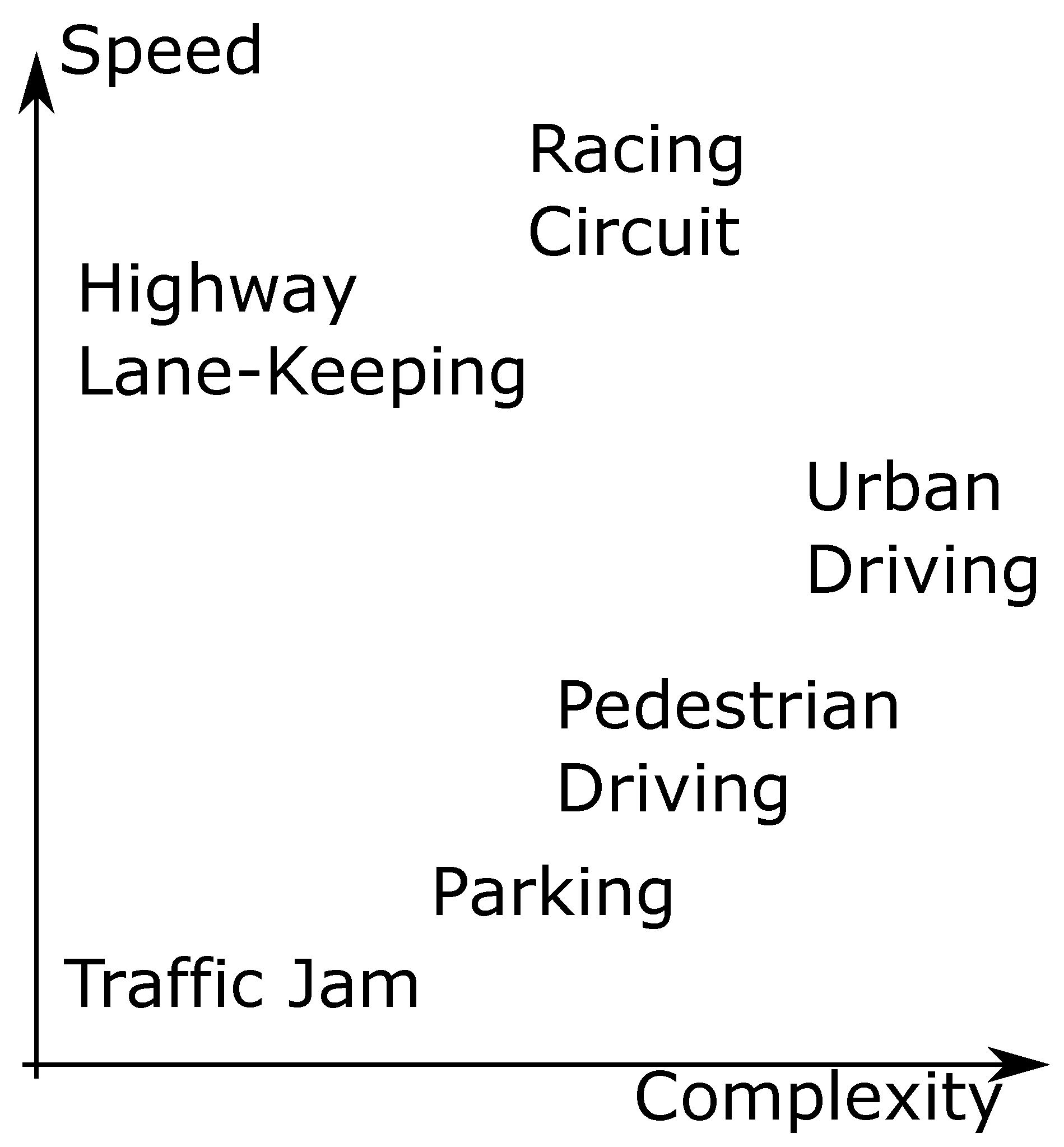
3.1. Autonomous Vehicle Planning Systems
3.2. Mission Planning
3.3. Behavioral Planning
3.4. Motion Planning
3.4.1. Combinatorial Planning
3.4.2. Sampling-Based Planning
3.5. Planning in Dynamic Environments
3.5.1. Decision Making Structures for Obstacle Avoidance
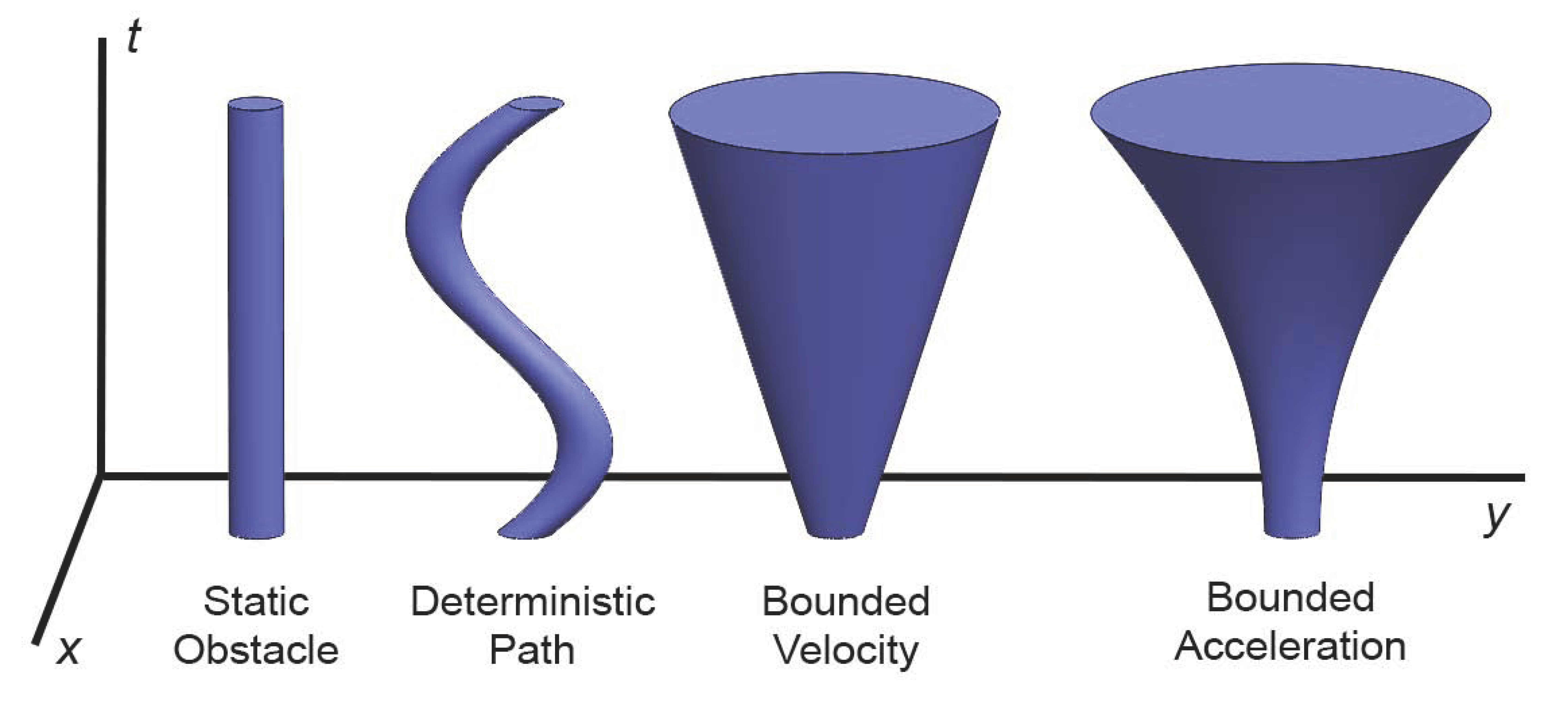
3.5.2. Planning in Space-Time
3.5.3. Control Space Obstacle Representations
3.6. Planning Subject to Differential Constraints
3.7. Incremental Planning and Replanning
4. Control
4.1. Classical Control
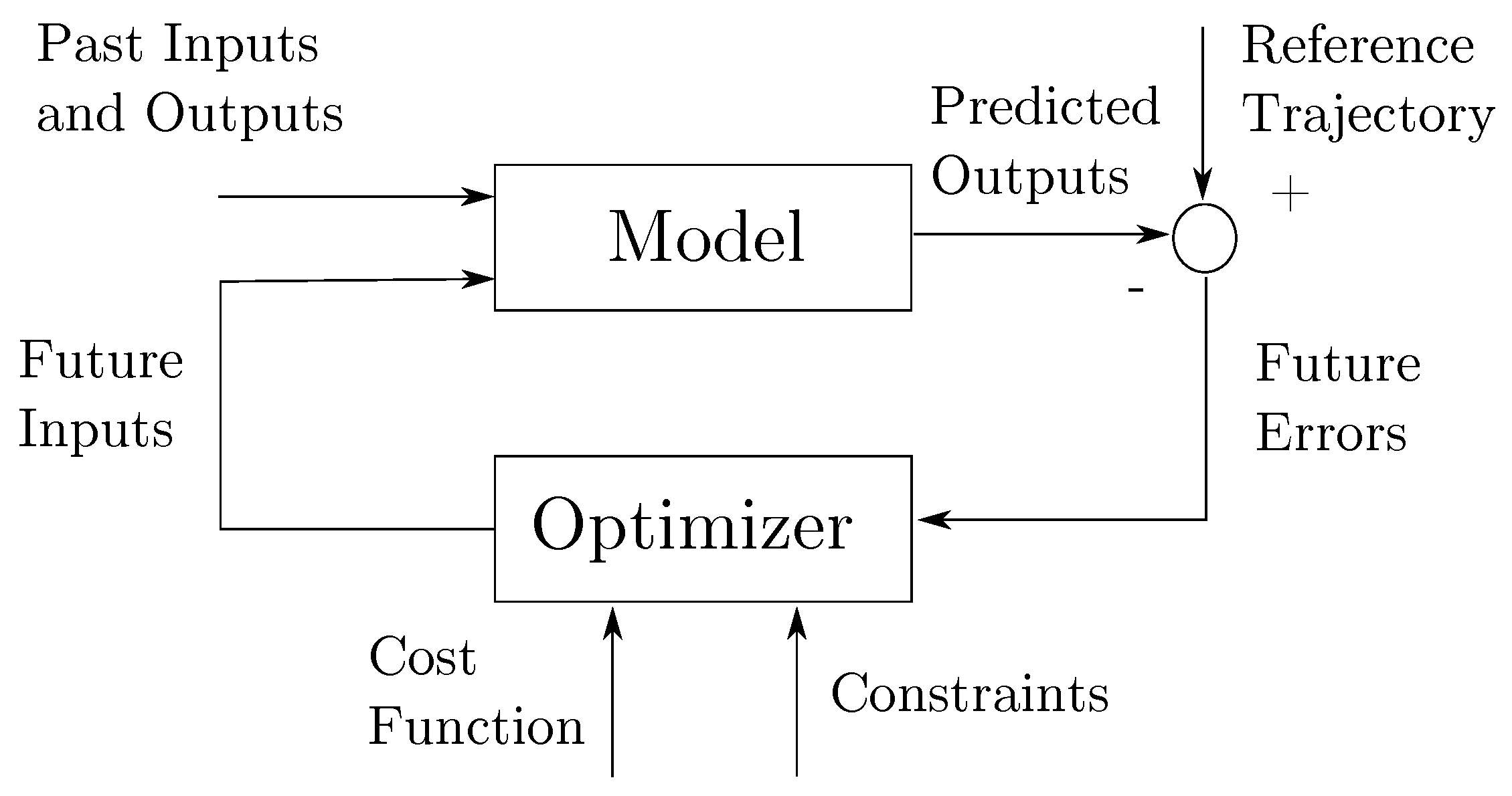
4.2. Model Predictive Control
4.3. Trajectory Generation and Tracking
4.3.1. Combined Trajectory Generation and Tracking
4.3.2. Separate Trajectory Generation and Tracking
Trajectory Generation
Trajectory Tracking
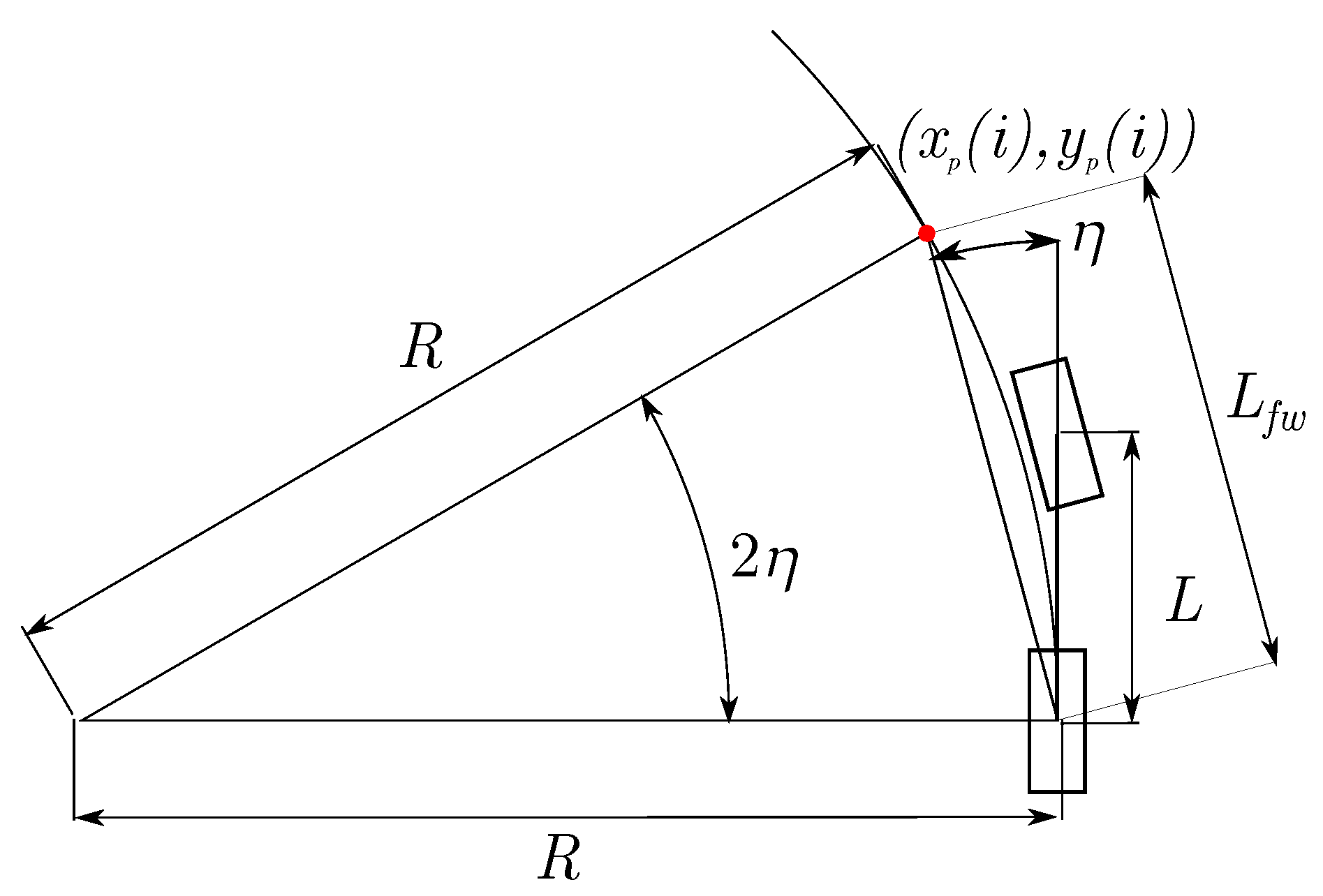
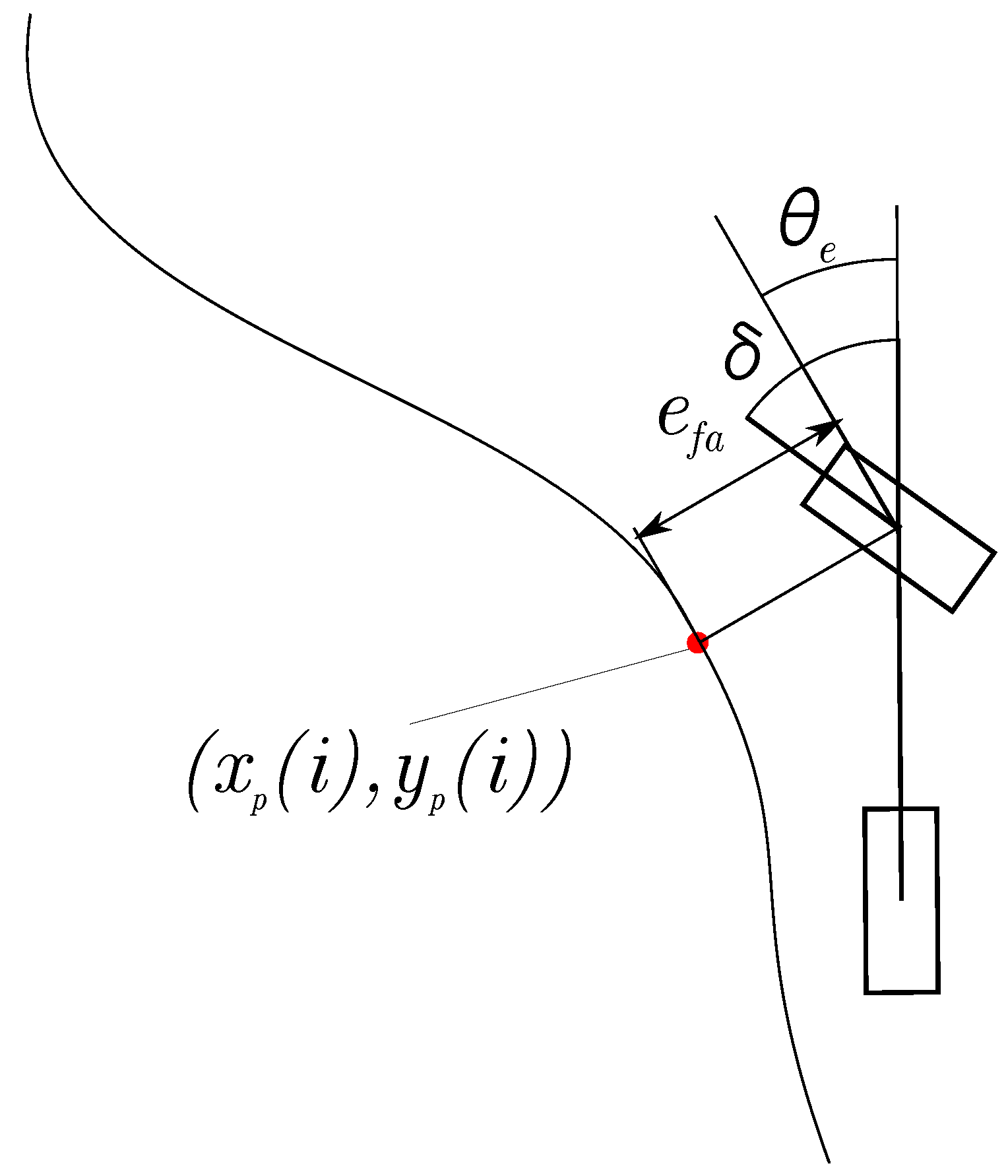
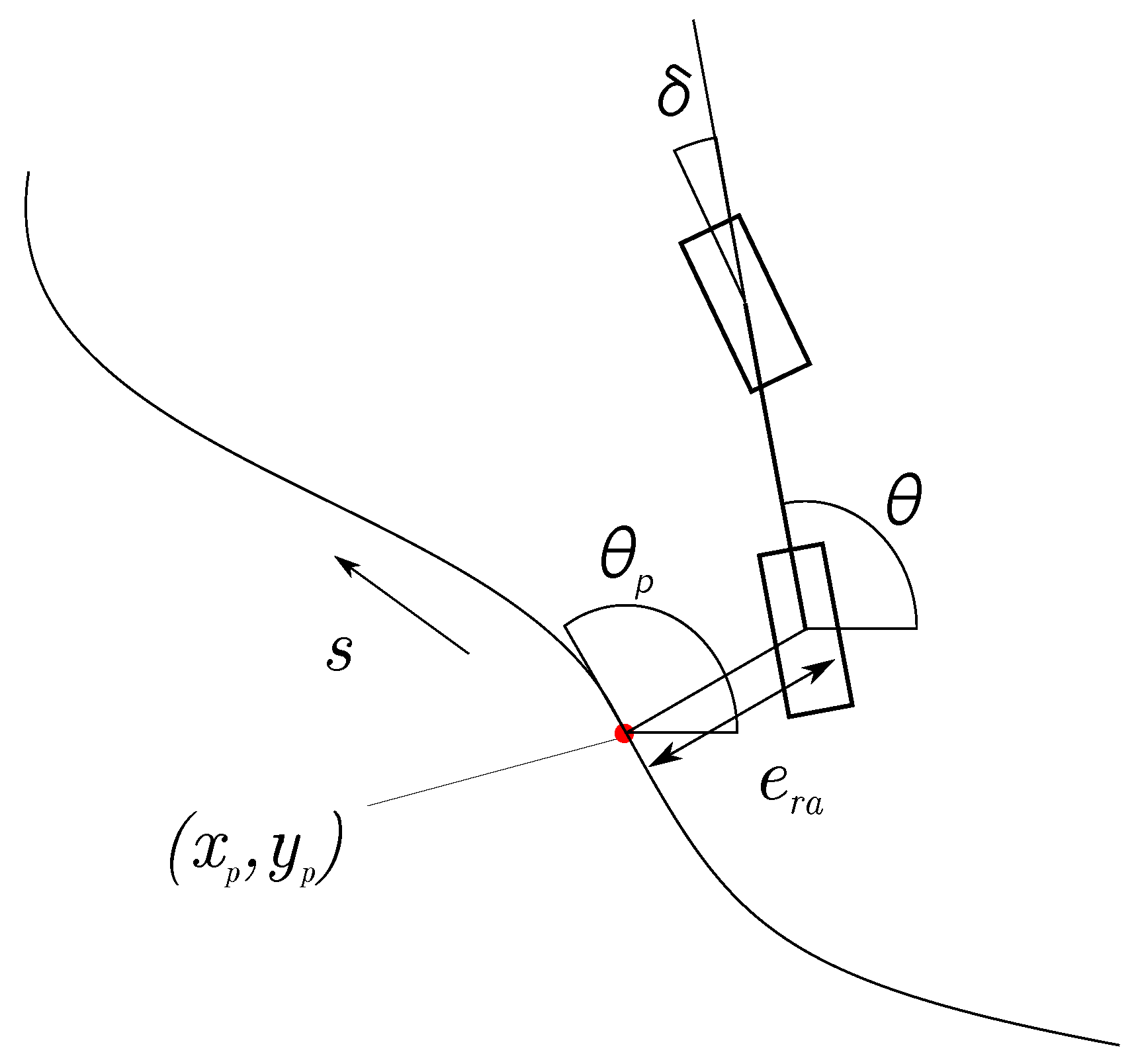
Geometric Path Tracking
Trajectory Tracking with a Model
- Path Tracking Model Predictive Controller : with a center of mass based linear model, Kim et al. [290] formulated an MPC problem for a path tracking and steering controller. The resulting integrated model is simulated with a detailed automatic steering model and a vehicle model in CarSim.
- Unconstrained MPC with Kinematic Model: by implementing CARIMA models without considering any input and state constraints, the computational burden can be minimized. The time-varying linear quadratic programming approach with no input or state constraints, using a linearized kinematic model, can be used to solve this sub class of problems, as demonstrated in [271].
- MPC Trajectory Controller with Dynamic Car Model : A wide array of methods are available in the literature. An approach with nonlinear tire behavior for tracking trajectory on various road conditions is explored in [267], and the simulation results suggest that the vehicle can be stabilized on challenging icy surfaces at a 20 Hz control frequency. The complexity of the model and inadequacy in available computing power at the time of publishing resulted in computational time that was more than the sample time of the system, hence only simulation results are available. The authors explored the linearization of the state of the vehicle about the state at the current time step in [291]. By reducing the complexity of the quadratic programming problem, a more reasonable computing time can be achieved, and the controller has been experimentally validated on challenging icy surfaces for up to 21 m/s driving speed. A linearization based approach was also investigated in [291] based on a single linearization about the state of the vehicle at the current time step. The reduced complexity of solving the quadratic program resulted in acceptable computation time, and successful experimental results are reported for driving in icy conditions at speeds up to 21 m/s.
5. Vehicle Cooperation
5.1. Vehicular Communication
5.2. Cooperative Localization
5.2.1. Vehicle Shape Information Utilization
5.2.2. Minimal Sensor Configuration
5.2.3. General Framework
5.3. Motion Coordination
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sousanis, J. World Vehicle Population Tops 1 Billion Units. Available online: http://wardsauto.com/ar/world_vehicle_population_110815 (accessed on 15 February 2015).
- Population Division of the Department of Economic; Social Affairs of the United Nations Secretariat. World Population Prospects: The 2012 Revision. Available online: http://esa.un.org/unpd/wpp/index.htm (accessed on 15 February 2015).
- Systematics, C. Crashes vs. Congestion–What’s the Cost to Society? American Automobile Association: Chicago, IL, USA, 2011. [Google Scholar]
- Schrank, D.; Eisele, B.; Lomax, T.; Bak, J. Urban Mobility Scorecard; Texas A&M Transportation Institute: College Station, TX, USA, 2015. [Google Scholar]
- Levy, J.I.; Buonocore, J.J.; Von Stackelberg, K. Evaluation of the public health impacts of traffic congestion: A health risk assessment. Environ. Health 2010, 9, 65. [Google Scholar] [CrossRef] [PubMed]
- Stenquist, P. The Motor Car of the Future. Oakl. Trib. 1918. Available online: https://www.scribd.com/document/20618885/1918-March-10-Oakland-Tribune-Oakland-CA?ad_group=&campaign=Skimbit%2C+Ltd.&content=10079&irgwc=1&keyword=ft500noi&medium=affiliate&source=impactradius (accessed on 15 February 2015).
- Clemmons, L.; Jones, C.; Dunn, J.W.; Kimball, W. Magic Highway U.S.A. Available online: https://www.youtube.com/watch?v=L3funFSRAbU (accessed on 30 December 2016).
- Thorpe, C.; Hebert, M.H.; Kanade, T.; Shafer, S.A. Vision and navigation for the Carnegie-Mellon Navlab. IEEE Trans. Pattern Anal. Mach. Intell. 1988, 10, 362–373. [Google Scholar] [CrossRef]
- Thrun, S.; Montemerlo, M.; Dahlkamp, H.; Stavens, D.; Aron, A.; Diebel, J.; Fong, P.; Gale, J.; Halpenny, M.; Hoffmann, G.; et al. Stanley: The robot that won the DARPA Grand Challenge. J. Field Robot. 2006, 23, 661–692. [Google Scholar] [CrossRef]
- Urmson, C.; Anhalt, J.; Bagnell, D.; Baker, C.; Bittner, R.; Clark, M.N.; Dolan, J.; Duggins, D.; Galatali, T.; Geyer, C.; et al. Autonomous driving in urban environments: Boss and the Urban Challenge. J. Field Robot. 2008, 25, 425–466. [Google Scholar] [CrossRef]
- Zhang, R.; Spieser, K.; Frazzoli, E.; Pavone, M. Models, Algorithms, and Evaluation for Autonomous Mobility-On-Demand Systems. In Proceedings of the American Control Conference, Chicago, IL, USA, 1–3 July 2015; pp. 2573–2587.
- Google Self-Driving Car Project. Available online: https://www.google.com/selfdrivingcar/ (accessed on 2 February 2017).
- Tesla Motors: Model S Press Kit. Available online: https://www.tesla.com/presskit/autopilot (accessed on 30 December 2016).
- Newton, C. Uber will eventually replace all its drivers with self-driving cars. Verge 2014, 5, 2014. [Google Scholar]
- Pittsburgh, Your Self-Driving Uber is Arriving Now. Available online: https://newsroom.uber.com/pittsburgh-self-driving-uber/ (accessed on 30 December 2016).
- De Graaf, M. PRT Vehicle Architecture and Control in Masdar City. In Proceedings of the 13th International Conference on Automated People Movers and Transit Systems, Paris, France, 22–25 May 2011; pp. 339–348.
- Alessandrini, A.; Cattivera, A.; Holguin, C.; Stam, D. CityMobil2: Challenges and Opportunities of Fully Automated Mobility. In Road Vehicle Automation; Springer: Berlin, Germany, 2014; pp. 169–184. [Google Scholar]
- Eggers, A.; Schwedhelm, H.; Zander, O.; Izquierdo, R.C.; Polanco, J.A.G.; Paralikas, J.; Georgoulias, K.; Chryssolouris, G.; Seibert, D.; Jacob, C. Virtual testing based type approval procedures for the assessment of pedestrian protection developed within the EU-Project IMVITER. In Proceedings of 23rd Enhanced Safety of Vehicles (ESV) Conference, Seoul, Korea, 27–30 May 2013.
- Makris, S.; Michalos, G.; Efthymiou, K.; Georgoulias, K.; Alexopoulos, K.; Papakostas, N.; Eytan, A.; Lai, M.; Chryssolouris, G. Flexible assembly technology for highly customisable vehicles. In Proceedings of the (AMPS 10), International Conference on Competitive and Sustainable Manufacturing, Products and Services, Lake Como, Italy, 11–13 October 2010.
- Buehler, M.; Iagnemma, K.; Singh, S. (Eds.) The Darpa Urban Challenge Autonomous Vehicle in City Traffic; Springer: Berlin, Germany, 2009.
- Furgale, P.; Schwesinger, U.; Rufli, M.; Derendarz, W.; Grimmett, H.; Muhlfellner, P.; Wonneberger, S.; Timpner, J.; Rottmann, S.; Li, B.; et al. Toward automated driving in cities using close-to-market sensors: An overview of the V-Charge Project. In Proceedings of the IEEE Intelligent Vehicles Symposium, Gold Coast City, Australia, 23–26 June 2013; pp. 809–816.
- Fisher, A. Google’s Self-Driving Cars: A Quest for Acceptance. Available online: http://www.popsci.com/cars/article/2013-09/google-self-driving-car (accessed on 18 September 2013).
- Asvadi, A.; Premebida, C.; Peixoto, P.; Nunes, U. 3D Lidar-based static and moving obstacle detection in driving environments: An approach based on voxels and multi-region ground planes. Robot. Auton. Syst. 2016, 83, 299–311. [Google Scholar] [CrossRef]
- Zhao, G.; Xiao, X.; Yuan, J.; Ng, G.W. Fusion of 3D-LIDAR and camera data for scene parsing. J. Vis. Commun. Image Represent. 2014, 25, 165–183. [Google Scholar] [CrossRef]
- Moosmann, F.; Pink, O.; Stiller, C. Segmentation of 3D lidar data in non-flat urban environments using a local convexity criterion. In Proceedings of the 2009 IEEE Intelligent Vehicles Symposium, Xi’an, China, 3–5 June 2009; pp. 215–220.
- Sack, D.; Burgard, W. A comparison of methods for line extraction from range data. In Proceedings of the 5th IFAC Symposium on Intelligent Autonomous Vehicles (IAV), Lisbon, Portugal, 5–7 July 2014; Volume 33.
- Oliveira, M.; Santos, V.; Sappa, A.D.; Dias, P. Scene Representations for Autonomous Driving: An Approach Based on Polygonal Primitives. In Proceedings of the Robot 2015: Second Iberian Robotics Conference, Lisbon, Portugal, 19–21 November 2015; Springer: Berlin, Germany, 2016; pp. 503–515. [Google Scholar]
- Wang, M.; Tseng, Y.H. Incremental segmentation of lidar point clouds with an octree-structured voxel space. Photogramm. Rec. 2011, 26, 32–57. [Google Scholar] [CrossRef]
- Vo, A.V.; Truong-Hong, L.; Laefer, D.F.; Bertolotto, M. Octree-based region growing for point cloud segmentation. ISPRS J. Photogramm. Remote Sens. 2015, 104, 88–100. [Google Scholar] [CrossRef]
- Nguyen, A.; Le, B. 3D point cloud segmentation: A survey. In Proceedings of the 2013 6th IEEE Conference on Robotics, Automation and Mechatronics (RAM), Manila, Philippines, 12–15 November 2013; pp. 225–230.
- Yao, W.; Deng, Z.; Zhou, L. Road curb detection using 3D lidar and integral laser points for intelligent vehicles. In Proceedings of the 2012 Joint 6th International Conference on Soft Computing and Intelligent Systems (SCIS) and 13th International Symposium on Advanced Intelligent Systems (ISIS), Kobe, Japan, 20–24 November 2012; pp. 100–105.
- Chen, X.; Deng, Z. Detection of Road Obstacles Using 3D Lidar Data via Road Plane Fitting. In Proceedings of the 2015 Chinese Intelligent Automation Conference, Fuzhou, China, 30 April 2015; Springer: Berlin, Germany, 2015; pp. 441–449. [Google Scholar]
- Yu, Y.; Li, J.; Guan, H.; Wang, C.; Yu, J. Semiautomated extraction of street light poles from mobile LiDAR point-clouds. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1374–1386. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, D.; Xie, X.; Ren, Y.; Li, G.; Deng, Y.; Wang, Z. A fast and accurate segmentation method for ordered LiDAR point cloud of large-scale scenes. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1981–1985. [Google Scholar] [CrossRef]
- Rusu, R.B. Semantic 3D object maps for everyday manipulation in human living environments. KI-Künstliche Intell. 2010, 24, 345–348. [Google Scholar] [CrossRef]
- Ioannou, Y.; Taati, B.; Harrap, R.; Greenspan, M. Difference of normals as a multi-scale operator in unorganized point clouds. In Proceedings of the 2012 Second International Conference on 3D Imaging, Modeling, Processing, Visualization & Transmission, Zurich, Switzerland, 13–15 October 2012; pp. 501–508.
- Hu, X.; Li, X.; Zhang, Y. Fast filtering of LiDAR point cloud in urban areas based on scan line segmentation and GPU acceleration. IEEE Geosci. Remote Sens. Lett. 2013, 10, 308–312. [Google Scholar]
- Vosselman, G. Point cloud segmentation for urban scene classification. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, XL-7/W2, 257–262. [Google Scholar] [CrossRef]
- Reddy, S.K.; Pal, P.K. Segmentation of point cloud from a 3D LIDAR using range difference between neighbouring beams. In Proceedings of the 2015 ACM Conference on Advances in Robotics, Goa, India, 2–4 July 2015; p. 55.
- Burgard, W. Techniques for 3D Mapping. In Slides from SLAM Summer School 2009; SLAM Summer School: Sydney, Australia, 20–23 January 2009. [Google Scholar]
- Hähnel, D.; Thrun, S. 3D Laser-based obstacle detection for autonomous driving. In Proceedings of the Abstract of the IEEE International Conference on Intelligent Robots and Systems (IROS), Nice, France, 22–26 Septempber 2008.
- Montemerlo, M.; Becker, J.; Bhat, S.; Dahlkamp, H.; Dolgov, D.; Ettinger, S.; Haehnel, D.; Hilden, T.; Hoffmann, G.; Huhnke, B.; et al. Junior: The stanford entry in the urban challenge. J. Field Robot. 2008, 25, 569–597. [Google Scholar] [CrossRef]
- Vieira, M.; Shimada, K. Surface mesh segmentation and smooth surface extraction through region growing. Comput. Aided Geom. Des. 2005, 22, 771–792. [Google Scholar] [CrossRef]
- Rabbani, T.; Van Den Heuvel, F.; Vosselmann, G. Segmentation of point clouds using smoothness constraint. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36, 248–253. [Google Scholar]
- Deschaud, J.E.; Goulette, F. A fast and accurate plane detection algorithm for large noisy point clouds using filtered normals and voxel growing. In Proceedings of the 3D Processing, Visualization and Transmission Conference (3DPVT2010), Paris, France, 17–20 May 2010.
- Biosca, J.M.; Lerma, J.L. Unsupervised robust planar segmentation of terrestrial laser scanner point clouds based on fuzzy clustering methods. ISPRS J. Photogramm. Remote Sens. 2008, 63, 84–98. [Google Scholar] [CrossRef]
- Teboul, O.; Simon, L.; Koutsourakis, P.; Paragios, N. Segmentation of building facades using procedural shape priors. In Proceedings of the 2010 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), San Francisco, CA, USA, 13–18 June 2010; pp. 3105–3112.
- Boulaassal, H.; Landes, T.; Grussenmeyer, P.; Tarsha-Kurdi, F. Automatic segmentation of building facades using terrestrial laser data. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2007, 36, W52. [Google Scholar]
- Broggi, A.; Cattani, S.; Patander, M.; Sabbatelli, M.; Zani, P. A full-3D voxel-based dynamic obstacle detection for urban scenario using stereo vision. In Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems (ITSC 2013), The Hague, The Netherlands, 6–9 October 2013; pp. 71–76.
- Azim, A.; Aycard, O. Layer-based supervised classification of moving objects in outdoor dynamic environment using 3D laser scanner. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium Proceedings, Dearborn, MI, USA, 8–11 June 2014; pp. 1408–1414.
- Asvadi, A.; Peixoto, P.; Nunes, U. Two-Stage Static/Dynamic Environment Modeling Using Voxel Representation. In Proceedings of the Robot 2015: Second Iberian Robotics Conference, Lisbon, Portugal, 19–21 November 2015; Springer: Berlin, Germany, 2016; pp. 465–476. [Google Scholar]
- Oniga, F.; Nedevschi, S. Processing dense stereo data using elevation maps: Road surface, traffic isle, and obstacle detection. IEEE Trans. Veh. Technol. 2010, 59, 1172–1182. [Google Scholar] [CrossRef]
- Vosselman, G.; Gorte, B.G.; Sithole, G.; Rabbani, T. Recognising structure in laser scanner point clouds. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 46, 33–38. [Google Scholar]
- Tarsha-Kurdi, F.; Landes, T.; Grussenmeyer, P. Hough-transform and extended ransac algorithms for automatic detection of 3d building roof planes from lidar data. In Proceedings of the ISPRS Workshop on Laser Scanning, Espoo, Finland, 12–14 September 2007; Volume 36, pp. 407–412.
- Rabbani, T.; Van Den Heuvel, F. Efficient hough transform for automatic detection of cylinders in point clouds. ISPRS WG III/3, III/4 2005, 3, 60–65. [Google Scholar]
- Yang, B.; Dong, Z. A shape-based segmentation method for mobile laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2013, 81, 19–30. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. (TIST) 2011, 2, 27. [Google Scholar] [CrossRef]
- Lafferty, J.; McCallum, A.; Pereira, F. Conditional random fields: Probabilistic models for segmenting and labeling sequence data. In Proceedings of the Eighteenth International Conference on Machine Learning, Williamstown, MA, USA, 28 June–1 July 2001; Volume 1, pp. 282–289.
- Golovinskiy, A.; Funkhouser, T. Min-cut based segmentation of point clouds. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision Workshops (ICCV Workshops), Kyoto, Japan, 27 September–4 October 2009; pp. 39–46.
- Golovinskiy, A.; Kim, V.G.; Funkhouser, T. Shape-based recognition of 3D point clouds in urban environments. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 27 September–4 October 2009; pp. 2154–2161.
- Riemenschneider, H.; Bódis-Szomorú, A.; Weissenberg, J.; Van Gool, L. Learning where to classify in multi-view semantic segmentation. In European Conference on Computer Vision; Springer: Berlin, Germany, 2014; pp. 516–532. [Google Scholar]
- Martinovic, A.; Knopp, J.; Riemenschneider, H.; Van Gool, L. 3D all the way: Semantic segmentation of urban scenes from start to end in 3d. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 4456–4465.
- Riegler, G.; Ulusoys, A.O.; Geiger, A. OctNet: Learning Deep 3D Representations at High Resolutions. arXiv 2016. [Google Scholar]
- Zhang, J.; Lin, X.; Ning, X. SVM-based classification of segmented airborne LiDAR point clouds in urban areas. Remote Sens. 2013, 5, 3749–3775. [Google Scholar] [CrossRef]
- Maturana, D.; Scherer, S. Voxnet: A 3d convolutional neural network for real-time object recognition. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–3 October 2015; pp. 922–928.
- Qi, C.R.; Su, H.; Niessner, M.; Dai, A.; Yan, M.; Guibas, L.J. Volumetric and Multi-View CNNs for Object Classification on 3D Data. arXiv 2016. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3D shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1912–1920.
- Hillel, A.B.; Lerner, R.; Levi, D.; Raz, G. Recent progress in road and lane detection: A survey. Mach. Vis. Appl. 2014, 25, 727–745. [Google Scholar] [CrossRef]
- McCall, J.C.; Trivedi, M.M. Video-based lane estimation and tracking for driver assistance: Survey, system, and evaluation. IEEE Trans. Intell. Transp. Syst. 2006, 7, 20–37. [Google Scholar] [CrossRef]
- Ranft, B.; Stiller, C. The Role of Machine Vision for Intelligent Vehicles. IEEE Trans. Intell. Veh. 2016, 1, 8–19. [Google Scholar] [CrossRef]
- Sivaraman, S.; Trivedi, M.M. Looking at Vehicles on the Road: A Survey of Vision-Based Vehicle Detection, Tracking, and Behavior Analysis. IEEE Trans. Intell. Transp. Syst. 2013, 14, 1773–1795. [Google Scholar] [CrossRef]
- Mukhtar, A.; Xia, L.; Tang, T.B. Vehicle detection techniques for collision avoidance systems: A review. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2318–2338. [Google Scholar] [CrossRef]
- Dollar, P.; Wojek, C.; Schiele, B.; Perona, P. Pedestrian detection: An evaluation of the state of the art. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 743–761. [Google Scholar] [CrossRef] [PubMed]
- Labayrade, R.; Douret, J.; Aubert, D. A multi-model lane detector that handles road singularities. In Proceedings of the Intelligent Transportation Systems Conference, ITSC’06, Toronto, ON, Canada, 17–20 September 2006; pp. 1143–1148.
- Du, X. Towards Sustainable Autonomous Vehicles. Ph.D. Thesis, National University of Singapore, Singapore, 2016. [Google Scholar]
- Nedevschi, S.; Schmidt, R.; Graf, T.; Danescu, R.; Frentiu, D.; Marita, T.; Oniga, F.; Pocol, C. 3D lane detection system based on stereovision. In Proceedings of the 7th International IEEE Conference on Intelligent Transportation Systems, Washington, DC, USA, 3–6 October 2004; pp. 161–166.
- Li, Q.; Zheng, N.; Cheng, H. An adaptive approach to lane markings detection. In Proceedings of the 2003 IEEE International Conference on Intelligent Transportation Systems, Shanghai, China, 12–15 October 2003; Volume 1, pp. 510–514.
- Tapia-Espinoza, R.; Torres-Torriti, M. A comparison of gradient versus color and texture analysis for lane detection and tracking. In Proceedings of the 2009 6th Latin American Robotics Symposium (LARS), Valparaiso, Chile, 29–30 October 2009; pp. 1–6.
- Sun, T.Y.; Tsai, S.J.; Chan, V. HSI color model based lane-marking detection. In Proceedings of the Intelligent Transportation Systems Conference, ITSC’06, Toronto, ON, Canada, 17–20 September 2006; pp. 1168–1172.
- Kim, Z. Robust lane detection and tracking in challenging scenarios. IEEE Trans. Intell. Transp. Syst. 2008, 9, 16–26. [Google Scholar] [CrossRef]
- Gopalan, R.; Hong, T.; Shneier, M.; Chellappa, R. A learning approach towards detection and tracking of lane markings. IEEE Trans. Intell. Transp. Syst. 2012, 13, 1088–1098. [Google Scholar] [CrossRef]
- Fritsch, J.; Kuhnl, T.; Kummert, F. Monocular road terrain detection by combining visual and spatial information. IEEE Trans. Intell. Transp. Syst. 2014, 15, 1586–1596. [Google Scholar] [CrossRef]
- Kang, D.J.; Jung, M.H. Road lane segmentation using dynamic programming for active safety vehicles. Pattern Recognit. Lett. 2003, 24, 3177–3185. [Google Scholar] [CrossRef]
- Kum, C.H.; Cho, D.C.; Ra, M.S.; Kim, W.Y. Lane detection system with around view monitoring for intelligent vehicle. In Proceedings of the 2013 International. SoC Design Conference (ISOCC), Busan, Korea, 17–19 November 2013; pp. 215–218.
- Cui, G.; Wang, J.; Li, J. Robust multilane detection and tracking in urban scenarios based on LIDAR and mono-vision. IET Image Process. 2014, 8, 269–279. [Google Scholar] [CrossRef]
- Lu, W.; Seignez, E.; Rodriguez, F.S.A.; Reynaud, R. Lane marking based vehicle localization using particle filter and multi-kernel estimation. In Proceedings of the 2014 13th International Conference on Control Automation Robotics & Vision (ICARCV), Singapore, 10–12 December 2014; pp. 601–606.
- Sivaraman, S.; Trivedi, M.M. Integrated lane and vehicle detection, localization, and tracking: A synergistic approach. IEEE Trans. Intell. Transp. Syst. 2013, 14, 906–917. [Google Scholar] [CrossRef]
- Du, X.; Tan, K.K. Vision-based approach towards lane line detection and vehicle localization. Mach. Vis. Appl. 2015, 27, 1–17. [Google Scholar] [CrossRef]
- Du, X.; Tan, K.K.; Htet, K.K.K. Vision-based lane line detection for autonomous vehicle navigation and guidance. In Proceedings of the 2015 10th Asian Control Conference (ASCC), Sabah, Malaysia, 31 May–3 June 2015; pp. 3139–3143.
- Du, X.; Tan, K.K. Comprehensive and practical vision system for self-driving vehicle lane-level localization. IEEE Trans. Image Process. 2016, 25, 2075–2088. [Google Scholar] [CrossRef] [PubMed]
- Borkar, A.; Hayes, M.; Smith, M.T. A novel lane detection system with efficient ground truth generation. IEEE Trans. Intell. Transp. Syst. 2012, 13, 365–374. [Google Scholar] [CrossRef]
- Danescu, R.; Nedevschi, S. Probabilistic lane tracking in difficult road scenarios using stereovision. IEEE Trans. Intell. Transp. Syst. 2009, 10, 272–282. [Google Scholar] [CrossRef]
- Topfer, D.; Spehr, J.; Effertz, J.; Stiller, C. Efficient Road Scene Understanding for Intelligent Vehicles Using Compositional Hierarchical Models. IEEE Trans. Intell. Transp. Syst. 2015, 16, 441–451. [Google Scholar] [CrossRef]
- Yoo, H.; Yang, U.; Sohn, K. Gradient-enhancing conversion for illumination-robust lane detection. IEEE Trans. Intell. Transp. Syst. 2013, 14, 1083–1094. [Google Scholar] [CrossRef]
- López, A.; Serrat, J.; Canero, C.; Lumbreras, F.; Graf, T. Robust lane markings detection and road geometry computation. Int. J. Automot. Technol. 2010, 11, 395–407. [Google Scholar] [CrossRef]
- Du, X.; Tan, K.K. Autonomous Reverse Parking System Based on Robust Path Generation and Improved Sliding Mode Control. IEEE Trans. Intell. Transp. Syst. 2015, 16, 1225–1237. [Google Scholar] [CrossRef]
- Labayrade, R.; Douret, J.; Laneurit, J.; Chapuis, R. A reliable and robust lane detection system based on the parallel use of three algorithms for driving safety assistance. IEICE Trans. Inf. Syst. 2006, 89, 2092–2100. [Google Scholar] [CrossRef]
- Wu, S.J.; Chiang, H.H.; Perng, J.W.; Chen, C.J.; Wu, B.F.; Lee, T.T. The heterogeneous systems integration design and implementation for lane keeping on a vehicle. IEEE Trans. Intell. Transp. Syst. 2008, 9, 246–263. [Google Scholar] [CrossRef]
- Huang, A.S.; Moore, D.; Antone, M.; Olson, E.; Teller, S. Finding multiple lanes in urban road networks with vision and lidar. Auton. Robots 2009, 26, 103–122. [Google Scholar] [CrossRef]
- Ding, D.; Yoo, J.; Jung, J.; Jin, S.; Kwon, S. Various lane marking detection and classification for vision-based navigation system? In Proceedings of the 2015 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 9–12 January 2015; pp. 491–492.
- Jiang, Y.; Gao, F.; Xu, G. Computer vision-based multiple-lane detection on straight road and in a curve. In Proceedings of the 2010 International Conference on Image Analysis and Signal Processing (IASP), Zhejiang, China, 12–14 April 2010; pp. 114–117.
- Jiang, R.; Klette, R.; Vaudrey, T.; Wang, S. New lane model and distance transform for lane detection and tracking. In Computer Analysis of Images and Patterns; Springer: Berlin, Germany, 2009; pp. 1044–1052. [Google Scholar]
- Ruyi, J.; Reinhard, K.; Tobi, V.; Shigang, W. Lane detection and tracking using a new lane model and distance transform. Mach. Vis. Appl. 2011, 22, 721–737. [Google Scholar] [CrossRef]
- Liu, G.; Worgotter, F.; Markelic, I. Stochastic lane shape estimation using local image descriptors. IEEE Trans. Intell. Transp. Syst. 2013, 14, 13–21. [Google Scholar] [CrossRef]
- Wang, Y.; Teoh, E.K.; Shen, D. Lane detection and tracking using B-Snake. Image Vis. Comput. 2004, 22, 269–280. [Google Scholar] [CrossRef]
- Sawano, H.; Okada, M. A road extraction method by an active contour model with inertia and differential features. IEICE Trans. Inf. Syst. 2006, 89, 2257–2267. [Google Scholar] [CrossRef]
- Borkar, A.; Hayes, M.; Smith, M.T. Robust Lane Detection and Tracking with Ransac and Kalman Filter. In Proceedings of the 2009 16th IEEE International Conference on Image Processing (ICIP), Cairo, Egypt, 7–11 November 2009; pp. 3261–3264.
- Sach, L.T.; Atsuta, K.; Hamamoto, K.; Kondo, S. A robust road profile estimation method for low texture stereo images. In Proceedings of the 2009 16th IEEE International Conference on Image Processing (ICIP), Cairo, Egypt, 7–11 November 2009; pp. 4273–4276.
- Guo, C.; Mita, S.; McAllester, D. Stereovision-based road boundary detection for intelligent vehicles in challenging scenarios. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 11–15 October 2009; pp. 1723–1728.
- Wedel, A.; Badino, H.; Rabe, C.; Loose, H.; Franke, U.; Cremers, D. B-spline modeling of road surfaces with an application to free-space estimation. IEEE Trans. Intell. Transp. Syst. 2009, 10, 572–583. [Google Scholar] [CrossRef]
- Ladickỳ, L.; Sturgess, P.; Russell, C.; Sengupta, S.; Bastanlar, Y.; Clocksin, W.; Torr, P.H. Joint optimization for object class segmentation and dense stereo reconstruction. Int. J. Comput. Vis. 2012, 100, 122–133. [Google Scholar] [CrossRef]
- Mendes, C.C.T.; Frémont, V.; Wolf, D.F. Vision-Based Road Detection using Contextual Blocks. arXiv 2015. [Google Scholar]
- Kühnl, T.; Kummert, F.; Fritsch, J. Spatial ray features for real-time ego-lane extraction. In Proceedings of the 2012 15th International IEEE Conference on Intelligent Transportation Systems, Anchorage, AK, USA, 16–19 September 2012; pp. 288–293.
- Freund, Y.; Schapire, R.E. A desicion-theoretic generalization of on-line learning and an application to boosting. In European Conference on Computational Learning Theory; Springer: Berlin, Germany, 1995; pp. 23–37. [Google Scholar]
- Vitor, G.B.; Victorino, A.C.; Ferreira, J.V. A probabilistic distribution approach for the classification of urban roads in complex environments. In Proceedings of the Workshop on IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014.
- Vitor, G.B.; Victorino, A.C.; Ferreira, J.V. Comprehensive performance analysis of road detection algorithms using the common urban Kitti-road benchmark. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium Proceedings, Dearborn, MI, USA, 8–11 June 2014; pp. 19–24.
- Fritsch, J.; Kuehnl, T.; Geiger, A. A New Performance Measure and Evaluation Benchmark for Road Detection Algorithms. In Proceedings of the International Conference on Intelligent Transportation Systems (ITSC), The Hague, The Netherlands, 6–9 October 2013.
- Jia, Y.; Shelhamer, E.; Donahue, J.; Karayev, S.; Long, J.; Girshick, R.; Guadarrama, S.; Darrell, T. Caffe: Convolutional architecture for fast feature embedding. In Proceedings of the 22nd ACM international conference on Multimedia, Orlando, FL, USA, 3–7 November 2014; pp. 675–678.
- Mendes, C.C.T.; Frémont, V.; Wolf, D.F. Exploiting Fully Convolutional Neural Networks for Fast Road Detection. In 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016.
- Brust, C.A.; Sickert, S.; Simon, M.; Rodner, E.; Denzler, J. Convolutional patch networks with spatial prior for road detection and urban scene understanding. arXiv 2015. [Google Scholar]
- Mohan, R. Deep deconvolutional networks for scene parsing. arXiv 2014. [Google Scholar]
- Oliveira, G.L.; Burgard, W.; Brox, T. Efficient deep models for monocular road segmentation. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 4885–4891.
- Laddha, A.; Kocamaz, M.K.; Navarro-Serment, L.E.; Hebert, M. Map-supervised road detection. In Proceedings of the 2016 IEEE Intelligent Vehicles Symposium (IV), Gotenburg, Sweden, 19–22 June 2016; pp. 118–123.
- Uijlings, J.R.; van de Sande, K.E.; Gevers, T.; Smeulders, A.W. Selective search for object recognition. Int. J. Comput. Vis. 2013, 104, 154–171. [Google Scholar] [CrossRef]
- Zitnick, C.L.; Dollár, P. Edge boxes: Locating object proposals from edges. In European Conference on Computer Vision; Springer: Berlin, Germany, 2014; pp. 391–405. [Google Scholar]
- Chen, X.; Kundu, K.; Zhang, Z.; Ma, H.; Fidler, S.; Urtasun, R. Monocular 3d object detection for autonomous driving. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 26 June–1 July 2016; pp. 2147–2156.
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, ON, Canada, 7–12 December 2015; pp. 91–99.
- He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial pyramid pooling in deep convolutional networks for visual recognition. In European Conference on Computer Vision; Springer: Berlin, Germany, 2014; pp. 346–361. [Google Scholar]
- Yang, F.; Choi, W.; Lin, Y. Exploit all the layers: Fast and accurate cnn object detector with scale dependent pooling and cascaded rejection classifiers. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 26 June–1 July 2016; pp. 2129–2137.
- Cai, Z.; Fan, Q.; Feris, R.S.; Vasconcelos, N. A unified multi-scale deep convolutional neural network for fast object detection. In European Conference on Computer Vision; Springer: Berlin, Germany, 2016; pp. 354–370. [Google Scholar]
- Xiang, Y.; Choi, W.; Lin, Y.; Savarese, S. Subcategory-aware Convolutional Neural Networks for Object Proposals and Detection. arXiv 2016. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. arXiv 2015. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S. SSD: Single Shot MultiBox Detector. arXiv 2015. [Google Scholar]
- Hall, D.L.; Llinas, J. An introduction to multisensor data fusion. Proc. IEEE 1997, 85, 6–23. [Google Scholar] [CrossRef]
- Schoenberg, J.R.; Nathan, A.; Campbell, M. Segmentation of dense range information in complex urban scenes. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Taipei, Taiwan, 18–22 October 2010; pp. 2033–2038.
- Xiao, L.; Dai, B.; Liu, D.; Hu, T.; Wu, T. CRF based road detection with multi-sensor fusion. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Korea, 28 June–1 July 2015; pp. 192–198.
- Premebida, C.; Carreira, J.; Batista, J.; Nunes, U. Pedestrian detection combining rgb and dense lidar data. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 4112–4117.
- Felzenszwalb, P.F.; Girshick, R.B.; McAllester, D.; Ramanan, D. Object detection with discriminatively trained part-based models. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1627–1645. [Google Scholar] [CrossRef] [PubMed]
- Premebida, C.; Monteiro, G.; Nunes, U.; Peixoto, P. A lidar and vision-based approach for pedestrian and vehicle detection and tracking. In Proceedings of the 2007 IEEE Intelligent Transportation Systems Conference, Bellevue, WA, USA, 30 September–03 October 2007; pp. 1044–1049.
- Premebida, C.; Nunes, U. A multi-target tracking and GMM-classifier for intelligent vehicles. In Proceedings of the 2006 IEEE Intelligent Transportation Systems Conference, Toronto, ON, Canada, 17–20 September 2006; pp. 313–318.
- Eitel, A.; Springenberg, J.T.; Spinello, L.; Riedmiller, M.; Burgard, W. Multimodal deep learning for robust rgb-d object recognition. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 681–687.
- Schlosser, J.; Chow, C.K.; Kira, Z. Fusing LIDAR and images for pedestrian detection using convolutional neural networks. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 2198–2205.
- Kelly, A. Mobile Robotics; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Najjar, M.E.E. A Road-Matching Method for Precise Vehicle Localization Using Belief Theory and Kalman Filtering. Auton. Robots 2005, 19, 173–191. [Google Scholar] [CrossRef]
- Guivant, J.; Katz, R. Global urban localization based on road maps. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems (IROS), San Diego, CA, USA, 29 October–2 November 2007.
- Bosse, M.; Newman, P.; Leonard, J.; Soika, M.; Feiten, W.; Teller, S. An Atlas Framework for Scalable Mapping. In Proceedings of the IEEE International Conference on Robotics and Automation, Taipei, Taiwan, 14–19 September 2003; pp. 1899–1906.
- Grisetti, G. Improving grid-based slam with rao-blackwellized particle filters by adaptive proposals and selective resampling. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Barcelona, Spain, 18–22 April 2005; pp. 2443–2448.
- Thrun, S.; Fox, D.; Burgard, W.; Dellaert, F. Robust Monte Carlo Localization for Mobile Robots. Artifi. Intell. 2001, 1–2, 99–141. [Google Scholar] [CrossRef]
- Walter, M.R.; Eustice, R.M.; Leonard, J.J. Exactly sparse extended information filters for feature-based SLAM. Proc. IJCAI Worksh. Reason. Uncertain. Robot. 2001, 26, 17–26. [Google Scholar] [CrossRef]
- Murphy, K. Bayesian Map Learning in Dynamic Environments. In Neural Info. Proc. Systems (NIPS); MIT Press: Cambridge, MA, USA; pp. 1015–1021.
- Grisetti, G.; Stachniss, C.; Burgard, W. Improved techniques for grid mapping with rao-blackwellized particle filters. IEEE Trans. Robot. 2007, 23, 2007. [Google Scholar] [CrossRef]
- Lu, F.; Milios, E. Globally Consistent Range Scan Alignment for Environment Mapping. Auton. Robots 1997, 4, 333–349. [Google Scholar] [CrossRef]
- Frese, U. Closing a million-landmarks loop. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 5032–5039.
- Grisetti, G.; Stachniss, C.; Burgard, W. Non-linear constraint network optimization for efficient map learning. IEEE Trans. Intell. Transp. Syst. 2009, 10, 428–439. [Google Scholar] [CrossRef]
- Kaess, M.; Ranganathan, A.; Dellaert, F. iSAM: Incremental Smoothing and Mapping. IEEE Trans. Robot. 2008, 24, 1365–1378. [Google Scholar] [CrossRef]
- Kaess, M.; Johannsson, H.; Roberts, R.; Ila, V.; Leonard, J.; Dellaert, F. iSAM2: Incremental Smoothing and Mapping Using the Bayes Tree. IJRR Int. J. Robot. Res. 2012, 31, 217–236. [Google Scholar] [CrossRef]
- Kummerle, R.; Grisetti, G.; Strasdat, H.; Konolige, K.; Burgard, W. G2o: A general framework for graph optimization. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 3607–3613.
- Grisetti, G.; Kümmerle, R.; Stachniss, C.; Burgard, W. A Tutorial on Graph-Based SLAM. IEEE Intell. Transp. Syst. Mag. 2010, 2, 31–43. [Google Scholar] [CrossRef]
- Callmer, J.; Ramos, F.; Nieto, J. Learning to detect loop closure from range data. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 15–22.
- Newman, P.; Cole, D.; Ho, K. Outdoor slam using visual appearance and laser ranging. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; pp. 1180–1187.
- Sünderhauf, N.; Protzel, P. Switchable Constraints for Robust Pose Graph SLAM. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems (IROS), Algarve, Portugal, 7–12 October 2012.
- Olson, E.; Agarwal, P. Inference on Networks of Mixtures for Robust Robot Mapping. Int. J. Robot. Res. 2013, 32, 826–840. [Google Scholar] [CrossRef]
- Latif, Y.; Cadena, C.; Neira, J. Robust loop closing over time. In Proceedings of the Robotics: Science and Systems (RSS), Sydney, Australia, 9–13 July 2012.
- Belongie, S.; Malik, J.; Puzicha, J. Shape Matching and Object Recognition Using Shape Contexts. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 24, 509–522. [Google Scholar] [CrossRef]
- Steder, B.; Grisetti, G.; Burgard, W. Robust place recognition for 3D range data based on point features. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Anchorage, AK, USA, 3–8 May 2010.
- Huber, D.; Hebert, M. Fully Automatic Registration Of Multiple 3D Data Sets. Image Vision Comput. 2001, 21, 637–650. [Google Scholar] [CrossRef]
- Magnusson, M.; Andreasson, H.; Nuchter, A.; Lilienthal, A.J. Appearance-based loop detection from 3D laser data using the normal distributions transform. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 23–28.
- Mozos, O.M.; Stachniss, C.; Burgard, W. Supervised Learning of Places from Range Data Using AdaBoost. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 1730–1735.
- Óscar Martínez, M.; Rottmann, A.; Triebel, R.; Jensfelt, P.; Burgard, W. Supervised semantic labeling of places using information extracted from sensor data. Robot. Auton. Syst. 2007, 55, 391–402. [Google Scholar] [CrossRef]
- Posner, I.; Schroeter, D.; Newman, P. Online generation of scene descrip tions in urban environments. Rob. Autom. Syst. 2008, 56, 901–914. [Google Scholar] [CrossRef]
- Sengupta, S.; Sturgess, P.; Ladický, L.; Torr, P.H.S. Automatic dense visual semantic mapping from street-level imagery. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Algarve, Portugal, 7–11 October 2012; pp. 857–862.
- Nüchter, A.; Hertzberg, J. Towards semantic maps for mobile robots. Rob. Autom. Syst. 2008, 56, 915–926. [Google Scholar] [CrossRef]
- Galindo, C.; Saffiotti, A.; Coradeschi, S.; Buschka, P.; Fernandez-Madrigal, J.A.; Gonzalez, J. Multi-hierarchical semantic maps for mobile robotics. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 2278–2283.
- Vasudevan, S.; Siegwart, R. Bayesian space conceptualization and place classification for semantic maps in mobile robotics. Rob. Autom. Syst. 2008, 56, 522–537. [Google Scholar] [CrossRef]
- Xie, D.; Todorovic, S.; Zhu, S.C. Inferring Dark Matter and Dark Energy from Videos. In Proceedings of the 2013 IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 2224–2231.
- Suganuma, N.; Uozumi, T. Precise position estimation of autonomous vehicle based on map-matching. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; pp. 296–301.
- Hentschel, M.; Wagner, B. Autonomous robot navigation based on OpenStreetMap geodata. In Proceedings of the 13th International IEEE Conference on Intelligent Transportation Systems, San Diego, CA, USA, 19–22 September 2010; pp. 1645–1650.
- Wulf, O.; Arras, K.O.; Christensen, H.I.; Wagner, B. 2D Mapping of Cluttered Indoor Environments by Means of 3D Perception. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; pp. 4204–4209.
- Levinson, J.; Thrun, S. Robust Vehicle Localization in Urban Environments Using Probabilistic Maps. In Proceedings of the IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–8 May 2010; pp. 4372–4378.
- Baldwin, I.; Newman, P. Road vehicle localization with 2D push-broom LIDAR and 3D priors. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St. Paul, MN, USA, 14–18 May 2012; pp. 2611–2617.
- Wulf, O.; Lecking, D.; Wagner, B. Robust Self-Localization in Industrial Environments Based on 3D Ceiling Structures. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; p. 8.
- Lecking, D.; Wulf, O.; Wagner, B. Localization in a wide range of industrial environments using relative 3D ceiling features. In Proceedings of the 2008 IEEE International Conference on Emerging Technologies and Factory Automation, Hamburg, Germany, 15–18 September 2008; pp. 333–337.
- Ozguner, U.; Acarman, T.; Redmill, K. Autonomous Ground Vehicles; Artech House: Norwood, MA, USA, 2011. [Google Scholar]
- Buehler, M.; Iagnemma, K.; Singh, S. The DARPA Urban Challenge: Autonomous Vehicles in City Traffic; Springer: Berlin, Germany, 2009; Volume 56. [Google Scholar]
- Bacha, A.; Bauman, C.; Faruque, R.; Fleming, M.; Terwelp, C.; Reinholtz, C.; Hong, D.; Wicks, A.; Alberi, T.; Anderson, D.; et al. Odin: Team victorTango’s entry in the DARPA urban challenge. J. Field Robot. 2008, 25, 467–492. [Google Scholar] [CrossRef]
- Kuwata, Y.; Teo, J.; Fiore, G.; Karaman, S.; Frazzoli, E.; How, J.P. Real-time motion planning with applications to autonomous urban driving. IEEE Trans. Control Syst. Technol. 2009, 17, 1105–1118. [Google Scholar] [CrossRef]
- Bohren, J.; Foote, T.; Keller, J.; Kushleyev, A.; Lee, D.; Stewart, A.; Vernaza, P.; Derenick, J.; Spletzer, J.; Satterfield, B. Little Ben: The Ben Franklin racing team’s entry in the 2007 DARPA urban challenge. J. Field Robot. 2008, 25, 598–614. [Google Scholar] [CrossRef]
- Miller, I.; Campbell, M.; Huttenlocher, D.; Kline, F.R.; Nathan, A.; Lupashin, S.; Catlin, J.; Schimpf, B.; Moran, P.; Zych, N.; et al. Team Cornell’s Skynet: Robust perception and planning in an urban environment. J. Field Robot. 2008, 25, 493–527. [Google Scholar] [CrossRef]
- Campbell, M.; Egerstedt, M.; How, J.P.; Murray, R.M. Autonomous driving in urban environments: Approaches, lessons and challenges. Phil. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2010, 368, 4649–4672. [Google Scholar] [CrossRef] [PubMed]
- Leonard, J.; How, J.; Teller, S.; Berger, M.; Campbell, S.; Fiore, G.; Fletcher, L.; Frazzoli, E.; Huang, A.; Karaman, S.; et al. A perception-driven autonomous urban vehicle. J. Field Robot. 2008, 25, 727–774. [Google Scholar] [CrossRef]
- Challenge, D.U. Route Network Definition File (RNDF) and Mission Data File (MDF) formats, 2007. Available online: https://www.grandchallenge.org/grandchallenge/docs/RNDF_MDF_Formats_031407.pdf (accessed on 15 February 2015).
- Qin, B.; Chong, Z.J.; Bandyopadhyay, T.; Ang, M.H. Metric mapping and topo-metric graph learning of urban road network. In Proceedings of the 2013 6th IEEE Conference on Robotics, Automation and Mechatronics (RAM), Manila, Philippines, 12–15 November 2013; pp. 119–123.
- Liu, W.; Kim, S.W.; Ang, M.H. Probabilistic road context inference for autonomous vehicles. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 1640–1647.
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Bast, H.; Delling, D.; Goldberg, A.; Müller-Hannemann, M.; Pajor, T.; Sanders, P.; Wagner, D.; Werneck, R.F. Route planning in transportation networks. arXiv 2015. [Google Scholar]
- Baker, C.R.; Dolan, J.M. Traffic interaction in the urban challenge: Putting boss on its best behavior. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 1752–1758.
- Broggi, A.; Debattisti, S.; Panciroli, M.; Porta, P.P. Moving from analog to digital driving. In Proceedings of the 2013 IEEE Intelligent Vehicles Symposium (IV), Gold Coast City, Australia, 23–26 June 2013; pp. 1113–1118.
- Furda, A.; Vlacic, L. Towards increased road safety: Real-time decision making for driverless city vehicles. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; pp. 2421–2426.
- Furda, A.; Vlacic, L. Enabling safe autonomous driving in real-world city traffic using multiple criteria decision making. IEEE Intell. Transp. Syst. Mag. 2011, 3, 4–17. [Google Scholar] [CrossRef]
- Wongpiromsarn, T.; Karaman, S.; Frazzoli, E. Synthesis of provably correct controllers for autonomous vehicles in urban environments. In Proceedings of the 2011 14th International IEEE Conference on Intelligent Transportation Systems (ITSC), Washington, DC, USA, 5–7 October 2011; pp. 1168–1173.
- Chaudhari, P.; Wongpiromsarny, T.; Frazzoli, E. Incremental minimum-violation control synthesis for robots interacting with external agents. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 1761–1768.
- Castro, L.I.R.; Chaudhari, P.; Tumova, J.; Karaman, S.; Frazzoli, E.; Rus, D. Incremental sampling-based algorithm for minimum-violation motion planning. In Proceedings of the 52nd IEEE Conference on Decision and Control, Florence, Italy, 10–13 December 2013; pp. 3217–3224.
- Latombe, J.C. Robot Motion Planning; Springer Science & Business Media: Berlin, Germany, 2012; Volume 124. [Google Scholar]
- Reif, J.H. Complexity of the mover’s problem and generalizations. In Proceedings of the 20th Annual Symposium on Foundations of Computer Science, San Juan, Puerto Rico, 29–31 October 1979; pp. 421–427.
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- LaValle, S.M.; Kuffner, J.J. Randomized kinodynamic planning. Int. J. Robot. Res. 2001, 20, 378–400. [Google Scholar] [CrossRef]
- Kavraki, L.; Latombe, J.C. Randomized preprocessing of configuration for fast path planning. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; pp. 2138–2145.
- Xu, W.; Wei, J.; Dolan, J.M.; Zhao, H.; Zha, H. A real-time motion planner with trajectory optimization for autonomous vehicles. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA), St. Paul, MN, USA, 14–18 May 2012; pp. 2061–2067.
- Wongpiromsarn, T.; Topcu, U.; Murray, R.M. Receding horizon control for temporal logic specifications. In Proceedings of the 13th ACM International Conference on Hybrid Systems: Computation and Control, Stockholm, Sweden, 12–16 April 2010; pp. 101–110.
- Tumova, J.; Hall, G.C.; Karaman, S.; Frazzoli, E.; Rus, D. Least-violating control strategy synthesis with safety rules. In Proceedings of the 16th International Conference on Hybrid Systems: Computation and Control, Philadelphia, PA, USA, 8–11 April 2013; pp. 1–10.
- Bandyopadhyay, T.; Won, K.S.; Frazzoli, E.; Hsu, D.; Lee, W.S.; Rus, D. Intention-aware motion planning. In Algorithmic Foundations of Robotics X; Springer: Berlin, Germany, 2013; pp. 475–491. [Google Scholar]
- Bandyopadhyay, T.; Jie, C.Z.; Hsu, D.; Ang, M.H., Jr.; Rus, D.; Frazzoli, E. Intention-aware pedestrian avoidance. In Experimental Robotics; Springer: Berlin, Germany, 2013; pp. 963–977. [Google Scholar]
- Ong, S.C.; Png, S.W.; Hsu, D.; Lee, W.S. Planning under uncertainty for robotic tasks with mixed observability. Int. J. Robot. Res. 2010, 29, 1053–1068. [Google Scholar] [CrossRef]
- Kurniawati, H.; Hsu, D.; Lee, W.S. SARSOP: Efficient Point-Based POMDP Planning by Approximating Optimally Reachable Belief Spaces; Robotics: Science and Systems: Zurich, Switzerland, 2008; Volume 2008. [Google Scholar]
- Kaelbling, L.P.; Littman, M.L.; Cassandra, A.R. Planning and acting in partially observable stochastic domains. Artif. Intell. 1998, 101, 99–134. [Google Scholar] [CrossRef]
- Bai, H.; Hsu, D.; Lee, W.S. Integrated perception and planning in the continuous space: A POMDP approach. Int. J. Robot. Res. 2014, 33, 1288–1302. [Google Scholar] [CrossRef]
- Kavraki, L.E.; Svestka, P.; Latombe, J.C.; Overmars, M.H. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef]
- LaValle, S.M. Rapidly-exploring random trees: A new tool for path planning. 1998. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.35.1853&rep=rep1&type=pdf (accessed on 15 February 2015).
- Kuffner, J.J.; LaValle, S.M. RRT-connect: An efficient approach to single-query path planning. In Proceedings of the IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 24–28 April 2000; Volume 2, pp. 995–1001.
- Urmson, C.; Simmons, R.G. Approaches for heuristically biasing RRT growth. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems, Las Vegas, Nevada, 27–31 October 2003; Volume 2, pp. 1178–1183.
- Janson, L.; Schmerling, E.; Clark, A.; Pavone, M. Fast marching tree: A fast marching sampling-based method for optimal motion planning in many dimensions. arXiv 2015. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Littlefield, Z.; Bekris, K.E. Sparse methods for efficient asymptotically optimal kinodynamic planning. In Algorithmic Foundations of Robotics XI; Springer: Berlin, Germany, 2015; pp. 263–282. [Google Scholar]
- Blackmore, L.; Ono, M.; Williams, B.C. Chance-constrained optimal path planning with obstacles. IEEE Trans. Robot. 2011, 27, 1080–1094. [Google Scholar] [CrossRef]
- Huynh, V.A.; Frazzoli, E. Probabilistically-sound and asymptotically-optimal algorithm for stochastic control with trajectory constraints. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 1486–1493.
- Roy, N.; Burgard, W.; Fox, D.; Thrun, S. Coastal navigation-mobile robot navigation with uncertainty in dynamic environments. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation, Detroit, MI, USA, 10–15 May 1999; Volume 1, pp. 35–40.
- Aoude, G.S.; Luders, B.D.; Levine, D.S.; How, J.P. Threat-aware path planning in uncertain urban environments. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Taipei, Taiwan, 18–22 October 2010; pp. 6058–6063.
- Luders, B.D.; Aoude, G.S.; Joseph, J.M.; Roy, N.; How, J.P. Probabilistically safe avoidance of dynamic obstacles with uncertain motion patterns. Available online: https://dspace.mit.edu/bitstream/handle/1721.1/64738/CCRRTwithRRGP2011.pdf?sequence=1&origin=publication_detail (accessed on 15 February 2015).
- Levinson, J.; Askeland, J.; Becker, J.; Dolson, J.; Held, D.; Kammel, S.; Kolter, J.Z.; Langer, D.; Pink, O.; Pratt, V.; et al. Towards fully autonomous driving: Systems and algorithms. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; pp. 163–168.
- Van Den Berg, J.; Abbeel, P.; Goldberg, K. LQG-MP: Optimized path planning for robots with motion uncertainty and imperfect state information. Int. J. Robot. Res. 2011, 30, 895–913. [Google Scholar] [CrossRef]
- Du Toit, N.E.; Burdick, J.W. Robotic motion planning in dynamic, cluttered, uncertain environments. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation (ICRA), Anchorage, AK, USA, 3–8 May 2010; pp. 966–973.
- Ferguson, D.; Howard, T.M.; Likhachev, M. Motion planning in urban environments. J. Field Robot. 2008, 25, 939–960. [Google Scholar] [CrossRef]
- Van Den Berg, J.; Overmars, M. Planning time-minimal safe paths amidst unpredictably moving obstacles. Int. J. Robot. Res. 2008, 27, 1274–1294. [Google Scholar] [CrossRef]
- Zucker, M.; Kuffner, J.; Branicky, M. Multipartite RRTs for rapid replanning in dynamic environments. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 1603–1609.
- Fiorini, P.; Shiller, Z. Motion planning in dynamic environments using velocity obstacles. Int. J. Robot. Res. 1998, 17, 760–772. [Google Scholar] [CrossRef]
- Van den Berg, J.; Lin, M.; Manocha, D. Reciprocal velocity obstacles for real-time multi-agent navigation. In Proceedings of the IEEE International Conference on Robotics and Automation, Nice, France, 22–26 September 2008; pp. 1928–1935.
- Van Den Berg, J.; Snape, J.; Guy, S.J.; Manocha, D. Reciprocal collision avoidance with acceleration-velocity obstacles. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 3475–3482.
- Alonso-Mora, J.; Breitenmoser, A.; Rufli, M.; Beardsley, P.; Siegwart, R. Optimal reciprocal collision avoidance for multiple non-holonomic robots. In Distributed Autonomous Robotic Systems; Springer: Berlin, Germany, 2013; pp. 203–216. [Google Scholar]
- Hsu, D.; Kindel, R.; Latombe, J.C.; Rock, S. Randomized kinodynamic motion planning with moving obstacles. Int. J. Robot. Res. 2002, 21, 233–255. [Google Scholar] [CrossRef]
- Kant, K.; Zucker, S.W. Toward efficient trajectory planning: The path-velocity decomposition. Int. J. Robot. Res. 1986, 5, 72–89. [Google Scholar] [CrossRef]
- Liu, W.; Weng, Z.; Chong, Z.; Shen, X.; Pendleton, S.; Qin, B.; Fu, G.M.J.; Ang, M.H. Autonomous vehicle planning system design under perception limitation in pedestrian environment. In Proceedings of the 2015 IEEE 7th International Conference on Cybernetics and Intelligent Systems (CIS) and IEEE Conference on Robotics, Automation and Mechatronics (RAM), Angkor Wat, Cambodia, 15–17 July 2015; pp. 159–166.
- Karaman, S.; Frazzoli, E. Sampling-based optimal motion planning for non-holonomic dynamical systems. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013; pp. 5041–5047.
- Webb, D.J.; van den Berg, J. Kinodynamic RRT*: Asymptotically optimal motion planning for robots with linear dynamics. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013; pp. 5054–5061.
- Schmerling, E.; Janson, L.; Pavone, M. Optimal sampling-based motion planning under differential constraints: The driftless case. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2368–2375.
- Dubins, L.E. On curves of minimal length with a constraint on average curvature, and with prescribed initial and terminal positions and tangents. Am. J. Math. 1957, 79, 497–516. [Google Scholar] [CrossRef]
- Reeds, J.; Shepp, L. Optimal paths for a car that goes both forwards and backwards. Pac. J. Math. 1990, 145, 367–393. [Google Scholar] [CrossRef]
- Jeon, J.H.; Karaman, S.; Frazzoli, E. Optimal sampling-based Feedback Motion Trees among obstacles for controllable linear systems with linear constraints. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 4195–4201.
- Allen, R.E.; Clark, A.A.; Starek, J.A.; Pavone, M. A machine learning approach for real-time reachability analysis. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2014), Chicago, IL, USA, 14–18 September 2014; pp. 2202–2208.
- Shkolnik, A.; Walter, M.; Tedrake, R. Reachability-guided sampling for planning under differential constraints. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 2859–2865.
- Chen, C.; Rickert, M.; Knoll, A. Kinodynamic motion planning with Space-Time Exploration Guided Heuristic Search for car-like robots in dynamic environments. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–3 October 2015; pp. 2666–2671.
- Narayanan, V.; Phillips, M.; Likhachev, M. Anytime safe interval path planning for dynamic environments. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Algarve, Portugal, 7–11 October 2012; pp. 4708–4715.
- Gonzalez, J.P.; Dornbush, A.; Likhachev, M. Using state dominance for path planning in dynamic environments with moving obstacles. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA), St. Paul, MN, USA, 14–18 May 2012; pp. 4009–4015.
- Bouraine, S.; Fraichard, T.; Azouaoui, O.; Salhi, H. Passively safe partial motion planning for mobile robots with limited field-of-views in unknown dynamic environments. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 3576–3582.
- Bruce, J.; Veloso, M. Real-time randomized path planning for robot navigation. In Proceedings of the 2002 IEEE/RSJ International Conference on Intelligent Robots and Systems, Lausanne, Switzerland, 30 September–4 October 2002; Volume 3, pp. 2383–2388.
- Ferguson, D.; Kalra, N.; Stentz, A. Replanning with rrts. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; pp. 1243–1248.
- Otte, M.; Frazzoli, E. RRTX: Real-Time Motion Planning/Replanning for Environments with Unpredictable Obstacles. In Algorithmic Foundations of Robotics XI; Springer: Berlin, Germany, 2015; pp. 461–478. [Google Scholar]
- Pendleton, S.; Uthaicharoenpong, T.; Chong, Z.J.; Ming, G.; Fu, J.; Qin, B.; Liu, W.; Shen, X.; Weng, Z.; Kamin, C.; et al. Autonomous Golf Cars for Public Trial of Mobility-on-Demand Service. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–3 October 2015; pp. 1164–1171.
- Martinez-Gomez, L.; Fraichard, T. Benchmarking Collision Avoidance Schemes for Dynamic Environments. In Proceedings of the ICRA Workshop on Safe Navigation in Open and Dynamic Environments, Kobe, Japan, 12–17 May 2009.
- Martinez-Gomez, L.; Fraichard, T. Collision avoidance in dynamic environments: An ics-based solution and its comparative evaluation. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 100–105.
- Large, F.; Laugier, C.; Shiller, Z. Navigation among moving obstacles using the NLVO: Principles and applications to intelligent vehicles. Auton. Robots 2005, 19, 159–171. [Google Scholar] [CrossRef]
- Seder, M.; Petrovic, I. Dynamic window based approach to mobile robot motion control in the presence of moving obstacles. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 1986–1991.
- Mayne, D.Q. Model predictive control: Recent developments and future promise. Automatica 2014, 50, 2967–2986. [Google Scholar] [CrossRef]
- Hrovat, D.; Di Cairano, S.; Tseng, H.; Kolmanovsky, I. The development of Model Predictive Control in automotive industry: A survey. In Proceedings of the 2012 IEEE International Conference on Control Applications, Dubrovnik, Croatia, 3–5 October 2012; pp. 295–302.
- Borrelli, F.; Bemporad, A.; Fodor, M.; Hrovat, D. An MPC/hybrid system approach to traction control. IEEE Trans. Control Syst. Technol. 2006, 14, 541–552. [Google Scholar] [CrossRef]
- Falcone, P.; Borrelli, F. A model predictive control approach for combined braking and steering in autonomous vehicles. In Proceedings of the IEEE 2007 Mediterranean Conference on Control & Automation (MED’07), Athens, Greece, 27–29 June 2007; pp. 1–6.
- Falcone, P.; Borrelli, F.; Asgari, J.; Tseng, H.E.; Hrovat, D. Predictive Acive Steering Control for Autonomous Vehicle Systems. Control 2007, 15, 566–580. [Google Scholar]
- Liu, C.; Carvalho, A.; Schildbach, G.; Hedrick, J.K. Stochastic Predictive Control for Lane Keeping Assistance Systems Using A Linear Time-Varying Model. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 3355–3360.
- Salazar, M.; Alessandretti, A.; Aguiar, A.P.; Jones, C.N. An Energy Efficient Trajectory Tracking Control of Car-like Vehicles. Annu. Conf. Decis. Control 2015, 1, 3675–3680. [Google Scholar]
- Faulwasser, T.; Findeisen, R. Nonlinear Model Predictive Control for Constrained Output Path Following. IEEE Trans. Autom. Control 2016, 61, 1026–1039. [Google Scholar] [CrossRef]
- Raffo, G.; Gomes, G.; Normey-Rico, J.; Kelber, C.; Becker, L. A Predictive Controller for Autonomous Vehicle Path Tracking. IEEE Trans. Intell. Transp. Syst. 2009, 10, 92–102. [Google Scholar] [CrossRef]
- Howard, T.M.; Green, C.; Kelly, A. Receding horizon model-predictive control for mobile robot navigation of intricate paths. In Proceedings of the 7th International Conferences on Field and Service Robotics, Cambridge, MD, USA, July 2010; pp. 69–78.
- Berntorp, K.; Magnusson, F. Hierarchical predictive control for ground-vehicle maneuvering. In Proceedings of the American Control Conference, Chicago, IL, USA, 1–3 July 2015; pp. 2771–2776.
- Verschueren, R.; Bruyne, S.D.; Zanon, M.; Janick, V.F.; Moritz, D. Towards Time-Optimal Race Car Driving using Nonlinear MPC in Real-Time. In Proceedings of the 2014 IEEE 53rd Annual Conference on Decision and Control (CDC), Los Angeles, CA, USA, 15–17 December 2014; pp. 2505–2510.
- Hespanha, J.P. Trajectory-tracking and path-following of underactuated autonomous vehicles with parametric modeling uncertainty. IEEE Trans. Autom. Control 2007, 52, 1362–1379. [Google Scholar]
- Kunz, T.; Stilman, M. Time-Optimal Trajectory Generation for Path Following with Bounded Acceleration and Velocity; MIT Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Talvala, K.L.R.; Kritayakirana, K.; Gerdes, J.C. Pushing the limits: From lanekeeping to autonomous racing. Annu. Rev. Control 2011, 35, 137–148. [Google Scholar] [CrossRef]
- Funke, J.; Brown, M.; Erlien, S.M.; Gerdes, J.C. Prioritizing collision avoidance and vehicle stabilization for autonomous vehicles. In Proceedings of the IEEE Intelligent Vehicles Symposium, Seoul, Korea, 28 June–1 July 2015; pp. 1134–1139.
- Erlien, S.M.; Funke, J.; Gerdes, J.C. Incorporating non-linear tire dynamics into a convex approach to shared steering control. In Proceedings of the American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 3468–3473.
- Subosits, J.; Gerdes, J.C. Autonomous vehicle control for emergency maneuvers: The effect of topography. In Proceedings of the American Control Conference, Chicago, IL, USA, 1–3 July 2015; pp. 1405–1410.
- Park, M.W.; Lee, S.W.; Han, W.Y. Development of Lateral Control System for Autonomous Vehicle Based on Adaptive Pure Pursuit Algorithm. In Proceedings of the International Conference on Control, Automation and Systems, Seoul, Korea, 22–25 October 2014; pp. 1443–1447.
- Wit, J.S. Vector Pursuit Path Tracking for Autonomous Ground Vehicles. Ph.D. Thesis, University of Florida, Gainesville, FL, USA, 2000. [Google Scholar]
- Campbell, S.F. Steering Control of an Autonomous Ground Vehicle with Application to the DARPA Urban Challenge. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2005. [Google Scholar]
- Kuwata, Y.; Teo, J.; Karaman, S. Motion planning in complex environments using closed-loop prediction. In Proceedings of the AIAA Guidance, Honolulu, HI, USA, 18–21 August 2008.
- Ollero, A.; Heredia, G.; Mercedes, A.R. Stability analysis of mobile robot path tracking. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Pittsburgh, PA, USA, 5–9 August 1995; Volume 3, pp. 461–466.
- Hoffmann, G.M.; Tomlin, C.J.; Montemerlo, M.; Thrun, S. Autonomous automobile trajectory tracking for off-road driving: Controller design, experimental validation and racing. In Proceedings of the American Control Conference, New York, NY, USA, 9–13 July 2007; pp. 2296–2301.
- Snider, J.M. Automatic Steering Methods for Autonomous Automobile Path Tracking. Available online: http://www.ri.cmu.edu/pub_files/2009/2/Automatic_Steering_Methods_for_Autonomous_Automobile_Path_Tracking.pdf (accessed on 15 February 2015).
- De Luca, A.; Oriolo, G.; Samson, C. Feedback Control of a Nonholonomic Car-like Robot. In Robot Motion Planning and Control; Laumond, J.P., Ed.; Springer: Berlin, Germany, 1998; Chapter 4; pp. 171–253. [Google Scholar]
- Murray, R.; Sastry, S. Steering nonholonomic systems in chained form. In Proceedings of the 30th IEEE Conference on Decision and Control, Brighton, UK, 11–13 December 1991; pp. 1121–1126.
- Kim, E.; Kim, J.; Sunwoo, M. Model predictive control strategy for smooth path tracking of autonomous vehicles with steering actuator dynamics. Int. J. Automot. Technol. 2014, 15, 1155–1164. [Google Scholar] [CrossRef]
- Falcone, P.; Borrelli, F.; Tseng, H.E.; Asgari, J.; Hrovat, D. Linear time-varying model predictive control and its application to active steering systems: Stability analysis and experimental validation. Int. J. Robust Nonlinear Control 2008, 18, 862–875. [Google Scholar] [CrossRef]
- Gerla, M.; Kleinrock, L. Vehicular networks and the future of the mobile internet. Comput. Netw. 2011, 55, 457–469. [Google Scholar] [CrossRef]
- Kim, S.W.; Chong, Z.J.; Qin, B.; Shen, X.; Cheng, Z.; Liu, W.; Ang, M.H. Cooperative perception for autonomous vehicle control on the road: Motivation and experimental results. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Tokyo, Japan, 3–7 November 2013; pp. 5059–5066.
- Kim, S.W.; Qin, B.; Chong, Z.J.; Shen, X.; Liu, W.; Ang, M.H.; Frazzoli, E.; Rus, D. Multivehicle Cooperative Driving Using Cooperative Perception: Design and Experimental Validation. IEEE Trans. Intell. Transp. Syst. 2015, 16, 663–680. [Google Scholar] [CrossRef]
- Shen, X.; Chong, Z.; Pendleton, S.; James Fu, G.; Qin, B.; Frazzoli, E.; Ang, M.H., Jr. Teleoperation of On-Road Vehicles via Immersive Telepresence Using Off-the-shelf Components. In Intelligent Autonomous Systems 13; Advances in Intelligent Systems and Computing; Springer International Publishing: Berlin, Germany, 2016; Volume 302, pp. 1419–1433. [Google Scholar]
- Tachet, R.; Santi, P.; Sobolevsky, S.; Reyes-Castro, L.I.; Frazzoli, E.; Helbing, D.; Ratti, C. Revisiting street intersections using slot-based systems. PLoS ONE 2016, 11, e0149607. [Google Scholar] [CrossRef] [PubMed]
- Knuth, J.; Barooah, P. Distributed collaborative localization of multiple vehicles from relative pose measurements. In Proceedings of the 47th Annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 30 Septermber–2 October 2009; pp. 314–321.
- Rekleitis, I.M.; Dudek, G.; Milios, E.E. Multi-robot cooperative localization: a study of trade-offs between efficiency and accuracy. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Lausanne, Switzerland, 30 September–4 October 2002; Volume 3, pp. 2690–2695.
- Madhavan, R.; Fregene, K.; Parker, L.E. Distributed heterogeneous outdoor multi-robot localization. In Proceedings of the IEEE International Conference on Robotics and Automation, Washington, DC, USA, 11–15 May 2002; Volume 1, pp. 374–381.
- Fox, D.; Burgard, W.; Kruppa, H.; Thrun, S. Collaborative multi-robot localization. In Mustererkennung 1999; Springer: Berlin, Germany, 1999; pp. 15–26. [Google Scholar]
- Martinelli, A.; Pont, F.; Siegwart, R. Multi-Robot Localization Using Relative Observations. In Proceedings of the IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 2797–2802.
- Fox, D.; Burgard, W.; Kruppa, H.; Thrun, S. A probabilistic approach to collaborative multi-robot localization. Auton. Robots 2000, 8, 325–344. [Google Scholar] [CrossRef]
- Walls, J.; Cunningham, A.; Eustice, R. Cooperative localization by factor composition over a faulty low-bandwidth communication channel. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 401–408.
- Webster, S.; Walls, J.; Whitcomb, L.; Eustice, R. Decentralized Extended Information Filter for Single-Beacon Cooperative Acoustic Navigation: Theory and Experiments. IEEE Trans. Robot. 2013, 29, 957–974. [Google Scholar] [CrossRef]
- Paull, L.; Seto, M.; Leonard, J. Decentralized cooperative trajectory estimation for autonomous underwater vehicles. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2014), Chicago, IL, USA, 14–18 September 2014; pp. 184–191.
- Li, H.; Nashashibi, F. Multi-vehicle cooperative localization using indirect vehicle-to-vehicle relative pose estimation. In Proceedings of the 2012 IEEE International Conference on Vehicular Electronics and Safety (ICVES), Istanbul, Turkey, 4–27 July 2012; pp. 267–272.
- Shen, X.; Pendleton, S.; Ang, M.H. Efficient L-shape fitting of laser scanner data for vehicle pose estimation. In Proceedings of the 2015 IEEE 7th International Conference on Cybernetics and Intelligent Systems (CIS) and IEEE Conference on Robotics, Automation and Mechatronics (RAM), Angkor Wat, Cambodia, 15–17 July 2015; pp. 173–178.
- Shen, X.; Pendleton, S.; Ang, M.H., Jr. Scalable Cooperative Localization with Minimal Sensor Configuration. In Distributed Autonomous Robotic Systems; Springer: Berlin, Germany, 2016; pp. 89–104. [Google Scholar]
- Switkes, J.P.; Gerdes, J.C.; Berdichevsky, G.; Berdichevsky, E. Systems and Methods for Semi-Autonomous Vehicular Convoys. U.S. Patent 8,744,666, 3 June 2014. [Google Scholar]
- Durrant-Whyte, H. A Beginner’s Guide to Decentralised Data Fusion. In Technical Document of Australian Centre for Field Robotics; University of Sydney: Sydney, Australia, 2000; pp. 1–27. [Google Scholar]
- Leung, K.; Barfoot, T.; Liu, H. Decentralized Localization of Sparsely-Communicating Robot Networks: A Centralized-Equivalent Approach. IEEE Trans. Robot. 2010, 26, 62–77. [Google Scholar] [CrossRef]
- Li, H.; Nashashibi, F. Cooperative Multi-Vehicle Localization Using Split Covariance Intersection Filter. IEEE Intell. Transp. Syst. Mag. 2013, 5, 33–44. [Google Scholar] [CrossRef]
- Shen, X.; Andersen, H.; Leong, W.; Kong, H.; Ang, M.H.; Rus, D. A General Framework for Multi-vehicle Cooperative Localization Using Pose Graph. IEEE Trans. Intell. Transp. Syst. 2016. submitted. [Google Scholar]
- Clark, C.M.; Rock, S.M.; Latombe, J.C. Motion planning for multiple mobile robots using dynamic networks. In Proceedings of the IEEE International Conference on Robotics and Automation, Taipei, Taiwan, 14–19 September 2003; Volume 3, pp. 4222–4227.
- Bennewitz, M.; Burgard, W.; Thrun, S. Optimizing schedules for prioritized path planning of multi-robot systems. In Proceedings of the IEEE International Conference on Robotics and Automation, Seoul, Korea, 21–26 May 2001; Volume 1, pp. 271–276.
- Van Den Berg, J.P.; Overmars, M.H. Prioritized motion planning for multiple robots. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 430–435.
- Velagapudi, P.; Sycara, K.; Scerri, P. Decentralized prioritized planning in large multirobot teams. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Taipei, Taiwan, 18–22 October 2010; pp. 4603–4609.
- LaValle, S.M.; Hutchinson, S.A. Optimal motion planning for multiple robots having independent goals. IEEE Trans. Robot. Autom. 1998, 14, 912–925. [Google Scholar] [CrossRef]
- Guo, Y.; Parker, L.E. A distributed and optimal motion planning approach for multiple mobile robots. In Proceedings of the IEEE International Conference on Robotics and Automation, Washington, DC, USA, 11–15 May 2002; Volume 3, pp. 2612–2619.
- Shen, X.; Chong, Z.J.; Pendleton, S.; Liu, W.; Qin, B.; Fu, G.M.J.; Ang, M.H. Multi-vehicle motion coordination using v2v communication. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Korea, 28 June–1 July 2015; pp. 1334–1341.
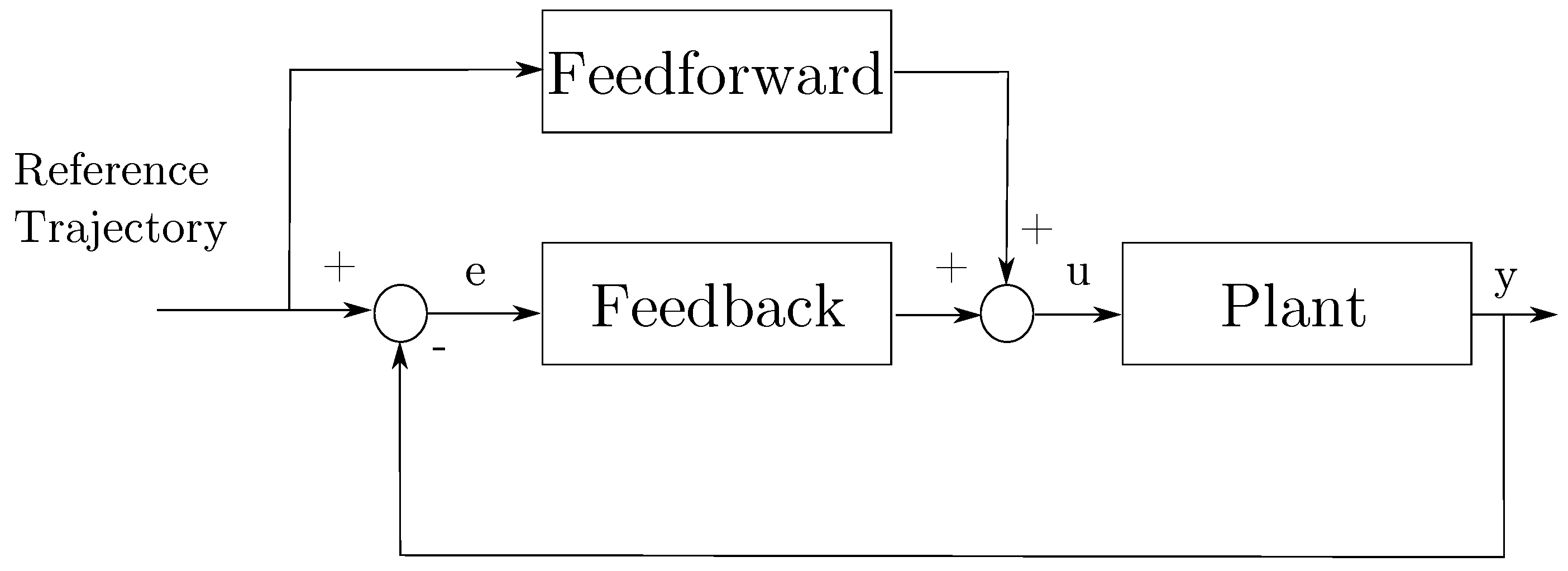
| Feedback | Feedforward | |
|---|---|---|
| Removes Unpredictable Errors and Disturbances | (+) yes | (−) no |
| Removes Predictable Errors and Disturbances | (−) no | (+) yes |
| Removes Errors and Disturbances Before They Happen | (−) no | (+) yes |
| Requires Model of a System | (+) no | (−) yes |
| Affects Stability of the System | (−) yes | (+) no |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pendleton, S.D.; Andersen, H.; Du, X.; Shen, X.; Meghjani, M.; Eng, Y.H.; Rus, D.; Ang, M.H. Perception, Planning, Control, and Coordination for Autonomous Vehicles. Machines 2017, 5, 6. https://doi.org/10.3390/machines5010006
Pendleton SD, Andersen H, Du X, Shen X, Meghjani M, Eng YH, Rus D, Ang MH. Perception, Planning, Control, and Coordination for Autonomous Vehicles. Machines. 2017; 5(1):6. https://doi.org/10.3390/machines5010006
Chicago/Turabian StylePendleton, Scott Drew, Hans Andersen, Xinxin Du, Xiaotong Shen, Malika Meghjani, You Hong Eng, Daniela Rus, and Marcelo H. Ang. 2017. "Perception, Planning, Control, and Coordination for Autonomous Vehicles" Machines 5, no. 1: 6. https://doi.org/10.3390/machines5010006
APA StylePendleton, S. D., Andersen, H., Du, X., Shen, X., Meghjani, M., Eng, Y. H., Rus, D., & Ang, M. H. (2017). Perception, Planning, Control, and Coordination for Autonomous Vehicles. Machines, 5(1), 6. https://doi.org/10.3390/machines5010006





